Cysteine-Cysteine Contact Preference Leads to Target-Focusing in Protein Folding

Abstract

We perform a statistical analysis of amino-acid contacts to investigate possible preferences of amino-acid interactions. We include in the analysis only tertiary contacts, because they are less constrained—compared to secondary contacts—by proteins' backbone rigidity. Using proteins from the protein data bank, our analysis reveals an unusually high frequency of cysteine pairings relative to that expected from random. To elucidate the possible effects of cysteine interactions in folding, we perform molecular simulations on three cysteine-rich proteins. In particular, we investigate the difference in folding dynamics between a Gō-like model (where attraction only occurs between amino acids forming a native contact) and a variant model (where attraction between any two cysteines is introduced to mimic the formation/dissociation of native/nonnative disulfide bonds). We find that when attraction among cysteines is nonspecific and comparable to a solvent-averaged interaction, they produce a target-focusing effect that expedites folding of cysteine-rich proteins as a result of a reduction of conformational search space. In addition, the target-focusing effect also helps reduce glassiness by lowering activation energy barriers and kinetic frustration in the system. The concept of target-focusing also provides a qualitative understanding of a correlation between the rates of protein folding and parameters such as contact order and total contact distance.

INTRODUCTION

Important tasks in a cell are mostly carried out by proteins. Given a cellular environment, the linear arrangement of amino acids in a protein determines its native structure and there is a characteristic time for this protein to reach its native state to conduct biological functions (1,2). However, despite decades of investigations in the research community, it still remains a challenge to use only the knowledge of the primary amino-acid sequence to either predict the relationship between structure and function or justify a characteristic folding time. In this regard, using bioinformatics approaches to extract information from protein structure database can be useful in investigation of functional roles of particular contact pairs in a protein. Using this strategy, several groups (3–5) have identified—using computational/experimental methods—various traits of disulfide bonds or cysteine-cysteine interactions. Here we follow these paths to perform a tertiary amino-acid contact analysis and find an unusually high contact frequency among cysteines. We further extend this information into molecular dynamics (MD) simulations, at least qualitatively, to investigate how protein dynamics in living systems may possibly benefit from cysteine-cysteine interactions.

The importance of disulfide bond formation in protein folding has been discussed (6,7). It was argued that disulfide bonds may enhance thermal stability of many disulfide-rich proteins. For instance, Mallick et al. (5) recently showed that the intracellular proteins of hyperthermophilic archea are disulfide-rich. Further, one may ask whether there could be other interesting roles for a cysteine pair to play. In this article, we investigate whether the cysteine-cysteine interaction can promote folding.

In terms of protein folding, disulfide bonds can be helpful if they form at a correct folding nucleus (4). On the other hand, nonnative disulfide bonds, if formed, can also hinder the folding. Nevertheless, in a radical environment such as in living systems, the bonds can form and break frequently at a biological timescale (8) if the bonding energy between a pair of cysteines is of order k_BT. This somewhat fast exchange rate makes it possible to offset a potentially detrimental consequence of misfolded proteins as a result of forming nonnative disulfide pairs. In this article, we investigate the possibility for such frequent formations and dissociation of disulfide bonds to assist protein folding at least in generic model systems.

Given the difficulties encountered in the pursuit of accurate quantification of the interactions among amino acids, many studies in this area use either statistics-based energetics or structure-specific energetics. A classic example of statistics-based potential is the Miyazawa-Jernigan interaction matrix (3,9). Inevitably, many specific features such as orientational dependence of the interactions and side-chain contact/packing are averaged out. The Gō model (10) is a representative of structure-specific models. Basically, given a protein π and its native structure S(π), the force between two amino acids in π is attractive (repulsive) if their three-dimensional separation in S(π) is within (outside) the so-called contact distance. An extra criterion needed for the two amino acids to be attractive is when no other amino acids stand between them. Aiming to provide a minimally frustrated folding energy landscape (11,12), the Gō potential has been commonly used in protein folding simulations (13,14). Structure-specific potentials, however, lack the generality of the fundamental physical forces. Apparently, there is a trade-off between strengths and limitations in both types of approaches.

Since our goal is to examine the generic effect of disulfide bond formation/dissociation on folding, we would like to employ a model that can fold protein within reasonable computational time. Designed for minimal frustration, the Gō model is known to quickly fold many proteins under MD simulations and is thus chosen as our starting model (wild-type model). A variant model that includes the nonspecific cysteine interactions can be readily constructed. We simply replace specific interactions between any cysteine pairs in a protein sequence with nonspecific attraction while leaving the rest of the pairwise interactions Gō-like. Intuitively, if the cysteine-cysteine attraction is much larger than solvent-averaged interactions between any two amino acids, nonnative contacts formed among cysteines will introduce energetic traps and the folding kinetics will be hindered. However, we find that if this nonspecific interaction is comparable to a solvent-averaged interaction, it helps proteins fold even faster than a standard Gō model.

This interesting finding prompts us to seek the possible mechanism for large heteropolymeric chains (such as proteins with >100 amino acids) to efficiently find their equilibrium conformations. A useful concept, termed “target-focusing,” is therefore introduced to elucidate, at least qualitatively, a plausible mechanism. The targets refer to monomer (e.g., amino acid) pairs whose effective mutual attractions are stronger than others. When the effective attraction is not too strong, the interacting targets on the polymer will loosely constrain the motion of other monomers on the chain and thus reduce the conformational entropy. In other words, the target-focusing helps reduce the size of search space that a heteropolymer needs to explore before reaching its equilibrium conformation.

In addition to search space reduction, target-focusing also enables a related feature: reduction of glassiness in folding. This phenomenon, resulting from lowering kinetic frustration and activation energy barriers, is analyzed in Results and Discussion. In the same section, we also further describe how the target-focusing concept may help us to understand the observed correlation between protein folding rate and other parameters such as contact order (15) and total contact distance (16).

MODELS AND METHODS

Pairwise tertiary contact analysis

From the Protein DataBank (PDB), we downloaded 4143 proteins (12,455 chains in total) with known three-dimensional structures. Because a protein may contain several chains (subunits), the number of chains is much larger than the number of proteins. To avoid overrepresentation of almost identical chains, we retain only one chain among highly similar chains. Using a score threshold of 200 bits, this procedure is done by “purge,” a preprocessing program of Gibbs motif sampling (17). After purging, the remaining 4142 proteins (5398 chains) are used for the contact analysis.

Compared to the contacts formed within a secondary structure, tertiary contacts among amino acids are less constrained by peptide backbone rigidity. Tertiary contact analysis is thus expected to provide information less relevant to secondary assembly within proteins but perhaps more relevant to proteins' tertiary assembly. In our analysis, a contact is defined plainly. Excluding the case when they are in the same secondary structure unit, two residues (amino acids) i and j (i, j = 1, 2, …, 20), are considered in contact if the distance between their C_α is smaller than a cutoff (7 Å) and if these two residues are separated by more than two amino acids in the primary sequence. This contact analysis is also useful in other applications such as multiple sequence alignment.

To quantify the tertiary contact preference between secondary structures of the same type, we first estimate the joint probability of contact involving amino acids i and j by

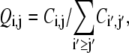(1)

where C_i,j is the number of contacts found between amino acids i and j while 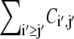sums the total number of contacts. The likelihood for an amino acid i to participate in a tertiary contact is estimated by the secondary-structure-specific background frequencies

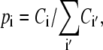(2)

where C_i counts amino acid i in one type of secondary structure. When considering contacts resulting from different types of secondary structures, C_i in Eq. 2 sums the counts of amino acid i in both types of secondary structures.

For a pair of amino acids i and j, the ratio of Q_i,j (the observed contact frequency) to p_i p_j (the expected contact frequency by chance),

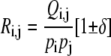(3)

quantifies the preference of residue contacts. The relative error δ associated R_i,j can be estimated by 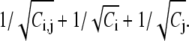For contacts among α-helices and among β-sheets, the 10 most preferred tertiary contact pairs are given in Table 1. The tertiary contacts resulting from different secondary structures are much less from our analysis of PDB data. Due to insufficient sample size, we refrain ourselves from showing those numbers in Table 1. Nonetheless, the major feature, such as the cysteine-pair ranks among top probability ratios, remains the same.

TABLE 1.

Top probability ratios

Contacts
Between helices
C-C	L-A	I-A	V-A	Y-C
16.55 ± 2.02	4.86 ± 0.19	4.05 ± 0.22	4.20 ± 0.19	3.70 ± 0.57
W-A	Y-A	A-C	F-C	F-W
3.51 ± 0.38	3.35 ± 0.24	3.40 ± 0.37	3.08 ± 0.48	3.05 ± 0.41
Between β-strands
C-C	C-W	V-I	F-W	V-F
36.95 ± 3.05	8.38 ± 1.27	7.54 ± 0.30	6.02 ± 0.65	4.99 ± 0.27
V-Y	V-C	F-C	I-C	V-V
4.91 ± 0.29	4.91 ± 0.45	4.83 ± 0.57	4.82 ± 0.49	4.5 ± 0.20

The top 10 probability ratios in contacts formed between various secondary structures.

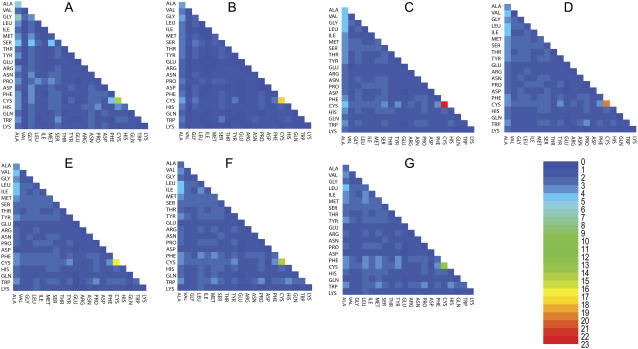
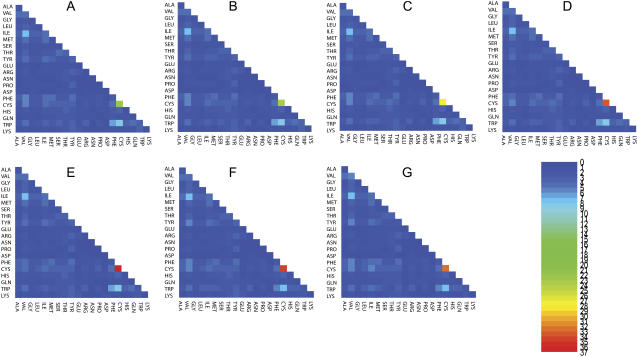
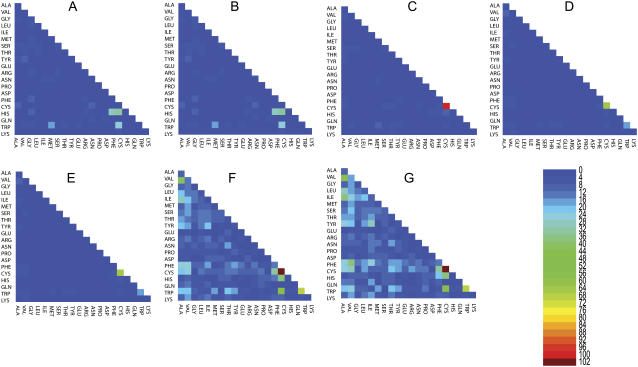
It is natural to ask how the probability ratios change when we change the cutoff distance used. Figs. 1–3 provide such information with cutoff distance ranging from 5 Å to 8 Å. Note that in both Fig. 1 and Fig. 2, the change of cutoff distance has little effect on the dominant pairs, indicating the generality of conclusions drawn.

FIGURE 1.

The probability ratios (explained in pairwise tertiary contact analysis) for tertiary contacts among helical secondary structures. The number key is given by the heat map. In the alphabetical order of the panels, from A to G, we display the probability ratios with different cutoff distances ranging from 5 Å to 8 Å with a 0.5 Å increment. Thus, panel A summarizes the results for using 5 Å as the cutoff distance, while panel G summarizes the results for using 8 Å as the cutoff distance.

FIGURE 2.

The probability ratios (explained in pairwise tertiary contact analysis) for tertiary contacts among β-sheet secondary structures. The number key is given by the heat map. In the alphabetical order of the panels, from A to G, we display the probability ratios with different cutoff distances ranging from 5 Å to 8 Å with a 0.5 Å increment. Thus, panel A summarizes the results for using 5 Å as the cutoff distance, while panel G summarizes the results for using 8 Å as the cutoff distance.

FIGURE 3.

The probability ratios (explained in Pairwise Tertiary Contact Analysis) for tertiary contacts formed between different secondary structures, i.e., contacts between helices and sheets. The number key is given by the heat map. In the alphabetical order of the panels, from A to G, we display the probability ratios with different cutoff distances ranging from 5 Å to 8 Å with a 0.5 Å increment. Thus, panel A summarizes the results for using 5 Å as the cutoff distance, while panel G summarizes the results for using 8 Å as the cutoff distance.

The overwhelming preference for cysteine-cysteine contact indicates that if a protein contains cysteines, the cysteines tend to be close in the folded structure of the protein. It is this observation that motivates our study of the role of cysteine contacts in the folding of cysteine-rich proteins.

It is worth noting that in our analysis the cysteine-cysteine pairing ratio is larger than observed in other analyses (3,9), where they actually documented other amino-acid pairs to have larger pairing ratios than the cysteine-cysteine pair. We attribute this difference to the fact that we use only tertiary contacts while the other analyses include secondary contacts. As we mentioned earlier, the tertiary contact is less constrained by the backbone rigidity than the secondary contacts, thus they may be able to better reflect, albeit statistically, the intrinsic interaction strengths among various amino acids.

Protein models

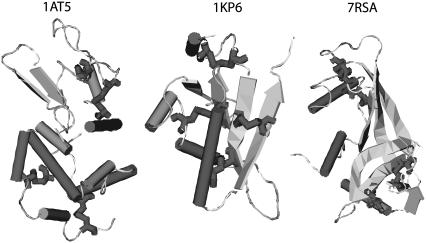
We first choose cysteine-rich proteins whose PDB files include the keyword SSBOND. We screen proteins based on the following criteria: 1), proteins with structures determined by x-ray crystallography but not solely determined by NMR; and 2), each protein must contain at least two pairs of cysteine-cysteine contacts in its native structure. Table 2 lists some details of three proteins selected: hen egg-white lysozyme (1AT5), Ustilago maydis killer toxin kp6 α-subunit (1KP6), and bovine pancreatic ribonuclease A (7RSA). The structures of these three proteins are displayed in Fig. 4.

TABLE 2.

Three cysteine-rich proteins selected

PDB identifier	No. A.A.	No. Cys.	Native cysteine-cysteine contact pairs
1AT5	129	8	(6,127) (30,115) (64,80) (76,94)
1KP6	79	8	(5,12) (16,74) (18,65) (35,51)
7RSA	124	8	(26,84) (40,95) (58,110) (65,72)

FIGURE 4.

The native structures, downloaded from the Protein DataBank, of the three proteins studies. Displayed from left to right are: the hen egg-white lysozyme (1AT5), U. maydis killer toxin kp6 α-subunit (1KP6), and bovine pancreatic ribonuclease A (7RSA). While the bulk of the proteins are in ribbon (β-strand) and cylinder (α-helix) representations, cysteine residues are shown using bond representation.

We use a simple Gō model (10) where each amino acid is represented by its C_α atom (13). The local structural Hamiltonian includes the regular bond-stretching, bond-rotation, bond-angle, and dihedral rotation terms describing the backbone deformation energy. For the pairwise interaction between two residues i and j separated by distance 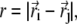the potential is given by

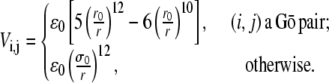(4)

Here r₀ is the contact distance between the Gō-pair residues i and j in native structure, and σ₀ is a parameter with dimensions of length. The Gō-type pairwise interaction is aimed to minimize energetic frustration, and thus is often expected to fold proteins the fastest. We call the model with this Gō-like potential the wild-type (wt).

As suggested by our tertiary contact analysis, we introduce unbiased interactions among all the cysteine residues in place of the Gō-like potential to produce a variant model. Precisely, cysteine m and cysteine n separated by distance r will have potential energy

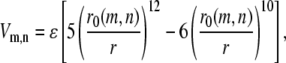(5)

regardless of whether m and n form a Gō pair or not. The energy parameter ɛ is allowed to vary from 2ɛ₀ to 20ɛ₀ to parameterize the strength of disulfide bond formation. Small ɛ mimics an environment that is more reducing for disulfide bonds. The distance parameter r₀(m, n) is defined as follows. When cysteines m and n form a Gō pair in the native structure, the native distance between these two cysteines has two equivalent names: R_N(m) and R_N(n), with R_N(m) = R_N(n), of course. In this case, the quantity r₀(m, n) is defined to be R_N(m), which is also equal to R_N(n). We then assume that cysteine m, influenced by its nearby amino acids, would contribute a preferred bonding length R_N(m)/2 while bonding to any another cysteine. This is a reasonable, albeit ad hoc, extrapolation from the original Gō model. Consequently, when cysteine m and cysteine n do not form a Gō pair, r₀(m, n) is chosen to be (R_N(m) + R_N(n))/2.

Molecular simulations

For thermodynamic simulations, we employ a standard molecular simulation method using AMBER6 program as an integrator (18). Descriptions of parameters and time steps can be found elsewhere (14). Thermodynamic properties, such as folding temperatures (T_f), are calculated by the weighted histogram analysis method (19). To study the kinetic effect of nonspecific cysteine-cysteine attraction in each protein, we employ Langevin dynamics (20) to simulate folding of both the wt and the variant.

For folding kinetics studies, initial structures are quenched at a high temperature (2.8 T_f). To avoid overrepresentation of similar initial configurations, we accept a new initial configuration only if the root mean-square distance (RMSD) between the new one and every existing one is larger than a phenomenological cutoff 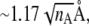where n_A is the number of amino acids in the protein considered. The idea here is to approximate the conformation of a denatured protein by that of a Gaussian chain. Since the gyration radius is proportional to the square root of the length of the chain, the natural length scale to discriminate two denatured states is proportional to 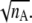The numerical factor 1.17 Å associated with the RMSD cutoff is chosen, after manually looking into many configurations differed by various RMSDs, to ensure that any two initial configurations are sufficiently distinct. We generated 100 initial configurations for each protein studied.

To minimize the errors due to biased sampling in initial configurations, for each protein studied we dictate both the wt and the variant to use the same set of initial configurations and the same temperature T_s for Langevin dynamics simulations. T_s is 0.9T_f, 0.9T_f, and 0.8T_f for 1AT5, 1KP6, and 7RSA, respectively. At T_s, the optimal folding temperature, folding rate reaches maximum for each wt model. The folding time in a simulation run is defined by a first passage time: when the potential energy first becomes lower than a threshold E_cut and all the native pairs of cysteines are formed. Loosely speaking, if the potential energy is lower than E_cut, it means that the current configuration and the lowest energy configuration shares >90% similarity in terms of amino-acid contacts.

Contact formation analysis

It was suggested that the cysteine-cysteine contacts, native or not, may play an important role in the folding of cysteine-rich proteins. For example, there exists phenomenological theory (21) that attempts to explain folding of cysteine-rich proteins considering only interactions among cysteines. For each protein, we analyze contact formation in all cysteine pairs to investigate the importance of individual cysteine pairs at various stages of the folding.

For each starting configuration s in the MD simulations, one may follow its time evolution and define the t-dependent contact percentage, averaged over a window size W, between two cysteines i and j as

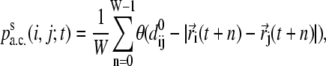(6)

where 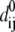is the native distance between cysteine i and cysteine j, θ(x) is the Heaviside step function taking value 1 if x ≥ 0 and value 0 otherwise, and 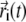is the position vector of cysteine i at time t in a MD simulation. This running average reveals which contact pairs are formed at various stages of the folding.

Taking the window size W to be the folding time for each of the folded trajectories, we may further calculate

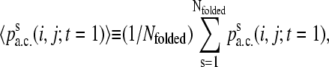which is the contact percentage averaged over the folded ensemble and abbreviated by 〈p_a.c.〉.

Moreover, we investigate how nonspecific cysteine interactions influence the contact between cysteines and other noncysteine residues. To investigate this effect, we monitor individual MD trajectories with special focus on cysteines and the noncysteine residues with the largest number of native contacts. For the i^th amino acid w_i along the primary sequence, we define its kinetic radius r(w_i) to be the largest residue-residue separation among all Gō pairs containing w_i. All the amino acids, whose C_α atoms are within distance r(w_i) of w_i in the native structures, are divided into two sets: those that form native Gō contacts with w_i and those that do not. The number of residues in the first set defines the expected contact numbers (ECN) of native kind, while the number in the second set defines ECN of nonnative kind. The deviations from ECN (DFECN) indicate whether the local region associated with a certain residue is crowded by native (nonnative) contacts or not.

RESULTS AND DISCUSSION

For the ease of referencing, we summarize all the abbreviations employed in this article in Table 3 before discussing the results.

TABLE 3.

Abbreviation summary

Abbreviation	Full term
MD	Molecular dynamics
wt	Wild-type
ECN	Expected contact number
DFECN	Deviation from ECN
NYF	Not-yet-folded

Folding rates and folding kinetics

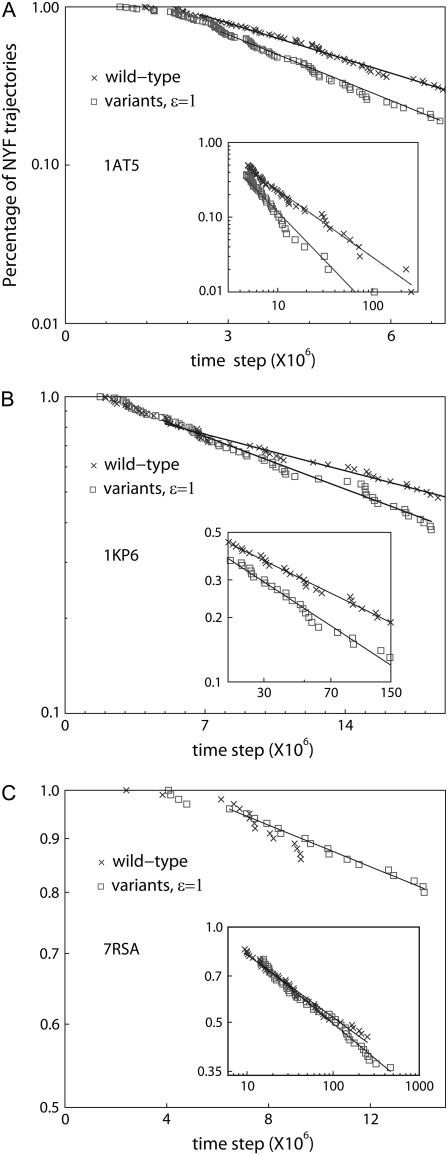
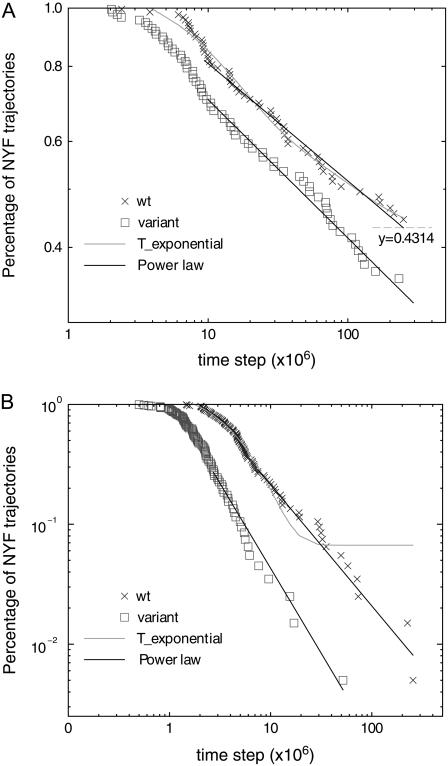
For small to intermediate attraction strength 0.25 < ɛ < 2 (see Eq. 5), we find that the folding rates of the variants are larger than those of the wt. This behavior dramatically changes (data not shown), as expected, once the amplitude of nonspecific attraction becomes very large (ɛ > 10). The effect, due to the nonnative cysteine-cysteine attraction, on the folding of a protein is studied in detail using an attraction strength that is approximately two-times the solvent-averaged energy in the Gō model (wt) used. Fig. 5 shows the percentages of not-yet-folded (NYF) trajectories versus time steps for the three proteins studied.

FIGURE 5.

Percentage of NYF trajectories versus time for the three proteins considered. Note that the percentage of NYF is always plotted in log scale while the time step is plotted in linear scale in the figure but in log scale in the insets. The exponents' α-values are obtained by fitting the power law in the insets. Both the α-values and the inverse characteristic timescales τ⁻¹ are given in Table 4.

We plot the percentage of NYF trajectories at T_s (defined in Models and Methods) versus time. As shown in Fig. 5, A and B, for proteins 1AT5 and 1KP6, the folding kinetics is largely characterized by single-transition-state behavior (the percentage of NYF trajectories is exponential in time P_{not yet folded}(t) ∼ exp(−t/τ)). However, the folding kinetics also exhibits a power-law tail 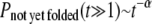(insets, Fig. 5, A and B) at large time, indicating the possibility of glassy kinetics. For the wt case of protein 7RSA, the percentage of NYF trajectories is almost purely power-law. When the nonspecific cysteine attraction is used, we see an increase in the number of data points characterizable by a single transition state. However, the majority of the points still fall in the realm that is characterizable by power law (see inset, Fig. 5 C). The large time kinetics, being closer to a power law than a single exponential, does indicate the possibility of glassy kinetics. However, we must emphasize that what we meant by glassiness here is in a broad sense. For example, a system with a large number of intermediate traps of energies not much higher than that of the ground state will be termed glassy in our definition. Therefore, systems that are kinetically frustrated by many potential traps will fall in this broad definition of glass. Kinetic frustration analysis will be made in the next subsection, followed by more discussions regarding other alternative explanations for the nonexponential kinetics as well as glassiness analysis.

Compared to its wt, the variant either reaches 100% folding within shorter simulation steps (1AT5) or enjoys a higher overall folded percentage (1KP6 and 7RSA) within the same maximum simulation steps. This result, documented in Table 4, demonstrates a special role played by cysteine contacts in protein folding kinetics. The MD simulation of 7RSA folding shows that a simple, minimally frustrated model is not enough to be rid of glassiness (in a broad sense) in the folding kinetics.

TABLE 4.

Summary of kinetics and glassiness analysis

PDB id.	MS (× 108) wt/variant	τ−1(× 10−6) wt/variant	α wt/variant	Total folded % wt/variant
1AT5	1.0/2.6	0.23 ± 0.02/0.32 ± 0.03	0.90 ± 0.08/1.32 ± 0.09	100/100
1KP6	1.5/1.5	0.038 ± 0.002/0.055 ± 0.003	0.42 ± 0.04/0.56 ± 0.05	86/90
7RSA	6.0/6.0	NA/0.23 ± 0.02	0.20 ± 0.02/0.23 ± 0.02	56/65

The maximum number of simulation steps (MS), folding rate 1/τ, power-law exponent α, and overall folded percentage of the three selected cysteine-rich proteins. The 1/τ entry for 7RSA in wt is not available because of the lack of sufficient data points to make a reliable estimate.

Contact formation analysis and kinetic frustration

The analysis of folding rates substantiates the importance of cysteine-cysteine contacts in protein folding. It is possible that both the native and nonnative cysteine contacts contribute positively to folding. We therefore analyzed contact formation of all cysteine pairs (four native and 24 nonnative) for each of the three proteins to investigate the importance of individual cysteine pairs at various stages of folding.

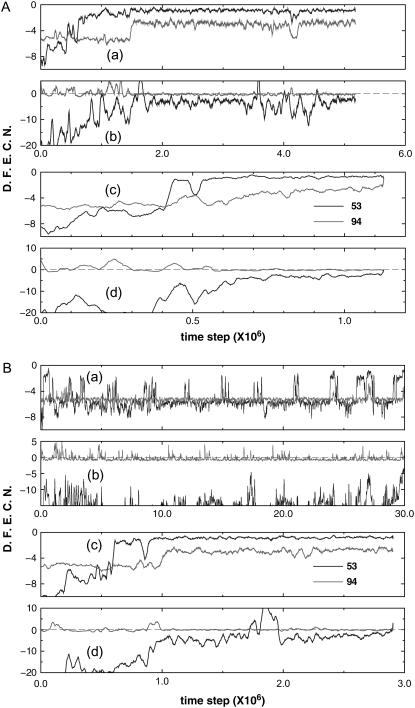
Fig. 6 A shows how nonspecific cysteine-cysteine interactions may facilitate the folding of protein 1AT5. Two folding trajectories, one for the wt and one for the variant, with identical initial configuration are used. DFECN is computed for noncysteine residue 53 that has the largest number of native Gō contacts and for residue 94 that is a cysteine. Fig. 6, A(a) and A(b), shows DFECN of native contacts and nonnative contacts for the wt, respectively; Fig. 6, A(c) and A(d), show DFECN of native contacts and nonnative contacts, respectively, for the variant. The variant folds faster than the wild-type because there is almost no positive DFECN of the nonnative kind for the variant.

FIGURE 6.

Deviation from expected contact numbers (DFECN) versus integration time steps for protein 1AT5. DFECN is computed for noncysteine residue 53 that has the largest number of native Gō contacts and for residue 94 that is a cysteine. Panels A(a) and A(b) show DFECNs of native contacts and nonnative contacts, respectively, from a folding trajectory of a wild-type protein; and panels A(c) and A(d) show DFECNs of native contacts and nonnative contacts, respectively, from another folding trajectory of the variant. The same initial structure is given for both the wild-type and the variant in folding simulations, and the variant folds faster than the wild-type. In addition, another set of folding simulations (B(a)–B(d)) is given to show that nonspecific cysteine-cysteine interactions facilitate folding. Particularly in this case, the wild-type trajectory did not reach the native state within the maximum folding time (i.e., 30 × 10⁶ time steps). However, the variant did. The legends of B(a)–B(d) are the same as those of panels A(a)–A(d). DFECN of native contacts associated with 53 is large and negative in panel B(a) while DFECN of nonnative contacts associated with 94 became frequently positive in panel B(b). It indicates that for a wild-type protein, contact pairing to 53 is far from nativelike, and contact pairing to 94 is overwhelmed by nonnative ones. Such conformations form kinetic traps that impede folding (B(a) and B(b)). However, when the nonspecific attraction among cysteines is introduced (i.e., variant B(c) and B(d)), it helps in circumventing such kinetic traps and allows the variant model to reach the native state in a much shorter time. DFECN is averaged over a window size of W = 1.5 × 10⁵.

Also shown in Fig. 6 B is another example, where foldings of the variant reached the native state but the wt did not, at least up to the maximum simulation time (i.e., 30 × 10⁶ time steps). The legends of Fig. 6 B(a) to 6 B(d) are the same as those of Fig. 6 A(a) to 6 A(d). For the wt, DFECN of both native and nonnative contacts for residue 53 is large and negative (Fig. 6 B(a,b)) while DFECN of nonnative contacts for residue 94 is frequently positive (Fig. 6 B(b)). It indicates that for the wt, native contact pairing to 53 is deficient and contact pairing to 94 is overwhelmed by nonnative ones. Such conformations form kinetic traps that impede folding. However, when nonspecific attraction between residue 94 and other cysteines is introduced, it helps to circumvent such kinetic traps. First, the number of native contact pairing to residue 53 increases (Fig. 6 B(c)). Second, the overwhelming number of nonnative contact pairing to residue 94 decreases. Consequently, the variant reaches the native state in a much shorter time. Similar analyses for the other two proteins, namely 1KP6 and 7RSA, can be found in Figs. 7 and 8 and their captions.

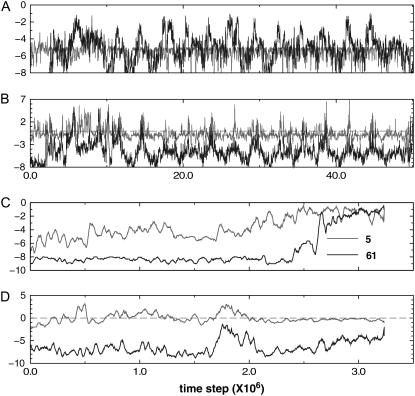
FIGURE 7.

Deviation from expected contact number (DFECN) versus integration time steps of protein 1KP6. In general, the variant model folds faster than the wild-type. DFECNs of residue 61 (which has the most content of native Gō contacts) and residue 5 (a cysteine) are plotted. Using the same initial configurations, we run MD simulations for the wt model and for the variant model. Panel A shows the DFECN of native kind of the wt; panel B shows the DFECN of nonnative kind of the wt; panel C shows the DFECN of native kind of the variant; and panel D shows the DFECN of nonnative kind of the variant. In essence, slow folders usually suffer more frequent kinetic frustration compared to the fast folders.

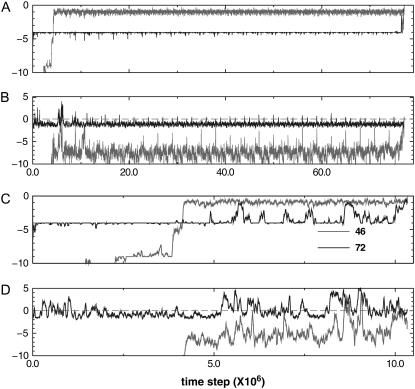
FIGURE 8.

Deviation from expected contact number (DFECN) versus integration time steps of protein 7RSA. In general, the variant model folds significantly faster than the wild-type. DFECNs of residue 6 (which has the most content of native Gō contacts) and residue 72 (a cysteine) are plotted. Using the same initial configurations, we run MD simulations for the wt model and for the variant model. Panel A shows the DFECN of native kind of the wt; panel B shows the DFECN of nonnative kind of the wt; panel C shows the DFECN of native kind of the variant; and panel D shows the DFECN of nonnative kind of the variant. DFECN is averaged over a window size of W = 1.5 × 10⁵.

In Table 5, we document 〈p_a.c.〉, the contact percentage averaged over the folded ensemble, for all cysteine pairs and seek qualitative connection to experimentally observed data. For protein 1AT5, the nonnative Cys⁶⁴-Cys⁷⁶ pair has highest contact percentage (∼70.60% in wt and 77.40% in its variant). The other higher contact percentages come from the native cysteine pairs Cys⁶⁴-Cys⁸⁰ and Cys⁷⁶-Cys⁹⁴. Interestingly, almost 30 years ago Anderson and Wetlaufer (22) suggested that two disulfide bonds involving Cys⁶⁴-Cys⁸⁰ and Cys⁷⁶-Cys⁹⁴ formed earlier than the pairs Cys⁶-Cys¹²⁷ and Cys³⁰-Cys¹¹⁵ in the folding of hen lysozyme. Further, Shioi et al. (23) suggested that the preferential formation of Cys⁶⁴-Cys⁷⁶ might facilitate the formation of Cys⁶⁴-Cys⁸⁰ and Cys⁷⁶-Cys⁹⁴. Upon introducing the nonspecific attraction among cysteines, we see a significant increase in contact percentage for all three pairs: Cys⁶⁴-Cys⁷⁶, Cys⁶⁴-Cys⁸⁰, Cys⁷⁶-Cys⁹⁴. The essential features of our results agree reasonably well with the experimental observations, indicating the important role of cysteine contacts in protein folding.

TABLE 5.

Contact formation analysis for all cysteine pairs

1AT5			1KP6			7RSA
Cysteine pair	Wild-type 〈pa.c.〉	Variant 〈pa.c.〉	Cysteine pair	Wild-type 〈pa.c.〉	Variant 〈pa.c.〉	Cysteine pair	Wild-type 〈pa.c.〉	Variant 〈pa.c.〉
6-30	5.38	9.13	5-12	67.11	74.28	26-40	1.97	2.25
6-64	0.16	0.24	5-16	1.22	1.87	26-58	0.15	0.10
6-76	0.26	0.37	5-18	0.34	0.80	26-65	0.09	0.36
6-80	0.13	0.28	5-35	0.63	1.71	26-72	0.13	0.23
6-94	0.46	0.81	5-51	0.26	0.73	26-84	35.67	44.06
6-115	0.43	0.83	5-65	0.19	0.37	26-95	0.88	2.73
6-127	1.29	1.65	5-74	0.24	0.58	26-110	0.15	0.23
30-64	0.16	0.30	12-16	1.89	2.62	40-58	0.21	0.04
30-76	0.08	0.23	12-18	0.08	0.06	40-65	0.09	0.09
30-80	0.40	0.52	12-35	1.56	6.25	40-72	0.19	0.07
30-94	0.30	0.52	12-51	0.59	1.44	40-84	0.61	1.51
30-115	10.5	13.13	12-65	1.11	0.91	40-95	33.45	50.29
30-127	0.70	1.08	12-74	0.56	1.08	40-110	0.19	0.19
64-76	70.60	77.40	16-18	97.93	97.92	58-65	0.56	0.94
64-80	66.5	73.10	16-35	5.85	10.23	58-72	53.46	64.32
64-94	2.10	3.30	16-51	30.17	28.95	58-84	0.21	0.09
64-115	0.16	0.30	16-65	5.25	9.75	58-95	0.08	0.26
64-127	0.08	0.33	16-74	4.71	4.82	58-110	26.35	26.03
76-80	5.97	7.25	18-35	1.45	2.46	65-72	96.44	97.55
76-94	50.73	58.27	18-51	6.18	8.72	65-84	0.42	0.50
76-115	0.25	0.86	18-65	15.86	19.93	65-95	0.08	0.14
76-127	0.25	0.86	18-74	2.05	2.88	65-110	5.62	11.36
80-94	1.58	2.07	35-65	1.34	1.16	72-84	0.19	0.36
80-115	0.17	0.14	35-74	0.78	1.13	72-95	0.04	0.13
80-127	0.11	0.33	35-51	75.70	77.86	72-110	31.72	32.16
94-115	0.68	1.03	51-65	1.38	1.94	84-95	1.38	2.66
94-127	0.79	1.65	51-74	1.06	2.15	84-110	0.09	0.22
115-127	1.28	2.20	65-74	0.73	1.14	95-110	0.12	0.15

The contact percentage of each pair is first calculated for each folded trajectory and then averaged over all folded trajectories to yield 〈p_a.c.〉. In addition to the native cysteine pairs, we also highlight, in boldface type, all the 〈p_a.c.〉 values that are >15%.

For protein 1KP6, the very high contact percentage for nonnative pair Cys¹⁶-Cys¹⁸ might be an artifact due to their closeness in the primary structure. The nonspecific attraction among cysteines again increases the contact percentage of native pairs but decreases that of Cys¹⁶-Cys⁵¹, a nonnative pair.

For protein 7RSA, the nonspecific attraction among cysteines again increases the contact percentages of native cysteine pairs. The native pair Cys⁶⁵-Cys⁷² has the highest contact percentage. Among other native pairs, the contact percentages of pairs Cys²⁶-Cys⁸⁴ and Cys⁴⁰-Cys⁹⁵ in the variant increase significantly when compared to their wt counterparts. From the structural point of view, the Cys⁴⁰-Cys⁹⁵ pair increases the protein core stability. For other pairs with high contact percentages, interesting comparisons to experiments may also be made. Shin et al. (24) showed that the pair Cys⁶⁵-Cys⁷² occurs in the early stage of folding. Further, Klink et al. (25) suggested that Cys²⁶-Cys⁸⁴ is very important to conformational stability. These experimental evidences lend support to the generic features of our results.

Nonexponential kinetics, glassiness, and barrier height

As we have show in the insets of Fig. 5, at long time all the protein models seem to display nonexponential kinetics, at least not describable by a single exponential. Although the late time kinetics data displayed seem to be easily characterized by a power law, indicating possible glassiness, we should first examine other alternative models that are known to exhibit nonexponential kinetics before firmly dwelling on the idea of glassiness.

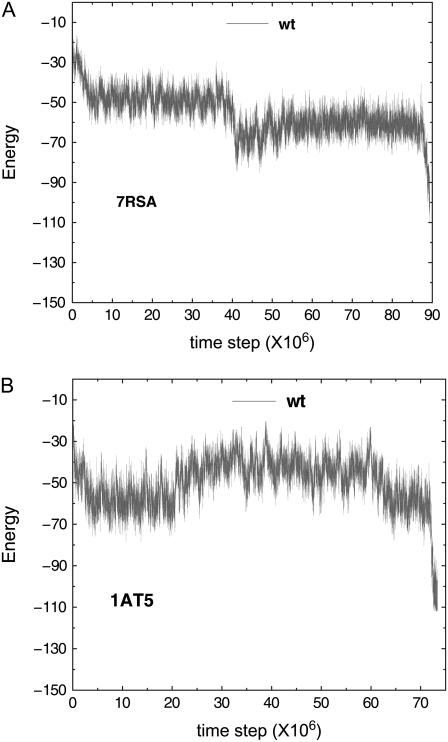
It has been observed that small proteins may exhibit fast but noncooperative folding that display nonexponential kinetics. Basically, in this type of process, it is believed that proteins will take trajectories strictly downhill in the free energy landscape, even though the downhill folding ensemble may consist of folding paths of different converging speed toward the native state (36). The question is: could this be the case in our minimally frustrated protein model? If folding is entirely downhill in a free-energy sense and free of glassy traps before reaching the native state, then the ensemble of intermediate structures becomes progressively more nativelike, indicating a reduction of entropy. Consequently, the energy gradient must completely overcome the entropy loss (37,38) to maintain the downhill folding in the free energy landscape. That said, for glassiness-free downhill folding, the energy itself, compared to free energy, must be an even steeper downhill toward native state for each trajectory. It turns out that testing this possibility is quite straightforward. We have randomly picked a few folding trajectories whose folding time fall in the range that is describable by power law. We found no evidence of glassiness-free downhill folding. This is shown in Fig. 9. As we can see from the two examples, typical energy variation over 1500 time steps is much smaller than the typical energy difference between nearby spikes and troughs in the figure. This indicates that the roughness in energy versus time cannot be attributed to stochastic noise and the scenario of glassiness-free downhill folding seems unlikely in the protein models shown.

FIGURE 9.

Energy versus time step for wt protein models. Panel A plots the energy versus time of a slow folding trajectory from protein model 7RSA wt; the folding time of this trajectory is within the range describable by power law. Panel B plots the energy versus time of a slow folding trajectory from protein model 1AT5 wt; the folding time of this trajectory again is within the range describable by power law. These typical energy versus time plots do not show any clear descending trend in energy and thus do not lend support to the glassiness-free down-hill folding scenario. In particular, the typical energy differences, 2.9 and 3.4 units for 7RSA wt and 1AT5 wt, respectively, over a time interval of 1500 time steps for both trajectories are approximately one order-of-magnitude smaller than their respective peak-to-valley values.

The other possibility would be to use multiexponential instead of a single exponential in describing the folding kinetics. However, we also need to remember that any power law over a finite data range can be mimicked by superimposing a number of exponentials. Because we have relatively few data points (100 for 1AT5 for both wt and variant, 53 for 7RSA wt, and 63 for 7RSA variant), we limit ourselves to triple exponential (which already contains six free parameters as opposed to two parameters for power law) to avoid over-fitting. Fig. 10, A and B, replot, respectively, the data for protein models associated with 7RSA and 1AT5. Theoretically speaking, a triple-exponential fitting should take the form

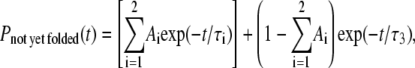(7)

with A_i ≥ 0, τ_i > 0 ∀ i and 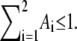However, with five free parameters, we still cannot get any decent fit even for the wt models. For better fitting, we therefore modify Eq. 7 to

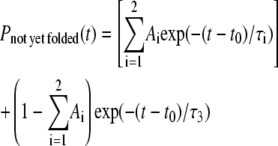(8)

to allow one more free parameter t₀. This modified triple exponential is only shown for wt protein models since it still does not fit the variant to any reasonable extent. However, power-law tails are fitted for both wt and variant models. Relevant fitting parameters are given in the figure caption. Although the triple-exponential fit for 7RSA wt model shown seems reasonably good, we have noticed that the third exponential (with τ₃ = 5 × 10⁴⁹ and (1 − A₁ − A₂) ≈ 0.4314) essentially is a constant over the range plotted. That is, if we allow those NYF trajectories to continue, extrapolating the triple-exponential fit will rule out the possibility for any of them to fold. Any appreciable folding event can only occur at another 10⁴⁸ time steps. This essentially means that there will be a large portion of denatured configurations that will never, in any realistic number of time steps, fold into the native state, contradicting the fundamental reason of introducing multiexponential fit instead of adopting the glassiness picture. Fig. 10 B shows the fitting results for protein model 1AT5. In this case, it is apparent that the triple-exponential fit does not fit as well as the power law. After examining two alternatives, we now proceed to examine the possibility of glassiness.

FIGURE 10.

Comparison of triple-exponential fitting and power-law fitting. The plots are shown in log-log scale. For visual clarity, we have divided the time steps associated with the variant models by a factor of two, resulting in a parallel shift to the left for all the variant models. (A) We plot the percentage of NYF trajectories versus simulation time steps for protein model 7RSA wt and 7RSA variant. At large time range, both the wt and variant are well fitted by power law. The wt is also fitted by triple exponentials with coefficients (see Eq. 8) given by t₀ = 3.92 × 10⁶, A₁ = 0.3515, A₂ = 0.21711, τ₁ = 1.2277 × 10⁷, τ₂ = 9.5925 × 10⁷, and τ₃ = 5 × 10⁴⁹. Although triple exponential seems a reasonable fit in the data range displayed, the largeness of τ₃ seems to contradict the purpose of triple-exponential fitting (see text for detail). (B) We plot the percentage of NYF trajectories versus simulation time steps. The best triple-exponential fitting, with parameters t₀ = 1.771 × 10⁶, A₁ = 2.19 × 10⁻⁵, A₂ = 0.933, τ₁ = 2.01 × 10⁶, τ₂ = 4.12 × 10⁶, and τ₃ = 5 × 10⁴², apparently does not fit the large time part. However, the large time regions for both the wt and the variant are well fitted by a power law.

It has been argued for some time that the covalently-bonded primary sequence is rigid and in fact acts like quenched disorder within the relevant temperature range for protein folding. The folding of a protein thus bears similarity to ground state formation in glass systems (26–30). The type of glassiness associated with protein folding, also termed structural glassiness, has the disorder quenched in kinetically as the glass is formed (31). Despite the seemingly difference between structural glasses and spin glasses, many experimental/theoretical studies (26,27) of applying the ideas of spin glasses to proteins seems to confirm the applicability of spin glasses to protein problems. In particular, a hierarchical structure in energy (similar to ultrametric structure) has been observed (26) in myoglobin of 153 amino acids. One important characteristic of a glassy system is the existence of many nearly degenerate ground states, which have been shown to exhibit ultrametric topology (32) and whose relaxation dynamics have been modeled and studied in detail (33).

A Gō-like potential, in some way, is designed to minimize the glassiness of the protein model by minimizing the energetic frustration. The insets in Figs. 5 and 10, however, suggest that the tail of the percentage of NYF trajectories is still characteristic of a power law. If we assume that the energetic frustration of structural glasses is largely similar to that of the regular spin glasses, as suggested by several studies (26–28), then the interesting study in Ogielski and Stein (33) will suggest that the percentage of NYF trajectories at large time t ≫ 1 behaves as

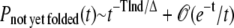(9)

with T being temperature, Δ being the activation energy barrier, and d the number of neighboring states that are separated by an energy barrier Δ from one another. In comparison to the power-law behavior of P_{not yet folded}(t) ∼ t^−α at large time t, we find α ∝ 1/Δ. For each protein, the MD simulations of both the wt and the variant are performed at the same temperature, the optimal folding temperature T_s of the wt. The ratio

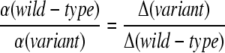(10)

reveals the change in the activation barrier.

The α-values in Table 4 suggest that nonspecific attraction among cysteines increases the protein-folding rate by lowering the activation energy barriers. Further, an interesting observation now becomes obvious. Despite the power-law kinetics, the glassy picture actually suggests a larger probability of folding at long time than suggested by triple-exponential fitting. It is possible that in the context of Gō model and the variant model, the level of glassiness may increase as the size of the protein increases.

THE TARGET-FOCUSING CONCEPT

Nonspecific attraction among all cysteines creates apparent energetic frustration in an otherwise Gō-like protein model. How can the frustrated proteins (variant) actually fold more effectively than the less frustrated proteins (wt) even at the optimal folding temperature T_s of the wt? It is commonly postulated that a foldable protein should have 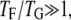i.e., the glass transition temperature T_G is much lower than the protein-folding temperature T_F, making glassiness less important at the relevant temperature range. Our simulations, however, indicate the existence of nonnegligible glassiness even when using the least frustrated protein model simulated at T_s.

Nonspecific attraction among cysteines, once introduced, seems to be able to alleviate glassiness in folding. We found that this nonspecific attraction does induce a qualitative change in folding behavior of the three cysteine-rich proteins studied, namely, 1AT5, 1KP6, and 7RSA. Not only do they fold faster, all three proteins have at least one nonnative cysteine pair that shows a higher percentage in contact formation than one of native cysteine pairs. These results suggest a concept, we termed “target-focusing”, as far as folding of a large protein is concerned.

What we meant by target-focusing is actually rather simple. Basically, the nonspecific attraction among cysteines tends to bring cysteines closer and thus reduce the available phase space of the peptide segment in between cysteines. When all the cysteine pairs formed are those in the native structure, the remaining trial space for noncysteine monomers is greatly reduced. When incorrect cysteine pairs are formed, the same reduction of phase space also turns out to be useful in reducing the basin of trapping. Therefore, we believe the native cysteine pairs (primary targets) are focused through the nonspecific attraction among cysteines. This effect is pertinent to the folding mechanism of large, cysteine-rich proteins where the system bears glassiness as mentioned above.

However, one may also ask whether the same effect, within the protein models we studied, can be easily produced by choosing a different amino-acid pair to have a nonspecific attractive potential (see Eq. 5). To answer that, it is natural to seek an alternative amino-acid pair to introduce the nonspecific interaction in one of our studied protein models. We therefore apply the tertiary contact analysis to a single protein 1AT5. As expected, one should anticipate a much larger statistical fluctuation since the sample size is now very small. We find that cysteine-cysteine pair, mainly due to a larger cysteine count, no longer has significantly larger probability ratio than others. There are 21 other pairs with larger probability ratios than the cysteine pair. We then randomly pick a methionine-tryptophan (MW) pair, with probability ratio only slightly larger than that of the cysteine pair. In 1AT5, there are eight cysteines, two methionines, and six tryptophans. Starting from Gō-like pairwise potential, we construct a new variant model for protein 1AT5 by replacing the Gō-like pairwise potential for each MW pair with nonspecific attractive potential. We study how differently the new variant behaves from our previous studies.

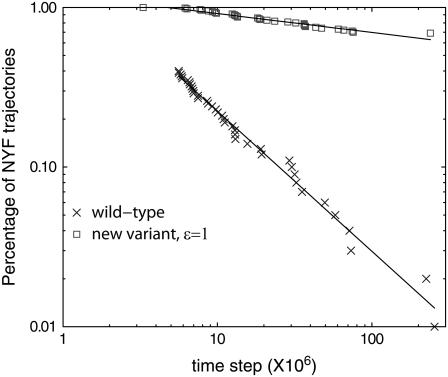
Interestingly, the MW mutant folds much slower than the wt. It exhibits a glassy behavior, as shown in Fig. 11. Folding of protein 1AT5 did not benefit from the addition of nonspecific MW attraction. This result indicates that cysteines in fact do play the target roles in cysteine-rich proteins and it seems nontrivial to find other alternatives. We should also point out that in our study the addition of nonnative cysteine interaction is based on the current database rather than on randomly chosen pairs (34). The nonspecific cysteine attraction may have an effect in terms of native state stability in the context of the Gō model. However, to study such an effect is beyond the scope of the current article. Generically speaking, the native state stability may be studied in terms of denaturing processes. In terms of folding process, enhanced native state stability may, in principle, increase the chance of pulling the protein conformation to be near its native state. We cannot, and probably should not, rule out this possibility. However, if we were to believe that faster folding is solely due to enhanced native state stability, we immediately learn from studying the MW pair a nontrivial lesson: despite the apparent lowering of contact energy in native state, not all the nonspecific attraction can increase the native state stability.

FIGURE 11.

Simulation steps for the wt model and the new variant model of protein 1AT5. The new variant model assigns a nonspecific attraction to every methionine-tryptophan pair with ε = 1 as in Eq. 5; nonspecific cysteine interactions are not included. In this log-log plot, for the wt only the trajectories finishing at late time are shown (see inset, Fig. 5 A). We note that the percentage NYF for the new variant remains 100% for a rather long time, and after that is well described by a power law, signifying a predominantly glassy system.

It is likely that the phenomenon of target-focusing can also be present in many other proteins. However, identification of the targets is most likely more difficult than that in the cysteine-rich proteins. Nevertheless, Table 1 suggests other amino-acid pairs—such as F-C and F-W—as generic target candidates. To test those new target candidates, however, one needs to select protein models based on the abundance of those target pairs, just as we studied the cysteine target pair using cysteine-rich proteins. Thus, to study the effect of F-C pair, one may need to choose proteins containing more F-C contacts in its native structure.

Some additional support for the generality of the target-focusing effect in protein folding is obtained from the studies (16,35) on the statistically significant correlation between a protein's folding rate and its contact order (CO) (15) or its total contact distance (TCD) (16). For any given protein, both CO and TCD are proportional to

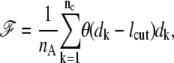(11)

where n_A denotes the total number of amino acids of the protein, n_c denotes the total number of native contacts, d_k denotes the separation on the primary sequence between the two residues that form contact k, and l_cut denotes the cutoff separation on primary sequence. Qualitatively speaking, ℱ is larger when the protein chain has a more complex/tangled topology (e.g., when native contacts are mainly formed by residues that are far apart on the primary sequences). In an average sense, a larger ℱ therefore indicates a larger conformational barrier for the two amino acids of any target to form contact. When this is the case, the folding slows down because the power of target-focusing is weakened. The observation made in Plaxco et al. (35)—some mutations that do not significantly alter CO still affect folding rates—can also be understood using the target-focusing idea. Even if the mutation does not affect the CO defined in Plaxco et al. (15), the folding rate can still have a nonnegligible change if the mutation does affect the targets.

CONCLUSIONS

From a bioinformatics study of tertiary contact, we have identified, along with other groups, that cysteine-cysteine contacts have a frequency much higher than expected by random pairing. Using molecular simulations, we investigate the effects of nonspecific cysteine attraction on the course of folding. Using three cysteine-rich protein models that are larger than a typical fast folding protein (e.g., containing <100 amino acids), we have found that an addition of nonspecific interactions can help promote folding and reduce glassiness of a protein. We come forward with the “target-focusing” concept, in which an addition of nonspecific interactions from evolutionarily selected contact pairs will help a large protein fold more efficiently. This is because interactions among “targets” are able to collectively reduce the search space of other nontarget monomers. Consequently, the effective time spent by a protein to search in conformational space to reach its native state is reduced.

Finally, as a cautionary note, one must acknowledge that the concept of target-focusing cannot enhance the prediction of how proteins fold given their primary structures unless (primary) targets can be identified via correct characterization of molecular interactions. Nevertheless, the notion of target-focusing may still be useful in analyzing protein evolution or even in protein design.