Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2007 May 4;93(3):1079–1088. doi: 10.1529/biophysj.106.102244

Single-Particle Tracking of Membrane Protein Diffusion in a Potential: Simulation, Detection, and Application to Confined Diffusion of CFTR Cl− Channels

Songwan Jin 1, Peter M Haggie 1, A S Verkman 1
PMCID: PMC1913154  PMID: 17483157

Abstract

Confined diffusion of membrane receptors and lipids can result from intramembrane barriers, skeletal interactions, rafts, and other phenomena. We simulated single-particle diffusion in two dimensions in an arbitrary potential, V(r), based on summation of random and potential gradient-driven motions. Algorithms were applied and verified for detection of potential-driven diffusion, and for determination of V(r) from radial particle density distributions, taking into account experimental uncertainties in particle position and finite trajectory recording. Single-particle tracking (SPT) analysis of the diffusion of cystic fibrosis transmembrane conductance regulator (CFTR) Cl− channels in mammalian cells revealed confined diffusion with diffusion coefficient ∼0.004 μm2/s. SPT data fitted closely to a springlike attractive potential, V(r) = kr2, but not to other V(r) forms such as hard-wall or viscoelastic-like potentials. The “spring constant”, k, determined from SPT data was 2.6 ± 0.8 pN/μm, and not altered significantly by modulation of skeletal protein architecture by jasplakinolide. However, k was reduced by a low concentration of latrunculin, supporting the involvement of actin in the springlike tethering of CFTR. Confined diffusion of membrane proteins is likely a general phenomenon suitable for noninvasive V(r) analysis of force-producing mechanisms. Our data provide the first measurement of actin elasticity, to the best of our knowledge, that does not involve application of an external force.

INTRODUCTION

Single-particle tracking (SPT) allows tracking of the microscopic motions of membrane proteins and lipids in living cells. SPT involves the selective labeling of proteins or lipids with fluorophores, such as quantum dots (Qdots), green fluorescent protein, or organic dyes (e.g., cyanine dyes), or probes visible with transmitted light (gold or latex beads), such that particle position can be measured with nanometer spatial and submillisecond temporal resolution using suitable camera detectors. Compared to ensemble-averaged methods to measure diffusion, such as fluorescence recovery after photobleaching and fluorescence correlation spectroscopy, SPT provides single-molecule information about the movements of many particles in an observation area with greater spatial resolution (1,2).

SPT is being used increasingly in living cells in which particle diffusion is often complex because of the presence of barriers (3–8), lipid rafts (9–12), intermolecular interactions (12,13), molecular crowding (14,15), and heterogeneity in membrane physical properties (16), as well as combinations of obstacles such as barriers and rafts (17). Confined diffusion has been seen for a variety of membrane proteins, such as components of the immunological synapse including Lck (an Src family tyrosine kinase), LAT (an adaptor protein that binds SH2 domain proteins upon T-cell activation), and CD2 (a protein involved in cell-cell adhesion) (12), synaptic receptors for glutamate and glycine (18–22), and, more recently, the epithelial cystic fibrosis transmembrane conductance regulator (CFTR) Cl− channel (13). Confined diffusion can result from a number of distinct physical mechanisms with quite different biological implications, such as physical barriers, tethering to fixed or relatively immobile skeletal elements, multimolecular complexation, and percolation in highly crowded media. SPT analysis of confined particle motion has been done largely by computation of mean-squared displacement (MSD) versus time relations, which provide information about diffusion coefficients and apparent confinement volumes, but not about confinement mechanisms. Some of these limitations of SPT are addressed by newer analysis methods such as particle spatial distribution analysis (23–25). Mechanical properties of membrane-associated proteins, which have not previously been measured using SPT, have been measured by applying external force using laser tweezers (4,26–28). Laser tweezers allows measurements of barrier free length and the forces required to move proteins in membranes (4,26). Particle tracking with optical tweezers has been used to estimate trapping potentials based on solution of the Boltzman distribution (27–29).

From these considerations it follows that information about the physical, force-producing mechanisms responsible for confined diffusion should be contained in single-particle trajectories, without the need to apply external forces. For example, confinement resulting from physical barriers within membranes would be describable by a “hard-wall” potential, whereas “softer” potentials would describe confinement resulting from springlike or viscoelastic-like particle tethering to relatively immobile structures such as the cytoskeleton. For this purpose mathematical methods were used to simulate confined single-particle diffusion in a potential and to deduce the potential function from experimental SPT data. Our approach was validated and applied to the analysis of confined diffusion of CFTR Cl− channels in cell membranes. Our data demonstrate the ability to distinguish barrier from tethering mechanisms using experimental SPT data, and they indicate springlike tethering of CFTR by the actin cytoskeleton.

METHODS

SPT simulations

The diffusion of particles in a potential can be simulated by Brownian dynamics methods (24,30). The displacement at each time step was determined as the sum of displacements from random diffusion and potential-driven motion. Noninteracting, point particles were placed at random positions initially. At each time step, x and y displacements from random diffusion were sampled from a Gaussian distribution with zero mean and standard deviation, (2DΔt)1/2, where the D is diffusion coefficient and Δt is the time step between two successive frames. We considered four different potentials: 1), “hard-wall potential”, where particles are confined by an impermeable wall; 2), “spring potential”, where particles are tethered to a springlike force-producing mechanism; 3), “cone potential”, where particles are trapped by softer, viscoelastic-like potential; and 4), “r4 potential”, which is harder than a spring potential but softer than a hard-wall potential,

graphic file with name M1.gif (1)
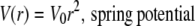graphic file with name M2.gif (2)
graphic file with name M3.gif (3)
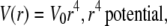graphic file with name M4.gif (4)

where V(r) is the potential function, r is the radius from the potential origin, V0 is the potential strength, and rc is the radius of confinement for a hard-wall potential.

The V(r)-driven displacement vector for time-step Δt was derived from the spatial derivative of V(r), Δr = vΔt = FΔt/ξ = −Δt × dV(r)/dr, where F is the force on the particle, v is particle velocity, and ξ is the friction coefficient (24,30). Net particle displacement was determined as the sum of V(r)-driven and random particle displacements. For some computations, diffusion coefficient, D, and potential strength, V0, were adjusted to give similar MSD versus time plots for each V(r) (Fig. 1, see legend for parameters). The “frame rate” for computations was 10 Hz. Computed trajectories were recorded over >300 s after “warm-up” to ensure steady state. The simulation was written in Matlab 7.2 (Mathworks, Natick, MA) and run on a PC.

FIGURE 1.

FIGURE 1

Open in a new tab

Simulation of confined diffusion in a potential, V(r). (A) Profiles of the four potential functions used in this study. (B) MSD versus time plots. (C) Representative single-particle trajectories shown in order of decreasing steepness of potential. White circles denote the potential center of each trajectory. Parameters: hard-wall potential, D = 0.012 μm2/s, rc = 0.347 μm; spring potential, D = 0.010 μm2/s, V0 = 0.17; cone potential, D = 0.012 μm2/s, V0 = 0.123; r4 potential, D = 0.011 μm2/s, V0 = 0.99; for all computations, frame rate was 10 Hz with >4000 time steps sampled.

V(r) determination from SPT

The radial particle density distribution, d(r), was used to determine V(r) from serial x,y coordinates in individual trajectories:

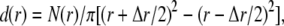graphic file with name M5.gif (5)

where r is the radial distance from the origin, Δr the distribution resolution, and N(r) the number of particles with radial distance, rp, in the range 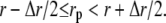Inline graphic d(r) was normalized by d(0) for nonlinear least-squares regression of Boltzmann distribution functions.

MSD for individual trajectories was computed as described (31,32),

graphic file with name M7.gif (6)

where x(t) and y(t) are the particle positions at time t, N is the total number of frames, n is the number of time intervals, and j is a positive integer. The diffusion coefficient of each trajectory was estimated from the slope of MSD versus time plots, slope = 4DΔt, obtained as linear fit to the first three time points of MSD plots. We refer to the diffusion coefficient, which is estimated by this method as D1–3. 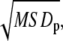For a 2-dimensional circular confined system, the MSD versus time plot saturates to Inline graphic with confinement size Inline graphic where the MSDp is the MSD value at plateau in the MSD plot (1). The mean MSD at Δt = 5–6 s was taken as MSDp. tp was defined as the time to reach plateau in the MSD plot.

SPT instrumentation and data acquisition

SPT was done as described in Haggie et al. (13) using a Nikon Eclipse TE2000U inverted epifluorescence microscope (Nikon, Tokyo, Japan) equipped with an Exfo X-Cite light source (Exfo, Quebec City, Canada), Nikon 100× TIRF oil immersion objective (numerical aperture 1.45), and Hamamatsu EM-CCD deep-cooled camera (Hamamatsu, Hamamatsu City, Japan). Qdot fluorescence was excited using a 420/40× excitation filter and 470DCXR dichroic mirror, and detected through a 655/40m emission filter (Chroma, Rockingham, VT). Data were obtained within 10 min of the final wash step after cell labeling. SPT was done using continuous 15-ms acquisitions for 20 s (62.5 frames/s). The spatial resolution of the system, determined as the standard deviation of “trajectories” obtained for immobilized Qdots on coverslips, was 20 nm (33). Image sequences were analyzed and trajectories constructed using IDL software (Research Systems, Boulder, CO) with algorithms available as shareware at http://www.physics.emory.edu/faculty/weeks/. Extracted trajectories were at least 6 s in duration, and intermittency (blinking) of Qdot fluorescence was used to verify that single fluorophores were analyzed. For V(r) analysis, although the analysis algorithms largely accounted for Qdot blinking, in some cases continuous trajectories were generated by manual linkage of shorter trajectories.

SPT measurements of CFTR diffusion

Cells lines used in this study express engineered CFTR constructs containing an external triplet hemagglutinin (HA) epitope tag in the fourth extracellular loop (CFTR-3HA), as described (13,34). Virally infected MDCK II (35) cells expressing CFTR-3HA were maintained in DMEM-H21 containing 10% FBS, 100 U/ml penicillin, 100 μg/ml streptomycin, and 1 mg/ml G418. COS7 cells were grown in DMEM H21 supplemented with 5% FBS, 100 U/ml penicillin, and 100 μg/ml streptomycin, and transfected with plasmid expressing CFTR-3HA using Lipofectamine 2000 (Invitrogen, Carlsbad, CA). MDCK II cells were also transfected with plasmid expressing CFTR-3HA-Δ26, a CFTR mutant that lacks its PDZ-binding domain, using JetPEI (Polyplus Transfection). Cells were grown at 37°C in a 5% CO2/95% air atmosphere and plated on 18-mm glass coverslips 2–3 days before experiments. CFTR-3HA at the cell surface was selectively labeled with Qdots after an initial blocking wash (PBS containing 6 mM glucose, 1 mM pyruvate, and 1% BSA, 5 min) by sequential room-temperature incubations with anti-HA antibody (Covance HA.11 mouse monoclonal antibody, 5–7 min, 0.05–0.1 μg/ml), goat antimouse biotin-SP-conjugated AffiniPure Fab fragment (Jackson ImmunoResearch, 5–7 min, 0.05–0.1 μg/ml), and 655 nm streptavidin-conjugated Qdots (2 min, 0.1 nM; Quantum Dot, Hayward, CA), in PBS containing 6 mM glucose and 1 mM pyruvate (PBS gluc/pyr). Cells were washed with PBS gluc/pyr three times between incubations and 6–10 times after Qdot incubations. For SPT measurements, coverglasses containing labeled cells bathed in PBS gluc/pyr were mounted in a custom chamber maintained at 37°C. In some experiments cells were treated with jasplakinolide (2.5 μM, 5–10 min) or with a low concentration of latrunculin (250 nM, 5–10 min), with the same compounds included in the bathing solution during tracking measurements. For experiments on fixed cells, proteins were chemically cross-linked with 4% paraformaldehyde for 30 min, washed three times in PBS, and labeled with Qdots using the same procedure as described above. For all maneuvers, data was obtained from 10–16 cell regions.

RESULTS

Particle density distributions

Fig. 1 A shows the four V(r) functional forms used in the computations, with MSD versus time plots shown in Fig. 1 B, and representative trajectories of individual particles shown in Fig. 1 C (trajectories of particles in hard-wall and spring potential are available in Supplementary Material, Movies 1 and 2). As shown in Fig. 1 B, diffusion coefficient and potential strengths can be chosen so that the plots of MSD versus time are indistinguishable on the scale of the figure, implying that different V(r) cannot necessarily be distinguished in MSD plots. However, examination of trajectories (Fig. 1 C) shows that the different V(r) produces different radial particle densities. The hard-wall potential is clearly distinguished from others because particle positions are evenly distributed over the confined region and the edge of the circular confinement area is well-demarcated. For the three non-hard-wall potentials, particle positions were distributed nonuniformly, with greater density near the centers of the trajectories. This tendency was less for the r4 potential, which is more similar than the others to the hard-wall potential. These simulations suggest that useful information about V(r) for confined diffusion is contained in radial particle density distributions.

Fig. 2 shows normalized radial particle density distributions (d(r)/d(0), open circles), defined by Eq. 5, for each of the four V(r). As expected, the d(r) functional forms were quite distinct for each V(r). In multiparticle systems, particles are generally distributed according to the Boltzmann distribution (24,28,29,36,37),

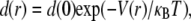graphic file with name M10.gif (7)

where κB is the Boltzmann constant (1.38 × 10−23 m2 kg/s2K) and T is absolute temperature. As shown in Fig. 2, simulated d(r)/d(0) were in good agreement with Boltzmann distributions for each V(r) (solid lines). For these computations the diffusion coefficient and potential strength were adjusted to make the MSD versus time plots nearly identical. Additional computations confirmed that d(r)/d(0) distributions can distinguish potentials for identical diffusion coefficients and potential strengths. Therefore, V(r) can be computed from the d(r) deduced from SPT data (28,29,36,37).

FIGURE 2.

FIGURE 2

Open in a new tab

Normalized radial particle density functions, d(r)/d(0). Open circles represent d(r) computed from simulations, and solid lines denote the Boltzmann distribution functions, 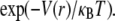Inline graphic

Theoretical considerations for determination of V(r) from experimental SPT data

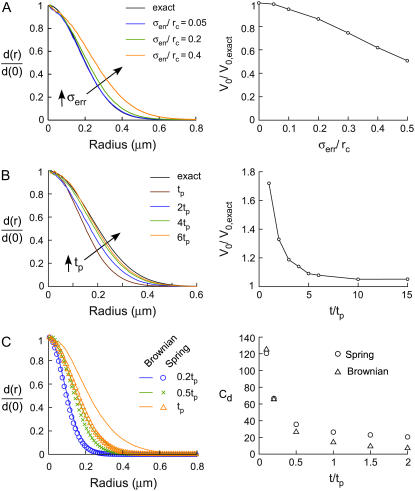
Several sources of error in real experimental data could influence d(r) and, hence, V(r) determination. Using the simulation methods developed here, we have modeled the three main sources of error, including: 1), uncertainty in particle centroid position (spatial resolution); 2), uncertainty in potential center position; and 3), finite measurement time.

Simulations were done using the spring potential (V(r) ≈ r2). Uncertainty in particle centroid was simulated by adding random errors to the trajectories, sampled from normal distributions with zero mean and standard deviation σerr. Fig. 3 A (left) shows radial density distributions, d(r)/d(0), with four different centroid position errors (including zero error). Increasing centroid error does not affect the shape of the distribution, 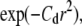Inline graphic where Cd is the density distribution coefficient, but produced broader d(r) with smaller Cd. The potential strength can be estimated from Cd = V0/κBT. Fig. 3 A (right) shows the effect of centroid position error (σerr/rc) on the error in deduced potential strength, V0/V0,exact.

FIGURE 3.

FIGURE 3

Open in a new tab

Theoretical considerations for V(r) analysis from experimental SPT data. (A) Error from uncertainty in particle centroid position (spatial resolution). Radial density distributions, d(r)/d(0), without and with three amounts of centroid position error (left). Effect of centroid position error on the error in potential strength, V0/V0,exact (right). (B) Error from uncertainty in potential center position. d(r)/d(0) for different tracking times, tp (left). Error from finite tracking time on the overestimation of potential strength, V0/V0,exact (right). (C) Error from finite measurement time. d(r)/d(0) for confined diffusion in a spring potential, as well as unconfined Brownian diffusion with different tracking times (left). Symbols and solid lines represent confined diffusion in a spring potential and Brownian diffusion, respectively, with colors representing the tracking time (blue, 0.2tp; green, 0.5tp; orange, tp). Density distribution coefficients, Cd, for confined diffusion in a spring potential (circle) and Brownian diffusion (triangle), for different tracking times (right).

Error in potential center position arises because the real r = 0 position of V(r) is not known in an experimentally measured particle trajectory. This type of error is minimized when large numbers of particle positions are contained in individual trajectories. Potential center position error was modeled by changing the total tracking time of individual particles, which is equivalent to changing the number of particle positions that are averaged to determine centroid position. Fig. 3 B (left) shows that increased tracking time (expressed as multiples of tp) produces more narrow d(r)/d(0), with shape closer to that for the “exact” simulated case with no centroid error. Fig. 3 B (right) shows the error in potential strength as a function of t/tp, which asymptotically approaches zero (V0/V0,exact = 1) for infinite tracking time. An error of <10% requires particle tracking for a time of at least 5tp.

Errors from finite tracking time result from a “non-steady-state” d(r) in which individual particles have not adequately sampled their confinement area. In the limit that tracking time is short compared with time to reach a plateau in MSD analysis, d(r) is similar to that for (unconfined) Brownian diffusion. Fig. 3 C (left) shows d(r)/d(0) for confined diffusion in a spring potential (open circles) and for Brownian diffusion (solid lines). For Brownian diffusion, the center of the trajectory for computation of d(r) was defined by mean particle x and y positions. Notably, d(r) for simple Brownian diffusion was similar to that for confined diffusion in a spring potential for the case of 0.2tp. However, differences in d(r) became evident as tracking time increased. Fig. 3 C (right) shows the density distribution coefficient, Cd, for confined diffusion in a spring potential and for Brownian diffusion. As tracking time was increased, Cd for Brownian diffusion decreased more rapidly and the differences in Cd increased. Fortunately, if the tracking time is long enough to measure the potential center position accurately (>5tp), the differences in Cd are large. However, Fig. 3 C (left) indicates that d(r) shape is nearly indistinguishable for Brownian diffusion versus confined diffusion in a weak spring potential. Computation of MSD is thus needed to verify confined diffusion before V(r) analysis is undertaken.

These simulations provide a prescription to determine V(r) from SPT data, as was used for analysis of CFTR SPT data in the next section. MSD analysis for individual trajectories is done initially to compute diffusion coefficient and to confirm confined diffusion and adequate tracking time. If a trajectory is judged to be acceptable for V(r) analysis based on these criteria, then the center of the potential (r = 0 location) is computed for calculation of d(r). The possible influence of errors in particle centroid and trajectory center is considered according to the simulations in Fig. 3. Finally, V(r) is computed from d(r) using Eq. 7.

Confined membrane diffusion of CFTR Cl− channels

We previously investigated the diffusion of CFTR in several cell lines, including airway epithelial cells, and reported highly confined CFTR diffusion in the plasma membrane (13). The CFTR interactions that result in its near immobilization are depicted in Fig. 4 A (upper), and include interaction of the CFTR C-terminal region (PDZ-binding domain) with PDZ domain binding protein EBP50, and then with ezrin and the actin cytoskeleton.

FIGURE 4.

FIGURE 4

Open in a new tab

Tracking of CFTR diffusion in cell membranes. (A, upper) Schematic of CFTR in the plasma membrane showing its C-terminal PDZ binding domain, the PDZ-domain protein EBP50, the actin-binding protein ezrin, and the actin cytoskeleton. The location of the epitope (3HA) in the fourth extracllular loop is also shown. (A, lower) Fluorescence micrographs of MDCK cells stably expressing CFTR-3HA (left) and nontransfected control cells (right), labeled with anti-HA antibody, secondary biotinylated Fab fragment, and streptavidin-conjugated Qdots. Image acquisition time was 15 ms, as used in SPT measurements. (B) Representative trajectories for CFTR-3HA diffusion in the plasma membrane of MDCK cells (upper) and COS7 fibroblasts (middle). Total trajectory time >12 s. For comparison, trajectories of immobilized Qdots and for parformaldehyde-fixed cells are shown (lower), acquired using the same parameters as for live cells. Scale bar applies to all trajectories. (C) MSD versus time plots for CFTR-3HA in MDCK cells (solid line), immobilized Qdots (dotted line), and CFTR mutant CFTR-Δ26 that lacks its C-terminal PDZ binding domain (dashed line). Plots are averaged for 16–38 individual trajectories.

To obtain experimental SPT data for V(r) analysis of CFTR diffusion, externally epitope-tagged CFTR was labeled with Qdots using a primary antibody, a secondary biotinylated Fab fragment, and streptavidin conjugated Qdots. This labeling method produced highly selective Qdot labeling of CFTR as seen by the absence of nonspecific labeling in identically treated nontransfected cells (Fig. 4 A, lower). Our previous analysis indicated that this labeling strategy does not cross-link CFTR in a manner that alters its diffusion, since similar diffusion was found for CFTR labeled with monomeric Fab fragments against the HA-epitope or with primary Fab fragments and Cy3-labeled secondary Fab fragments (13). Also, several maneuvers (actin disruption by high concentrations of latrunculin, CFTR overexpression, expression of dominant negative mutants of EBP50) greatly increased the mobility Qdot-labeled CFTR, indicating the absence of large-long crosslinking effects (13).

CFTR diffusion was measured using continuous imaging with 15-ms acquisitions (see Supplementary Material, movie 3). Representative trajectories for CFTR-3HA diffusion in the plasma membrane of MDCK cells are shown in Fig. 4 B (upper). Similar trajectories were seen in other transfected cell types, including COS7 fibroblasts (Fig. 4 B, middle) and BHK fibroblasts (data not shown). For comparison, “trajectories” for immobilized Qdots are shown in Fig. 4 B (lower). The uncertainty in defining the Qdot centroid, which is related to the fluorescence signal, defines the spatial resolution of the system (33,38). Trajectories are also shown for paraformaldehyde-fixed cells that were subsequently labeled with primary antibody, secondary biotinylated Fab fragment, and streptavidin conjugated Qdots (Fig. 4 B, lower). Trajectories from fixed cells were similar to those for immobilized Qdots, indicating that “molecular flexibility” of the labeling complex has little influence in derived trajectories. The MSD analysis in Fig. 4 C indicates confined CFTR diffusion. For comparison, MSD analysis for immobilized Qdots is shown, as well as that for nonconfined diffusion of CFTR-3HA-Δ26, a mutated CFTR that lacks its C-terminus PDZ-binding domain.

Fig. 5 A gives four examples of particle positions for individual CFTR trajectories, shown as dots, and corresponding normalized radial particle density distributions, d(r)/d(0) (open circles). These trajectories appear to be confined, as verified by MSD analysis. Solid lines show very close regressions to each of the distribution functions to a spring potential, 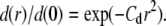Inline graphic Fig. 5 B shows the mean d(r)/d(0) from 65 trajectories of different CFTR molecules, each of which was confirmed by MSD analysis as undergoing confined diffusion. The solid line is the best fit to the spring potential, which is clearly superior to fits to the cone and r4 potentials (dashed lines), and hard-wall potential (not shown). Fig. 5 C shows histograms of spring constant (k = 2V0), confinement radius rc (defined as 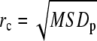Inline graphic), and diffusion coefficient D1–3 (see Methods). The average value of the spring constant, k, was 2.6 ± 0.8 pN/μm, which is in the range 2.4–10 pN/μm reported previously for skeletal interactions by optical trap methods (27,28).

FIGURE 5.

FIGURE 5

Open in a new tab

Determination of V(r) for confined diffusion of CFTR. (A) Particle positions and corresponding d(r)/d(0) for four CFTR molecules. Solid lines represent best fits to the distribution function for a spring potential. (B) Mean d(r)/d(0) from 65 trajectories of individual CFTR molecules. Best fits to distribution functions for indicated potentials are shown. For the spring potential, k = 2.6 ± 0.8 pN/μm. (C) Histograms of distribution coefficient k, confinement radius rc, and diffusion coefficient D1–3. (D) Particle positions and corresponding d(r)/d(0), as in A, for CFTR after treatment of cells with a low concentration of latrunculin. (E) Mean d(r)/d(0) and best fits to spring potential shown for control cells (same data as in panel B), and cells treated with jasplakinolide (k = 2.4 ± 0.8 pN/μm, 42 trajectories) or latrunculin (k = 1.9 ± 0.6 pN/μm, 27 trajectories). (F) MSD plot for control versus latrunculin-treated cells.

Fig. 5 D gives additional examples of CFTR particle positions and radial density functions, but after cell treatment with a low concentration of latrunculin to partially disrupt the actin cytoskeleton. Of 64 trajectories analyzed, ∼40% showed relatively “looser” distributions, as seen for the two examples at the top. Fig. 5 E summarizes averaged radial distribution functions for CFTR from many latrunculin-treated cells, as well as cells treated with jasplakinolide, an agent that promotes actin polymerization (39). Compared to control (untreated) cells, the spring potential fit to latrunculin-treated cells gave an ∼25% lower spring constant, k, for trajectories showing “looser” distributions. There was no significant effect of jasplakinolide, suggesting that although this compound dramatically alters the macroscopic properties of the actin cytoskeleton (39), the properties of short actin branches that interact indirectly with CFTR are not changed. The MSD analysis in Fig. 5 F shows greater CFTR range in latrunculin-treated versus control cells.

DISCUSSION

Our studies utilize particle spatial distributions to extend the information available from SPT measurements of confined diffusion. The deduced energy potential, V(r), provides a quantitative description of the forces (proportional to dV(r)/dr) encountered by a diffusing particle in its confinement zone. We considered four biologically relevant forms of V(r), including a hard-wall potential representing membrane “corrals”, barriers, or nonelastic tethering (2,5,32,40,41), a spring potential representing tethering with a springlike force-producing mechanism (28,37,42), a cone potential representing a nonlinear elastic force-producing mechanism, as can be seen in complex biopolymer networks (43,44), and an r4 potential. We found that the major biologically relevant forms of V(r) are readily distinguishable using the analysis approach developed here. V(r) of arbitrary functional form can thus be deduced from SPT data for permanently or transiently confined diffusion.

As described in many previous studies (24,28,29,36,37), V(r) can be deduced from d(r) by thermodynamic Boltzmann considerations, as confirmed in simulations of diffusion in defined V(r). Our simulation approach involved vectorial summation of Brownian and potential-driven particle displacements in two dimensions. The simulation allowed examination of the requirements and limitations of V(r) analysis from SPT trajectory data. The key requirements for meaningful V(r) determination include adequacy of the statistics and spatial/temporal resolution of the SPT measurement, and verification that trajectories included in the V(r) analysis represent bona fide confined diffusion. Our analysis indicated that spatial (x,y) resolution is generally the most important source of error for potential strength measurement. Our experimental data for CFTR showed strong confinement with a very small radius, rc, of ∼60 nm (Fig. 5 C, middle). As shown in Fig. 4 B, even though our SPT measurement had good spatial resolution (σerr = 20 nm), the normalized uncertainty in centroid, σerr/rc, is ∼0.33, indicating that the spring constant could be underestimated by up to 30%. Correcting for this error, the spring constant becomes 3.6 ± 1.1. To achieve 90% accuracy of the spring constant, the spatial resolution should be <10 nm in this system. According to Fig. 3 B, the measurement time should be long enough (>5tp) to avoid significant error, which was not a problem in the CFTR system. Adequate numbers of particle positions per trajectory (generally >400) are required to construct well-resolved d(r) (and deduced V(r)), both for accurate centroid determination and for narrow binning. Finally, only trajectories showing clear confinement by MSD analysis are suitable for d(r) and V(r) determination. In addition to downward curvature and approach to constant MSD, data collection over a time much greater (generally more than five times) than the “time” for MSD saturation is required to ensure a fully developed, steady-state d(r).

We found that CFTR motion is sufficiently confined to allow for meaningful analysis of V(r). Whereas CFTR shows long-term confinement (timescales greater than seconds), some membrane constituents show transient confinement. Phospholipids display “hop diffusion” characterized by periods of free diffusion (termed Dmicro) in putative actin-demarcated membrane compartments interspersed by “hops” between compartments (2,33). The data of Kusumi and co-workers indicating transient confinement of phospholipids at 25 μs resolution is suitable for V(r) analysis, since confinement is seen for ∼10 ms (i.e., 400 data points) in areas of 230-nm diameter (>14 times the 17-nm optical resolution of their system at 25 μs (33)). V(r) analysis should also be suitable for the μ-opioid receptor, a G-protein-coupled receptor, based on published results acquired at 40 kHz (45 ms residency, 210 nm confinement zone (45)). The possible finding of a hard-wall potential in these systems would provide support for the hypothesis that actin and associated proteins form a picket fence in the plasma membrane (46). V(r) analysis may also be useful to analyze the motions of a variety of neuronal receptors (20), including the α-amino-3-hydroxy-5-methyl-4-isoxazole propionic acid receptor (47) and the glycine receptor (21), both of which demonstrate transient confinement. The applicability of V(r) analysis depends on many factors, including, but not limited to, compartment size, duration of confinement, temporal and spatial resolution, and duration of data acquisition.

In this study, we assumed circular symmetry for computations and analysis of confined diffusion in a potential. Preliminary inspection of CFTR trajectories indicated that the vast majority had grossly circular symmetry, which directed the analysis methods of our study. The conclusion that CFTR is “tethered” and not “corralled” is consistent with circular symmetry. There are likely instances where circular symmetry is not valid, as reported by Morone et al. (46), in which case the analysis methods developed here would require modification.

SPT analysis of confined diffusion was applied to determine apparent V(r) for diffusion of CFTR Cl− channels at the cell plasma membrane. The CFTR protein is a 1480-amino acid, cAMP-regulated Cl− channel expressed in the apical membrane in many epithelial cell types, which when mutated can cause the genetic disease cystic fibrosis. Interactions between the intracellular C-terminus of CFTR (a class I PDZ (PSD95/Dlg/ZO-1) binding domain) and PDZ domain binding proteins, such as EBP50/NHERF1, have been reported (reviewed in (48)). Association between the CFTR C-terminus, EBP50, ezrin, and the actin cytoskeleton has been proposed to physically tether CFTR. We recently found direct evidence for these interactions in living cells (13), in which CFTR diffusion was highly confined under control conditions, but its diffusion was greatly increased after C-terminus truncations or blocking, EBP50 mutation, or cytoskeletal disruption. Expression of excess CFTR also greatly increased its diffusion, which was interpreted in terms of a saturable tethering system. These results accounted for prior photobleaching results in highly expressing CFTR-transfected cells in which CFTR was found to be quite mobile (49,50).

As for other PDZ-interactions, CFTR-PDZ associations have been implicated in channel polarization/targeting, regulation, recycling, and protein-protein association (reviewed in (48)). We found previously that CFTR tethering did not depend on its phosphorylation state (13), suggesting that CFTR complex formation is constitutive rather than regulated. Naturally occurring CFTR mutants lacking their C-terminal PDZ-interacting domains (such as CFTR-Δ26) were not immobilized by activation, indicating that CFTR immobilization is not necessary for its Cl− channel function (13,34,51,52). Similarly, the finding of similar diffusion of stable PDZ-binding domain CFTR mutants (CFTR-Δ26) and unstable mutants (CFTR-Δ70) suggests that C-terminal interactions do not have a role in CFTR degradation (13,51–54). As such, the functional consequences of CFTR immobilization are not clear at this time. In neurons, the immobilization of receptors has been proposed to be involved in synaptogenesis, long-term potentiation and long-term depression (20).

The SPT data here show that most CFTR molecules undergo confined diffusion that is described well by a springlike potential, V(r) ≈ r2. The cortical actin cytoskeleton with which CFTR associates is complex, with actin monomers assembling into polarized filaments that are organized by multiple actin binding proteins into branched, bundled, and cross-linked/orthogonal networks (55–58). The physical properties of the actin cytoskeleton are also very complex. Measurements of cell surface receptor displacements in response to applied forces and atomic force microscopy suggest that cortical actin is essentially elastic, although fluid/viscous behavior has also been observed (43,44). Laser tweezers measurements have also indicated elastic (non-hard-wall) boundaries for diffusion of several actin-associated proteins, including the transferrin receptor and major histocompatibility class I molecules (4,59). Actin-dependent elastic behavior has also been observed upon application of twisting forces to cell-surface integrins using magnetic beads (60).

According to polymer theory, filaments can be described by two parameters: persistence length (lp), which relates to polymer stiffness and defines the average length over which the filament length changes due to thermal fluctuations, and contour length (lc), which relates to filament size in an extended conformation. Most biologically important filaments, including actin, are “semiflexible”, such that lp and lc are comparable (for actin, lp is ∼17 μm (61,62) and lc is ∼0.5–1 μm (63–65)). Filaments are considered flexible if lp ≪ lc, and rigid if lp ≫ lc. Flexible and semiflexible filaments respond to applied force in an elastic manner driven by entropy (42,66). In vitro, cross-linked actin filaments demonstrate elastic behavior and strain hardening that is dependent on proteins such as α-actinin (67,68), fascin (69), scruin (42,70), filamin (71,72), myosin (73), and ActA (74). To best recapitulate the mechanical behavior of living cells, actin networks need to be bundled (42) or prestressed (72). Cross-linked and bundled actin networks possess two elastic regimes that are related to bending of individual filaments and (entropic) filament stretching (42). Robust models that faithfully recapitulate the properties of cellular actin assume elastic behavior of actin (42,66). Our data indicating a springlike, elastic potential (V(r) ≈ r2) for confined CFTR diffusion support the notion that elastic CFTR tethering by actin is responsible for its confined diffusion, as opposed to other mechanisms such as hard-wall fences.

In summary, analysis of SPT data for confined diffusion using a potential function can provide useful information about the mechanical forces that confine particle movement and thus about cellular mechanisms of confined diffusion. Our experimental analysis of CFTR diffusion at the cell plasma membrane supports a model of confined diffusion produced by interactions with the actin cytoskeleton, resulting in springlike forces that attempt to immobilize CFTR. Notwithstanding the caveats about the need for SPT data collection with adequate spatial and temporal resolution, as well as the need to distinguish between confined and other types of anomalous subdiffusion, computation of V(r) should be useful to characterize confinement and force-producing mechanisms for a wide variety of integral membrane proteins.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.

Supplementary Material

[Supplement]
biophysj_106.102244_index.html (1KB, html)

Acknowledgments

The work was supported by National Institutes of Health grants EB00415, HL73856, DK35124, HL59198, and EY13574, Cystic Fibrosis Research and Translational Core Center grant DK72517, and Research Development Program and Drug Discovery grants from the Cystic Fibrosis Foundation.

Editor: David W. Piston.

References

  • 1.Saxton, M. J., and K. Jacobson. 1997. Single-particle tracking: applications to membrane dynamics. Annu. Rev. Biophys. Biomol. Struct. 26:373–399. [DOI] [PubMed] [Google Scholar]
  • 2.Kusumi, A., C. Nakada, K. Ritchie, K. Murase, K. Suzuki, H. Murakoshi, R. S. Kasai, J. Kondo, and T. Fujiwara. 2005. Paradigm shift of the plasma membrane concept from the two-dimensional continuum fluid to the partitioned fluid: high-speed single-molecule tracking of membrane molecules. Annu. Rev. Biophys. Biomol. Struct. 34:351–378. [DOI] [PubMed] [Google Scholar]
  • 3.Sheetz, M. P. 1993. Glycoprotein motility and dynamic domains in fluid plasma membranes. Annu. Rev. Biophys. Biomol. Struct. 22:417–431. [DOI] [PubMed] [Google Scholar]
  • 4.Sako, Y., and A. Kusumi. 1995. Barriers for lateral diffusion of transferrin receptor in the plasma membrane as characterized by receptor dragging by laser tweezers: fence versus tether. J. Cell Biol. 129:1559–1574. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Saxton, M. J. 1995. Single-particle tracking: effects of corrals. Biophys. J. 69:389–398. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Winckler, B., P. Forscher, and I. Mellman. 1999. A diffusion barrier maintains distribution of membrane proteins in polarized neurons. Nature. 397:698–701. [DOI] [PubMed] [Google Scholar]
  • 7.Tang, Q., and M. Edidin. 2003. Lowering the barriers to random walks on the cell surface. Biophys. J. 84:400–407. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Ritchie, K., R. Iino, T. Fujiwara, K. Murase, and A. Kusumi. 2003. The fence and picket structure of the plasma membrane of live cells as revealed by single molecule techniques. Mol. Membr. Biol. 20:13–18. [DOI] [PubMed] [Google Scholar]
  • 9.Dietrich, C., B. Yang, T. Fujiwara, A. Kusumi, and K. Jacobson. 2002. Relationship of lipid rafts to transient confinement zones detected by single particle tracking. Biophys. J. 82:274–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Kenworthy, A. K., B. J. Nichols, C. L. Remmert, G. M. Hendrix, M. Kumar, J. Zimmerberg, and J. Lippincott-Schwartz. 2004. Dynamics of putative raft-associated proteins at the cell surface. J. Cell Biol. 165:735–746. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Zhang, L., and S. Granick. 2005. Slaved diffusion in phospholipid bilayers. Proc. Natl. Acad. Sci. USA. 102:9118–9121. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Douglass, A., and R. D. Vale. 2005. Single-molecule microscopy reveals plasma membrane microdomains created by protein-protein networks that exclude or trap signaling molecules in T cells. Cell. 121:937–950. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Haggie, P. M., J. K. Kim, G. L. Lukacs, and A. S. Verkman. 2006. Tracking of quantum dot-labeled CFTR shows near immobilization by C-terminal PDZ interactions. Mol. Biol. Cell. 17:4937–4945. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Ryan, T. A., J. Myers, D. Holowka, B. Baird, and W. W. Webb. 1988. Molecular crowding on the cell surface. Science. 239:61–64. [DOI] [PubMed] [Google Scholar]
  • 15.Banks, D. S., and C. Fradin. 2005. Anomalous diffusion of proteins due to molecular crowding. Biophys. J. 89:2960–2971. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Cao, J. 2001. Single molecule tracking of heterogeneous diffusion. Phys. Rev. E. 63:041101. [DOI] [PubMed] [Google Scholar]
  • 17.Nicolau, D. V., Jr., J. F. Hancock, and K. Burrage. 2007. Sources of anomalous diffusion on cell membranes: a Monte Carlo study. Biophys. J. 92:1975–1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Sergé, A., L. Fourgeaud, A. Hémar, and D. Choquet. 2002. Receptor activation and Homer differentially control the lateral mobility of metabotropic glutamate receptor 5 in the neuronal membrane. J. Neurosci. 22:3910–3920. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Tardin, C., L. Cognet, C. Bats, B. Lounis, and D. Choquet. 2003. Direct imaging of lateral movements of AMPA receptors inside synapses. EMBO J. 22:4656–4665. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Choquet, D., and A. Triller. 2003. The role of receptor diffusion in the organization of the postsynaptic membrane. Nat. Rev. Neurosci. 4:251–265. [DOI] [PubMed] [Google Scholar]
  • 21.Dahan, M., S. Lévi, C. Luccardini, P. Rostaing, B. Riveau, and A. Triller. 2003. Diffusion dynamics of glycine receptors revealed by single-quantum dot tracking. Science. 302:442–445. [DOI] [PubMed] [Google Scholar]
  • 22.Groc, L., M. Heine, L. Cognet, K. Brickley, F. A. Stephenson, B. Lounis, and D. Choquet. 2004. Differential activity-dependent regulation of the lateral mobilities of AMPA and NMDA receptors. Nat. Neurosci. 7:695–696. [DOI] [PubMed] [Google Scholar]
  • 23.Forstner, M. B., D. S. Martin, A. M. Navar, and J. A. Käs. 2003. Simultaneous single-particle tracking and visualization of domain structure on lipid monolayers. Langmuir. 19:4876–4879. [Google Scholar]
  • 24.Selle, C., C. F. Rückerl, D. S. Martin, M. B. Forstner, and J. A. Käs. 2004. Measurement of diffusion in Langmuir monolayers by single-particle tracking. Phys. Chem. Chem. Phys. 6:5535–5542. [Google Scholar]
  • 25.Jin, S., and A. S. Verkman. 2007. Single particle tracking of complex diffusion in membranes: simulation and detection of barrier, raft and interaction phenomena. J. Phys. Chem. B. 111:3625–3632. [DOI] [PubMed] [Google Scholar]
  • 26.Edidin, M., S. C. Kuo, and M. P. Sheetz. 1991. Lateral movements of membrane glycoproteins restricted by dynamic cytoplasmic barriers. Science. 254:1379–1382. [DOI] [PubMed] [Google Scholar]
  • 27.Peters, I. M., Y. van Kooyk, S. J. van Vliet, B. G. de Grooth, C. G. Figdor, and J. Greve. 1999. 3D single-particle tracking and optical trap measurements on adhesion proteins. Cytometry. 36:189–194. [DOI] [PubMed] [Google Scholar]
  • 28.Oddershede, L., J. K. Dreyer, S. Grego, S. Brown, and K. Berg-Sørensen. 2002. The motion of a single molecule, the λ-receptor, in the bacterial outer membrane. Biophys. J. 83:3152–3161. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Florin, E.-L., A. Pralle, E. H. K. Stelzer, and J. K. H. Hörber. 1998. Photonic force microscope calibration by thermal noise analysis. Appl. Phys. A. 66:S75–S78. [Google Scholar]
  • 30.McCammon, J. A., and S. C. Harvey. 1987. Dynamics of proteins and nucleic acids. Cambridge University Press, New York.
  • 31.Qian, H., M. P. Sheetz, and E. L. Elson. 1991. Single particle tracking. Analysis of diffusion and flow in two-dimensional systems. Biophys. J. 60:910–921. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Kusumi, A., Y. Sako, and M. Yamamoto. 1993. Confined lateral diffusion of membrane receptors as studied by single particle tracking (Nanovid microscopy). Effects of calcium-induced differentiation in cultured epithelial cells. Biophys. J. 65:2021–2040. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Fujiwara, T., K. Ritchie, H. Murakoshi, K. Jacobson, and A. Kusumi. 2002. Phospholipids undergo hop diffusion in compartmentalized cell membrane. J. Cell Biol. 157:1071–1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Benharouga, M., M. Sharma, J. So, M. Haardt, L. Drzymala, M. Popov, B. Schwapach, S. Grinstein, K. Du, and G. L. Lukacs. 2003. The role of the C-terminus and Na+/H+ exchanger regulatory factor in the functional expression of cystic fibrosis transmembrane conductance regulator in nonpolarized cells and epithelia. J. Biol. Chem. 278:22079–22089. [DOI] [PubMed] [Google Scholar]
  • 35.Mohamed, A., D. Ferguson, F. S. Seibert, H. M. Cai, N. Kartner, S. Grinstein, J. R. Riordan, and G. L. Lukacs. 1997. Functional expression and apical localization of the cystic fibrosis transmembrane conductance regulator in MDCK I cells. Biochem. J. 322:259–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Sasaki, K., M. Tsukima, and H. Masuhara. 1997. Three-dimensional potential analysis of radiation pressure exerted on a single microparticle. Appl. Phys. Lett. 71:37–39. [Google Scholar]
  • 37.Scholz, T., S. M. Altmann, M. Antognozzi, C. Tischer, J.-K. Heinrich Hörber, and B. Brenner. 2005. Mechanical properties of single myosin molecules probed with the photonic force microscope. Biophys. J. 88:360–371. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Thompson, R. E., D. R. Larson, and W. W. Webb. 2002. Precise nanometer localization analysis for individual fluorescent probes. Biophys. J. 82:2775–2783. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Okamoto, K.-I., T. Nagai, A. Miyawaki, and Y. Hayashi. 2004. Rapid and persistent modulation of actin dynamics regulates postsynaptic reorganization underlying bidirectional plasticity. Nat. Neurosci. 7:1104–1112. [DOI] [PubMed] [Google Scholar]
  • 40.Schmidt, K., and B. J. Nichols. 2004. A barrier to lateral diffusion in the cleavage furrow of dividing mammalian cells. Curr. Biol. 14:1002–1006. [DOI] [PubMed] [Google Scholar]
  • 41.Ritchie, K., X.-Y. Shan, J. Kondo, K. Iwasawa, T. Fujiwara, and A. Kusumi. 2005. Detection of non-Brownian diffusion in the cell membrane in single molecule tracking. Biophys. J. 88:2266–2277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Gardel, M. L., J. H. Shin, F. C. MacKintosh, L. Mahadevan, P. Matsudaira, and D. A. Weitz. 2004. Elastic behavior of cross-linked and bundled actin networks. Science. 304:1301–1305. [DOI] [PubMed] [Google Scholar]
  • 43.Bausch, A. R., F. Ziemann, A. A. Boulbitch, K. Jacobson, and E. Sackmann. 1998. Local measurements of viscoelastic parameters of adherent cell surfaces by magnetic bead microrheometry. Biophys. J. 75:2038–2049. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Alcaraz, J., L. Buscemi, M. Grabulosa, X. Trepat, B. Fabry, R. Farré, and D. Navajas. 2003. Microrheology of human lung epithelial cells measured by atomic force microscopy. Biophys. J. 84:2071–2079. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Suzuki, K., K. Ritchie, E. Kajikawa, T. Fujiwara, and A. Kusumi. 2005. Rapid hop diffusion of a G-protein-coupled receptor in the plasma membrane as revealed by single-molecule techniques. Biophys. J. 88:3659–3680. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.Morone, N., T. Fujiwara, K. Murase, R. S. Kasai, H. Ike, S. Yuasa, J. Usukura, and A. Kusumi. 2006. Three-dimensional reconstruction of the membrane skeleton at the plasma membrane interface by electron tomography. J. Cell Biol. 174:851–862. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Borgdorff, A. J., and D. Choquet. 2002. Regulation of AMPA receptor lateral movements. Nature. 417:649–653. [DOI] [PubMed] [Google Scholar]
  • 48.Guggino, W. B., and B. A. Stanton. 2006. New insights into cystic fibrosis: molecular switches that regulate CFTR. Nat. Rev. Mol. Cell Biol. 7:426–436. [DOI] [PubMed] [Google Scholar]
  • 49.Haggie, P. M., B. A. Stanton, and A. S. Verkman. 2004. Increased diffusional mobility of CFTR at the plasma membrane after deletion of its C-terminal PDZ binding motif. J. Biol. Chem. 279:5494–5500. [DOI] [PubMed] [Google Scholar]
  • 50.Bates, I. R., B. Hébert, Y. Luo, J. Liao, A. I. Bachir, D. L. Kolin, P. W. Wiseman, and J. W. Hanrahan. 2006. Membrane lateral diffusion and capture of CFTR within transient confinement zones. Biophys. J. 91:1046–1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 51.Haardt, M., M. Benharouga, D. Lechardeur, N. Kartner, and G. L. Lukacs. 1999. C-terminal truncations destabilize the cystic fibrosis transmembrane conductance regulator without impairing its biogenesis. J. Biol. Chem. 274:21873–21877. [DOI] [PubMed] [Google Scholar]
  • 52.Ostedgaard, L. S., C. Randak, T. Rokhlina, P. Karp, D. Vermeer, K. J. A. Excoffon, and M. J. Welsh. 2003. Effects of C-terminal deletions on cystic fibrosis transmembrane conductance regulator function in cystic fibrosis airway epithelia. Proc. Natl. Acad. Sci. USA. 100:1937–1942. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53.Benharouga, M., M. Haardt, N. Kartner, and G. L. Lukacs. 2001. COOH-terminal truncations promote proteasome-dependent degradation of mature cystic fibrosis transmembrane conductance regulator from post-Golgi compartments. J. Cell Biol. 153:957–970. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 54.Sharma, M., F. Pampinella, C. Nemes, M. Benharouga, J. So, K. Du, K. G. Bache, B. Papsin, N. Zerangue, H. Stenmark, and G. L. Lukacs. 2004. Misfolding diverts CFTR from recycling to degradation; quality control at early endosomes. J. Cell Biol. 164:923–933. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 55.Pollard, T. D., S. Almo, S. Quirk, V. Vinson, and E. E. Lattman. 1994. Structure of actin binding proteins: insights about function at atomic resolution. Annu. Rev. Cell Biol. 10:207–249. [DOI] [PubMed] [Google Scholar]
  • 56.Higgs, H. N., and T. D. Pollard. 2001. Regulation of actin filament network formation through ARP2/3 complex: activation by a diverse array of proteins. Annu. Rev. Biochem. 70:649–676. [DOI] [PubMed] [Google Scholar]
  • 57.Pollard, T. D., and G. G. Borisy. 2003. Cellular motility driven by assembly and disassembly of actin filaments. Cell. 112:453–465. [DOI] [PubMed] [Google Scholar]
  • 58.Janmey, P. A., and D. A. Weitz. 2004. Dealing with mechanics: mechanisms of force transduction in cells. Trends Biochem. Sci. 29:364–370. [DOI] [PubMed] [Google Scholar]
  • 59.Suzuki, K., and M. P. Sheetz. 2001. Binding of cross-linked glycosylphosphatidylinositol-anchored proteins to discrete actin-associated sites and cholesterol-dependent domains. Biophys. J. 81:2181–2189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 60.Wang, N., J. P. Butler, and D. E. Ingber. 1993. Mechanotransduction across the cell surface and through the cytoskeleton. Science. 260:1124–1127. [DOI] [PubMed] [Google Scholar]
  • 61.Gittes, F., B. Mickey, J. Nettleton, and J. Howard. 1993. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J. Cell Biol. 120:923–934. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 62.Ott, A., M. Magnasco, A. Simon, and A. Libchaber. 1993. Measurement of the persistence length of polymerized actin using fluorescence microscopy. Phys. Rev. E. 48:R1642–R1645. [DOI] [PubMed] [Google Scholar]
  • 63.Podolski, J. L., and T. L. Steck. 1990. Length distribution of F-actin in Dictyostelium discoideum. J. Biol. Chem. 265:1312–1318. [PubMed] [Google Scholar]
  • 64.Svitkina, T. M., and G. G. Borisy. 1999. Arp2/3 complex and actin depolymerizing factor/cofilin in dendritic organization and treadmilling of actin filament array in lamellipodia. J. Cell Biol. 145:1009–1026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 65.Medalia, O., I. Weber, A. S. Frangakis, D. Nicastro, G. Gerisch, and W. Baumeister. 2002. Macromolecular architecture in eukaryotic cells visualized by cryoelectron tomography. Science. 298:1209–1213. [DOI] [PubMed] [Google Scholar]
  • 66.Storm, C., J. J. Pastore, F. C. MacKintosh, T. C. Lubensky, and P. A. Janmey. 2005. Nonlinear elasticity in biological gels. Nature. 435:191–194. [DOI] [PubMed] [Google Scholar]
  • 67.Xu, J., D. Wirtz, and T. D. Pollard. 1998. Dynamic cross-linking by α-actinin determines the mechanical properties of actin filament networks. J. Biol. Chem. 273:9570–9576. [DOI] [PubMed] [Google Scholar]
  • 68.Xu, J., Y. Tseng, and D. Wirtz. 2000. Strain hardening of actin filament networks. Regulation by the dynamic cross-linking protein α-actinin. J. Biol. Chem. 275:35886–35892. [DOI] [PubMed] [Google Scholar]
  • 69.Tseng, Y., B. W. Schafer, S. C. Almo, and D. Wirtz. 2002. Functional synergy of actin filament cross-linking proteins. J. Biol. Chem. 277:25609–25616. [DOI] [PubMed] [Google Scholar]
  • 70.Shin, J. H., M. L. Gardel, L. Mahadevan, P. Matsudaira, and D. A. Weitz. 2004. Relating microstructure to rheology of a bundled and cross-linked F-actin network in vitro. Proc. Natl. Acad. Sci. USA. 101:9636–9641. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 71.Wagner, B., R. Tharmann, I. Haase, M. Fischer, and A. R. Bausch. 2006. Cytoskeletal polymer networks: the molecular structure of cross-linkers determines macroscopic properties. Proc. Natl. Acad. Sci. USA. 103:13974–13978. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 72.Gardel, M. L., F. Nakamura, J. H. Hartwig, J. C. Crocker, T. P. Stossel, and D. A. Weitz. 2006. Prestressed F-actin networks cross-linked by hinged filamins replicate mechanical properties of cells. Proc. Natl. Acad. Sci. USA. 103:1762–1767. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 73.Mizuno, D., C. Tardin, C. F. Schmidt, and F. C. MacKintosh. 2007. Nonequilibrium mechanics of active cytoskeletal networks. Science. 315:370–373. [DOI] [PubMed] [Google Scholar]
  • 74.Chaudhuri, O., S. H. Parekh, and D. A. Fletcher. 2007. Reversible stress softening of actin networks. Nature. 445:295–298. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplement]
biophysj_106.102244_index.html (1KB, html)
Download video file (692.1KB, avi)
Download video file (793.5KB, avi)
Download video file (1.7MB, avi)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES