Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2007 May 4;93(3):930–937. doi: 10.1529/biophysj.106.096982

Free Energy of Membrane Protein Unfolding Derived from Single-Molecule Force Measurements

Johannes Preiner *, Harald Janovjak †, Christian Rankl *, Helene Knaus †, David A Cisneros †, Alexej Kedrov †, Ferry Kienberger *, Daniel J Muller †, Peter Hinterdorfer *
PMCID: PMC1913163  PMID: 17483176

Abstract

Mechanical single-molecule techniques offer exciting possibilities to investigate protein folding and stability in native environments at submolecular resolution. By applying a free-energy reconstruction procedure developed by Hummer and Szabo, which is based on a statistical theorem introduced by Jarzynski, we determined the unfolding free energy of the membrane proteins bacteriorhodopsin (BR), halorhodopsin, and the sodium-proton antiporter NhaA. The calculated energies ranged from 290.5 kcal/mol for BR to 485.5 kcal/mol for NhaA. For the remarkably stable BR, the equilibrium unfolding free energy was independent of pulling rate and temperature ranging between 18 and 42°C. Our experiments also revealed heterogeneous energetic properties in individual transmembrane helices. In halorhodopsin, the stabilization of a short helical segment yielded a characteristic signature in the energy profile. In NhaA, a pronounced peak was observed at a functionally important site in the protein. Since a large variety of single- and multispan membrane proteins can be tackled in mechanical unfolding experiments, our approach provides a basis for systematically elucidating energetic properties of membrane proteins with the resolution of individual secondary-structure elements.

INTRODUCTION

Biological membranes are essential to all organisms as they provide permeability barriers and specialized environments for a multitude of crucial processes. Transmembrane proteins fulfill many of these functions, as they act, for example, as sensors, receptors, and channels. In line with their important roles, membrane proteins comprise ∼20–30% of all cellular proteins (1). Detailed knowledge of their three-dimensional structures and folding is, however, still lacking: Less than 1% of the structures deposited within the Protein Data Bank are membrane proteins, and mechanistic information of the folding in the anisotropic environment of the lipid bilayer is only available for a few of these (2,3).

Considerable effort has been devoted to investigating the unfolding of membrane proteins in thermal and chemical denaturation experiments (4–7). Despite their suitability for studying globular proteins, these methods are often unable to fully denature membrane proteins. In contrast to the natively folded state of the protein, the unfolded state is structurally not defined. Thus, substantial amounts of secondary structures of a denatured protein remain folded or partly folded, and the free energy of the natively folded protein is most often inaccessible (4,7). From thermodynamic predictions and experiments, it was postulated that the transfer of hydrophobic amino acid (aa) residues to the core regions of the membrane is linked to a free-energy gain of ∼1 kcal/mol (8,9). However, from the few macroscopic studies of membrane protein unfolding, complete measurements of their insertion and folding energies are not available.

Single-molecule force spectroscopy has been widely used to probe the mechanical properties of individual molecules by exerting mechanical forces that induce conformational changes in proteins, nucleic acids, and polysaccharides (10–12). In mechanical unfolding experiments of membrane proteins (13–17), an external pulling force applied through the cantilever of an atomic force microscope (AFM) plays the role of the chemical/thermal denaturant. The high sensitivity of this method allows the interactions that stabilize secondary structures such as transmembrane α-helices and small helical segments to be detected (15,16,18). In contrast to ensemble approaches, which inherently probe the average behavior of large numbers of molecules, single-molecule experiments detect coexisting unfolding pathways and nonaccumulative folding intermediates that are populated in multidimensional energy landscapes and folding funnels (19–22). However, due to the finite force loading rate, mechanical unfolding studies are typically nonequilibrium experiments, supposing that only irreversible work can be calculated from force-extension traces (12).

In 1997, Jarzynski derived an identity relating the irreversible work of multiple measurements to equilibrium-free-energy differences (Jarzynski's identity (23)). The remarkable theoretical result opens the possibility to obtain equilibrium thermodynamic parameters from processes carried out arbitrarily far from equilibrium, provided that multiple measurements at a sufficiently high signal/noise ratio are available. In 2001, Hummer and Szabo (24) adapted Jarzynski's identity for the analysis of single-molecule pulling experiments, and in 2002 Liphardt et al. (25) tested Jarzynski's equality by comparing the work performed in the reversible and irreversible mechanical unfolding of a single RNA molecule.

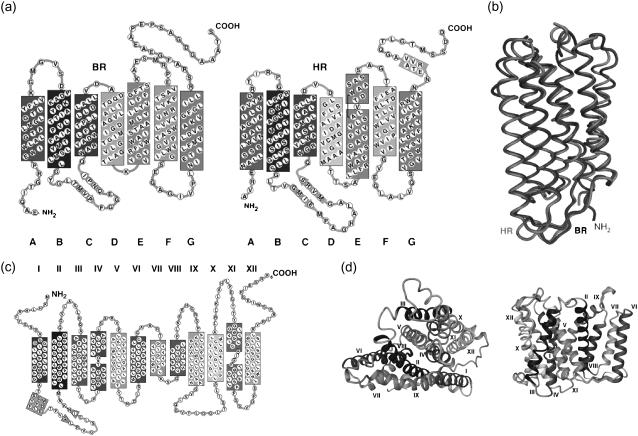
Here we applied Jarzynski's identity as adopted recently by Hummer and Szabo (26) to characterize the stability of three membrane proteins (bacteriorhodopsin (BR), halorhodopsin (HR), and the Na+/H+ antiporter NhaA) by calculating the unfolding free energies (i.e., the energy difference between the folded and unfolded state) of their transmembrane helices from single-molecule force measurements. The reversibility of BR and NhaA protein unfolding was shown in two recent studies (27,28). Because of the high structural and functional similarities of HR and BR (16), it might be assumed that HR shows reversible unfolding pathways as well. BR and HR are two highly similar heptaspan light-driven ion pumps from the archaebacteria Halobacter salinarum, and NhaA is a dodecaspan ion antiporter from Escherichia coli. The topologies and tertiary structures of BR (29), HR (30), and NhaA (31) are shown in Fig. 1.

FIGURE 1.

FIGURE 1

Open in a new tab

Topologies and three dimensional structures of (a and b) the halophilic heptaspan membrane proteins BR (PDB-code 1C3W) and HR (PDB-code 1E12), and (c and d) the dodecaspan sodium-proton antiporter NhaA (PDB-code 1ZCD) from Escherichia coli. The helices are labeled A–G in the case of BR and HR and I–XII in the case of NhaA.

METHODS

Unfolding data

For BR unfolding at different pulling rates (see Fig. 3), 60 deflection traces at 654 nm/s, 60 at 1310 nm/s, and 59 at 2620 nm/s, recorded at 18°C, were analyzed. Temperature dependence (see Fig. 4) was investigated using additional 45 deflection traces at 87 nm/s, 49 at 654 nm/s, 57 at 1310 nm/s, 18 at 2620 nm/s, and 63 at 5230 nm/s, recorded at 25°C; and 57 deflection traces at 300 nm/s, 64 at 654 nm/s, and 61 at 1310 nm/s, recorded at 42°C (data taken from Janovjak et al. (32)). We analyzed 41 deflection traces recorded at 90 nm/s for HR (data taken from Cisneros et al. (16)) and 56 deflection traces recorded at 120 nm/s for NhaA (data taken from Kedrov et al. (15)). The part of the deflection trace after extracting the last helix was used to determine and correct the slope of the baseline and the deflection offset (33). The alignment of the curves was done by fitting a straight line to cantilever deflections (z(t) − q(t)) > 1 nm in the contact region (negative piezomovement, Fig. 2 a), and then shifting the so-determined point of contact to zero piezomovement for each curve (e.g., (34)). This ensures a defined initial condition for all traces, as required by the Jarzynski analysis (23).

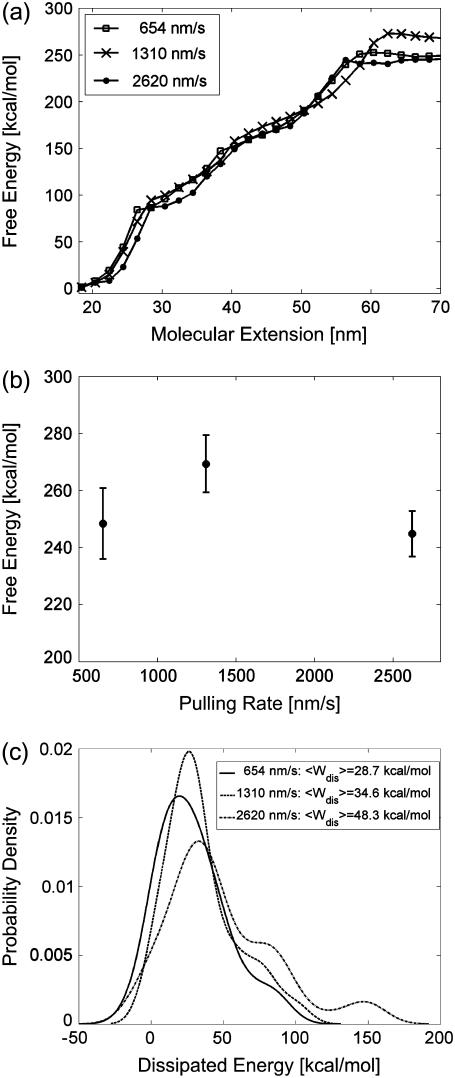
FIGURE 3.

FIGURE 3

Open in a new tab

Pulling-rate dependence of the free-energy profile of BR unfolding. (a) Free-energy profiles of BR at three different pulling rates, acquired at 18°C. (b) Free-energy difference 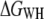Inline graphic as a function of the pulling rate, examined at 70 nm extension. Error bars were obtained via Bootstrap analysis (cf. Methods). (c) Probability densities of the dissipated work for 654 nm/s (solid line), 1310 nm/s (dashed line), and 2620 nm/s (dot-dashed line).

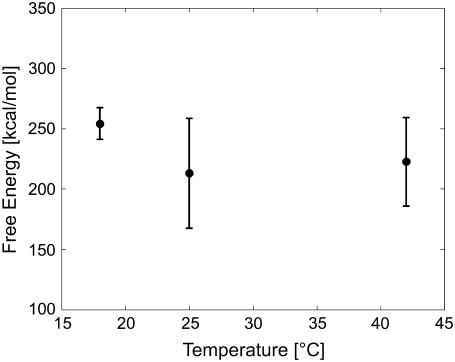
FIGURE 4.

FIGURE 4

Open in a new tab

Temperature dependence of the free-energy profile of BR unfolding. The average free-energy difference between folded and unfolded states is plotted as a function of temperature (18°C, 25°C, and 42°C; examined at an extension of 70 nm) and the corresponding mean (solid line). Error bars were obtained by averaging over different pulling rates at each temperature.

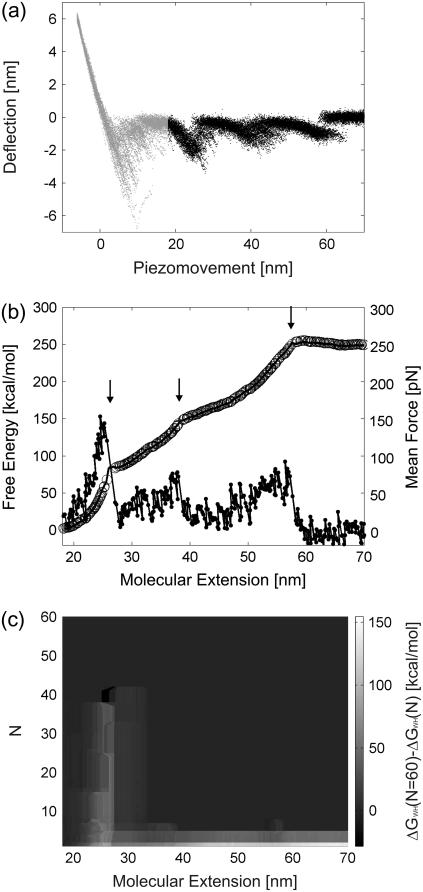
FIGURE 2.

FIGURE 2

Open in a new tab

Reconstruction of the free-energy profile of BR unfolding. (a) Ensemble plot of 60 single unfolding curves (deflection z(t) − q(t) versus piezomovement z(t)) recorded at a pulling rate of 654 nm/s. The unfolding steps of helices E and D (at 27 nm extension), C and B (at 42 nm extension), and A (at 62 nm extension) are clearly observed. Because of unspecific interactions between the AFM stylus and the membrane surface, the unfolding of helices G and F is scattered at extensions <18 nm. For energy calculations, the first peak (helices G and F, gray regions) is omitted. (b) Free-energy profile for the unfolding of helices E and D, C and B, and A computed from a using 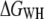Inline graphic (solid line), 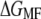Inline graphic (circles), and the corresponding mean force (dots). Arrows indicate the transition points. (c) Color-coded convergence of 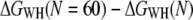Inline graphic along the molecular extension coordinate as a function of the number of pulling cycles for the data from a.

Energy calculations and error estimations

The integral in Eq. 2 was evaluated using a standard trapezoidal numerical integration algorithm. Error bars (Fig. 3 b, HR and NhaA) were calculated using a nonparametric bootstrap analysis. This method allows sampling distributions and standard errors to be calculated without making any assumptions about the underlying distributions. In this analysis, the sampling distribution (i.e., the mean and the standard deviation) of the value of interest was approximated using replicate data sets of the same size as the original data set (35).

The dissipated energy values were calculated from the difference of irreversible works (for each trajectory) and the equilibrium free energy obtained using the weighted histogram estimator for 654-nm/s, 1310-nm/s, and 2620-nm/s pulling rate. Probability densities were then calculated using a kernel estimator (36).

The error of a single-cantilever spring constant determination is typically ±10% (37) and increases for n cantilevers to 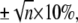Inline graphic which agrees with the observed error bars in Fig. 3 (up to two cantilevers used per dataset). To prove that the mean free energies at different temperatures (Fig. 4) were statistically not distinguishable, an ANOVA test was performed to check that all samples were drawn from the same population (P-value 0.36). All calculations were performed using MATLAB Version 7.1 (MathWorks, Natick, MA).

RESULTS

Application of Jarzynski's identity to the forced unfolding of BR

Jarzynski derived a relation between the free-energy difference of two states at different times and appropriately weighted averages of the work required to shuttle between these states measured for many repetitions of a nonequilibrium process (23). An extension of this relation was developed by Hummer and Szabo to calculate free-energy profiles along mechanical reaction coordinates obtained from single-molecule pulling experiments (24,26). Following methods used in their work, we applied the weighted histogram method and the momentum-based approach (26). The weighted histogram method results in the equation

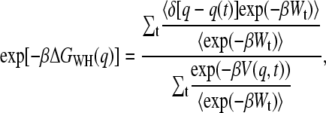graphic file with name M6.gif (1)

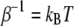where Inline graphic (T is the temperature, 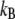Inline graphic is the Boltzmann constant), q is the pulling coordinate (molecular extension), 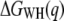Inline graphic is the free-energy profile along q, and the sums are over the histograms collected at different times t. 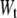Inline graphic is the accumulated work calculated by

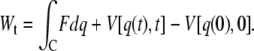graphic file with name M11.gif (2)

Here, F = k(z(t) − q(t)) denotes the restoring force, where k is the cantilever spring constant, z(t) = vt is the product of pulling rate v and time, 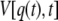Inline graphic is the harmonic biasing potential of the cantilever, and the integral over q is along the position versus time contour connecting q(0) and q(t). If the cantilever is relatively stiff, most trajectories will be clustered near z(t), the position of the piezo actuator (25). In this case one can approximate the weighted distribution of molecular extensions by a Gaussian with mean

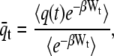graphic file with name M13.gif (3)

and corresponding variance 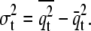Inline graphic Using this approximation (momentum-based approach), the first derivative of the potential of mean force (i.e., the mean force) can be calculated according to

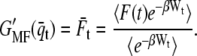graphic file with name M15.gif (4)

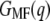Inline graphic is then calculated by the cumulative integral of Eq. 4.

Formalism was applied to unfolding traces of individual BR molecules from native purple membrane patches of H. salinarum (data taken from (32)). Fig. 2 a shows an ensemble plot of 60 curves obtained from unfolding single BR molecules at a pulling rate of 654 nm/s (32) and 18°C. In previous studies, the four groups of peaks were assigned to the unfolding of helices G and F (at extensions <18 nm), E and D (at ∼27 nm extension), C and B (at ∼42 nm extension), and helix A (at ∼62 nm extension) (13,14). From such unfolding spectra, the energy difference between the folded state in the membrane and an unfolded state outside the membrane can be determined.

Since the first group of peaks (unfolding of helices G and F) is scattered due to interactions occurring between the AFM stylus and the protein membrane (Fig. 2 a, gray regions) (18,38), we omitted these data points in the calculations and set 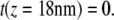Inline graphic Assuming that a quasiequilibrium was established at this point, Eqs. 1–4 can be applied to determine the free energy profile along the molecular extension coordinate. Fig. 2 b shows the Jarzynski reconstruction of the Gibbs free energy profile using the weighted histogram method, 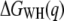Inline graphic (solid line), the estimator based on the mean force, 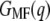Inline graphic (circles), and the underlying mean force (dots). Three pronounced energy steps of 84.1 ± 3.6 kcal/mol (helices E and D), 63.0 ± 5.1 kcal/mol (helices C and B), and 101.6 ± 5.3 kcal/mol (helix A) were found for the unfolding and extraction of the corresponding helices (mean ± SD obtained via Bootstrap analysis, cf. Methods). In total, an energy of 248.4 ± 3.9 kcal/mol is required to extract and unfold a single BR molecule at a pulling rate of 654 nm/s. It should be noted that possible energetic contributions of helices G and F could not be included in this estimation (cf. Discussion). The mean-force-based estimator performs comparably to the weighted histogram method, with the exception of cusplike features in the free-energy reconstruction (Fig. 2 b, arrows) since the Gaussian approximation performs poorly in these regions (26).

Although Jarzynski's equality applies in theory to systems driven arbitrarily far from equilibrium, a sufficiently large number of unfolding experiments N must be available, either obtained from the same molecule (time average) (25), or from an ensemble of molecules (ensemble average). To show that 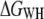Inline graphic approaches the equilibrium free-energy difference, Fig. 2 c depicts the convergence (color code) of the difference 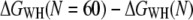Inline graphic along the molecular extension as the number of curves included in the calculation is increased from 1 to 60. In general, the more work is dissipated, the more curves are required for proper convergence (25). In the region where most work is dissipated (20–30 nm extension) the convergence is slow, in contrast to regions where convergence is essentially reached after N ≈ 8. However, the overall free energy does not change significantly for N > 40 (Fig. 2 c), indicating proper convergence.

The unfolding free energy of BR is pulling-rate-independent

In the next step, free-energy profiles 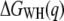Inline graphic were computed from force traces recorded on BR at three different pulling rates ranging from 654 nm/s to 2620 nm/s (Fig. 3 a). In Fig. 3 b, the free energy required for extracting helices E and D, C and B, and A, is plotted against the pulling rate. It can be seen that the calculated free-energy values do not depend on the pulling rate; deviations are primarily given by the accuracy of the cantilever-spring-constant determination (cf. Methods). An average free energy 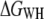Inline graphic of 254.1 ± 13.3 kcal/mol (mean ± SD) was obtained for the extraction and unfolding of BR (neglecting helices G and F). Fig. 3 c shows the probability density for the energy dissipated during the extraction and unfolding of helices E and D.

The unfolding free energy of BR is temperature-independent

In addition to the pulling-rate dependence, the influence of temperature on the unfolding free energy of BR was investigated (Fig. 4). Unfolding traces recorded at three different temperatures (18°C, 25°C, and 42°C) and different pulling rates were used (cf. Methods), and 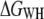Inline graphic values were computed and averaged over the pulling rates at each temperature. Within experimental error, the unfolding free energies remained unchanged in this temperature range, as assessed using an ANOVA test (cf. Methods).

Unfolding free energies of HR and NhaA

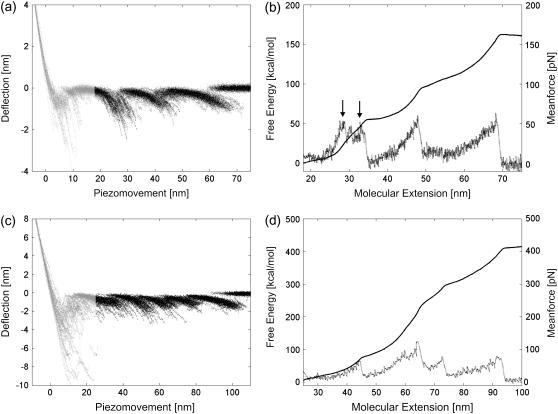
The same procedure was applied to unfolding deflection data of the light-driven chloride pump HR from H. salinarum (Fig. 5 a) and the sodium-proton antiporter NhaA from E. coli (Fig. 5 c). Fig. 5 b shows the mean force (dashed line) and the corresponding energy profile 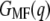Inline graphic of HR (solid line), with energy steps corresponding to the unfolding of helices E and D (55.1 ± 2.3 kcal/mol), C and B (40.1 ± 3.3 kcal/mol), and A (67.1 ± 2.7 kcal/mol). In total, a free energy of 162.3 ± 2.7 kcal/mol was obtained for HR (neglecting helices G and F), which lies within the range determined for BR. However, in contrast to BR (Fig. 2 b, mean force, dots), a two-step unfolding of helices E and D at an extension of 30 nm was observed.

FIGURE 5.

FIGURE 5

Open in a new tab

Free-energy profile of halorhodopsin (HR) and NhaA unfolding. (a) Ensemble plot of 41 single unfolding deflection curves of HR recorded at a pulling rate of 90 nm/s (for calculations, traces were cut at extensions <18 nm, gray region). (b) Free-energy profile of HR unfolding (solid line) and the corresponding mean force (dashed line). The unfolding of helices E and D occurs in two steps (arrows), with a corresponding energy step of 24.4 kcal/mol. (c) Ensemble plot of 56 single unfolding deflection curves of NhaA recorded at a pulling rate of 120 nm/s (for calculations, traces were cut at extensions <25 nm, gray region). (d) Free-energy profile of NhaA (solid line) and the corresponding mean force (dashed line). Five energy steps relating to the five helical pairs can be clearly observed (helices X and IX, VIII and VII, VI and V, IV and III, and II and I)

The mean force (Fig. 2 b, dashed line) and the free-energy profile 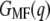Inline graphic of NhaA is shown in Fig. 5 d. From the unfolding force pattern, five energy steps corresponding to the unfolding of helices X and IX, VIII and VII, VI and V, IV and III, and II and I (28) with 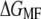Inline graphic values of 69.9 ± 11.2 kcal/mol, 88.0 ± 25.9 kcal/mol, 49.2 ± 27.9 kcal/mol, 91.2 ± 15.9 kcal/mol, and 112.0 ± 6.9 kcal/mol, respectively, were obtained. Neglecting the scattered unfolding peak (helices XII and XI), a total energy of 410.4 ± 5.1 kcal/mol was found for the unfolding of NhaA.

DISCUSSION

Mechanical single-molecule experiments are seen as a promising way to study the stability and folding mechanism of individual globular (39–41) and membrane proteins (14,27,28). Here, we applied a formalism developed by Jarzynski (23) using an extension of Hummer and Szabo (24,26) to derive the free energy of transmembrane protein unfolding. We used two different estimators, the first based on the weighted histogram method, 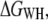Inline graphic and the second on mean force, 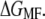Inline graphic Both performed with comparable accuracy, even though the distributions of q are not always Gaussian (also see below). In the end of the pulling interval, 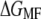Inline graphic exceeded 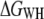Inline graphic by <2%, which can be explained by the expected bias of the former estimator (26).

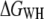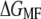We showed that the free energy for unfolding BR is independent of pulling rate in the range between 654 and 2620 nm/s and temperature range between 18 and 42°C. This result demonstrates that Inline graphic and Inline graphic values indeed reflect equilibrium properties. BR is an interesting model system to study temperature effects, since neither significant changes in protein structure nor a change in heat capacity were detected for native BR membranes within physiological temperature ranges (6,7,32,42). Thus, a temperature-independent unfolding free energy is not surprising and may serve as an additional validation of the method presented here.

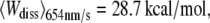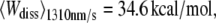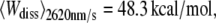The probability densities of the dissipated work during the unfolding of helices E and D of BR were calculated and compared for different pulling velocities. The expectation values increased from Inline graphic over Inline graphic to Inline graphic reflecting that additional work is dissipated as a result of friction when the molecule is unfolded more rapidly. The free energy required to unfold this helical pair (E and D) was 83.3 ± 8.4 kcal/mol (mean ± SD). In 2001, Hummer and Szabo (24) applied their formalism to linear approximations of force-distance curves of these helices recorded in a different experiment (13). Their value of 64 kcal/mol compares well with our result, and the difference can be attributed to the simplification of the shape of the force-distance curves as well as experimental uncertainties. When averaged over all different pulling rates and temperatures, 226.8 ± 38.2 kcal/mol (mean ± SD) were required to unfold BR (neglecting helices G and F). This value corresponds to a free energy of ∼1.32 kcal/mol per amino acid residue (171 aa). Because unspecific interactions between AFM tip and membrane surface overlapped with the unfolding data at extensions below 18 nm, the energetic contribution of the first helical pair (G and F) could not be reliably calculated. Therefore, an estimation of the total free energy of an entire BR molecule can be given using the number of amino acids of the first helical pair (48 aa) and the average free energy per residue, resulting in 63.7 kcal/mol. In this way, an estimate of 290.5 ± 48.9 kcal/mol was obtained for the entire BR molecule.

Despite the obvious differences in the measurement principles, our results compare well to biochemical ensemble experiments where the denaturation of BR is accompanied by an enthalpy of 100–179 kcal/mol, depending on the method of measurement (8). Typical contributions to the denaturation energy include hydrophobicity and hydrogen-bond interactions. Using the position-independent amino acid hydrophobicity scale introduced by White and Wimley (8), we estimated the cumulative transfer energy of all residues of each helix of BR into the membrane core and interface resulting in values between −15.7 and 3.9 kcal/mol (Supplementary Material). Assuming 5 kcal/mol for the stability of a single hydrogen bond within the membrane (8) and 40 hydrogen bonds per helix, a contribution of ∼200 kcal/mol per helix was estimated. Our experimental values (∼30 kcal/mol per helix) lie between these two extremes and clearly, other contributions (e.g., intrahelical hydrogen-bonding and interhelix contacts) need to be considered in a more detailed analysis.

The mean force of BR shows three main unfolding events located at 25, 38, and 58 nm (Fig. 2 b). In comparison to the nonequilibrium unfolding traces, no shoulder peaks between the main peaks are observed. This finding is in good agreement with a recent study (18) where a smaller occurrence of the shoulder peaks was observed upon reducing the pulling rate, i.e., working closer to equilibrium. We also noticed that the work distribution of helices E and D appears multimodal (Fig. 3 c). In one of these cases (v = 2620 nm/s), all unfolding traces were recorded in a single experiment, suggesting that the observed subpopulations may not be attributed to instrumental uncertainties. In this context, we would like to point out that these helices play a crucial role in intermonomeric interactions in the purple membrane trimers. Thus, one could speculate that the subpopulations may represent the unfolding of BR monomers in trimers where one or two monomers are already unfolded. A similar multimodal distribution of relative unfolding forces of helices E and D was recently observed using a different data analysis approach (43).

As shown in Fig. 5 b, the total unfolding free energy for HR was in the same range as for BR. The obtained value to extract and unfold HR (neglecting helices G and F) was 162.3 ± 2.7 kcal/mol, corresponding to 0.92 kcal/mol per amino acid (176 aa). By estimating the energy of the first helical pair (helices G and F; 47 aa), a total free energy of 205.7 ± 3.3 kcal/mol can be obtained for the entire HR unfolding. However, the unfolding of helices E and D of HR occurs in two well-separated steps (Fig. 5 b, arrows), in contrast to that of BR. Cisneros et al. (16) recently addressed this point and showed that the structure of HR resembles that of BR, but with one difference: HR exhibits an additional pi-bulk interaction that splits helix E into two structurally distinct segments. The splitting of the force peak of helix E was observed in the unfolding curves (Fig. 5 a) with high probability (80%) (16). Accordingly, we can attribute the splitting of the mean force of helices E and D of HR (Fig. 5 b, arrows) to the stepwise unfolding of the helix and an energy step of ∼24 kcal/mol. This example highlights that the combination of single-molecule manipulation and the Jarzynski equality is capable of detecting the stability of individual helices in terms of a unique signature in the energy profile.

Finally, we derived the unfolding free energy of the sodium-proton antiporter NhaA (Fig. 5 d). The energy required to unfold the five helical pairs was 410.4 ± 5.1 kcal/mol, corresponding to ∼1.25 kcal/mol per amino acid (328 aa). By estimating the first helical pair (helices XII and XI, 60 aa), a total free energy of 485.0 ± 6.0 kcal/mol was obtained for NhaA unfolding, which lies significantly above the free energies revealed for BR and HR. It is interesting to note that NhaA shows a markedly different mean force profile (Fig. 5 d) compared to the nonequilibrium force traces (Fig. 5 c). In the nonequilibrium case, a series of more or less regularly spaced force peaks with comparable intensities are observed (15), whereas the mean-force curve emphasizes a central region of the spectrum centered around an intensive peak located at ∼65 nm. Recent ensemble (44) and single-molecule (34,45) activation and inhibition experiments reported that this location can be correlated to the functionally important residues in helix V.

CONCLUSIONS

Mechanical single-molecule experiments are powerful tools to probe the stability and (near-equilibrium) refolding of single- and multispan membrane proteins (46–49). Here, for the first time that we know of, we determined the free energy differences associated with the mechanical unfolding of three multispan membrane proteins. The free-energy differences revealed from our approach reflect the overall stability of the proteins, including the extraction and unfolding of membrane helices with contributions from hydrophobic interactions, hydrogen bonds, and helix-helix contacts. Future developments will yield approaches that may separate the individual contributions of different types of molecular interactions that guide the (un-)folding, (de-)stabilization, and functional state of membrane proteins.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

Supplementary Material

[Supplement]
biophysj_106.096982_index.html (817B, html)

Acknowledgments

We thank S. White and two anonymous reviewers for constructive comments.

This work was supported by the Deutsche Forschungsgemeinschaft (DFG) and the European Union.

Editor: Jane Clarke.

References

  • 1.Wallin, E., and G. von Heijne. 1998. Genome-wide analysis of integral membrane proteins from eubacterial, archaean, and eukaryotic organisms. Protein Sci. 7:1029–1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Bowie, J. U. 2005. Solving the membrane protein folding problem. Nature. 438:581–589. [DOI] [PubMed] [Google Scholar]
  • 3.Sadlish, H., D. Pitonzo, A. E. Johnson, and W. R. Skach. 2005. Sequential triage of transmembrane segments by Sec61α during biogenesis of a native multispanning membrane protein. Nat. Struct. Mol. Biol. 12:870–878. [DOI] [PubMed] [Google Scholar]
  • 4.Chen, G. Q., and E. Gouaux. 1999. Probing the folding and unfolding of wild-type and mutant forms of bacteriorhodopsin in micellar solutions: evaluation of reversible unfolding conditions. Biochemistry. 38:15380–15387. [DOI] [PubMed] [Google Scholar]
  • 5.Cladera, J., M. L. Galisteo, M. Sabes, P. L. Mateo, and E. Padros. 1992. The role of retinal in the thermal stability of the purple membrane. Eur. J. Biochem. 207:581–585. [DOI] [PubMed] [Google Scholar]
  • 6.Shnyrov, V. L., and P. L. Mateo. 1993. Thermal transitions in the purple membrane from Halobacterium halobium. FEBS Lett. 324:237–240. [DOI] [PubMed] [Google Scholar]
  • 7.Taneva, S. G., J. M. Caaveiro, A. Muga, and F. M. Goni. 1995. A pathway for the thermal destabilization of bacteriorhodopsin. FEBS Lett. 367:297–300. [DOI] [PubMed] [Google Scholar]
  • 8.White, S. H., and W. C. Wimley. 1999. Membrane protein folding and stability: physical principles. Annu. Rev. Biophys. Biomol. Struct. 28:319–365. [DOI] [PubMed] [Google Scholar]
  • 9.Hessa, T., H. Kim, K. Bihlmaier, C. Lundin, J. Boekel, H. Andersson, I. Nilsson, S. H. White, and G. von Heijne. 2005. Recognition of transmembrane helices by the endoplasmic reticulum translocon. Nature. 433:377–381. [DOI] [PubMed] [Google Scholar]
  • 10.Rief, M., and H. Grubmuller. 2002. Force spectroscopy of single biomolecules. Chem. Phys. Chem. 3:255–261. [DOI] [PubMed] [Google Scholar]
  • 11.Janshoff, A., M. Neitzert, Y. Oberdorfer, and H. Fuchs. 2000. Force spectroscopy of molecular systems. Single-molecule spectroscopy of polymers and biomolecules. Angew. Chem. Int. Ed. Engl. 39:3212–3237. [DOI] [PubMed] [Google Scholar]
  • 12.Bustamante, C., Y. R. Chemla, N. R. Forde, and D. Izhaky. 2004. Mechanical processes in biochemistry. Annu. Rev. Biochem. 73:705–748. [DOI] [PubMed] [Google Scholar]
  • 13.Oesterhelt, F., D. Oesterhelt, M. Pfeiffer, A. Engel, H. E. Gaub, and D. J. Muller. 2000. Unfolding pathways of individual bacteriorhodopsins. Science. 288:143–146. [DOI] [PubMed] [Google Scholar]
  • 14.Muller, D. J., M. Kessler, F. Oesterhelt, C. Moller, D. Oesterhelt, and H. Gaub. 2002. Stability of bacteriorhodopsin α-helices and loops analyzed by single-molecule force spectroscopy. Biophys. J. 83:3578–3588. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Kedrov, A., C. Ziegler, H. Janovjak, W. Kühlbrandt, and D. J. Muller. 2004. Controlled unfolding and refolding of a single sodium-proton antiporter using atomic force microscopy. J. Mol. Biol. 340:1143–1152. [DOI] [PubMed] [Google Scholar]
  • 16.Cisneros, D. A., D. Oesterhelt, and D. J. Muller. 2005. Probing origins of molecular interactions stabilizing the membrane proteins halorhodopsin and bacteriorhodopsin. Structure. 13:235–242. [DOI] [PubMed] [Google Scholar]
  • 17.Kienberger, F., G. Kada, H. Mueller, and P. Hinterdorfer. 2005. Single molecule studies of antibody-antigen interaction strength versus intra-molecular antigen stability. J. Mol. Biol. 347:597–606. [DOI] [PubMed] [Google Scholar]
  • 18.Janovjak, H., J. Struckmeier, M. Hubain, A. Kedrov, M. Kessler, and D. J. Muller. 2004. Probing the energy landscape of the membrane protein bacteriorhodopsin. Structure. 12:871–879. [DOI] [PubMed] [Google Scholar]
  • 19.Muller, D. J., H. Janovjak, T. Lehto, L. Kuerschner, and K. Anderson. 2002. Observing structure, function and assembly of single proteins by AFM. Prog. Biophys. Mol. Biol. 79:1–43. [DOI] [PubMed] [Google Scholar]
  • 20.Dietz, H., and M. Rief. 2004. Exploring the energy landscape of GFP by single-molecule mechanical experiments. Proc. Natl. Acad. Sci. USA. 101:16192–16197. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Dill, K. A., and H. S. Chan. 1997. From Levinthal to pathways to funnels. Nat. Struct. Biol. 4:10–19. [DOI] [PubMed] [Google Scholar]
  • 22.Bryngelson, J. D., J. N. Onuchic, N. D. Socci, and P. G. Wolynes. 1995. Funnels, pathways, and the energy landscape of protein folding: a synthesis. Proteins. 21:167–195. [DOI] [PubMed] [Google Scholar]
  • 23.Jarzynski, C. 1997. Nonequillibrium equality for free energy differences. Phys. Rev. Lett. 78:2690–2693. [Google Scholar]
  • 24.Hummer, G., and A. Szabo. 2001. Free energy reconstruction from nonequilibrium single-molecule pulling experiments. Proc. Natl. Acad. Sci. USA. 98:3658–3661. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Liphardt, J., S. Dumont, S. B. Smith, I. Tinoco, Jr., and C. Bustamante. 2002. Equilibrium information from nonequilibrium measurements in an experimental test of Jarzynski's equality. Science. 296:1832–1835. [DOI] [PubMed] [Google Scholar]
  • 26.Hummer, G., and A. Szabo. 2005. Free energy surfaces from single-molecule force spectroscopy. Acc. Chem. Res. 38:504–513. [DOI] [PubMed] [Google Scholar]
  • 27.Kessler, M., K. E. Gottschalk, H. Janovjak, D. J. Muller, and H. E. Gaub. 2006. Bacteriorhodopsin folds into the membrane against an external force. J. Mol. Biol. 357:644–654. [DOI] [PubMed] [Google Scholar]
  • 28.Kedrov, A., H. Janovjak, C. Ziegler, W. Kuhlbrandt, and D. J. Muller. 2006. Observing folding pathways and kinetics of a single sodium-proton antiporter from Escherichia coli. J. Mol. Biol. 355:2–8. [DOI] [PubMed] [Google Scholar]
  • 29.Luecke, H., B. Schobert, H. T. Richter, J. P. Cartailler, and J. K. Lanyi. 1999. Structure of bacteriorhodopsin at 1.55 Å resolution. J. Mol. Biol. 291:899–911. [DOI] [PubMed] [Google Scholar]
  • 30.Kolbe, M., H. Besir, L. O. Essen, and D. Oesterhelt. 2000. Structure of the light-driven chloride pump halorhodopsin at 1.8 Å resolution. Science. 288:1390–1396. [DOI] [PubMed] [Google Scholar]
  • 31.Hunte, C., E. Screpanti, M. Venturi, A. Rimon, E. Padan, and H. Michel. 2005. Structure of a Na+/H+ antiporter and insights into mechanism of action and regulation by pH. Nature. 435:1197–1202. [DOI] [PubMed] [Google Scholar]
  • 32.Janovjak, H., H. Knaus, and D. J. Muller. 2007. Transmembrane helices have rough energy surfaces. J. Am. Chem. Soc. 129:246–247. [DOI] [PubMed] [Google Scholar]
  • 33.Kuhn, M., H. Janovjak, M. Hubain, and D. J. Muller. 2005. Automated alignment and pattern recognition of single-molecule force spectroscopy data. J. Microsc. 218:125–132. [DOI] [PubMed] [Google Scholar]
  • 34.Kedrov, A., M. Krieg, C. Ziegler, W. Kuhlbrandt, and D. J. Muller. 2005. Locating ligand binding and activation of a single antiporter. EMBO Rep. 6:668–674. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Press, W. H., S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. 1988. Numerical Recipes in C. Cambridge University Press, Cambridge, UK.
  • 36.Bowman, A. W., and A. Azzalini. 1997. Applied Smoothing Techniques for Data Analysis. Oxford University Press, Oxford, UK.
  • 37.Burnham, N. A., X. Chen, C. S. Hodges, G. A. Matei, E. J. Thoreson, C. J. Roberts, M. C. Davies, and S. J. B. Tendler. 2003. Comparison of calibration methods for atomic-force microscopy cantilevers. Nanotechnology. 14:1–6. [Google Scholar]
  • 38.Muller, D. J., J. B. Heymann, F. Oesterhelt, C. Moller, H. Gaub, G. Buldt, and A. Engel. 2000. Atomic force microscopy of native purple membrane. Biochim. Biophys. Acta. 1460:27–38. [DOI] [PubMed] [Google Scholar]
  • 39.Schwaiger, I., M. Schleicher, A. A. Noegel, and M. Rief. 2005. The folding pathway of a fast-folding immunoglobulin domain revealed by single-molecule mechanical experiments. EMBO Rep. 6:46–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Rief, M., M. Gautel, F. Oesterhelt, J. M. Fernandez, and H. E. Gaub. 1997. Reversible unfolding of individual titin immunoglobulin domains by AFM. Science. 276:1109–1112. [DOI] [PubMed] [Google Scholar]
  • 41.Marszalek, P. E., H. Lu, H. Li, M. Carrion-Vazquez, A. F. Oberhauser, K. Schulten, and J. M. Fernandez. 1999. Mechanical unfolding intermediates in titin modules. Nature. 402:100–103. [DOI] [PubMed] [Google Scholar]
  • 42.Janovjak, H., M. Kessler, D. Oesterhelt, H. Gaub, and D. J. Muller. 2003. Unfolding pathways of native bacteriorhodopsin depend on temperature. EMBO J. 22:5220–5229. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Janovjak, H., K. T. Sapra, and D. J. Muller. 2005. Complex stability of single proteins explored by forced unfolding experiments. Biophys. J. 88:L37–L39. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Inoue, H., T. Noumi, T. Tsuchiya, and H. Kanazawa. 1995. Essential aspartic acid residues, Asp-133, Asp-163 and Asp-164, in the transmembrane helices of a Na+/H+ antiporter (NhaA) from Escherichia coli. FEBS Lett. 363:264–268. [DOI] [PubMed] [Google Scholar]
  • 45.Kedrov, A., C. Ziegler, and D. J. Muller. 2006. Differentiating ligand and inhibitor interactions of a single antiporter. J. Mol. Biol. 362:925–932. [DOI] [PubMed] [Google Scholar]
  • 46.Kedrov, A., H. Janovjak, K. T. Sapra, and D. J. Muller. 2007. Deciphering molecular interactions of native membrane proteins by single-molecule force spectroscopy. Annu. Rev. Biophys. Biomol. Struct. 36:233–260. [DOI] [PubMed] [Google Scholar]
  • 47.Janovjak, H., A. Kedrov, D. A. Cisneros, K. T. Sapra, J. Struckmeier, and D. J. Muller. 2006. Imaging and detecting molecular interactions of single transmembrane proteins. Neurobiol. Aging. 27:546–561. [DOI] [PubMed] [Google Scholar]
  • 48.Contera, S. A., V. Lemaitre, M. R. de Planque, A. Watts, and J. F. Ryan. 2005. Unfolding and extraction of a transmembrane α-helical peptide: dynamic force spectroscopy and molecular dynamics simulations. Biophys. J. 89:3129–3140. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 49.Ganchev, D. N., D. T. Rijkers, M. M. Snel, J. A. Killian, and B. de Kruijff. 2004. Strength of integration of transmembrane α-helical peptides in lipid bilayers as determined by atomic force spectroscopy. Biochemistry. 43:14987–14993. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplement]
biophysj_106.096982_index.html (817B, html)
biophysj_106.096982_1.pdf (95.1KB, pdf)
biophysj_106.096982_96982_Supplementary_Reference_02April2007.doc (23.5KB, doc)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES