Two Stereoisomers of Spheroidene in the Rhodobacter sphaeroides R26 Reaction Center: A DFT Analysis of Resonance Raman Spectra

Abstract

From a theoretical analysis of the resonance Raman spectra of 19 isotopomers of spheroidene reconstituted into the reaction center (RC) of Rhodobacter sphaeroides R26, we conclude that the carotenoid in the RC occurs in two configurations. The normal mode underlying the resonance Raman transition at 1239 cm⁻¹, characteristic for spheroidene in the RC, has been identified and found to uniquely refer to the cis nature of the 15,15′ carbon-carbon double bond. Detailed analysis of the isotope-induced shifts of transitions in the 1500–1550 cm⁻¹ region proves that, besides the 15,15′-cis configuration, spheroidene in the RC adopts another cis-configuration, most likely the 13,14-cis configuration.

INTRODUCTION

Carotenoids in the membranes of purple photosynthetic bacteria are found both in the light-harvesting complexes and in the photosynthetic reaction centers (RC) (1,2). For anaerobically grown Rhodobacter sphaeroides wild-type strain 2.4.1, the carotenoid bound to the RC is spheroidene (3). It takes part in light harvesting and protects the bacteriochlorophyll pigments from photodestruction by preventing the formation of singlet oxygen (1,4).

Spheroidene in the light-harvesting complexes is known to occur in the all-trans form (5,6). As early as 1976, Lutz et al. suggested on the basis of resonance Raman scattering that in the RC, spheroidene adopts a cis conformation (5), probably 15,15′-cis (7). They studied spheroidene reconstituted in the carotenoidless R26 Rb. sphaeroides RC. The latter was shown to have the same characteristics and structure after reconstitution as the wild-type RC, which naturally contains spheroidene (8–11). Lutz et al. (12) later combined resonance Raman and ¹H-NMR spectroscopy on spheroidene extracted from the RC to conclude that the RC contained 15,15′-cis spheroidene. To determine the precise location of the cis bond in the conjugated system, Koyama et al. (13,14) compared resonance Raman data for the RC and various cis-isomers of β-carotenes. De Groot et al. (15) relied on the same principle for the interpretation of ¹³C magic angle spinning NMR data of the RC. Such investigations have indicated with increasing confidence that spheroidene adopts a 15,15′-cis conformation. Bautista et al. (16) demonstrated that the natural selection of a cis-isomer of spheroidene for incorporation into RCs is mainly determined by the actual structure of the RCs. The crystallization and x-ray diffraction of the Rb. sphaeroides RC allowed for ever more accurate determination of the structure of the RC (11,17–20). The resolution of the derived electron density maps around the spheroidene molecule, however, does not suffice to unequivocally determine the structure of the carotenoid. As late as 2000, McAuley et al. (20) considered the 13,14-cis conformer as a possible (though less likely) fit of their data.

To understand the function of spheroidene in the photophysical cycle of the photosynthetic complex, one needs to know its structure. Despite the impressive indirect evidence of the 15,15′-cis conformer occurring in the RC, this configuration still remains to be observed directly. Some time ago, we embarked on a project that involves (1) the synthesis of specific ¹³C and ²H labeled spheroidenes, (2) the reconstitution of these spheroidenes into the R26 RC, and (3) recording resonance Raman spectra of the spheroidene isotopomers both in solution and bound to the RC. We have reported the spectra for a range of ¹³C and ²H labeled spheroidenes in earlier articles (21,22). Since then we have measured the spectra of many more isotopomers of spheroidene in the RC. Recently, we have also demonstrated that a complete description of the resonance Raman spectra of isotope labeled all-trans-spheroidene in solution could be obtained, using DFT geometry optimization and frequency calculations (23). This success has inspired confidence that we can use the same theoretical approach to analyze the resonance Raman spectra of the spheroidene isotopomers in the R26 RC, to learn more about the structure of the carotenoid.

In this article, we report on the progress we have made using DFT analysis for determining the structure of spheroidene in the RC. In our attempts to reproduce the experimental spectra, we have calculated spectra for a variety of structures and isotopomers. Our analysis will demonstrate that the RC must contain nonplanar 15,15′-cis spheroidene. If we suppose that all spheroidene in the RC exists in the 15,15′-cis configuration, we cannot explain all isotope-induced shifts, particularly in the 1500–1550 cm⁻¹ region. Another configuration, probably 13,14-cis, also occurs in significant proportion.

Before commencing with the DFT analysis of the resonance Raman spectra of spheroidene in the RC, we present certain relevant experimental details and will briefly discuss several representative spectra. The computational methods used to optimize the molecular geometries and calculate the normal modes and frequencies are described afterwards.

RESONANCE RAMAN SPECTRA

The synthesis of isotope-labeled spheroidenes and their reconstitution into the Rhodobacter sphaeroides R26 photosynthetic reaction center have been described in previous publications (24–27). Resonance Raman spectra of spheroidene in the reaction centers (RC) were obtained in a bath cryostat at 1.8 K from a glass of 30–50% glycerol and the RC/Tris-buffer solution. In addition to the natural abundance (NA) spectrum we have determined the spectra for a total of 18 isotopomers of reconstituted spheroidene, 11 labeled with ²H and 7 labeled with ¹³C. These isotopomers are: 10-²H, 11-²H, 12-²H, 14-²H, 15-²H, 15′-²H, 14′-²H, 11′-²H, 10,12-²H₂, 12,14-²H₂, 15,15′-²H₂, 8-¹³C, 10-¹³C, 11-¹³C, 13-¹³C, 15′-¹³C, 14′-¹³C, and 13,14-¹³C₂.

For the resonance Raman measurements we excited at 496.5 nm, in resonance with the first allowed π* ← π (S₂ ← S₀) transition. Only transitions corresponding to vibrational modes that contain conjugated C–C or C=C stretch character are resonance-enhanced in the spectra. For the normal-mode analysis we consider a truncated structure, comprising the C₃ to C_9′ part of the molecule (see Fig. 1) terminated by carbon atoms that were assigned the masses of the corresponding terminal groups (87 and 151 for C₅H₉O and C₁₁H₁₇, respectively). This truncation is justified by the fact that the modes in the outer parts of the molecules are decoupled from those in the conjugated part of the molecule. This theoretical consideration has been corroborated for all-trans spheroidene. Calculations on all-trans spheroidene showed no new modes in the relevant frequency ranges, hardly any change of mode-character, and shifts of only a few wavenumbers as compared to calculations on the corresponding truncated molecule. Fig. 1 contains a schematic representation of spheroidene and explains our labeling. For simplicity, spheroidene is shown in the all-trans form.

FIGURE 1.

Schematic representation of the spheroidene molecule and our labeling system. The molecule is shown in the all-trans form. The conjugated part of spheroidene is indicated between dashed lines.

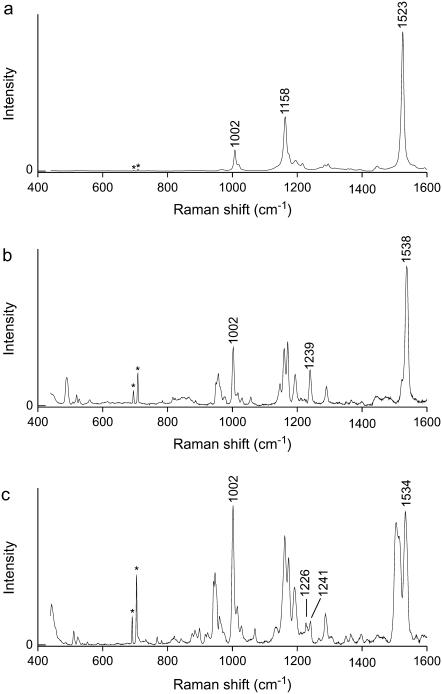
In Fig. 2 the resonance Raman spectra in the range 400–1600 cm⁻¹ are displayed for NA spheroidene in petroleum ether, and NA and 15,15′-²H₂ labeled spheroidene in the R26 reaction center. Three regions can be recognized in the spectrum of all-trans spheroidene in Fig. 2 a. Between 1500 and 1600 cm⁻¹ transitions are seen that correspond to C=C stretch vibrations. The so-called fingerprint region between 1100 and 1300 cm⁻¹ is where normal modes comprising stretch vibrations of C–C bonds and in-plane H-bend vibrations are found. In the region at ∼1000 cm⁻¹, there is a band at 1002 cm⁻¹, which belongs to a normal mode composed of methyl-rock vibrations. The absence of out-of-plane H-bend transitions, normally found at ∼950 cm⁻¹, indicates that this structure is planar. For planar spheroidene, symmetry rules forbid the mixing of out-of-plane modes with the C–C and C=C stretch modes, and they cannot gain intensity in the resonance Raman spectrum.

FIGURE 2.

Resonance Raman spectra of (a) NA spheroidene in petroleum ether, and (b) NA spheroidene and (c) 15,15′-²H₂ spheroidene in the photosynthetic reaction center of Rb. sphaeroides. Peaks denoted with * are argon plasma lines.

The spectra of the spheroidenes in the RC in Fig. 2 do clearly show out-of-plane H-bend transitions at ∼950 cm⁻¹, and hence these spheroidene structures cannot be planar. In general, these two spectra are much richer in transitions in all three aforementioned regions than the spectrum in Fig. 2 a. In the fingerprint region, among the signals that stand out in comparison to the all-trans spectrum, we see one or several bands at or slightly below 1240 cm⁻¹. In the C=C stretch region we see two or more transitions appear.

The spectrum for NA spheroidene in the RC displays an intense C=C stretch band at 1538 cm⁻¹ with a clear shoulder at 1523 cm⁻¹. The peak at 1538 cm⁻¹ has a width of 11 cm⁻¹, which could indicate the presence of two overlapping transitions. The shift of the most intense transition to a higher frequency for spheroidene in the RC with respect to all-trans-spheroidene (1523 cm⁻¹) is larger than expected upon introducing a cis double bond in the conjugated part of the molecule. Such upward shifts are related to a reduced conjugation length and are normally found to be ∼10 cm⁻¹ for β-carotenes (13,14,28). The fact that the most intense peak shifts upward by 16 cm⁻¹ is most probably due to the nonplanarity of the structure of RC spheroidene. In Fig. 2 c, more than the aforementioned two bands are apparent in the region between 1500 and 1540 cm⁻¹. This is also the case for many other isotopomers of spheroidene in the RC, most notably all those labeled at or somewhere between chain positions 11 and 14′. We have checked the possibility that C=C stretch signals arise from residual isotope-labeled all-trans spheroidene present in our samples. Careful comparison of the spectra of spheroidene isotopomers in the RC and in petroleum ether has shown that this is not the case. The positions of transitions and distinct shoulders in the C=C stretch regions of the resonance Raman spectra displayed in Fig. 2, as well as for all other isotopomers, are listed in Table 1. For some isotopomers, denoted with an asterisk symbol in Table 1, the spectra display broad peaks in this region as a result of the close proximity of various transitions. The overlap of signals therefore prohibits the determination of the precise frequencies associated with these transitions. Note that this is not a consequence of limited resolution of our monochromator, but of the intrinsic width of the signals associated with molecular transitions. For the marked isotopomers the peak width (FWHM) is given in the caption of Table 1. The width of a single transition is ∼8 cm⁻¹, so any significantly broader band in principle consists of more than one transition. Some of the indicated spectra will be treated in more detail in the discussion of the normal-mode analysis.

TABLE 1.

This table lists the positions and intensities for peaks and visible shoulders in the C=C stretch regions of the experimental resonance Raman spectra of spheroidene in the RC

					Calc. C=C str. frequency
Isotopomer	Experimental C=C stretch frequencies (% max int.)				15,15′-cis		13,14-cis
NA	1523 (19)		1538 (100)		1525	1537	1526	1539
8-13C	1524 (100)	1533 (55)	1538 (29)	1550 (19)	1523	1535	1525	1532
10-2H*	1534 (100)				1525	1531	1523	1539
10-13C*	1518 (100)				1525	1528	1522	1539
11-2H	1516 (54)	1529 (100)	1540 (46)		1516	1534	1524	1528
11-13C	1519 (76)	1528 (100)			1517	1536	1525	1529
12-2H*	1524 (100)				1519	1534	1519	1531
13-13C	1524 (93)	1528 (100)	1537 (81)		1522	1529	1512	1539
14-2H	1522 (26)	1532 (100)			1523	1531	1516	1539
15-2H	1514 (26)	1529 (100)	1535 (87)		1517	1535	1524	1529
15′-2H	1514 (22)	1529 (100)	1537 (82)		1517	1537	1525	1531
15′-13C	1508 (11)	1522 (32)	1539 (100)		1511	1537	1522	1533
14′-2H*	1520 (25)	1531 (100)	1535 (86)	1541 (34)	1523	1535	1523	1538
14′-13C*	1529 (100)		1534 (85)	1555 (10)	1525	1533	1521	1539
11′-2H	1528 (51)		1538 (100)		1523	1537	1525	1537
10,12-2H2*	1518 (100)				1517	1530	1516	1531
12,14-2H2*	1519 (100)				1514	1530	1509	1530
15,15′-2H2	1506 (92)	1515 (81)	1534 (100)	1551 (9)	1506	1535	1514	1524
13,14-13C2	1505 (40)	1511 (90)	1526 (78)	1539 (100)	1514	1526	1499	1539

The intensity value between brackets is proportional to the most intense peak in the spectrum. The calculated frequencies in the last four columns concern 15,15′-cis spheroidene and 13,14-cis spheroidene.

^*Due to the proximity of transitions, a single experimental peak is found for which assignments of maxima and shoulders are tentative or even impossible. The widths (FWHM) are: 10-²H 16 cm⁻¹, 10-¹³C 18 cm⁻¹, 12-²H 17 cm⁻¹, 14′-²H 14 cm⁻¹, 14′-¹³C 20 cm⁻¹, 10,12-²H₂ 18 cm⁻¹, and 12,14-²H₂ 18 cm⁻¹.

COMPUTATIONAL METHODS

In a previous article we described our method for the calculation and subsequent analysis of the resonance Raman spectra of spheroidene in solution (23). The success of our method in quantitatively describing the resonance Raman spectra of a large conjugated molecule like all-trans-spheroidene makes us confident that this method can also be applied to analyze cis-spheroidene bound to the RC. Furthermore, we have performed test calculations on 9- and 11-cis-retinal and found that the calculated frequencies agree well with experimental resonance Raman frequencies (28). The spectra are calculated in four steps:

Step 1: Geometry optimization

The Gaussian 98 package, Rev. A.5 on an IBM SP2 computer, and later the Gaussian 03 package, Rev. B.05 (29) were used for performing the DFT calculations on a Beowulf cluster consisting of 17 nodes each equipped with two 1.7 GHz Intel Xeon processors. We used a 6-31G* basis set combined with the hybrid B3LYP functional. Geometry optimization was done in Cartesian coordinates and carried out with the Berny algorithm and an ultra-fine integration grid for numerical calculation of the two-electron integrals.

Our starting structure was taken from the x-ray structure of the reaction center as determined by McAuley et al. (20) for a mutant bacterium at a resolution of 2.1 Å. This structure is deposited in the RSCB Protein DataBank as 1QOV. The Rb. sphaeroides bacterium whose RC was studied by McAuley et al. (20) was grown under semiaerobic conditions in the dark and therefore the bound carotenoid is actually spheroidenone (C₄₁H₅₈O₂) instead of spheroidene (C₄₁H₆₀O₁). Spheroidenone contains an additional carbonyl group bound to C-atom 2 (see Fig. 1). The carbonyl group does not appear to interact with the surrounding protein (20) so as to significantly affect the spheroidenone configuration compared to that of spheroidene. The conjugated part of the spheroidenone structure upon which we have based our calculations can therefore be considered the same as that of spheroidene.

As mentioned in Resonance Raman Spectra, the presence of out-of-plane H-bends in the resonance Raman spectra of incorporated spheroidenes indicates that the molecule cannot be planar. Geometry optimizations of isolated 15,15′-cis spheroidene all resulted in a planar structure, due to the absence of a protein scaffold. To prevent the DFT optimized structures from becoming planar we have fixed the Cartesian coordinates of C-atoms of methyl groups in our calculations. These coordinates were taken from the x-ray file.

Step 2: Calculation of Hessian

Numerical calculation of the Hessian in Cartesian coordinates and transformation to mass-weighted coordinates, using Gaussian 98 or Gaussian 03 with the Freq(ReadIsotopes) keyword and option.

Step 3: Calculation of normal modes

Calculation of the normal modes and corresponding frequencies for all isotopomers, using the Wilson GF formalism. In this article we refer to calculated spectra for spheroidene containing only the most abundant isotopes ¹H and ¹²C as natural abundance (NA) spectra, despite the fact that in actuality naturally occurring carbon contains 1.1% ¹³C and hydrogen 0.015% ²H. The DFT calculated frequencies are scaled by a factor of 0.963 (30).

Step 4: Estimation of resonance Raman intensities

We estimated the intensity of a normal mode I_a according to Eq. 1:

(1)

In this equation, which is only an approximation (23,31), ν_α is the frequency of normal mode α, A represents the transformation matrix from internal into normal coordinates that was determined in Step 3, and δ_i equals the change in internal coordinate i as a result of the (near-)resonant electronic π* ← π (HOMO to LUMO) transition.

Reproduction of the experimental frequencies for all isotopomers is, in fact, the most significant indicator that we have obtained a correct molecular structure. For this reason, the primary goal of our work was to reproduce the frequencies of the experimental spectra in our calculations. The intensity estimation in Step 4 mainly served to reveal which transitions display any resonance Raman intensity at all. We have used the same set of δ_i-values (for the C–C and C=C bonds) as for all-trans-spheroidene (23). In that case, the δ_i-values were determined from the best fit between experimental and calculated resonance-Raman intensities. Later on, electronic calculations (semiempirical ZINDO method) showed that these values could be rationalized on the basis of the increase/decrease of the double-bond character of each carbon-carbon bond from the HOMO to the LUMO. Similar calculations for cis-spheroidenes revealed negligible changes compared to all-trans-spheroidene.

DFT ANALYSIS

In this section we will discuss the results from our calculations. Presently, the consensus in literature is that spheroidene in the Rb. sphaeroides photosynthetic reaction center exists in the 15,15′-cis configuration. We have therefore started our analysis from the same assumption. In our discussion we will show that, especially for the C=C stretch region, although the calculated frequencies nicely reproduce some resonance Raman bands and their shifts upon isotope substitution, other peaks remain that cannot be explained with a 15,15′-cis configuration.

C=C stretch region

As Fig. 2 and Table 1 illustrate, reconstituted NA and isotopically labeled spheroidenes in the R26 RC show two or more C=C stretch modes in the region between 1500 and 1540 cm⁻¹. For several experimental spectra the bands in this region are quite broad (>10 cm⁻¹) and probably contain more than one normal-mode peak. The relevant isotopomers have been denoted with an asterisk symbol in Table 1. In this section, we focus on how our calculations reproduce the transitions associated with C=C stretch modes.

Although Fig. 2 shows that spheroidene in the RC is not planar, we have started our calculations with a planar 15,15′-cis spheroidene configuration. The calculations, as expected, result in two NA C=C stretch frequencies that are too low, giving 1520 and 1530 cm⁻¹. The earlier work on all-trans-spheroidene also revealed two C=C stretch normal modes, visible as distinct transitions only in the spectra of some isotopomers. The two C=C stretch modes were shown by Dokter et al. (23) to consist of two in-phase combinations, one containing stretch vibrations of double bonds that are substituted with a methyl group, and one containing stretch vibrations of unsubstituted C=C bonds. The calculations for cis-spheroidene yield similar mode compositions, except that already for NA they are calculated at more separated frequencies. For planar 15,15′-cis spheroidene, the mode at 1520 cm⁻¹ corresponds to the normal mode that comprises unsubstituted local C=C stretch modes and the mode at 1530 cm⁻¹ to the normal mode that consists of a linear combination of local methyl-substituted C=C stretch modes. For brevity, we will, in the following discussion, refer to the former as the C=C stretch mode and the latter as the Me–C=C stretch mode.

To prevent optimized 15,15′-cis spheroidene structures from becoming planar, we have frozen the carbon positions of all five methyl groups at the coordinates found for the x-ray structure. The positions of the methyl groups show up clearly in the electron density map as protrusions, making them probable points of fixture. The nonplanar 15,15′-cis structure obtained this way yielded two NA frequencies, 1525 and 1537 cm⁻¹. The former is the C=C stretch mode and the latter the Me–C=C stretch mode. Fig. 3 shows the compositions of these two modes. As predicted, nonplanarity results in higher stretch frequencies and these correspond well with the experimental values of 1523 cm⁻¹ and 1538 cm⁻¹. No normal modes are calculated to occur in this region other than these two modes. The calculated frequencies between 1500 and 1550 cm⁻¹ for all isotopomers of this structure have been summarized in Table 1. The bond lengths, bond angles, and dihedral angles of the optimized geometry are given in Table 2 in the Supplementary Material. Our calculations invariably produce two normal modes in the C=C stretch region for each isotopomer. The experimental spectra of isotope-labeled spheroidenes in the RC, however, often show three or four bands in the C=C stretch region.

FIGURE 3.

Mode compositions for the C=C stretch (a) and Me–C=C stretch modes (b) of nonplanar 15,15′-cis spheroidene. Double bonds have been drawn as thicker sticks. Atom sizes and bond lengths have not been drawn to scale. Arrows indicate relative displacement, but are also not drawn to scale. Displacement for hydrogen atoms has been scaled down.

We have established that major changes of the structure of 15,15′-cis spheroidene (e.g., the 15=15′ bond length and the 14–15=15′–14′ dihedral angle) do not give rise to extra modes for isotope-labeled spheroidenes, although such changes do influence the position of the calculated modes in the C=C stretch region (32). Additionally, we have investigated a range of alternative configurations that might be compatible with the electron density map as determined by McAuley et al. (20) and refined by Roszak et al. (11): 13,14 cis, 13,14-15,15′-13′14′-triple-cis, and 15,15′-cis-10,11-12,13-double-s-cis. None of the calculations on these structures result in more than two bands in the C=C stretch region, again contrary to what we have observed experimentally. This discrepancy between experiment and calculation has led us to consider the possibility of spheroidene occurring in the RC simultaneously in two configurations—the second one with the cis double-bond in a position other than the 15,15′-cis configuration. Because 13,14-cis spheroidene turned out to be a good candidate, we will examine in detail the results of our DFT calculations for the 15,15′-cis and 13,14-cis configurations.

The nonplanar 13,14-cis spheroidene structure was obtained by restraining methyl groups in a similar way as for the 15,15′-cis structure discussed above. In this case, we fixed the four methyl groups at the 5,9,13 and 13′ positions. The results of the calculations are included in Table 1. For NA spheroidene, the calculated frequencies for the 13,14-cis structure come close to those for the 15,15′-cis structure and fit the experimental results almost as well. For 13,14-cis spheroidene, the calculations reveal that the low frequency mode corresponds to the Me–C=C stretch mode and the high frequency mode to the C=C stretch mode. This is the inverse of the order calculated for 15,15′-cis spheroidene. This mode reversal of course has consequences for the shift of the bands upon isotope labeling, which are most relevant for the argument in the next paragraphs.

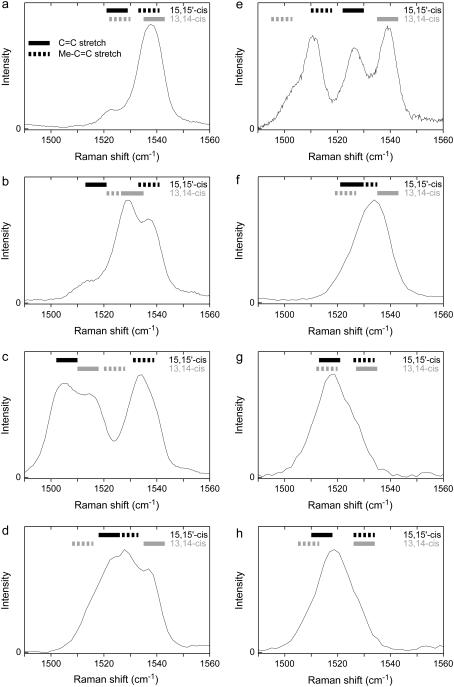
Our calculations for 15,15′-cis and 13,14-cis spheroidene show that the compositions of the C=C stretch modes for the various isotopomers remain roughly the same, while frequencies shift as expected from mass-effects upon isotope-substitution. The discussion will focus on the C=C stretch regions of the experimental spectra of NA spheroidene and seven isotopomers in the RC, as displayed in Fig. 4. These seven isotopomers have been chosen because their spectra are representative for those of all isotopomers and nicely illustrate the different shift patterns observed. Above each spectrum, 8-cm⁻¹-wide bars show the calculated frequencies from Table 1 for the respective isotopomer. Continuous bars denote C=C stretch modes and dashed bars Me–C=C stretch modes.

FIGURE 4.

The C=C stretch regions of the resonance Raman spectra of reconstituted spheroidene in the Rb. sphaeroides R26 photosynthetic reaction center. (a) NA, (b) 15′-²H, (c) 15,15′-²H₂, (d) 13-¹³C, (e) 13,14-¹³C₂, (f) 10-²H, (g) 10,12-²H₂, and (h) 12,14-²H₂. Calculated frequencies have been indicated above each spectrum by bars. Values calculated for the 15,15′-cis structure are displayed in solid representation and values for the 13,14-cis structure in shaded representation.

First, consider 15′-²H spheroidene and 15,15′-²H₂ spheroidene. The spectrum for 15′-²H spheroidene in the RC in Fig. 4 b displays at least three transitions, at 1514, 1529, and 1537 cm⁻¹. The spectrum for 15,15′-²H₂ spheroidene in the RC in Fig. 4 c also shows three transitions, at 1506, 1515, and 1534 cm⁻¹. Moreover, the signal does not approach zero at 1524 cm⁻¹, despite the fact that the maxima to either side are 19 cm⁻¹ apart. As was mentioned earlier, each transition is expected to give rise to a peak of ∼8 cm⁻¹ width (FWHM). This indicates the presence of a fourth transition at ∼1524 cm⁻¹. The maximum at 1506 cm⁻¹ for 15,15′-²H₂ spheroidene is probably a C=C stretch mode related to the one found at 1514 cm⁻¹ in the singly labeled 15′-²H spectrum, as it has shifted roughly twice as far from the NA-position. For both isotopomers, our calculations for 15,15′-cis spheroidene produce two normal modes in this spectral region, whose frequencies correspond to the two outermost signals quite well (solid bars in Fig. 4, b and c). The signal at the lowest frequency derives from the C=C normal mode, the signal at the highest frequency from the Me–C=C normal mode. The calculations on the 13,14-cis configuration produce features complementary to those for the 15,15′-cis configuration (shaded bars in Fig. 4, b and c). Due to the reversed mode structure, the signal that shifts upon ²H substitution in the 13,14-cis calculation is the opposite of that in the 15,15∼-cis calculation (see Table 1). The strong signal at 1529 cm⁻¹ for the 15′-²H isotopomer in Fig. 4 b that does not show up in the 15,15′-cis calculations is reproduced for the 13,14-cis configuration (1531 cm⁻¹). The calculated Me–C=C frequency of 1525 cm⁻¹ is not visible, but might be drowned out by the signal at 1529 cm⁻¹. The fact that the signal for the 15,15∼-²H₂ isotopomer in Fig. 4 c does not approach zero at 1524 cm⁻¹ is consistent with the Me–C=C mode calculated at 1524 cm⁻¹ for the 13,14-cis configuration.

Secondly, consider 13-¹³C spheroidene and 13,14-¹³C₂ spheroidene, both labeled on a methyl-substituted double bond. The spectrum for 13-¹³C spheroidene in the RC in Fig. 4 d shows two maxima and two shoulders. The spectrum for 13,14-¹³C₂ spheroidene in the RC in Fig. 4 e also reveals four transitions. A shoulder is clearly visible at 1505 cm⁻¹ and three distinct peaks each display a width characteristic of a single transition. For both isotopomers, our calculations for 15,15′-cis spheroidene reproduce the two innermost features in the experimental spectrum (solid bars in Fig. 4, d and e), as opposed to when we label the unsubstituted double bonds. As may be expected, the C=C stretch mode is largely unaffected by this labeling, whereas the Me–C=C mode shifts to a lower frequency. Again, the calculations on the 13,14-cis configuration reproduce the transitions visible in the spectra that have not been reproduced in the calculations for the 15,15′-cis configuration (shaded bars in Fig. 4, d and e). Although the Me–C=C stretch mode for 13,14-¹³C₂ spheroidene in the 13,14-cis configuration is calculated somewhat too low at 1499 cm⁻¹, this mode provides the explanation of the shoulder at 1505 cm⁻¹ in Fig. 4 e.

Thirdly, consider 10-²H labeled spheroidene. In Table 1, this entry was denoted with an asterisk, implying that the experimental spectrum does not allow for an unambiguous determination of the frequencies corresponding to the overlapping transitions. Fig. 4 f shows the C=C stretch region of the experimental spectrum of this isotopomer, which comprises a single peak with a maximum at 1534 cm⁻¹. The peak's width (16 cm⁻¹ FWHM) indicates that it encompasses more than a single resonance Raman transition. The calculated frequencies, 1525 and 1531 cm⁻¹ for the 15,15′-cis configuration and 1523 and 1539 cm⁻¹ for the 13,14-cis configuration, all lie within the range corresponding to the broad experimental band.

Finally, consider 10,12-²H₂ spheroidene and 12,14-²H₂ spheroidene. Their spectra in Fig. 4, g and h, illustrate another striking phenomenon in our experimental spectra. Instead of showing three or four distinct resonances over the range of 1500–1540 cm⁻¹, like for the doubly labeled 15,15′-²H₂ and 13,14-¹³C₂ spheroidenes in Fig. 4, c and e, these spectra display a relatively narrow signal at ∼1518 cm⁻¹. The 10,12-²H₂ and 12,14-²H₂ isotopomers are distinct in that they have been labeled on both a C=C and a Me–C=C band. Consistently, our calculations for these isotopomers produce nearly the same values and shifts for both the 13,14-cis and the 15,15′-cis spheroidene configurations.

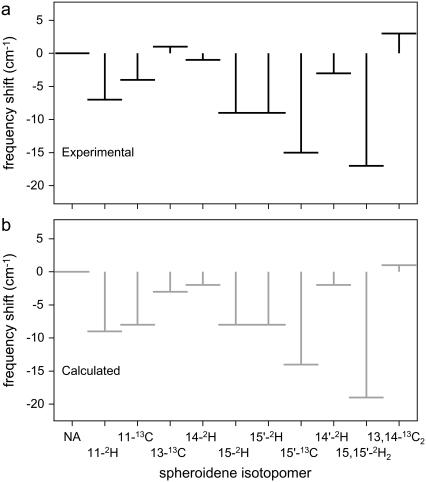
The combination of frequencies calculated for the 15,15′-cis and 13,14-cis structures of spheroidene provides a consistent description of the resonance Raman spectra of spheroidene in the RC, as summarized in Table 1 and visualized for the isotopomers in Fig. 4 by the bars above the resonance Raman signals in the carbon-carbon double-bond stretch region. The interpretation of the experimental results as originating from two structures enables us to assign specific transitions in this region of the spectra to the 15,15′-cis spheroidene, and to a C=C or Me–C=C stretch mode. Fig. 5 shows a comparison of experimental shifts of the C=C stretch mode of 15,15′-cis spheroidene to the shifts that we calculated for this mode. We have included shifts of only 11 out of 19 isotopomers. The resonance Raman spectra of the displayed isotopomers show clearly resolved transitions for the assigned mode, whereas the other spectra do not (e.g., Fig. 4, f–h). The close correspondence of the experimental and the calculated values, comparable to that found for all-trans spheroidene (23), serves to illustrate that our 15,15′-cis calculations correctly reproduce the frequencies found in the C=C stretch region of the resonance Raman spectra, as long as we assume that another spheroidene configuration is present as well. The same holds true for the Me–C=C stretch mode of 15,15′-cis spheroidene (not shown here).

FIGURE 5.

A comparison of experimental (a) and calculated (b) shifts for the C=C stretch mode of 15,15′-cis spheroidene with respect to the NA values. The experimental NA frequency is 1523 cm⁻¹ and the calculated one is 1525 cm⁻¹. Only for the isotopomers shown is it possible to assign a transition, whereas in the other spectra the C=C stretch and Me–C=C stretch modes show too much overlap.

Fingerprint region: 1150–1240 cm⁻¹

The normal modes visible in the fingerprint regions of the resonance Raman spectra (see Fig. 2 between 1150 and 1300 cm⁻¹) comprise in-plane C–C stretch and C–H bend vibrations. The spectra reveal intense signals lying close together between 1150 and 1180 cm⁻¹ for all isotopomers. Our calculations for the 15,15′-cis structure reveal several strong transitions in this region, which are delocalized throughout the conjugated part of the chain. The transitions calculated in this region are found close together and consist of many local modes. As a result, the compositions and frequencies of the calculated vibrational modes are found to be quite sensitive to even minor changes in the spheroidene structure. For this part of the spectrum, the correspondence of the calculated frequencies with the experimental spectra is less quantitative than for the C=C stretch region. This is to be expected, as it was already found to be the case for all-trans-spheroidene (23).

There is one strong transition in the NA spectrum at 1193 cm⁻¹ (Fig. 2 b), which is observed at roughly the same frequency for all isotopomers. This transition can also be seen in the spectrum of all-trans-spheroidene (Fig. 2 a). The corresponding normal mode is an in-phase combination of in-plane bend vibrations of the C–H bonds and stretch vibrations of the C–C bonds on the nonprime side of the conjugated chain (for 15,15′-cis spheroidene). Our calculations for 15,15′-cis spheroidene reproduce this transition quite well for NA (at 1189 cm⁻¹) as well as the isotope-labeled spheroidenes.

A distinctive transition observed in the resonance Raman spectra of spheroidene in the Rb. sphaeroides RC (see Fig. 2) is found at 1239 cm⁻¹ (7,12,14). For the 15,15′-cis structure we calculate a mode at 1242 cm⁻¹. Just like in the experimental NA spectrum, it is the only transition in the calculated spectrum between 1200 and 1250 cm⁻¹ with non-zero intensity. Fig. 6 shows that the normal mode calculated at 1242 cm⁻¹ consists of a linear combination of local modes in the 14–15=15′–14′ section of the spheroidene molecule. This makes it the only intense mode in the entire calculated spectrum that is not considerably delocalized across the conjugated chain. Note that a similar mode composition could not occur for a different cis-spheroidene structure, like 13,14-cis spheroidene, for example. Indeed, the occurrence of the transition at 1239 cm⁻¹ in the NA resonance Raman spectrum seems to refer uniquely to the cis nature of the 15=15′ bond.

FIGURE 6.

The composition of the normal mode corresponding to the transition calculated to occur at 1242 cm⁻¹ for the 15,15′-cis structure. The mode is composed almost exclusively of the 14′–15′ and 15–14 stretches and the C–H bend vibrations at the 15 and 15′ positions.

The calculated frequency was found to depend only weakly on the 14–15=15′–14′ dihedral angle for values between 0 and 10°. Such changes to the dihedral angle have no effect on the composition of the mode. We do expect the normal mode to be strongly influenced by ²H substitution at the 15 or 15′ positions, however, since this would significantly lower the frequencies of the local C–H bend vibrational modes. Indeed, the mode at ∼1240 cm⁻¹ disappears altogether in our calculations for 15-²H, 15′-²H, and 15,15′-²H₂ labeled spheroidene. The only mode with non-zero intensity at ∼1240 cm⁻¹ is calculated at 1223 cm⁻¹ for 15,15′-²H₂ spheroidene. A similar result is found for 15-²H and 15′-²H spheroidene. The mode at 1223 cm⁻¹ is a rather delocalized mode consisting of many different local modes. The corresponding mode is not found to have any intensity in the calculation for NA spheroidene, nor is it seen in the experimental NA spectrum. It is observed in the spectra of 15-²H, 15′-²H, and 15,15′-²H₂ labeled spheroidene, as well as for several other isotopomers for which it is also calculated. Thus far the 15,15′-cis calculations agree well with the experimental observations. Our experimental spectra, however, still show remaining signals at roughly 1240 cm⁻¹ for the 15-²H, 15′-²H, and 15,15′-²H₂ isotopomers, where our calculations do not calculate any vibrational mode. In the 15-²H and 15,15′-²H₂ spectra the transitions are considerably weaker than in all other spectra. The corresponding modes must be composed of different local modes than those constituting the mode shown in Fig. 6 and are therefore likely to be more delocalized. Since no such mode is calculated for the 15,15′-cis structure, this again provides an indication of another cis-structure present in the RC. As in the subsection on the C=C stretch region (see above), we have considered the 13,14-cis structure of spheroidene as a candidate.

In the frequency range between 1200 and 1245 cm⁻¹, the calculations for NA 13,14-cis spheroidene only produce a transition with non-zero intensity at 1209 cm⁻¹. This transition does not appear in the experimental NA spectrum. It is observed, however, in the spectra of 8-¹³C, 10-²H, 11-²H, 11-¹³C, 13-¹³C, 15-²H, 14′-¹³C, 11′-²H, 13,14-¹³C₂, and 15′-²H labeled spheroidene, for which the transition is also calculated with considerable intensity. The fact that our calculations do not produce a transition at ∼210 cm⁻¹ for the 15,15′-cis structure suggests that the calculations for the two structures are complementary, as was the case for the C=C stretch region. The 13,14-cis structure, however, does not yield any transitions at ∼1240 cm⁻¹, and fails to explain the observed transition around this frequency in the resonance Raman spectra of the 15-²H, 15′-²H, and 15,15′-²H₂ isotopomers.

The calculated results for the fingerprint region support the presence of a 15,15′-cis spheroidene structure in the reconstituted R26 RCs. The transitions found in this region are not as easily assigned as those in the C=C stretch region. Nonetheless, our analysis has revealed that the transition at 1239 cm⁻¹, which is reproduced at 1242 cm⁻¹, is not only indicative of spheroidene in the RC, but also a unique marker of the 15,15′-cis stereoisomer. Other expected transitions in the fingerprint region are also obtained, although they do not correspond as closely to experimental values as for the C=C stretch region. The signal at 1193 cm⁻¹ is accurately reproduced at 1189 cm⁻¹, but between 1150 and 1180 cm⁻¹ the agreement is less quantitative. Calculations for a 13,14-cis stereoisomer in the fingerprint region do not disagree with the possibility of the additional structure being 13,14-cis.

CONCLUSIONS

The theoretical analysis of the resonance Raman spectra of reconstituted spheroidene in the R26 photosynthetic reaction center has demonstrated conclusively that the RC contains 15,15′-cis spheroidene. The DFT optimized geometry, obtained by fixing the five methyl groups at the coordinates from the x-ray structure of Roszak et al. (11,20), accurately reproduces the trends of isotope-induced shifts for two transitions in the C=C stretch region. Furthermore, our calculations have revealed that the transition at 1239 cm⁻¹, which was hitherto already known to be distinctive of spheroidene in the RC, in fact corresponds to a normal mode unique to the 15,15′-cis stereoisomer. It is calculated at 1242 cm⁻¹ for NA spheroidene.

The resonance Raman spectra of several isotopomers of spheroidene contain additional transitions that we do not observe in our calculations for 15,15′-cis spheroidene. Most notably the C=C stretch regions in our spectra display a pattern of isotope-induced shifts, which our analysis has shown cannot result from a 15,15′-cis structure. This fact has led us to conclude that some RCs contain an alternative stereoisomer of spheroidene. The explanation of the complete resonance Raman spectra is not possible by presuming spheroidene is bound in one form only.

There can be no doubt concerning the purity of the isotope-labeled spheroidenes used in reconstituting spheroidene in the R26 RC. Our earlier work on spheroidene in petroleum ether (23) has demonstrated the presence of only single isotopomers in the samples and the same compounds were used in the process of reconstitution. Moreover, we are confident that the discrepancies between our calculations and experimental results are not related to faults in the computational method used. We base this conclusion on our success in describing the spectra of 19 isotopomers of spheroidene in organic solvent, combined with positive test results from calculations of the resonance Raman spectra of 9- and 11-cis-retinal.

To the best of our knowledge, the possibility of spheroidene incorporated in the RC occurring in two different cis configurations has never been considered in earlier studies. As such, our conclusions are not incompatible with findings from previous publications. On the other hand, for the excited triplet state of spheroidene in the RC, multiple conformations have been reported. In 1989, Kolaczkowski (33) noticed additional shoulders in the electron-paramagnetic-resonance spectrum of spheroidene in its excited triplet state in the fully deuterated RC of Rb. sphaeroides 2.4.1. He interpreted these shoulders as originating from a second conformer that had undergone a twist around a σ-bond near one of the ends of the conjugated part of the spheroidene molecule (33). Recently Kakitani et al. (34) performed time-resolved electron-paramagnetic-resonance experiments on the same RCs from which they concluded that the spheroidene in the triplet state undergoes conformational changes in the C₁₁ to C_15′ part of the conjugated chain. The experiments on the triplet state might well deserve further consideration in relation to our observation of two configurations of spheroidene being present already in the ground state.

The presence of two stereoisomers in the RC crystals might be the cause of the lower resolution of the electron density maps at the carotenoid position compared to that for other cofactors in the RC (11,20). As a candidate for the additional structure present in our samples, we have considered 13,14-cis spheroidene, which seems compatible with the x-ray density map determined by McAuley et al. (20) and refined by Roszak et al. (11). If we superimpose the results from the theoretical analysis of the 15,15′-cis and 13,14-cis structures, all transitions in the C=C stretch regions of the resonance Raman spectra and trends upon isotope substitution are well reproduced and understood. This is clearly illustrated by the calculated frequency bars plotted over the spectra in Fig. 4 and the close correspondence between the experimental and calculated shifting patterns in Fig. 5. The intensities of the transitions in the C=C stretch region that are not related to the 15,15′-cis structure suggest that the additional structure makes up a significant proportion of the spheroidene bound to the RC. It should be noted that as far as the C=C stretch results are concerned, any additional configuration might do, provided the mode composition of the two C=C stretch modes is reversed with respect to that of a 15,15′-cis structure. The 13,14-cis stereoisomer is a possibility, but not a necessity. To ascertain that it is indeed present in our samples, further attention needs to be given to the geometry optimization of the 13,14-cis structure in the RC environment.

Resonance Raman and electronic absorption spectra indicate that the carotenoid binds to the R26 RC in a way similar to the binding of the carotenoid in the wild-type RC (8). Whether two cis configurations occur in the latter case as well remains to be established. To investigate this question, techniques other than resonance Raman spectroscopy might well be useful, because the differences between the resonance Raman spectra of the two cis isomers for natural abundance spheroidene are (too) subtle. If our observation of two cis configurations of spheroidene in the reaction center turns out to be more general, an intriguing question arises concerning the biological relevance.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.