Perceptual classification of chromatic modulation

Abstract

We measured the regions of the equiluminant plane that are exploited by observers during a Yes/No detection task. The signal was a 640 ms Gaussian modulation (σ_t = 160 ms) of a Gaussian spatial patch (σ_s = 2.4 deg) presented in chromatically bivariate uniform noise. One component of the noise was along the direction axial with the signal in color space, the other perpendicular. Four signal directions were tested: along cardinal LM and S axes and two intermediate directions to which the cardinal axes were equally sensitive. The distribution of noise chromaticities from each trial was correlated with the observers’ responses and the presence and absence of the signal to build a classification image of the distribution of chromaticities on which the decision of the observer was based. The images show a narrowly selective peak in the signal direction flanked by regions with a broader selectivity. These results raise the possibility that detection judgments are mediated by both linear and nonlinear mechanisms with peak sensitivities between the cardinal directions.

1 Introduction

The fundamental notion of trichromacy, that humans must manipulate three variables in order to perform color matches, is widely understood to imply that spectral differences between lights are encoded within three independent visual channels, each with a different spectral sensitivity (Kaiser & Boynton, 1996; Knoblauch, 2002; Wyszecki & Stiles, 1982). This hypothesis has been confirmed by demonstrations of three classes of cone photopigment in the retina (Dartnall et al., 1983;, Schnapf et al., 1987) whose opsins are under the control of three separate genes (Nathans et al., 1986) and the identification of three sub-cortical pathways within which cone signals are recoded, (Dacey & Lee, 1994; Derrington et al, 1984; Shapley, 1990).

Given only three spectral coding mechanisms at the input to vision, it is, at first glance, surprising that more than three might be required to account for discrimination behavior. If discrimination were mediated by linear mechanisms at all stages of visual processing, then indeed it would be difficult to explain. Certain nonlinearities, however, reduce the bandwidth of a mechanism in color space. Thus, more mechanisms could be required to avoid sensitivity losses in specific regions of color space. For example, a simple half-wave, rectifying nonlinearity, renders a mechanism sensitive to modulations in only half of color space and would require complementary mechanisms to code increments and decrements along an axis in color space. As a second example, cone signals that undergo a compressive nonlinearity prior to combining linearly produce a mechanism with narrower spectral selectivity than a linear mechanism. Again, additional mechanisms might be required in order to avoid a chromatic “blind spot” in color space. Both of the above mentioned nonlinearities are reasonable in physiological terms and appear frequently in models of early visual coding.

Recent studies have focused on two questions. First, are more than three mechanisms required to explain chromatic discrimination behavior? Second, are the bandwidths of the underlying mechanisms indicative of linear (broad band) or nonlinear (narrow band) integrative mechanisms? Physiological data show that the spectral sensitivities of subcortical cells tend to cluster around three axes, corresponding to mechanisms with cones inputs L+M, L−M and S− (L+M) (Derrington et al, 1984; DeValois et al, 1966). These cells display a half-wave, rectifying nonlinearity, though they tend to integrate chromatic information linearly in the half-space to which they are sensitive. Two new features emerge in visual cortex. First, the spectral sensitivities of cells in cortical area V1 are more uniformly distributed in color space (DeValois et al., 2000; Lennie et al., 1990; Zeki, 1980). Second, some cortical cells display tuning curves that are too narrow to be explained by linearity (DeValois et al., 2000; Kiper et al., 1997; Lennie et al., 1990; Zeki, 1980). Thus, tuning to axes intermediate to those found subcortically and narrow spectral bandwidth are taken to be characteristics of cortical color vision mechanisms.

The results from psychophysical studies are less clear. As early as the 1950’s, Stiles (1953) found it necessary to postulate more than three mechanisms mediating discrimination behavior to explain two-color increment threshold data. Recently, psychophysical investigations of discrimination employing diverse techniques have addressed these questions with some studies showing evidence for numerous mechanisms (D’Zmura & Knoblauch, 1998; Gegenfurtner & Kiper, 1992; Krauskopf et al., 1986; Monaci et al., submitted) and some not (Eskew et al., 2001; Guillanni & Eskew, 1998; Sankaralli & Mullen, 1997), some showing evidence for linear, broad-band mechanisms (Cardinal & Kiper, 2003; D’Zmura & Knoblauch, 1998; Monaci et al., submitted) and some narrow-band (Gegenfurtner & Kiper, 1992; Goda & Fuji, 2001). The results may depend on the tasks studied as well as the stimulus conditions employed. Given the changes in coding across the various stages of visual processing, it would not be surprising to find the diversity of results observed if different tasks are constrained by different levels in the visual system or are mediated by different cell classes within a given cortical visual area.

The paradigms of habituation (Krauskopf et al., 1982), adaptation (Webster & Mollon, 1994) visual search (D’Zmura, 1991) and masking (Gegenfurtner & Kiper, 1992), have typically been used to evaluate how the characteristics of a conditioning stimulus influence the sensitivity of the observer while discriminating a test signal. The logic is that if the conditioning stimulus is processed by the same channels as the test, it will interfere with discrimination and the observer will require a greater signal strength to achieve a criterion performance. Systematically changing the characteristics of the conditioning stimulus reveals the sensitivity profile of the mechanism(s) mediating the discrimination. In the present study, we used a complementary approach, the classification image paradigm (Ahumada, 2002; Ahumada & Lovell, 1971), in which, a signal of fixed strength is presented in a masking noise with fixed statistical characteristics. The responses of the observer are correlated with the noise profile on individual trials to reveal the manner in which the stimulus distribution influences the observer’s decisions as to the presence or absence of the signal. Knowledge of the stimulus characteristics that form the basis of the observer’s decision permits us to impose constraints on the coding properties of early visual mechanisms.

2 Methods

2.1 Observers

Two observers (CB: female, age 25 and RB: male, age 24 years) with normal color vision and normal or corrected to normal acuity participated in the study. Observer RB was an author but remained naïve to the results except as discussed below. CB remained naïve to the experimental goals and results until all testing was completed.

2.2 Equipment

The stimulus set-up has previously been described in detail (D’Zmura & Knoblauch, 1998). In brief, all stimuli were presented on an Eizo FlexScan T562-T color monitor driven by software on a PC computer under the control of a Cambridge Research Systems VSG/2 color graphics card that provides 12 bits of resolution for each phosphor of the 800 × 600 pixel display. The screen was run at a field rate of 100 Hz, non-interlaced. The voltage-phosphor luminance relationship was linearized with look-up tables. Calibration of the screen was performed with a Minolta CS-100 chromameter and a silicone photo-diode used with the optical software (CRS). The screen was set to a steady background with luminance 65 cd/m² and chromaticity (0.294, 0.303) for the CIE 1931 standard observer.

2.3 Stimulus

The chromatic properties of the stimulus are described in DKL color space (Derrington et al, 1984) which is based on the MacLeod and Boynton color diagram (1979). Lights are represented in this space relative to the coordinates of the steady background, B, to which the visual system is adapted. The color space has three axes that intersect at B and correspond to a luminance axis (L+M), an LM axis, along which S cone and luminance modulation are constant and an S axis, along which L and M cone modulations are constant. The latter two axes lie in the equiluminant plane. All stimuli used in the current experiments were constrained to lie in this plane and are described as modulations with respect to B along axes defined by their angle with respect to the LM axis. Unit vectors were defined in terms of threshold units along the LM and S axes.

The stimulus was a spatially isotropic Gaussian with σ_s = 2.4 deg of visual angle presented in the center of the screen and modulated by the signal and noise chromaticities over time. The signal had a Gaussian time course with σ_t = 160 ms and a duration of 640 ms. The noise was a rapid time-varying modulation of the chromaticity of the Gaussian patch with each noise sample of 20 ms duration, or 32 samples per stimulus. It was composed of the vector sum of two independent chromatic components, distributed uniformly, along the signal and orthogonal axes, respectively. Figure 1 shows a schematic representation of the relation between signal and noise axes for a signal at 45 deg. The solid short arrow indicates the axis along which the signal is modulated. The long dashed arrows show the axes along which the independent noise samples are drawn. The distribution in the equiluminant plane of the instantaneous vector sum of the two noise samples is indicated by the gray diamond shaped region. On signal present trials, the signal vector and noise vector were added.

Figure 1.

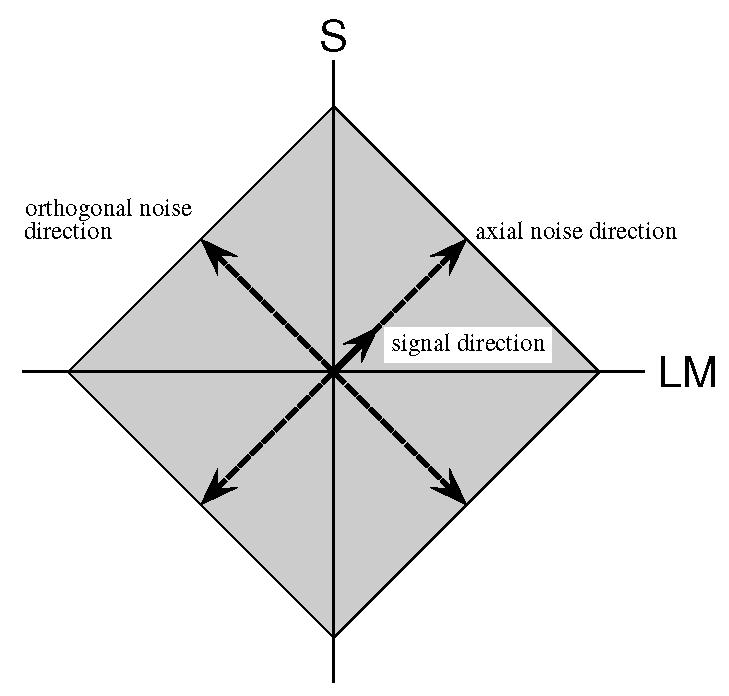
A schematic representation of the stimulus in the equiluminant plane. All stimuli are defined with respect to the LM and S axes. The signal is indicated by the short solid arrow. The masking noise is composed of two independent, uniform noise components, one axial with the signal and the other orthogonal. The grey diamond indicates the region over which the noise may vary. To represent a signal in a different direction, the diagram would be rotated.

In the experiment, four signal directions were tested: along the LM and S axes (0 and 90 deg, respectively) and along two intermediate directions estimated for both observers. The first of these was chosen on the basis of preliminary experiments to be in a direction to which the LM and S axes were equally sensitive or 45 deg in threshold units. The second intermediate direction was chosen as 90 deg clockwise to the first, or 315 deg. The variance or modulation depth of the axial uniform noise was chosen to raise the threshold amplitude of the signal by a factor of two, which under our conditions corresponded to approximately 10 threshold units. This modulation depth was also used when the signal was orthogonal to the noise. The signal amplitude in each direction was chosen to yield a detection performance of d′ = 1 when added to the noise.

2.4 Task

At the start of each session, the observer was seated 57 cm from the screen in a dark room and light adapted to the mean luminance of the screen for two minutes. The observer performed a Yes/No detection task for which the signal was present on half of the trials. Feedback was provided after each trial as to the presence or absence of the signal. The four signal directions were tested in random order in four consecutive blocks of 224 trials, in each session. Prior to each block, the observer was shown an example of the signal modulation for that block and instructed to judge each trial as to its presence. Sixteen sessions were run for each observer. After having completed the set and analyzing the data, observer RB performed a second set of sixteen sessions. As our analysis revealed no significant differences in the two sets of results, the thirty-two sessions were combined to reduce overall variability.

2.5 Analysis

Each trial was coded as to the presence or absence of the signal and the response of the observer. The axial and orthogonal noise distributions from each trial were recorded as 32-element vectors. In an initial analysis, axial and orthogonal vectors were averaged individually within each of the four categories: Hit, False Alarm, Miss, Correct Rejection. The average vectors were then combined in a weighted sum to yield separate temporal classification images, CI for modulation along the axial and orthogonal directions.

$$\mathrm{CI}={\overrightarrow{\mu }}_H+{\overrightarrow{\mu }}_F-{\overrightarrow{\mu }}_M-{\overrightarrow{\mu }}_C,$$ (1)

where μ⃗_H is the mean noise vector for the Hit trials, μ⃗_F the mean vector for the False Alarms, etc (Ahumada, 2002). The classification images were then converted into z-scores by dividing them by the standard deviation of the noise modulations, computed under the assumption that trials were classified randomly.

In a second analysis, the axial and orthogonal noise vectors were combined to give the temporal sequence of random positions in the equiluminant plane occupied by the noise vector on each trial. Within each of the four categories, 32 two-dimensional histograms were created by cumulating the positions for each sequence, for each of the 32 elements of the noise vector. In order to generate sufficient data, the equiluminant plane was subdivided into 9×9 bins.

Under the hypothesis that an observer classifies trials randomly, the number of counts in each bin will follow a binomial distribution with N, the number of trials on which the signal was present or absent and p = 1/81. Given the large number of trials, however, we treat the counts as Gaussian variables, based on the central limit theorem, distributed as

$$\mathcal{N}\left(\frac{N}{81},\frac{80N}{{81}^2}\right).$$

Under the Gaussian assumption, we can combine the histograms from each category according to the optimal rule in Equation 1 (Ahumada, 2002) to form a classification image showing how the distribution of chromatic modulations influences the observer’s decision on each trial. In addition, we combined the images over time to increase the number of counts in each bin, with the goal of increasing the signal to noise ratio in the classification image.

3 Results

The observers’ sensitivity to the signal was stable with d′ not significantly different from 1.0 and showed no trends over sessions. Similarly, the criterion, c, did not differ significantly from 0, indicating that the observers were unbiased. Average values and standard deviations for these measures are shown for each signal direction and observer in Table 1.

Table 1.

Average estimates of sensitivity, d′ and criterion, c, for all conditions

		Signal Direction	0	45	90	315
Obs
RB	d′		1.02	0.92	0.97	1.03
	sd		0.15	0.14	0.12	0.13
	c		−0.01	−0.07	−0.08	−0.10
	sd		0.05	0.05	0.05	0.06
CB	d′		0.93	0.92	1.05	1.18
	sd		0.13	0.18	0.18	0.19
	c		0.8 10−3	0.02	−0.01	0.01
	sd		0.03	0.03	0.05	0.06

Figure 2a shows the classification images in z-score units as a function of time for the axial (unfilled circles) and orthogonal (filled circles) components of the noise, when the signal was along the S axis (90 deg) for observer RB. The axial component approximately follows the Gaussian profile of the signal while the orthogonal component varies randomly near a value of zero. The results demonstrate that the observer can integrate information along the signal axis while ignoring the orthogonal axis. The second observer displayed similar results as did both observers when the signal was along the LM axis. These results were not unexpected as there is considerable evidence for independent, linear mechanisms that mediate detection tuned to these axes.

Figure 2.

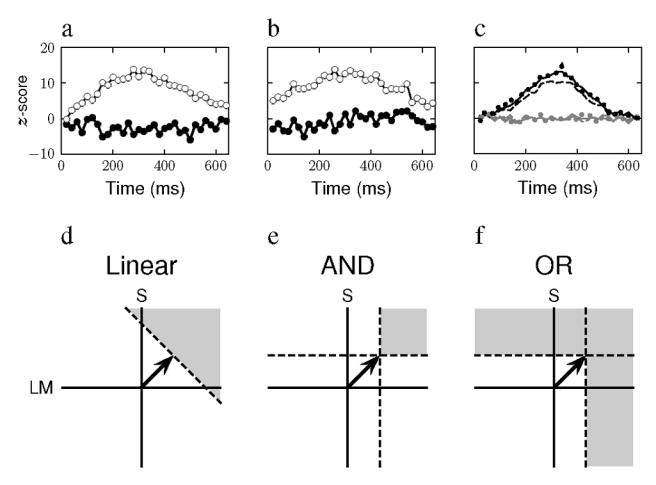
a) The classification images calculated from the axial (unfilled circles) and the orthogonal (filled circles) noise components for observer RB, for detection of a Gaussian signal modulated in time along the S axis. (90 deg). b) The classification images calculated for observer RB, for detection of a Gaussian signal modulated in time along the intermediate axis of 315 deg. The symbols have the same meaning as in (a), c) The classification images calculated from the axial (black) and orthogonal (gray) noise components for a model observer. The solid curves show the images for an observer who bases his judgment on the response of a single linear mechanism tuned to the signal direction. The dashed and dotted curves show the images for an observer whose judgments are based on the responses in two mechanisms tuned to directions to either side of the signal direction. For the dashed curves, the observer requires that the responses of both mechanism be superior to a criterion value to judge the signal present. For the dotted curves, the observer judges the signal present if the response of at least one mechanism is greater than the criterion, d) The decision space for a model observer whose decisions are based on the responses of a single linear mechanism tuned to the signal direction, denoted ’Linear’. The signal direction is indicated by the solid arrow. The dashed line indicates a criterion level of response of the mechanism. Stimulus chromaticities that fall in the gray region are more likely to lead the observer to respond that the signal is present, e) The decision space for a model observer whose decisions are based on the responses of linear mechanisms tuned to the LM and S axes and whose judgment that the signal is present requires that the response be greater than a criterion on both mechanism axes, indicated by the horizontal and vertical dashed lines. This decision rule is called an ‘AND’ criterion, f) The decisions of a model observer who employs an ‘OR’ criterion also depend on the responses of linear mechanisms tuned to the LM and S axes, but this observer will judge the signal present when the criterion response is exceeded on at least one axis.

Figure 2b shows the results of the same observer when the signal was along an intermediate axis, 315 deg. The results resemble those in 2a, indicating again that the observer’s judgments are based on chromatic modulation along the signal axis and not along the orthogonal axis. The second observer displays similar results for this condition as do both for the other intermediate direction. Can these data, then, be taken to indicate the presence of mechanisms tuned to intermediate directions? To address this question, we performed the same experiment on a simulated observer whose decisions were based either on a single, linear mechanism tuned to the signal direction or, alternatively, on the modulations of two linear mechanisms tuned to either side of the signal direction.

The decision space for the first hypothesis, that the observer bases his detection judgments on a single, linear, axial mechanism, is shown in Figure 2d, labeled ‘Linear’. The signal direction and mechanism spectral sensitivity are indicated by the arrow at 45 deg. On each trial, the chromaticity values of the stimulus are initially projected on this axis and then weighted by a Gaussian template and summed over time to yield the decision variable. The dashed line indicates the observer’s criterion. When the decision variable exceeds the criterion, the observer reports that the signal is present. The grey area indicates the region of the equiluminant plane in which modulations are most likely to lead to a present response.

Under the second hypothesis, the stimulus is projected on the two off-axis mechanism spectral sensitivity axes, LM and S. Each mechanism’s temporal response is then integrated with the Gaussian template to yield a response variable for each mechanism. The judgment of the observer will depend on the way the two responses are combined. We investigated two extreme cases. In the first case, shown in Figure 2e, the observer decides that the signal is present if the response variable of both mechanisms exceeds a criterion. We label this an ‘AND’-criterion. Note that under this hypothesis, the bandwidth of the region of the equiluminant plane in which modulations are most likely to lead to a present response is narrower than for the Linear hypothesis. Alternatively, the observer could respond present when the response on either axis exceeds a criterion. We label this an ‘OR’-criterion and display the decision space in Figure 2f.

We adjusted the signal strength so that the simulated observer’s performance level was at d′ = 1′. Based on the observer’s judgments and the presence and absence of the signal, we classified the noise vectors and computed classification images just as with the real observers. The results based on 5000 trials are shown in Figure 2c, with the Linear hypothesis as a solid line, the AND hypothesis as a dashed line and the OR hypothesis as a dotted line. The classification image of the axial noise component is in black and of the orthogonal component in gray. Surprisingly, all three simulated observers perform in a similar fashion. Specifically, they each base their decisions on the modulations along the signal axis and ignore the modulations along the orthogonal axis. These results are, perhaps, less surprising if we note that this analysis indicates essentially in what part of the equiluminant plane the classification image peaks and all three hypotheses display peak sensitivity along the signal axis.

Nevertheless, the decision space diagrams of Figures 2d–f suggest that the hypotheses might be differentiated by examining how the distribution of modulations in the equiluminant plane influences the observer’s decisions. Thus, we evaluated the frequency with which modulations of different regions of the equiluminant plane lead to signal present or absent judgments.

Figure 3 shows four examples of classification images based on the frequencies with which different regions of the equiluminant plane contribute to the observer’s decision. Bright pixels indicate chromaticities whose presence increases the tendency to respond ‘Present’; dark pixels indicate chromaticities whose presence increases the tendency to respond ‘Absent’. The differential frequency information in these images has been transformed to z-scores (indicated by the greyscale bars beside each image), and the images were thresholded to display only those regions outside of a 95%-confidence interval. The orientation differences of the images reflect the change in orientation of the noise components with the signal direction. The signal direction is indicated by a gray arrow attached to a side of the image.

Figure 3.

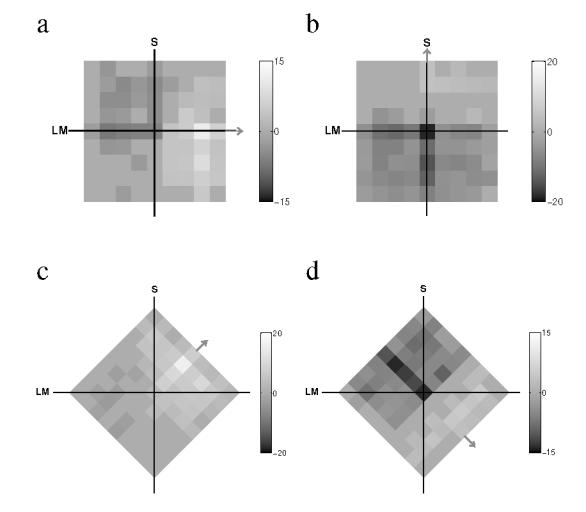
Classification images showing the regions of the equiluminant plane most likely to lead to a present (brighter) or an absent response (darker). The images are oriented so that the noise components are aligned with the sides of the square region. The signal direction or azimuth is indicated by a gray arrow. The gray-level scale indicates the number of standard deviations from the expected unbiased, random observer, a) Obs: CB, Signal: 0 deg. b) Obs: RB, Signal: 90 deg. c) Obs: CB, Signal: 45 deg d) Obs: RB, signal 315 deg.

The light and dark regions of each image appear to be distributed in a horizontal band perpendicular to the signal direction, as would be predicted if decisions were based on a linear mechanism axial with the signal. All of the images, however, show an increase in intensity on the signal axis, which might provide evidence for a narrowing of selectivity near the signal axis. Interestingly, along some axes (Figures 3b and d) decisions seem to depend more on the chromaticities that lead to an ‘Absent’ than a ‘Present’ response, based on the tendency for darker regions to accumulate in the direction negative to the signal. Modulations in the direction complementary to the signal are as informative as those in the same direction in a Yes/No paradigm, and the observers appear to have integrated such information in their classification strategy.

To evaluate whether these images favor one of the three hypotheses, we applied linear contrasts to each image under the assumption that the z-scores in the images are drawn from a standard normal distribution (Hays, 1973), with weights chosen based on the decision spaces shown for the three hypotheses in Figures 2d–f. The distribution of positive and negative weights used in the three contrasts are shown in the legend of Figure 4 with white and black regions indicating positive and negative weights, respectively. The positive and negative weights were adjusted to sum to zero. The results for all three hypotheses are shown in Figure 4 for all signal directions and for both observers as bar graphs. As the three hypotheses are not orthogonal and overlap considerably, all three lead to high values. The Linear hypothesis, however, results in the largest response in every single case. If we suppose that each of the three hypotheses is equally likely to have produced the highest value, then the probability of the observed outcome is (1/3)⁸ = 1.5 × 10⁻⁴.

Figure 4.

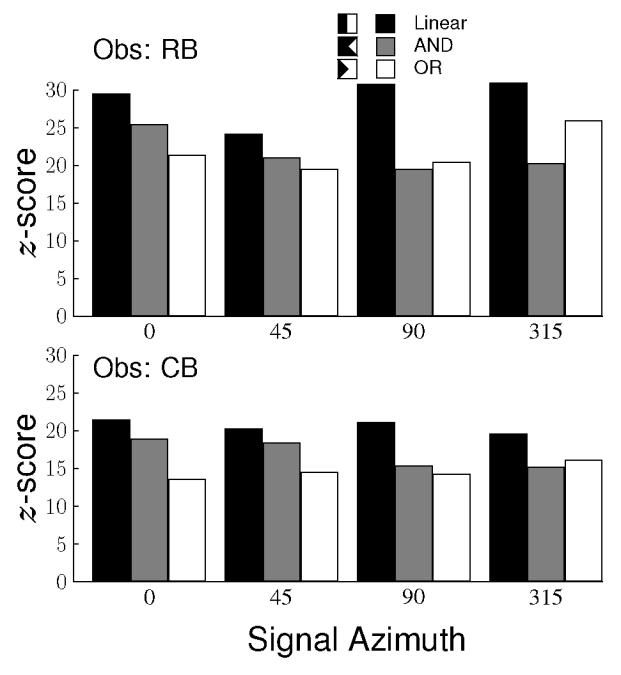
Weighted contrasts of the classification images under three hypotheses for each signal direction and for both observers. The black bars are calculated under the hypothesis that decisions are based on the response of a single, linear mechanism tuned to the signal. The gray bars are calculated under the hypothesis that decisions are based on the responses in two mechanisms tuned along cardinal axes and that their responses are combined by an ’AND’ rule. The white bars are also calculated based on the same two mechanisms except that the responses are combined with an ’OR’ rule.

While the Linear hypothesis describes the data better than either of those based on two off-axis mechanisms, there was a tendency in Figure 3, as noted above, for selectivity along the signal axis. Since such selectivity would be indicative of nonlinearity, we investigated it further. The Linear hypothesis would predict that the 1D profiles across the signal axis (i.e., projected on the orthogonal axis) are constant at each position along the signal axis. We calculated a weighted profile with the levels in the signal direction given a positive weight and those in the complementary direction a negative weight. The calculated profiles are shown in the four panels of Figure 5 for the two observers and for the four signal directions in terms of z-scores as a function of noise modulation along the orthogonal axis. Recall that the maximum modulation along each axis was equivalent to ten times the signal modulation at threshold. Both observers display a similar profile for each signal direction with a narrow peak in the signal direction sitting on a more broadly tuned baseline.

Figure 5.

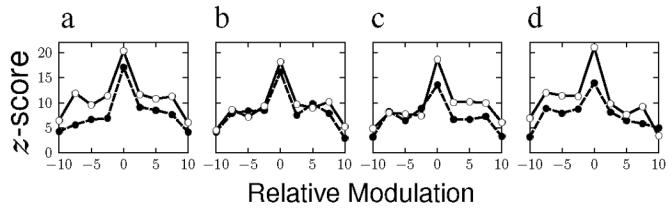
Classification images calculated parallel to the signal direction as a function of the relative chromaticity difference from the signal direction along the orthogonal axis, for two observers (RB unfilled circles, CB filled circles). Each panel shows the results obtained from a different signal direction: a) 0 deg, b) 45 deg, c) 90 deg, d) 315 deg.

4 Discussion

In the experiments reported here, we find that classification images for detecting a chromatic pulse are tuned to the signal modulation direction in chromaticity space. A similar result has recently been reported for detection of a spatial, chromatic stimulus (Hansen & Gegenfurtner, 2003). This result, in itself, is not revealing since our first analysis demonstrates at least three different models of sensory coding predict this outcome. The three models do differ, however, in the distribution in the equiluminant plane over which information is expected to lead to a positive or negative decision by the observer. The results for all signal modulations most closely resemble the predictions of a model observer whose decisions are based on a single, linear mechanism tuned to the signal direction.

The two-mechanism models examined were simplified and did not, for example, incorporate the influence of probability summation between mechanisms. It is unlikely that doing so would have influenced the results, however, as probability summation is largest where the two mechanisms are, equally sensitive, i.e., along the signal direction and, as noted previously, the three hypotheses cannot be differentiated along this direction.

A closer examination of the Linear hypothesis, however, indicated a narrowing of selectivity around the signal axis. The profile of the classification images suggests the possibility that both broad band, linear and narrow band, nonlinear mechanisms contribute to the observer’s decision. The current results, however, do not indicate whether the two parts of the profile that we have identified correspond to separate and independent processes.

The results reported here complement those obtained previously using sectored noise to mask detection of a chromatic pulse in the equiluminant plane, that demonstrate that sensitivity is independent of noise bandwidth around the signal direction, as would be predicted were detection mediated by a single, linear mechanism, axial to the signal direction (Bouet & Knoblauch, 2003; D’Zmura & Knoblauch, 1998: Monaci et al., submitted). In contrast to these masking studies, the classification image data raise the possibility that the observer’s decisions are based on both broad band and narrow band mechanisms. Perhaps, the narrow band mechanisms were not evident in the masking studies because the linear mechanisms continued to support detection under conditions of noise masking away from the signal axis. Neither those results nor the current ones, however, permit a decision as to whether mechanisms tuned to intermediate directions result from dynamically deployed combinations of cardinal mechanisms or are distinct, hard-wired visual mechanisms, although ample evidence for the latter is available in recent cortical studies (DeValois et al, 2000; Lennie, et al, 1990).

It might be thought that classification images are interesting only insomuch as they do not resemble the signal. We would argue that such an interpretation is too restrictive. Classification images reveal the distribution of information in the stimulus that an observer exploits during a decision. As such, they permit the evaluation of hypotheses concerning how such information is transmitted through the visual system. The analyses from the present study suggest a detection model in which this information is transmitted through both linear and nonlinear mechanisms tuned to the signal direction.