The network of sequence flow between protein structures

Abstract

Sequence–structure relationships in proteins are highly asymmetric because many sequences fold into relatively few structures. What is the number of sequences that fold into a particular protein structure? Is it possible to switch between stable protein folds by point mutations? To address these questions, we compute a directed graph of sequences and structures of proteins, which is based on 2,060 experimentally determined protein shapes from the Protein Data Bank. The directed graph is highly connected at native energies with “sinks” that attract many sequences from other folds. The sinks are rich in β-sheets. The number of sequences that transition between folds is significantly smaller than the number of sequences retained by their fold. The sequence flow into a particular protein shape from other proteins correlates with the number of sequences that matches this shape in empirically determined genomes. Properties of strongly connected components of the graph are correlated with protein length and secondary structure.

As data on protein sequences and their variations become more accessible (following the abundance of large-scale sequencing and gene expression projects), it is clear that protein structures serve as evolutionary templates. Similar protein backbones are used again and again to create proteins with adjusted functions in response to environmental variations or at random. This asymmetric relationship is of considerable interest in the study of protein evolution and design and has received considerable attention. How many sequences fold to a common structure, or equivalently, what is the sequence capacity (or designability) of a known fold? Past theoretical and computational studies primarily are focused on the thermal stability of the proteins. The stability is estimated by an energy calculation of threaded sequences in a known structure. The theory and calculations can be divided (roughly) into two categories: (i) general theories (1–6) and exhaustive simulations of simple model systems (7–11) and (ii) accurate and detailed modeling of a few proteins (12–16). The studies of class i provide a universal view of sequence–structure matches and their variations. Investigations of class ii made specific predictions on protein folds that are straightforward to test experimentally. The function of interest, protein designability or sequence capacity, was estimated theoretically and by computations. However, neither of these calculations consider explicitly all structures of the Protein Data Bank (PDB) (17). Quantitative extrapolations from approximate theories, lattice models, or detailed simulations of a few proteins to other folds may not be obvious. Furthermore, collective behavior of the evolutionary process, not restricted to a single or a few proteins, may go unnoticed.

Explicit calculation of sequence capacity of all protein folds is of particular interest because genomic-scale experiments are emerging, making it possible to determine sequence selection mechanisms (18–20). The experiments assess the contribution of sequence capacity, estimated from theory or simulation, and compare it to natural mutation rates. We have developed a computational model in which the sequence capacity was computed directly for a representative set of structures from the PDB (3,660 folds) (21). In the calculation, only the energy function is approximate whereas the PDB structures and their corresponding sequences are sampled significantly. The sampling allowed for statistical convergence of the capacity. In addition to sequence capacities of all folds, we computed an intriguing temperature relationship between the folds.

We sampled only experimentally determined structures from the PDB, so an obvious question is the completion of the set. Arguments were made that the PDB is indeed complete (22, 23) with the current thousands of distinct folds. This argument further supports the creation of a comprehensive model of protein structure space and their sequence capacities and the progressive refinement of this model. In ref. 21 we did not consider the possibility that mutated sequences of a particular structure will fold to different shapes (sequence migration; we use “migration” to denote sequences that evolve in one fold and end up in another structure). This analysis of sequence migration is particularly timely with the growing experimental evidence for pairs of proteins with a high percentage of sequence identity and alternate structures. These “interface” sequences were illustrated experimentally on model systems (24–26) and on proteins (26–30). What is the impact of the interfaces on protein evolution and design? Interesting analyses of existing structures and identification of continuous evolutionary changes are presented in refs. 31 and 32, suggesting the mixing of folds during the evolutionary processes. The major goal of the present article is the development of a complete computational model for protein space as a network, with the nodes of the graph representing the protein folds and directed edges accounting for the flow of sequences in and out of the folds. The “in-degree” of a fold is the number of edges that point to it or the number of other folds that lose sequences to that structure as a result of point mutations. Similarly the “out-degree” of a fold is the number of edges that carry sequences from that fold to other proteins shapes. An edge indicates loss of sequences that are energetically compatible with one structure to another fold. Although other interesting network models for protein space have been proposed in the past (33–36), they were not based on explicit modeling of the kinetics of evolution (i.e., sequence mutations and migration between structures), which is done here.

Computational Model

We first summarize the basic components of the computational model. We directly compute the absolute number of sequences that fold to each member of a comprehensive sample of protein structures. We also calculate the number of transitional sequences between folds. A transitional sequence allows, with a single point mutation, to flip between alternative stable structures. The computation is based on a stochastic sampling of sequences with provable polynomial convergence in the sequence length. The sampling is done one structure at a time. A sequence evolves in one particular structure, and the number of sequences (sequence capacity) below a particular energy is estimated as well as the number of sequences that were lost to other folds. Our selection criterion is based on a threading energy function that makes it possible to estimate microcanonical partition functions of sequence space in the neighborhood of each stable basin (a protein structure) and the entropy of the transition state between pairs of folds. The numbers of sequences of a fold and of the transitional sequences between pairs of folds form the network of sequence flow, which is the prime result of the present article.

To estimate the sequence capacity of a representative set of structures, we selected chains from the PDB covering over 90% of the protein families in the Structural Classification of Proteins (SCOP) database classes a–e (37) (representing single and multidomain α- and β-proteins). We started with a large subset of 14,000 chains from the PDB, chosen so that no two chains have >70% sequence identity. We compared this subset against the families in SCOP and eliminated chains that yielded redundant representations while making sure that our coverage of SCOP families remained as high as possible. Afterward, we compared the remaining chains by using the TM-Align algorithm (38). The range of the TM-score is between 0 and 1, where 1 is identity. Of every pair of proteins with TM-Score >0.8, we removed one, thereby eliminating structural redundancies. The resulting data set used in this work contains 2,060 protein chains.

In our earlier study (21), we considered the sequence capacity N_i(E), which is the number of sequences with energy lower than E of fold i. To characterize the properties of the new set, we define the sequence capacity with competition, C_i(E) as follows: it is the number of sequences for which the energy E_i in fold i is lower than E and also lower than the energy E_j in any of the competing folds j. In the present study, we are using a model close to gapless threading (39) to check for competing folds. We do not allow general alignments with deletions and insertions when we fit sequences into structures. The shorter sequence of two matched proteins is continuous and considered in full. Deletions and insertions at the beginning and the end of sequences score zero, which is a penalty because the THOM2 energy function (see below) is negative on the average. Hence, gaps do not make energetic contributions in our model.

The energy used in the present study is THOM2 (40). It was used in an earlier study of N_i(E), which is extended here to the study of C_i(E) and the stability network. It also is an integral part of our structure prediction program LOOPP (http://cbsuapps.tc.cornell.edu/loopp.aspx) and provides a useful signal to detect similarities between folds of proteins. THOM2 captures the environment of each structural site by assigning a score, u(α, m), for each contact to a structural site. A contact is assumed if the distance between the geometric centers of two amino acid side chains is <6.4 angstrom. The score is determined from a lookup table by using the type of amino acid, α, at the site of interest and the number of neighbors m to the contact site. The total energy of a protein is a sum of the site contributions:

where the index l is running over the structural sites and the index k over the contacts of the site l. THOM2 performs quite well on the set of folds we considered. It recognizes in 1,885 of the 2,060 proteins the native structure as the best fold of the native sequence. The remaining 175 structures are not competitive for sequences within the network and therefore do not influence its behavior significantly. The 175 folds have fewer than 10 sequences with better energy than the native sequence. From a bioinformatic perspective, the THOM2 energy is particularly useful because an efficient alignment algorithm [dynamic programming (41)] is known. From the perspective of estimating N(E) and C(E), this energy function also is of significant value. It was shown (42) that the Markov chain of the algorithm described below that relies on THOM2 is well mixed (approaching the desired distribution) after a polynomial number of steps in the sequence length. It therefore is expected that an efficient calculation of the sequence capacity can be made with THOM2. In contrast, we cannot demonstrate that the Markov chain for pairwise potentials is ergodic.

Consider a protein sequence A_t of length L, a fold X_i, and energy function E_t ≡ E(A_t, X_i). We set two upper energy boundaries for an intermediate estimate of the number of sequences, E_s and E_s+1, (E_s < E_s+1). Both boundaries are chosen empirically, such that E_t < E_s+1 and the ratio N(E_s+1)/N(E_s) is of order one (between 1 and 20). Note that typically N(E) grows exponentially with the protein length L, and its maximum is 20^L, which can make the choices of the energies a little tricky. The determination of the ratios of N(E_s+1)/N(E_s) for different energies E_s and E_s+1 is the target of the current calculation. Each individual ratio is estimated with a randomized algorithm (21, 42) as described below. Starting from A_t, we modify at random one of its amino acids. If the energy of the new sequence is larger than E_s+1, the new sequence is rejected, and a new trial is made based on A_t. If the new energy is lower or equal E_s+1, the step is accepted, and we add one to the counter l_s+1. In this way, we performed a random sampling on the space of sequences with energy below E_s+1. We keep track of the number of steps that this walk spends below energy E_s in a second counter l_s; the ratio l_s+1/l_s then can be shown to give a polynomial-time approximation to N(E_s+1)/N(E_s).

In a previous study, we approximated N(E_n), the number of sequences with energy lower than the energy of the native sequence, A_n, by a successive ratio

where N(E_ref) is the number of sequences at a reference energy that we can estimate directly. For example, the average energy, E_mean, and N(E_mean) can be determined by direct random sampling of sequences. The capacity N(E_mean) is quite close to 1/2·20^L (although we compute it for every fold in the set). Because the difference between N(E_ref) and N(E_n) can be exponential in the protein length, we establish S intermediate ratios to satisfy the above requirement that each individual ratio is O(1). For each intermediate ratio, we typically generate a sample of a few million sequences. We repeat this calculation for every fold in the set.

In the calculations of C_i(E), the number of sequences that fit a fold X_i with competition, we adjust the counting as follows. As before, we generate a Markov chain in sequence space such that E_t < E_s+1, and we compute the ratio l_s+1/l_s. In addition to previous calculation (21, 42), we check for each sequence whether one of the alternative folds X_j has energy E_j < E_t. We define c_s+1 as the number of sequences sampled below E_s+1 that do not have better energies in other folds, and r_s+1 as the total number of sequences sampled below the energy E_s+1. We compute the estimate C(E_s+1) ≈ N(E_s+1)c_s+1/r_s+1, and estimate C(E_s) in the same manner. We also compute m_s(i → j), the number of sequences that migrate from structure i to structure j. This information is sufficient to describe the directed graph we are after.

The above procedure can increase the computational cost by several orders of magnitude compared with counting without competition (instead of a single energy evaluation per sequence, we may need thousands of evaluations). However, we can employ additional heuristics to significantly reduce the running time of our algorithm. For instance, we observe that a structure j that cannot compete with structure i in the energy interval E_s is highly unlikely to be competitive at any interval E_s′ such that E_s′ < E_s. Therefore, whenever a structure j has been noncompetitive for three successive energy intervals, we will remove it from the list of competitors for the next two intervals (rounds). After “sitting out” for two rounds, the structure j will reenter the competition; however, if it remains noncompetitive, it will be eliminated again for four rounds, then for eight rounds, etc. Empirically, we observe that reentering structures almost are always eliminated outright and never have any significant effect on the competition (e.g., m_s(i → j) is close to zero for all s′ < s). The heuristic allows us to significantly cut down on the number of structures we need to consider at any given time and generally increases the efficiency of our algorithm.

Results

In Fig. 1 we show a schematic view of the two largest strongly connected components of the graph (a strongly connected component of a directed graph is a maximal set inside which every node has a path to every node). A directed edge is drawn from protein i to j if at least a fraction c of the sequences with energy below the native energy of i migrate to j. The minimal fraction c to establish an edge in Fig. 1 (0.00375) was chosen for clearer visualization. The size of the largest component is 320 structures, and the second largest is 90 (the third is 39). For clarity in this image, at most five outgoing edges with the largest weights were kept for each node.

Fig. 1.

The two largest strongly connected components of the network of sequence flow between protein folds. Protein space is presented as a directed graph in which a node is a protein shape and the directed edge denotes a flow of sequences from one fold to another. Sequence flow is created when a sequence that is energetically compatible with one structure becomes more compatible with another structure as the result of a single point mutation.

Examining the properties of the components, we realize that the largest of the two includes proteins that are unusually long. The average length of proteins of the largest component is 516 aa, whereas the average length of the whole set is 260 aa. However, the average length of proteins in the second component is only 200 aa. This length is shorter than the average length of the set, which suggests that the length is not the only factor leading to the strong connectivity. We define the secondary structure content as the fractions of residues in an α-helix or a β-sheet configuration according to the DSSP program (43). The largest component is slightly richer with helical content compared with the second-largest component (0.276 versus 0.252) and slightly poorer with sheets (0.232 versus 0.276). The contribution of the secondary structure to in-degrees is clearer when correlations are examined. We emphasize that no correlation is observed between secondary structure and protein length (ρ = −0.002 and P = 0.1). The Spearman correlation coefficient of β-sheet content and in-degree is ρ = 0.215 with P < 10⁻¹². Another piece of evidence for the importance of protein length and β-sheet content for in-degree are the “sinks.” The graph clearly shows the existence of structures that attract sequences from many other folds. The potential existence of sinks was noted in the past based on 3 × 3 × 3 lattice simulations (6, 33). All of the top attractors are in the largest component. The PDB identifiers of the proteins with at least 100 in-degrees are: 1TYV (272 in-degrees, length of 542 aa, and high β-sheet content), 1IDK, which is similar in its characteristics (152 in-degrees, length of 359 aa, and high β-sheet content), and 1OFL:A, the next in line (100 in-degrees, 481 aa, and a β-protein). Yet another example is 1RWR, which is the fifth-strongest attractor with 64 in-degrees and moderate length (301 aa and a β-protein). A useful property that strongly correlates with the graph in-degree is the contact density (the total number of contacts of a protein divided by the sequence length). It is higher for the largest component (1.626 versus 1.531), which is not surprising because higher contact density is expected for longer proteins with smaller surface–volume ratios. Indeed, the contact density is highly correlated with the protein length. One may expect that the in-degree of a structure will strongly correlate with the sequence capacity. The correlation, however, is not so strong once the length effect is factored out. The correlation coefficient of log[C(E)/20^L] with the in-degree is 0.468 and of log[N(E)/20^L] is −0.169.

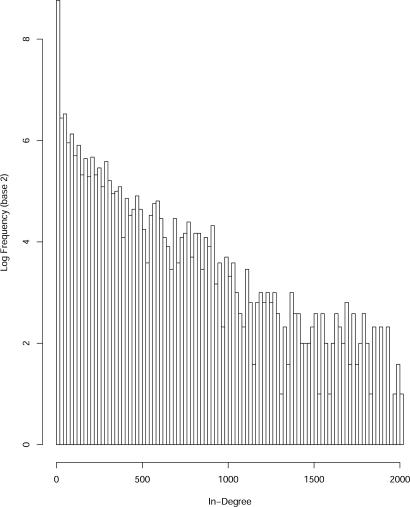
The above analysis focused on a particular definition of an edge that was useful for graphical purposes. Another definition that we examined in detail is based on the size of the network. Two nodes i and j are connected by a directed edge if the fraction of sequences that migrate from i to j is larger or equal to 1/K (K is the total number of folds in our set). In Fig. 2 we show the distribution of the number of “in” edges.

Fig. 2.

The log of the number of proteins (the number of nodes in the directed graph) as a function of in-degree (the total number of edges directed into a fold). The in-degree is an indicator of the stability of a particular shape and its ability to “steal” sequences from other structures.

The total number of in-edges is 785,182, suggesting that the connectivity of the graph is dense. Besides the dominant feature at zero, the distribution also shows a long tail to much higher values (up to 2,002 in edges). The proteins that feature in this high number of in-degree class (e.g., 1K32:A) are (again) enriched with β-sheet structures compared with the rest of the proteins. This observation suggests that the properties of the sinks are not sensitive to the edge cutoff value. The Spearman correlation coefficient of length and in-degrees is highly significant ρ = 0.623 with P value significantly <10⁻¹². It is interesting to note that the distribution of the number of out-edges is considerably more focused, and no long tails are observed. It is peaked at a value of ≈470 for the degree and is not correlated with the number of in edges of a particular fold.

Because the in-degrees show such a striking behavior, we examined whether there are correlations between the distribution of in-degrees and the number of sequences for each fold family that are observed experimentally. For every native sequence in our database, we identify all related sequences in the NR database (44). The matching was done with BLAST (45) with an E value of 0.001 and the BLOSUM 60 substitution matrix (46) (no significant changes in the results reported below were found for an E value of 0.01). Because longer proteins may have more than one domain (and therefore may have independent BLAST hit to different domains), we divided the number of sequence hits by the number of domains. The sampling of sequences is significant, and on the average we assigned ≈340 sequences to one fold. We have found that the number of sequences that match a particular fold correlates with the number of in-edges with Spearman's correlation coefficient of 0.223. Although this correlation suggests that many other factors are involved in evolutionary processes (besides stability) in accord with observations of others (19), it nevertheless is highly significant (P < 10⁻¹²).

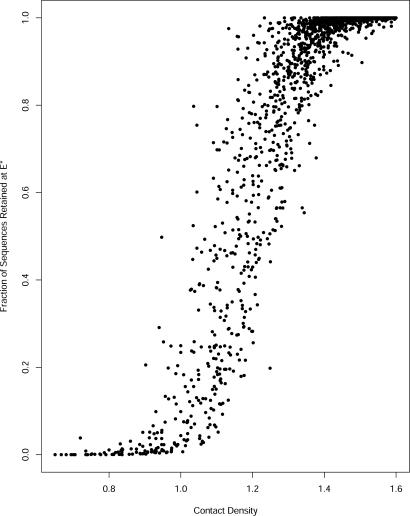
For every fold we also can determine an ideal energy E* where the fraction of retained sequences [i.e., the quantity C(E*)/N(E*)] is maximized. This energy always is lower than the energy of the native sequence and for a large number of proteins C(E*)/N(E*) = 1. Hence, some proteins are able to retain all their sequences at the ideal energy. In a sharp contrast, the other folds retain only a small fraction of their sequences as demonstrated in Fig. 3, dividing the fold family into two broad classes. The proteins with high retention factors also are with high contact density.

Fig. 3.

Sequence retention at the energy E* as a function of the contact density. For every fold, E* is the energy at which the fraction of sequences retained by that fold is maximal. In our model, some proteins retain all sequences at E* and all energy levels below. For other proteins, the fraction of retained sequences reaches a maximum at their E* and then falls again as energy is lowered. Some protein folds even have zero sequence retention rate throughout the energy landscape, meaning that they are almost entirely energetically dominated by other folds.

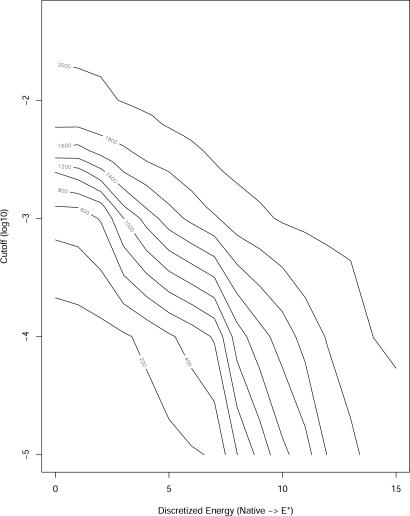
From the discussion above, it is clear that the edges of the graph are a function of an ad hoc cutoff value of the transmission probability between nodes and the energy of the calculation (at E* the number of edges is likely to be minimal). It therefore is useful to explore different values of cutoff and of sequence-counting energy (between E* and E_nat). In Fig. 4 we plot the number of components of the graph computed as we varied these parameters

Fig. 4.

A contour plot of the number of strongly connected components in the graph as a function of the log of the cutoff value for establishing an edge (y axis) and as a function of the energy in the range E* and E_nat (x axis). An edge is established when the fraction of sequences that flow between one protein to the next exceed a cutoff value. (A strongly connected component of a directed graph is a maximal set inside which every node has a path to every node).

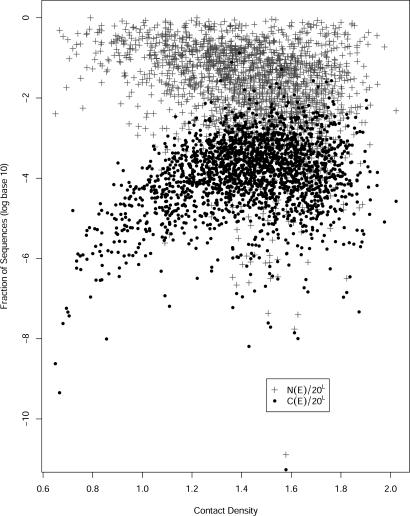
In Fig. 5 we show the functions log[N(E_n)/20^L] and log[C(E_n)/20^L] for all proteins in the set plotted as a function of the contact density (the total number of contacts of a protein molecule divided by the protein length L). We call these functions “the density of capacity” (with or without competition).

Fig. 5.

The density of sequence capacity (without and with competition log[N(E_n)/20^L] and log[C(E_n)/20^L]) as a function of the contact density (the total number of contacts divided by the number of amino acids).

We observe that log[N(E_n)/20^L] is a nonincreasing function (on the average) of the contact density. This finding is easy to explain because structural sites of amino acids with higher contact density are more selective, and a smaller fraction of sequences is found below the native energy. The function C(E_n)/20^L behaves differently and shows a maximum as a function of the contact density. The deviation of C(E_n)/20^L from N(E_n)/20^L is the clearest for low contact density, whereas at high values both functions are more similar. At low contact density the native structure is only marginally stable, making N(E_n)/20^L large (it is easy to find sequences with better or comparable energy to the native energy for this particular fold). However, the marginal stability of structures with low contact density suggests that it is easy to find alternative folds with lower energies for the probe sequence. The availability of alternative folds in the calculation of C(E_n) significantly reduces the number of sequences for marginally stable proteins compared with the results of N(E_n). On the other hand, when the contact density is large, the fraction of sequences acceptable to that fold is smaller, and their energies are lower making it more difficult to find alternative folds for a particular sequence. Hence, for large contact density the two densities of capacity are more similar. The more accurate function for estimating sequence capacity, C(E), has an intriguing maximum at ≈1.5 for the contact density, which is the largest value observed for the density of sequence capacity or protein designability.

Finally, we discuss potential sources of errors in our calculations. Although the convergence of our sampling procedure is mathematically sound, two other components of the model may have significant errors. First, our set of alternative structures is incomplete even if the PDB is, because in our studies we use only gapless alignments. The presence of gaps will significantly increase the number of alternate structures (47). Second, our energy function, which is a one-body potential, is less accurate than more sophisticated energy models that are available. The first point will tend to make the network more dense, whereas the second point probably more diluted. Both of these choices were made to facilitate the construction of the network. We examine tens to hundreds of millions of sequences for each particular fold. It would not be practical for us to create a network at the same level of sampling accuracy and a comprehensive view of the PDB with significantly more complex models.

Discussion

Perhaps the most striking observation of the present article is the high connectivity between protein folds induced by sequence migration. Both the usual notion of a unique and stable protein fold and the success of homology modeling (many sequences fold into one particular shape) are in conflict with the picture of a densely connected space of protein structures by sequence evolution. This conflict is easily resolved. The number of sequences that migrates between folds is significantly smaller than the total number of sequences available to a particular fold. For longer proteins the probability of structural flip is particularly small. Given that the number of homologous proteins known today to a particular fold is in the hundreds to thousands, experimental detection of a transition would be hard to come by. Nevertheless, a number of intriguing sequence migration and structural shifts already were observed (26–30). Further searches for such transitions can benefit from interactions between experiment and simulations; the simulations might be able to guide the search for these rare events.

The high connectivity that we observed is for energies that are below the native energies of these proteins. These transitions therefore are direct with a single point mutation. They are possible, within our energy model, without causing unfolding. Obviously, additional possibilities for these exchanges will be open once more complex moves are considered (such as domain swap). However, even with the highly restricted move set, the connectivity is quite significant and may serve a purpose. It is well known that proteins have native sequences that are far from optimal in their correct folds. A number of speculations were suggested to explain this observation, such as making sure that the protein folds even after a potentially damaging point mutation (large sequence capacity), retaining flexibility necessary for function, etc. Here we are adding one more speculation. The native sequences of experimental folds are far from optimal to retain the possibility of structural flexibility, adjusting protein shapes by local mutations in response to environmental pressure. These transitions will be obviously rare but still possible according to our calculations and to a few experimental examples listed above. Hence, the present article opens the way for speculation on structural evolution that results from point mutations. The observed structural flips are not necessarily restricted to proteins, and it is possible that molecules like RNA will show similar behavior.

Abbreviation

PDB

Protein Data Bank.