Skip to main content
PMC home page
Springer logoLink to Springer
. 2007 Feb 27;36(6):589–599. doi: 10.1007/s00249-006-0126-y

Free energies of binding of R- and S-propranolol to wild-type and F483A mutant cytochrome P450 2D6 from molecular dynamics simulations

Chris de Graaf 1, Chris Oostenbrink 1, Peter H J Keizers 1, Barbara M A van Vugt-Lussenburg 1, Jan N M Commandeur 1, Nico P E Vermeulen 1,✉
PMCID: PMC1914272  PMID: 17333164

Abstract

Detailed molecular dynamics (MD) simulations have been performed to reproduce and rationalize the experimental finding that the F483A mutant of CYP2D6 has lower affinity for R-propranolol than for S-propranolol. Wild-type (WT) CYP2D6 does not show this stereospecificity. Four different approaches to calculate the free energy differences have been investigated and were compared to the experimental binding data. From the differences between calculations based on forward and backward processes and the closure of thermodynamic cycles, it was clear that not all simulations converged sufficiently. The approach that calculates the free energies of exchanging R-propranolol with S-propranolol in the F483A mutant relative to the exchange free energy in WT CYP2D6 accurately reproduced the experimental binding data. Careful inspection of the end-points of the MD simulations involved in this approach, allowed for a molecular interpretation of the observed differences.

Electronic supplementary material

The online version of this article (doi:10.1007/s00249-006-0126-y) contains supplementary material, which is available to authorized users.

Introduction

The superfamily of cytochrome P450 (CYP) enzymes constitutes the most important phase I metabolic enzymes. CYPs generally detoxify pharmacologically active and potentially hazardous compounds, but in a number of cases non-toxic parent compounds are bioactivated into pharmacologically or toxicologically active metabolites, or procarcinogens into their ultimate carcinogens (Sheweita 2000; Vermeulen 1996). Although the expression levels of CYP2D6 represent only 2% of all hepatic CYPs, it is the second most important drug metabolizing enzyme, after CYP3A4, and involved in the metabolism of about 15–30% of the currently marketed drugs (Bertilsson et al. 2002; Zanger et al. 2004). Large interindividual differences exist in CYP2D6 activity, due to gene multiplicity and polymorphisms further emphasizing its clinical importance (Ingelman-Sundberg 2004; Oscarson and Ingelman-Sundberg 2002; Wormhoudt et al. 1999). The early identification of potential CYP2D6 substrates and prediction of their metabolism is therefore advantageous in the discovery and development of new drugs.

Experimentally, the active site of CYP2D6 can be probed by site directed mutagenesis studies as described in e.g. Flanagan et al. (2004), Keizers et al. (2004, 2005b), Lussenburg et al. (2005) and Paine et al. (2003). Such experiments can be designed from structural models of enzyme–substrate complexes and the observed effect of mutations on metabolism and inhibition can subsequently be rationalized at an atomic resolution by modeling approaches. One mutant of CYP2D6 that was proposed based on computational models, is the F483A mutant (Lussenburg et al. 2005). The effect of this mutation on substrate binding affinities and orientations was shown to be strongly dependent on the substrate. For example, the metabolism of MAMC was no longer observed in the F483A mutant and metabolism of bufuralol was reduced. On the other hand no effects on the MDMA metabolism were found, while for dextrometorphan several alternative metabolites were observed. The binding affinity of these compounds did not seem to be influenced significantly by the mutation. For the substrate R-propranolol, however, the affinity is reduced by a factor 20 upon mutation. Interestingly, a large stereospecific affinity is observed in the mutant CYP2D6, but not in wild-type (WT). The metabolites formed from both R- and S-propranolol remain the same upon mutation of the enzyme (unpublished data).

In this study, we explore the stereospecific binding of propranolol to wild-type CYP2D6 and the F483A mutant. The spectral dissociation constants obtained were computationally rationalized. Computational tools may offer an atomic resolution often lacking in experiments. In the present case, one expects that subtle differences in the protein–ligand interactions in WT CYP2D6 or in the F483A mutant have a determining influence on the observed affinities. In order to catch such subtle differences a static approach based on protein–ligand structures only will not likely suffice, but rather the structure and dynamics of protein–ligand interactions have to be taken into account, for instance by molecular dynamics (MD) simulation. In CYPs it was shown that docking and scoring strategies can be applied to accurately predict binding modes and to select high affinity compounds from chemical databases (e.g. CYP101, CYP2D6 and CYP3A4) (de Graaf et al. 2006; DeVoss and Demontellano 1995; DeVoss et al. 1997; Kemp et al. 2004; Keseru 2001; Zhang et al. 1998). However, the scoring functions available in docking programs show little or no correlation with (experimental) binding affinity for these CYPs (Kemp et al. 2004; Keseru 2001). In the case of MDMA binding to CYP2D6 (WT and F120A mutant) it was shown that a dynamic view on the interaction was required to rationalize experimental findings (Keizers et al. 2005a). Detailed MD simulations also offer the possibility to calculate the free energy difference between complexes of different proteins and ligands.

Previously, successful free energy calculations have been reported using different methods. The linear interaction energy (LIE) method (Aqvist et al. 1994) was used for CYP101 (Paulsen and Ornstein 1996), CYP1A1 (Szklarz and Paulsen 2002); free energy perturbation (FEP) calculations (Beveridge and DiCapua 1989; Zwanzig 1954) for CYP101 (Helms and Wade 1995; Jones et al. 1993) and a combination of MD simulations, entropy estimates and Poisson–Boltzmann calculations (MMPB-SA) (Kollman et al. 2000) for CYP2B4 (Harris et al. 2004).

A remaining hurdle in the accurate calculation of CYP ligand binding affinity, however, is the diversity of binding modes of substrates, stemming from a flexible binding cavity that is large in relation to the size of the substrates. Subsequently, for many substrates the binding mode in CYPs is not as strictly defined as is the case for many other more substrate specific enzymes. This introduces sampling problems, prohibiting the application of MD based methods that can provide the most accurate free-energy calculations.

In the case of R- and S-propranolol binding to WT CYP2D6 and the F483A mutant, several approaches can be made, making use of different thermodynamic cycles (Tembe and McCammon 1984). We distinguish four of such approaches, which are exemplified in Fig. 1.

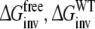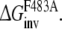  1. Calculate the free energy of inversion of R-propranolol into S-propranolol in solution and when bound to protein (WT or F483): Inline graphic and Inline graphic From this approach the relative binding affinities of R- and S-propranolol in protein (WT or F483A) can be obtained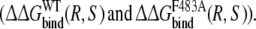 Inline graphic

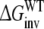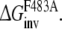  2. Calculate the free energy of inversion of R-propranolol into S-propranolol when bound to WT and when bound to the F483A mutant: Inline graphic and Inline graphic From this the relative free energy of transfer from WT to F483A for R- and S-propranolol can be obtained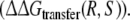 Inline graphic

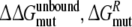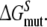  3. Calculate the free energy of mutating the phenylalanine sidechain into an alanine at position 483 in a substrate free protein model and a substrate (R- or S-propranolol) bound protein model Inline graphic and Inline graphic From this the relative binding affinities of the ligand (R- or S-propranolol) to WT and F483A can be obtained (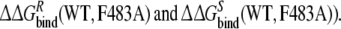Inline graphic

  4. Calculate the free energy of mutating the phenylalanine side chain into an alanine at position 483 in a R-propranolol bound protein model and in a S-propranolol bound protein model: 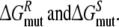Inline graphic From this the relative free energy of exchanging R-propranolol by S-propranolol in WT and the F483A mutant can be obtained (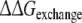Inline graphic (WT,F483A)).

Each of these approaches yields information that can be compared directly to the experimentally determined differences in binding affinities of R- and S-propranolol to WT and F483A CYP2D6. 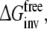Inline graphic representing the inversion of the stereocenter of propranolol free in solution, should equal zero. Because free energy is a state function, combinations of individual free energy terms defined above can be found that should sum up to exactly zero 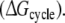Inline graphic Comparisons of calculated to experimental values and to theoretically defined values will be used to determine which of the approaches is most accurate and can be used to rationalize the stereospecificity of the F483A mutant.

Fig. 1.

Fig. 1

Open in a new tab

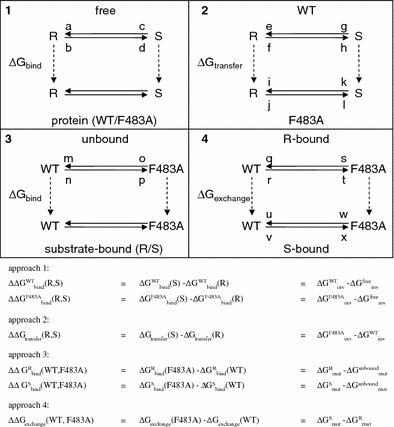
Four different approaches to calculate the differences in binding affinities of R-propranol (R) and S-propranolol (S) to wild-type (WT) and F483A mutant (F483A) CYP2D6, making use of different thermodynamic cycles (described in the text). Simulations at the initial and final stages along the solid arrows are labeled with a small letter (also referred to in the text and in Table 2)

Methods

Optical titrations

Dissociation constants of the substrates to the enzymes were determined by spectral titration, according to the method of Jefcoate (1978). Spectra were taken at room temperature on a Pharmacia Ultrospec 2000 spectrometer. In short, 1 ml of 0.5 μM purified enzyme in a 50 mM potassium phosphate buffer, pH 7.4 containing 10% glycerol, was divided over two cuvettes, to the first 5 μl of a 1 mM solution of R- or S-propranolol in the same buffer was added, to the second the same volume of just buffer. Difference spectra from 350 to 450 nm were taken before, and after each addition of compound. The substrates themselves did not show absorbance in this spectral range at the concentrations used. The difference between the absorbance at 390 and 425 nm was plotted against the substrate concentration to estimate the dissociation constant (Ks) using the following equation:

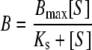graphic file with name M14.gif 1

where B is the absorbance difference (390–425) and Bmax is the absorbance difference when [S] → ∞.

CYP2D6-propranolol model

Coordinates for a ligand bound model of cytochrome P450 were obtained from homology modeling as described in (de Graaf et al. 2007; Keizers et al. 2005a). Very recently a model based on the crystal structure of this isoenzyme has been published, but this involves a ligand-free conformation of the protein (Rowland et al. 2005). Our homology model was found to agree with most of the details of the recently solved substrate-free CYP2D6 crystal structure. Structural differences between the homology model and crystal structure were the same differences observed between substrate-free and substrate-bound structures of other CYPs (e.g. 2C5; Wester et al. 2003a, 2003b; Williams et al. 2000), suggesting that these conformational changes are required upon substrate binding (de Graaf et al. 2007). For this reason we chose to rather use the ligand-bound homology model, which was validated in earlier MD simulations (Keizers et al. 2005a). Initial coordinates for R-propranolol in complex with the protein model were obtained by an automated docking approach as described in (de Graaf et al. 2005a, 2006).

Molecular dynamics simulations

Molecular dynamics simulations and free energy calculations were performed along all solid angles in the thermodynamic cycles in Fig. 1. All molecular dynamics simulations were performed using a preliminary version of the GROMOS05 programme (Christen et al. 2005). Interaction parameters were taken from the GROMOS 43A1 force field (Van Gunsteren et al. 1996). For propranolol, parameters were determined according to analogy to protein functional groups (see supplementary material). The GROMOS force field is a united atom force field, treating aliphatic hydrogen atoms together with the carbon atoms to which they are bound as a single interaction site. The wild-type protein was solvated in a rectangular periodic box containing 5,314 (ligand free simulation) or 5,306 (with R-propranolol bound) SPC water molecules (Berendsen et al. 1981). For the simulations of propranolol free in solution, the simulation box contained 2,367 water molecules. After an initial energy minimization in which the protein was positionally restrained, simulations were started at a temperature of 300 K, maintaining harmonic restraints with force constant 2,500 kJ mol−1 nm−2 on all solute atoms.

The system was carefully heated up and equilibrated as described in (Keizers et al. 2005a). Bond lengths were constrained at their minimum energy values using the SHAKE algorithm (Ryckaert et al. 1977) allowing for a time step of 2 fs. Nonbonded interactions were calculated using a triple range cutoff scheme. Interactions within a short range cutoff of 0.8 nm were calculated at every time step from a pairlist that was generated every five steps. Longer range interactions within a cutoff of 1.4 nm were calculated at pairlist generation and kept constant between updates. To account for electrostatic interactions beyond the long range cutoff, a reaction field contribution to the energies and the forces was calculated (Tironi et al. 1995). The temperature was kept constant by coupling solute and solvent degrees of freedom separately to a temperature bath of 300 K and using a relaxation time of 0.1 ps (Berendsen et al. 1984). Constant pressure was maintained by isotropically coupling to a weak pressure bath of 1 atm using a relaxation time of 0.5 ps and an estimated isothermal compressibility of 4.575 × 10−4 (kJ mol−1 nm−3)−1.

Free energy calculations

Free energies were calculated along the solid arrows in Fig. 1, using the thermodynamic integration method (Beveridge and DiCapua 1989; Kirkwood 1935). The arrows in this figure connect an initial (A) and a final (B) state, which can be defined as: (1) R-propranolol (A) versus S-propranolol (B) free in solution; (2) R-propranolol (A) versus S-propranolol (B) bound to wild-type and F483A mutant CYP2D6, respectively; (3) unbound wild-type (A) versus unbound F483A mutant (B) CYP2D6; (4) wild-type (A) versus F483A mutant (B) binding R- and S-propranolol, respectively. The Hamiltonians describing the initial and final states of each process were related using a coupling parameter λ, such that at λ = 0 the Hamiltonian described the initial state and at λ = 1, it described the final state of the process. Simulations were performed at a number of discreet λ-values and the free energy was obtained by numerical integration of the derivative of the Hamiltonian with respect to λ:

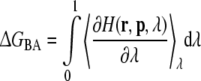graphic file with name M15.gif 2

where 〈∂H(r, p, λ)/∂λ〉λ represents an ensemble average obtained at the specified value of λ, r and p are the positions and momenta of all particles in the system. Free energies of mutating residue 483 and of R/S inversion of propranolol were calculated as shown Fig. 2. Processes involving the inversion of the chiral center of propranolol were performed in a two-step process (Zhou et al. 2005, 2006). First one stereoisomer was transformed into a planar intermediate (I), using six simulations for the integration of Eq. 2. The intermediate state was subsequently transformed into the alternative stereoisomer, using again six equidistant values of λ. Processes involving the transformation of residue 483 were obtained from 11 simulations at equidistant λ-values. Aromatic atoms in F483 were changed into non-interacting dummy atoms, while Cβ was changed from a CH2 group into a CH3 group. The nonbonded interactions at intermediate λ-values were described using the soft-core approach to avoid singularities in the derivative (Beutler et al. 1994). No changes were made in the covalent interactions. Twenty ps of equilibration were followed by 200 ps of data collection at every λ-value. Statistical error estimates on the ensemble averages were obtained using block averages (Allen and Tildesley 1987). Simulations with relatively large statistical errors were prolonged for another 200 ps, and additional points were added wherever needed to obtain a smooth profile of 〈∂H/∂λ〉 as a function of λ. A more empirical error estimate was obtained by comparing calculated free energy values associated with a forward process and the corresponding reverse process, also called hysteresis. An average free energy estimate from the forward and backward processes can be calculated using Boltzmann weighted averages using (Jarzinsky 1997; Lu et al. 2003):

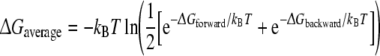graphic file with name M16.gif 3

A total of 76 simulations (6 × 2 × 6 + 4 added λ-points) were performed involving R/S inversions and 72 simulations (6 × 11 + 6 added λ-points) were performed involving F/A mutations. This leads to an overall simulation time of 33 ns.

Fig. 2.

Fig. 2

Open in a new tab

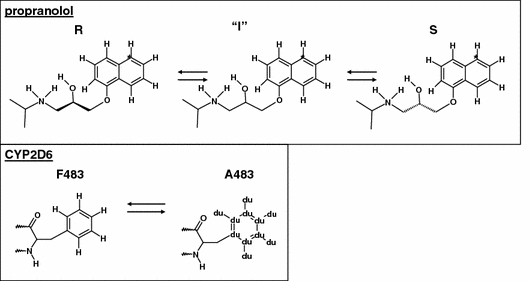
Schemes describing the (reversible) inversion of R- into S-propranolol and the (reversible) mutation of the residue on position 483 in CYP2D6 (F (WT) into A (mutant)). The planar propranolol intermediate is indicated by “I”, non-interacting dummy atoms in the A483 residue are indicated by “ du”. An asterisk indicates atom C5 of propranolol

Results

Experimental results

Both the propranolol enantiomers displayed a type I binding spectrum when added to wild-type CYP2D6, as derived from a decrease of the Soret maximum at 417 nm, and the appearance of a shoulder at 380 nm, which is typical for type I binding of a substrate (Jefcoate 1978). The affinity of the wild-type enzyme for the R- and S-enantiomers was similar (Table 1).

Table 1.

Ks values (μM) of S- and R-propranolol for wild-type and F483A mutant CYP2D6

Ligand Ks (μM)
Wild-type F483A
S-propranolol 26 ± 6 23 ± 2
R-propranolol 19 ± 3 376 ± 26
Open in a new tab

All values are the means of at least two independent experiments; ±SD as described in the experimental procedures

The addition of S-propranolol to the F483A mutant gave the same results as obtained for wild-type CYP2D6. The addition of R-propranolol to the F483A mutant of CYP2D6 did also lead to a type I spectrum, however, the affinity was 20-fold lower compared to the wild-type enzyme.

Computational approaches

Simulations at the initial and final stages along the solid arrows in Fig. 1 have been analyzed in detail. For every combination of R- or S-propranolol and WT or F483A mutant, four of such simulations of 200 ps were performed, labeled with small letters in Fig. 1. The four simulations included the end points of at least two different processes (R/S-inversion or F/A mutation) allowing for a comparison of convergence at every state.

The atom-positional root-mean-square deviation of Cα atoms with respect to the initial homology model, remained stable throughout the simulations, with maximum values of 0.25 nm. For a 464 residue protein (the N-terminus of the homology model is truncated by 33 residues) such values are reasonable and indicate simulations of a stable protein structure.

Binding mode orientation

The active site of CYP2D6 is formed by substrate recognition sites (SRS) 1 (B–C loop), 2 (F-helix), 4 (I-helix), 5 (β1-4) and 6 (β4-1). Figure 3 displays a top view of the active site with interacting residues displayed in stick. The protonated nitrogen atom and the hydroxyl group of propranolol can form a hydrogen bond network with the negatively charged carboxylate of E216 (not visible in Fig. 3, but shown in Fig. 5). Two binding modes for the naphthalene moiety can be distinguished (see Fig. 3). In WT CYP2D6, propranolol occupies a hydrophobic cavity formed by F120, V308, V370, and F483 (binding mode 1). In the F483A mutant, a larger cavity becomes available and SRS5 slightly shifts. The naphthalene moiety of propranolol now occupies a cavity formed by F120, V374, V370 and A483 (binding mode 2). In order to distinguish these binding modes, an atomic distance and an angle are defined in Fig. 3. The distance between the heme NB atom and the C5 atom of propranolol will be larger in binding mode 2. The angle defined by the Cξ atom in F120, the C5 atom of propranolol and the Cβ in V370 will approach 180 in binding mode 2. All simulations originated from the WT protein and R-propranolol occupying binding mode 1. During the free energy calculations, the ligand was seen to move to binding mode 2. Table 2 presents the average values of the NB-C5 distance and the Cξ–C5–Cβ angle over the end-point simulations, together with the average number of hydrogen bonds between propranolol and E216. The presence of a hydrogen bond was determined using geometric criteria: a donor–acceptor distance of at most 0.25 nm and a H-bond angle of at least 135°. Alternative hydrogen bonds partners of propranolol were not observed for significant periods of time.

Fig. 3.

Fig. 3

Open in a new tab

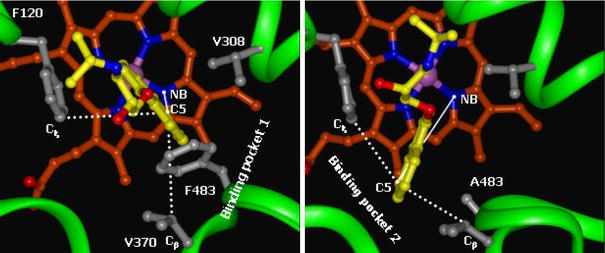
Representative snapshots of two distinct binding modes observed in simulations of WT CYP2D6 (binding mode 1, left panel) and the F483A mutant (binding mode 2, right panel). Propranolol is depicted in yellow sticks and hydrophobic substrate binding amino acid residues are depicted in grey ball-and- sticks. Two geometric features used to discriminate between the two binding modes are displayed: the distance between the nitrogen atom of heme pyrrole ring B (NB) and the C5 atom of R-propranolol and the angle defined by the Cξ atom in F120, the C5 atom in R-propranolol and the Cβ in V370

Fig. 5.

Fig. 5

Open in a new tab

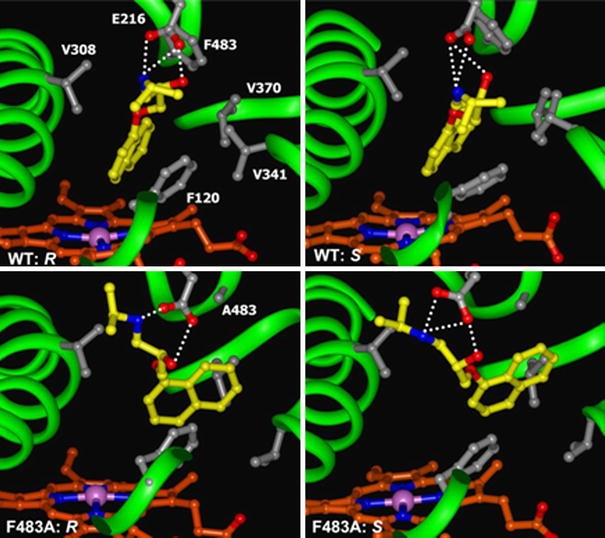
Representative orientations of R- and S-propranolol in the binding cavities of WT and mutant CYP2D6 observed during the MD-simulations at points defined in Fig. 1 and included in approach 2: e (WT: R), g (WT: S), i (F483A: R), and k (F483A: S). R-propranolol forms fewer hydrogen bonds than S-propranolol in the F483A mutant. The F483A mutation also causes a loss of favourable hydrophobic interactions, which can be compensated by increased hydrogen bond formation by S-propranolol, but not by R-propranolol

Table 2.

Average values and standard deviations of the geometric features defined in Fig. 3 together with the average number of hydrogen bonds between propranolol and E216 for the different MD-simulations at the initial and final stages of the inversion and mutation processes defined in Fig. 1

Simulations Propranolol CYP2D6 Average H-bonds NB-C5 distance (Å) F120 Cξ–C5–V370Cβ angle (deg)
e R-propranolol WT 2.2 4.7 ± 0.3 90 ± 6
f 2.2 5.4 ± 0.4 111 ± 9
g S-propranolol WT 2.4 4.7 ± 0.3 92 ± 5
h 2.6 4.5 ± 0.3 87 ± 4
i R-propranolol F483A 2.1 8.3 ± 0.5 159 ± 10
j 2.4 8.0 ± 1.9 138 ± 27
k S-propranolol F483A 2.7 10.5 ± 0.7 117 ± 12
l 2.1 8.6 ± 1.8 134 ± 23
q R-propranolol WT 2.4 6.6 ± 0.5 157 ± 13
r 2.2 4.8 ± 0.3 103 ± 6
s S-propranolol WT 1.5 4.6 ± 0.3 88 ± 5
t 2.2 4.8 ± 0.3 83 ± 4
u R-propranolol F483A 2.5 4.9 ± 0.6 104 ± 11
v 2.5 5.2 ± 0.7 101 ± 21
w S-propranolol F483A 1.7 5.0 ± 0.5 90 ± 6
x 1.7 4.9 ± 0.4 89 ± 5
Open in a new tab

The results belonging to approach 2 (defined in Fig. 1) are displayed in bold

Free energy calculations

The values of 〈∂H/∂λ〉 as a function of λ are displayed in Fig. 4 for all thermodynamic integration simulations. Values for the backward processes are multiplied by −1, for ease of comparison to the forward processes. Free energy estimates for all processes were obtained by a simple trapezoid integration of these curves and the resulting free energies are presented in Table 3. Using the definitions in Fig. 1, the different relative free energies are calculated and compared to experimental values.

Fig. 4.

Fig. 4

Open in a new tab

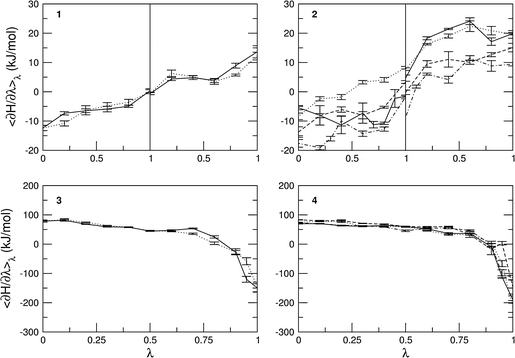
The values of 〈∂H/∂λ〉 as a function of λ for the calculation of the following free energy values. Panel 1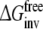Inline graphic forward (solid) and backward (dotted). Panel 2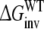Inline graphic forward (solid) and backward (dotted), 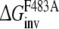Inline graphic forward (dashed) and backward (dash-dot). Panel 3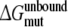Inline graphic forward (solid) and backward (dotted). Panel 4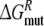Inline graphic forward (solid) and backward (dotted); 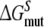Inline graphic forward (dashed) and backward (dash-dot)

Table 3.

Free energy estimates, the resulting average free energies, and the relative free energies for all processes defined in Fig. 1 and compared to experimentally determined values

  Forward Backward Averagea Hysteresisb
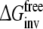Inline graphic −0.4 ± 1.5 −1.0 ± 1.8 −0.7 0.6
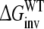Inline graphic 10.6 ± 1.5 19.1 ± 1.7 12.2 8.5
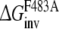Inline graphic 3.6 ± 2.1 6.8 ± 1.9 4.7 3.2
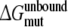Inline graphic 35.8 ± 3.0 36.0 ± 3.5 35.9 0.2
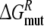Inline graphic 36.8 ± 2.0 40.2 ± 2.7 38.0 3.4
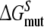Inline graphic 50.5 ± 4.3 41.3 ± 2.5 42.9 9.2
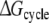Inline graphic 20.7 ± 11.4 13.4 ± 8.8 12.5
Averagea Experimental
Approach 1
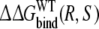Inline graphic 12.9 0.8
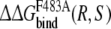Inline graphic 5.4 −6.9
Approach 2
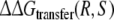Inline graphic −7.5 −7.7
Approach 3
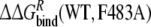Inline graphic 2.1 7.4
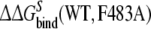Inline graphic 7.0 0.3
Approach 4
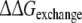Inline graphic (WT,F483A) 5.0 −7.1
Open in a new tab

aAverage determined according to Eq. 3

bHysteresis, defined as the difference between performing a process in the forward and backward directions, yields information on the convergence of the two independent calculations

Discussion

The primary aim of this study was to reproduce and rationalize the experimental finding that the F483A mutant of CYP2D6 has lower affinity for R-propranolol than for S-propranolol, using detailed molecular dynamics (MD) simulations. From these simulations, free energy estimates for all processes in Fig. 1 have been derived, which are presented in Table 3. The error estimates in Table 3 should be considered as statistical error estimates, indicating the statistical precision of the calculation. The absolute accuracy, however, is more difficult to determine. Three criteria that may give an indication of the accuracy can be distinguished. First, the hysteresis, defined as the difference between performing a process in the forward and backward directions, yields information on the convergence of the directions. At infinite sampling times, the hysteresis will be equal to zero. In Table 3, two cases can be observed with relatively large hystereses, the R/S inversion of propranolol in WT CYP2D6 and the F/A mutation in S-propranolol bound protein. In the other cases the hysteresis falls within the statistical uncertainty. Second, using the studied processes, one can obtain cyclic pathways along which the sum of free energies should be equal to zero. In Table 3, such a pathway is presented as 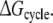Inline graphic It is clear that the present calculations do not meet this criterion, with values of 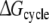Inline graphic larger than the statistical uncertainty. This indicates that not all free energy calculations have converged properly. The third criterion is the ability to reproduce experimental data. Knowing that not all simulations have reached convergence, this last criterion allows us to determine if any of the four approaches mentioned in the introduction can still be used to rationalize the experimental data at an atomic level.

Free energies of binding: approaches 1 and 3

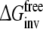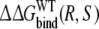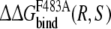In the first approach, the relative free energies of binding R- and S-propranolol are determined for both proteins. This approach uses a simulation of the R/S-inversion free in solution, of which the free energy value should fundamentally equal zero. As can be seen in Table 3, indeed Inline graphic is calculated to be 0 within the error estimate. However, the relative free energies Inline graphic and Inline graphic do not correspond to the experimentally determined value. The inversion process of propranolol when bound to the protein seems to be too unfavourable. Still, this may be due to a systematic contribution in the protein simulations, which would cancel in approach 2, where only free energies resulting from simulations of the propranolol inversion when bound to the protein are compared.

In the third approach, the relative free energies of binding R- and S-propranolol to the WT and mutant CYP2D6 protein are calculated and compared. The mutation in the ligand-free protein shows the smallest hysteresis in Table 3. The obtained value of 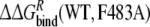Inline graphic is within 4 kJ mol−1 of the experimental value, which is within the statistical uncertainty, but not satisfactory. The value of 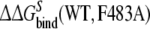Inline graphic is even further from the experimental value. Note that the value of 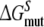Inline graphic shows the largest hysteresis, indicating that particularly these simulations may not have converged properly. An indication of the convergence can be obtained by comparing simulations k and l to simulations w and x in Fig. 1 in terms of the structural properties. From the average distance and angle in Table 2, we can see that in simulations k and l, the naphthalene moiety of S-propranolol binds in binding mode 2, while in simulations w and x, S-propranolol still orients according to binding mode 1 (see Fig. 2). This difference indicates that the processes (R/S inversion in the mutant protein, or F/A mutation with S-propranolol bound) do not converge to the same end point. This is also reflected by significant differences in H-bond counts (see Table 3): S-propranolol forms more H-bonds with E216 in the F483A mutant in simulations k and l than it does in simulations w and x. A similar difference in the average number of hydrogen bonds between S-propranolol and E216 in WT is observed when comparing simulations g and h with simulations s and t. This indicates that S-propranolol occupies a different area in phase space during the F/A mutation than during the other simulations leading to the same end-points. With these observations, we also find an explanation for the non-zero value of 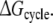Inline graphic Since not all end-points of the simulations are connected, the calculated cycle is not complete.

Free energies of transfer and exchange: approaches 2 and 4

Approach 4 uses the same mutational processes with propranolol bound to the protein as were used in approach 3. From these values the free energies of exchanging R-propranolol by S-propranolol in the mutant relative to WT (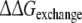Inline graphic (WT,F483A)) can be obtained. As was discussed above, the F/A mutation with S-propranolol bound does not converge to the same end-points. For this reason it should not be expected that the value of 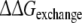Inline graphic (WT,F483A) will correspond to the experimental data (Table 3).

The only approach for which the calculated free energies match the experimental data appears to be approach 2. In this approach, the free energy of transferring R-propranolol from WT CYP2D6 to the F483 mutant is calculated relative to the free energy of transferring S-propranolol 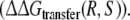Inline graphic The obtained value lies only 0.2 kJ mol−1 from the experimental value, which is well within the statistical error estimate of the calculations. It is also within kBT (∼2.5 kJ mol−1), corresponding to thermal fluctuations, which is the accuracy that can be expected from free energy calculations (Brandsdal et al. 2003; van Gunsteren et al. 2002).

In summary, the approaches using protein mutations (i.e., 3 and 4) do not converge sufficiently to reproduce the experimental data. A systematic error in the R/S inversion for protein-bound propranolol disqualifies approach 1, but still allows for a comparison with approach 2 (the inversion in the different proteins), which does yield free energy values in agreement with the experimental data. From Fig. 4 it can be seen that 〈∂H/∂λ〉 takes much larger values in the processes involving a mutation than in the processes involving an inversion. It has been shown earlier that free energy calculations involving smaller structural changes and smaller energy barriers yield more accurate free energy estimates than integrations involving large changes in 〈∂H/∂λ〉 (Mark et al. 1991; Zhou et al. 2005).

Possibly, better results with lower hysteresis and cycle closure, could be obtained by further extending the length of the simulations and by adding more λ-points (Mark et al. 1991; Oostenbrink and Van Gunsteren 2006). Another possible source of error could be the fact that a (substrate-bound) homology model was used, which has slightly different properties than the recently solved substrate-free crystal structure. However, we conclude that the changes required in the active site of CYP2D6 upon ligand binding are so large (de Graaf et al. 2007; Rowland et al. 2005) that the use of the homology model is justified. In addition, CYP2D6 will remain a challenging target for computational approaches, because of the broad range of inhibitors and substrates and the multiple binding modes observed for these (de Graaf et al. 2005b).

Now that we have determined that approach 2 reproduces the experimental data best, it is of interest to investigate the molecular basis for the calculated free energies in this approach.

Structural rationalization

In order to rationalize the difference in affinity for R- and S-propranolol upon mutation of residue 483, we can compare the observed binding modes in simulations e − l in Fig. 1. Representative orientations of propranolol in the binding cavities of WT and mutant protein in these simulations are presented in Fig. 5. In all simulations propranolol is involved in a salt bridge between the protonated nitrogen atom and the negatively charged E216 in the protein. Together with the propranolol hydroxyl group, these three moieties form a dynamic hydrogen bond network. The average number of hydrogen bonds observed throughout the simulations, however varies for different combinations of R/S-propranolol and WT/F483A proteins. Already in WT (simulations e − h), we observed fewer hydrogen bonds for R-propranolol than for S-propranolol (see Table 2 and Fig. 5).

For both stereoisomers, the naphthalene moiety orients itself according to binding mode 1, it fits snugly into a hydrophobic pocket formed by V308, V370, and F483 (pocket 1, see Figs. 3, 5). Upon the F483A mutation, the size of the pocket increases, which opposes tight hydrophobic interactions. The naphthalene moiety now occupies the pocket formed by F120, V370, V374 and A483 (pocket 2), according to binding mode 2, as indicated by a larger value of the heme-NB to propranolol-C5 distance (see Table 2). A large value of the Cξ–C5–Cβ angle indicates that a position between F120 and V370 is occupied. In the F483A mutant, R-propranolol binds in pocket 2 without significant decrease in the average number of hydrogen bonds (simulations i and j), compared to the simulations performed in WT (e and f). When S-propranolol binds in pocket 2 in F483A, hydrogen bond interactions are lost, in particular the propranolol-OH to E216-Oɛ hydrogen bond is observed only for 50% of the time in simulation l. This hydrogen bond can be regained by moving away from F120 and V370 (angle Cξ–C5–Cβ decreases) in simulation k. In fact the average number of hydrogen bonds in this simulation is even larger than for S-propranolol in WT, compensating the lack of tight hydrophobic interactions at the naphthalene moiety. R-propranolol cannot compensate for this loss.

In summary, the following picture arises. R-propranolol forms fewer hydrogen bonds than S-propranolol, both in WT and in the F483A mutant. The mutation causes a loss of favourable hydrophobic interactions, which can be compensated by increased hydrogen bond formation by S-propranolol, but not by R-propranolol.

Conclusions

Detailed molecular dynamics (MD) simulations have been performed to reproduce and rationalize the experimental finding that the F483A mutant of CYP2D6 has lower affinity for R-propranolol than for S-propranolol. Wild-type (WT) CYP2D6 does not show this stereospecificity. Four different approaches to calculate the free energy differences have been investigated and were compared to the experimental binding data. From the differences between calculations based on forward and backward processes and the closure of the thermodynamic cycles, it was clear that not all simulations have converged sufficiently. The approach that calculates the free energies of exchanging R-propranolol with S-propranolol in the F483A mutant relative to the exchange free energy in WT accurately reproduced the experimental binding data. Careful inspection of the end-points of the simulations involved in this approach, allowed for a molecular interpretation of the observed differences.

Electronic supplementary material

Footnotes

Electronic supplementary material

The online version of this article (doi:10.1007/s00249-006-0126-y) contains supplementary material, which is available to authorized users.

References

  1. Allen MP, Tildesley DJ (1987) Computer simulations of liquids. Clarenden Press, Oxford
  2. Aqvist J, Medina C, Samuelsson JE (1994) A new method for predicting binding affinity in computer-aided drug design. Protein Eng 7:385–391 [DOI] [PubMed]
  3. Berendsen HJC, Postma JPM, Van Gunsteren WF, Hermans J (1981) Ìnteraction models for water in relation to protein hydration intermolecular forces. Reidel, Dordrecht, pp 331–342
  4. Berendsen HJC, Postma JPM, Van Gunsteren WF, DiNola A, Haak JR (1984) Molecular dynamics with coupling to an external bath. J Chem Phys 81:3684–3690 [DOI]
  5. Bertilsson L, Dahl ML, Dalen P, Al-Shurbaji A (2002) Molecular genetics of CYP2D6: clinical relevance with focus on psychotropic drugs. Br J Clin Pharmacol 53:111–122 [DOI] [PMC free article] [PubMed]
  6. Beutler TC, Mark AE, van Schaik RC, Gerber PR, Van Gunsteren WF (1994) Avoiding singularities and numerical instabilities in free energy calculations based on molecular simulations. Chem Phys Lett 222:529–539 [DOI]
  7. Beveridge DL, DiCapua FM (1989) Free energy via molecular simulation: applications to chemical and biomolecular systems. Annu Rev Biophys Biophys Chem 18:431–492 [DOI] [PubMed]
  8. Brandsdal BO, Osterberg F, Almlof M, Feierberg I, Luzhkov VB, Aqvist J (2003) Free energy calculations and ligand binding. Protein Simul 66:123–158 [DOI] [PubMed]
  9. Christen M, Hunenberger PH, Bakowies D, Baron R, Burgi R, Geerke DP, Heinz TN, Kastenholz MA, Krautler V, Oostenbrink C, Peter C, Trzesniak D, van Gunsteren WF (2005) The GROMOS software for biomolecular simulation: GROMOS05. J Comput Chem 26:1719–1751 [DOI] [PubMed]
  10. DeVoss JJ, Demontellano PRO (1995) Computer-assisted, structure-based prediction of substrates for cytochrome P450(Cam). J Am Chem Soc 117:4185–4186 [DOI]
  11. DeVoss JJ, Sibbesen O, Zhang ZP, deMontellano PRO (1997) Substrate docking algorithms and prediction of the substrate specificity of cytochrome P450(cam) and its L244A mutant. J Am Chem Soc 119:5489–5498 [DOI]
  12. Flanagan JU, Marechal JD, Ward R, Kemp CA, McLaughlin LA, Sutcliffe MJ, Roberts GC, Paine MJ, Wolf CR (2004) Phe120 contributes to the regiospecificity of cytochrome P450 2D6: mutation leads to the formation of a novel dextromethorphan metabolite. Biochem J 380:353–360 [DOI] [PMC free article] [PubMed]
  13. de Graaf C, Pospisil P, Pos W, Folkers G, Vermeulen NP (2005a) Binding mode prediction of cytochrome p450 and thymidine kinase protein–ligand complexes by consideration of water and rescoring in automated docking. J Med Chem 48:2308–2318 [DOI] [PubMed]
  14. de Graaf C, Vermeulen NP, Feenstra KA (2005b) Cytochrome p450 in silico: an integrative modeling approach. J Med Chem 48:2725–2755 [DOI] [PubMed]
  15. de Graaf C, Oostenbrink C, Keizers PHJ, van der Wijst T, Jongejan A, Vermeulen NP (2006) Catalytic site prediction of and virtual screening accuracy of cytochrome P450 2D6 substrates by consideration of water and rescoring in automated docking. J Med Chem 49:2417–2430 [DOI] [PubMed]
  16. de Graaf C, Oostenbrink C, Keizers PHJ, Vugt-Lussenburg BM, van Waterschoot RAB, Tschirret-Guth RA, Commandeur JNM, Vermeulen NPE (2007) Molecular modeling-guided site-directed mutagenesis of cytochrome P450 2D6. Curr Drug Metab 18:59–77 [DOI] [PubMed]
  17. van Gunsteren WF, Daura X, Mark AE (2002) Computation of free energy. Helv Chim Acta 85:3113–3129 [DOI]
  18. Harris DL, Park JY, Gruenke L, Waskell L (2004) Theoretical study of the ligand–CYP2B4 complexes: effect of structure on binding free energies and heme spin state. Proteins 55:895–914 [DOI] [PubMed]
  19. Helms V, Wade RC (1995) Thermodynamics of water mediating protein–ligand interactions in cytochrome P450cam: a molecular dynamics study. Biophys J 69:810–824 [DOI] [PMC free article] [PubMed]
  20. Ingelman-Sundberg M (2004) Human drug metabolising cytochrome P450 enzymes: properties and polymorphisms. Naunyn Schmiedebergs Arch Pharmacol 369:89–104 [DOI] [PubMed]
  21. Jarzinsky C (1997) Non equilibrium equality for free energy differences. Phys Rev Lett 87:2690–2693 [DOI]
  22. Jefcoate CR (1978) Measurement of substrate and inhibitor binding to microsomal cytochrome P-450 by optical-difference spectroscopy. Methods Enzymol 52:258–279 [DOI] [PubMed]
  23. Jones JP, Trager WF, Carlson TJ (1993) The binding and regioselectivity of reaction of (R)-nicotine and (S)-nicotine with cytochrome-P-450cam—parallel experimental and theoretical-studies. J Am Chem Soc 115:381–387 [DOI]
  24. Keizers PH, Lussenburg BM, de Graaf C, Mentink LM, Vermeulen NP, Commandeur JN (2004) Influence of phenylalanine 120 on cytochrome P450 2D6 catalytic selectivity and regiospecificity: crucial role in 7-methoxy-4-(aminomethyl)-coumarin metabolism. Biochem Pharmacol 68:2263–2271 [DOI] [PubMed]
  25. Keizers PH, de Graaf C, de Kanter FJ, Oostenbrink C, Feenstra KA, Commandeur JN, Vermeulen NP (2005a) Metabolic regio- and stereoselectivity of cytochrome P450 2D6 towards 3,4-methylenedioxy-it N-alkylamphetamines: in silico predictions and experimental validation. J Med Chem 48:6117–6127 [DOI] [PubMed]
  26. Keizers PH, Schraven LH, de Graaf C, Hidestrand M, Ingelman-Sundberg M, van Dijk BR, Vermeulen NP, Commandeur JN (2005b) Role of the conserved threonine 309 in mechanism of oxidation by cytochrome P450 2D6. Biochem Biophys Res Commun 338:1065–1074 [DOI] [PubMed]
  27. Kemp CA, Flanagan JU, van Eldik AJ, Marechal JD, Wolf CR, Roberts GCK, Paine MJI, Sutcliffe MJ (2004) Validation of model of cytochrome p450 2D6: an in silico tool for predicting metabolism and inhibition. J Med Chem 47:5340–5346 [DOI] [PubMed]
  28. Keseru GM (2001) A virtual high throughput screen for high affinity cytochrome P450cam substrates. Implications for in silico prediction of drug metabolism. J Comput Aided Mol Des 15:649–657 [DOI] [PubMed]
  29. Kirkwood JG (1935) Statistical mechanics of fluid mixtures. J Chem Phys 3:300–313 [DOI]
  30. Kollman PA, Massova I, Reyes C, Kuhn B, Huo S, Chong L, Lee M, Lee T, Duan Y, Wang W, Donini O, Cieplak P, Srinivasan J, Case DA, Cheatham TE, 3rd (2000) Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models. Acc Chem Res 33:889–897 [DOI] [PubMed]
  31. Lu N, Adhikari J, Kofke DA (2003) Variational formula for the free energy based on incomplete sampling in a molecular simulation. Phys Rev E Stat Nonlinear Soft Matter Phys 68:026122 [DOI] [PubMed]
  32. Lussenburg BM, Keizers PH, de Graaf C, Hidestrand M, Ingelman-Sundberg M, Vermeulen NP, Commandeur JN (2005) The role of phenylalanine 483 in cytochrome P450 2D6 is strongly substrate dependent. Biochem Pharmacol 70:1253–1261 [DOI] [PubMed]
  33. Mark AE, Van Gunsteren WF, Berendsen HJC (1991) Calculation of relative free energy via indirect pathways. J Chem Phys 94:3808–3816 [DOI]
  34. Oostenbrink C, Van Gunsteren WF (2006) Calculating zeros: Non-equilibrium free energy calculations. Chem Phys 323:102–108 [DOI]
  35. Oscarson M, Ingelman-Sundberg M (2002) CYPalleles: a web page for nomenclature of human cytochrome P450 alleles. Drug Metab Pharmacokinet 17:491–495 [DOI] [PubMed]
  36. Paine MJ, McLaughlin LA, Flanagan JU, Kemp CA, Sutcliffe MJ, Roberts GC, Wolf CR (2003) Residues glutamate 216 and aspartate 301 are key determinants of substrate specificity and product regioselectivity in cytochrome P450 2D6. J Biol Chem 278:4021–4027 [DOI] [PubMed]
  37. Paulsen MD, Ornstein RL (1996) Binding free energy calculations for P450cam-substrate complexes. Protein Eng 9:567–571 [DOI] [PubMed]
  38. Rowland P, Blaney FE, Smyth MG, Jones JJ, Leydon VR, Oxbrow AK, Lewis CJ, Tennant MM, Modi S, Eggleston DS, Chenery RJ, Bridges AM (2005) Crystal structure of human cytochrome P450 2D6. J Biol Chem 281(11):7614–7622 [DOI] [PubMed]
  39. Ryckaert J-P, Cicotti G, Berendsen HJC (1977) Numerical integration of cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J Comput Phys 23:327–341 [DOI]
  40. Sheweita SA (2000) Drug-metabolizing enzymes: mechanisms and functions. Curr Drug Metab 1:107–132 [DOI] [PubMed]
  41. Szklarz GD, Paulsen MD (2002) Molecular modeling of cytochrome P450 1A1: enzyme–substrate interactions and substrate binding affinities. J Biomol Struct Dyn 20:155–162 [DOI] [PubMed]
  42. Tembe BL, McCammon JA (1984) Ligand–receptor interaction. Comput Chem 8:281–283 [DOI]
  43. Tironi IG, Sperb R, Smith PE, Van Gunsteren WF (1995) A generalized reaction force field method for molecular dynamics simulations. J Chem Phys 102:5451–5459 [DOI]
  44. Van Gunsteren WF, Billeter SR, Hünenberger PH, Krüger PM, A.E., Scott WRP, Tironi IG (1996) Biomolecular simulations: the GROMOS96 manual and user guide. Vdf blochschulverlag AG an der ETH Zürich, Zürich
  45. Vermeulen NPE (1996) Role of metabolism in chemical toxicity. In: Ioannides C (ed) Cytcochromes P450: metabolic and toxicological aspects. CRC Press, Boca Raton, FL, pp 29–53
  46. Wester MR, Johnson EF, Marques-Soares C, Dansette PM, Mansuy D, Stout CD (2003a) Structure of a substrate complex of mammalian cytochrome P450 2C5 at 2.3 A resolution: evidence for multiple substrate binding modes. Biochemistry 42:6370–6379 [DOI] [PubMed]
  47. Wester MR, Johnson EF, Marques-Soares C, Dijols S, Dansette PM, Mansuy D, Stout CD (2003b) Structure of mammalian cytochrome P450 2C5 complexed with diclofenac at 2.1 A resolution: evidence for an induced fit model of substrate binding. Biochemistry 42:9335–9345 [DOI] [PubMed]
  48. Williams PA, Cosme J, Sridhar V, Johnson EF, McRee DE (2000) Mammalian microsomal cytochrome P450 monooxygenase: structural adaptations for membrane binding and functional diversity. Mol Cell 5:121–31 [DOI] [PubMed]
  49. Wormhoudt LW, Commandeur JN, Vermeulen NP (1999) Genetic polymorphisms of human N-acetyltransferase, cytochrome P450, glutathione-it S-transferase, and epoxide hydrolase enzymes: relevance to xenobiotic metabolism and toxicity. Crit Rev Toxicol 29:59–124 [DOI] [PubMed]
  50. Zanger UM, Raimundo S, Eichelbaum M (2004) Cytochrome P450 2D6: overview and update on pharmacology, genetics, biochemistry. Naunyn Schmiedebergs Arch Pharmacol 369:23–37 [DOI] [PubMed]
  51. Zhang Z, Sibbesen O, Johnson RA, Ortiz de Montellano PR (1998) The substrate specificity of cytochrome P450cam. Bioorg Med Chem 6:1501–1508 [DOI] [PubMed]
  52. Zhou Y, Oostenbrink C, Van Gunsteren WF, Hagen WR, De Leeuw SW, Jongejan JA (2005) Relative stability of homochiral and heterochiral dialanine peptides. Effects of perturbation pathways and force-field parameters on free energy calculations. Mol Phys 103:1961–1969
  53. Zhou Y, Oostenbrink C, Jongejan A, Van Gunsteren WF, Hagen WR, De Leeuw SW, Jongejan JA (2006) Computational study of ground-state chiral induction in small peptides: comparison of the relative stability of selected amino acid dimers and oligomers in homochiral and heterochiral combinations. J Comput Chem 27:857–867 [DOI] [PubMed]
  54. Zwanzig RW (1954) High-temperature equation of state by a perturbation method. I. Nonpolar gases. J Chem Phys 22:1420–1426 [DOI]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

249_2006_126_MOESM1_ESM.doc (178.5KB, doc)

Articles from European Biophysics Journal are provided here courtesy of Springer

RESOURCES