Bending Dynamics of Fluctuating Biopolymers Probed by Automated High-Resolution Filament Tracking

Abstract

Microscope images of fluctuating biopolymers contain a wealth of information about their underlying mechanics and dynamics. However, successful extraction of this information requires precise localization of filament position and shape from thousands of noisy images. Here, we present careful measurements of the bending dynamics of filamentous (F-)actin and microtubules at thermal equilibrium with high spatial and temporal resolution using a new, simple but robust, automated image analysis algorithm with subpixel accuracy. We find that slender actin filaments have a persistence length of ∼17 μm, and display a q⁻⁴-dependent relaxation spectrum, as expected from viscous drag. Microtubules have a persistence length of several millimeters; interestingly, there is a small correlation between total microtubule length and rigidity, with shorter filaments appearing softer. However, we show that this correlation can arise, in principle, from intrinsic measurement noise that must be carefully considered. The dynamic behavior of the bending of microtubules also appears more complex than that of F-actin, reflecting their higher-order structure. These results emphasize both the power and limitations of light microscopy techniques for studying the mechanics and dynamics of biopolymers.

INTRODUCTION

Actin filaments and microtubules are semiflexible biopolymers that form the elastic cytoskeletal network within cells that controls cell migration, division, cargo transport, and mechanosensing (1). Understanding the mechanical behavior of these filaments is thus of central importance for establishing how they function as a dynamic mechanical scaffold within living cells. Indeed, mechanical models of the cell require accurate measurements of the stiffness and dynamical behavior of the component filaments (2–4). However, the semiflexible macromolecular backbone of microtubules and actin filaments results in physical behavior that remains incompletely understood.

Using light microscope images to directly measure the shape fluctuations of individual biopolymers is a powerful technique for studying their dynamics and mechanical behavior (5–9). By extracting a set of filament coordinates from each image, the variance of the curvature fluctuations induced by thermal motion can be used to obtain the bending rigidity. The rigidity is typically expressed in terms of the length scale beyond which the filament shows significant curvature due to thermal forces, known as the persistence length, 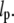Changes in thermally-induced curvature occur on a timescale that is set by viscous drag from the surrounding fluid. This time can be obtained from the relaxation time of a shape autocorrelation function, such as the mean-squared difference in curvature calculated for increasing lag times. Utilizing variations of this technique, actin filaments have been shown to have a persistence length of ∼17 μm (5,8,10), although they were initially suggested to have a length scale-dependent rigidity (11). Microtubules have been shown to be orders of magnitude more stiff, with a persistence length on the order of millimeters (8). However, recent studies have suggested that microtubule rigidity may depend on their growth velocity (7) and other factors related to their macromolecular structure (12–14). Indeed, it was recently suggested that inter-protofilament shearing leads to a softening of shorter microtubules (15). Other studies have suggested that internal dissipation mechanisms may dominate over hydrodynamic drag to increase the relaxation times of microtubules on short length scales (7,16).

Successfully extracting such mechanical information from microscope images is limited by position uncertainties resulting from image noise, requiring precise filament tracking. Despite the need for accurate filament localization, reports utilizing this technique often use semi-manual filament tracking methods and do not report a noise floor. Automated video tracking of objects with spherical symmetry, such as colloidal particles and fluorescent point-sources, is a well-developed technique for quantifying their dynamic behavior. Tracking of large numbers of spherical probe particles is central to microrheological measurements of the mechanical behavior of soft materials such as biopolymer gels and even living cells (17–19). Particle tracking algorithms typically employ an initial particle localization, such as intensity maxima, followed by particle position refinement using an intensity weighted center of mass (20) or fitting to a Gaussian or parabolic function. These algorithms can be used to obtain particle positions with subpixel accuracy. Positions are then linked in time to establish the trajectories of the particles. Precise tracking of objects with nonspherical symmetry, such as biopolymer filaments, presents more of a challenge. Unlike colloidal particles, the shape of the filament is not known a priori and thus conventional automated fitting techniques are no longer applicable. There is an extensive computer vision literature that describes identification of linear structures, such as roads or capillary tubes, from complex landscapes (21). A related technique for automated tracking of differential interference contrast (DIC) images of linear structures such as microtubules has been described (22). A recent study describes automated tracking of uniformly-sized fluorescent colloidal rods (23). There are also a number of papers describing filament-centroid tracking routines for in vitro motility assays of fluorescent actin filaments gliding over myosin-coated surfaces (24,25). However, to our knowledge there have been no reports describing automated contour tracking of fluctuating fluorescent filaments with sub-pixel accuracy.

In this paper, we develop and utilize a robust automated image analysis algorithm for tracking fluorescently-labeled biopolymer filaments with subpixel accuracy. We first demonstrate the accuracy of this technique by tracking immobilized fluorescent biopolymers and show that we obtain a root mean-square precision of ∼0.15 pixel (∼20 nm), even as the filaments begin to be photobleached after hundreds of exposures. We then use this technique to study the shape fluctuations of microtubules and actin filaments at thermal equilibrium down to short length and time scales. This allows us to address recent conflicting reports of the mechanics and dynamics of biopolymer bending fluctuations, particularly those of microtubules. The persistence length of actin filaments obtained from our measurements agrees well with previous experiments (5,8,10), l_p≈17 μm. We obtain microtubule persistence lengths on the order of a few mm, also in agreement with previous measurements (7,8,13,14). Our data show a slight correlation between filament length and stiffness, consistent with a recent study (15). However, we demonstrate that this correlation can in principle arise from inherent noise limitations that occur even with high precision measurements. Thus, over the range we study, there does not appear to be a systematic dependence of the bending rigidity on length or wavevector, in agreement with other studies (7,8,13,14). However, after a careful analysis of the relaxation times of the fluctuating normal modes, we find evidence that microtubules do display anomalous bending dynamics that reflects their more complex molecular structure (26) compared to actin filaments. Although the relaxation times of fluctuating actin filaments are consistent with simple viscous drag, for microtubules they are much longer than expected from hydrodynamic drag on short length scales. This effect may be due to a surprisingly large internal dissipation that dominates the relaxation times of microtubules on biologically relevant length and time scales. Our findings emphasize both the power and limitations of light microscopy techniques for probing the complex mechanical behavior of semiflexible polymers.

Filament tracking algorithm

The analysis algorithm used to track the shape of fluorescently labeled biopolymers in successive images consists of the steps detailed below. Briefly, an initial rough estimate of the position of a filament is first determined by thresholding the image. Pixels above threshold are then skeletonized to obtain a 1-pixel-wide representation of the filament. A polynomial fit to this skeleton is then used to walk along the contour of the filament, refining the position estimate by finding the intensity maximum along perpendicular cuts across the filament.

Background noise reduction

We first performed an image noise reduction by convolving each pixel of the image with a Gaussian kernel over a local region of size w:

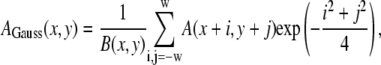(1)

where 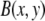is an appropriate normalization. The long wavelength background intensity variation is also accounted for by averaging each pixel of the unfiltered image over a local region of size w, to obtain 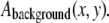The final filtered image is then obtained from: 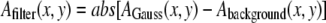(20). For initial filament localization, the size w was set to be around three times larger than the width of the filament, ∼5 pixels in our system. For refinement of the initial filament localization, we limit the convolution of local position information with neighboring position information by setting the filter size to approximately the width of the filament. An example of the result of this procedure for a typical image of a fluorescently labeled microtubule (Fig. 1 A) is shown in Fig. 1 B. Filters designed specifically for highlighting linear structures are another alternative (27).

FIGURE 1.

Example of the initial image processing stages of the filament localization algorithm for a typical fluorescence micrograph of an Alexa-488 dye-labeled microtubule constrained to move in a quasi-two-dimensional chamber. (A) Unprocessed image, and image after bandpassing, as in Eq. 1 (B), followed by thresholding (C), and skeletonization (D). Note that the spurious speck in the thresholded image is eliminated upon skeletonization.

Thresholding

Thresholding was done to separate the filament from the remaining background intensity fluctuations. Pixels with a value greater than the threshold value are assigned a value of 1, whereas those with a value less than the threshold value are assigned a value of 0. The threshold value is given by 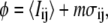where 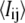is the average intensity value of all pixels ij, and 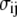is the standard deviation of the pixel intensity, both of which are dominated by the nonfilament background pixels. For high-frequency image acquisition, the signal/noise ratio (s/n) is usually small; thus, it is critical to determine an appropriate threshold value by determining the number of standard deviations away from the average, m. If m is too small, some background may be included, whereas if it is large, the entire filament may not be included. We typically start with a small value of m(∼3) and successively increase its value in small increments (0.2) until the backbone of the thresholded region is well fit by a polynomial. An example of thresholding is shown in Fig. 1 C.

Skeletonization

For good s/n and an appropriate threshold value, pixels above threshold will cover the fluorescent filament in a cluster several pixels wide. This cluster can be thinned to a 1-pixel-wide line using a skeletonization routine that erodes pixels while maintaining cluster connectedness (28). Skeletonization has the advantage that small clusters corresponding to nonfilament background fluctuations above threshold are typically eliminated by the erosion process. Persistent fluorescent specks that are still not eliminated are ignored using a simple routine to exclude objects above threshold from specific regions of the image. If necessary, more complex pixel clustering algorithms may be used to identify pixels associated with the desired filament (28). An example of skeletonization of a thresholded filament is shown in Fig. 1 D. This line, corresponding to a set of position coordinates x = i, y = j such that 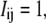provides a first, imprecise, estimate of the filament location.

Polynomial fitting and filament rotation

We refine the initial position estimate by analyzing the intensity distribution of sections taken perpendicular to the local slope of the filament (Fig. 2 A). To obtain the local slope, we fit the xy coordinates of the skeleton with a polynomial of order p. The polynomial degree required depends on the amount of curvature in the filaments under study; we typically use p = 3–5 for microtubules and actin filaments. We thus obtain a curve 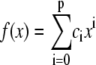that can be differentiated to obtain an estimate of the local slope of the filament at position 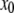: 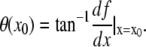To obtain the intensity profile of the filament perpendicular to this local slope, we rotate the original image by an angle 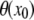around the position, 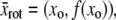to orient the filament horizontally. Successful image rotation requires the use of a good interpolation algorithm that maps the intensity of all pixels onto the rotated image without introducing artifacts. Image rotation routines implementing good interpolation algorithms accompany software packages such as IDL and Matlab. The process is computationally intensive, and thus we restrict image rotation to a local region of interest around the filament with coordinates 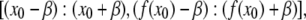where β is larger than the extent of the Gaussian kernel, w.

FIGURE 2.

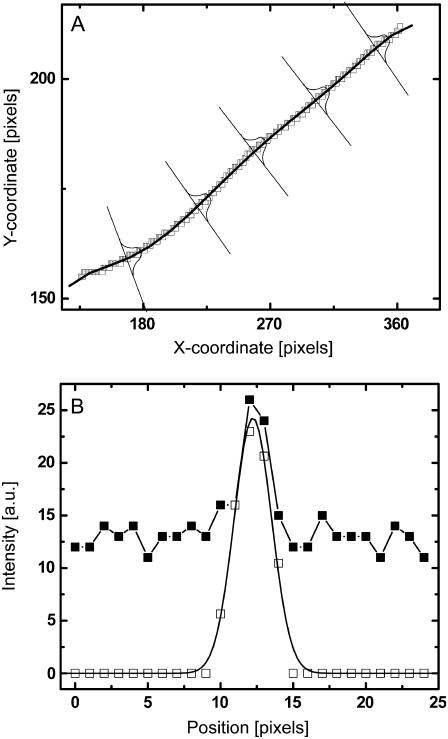
Example of filament position refinement by fitting Gaussian intensity profiles along cuts perpendicular to the filament contour. (A) Skeleton (see Fig. 1 D) in the xy coordinate frame with polynomial fit and schematic perpendicular cuts. (B) The intensity profile along a perpendicular cut of an unprocessed image is shown (solid squares). After bandpassing the image, the intensity distribution (open squares) is fit to a Gaussian (solid line). The filament location is taken to be the maximum of the Gaussian.

Because the skeletonization procedure erodes pixels at the ends of the thresholded filament, we sample perpendicular sections along the polynomial backbone from, typically, 4 pixels before to 4 pixels after the end points of the skeleton. We calculate the integrated signal along the perpendicular column of pixels k, 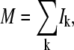and set a threshold value (“masscut”) for identified filament positions. The first and last filament positions with a signal mass above threshold define the two ends of the filament. Because fluorescently labeled biopolymers frequently display nonuniform labeling along their length, masscut thresholding often leaves holes in the position identification of the filament, particularly in low-s/n images. We fill in these gaps by linear interpolation between the nearest successfully sampled points.

Position refinement by Gaussian fitting

We proceed to analyze the intensity distribution of the vertical column of pixels in each rotated region. An example of such an intensity distribution is shown in Fig. 2 B (solid squares). By applying the Gaussian convolution kernel and background subtraction to this rotated local region, we improve the s/n ratio by eliminating both high- and low-frequency noise (Fig. 2 B, open squares). The center of the filament can be identified from this intensity distribution using either functional fitting or an intensity-weighted center of mass. It is important to note that the Gaussian filter leads to averaging of pixel intensities over a local region defined by the size of the Gaussian kernel (∼5–10 pixels); averaging the filament centroid obtained from adjacent perpendicular cuts of unbandpassed images could provide an alternative s/n improvement, without undesirable averaging in the perpendicular direction. We choose to fit the intensity distribution to a Gaussian intensity profile (Fig. 2 B, solid line), which yields the highest precision for tracking of spherical objects (29). We find that the primary advantage of Gaussian fitting over an intensity-weighted center-of-mass approach is its relative insensitivity to any residual background signal. The position of the center of the Gaussian, 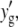identifies the position of the filament in the rotated frame. This center position is then mapped back onto the unrotated full image coordinate system to obtain the real-space position of the m^th sampled point 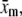using 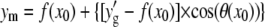and 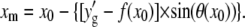This procedure is repeated along the polynomial at the desired sampling frequency, typically in steps of size 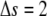pixels, until a full set of refined filament coordinates is obtained.

MATERIALS AND METHODS

Monomeric (G) actin was purified from rabbit skeletal muscle (30), with an additional gel-column chromatography step (Sephacryl S-200) to remove residual cross-linking and capping proteins. Actin filaments stabilized with phalloidin were prepared by polymerizing G-actin in AB-buffer (25 mM imidazole, 50 mM KCl, 2 mM MgCl₂, 1 mM EGTA, and 1 mM dithiothreitol, pH 7.4). Filaments were fluorescently labeled by using Alexa-488-modified G-actin, or by stabilizing unlabeled actin filaments with Alexa-488 phalloidin (Molecular Probes). We analyzed actin filaments with contour lengths between 8 and 15 μm. Tubulin was purified from bovine brain according to standard procedures and fluorescently labeled with Alexa-488. Microtubules were polymerized in K-Pipes buffer (80 mM K-Pipes, 1 mM EGTA, and 1 mM MgCl₂, pH 6.8) at 37°C and stabilized with 10 μM taxol.

Microtubules were imaged in a quasi-two-dimensional sample chamber that was made by placing a small volume (typically 0.3 μL) of a dilute solution of stabilized filaments augmented with a standard antioxidant mixture (glucose oxidase, catalase, glucose, 2-mercaptoethanol) (31) to slow photobleaching between a microscope slide and coverslip. The edges of the coverslip were sealed with mineral oil to prevent fluid flow due to evaporation. Adsorption of filaments onto the glass surfaces was avoided by passivating the glass with adsorbed bovine serum albumin or covalently attached poly-(ethylene glycol) chains (MPEG-silane-5000, Nektar, San Carlos, CA). All experiments were performed at room temperature.

Fluorescent images of microtubules were acquired on a Leica DM-IRB inverted microscope equipped with either a Hamamatsu intensified charge-coupled device (CCD) camera C7190-21 (exposure time 33 ms, 0.136 μm/pixel) or a Hamamatsu ORCA CCD camera C4742-95 (exposure time 59 ms, 0.128 μm/pixel) (Hamamatsu City, Japan). Images of actin filaments and some microtubules were obtained using a Nikon inverted microscope with Coolsnap HQ camera (exposure time of 5–100 ms, 0.129–0.194 μm/pixel). Microtubules were also imaged with a 10-ms exposure using a high-speed camera (Phantom V7, Vision Research, Wayne, NJ) equipped with an image intensifier (Model VS4-1845HS, Video Scope International, Dulles, VA). Some actin filament bending data (see Fig. 7) was obtained using a second method to slow down the filament dynamics by adding nonadsorbing polymer (2–3%, Dextran 500,000 g/mol). The polymer induces an attractive depletion interaction between the coverglass and the filaments, leading to confinement of the filaments close to the bottom surface. Using these samples, we were able to acquire images with either epi-illumination or total internal reflection fluorescence (TIRF) illumination. Due to the low levels of background fluorescence, we were able to decrease exposure time with TIRF illumination to a few milliseconds.

FIGURE 7.

Saturation values of the mean-square amplitudes of the bending modes of 12 actin filaments imaged using different ratios of exposure time to mode relaxation time. Light gray squares were imaged with 100 ms exposure in aqueous buffer, gray triangles were imaged with 100 ms exposure time in a viscous background solution. Black circles were imaged with 5–10 ms exposure time using TIRF illumination. The onset of deviation from q²-scaling (black line, slope 1/l_p = 17 μm) corresponds to wavevectors for which the relaxation time roughly equals the exposure time; fluctuations for larger wavevectors are blurred and register as smaller values.

The data in Fig. 11 B were fit to a line to obtain a slope of −0.050 ± 0.066, indicating no statistically significant correlation between persistence length, 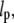and wavevector, q. In addition, the correlation coefficient was calculated using 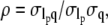where 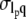is the covariance between l_p and q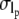, and and 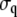is the standard deviation of l_p and q, respectively. The values of ρ vary from 1 (strongly correlated) to −1 (strongly anticorrelated). We obtained a value of −0.096, which is a statistically insignificant correlation (p > 0.005).

FIGURE 11.

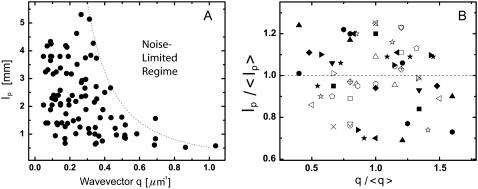
Persistence length of microtubule bending modes as a function of the corresponding wavevector q. (A) The persistence length appears to be lower at higher wavevectors, but this is likely due to a bias caused by intrinsic noise limitations. The dotted line denoting the noise-limited regime was obtained using conservative values for the noise floor (RMS error of 0.5 pixel) in Eq. 3. (B) Within individual filaments, there is no dependence of the persistence length obtained from each mode (normalized by the persistence length averaged over all modes) on wavevector (normalized by the wavevector averaged over all modes). Each filament is shown with a different symbol.

RESULTS

Evaluation of tracking precision

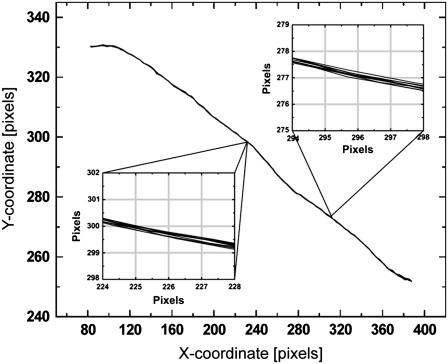
As a first test to evaluate the performance of our algorithm we determined the uncertainty in filament localization arising from camera shot noise and tracking limitations. This was accomplished by analyzing the shape fluctuations of microtubules that were immobilized by physically adhering them to poly-L-lysine coated surfaces. These microtubules were locked tightly to the glass coverslip surface, so any residual filament shape fluctuations that we measured would be due to uncertainty in filament localization inherent in our technique. To visualize the typical noise level, we overlay the extracted shapes of an immobilized filament for 10 consecutive frames of a movie in Fig. 3. The insets show higher-magnification views of two representative positions along the filament against a pixel-sized grid. This explicitly demonstrates that we obtained subpixel tracking accuracy with a noise level of ∼0.1–0.2 pixels (∼20 nm). This degree of accuracy is representative of the filaments we track in typical conditions, although, as we quantify below, the tracking accuracy decreased with decreasing s/n. Since spherically symmetric colloidal particles are much more straightforward to track, and typically result in ∼0.1-pixel accuracy, our filament tracking algorithm performed well, with a comparable root mean-squared (RMS) noise level.

FIGURE 3.

Filament contours for a microtubule fixed to an oppositely charged, poly-L-lysine-coated glass surface. (Insets) Higher-magnification views of 10 consecutive filament contours from a video acquisition; the pixel size is represented by the gray grid, demonstrating that the filament tracking algorithm performs with subpixel accuracy.

Bending rigidity of microtubules and actin filaments from mode analysis

We track microtubules and actin filaments freely fluctuating in quasi-two-dimensional chambers. We obtain the filament bending rigidities by analyzing the shape fluctuations using a Fourier decomposition technique developed in previous studies (8,9). From the pixel coordinates 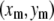of the filaments we first calculate the tangent angle 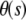as a function of arclength s, using: 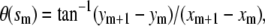where

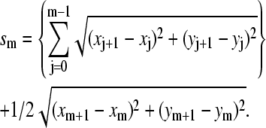The tangent angle is then decomposed into a sum of cosines,

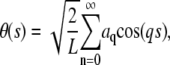(2)

where the wave vector q is defined as 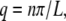with n the mode number and L the filament contour length (8). A cosine expansion of the tangent angle using different normalization prefactors has been used in other studies (9), but we find the normalization used by Gittes et al. most natural since it results in a length-independent variance of the mode amplitude. Use of this pure cosine mode decomposition assumes a zero-curvature boundary condition at the free filament ends, appropriate for freely fluctuating filaments.

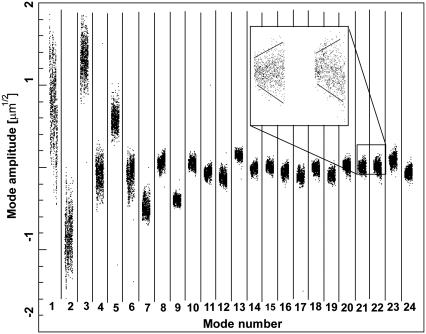
The amplitudes, 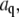of the first 24 bending modes of a freely fluctuating microtubule are plotted as a function of time in each of the subpanels of Fig. 4. The microtubule has a nonzero intrinsic curvature, 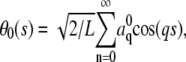resulting in a nonzero mean amplitude. The variance of the lower modes contains information about the flexural rigidity, whereas the amplitude of the higher modes is dominated by experimental noise. The amplitudes of these higher modes widen with time (Fig. 4, inset) due to photobleaching and concomitant reduction of the s/n.

FIGURE 4.

The amplitude of 24 bending modes for the microtubule shown in Fig. 1, plotted as a function of time in each of the subpanels. The microtubule has intrinsic curvature, resulting in a nonzero mean amplitude. The variance of the lower modes contains information about the flexural rigidity, whereas the amplitude of the higher modes is dominated by experimental noise. The amplitudes widen with time (see inset) due to photobleaching and concomitant reduction of the signal/noise ratio.

A convenient feature of the cosine expansion in Eq. 2 is that random noise due to errors in filament localization obeys the following simple relation (8):

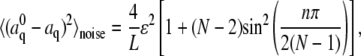(3)

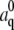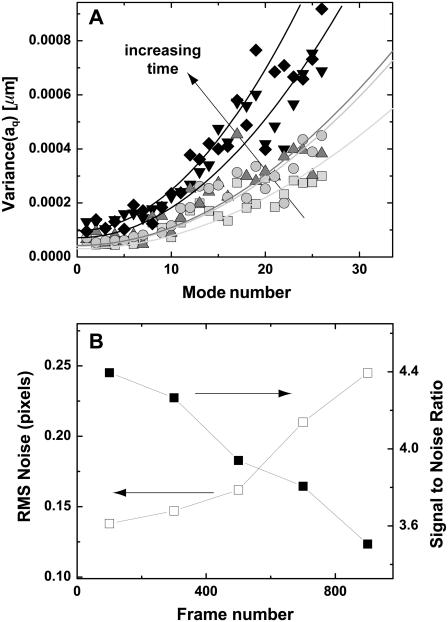
where is the mode amplitude corresponding to the filament's intrinsic curvature, 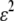is the mean-squared error in filament localization, and N is the number of position points sampled along the filament. We tested the validity of Eq. 3 by performing a mode analysis on immobilized microtubules. The variance in mode amplitude due to noise could be well fit to the above expression, as shown in Fig. 5 A. From this fit, we obtain a RMS error 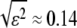pixels, in good agreement with the direct measurement of the noise floor shown in Fig. 3.

FIGURE 5.

(A) Variance of the Fourier coefficients 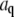of each mode amplitude plotted as a function of mode number n, for an individual immobilized microtubule. (B) The error in filament localization increases with frame number (i.e., time) as the signal/noise ratio of the video images is reduced due to photobleaching. Squares, frames 0–200; circles, frames 200–400, triangles, frames 400–600, inverted triangles, frames 600–800, diamonds, frames 800–1000. Filaments can be tracked with subpixel accuracy for a duration of typically 2000 frames.

By fitting the variance in the mode amplitude obtained from later frames of a movie sequence of an immobilized microtubule, we were able to evaluate the robustness of our tracking algorithm to decreasing s/n caused by photobleaching. Fig. 5 B shows that, as expected, the variance increases with time, reflecting the decreasing ability to precisely localize the position of the filament as it photobleaches. However, even after 900 frames, when the s/n has decreased by ∼20%, the error in pixel position is still only 0.25 pixels. With a high-sensitivity CCD camera, the s/n and corresponding tracking precision can be improved and maintained for many frames; we have successfully tracked filaments for over 7000 frames.

We note that the error in filament localization introduces an increase in the measured contour length of the filament, ΔL, which is of order 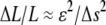(8). With the high tracking accuracy of our algorithm, this error should be <1% and can thus be neglected. A more important source of error is the fact that the ends of the filaments must be defined in each successive image by setting a masscut value. However, we find fluctuations in the measured length of the filament to be of order 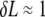pixel. For filaments of 10 μm or longer, this corresponds to an error in length of <1%, which is negligibly small.

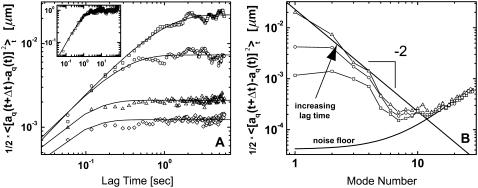
To investigate the time dependence of the mode amplitudes, 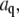we plot the mean-squared amplitudes of the first four modes of a 30-μm-long microtubule as a function of lag time in Fig. 6 A. The fluctuations in mode amplitude at a given lag time display a Gaussian distribution, suggesting that small intrinsic curvature on long length scales helps avoid artifacts from filament rotation (8). The variance of the distribution was therefore obtained by fitting a Gaussian to a histogram of the data; direct calculation of the variance is less precise due to occasional filament misidentification that greatly exaggerates a direct calculation of the variance.

FIGURE 6.

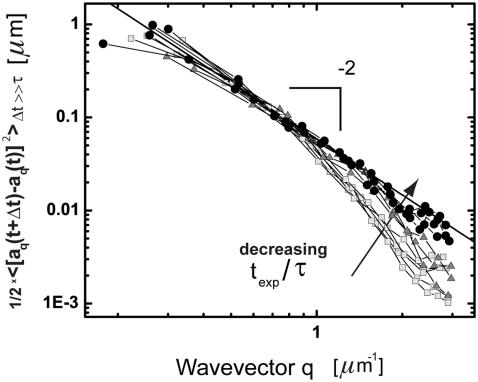
(A) Time dependence of the mean-square amplitude of Fourier coefficients 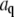of the first four bending modes of a 30-μm -long microtubule, with fits to Eq. 6. (Inset) Note that data scale together when plotted as a function of the scaled variables 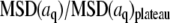and t/τ. (B) Mean-square amplitudes of the Fourier coefficients 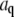plotted as a function of mode number n, for increasing lag times Δt = 0.059 s, 0.0177 s, and 5.9 s. At longer lag times, the variance of the amplitude for the first few modes approaches the expected q²-dependence of Eq. 6, with a persistence length of 4 mm (decreasing solid line). At higher mode numbers, the amplitudes are dominated by a RMS noise of 0.15 pixel (increasing solid line).

We first analyze the long-time limit, where the bending mode amplitudes have decorrelated. To understand this limit, we note that the bending energy U of a curved filament can be expressed as an integral of its deviation in curvature from the intrinsic curvature along the filament backbone (8,32):

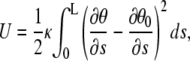(4)

where 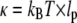is the bending rigidity; this is known as the worm-like chain Hamiltonian. By differentiation of Eq. 2 and subsequent integration, one obtains: 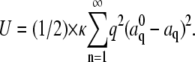By the equipartition theorem, the saturating values of the mean-square difference of the mode amplitude fluctuations are

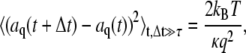(5)

where k_B is Boltzmann's constant, T is the temperature, 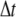is the lag time between different images, and τ is the relaxation (correlation) time of the mode. The modes must be fully decorrelated to accurately obtain the saturating variance, requiring the long-time limit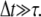

The saturation levels of the mean-square amplitudes extracted from the data in Fig. 6 A, plotted as a function of mode number, are shown in Fig. 6 B. Long-wavelength fluctuations corresponding to the first few modes of typical filaments are well above the noise floor and reflect curvature fluctutions due to thermal energy. The saturating amplitudes of the first few modes scale with the expected 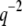dependence of Eq. 5 (Fig. 2 B, solid line). Higher modes cannot be used if their relaxation timescale, 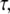is similar to or shorter than the exposure time 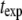(5–100 ms in our studies). The fluctuations of these modes are effectively blurred, causing them to appear stiffer. We were able to extend the measurable q range to higher q values by using short exposure times, either with TIRF illumination (33,34), or by using a high-speed camera equipped with an intensifier. As expected, for data acquired using short exposure times, the regime displaying the expected 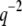dependence is extended, as demonstrated in Fig. 7.

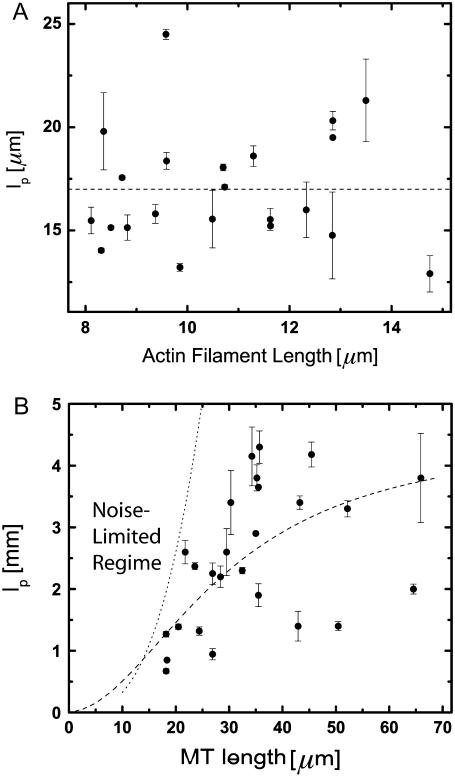
We obtain the persistence length of filaments by fitting the saturating mean-square amplitude versus q to Eq. 5. The fits were extended over the range of modes for which no systematic deviation below 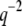was observed, i.e., 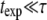(typically, the first three to five modes). From these fits, we find a persistence length l_p of 17.0 ± 2.8 μm (mean ± SD) for actin filaments, in good agreement with previous studies (5,8,10). This persistence length is independent of the length of the actin filaments within the observed range of 8–15 μm, as shown in Fig. 8 A. In contrast, for microtubules, we find a small apparent correlation between l_p and length: short filaments tend to appear softer, as shown in Fig. 8 B. Microtubules with lengths between 25 and 66 μm have an average persistence length of 2.8 ± 1 mm (mean ± SD), similar to previously reported values (7,8,14) (Fig. 8 B). Shorter filaments with lengths in the range 18–25 μm have a lower average persistence length of 1.5 ± 0.7 mm. The data are thus in qualitative agreement with a recent report suggesting that the internal protofilament structure of microtubules leads to a bending rigidity that depends on total microtubule length (15). 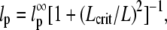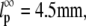Indeed, our data can be fit reasonably well to the reported functional form of this dependence with and 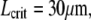as shown by the dashed line in Fig. 8 B. However, the close proximity of the noise floor both in our measurements (Fig. 8 B, dotted line) and in those of Pampaloni et al. (15) suggest a cautious interpretation of these results.

FIGURE 8.

Persistence length of 22 actin filaments and 26 microtubules plotted as a function of filament length. (A) Actin filaments show a relatively narrow distribution of persistence lengths with an average 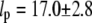μm (dashed line). There does not appear to be any dependence on filament length over the range studied. (B) Microtubules display a broader distribution of persistence lengths, and there is an apparent small correlation between the bending rigidity and filament length, with shorter filaments appearing softer. 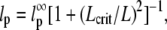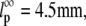Our data can be fit to a length-dependent expression for the persistence length, with and 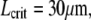as shown by the dashed line (15). However, the dotted line, denoting a conservative estimate of the intrinsic noise limitations, suggests that this correlation may only reflect a noise limitation.

Bending relaxation timescales

By using a Fourier decomposition of the filament shape, we can readily determine mode relaxation times from the autocorrelation function, as shown in Fig. 6 A. However, these Fourier modes are only approximations of the true normal modes of the dynamical equation of motion (see Appendix). Although a Fourier decomposition is suitable for determining the static behavior, as described above, Fourier modes are not normal modes of the system. Instead, Fourier modes will reflect the combined behavior of different normal modes relaxing on different timescales. Nevertheless, the Fourier modes are a convenient basis set that completely captures the instantaneous filament shape. It is therefore possible to express the true normal-mode amplitudes in terms of our measured amplitudes 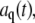and thus to measure the normal-mode relaxation rates. A more complete description of this procedure is provided in the Appendix.

Surprisingly, we found that over all experimentally accessible timescales, mode-mixing effects arising from the fact that these Fourier modes are not pure normal modes were small. This can be understood as follows. By symmetry, the odd (even) Fourier modes decompose into only odd (even) normal modes 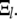Strictly speaking, this means that the amplitudes in Eq. 5 for finite 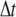exhibit non-single-exponential relaxation. For the lowest Fourier modes, n = 1, 2; however, only the corresponding l = 1, 2 normal modes are apparent at later stages of relaxation, since the higher-order normal modes relax more quickly. A comparison between the first Fourier mode and the corresponding normal mode of a microtubule is shown in Fig. 9 A. The relaxation times obtained from fits to a single exponential are very similar: 0.84 s for the Fourier mode and 0.82 s for the normal mode. For the higher Fourier modes, n = 3, 4…, the filament end effects are less apparent, and the normal modes are better approximated by Fourier modes. However, as discussed in the Appendix, since these modes mix with more slowly decaying modes the non-single-exponential behavior may be apparent at longer times in the relaxation. Nevertheless, these non-single-exponential corrections can be shown to be of order 10–15%. Thus, in practice, the dynamical behavior of the cosine modes is well approximated by the single-exponential relaxation of the normal modes:

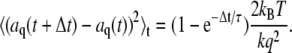(6)

FIGURE 9.

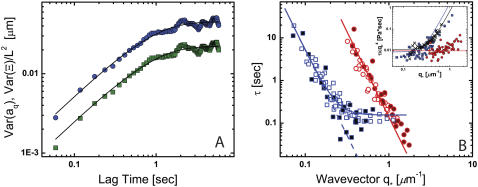
(A) Comparison between the decorrelation of the first Fourier mode (green squares) and the corresponding normal mode (blue circles) of the microtubule shown in Fig. 6 A. The normal mode was obtained from a sum of odd Fourier modes, as described in the Appendix. The relaxation time obtained from a fit to a single exponential is 0.84 s for the Fourier mode and 0.82 s for the normal mode. (B) Relaxation times of bending modes of actin filaments (circles) and microtubules (squares) plotted as a function of wavevector 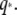Solid symbols represent data obtained using short exposure times (5–10 ms). The data for actin filaments are consistent with a 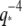dependence (solid line) expected from simple hydrodynamic drag (Eq. 7). For microtubules, we find a deviation from 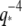at 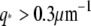(solid line, fit to Eq. 9; dotted line, fit to 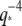). 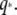The inset shows the same data normalized as plotted versus Black crosses are data for microtubules from Janson and Dogterom (7).

As shown in the appendix, the mode relaxation times τ are given by:

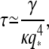(7)

where 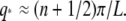The hydrodynamic drag coefficient for a rod confined between two surfaces is approximated by

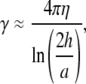where η is the buffer viscosity, h is the distance between the filament and the coverslips (∼1 μm), and 2a is the filament diameter (8,10). The mean-square fluctuation of the mode amplitudes can indeed be well fit to Eq. 6 (Fig. 6 A, lines).

The collected data for the relaxation times τ of 26 microtubules and 22 actin filaments, obtained from fits to Eq. 6, are shown in Fig. 9. For actin filaments (circles), the relaxation times decay rapidly with 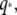consistent with the expected 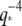-dependence. We fit the data to Eq. 7; using the average persistence length, 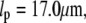we obtain a drag coefficient of 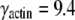mPa·s, in reasonable agreement with the calculated value of 1.8 mPa·s obtained from the approximate hydrodynamic expression. The inset shows the normalized relaxation timescales, 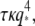which are roughly constant. This indicates that the bending relaxation timescale for actin filaments is set by hydrodynamic drag. The relaxation timescales of microtubules show a similar behavior (Fig. 9, squares) at the smallest wavevectors, with the relaxation times decreasing rapidly as 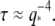However, at larger wavectors, the relaxation times are much larger than expected and appear to become wavevector-independent. Data taken with faster acquisition time also show this trend, although some points remain consistent with a simple 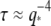scaling, suggesting that the dynamic behavior of microtubules is heterogeneous.

For microtubules, a similar deviation from 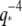-dependence was recently reported for the relaxation times of thermally fluctuating microtubules clamped at one end (7). A possible explanation for the origin of these anomalous relaxation times comes from a recent study (16) that incorporates an additional friction term in the Langevin equation (see Appendix), describing the bending dynamics of thermally fluctuating biopolymers:

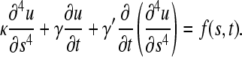(8)

This additional third term represents internal friction within the biopolymer. The mode relaxation times (Eq. 7) now become:

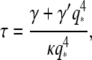(9)

where 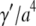can be considered an effective internal viscosity. Equation 9 implies that at wavevectors larger than 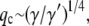internal friction will dominate and the relaxation times correspondingly become 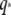-independent. The microtubule relaxation time data can be fit to Eq. 9, as shown in Fig. 9 B; using the average persistence length, l_p = 2.5 mm, we obtain a drag coefficient of 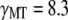mPa·s, in fair agreement with the value of 2.4 mPa·s estimated from the approximate hydrodynamic expression. From the fit, we also obtain an internal dissipation of 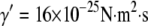, corresponding to an internal viscosity of 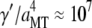mPa·s. Interestingly, this value is similar to that obtained in the previous study, 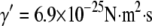(7) (fit shown in Fig. 9 B, inset). Thus, in both cases, microtubules appear to cross over to a wavevector-independent relaxation regime at 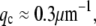on a length scale corresponding to 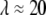μm.

Microtubules in cells

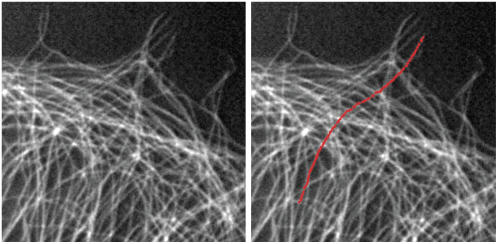
Our tracking algorithm can also be extended to extract the contours of fluorescently labeled microtubules within living cells. Because the cytoskeleton of living cells is typically packed with a dense network of microtubules with a mesh size of ∼1 μm, initial filament localization using a thresholding/skeletonization routine is insufficient. However, with a graphical interface that enables the user to provide an initial estimate of the filament position, it is possible to implement our simple algorithm with minor modifications. Alternatively, the initial filament localization may be accomplished with automated edge-detection routines (21). A modification for handling filament intersections must also be added to our algorithm for complex networks. This can be accomplished by introducing a χ² goodness-of-fit parameter for the Gaussian fit to the intensity profile of the filament cross-section. In this way, filament intersections, for which the intensity profile is poorly fit to a Gaussian, can be easily distinguished from nonoverlapping segments of the filament. Such filament positions can then be interpolated between neighboring sampled positions. In Fig. 10, we demonstrate that we can track a single microtubule through the dense network in a fixed tissue-culture cell using such an approach (4).

FIGURE 10.

Fluorescence image of a monkey kidney epithelial cell that has been fixed and stained, showing microtubules near the cell edge. We track one microtubule by combining the automated filament tracking algorithm with a manual initial filament identification. On the right is the fluorescence image with the filament coordinates overlaid in red.

DISCUSSION

We have developed and characterized a simple but robust algorithm for precisely tracking fluorescent filaments. To study biopolymer bending dynamics using this algorithm, we took care to identify and characterize the main sources of error that arise in these measurements.

1. Intrinsic noise makes the bending fluctuations appear larger and therefore makes the filament look softer.

2. Correlated fluctuations appear to have a smaller variance than uncorrelated fluctuations evaluated at longer times, and thus cause error since the filament appears stiffer.

3. Long exposure times relative to relaxation time can cause the filament to blur, making the fluctuations appear smaller and, thus, the filament appear stiffer.

4. Improper mode decomposition can lead to mode-mixing effects that hinder interpretation of the dynamic behavior of filaments.

Each of these sources of error can affect measurements of bending rigidity and/or relaxation time, and need to be carefully considered.

Filament bending rigidity

Using our precise tracking algorithm, we determine the persistence length and relaxation timescales of thermally fluctuating actin filaments and microtubules. Consistent with previous studies, we find that microtubules are two orders of magnitude stiffer than actin filaments. Both actin filaments and microtubules show a wavevector dependence of their bending amplitude that agrees well with expectations from the wormlike chain model. Actin filaments have a persistence length of ∼17 μm, independent of filament length. Interestingly, for microtubules we find a weak dependence on the filament length, with short microtubules appearing softer than long ones.

The persistence lengths plotted in Fig. 8, A and B, are essentially averages over multiple q-values, since they are obtained by fitting multiple bending modes to Eq. 5 (see Fig. 6 B). Thus, the apparent length dependence of the bending rigidity of microtubules in Fig. 8 B could actually reflect a q-dependence. To test this, we plot the persistence length obtained from the variance of each mode as a function of the corresponding wavevector, as shown in Fig. 11 A. Although there does not appear to be a strong correlation at small wavevector, high-wavevector fluctuations indeed appear to be softer. These soft high-wavevector modes would tend to make shorter filaments appear softer, since their relative contribution to the average stiffness (obtained from a fit of multiple modes to Eq. 5) would be larger. One possible explanation for this wavevector dependence is that at sufficiently high wavevectors, mode amplitude fluctuations due to filament tracking noise dominate over thermal bending fluctuations. This is unlikely, however, since modes in the noise regime obey the noise relationship (Eq. 3) that is easily identifiable, as illustrated in Fig. 6 B. Moreover, we only considered modes that clearly decorrelated with lag time, which is never true for modes in the noise regime. Thus, the high wavevector fluctuations we measure are not directly affected by intrinsic noise fluctuations.

Although intrinsic noise does not directly contribute to the measured fluctuations, it is possible that noise still indirectly affects the measurements, since it introduces a bias: high wavevector fluctuations can be detected above the noise floor only if the filament is sufficiently soft. This effect is likely to arise for microtubules in particular because of the large filament-to-filament variability of the persistence length. Indeed, using conservative values for the noise floor (taking an RMS noise of 0.5 pixel), an estimate of the location of this bias agrees with the trend in Fig. 11 A (solid line). Further support for this comes from the fact that within individual filaments there is no detectable wavevector dependence of the bending rigidity, as can be seen in the rescaled data in Fig. 11 B. As expected from the plot, linear regression shows no statistically significant correlation. Interestingly, although our data are consistent with the findings of Pampaloni et al. (15), intrinsic noise biasing likely contributes to the small correlation we find between total filament length and rigidity, as shown by the corresponding noise boundary in Fig. 8 B. Indeed, such artifacts introduced by noise limitations could also contribute to the bending rigidity/length correlation found in this recent study. Further experimental work incorporating a careful analysis of the noise will be required to determine whether there is indeed a significant dependence of the rigidity on microtubule length, and to elucidate the precise origin of this potentially interesting finding (15).

Bending relaxation timescales

By studying the time evolution of the mode amplitudes, we found that actin filaments display relatively simple bending dynamics, whereas microtubule bending reflects a more complex mechanical behavior. The relaxation times of actin filaments are consistent with the 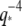-wavevector dependence expected from hydrodynamic drag. Microtubules, however, appear to cross over from a hydrodynamically-dominated relaxation regime at long length scales, 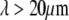to a wavevector-independent relaxation regime at shorter length scales,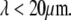

These anomalous relaxation timescales do not appear to be due to any of the sources of measurement error we identified. In particular, if high-wavevector relaxation timescales were affected by the exposure time of the camera, then the relaxation timescales would become smaller and not larger, as we have observed. We addressed the possibility of exposure time effects by obtaining data using much shorter exposure times (Fig. 9 B, solid symbols). These data show a similar trend, although some points remain consistent with a simple 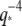scaling. Although the actin relaxation timescale data show a very slight deviation from a perfect 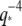-dependence possibly due to measurement errors, for microtubules the marked spread in the data showing deviation from the expected 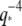-dependence does not appear to result from measurement error, and highlights the heterogeneity of the dynamic behavior of microtubules.

As discussed above, it was recently suggested that structural changes in the form of interprotofilament shearing lead to a filament-length-dependent stiffness (15). Interestingly, the model described there would seem to lead to a reduced effective stiffness, and therefore reduced relaxation rate for short wavelength modes. However, we find no evidence for a true wavevector-dependent rigidity (Fig. 11). Moreover, the strong trend in our microtubule relaxation time data could not be explained by the small stiffness bias we observe, since the normalized relaxation times (Fig. 9, inset) remain consistent with a wavevector-independent relaxation regime. The anomalous microtubule relaxation times thus appear to reflect some form of viscous dissipation within a heterogeneous population of microtubules.

To estimate the dissipative parameter γ′ in Eq. 8, we adopt a simple physical picture for the microtubules (16). For an elastic filament composed of a porous or viscoelastic gel-like material, internal dissipation results from the flow of a fluid of viscosity η′ through pores of size 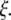This leads to 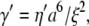where 2a is the filament diameter. Wavevector-independent relaxation times for bulky mitotic chromosomes appear to be described by such a picture (16). Because the diameter of microtubules is ∼25 nm, whereas actin filaments are a more slender 7 nm, similar internal dissipation should be more apparent for microtubules; this is qualitatively consistent with our findings. However, the high-frequency rheology of actin solutions (35–37) shows no evidence of deviations from pure hydrodynamic drag up to frequencies as high as 100 kHz, corresponding to relaxation times up to four orders of magnitude smaller than for microtubules in this study. This fact cannot be explained by the difference between microtubule and actin diameters alone. Specifically, the bending moduli of both microtubules and actin are consistent with the simple prediction 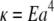of elasticity theory, where the Young's modulus 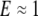GPa for both. Thus, the model above for porous filaments would result in a relaxation rate of order 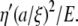It seems more likely that anomalously large values of γ′ for microtubules, as compared with actin, are due to slow structural fluctuations or conformational changes (16).

CONCLUSIONS

We have demonstrated that bending fluctuations of fluorescently-labeled biopolymers can be tracked with high spatial and temporal resolution using a simple and robust automated subpixel tracking algorithm. Using this algorithm, we confirmed previous studies reporting a persistence length of actin filaments of ∼17 μm, and microtubule persistence lengths on the order of a few millimeters. For microtubules, we found that a correlation between persistence length and filament length can arise due to biasing from intrinsic noise limitations. By studying the time evolution of actin bending fluctuations, we found that their relaxation times display a 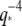hydrodynamic scaling, whereas some microtubules appear to transition into a high-wavevector regime dominated by surprisingly large internal viscous dissipation. These results emphasize the heterogeneous mechanical behavior of microtubules, and suggest that microtubules display anomalous bending dynamics that reflect their complex molecular structure.

APPENDIX

To understand the time dependence of the mode amplitude fluctuations (Fig. 6 A), we consider the following Langevin equation for changes in the transverse position u(s,t) of the filament as a function of arclength, s, and time, t (5,8,10,38):

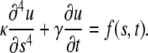(A1)

The first term accounts for the elastic restoring force prescribed by Eq. 4, the second term is the hydrodynamic drag on the filament as it moves through the viscous buffer, and the third term is the δ-function correlated random thermal noise acting along the filament.

Following Aragon and Pecora (38), we find solutions to the equation of motion (Eq. A1) in terms of normal modes 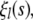which are solutions to the eigenvalue equation

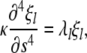(A2)

with the boundary conditions corresponding to no net forces or torques on the ends,

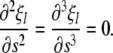(A3)

Here, the eigenvalues are given by 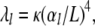where 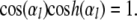To within better than 0.4%, the solutions of the latter are approximately given by 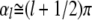for 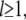where this approximation becomes increasingly accurate for the higher modes. Thus, even though the 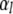will appear raised to the power of four in the expressions below, we will make no more than ∼1.5% error using the approximation above.

The solutions to Eq. A2 are orthogonal. Thus, we can construct an orthonormal basis for functions on 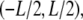given by

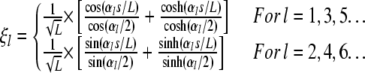(A4)

The solutions we seek can be expressed as

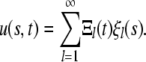(A5)

The Langevin equation can also be written now in terms of the amplitudes

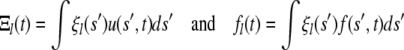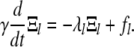(A6)

The solutions to this are of the form

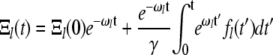(A7)

for 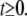This allows us to calculate the correlation functions

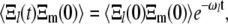(A8)

since 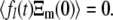However, given the time translation invariance of this result, as well as the nondegenerate spectrum of relaxation rates 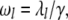this only makes sense if 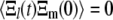for all 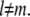This can also be seen from the fact that the bending energy

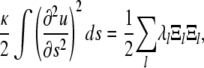(A9)

which results in Gaussian distributed amplitudes

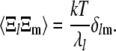(A10)

Here, we have used partial integration for the bending energy, together with the force- and torque-free boundary conditions.

Of course, we could have also used the more familiar Fourier modes

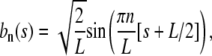(A11)

but only for the statics. These are not normal modes for the dynamics. The Fourier amplitudes 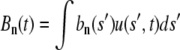now satisfy

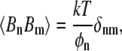(A12)

where this is an equal-time correlation function and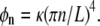

We note that the last two terms of Eq. A1 both depend on the local position/velocity of the polymer. As these variables are nonlocal in the tangent angle variables, it is not possible to write this Langevin equation in terms of θ(s). However, for weakly bending filaments, the local slope of the filament 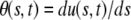can also be used to describe the shape. This shape can be further described by the Fourier amplitudes above:

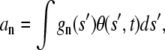(A13)

where

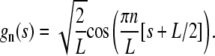(A14)

In terms of the normal modes, the amplitudes 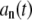can be expressed as

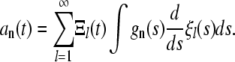(A15)

We define the matrix

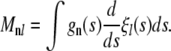(A16)

Thus, the correlation of amplitudes 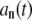can be found in terms of the normal modes:

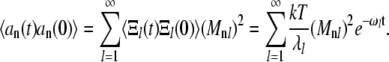(A17)

We note that the functions 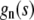are alternately odd and even, whereas the functions 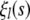are alternately even and odd. Thus, 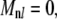unless n and l are either both odd or both even. For example, 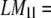7.05, 0, 5.69, 0, 5.66, 0, for l = 1, 2, … 6, whereas 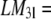−0.377, 0, 12.29, 0, 6.21, 0, for l = 1, 2, … 6.

Alternatively, the matrix inverse 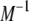can be used to express the normal mode amplitudes 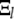in terms of the measured amplitudes :

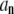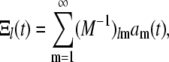(A18)

so that

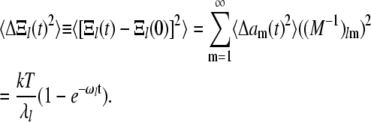(A19)

Since the matrices describing the linear transformations between 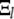and 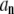are easily evaluated, this procedure provides a practical way to determine the normal-mode relaxation spectrum in terms of the 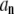that can be measured as discussed above.

For large l, the dominant term in this sum is for m = l, since the effect of the ends of the filament become negligible in this limit. Thus, we expect that for large enough n, the relaxation of 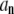is approximately single-exponential with relaxation rate

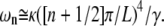(A20)

At the other end of the spectrum, for n = 1, 2, the relaxation of 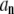will also be approximately single-exponential with relaxation rate 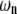for long times, since the most slowly relaxing mode in Eq. A17 is for l = n when n = 1, 2. The corrections to this approximate single-exponential behavior, due to modes l = n + 2, both have amplitudes smaller by approximately 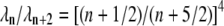and relax substantially faster (specifically, by a factor of 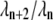). Using the matrix entries 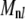above, we find that the second term in Eq. A17 is smaller than the first by a factor of 0.022 (0.036) for n = 1 (2). Perhaps surprisingly, even though the n = 3, 4 modes mix with the slowly relaxing l = 1, 2 normal modes in Eq. A17, using the 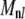above, we find the relative contribution of these slow modes to be 0.027 and 0.048, respectively. Including other subdominant terms in Eq. A17, we expect that it is sufficient to keep only the l = n term, to within ∼10–15%. This explains why we find little evidence, in practice, for non-single-exponential relaxation for any of the modes we examined. We have directly implemented the procedure described above for several data sets for n = 1–6 and find that the correction is within our error bars. However, accounting for the correct normal mode relaxation using Eq. A20 is essential for interpretation of the dynamics of both microtubules and F-actin in our experiments.