Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2007 Apr 13;93(1):54–61. doi: 10.1529/biophysj.106.103143

The Shape and Dynamics of the Leptospiraceae

Wanxi Kan 1, Charles W Wolgemuth 1
PMCID: PMC1914434  PMID: 17434949

Abstract

Most swimming bacteria produce thrust by rotating helical filaments called flagella. Typically, the flagella stick out into the external fluid environment; however, in the spirochetes, a unique group that includes some highly pathogenic species of bacteria, the flagella are internalized, being incased in the periplasmic space; i.e., between the outer membrane and the cell wall. This coupling between the periplasmic flagella and the cell wall allows the flagella to serve a skeletal, as well as a motile, function. In this article, we propose a mathematical model for spirochete morphology based on the elastic interaction between the cell body and the periplasmic flagella. This model describes the mechanics of the composite structure of the cell cylinder and periplasmic flagella and accounts for the morphology of Leptospiraceae. This model predicts that the cell cylinder should be roughly seven times stiffer than the flagellum. In addition, we explore how rotation of the periplasmic flagellum deforms the cell cylinder during motility. We show that the transition between hook-shaped and spiral-shaped ends is purely a consequence of the change in direction of the flagellar motor and does not require flagellar polymorphism.

INTRODUCTION

Bacterial swimming is often driven by long helical filaments that are rotated at one end by a molecular motor. In most flagellated bacteria, the flagella protrude into the fluid environment. Rotation of the flagellar filament or filaments exerts force on the fluid, producing thrust. This mechanism of motility works well if the bacterium lives in a bulk fluid, but for those bacteria that prefer to invade a host there are at least two disadvantages to this mechanism. First, the extracellular environment of mammals is not a pure fluid, but is typically gel-like, which slows down or halts many swimming bacteria (1,2). Second, the immune system of mammals naturally identifies the protein, flagellin, that composes the flagellar filament and this interaction can lead to the innate immune response (3,4).

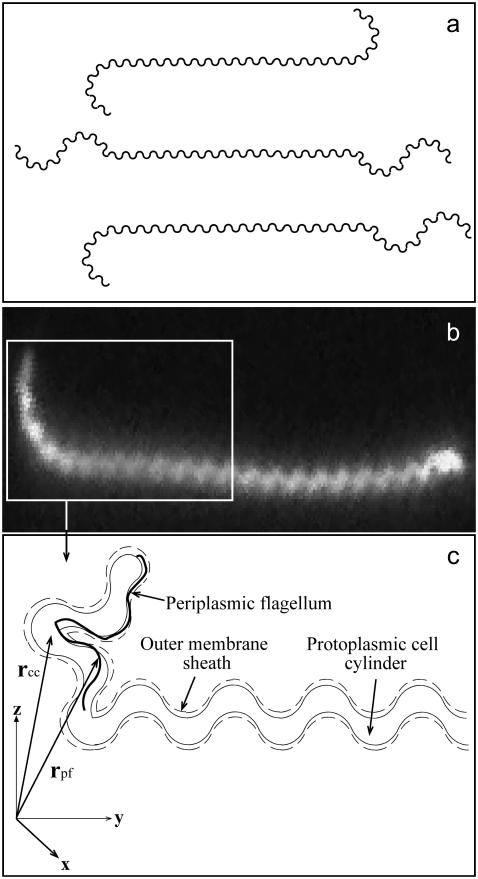
Modifications of the same apparatus, though, can overcome these difficulties. The spirochetes, a unique group of bacteria, with some members being highly virulent in humans, embed their flagella inside their periplasmic space (the space between the inner membrane-cell wall complex—i.e., cell cylinder—and outer membrane sheath; Fig. 1 c). In this article, we focus on the Leptospiraceae, such as Leptonema illini, Leptospira interrogans, and Leptospira biflexa. These bacteria have a short, single periplasmic flagellum (PF) attached subterminally that extends toward the center of the cell, which is not long enough to overlap at the center with the flagellum from the other end (5). The flagella are structurally similar to those of rod-shaped bacteria, but when observed by negative-stain electron microscopy, they form a tight coil rather than being wavelike as are most bacterial flagella (5–10). When the cells are at rest, fixed, or dead, the ends of the cell are hook-shaped (Fig. 1, a–c) (7,11,12). Mutants that form uncoiled PFs or lack PFs are still helically shaped but have ends that are straight (i.e., they do not form hook-shaped ends) (5,13). In addition, cells with their outer membrane sheath removed are still helically shaped (14).

FIGURE 1.

FIGURE 1

Open in a new tab

(a) Schematic diagram of the shapes of the Leptospiraceae. The cell body of Leptonema illini is a right-handed helix with ends that are bent into either a hook shape or a spiral shape. If both ends are bent into a hook (top shape) or a spiral (middle shape), then the cell does not translate. If one end is bent into a hook and the other end is bent into a spiral (bottom shape), then the cell propagates in the direction of the spiral end. (b) A dark field image of a cell with two hook-shaped ends. Image courtesy of Stuart Goldstein. (c) Schematic diagram of the relative position of the periplasmic flagellum to the cell body and the coordinate system used for our calculations. Leptospira spp. have one short flagellum at each end that is attached to a flagellar motor located at the end of the cell in the inner membrane.

Rotation of the PF by a flagellar motor is believed to induce deformations in and counter-rotation of the CC. The combination of these deformations and rotations of the CC produce the thrust that drives motility. Swimming Leptospiraceae exhibit a number of different cell shapes. In cells that are translating, the anterior end is spiral-shaped and the posterior end is hook-shaped (Fig. 1 a) (7,12,15). Cells readily reverse directions, with the spiral end becoming hook-shaped and the hook-shaped end becoming spiral-shaped. Nontranslating forms are also seen where both ends of the cell are either hook-shaped or spiral-shaped (Fig. 1 a) (7,12,15). Several lines of evidence indicate that the spiral-shaped end is associated with counter-clockwise rotation (the frame of reference is viewing the flagella along its length from its distal end to the insertion point on the cell cylinder) of its associated PF, and the hook-shaped end is associated with clockwise rotation. Thus, translating cells are associated with cells that rotate their PFs in opposite direction. Taken together, the results indicate that the direction of rotation of the PF and its interaction with the cell cylinder determines the morphology of the end (7,11,12,16,17).

THE MODEL

In this article, we explore the role of the elasticity of the cell cylinder (CC) and its interaction with the PF in determining the morphology of the Leptospiraceae. Since these bacteria are thin, right-handed helical bacteria with a length of 6–20 μm and a diameter of 0.1–0.2 μm (11,12,18,19), we consider the CC to be an elastic filamentary object that prefers to be helical with curvature, 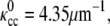Inline graphic and torsion, 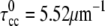Inline graphic (19). The position of the CC can be defined by the position of its centerline, rcc(s), where s is the arclength (Fig. 1 c). We also consider the bacterial flagellum to be a tightly-coiled elastic filament with preferred curvature, 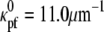Inline graphic (5). The outer membrane sheath is proposed to hold the PF at the radius of the CC. Since this radius is smaller than the other length scales (the lengths of the PF and CC, and the radius of curvature and the pitch for the CC), we ignore the displacement of the flagellum from the centerline of the CC and set rpf = rcc.

It is convenient to define a material, orthonormal triad, (e1, e2, e3), with respect to the CC and a separate triad for the PF. Here, e3 is the tangent vector, e1 points to an imaginary painted line on the surface of the bacterium, and e2 = e3 × e1. The curvature and twist of the CC can be defined by a strain vector, Ωcc(s), where Ω1,cc and Ω2,cc are the curvatures about e2 and e1, respectively, and Ω3,cc is the twist per length about the tangent vector. We assume that the PF is free to rotate with respect to the cell body and define the angle, α, between the PF orthonormal triad and that of the CC. Therefore, the strain vector for the PF can be written as

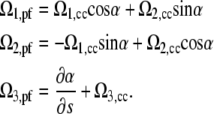graphic file with name M4.gif (1)

Assuming linear elasticity, the energy required to deform an elastic filament is proportional to the square of the deviation of the curvatures and twist from the preferred values,

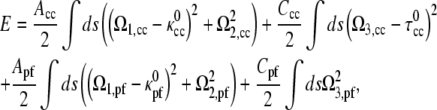graphic file with name M5.gif (2)

where Acc and Apf are the bending moduli for the CC and PF and Ccc and Cpf are the twist moduli for the CC and PF. In general, the moment along the centerline, M, is the functional derivative of the energy with respect to Ω,

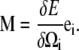graphic file with name M6.gif (3)

This moment satisfies the dynamic Kirchoff rod equations

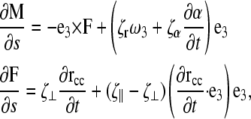graphic file with name M7.gif (4)

where F is the force on the filament, ζr is the drag coefficient for rotation about the tangent vector, ζα is the drag coefficient for rotation of the PF with respect to the CC, ζ⊥ is the drag coefficient for translational motion perpendicular to the tangent vector, and ζ‖ is the drag coefficient for motion parallel to the tangent vector (see the Appendices for the full derivation of this result). In addition, the dynamics for the rotation of the PF around the CC is given by

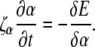graphic file with name M8.gif (5)

RESULTS

We begin by examining the behavior of the model equations in the absence of applied forces and torques. We expect that this scenario should reproduce the hook-shaped end morphology that arises when the flagella are not rotating, i.e., the bacterium is at rest, fixed, or dead (Fig. 2 a) (7,8,12). Setting the elastic moment equations (Eq. 3) equal to zero, we find the dependence of the strain vector on α,

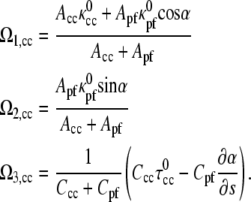graphic file with name M9.gif (6)

FIGURE 2.

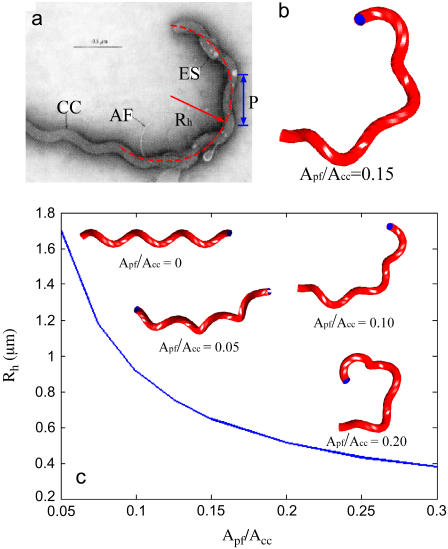
FIGURE 2

Open in a new tab

(a) Electron micrograph image of the hook region of a serotype illini cell showing the protoplasmic cell cylinder (CC), the axial filament (AF), and the external sheath (ES). The hook region has a radius of curvature, Rh, and pitch, P. Electron micrograph originally published in Berg et al. (7) and reproduced with permission from N. Charon. (b) Computed shape of the hook region with Apf/Acc = 0.15. (c) Hook region radius of curvature as a function of the ratio of the PF bending modulus to the CC bending modulus, Apf/Acc. Insets show the computed shapes for different values of Apf/Acc.

Minimizing the energy equation, Eq. 2 with respect to α and using Eq. 6 leads to

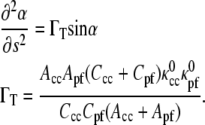graphic file with name M10.gif (7)

For most materials, the ratio of the twist modulus to the bending modulus is between 2/3 and 1 (20). Since the material properties for the CC and PF have not been measured, we use that Ccc/Acc = Cpf/Apf = 1. There remains one free parameter, the ratio of the PF bending modulus to the CC bending modulus, Apf/Acc.

Solving Eq. 7 over a total length of 3 μm (the approximate length of the PF determined by the length of the hook region) and using Apf/Acc = 0.15 leads to the hook-shaped morphology shown in Fig. 2 b. To compare the calculated morphology with the shape of the hook-shaped region of a L. illini cell, we measured the radius of curvature of the hook region, Rh, and the pitch, P, of the cell cylinder (See Fig. 2 a). For the calculated shape shown in Fig. 2 b, the radius of curvature of the hook region is 0.65 μm and the pitch of the CC is 0.64 μm. We measured Rh and P from an electron micrograph of the hook-region of L. illini shown in (7) (Fig. 2 a) and found Rh = 0.70 μm and P = 0.60 μm.

As the ratio, Apf/Acc, has not been measured, we explore the behavior of the end morphology for the Leptospiraceae as a function of this ratio. For Apf/Acc = 0, the flagellum has no effect on the morphology and the cell cylinder remains helical (Fig. 2 c). As Apf/Acc increases, the flagellum becomes stiffer and therefore has more effect on the shape, causing the cell cylinder to bend into a hook shape. To quantify this effect, we plot Rh as a function of Apf/Acc. Larger values of Apf/Acc produce a smaller radius of curvature for the hook shape (Fig. 2 c). As mentioned above, we find the best agreement between the model predictions and the end morphology of L. illini for values of Apf/Acc of ∼0.15.

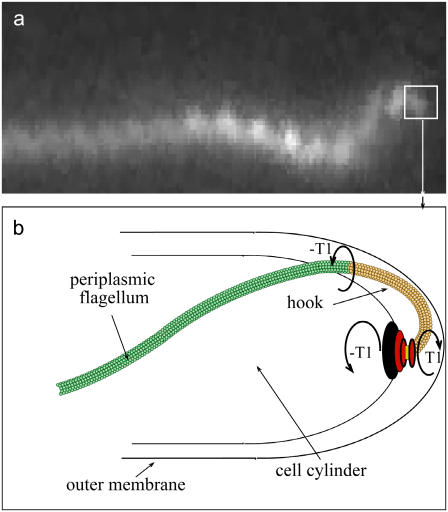
To swim, the bacterium rotates the flagellum that is located at either end of the cell using a rotary flagellar motor. Evidence suggests that clockwise rotation of the flagellum maintains the hook-shaped end morphology (Fig. 1 b), whereas counter-clockwise rotation results in a spiral-shaped end (Fig. 3 a). To test whether our model can account for these morphologies, we idealize the effect of the flagellar motor as a pure torque, with magnitude T1, applied to the flagellum along the tangent direction of the flagellum. We assume that the flagellum protrudes out of the inner cell membrane in a direction tangent to the long axis of the cell at the cell end (Fig. 3 b). Torque balance requires that the CC must feel an equal but opposite torque to that applied on the PF. In addition, since the PF resides in the periplasmic space, the PF must bend back 180° (Fig. 3 b). In rod-shaped bacteria, a flexible hook connects the flagellar filament to the flagellar motor. This hook acts like a universal joint (21) and redirects the torque on the flagellum. In the real system, the motor is a short distance from the tip and comes out of the side of the CC. This offset may induce an additional wobble of the tip that will not be accounted for in this model.

FIGURE 3.

FIGURE 3

Open in a new tab

(a) Dark field image of the spiral-shaped end of Leptonema illini. Image courtesy of Stuart Goldstein. (b) Schematic diagram showing how the flagellar motor torque, T1, gets transmitted from the hook (yellow) to the flagellar filament (green). We assume that the torque is applied tangent to both the cell cylinder and the periplasmic flagellum.

We explored the dynamic behavior of the model under an applied torque from the flagellar motor using two methods—steady-state analysis and the full dynamic model. We began by solving the steady-state form of Eqs. 4 and 5 with a torque, T1, applied to the hook portion of the flagellum (which corresponds to a torque −T1 acting on the flagellar filament and the cell cylinder; see Fig. 3 b and Appendices for details). For all simulations, we used that Apf = 0.15 Acc, since this value gave the closest agreement for the end morphology in the absence of external forces or torques. We solved the equations in the region of the PF (a 3-μm length) and assumed that the remainder of the cell is rigidly fixed in space (Fig. 4 a). By treating the rest of the cell as being fixed, we do not expect the model to provide quantitative agreement with measurable quantities for translating Leptospiraceae. However, since L. illini cells tethered to the coverslip via antibody-coated microspheres still dynamically transition between hook- and spiral-shaped ends (17), we expect the model to provide qualitative or semiquantitative results for the morphology of the ends of the cell during flagellar rotation. Because we are assuming that the region of the cell away from the end of the cell is stationary, this treatment does not allow us to calculate the translational or rotational velocities for the cell. However, it is possible to calculate the total force and moment that are required to prevent the motion of the cell. This total force and moment can be used to estimate the propulsive thrust and rotational velocity that would occur if the fixed position constraint were removed.

FIGURE 4.

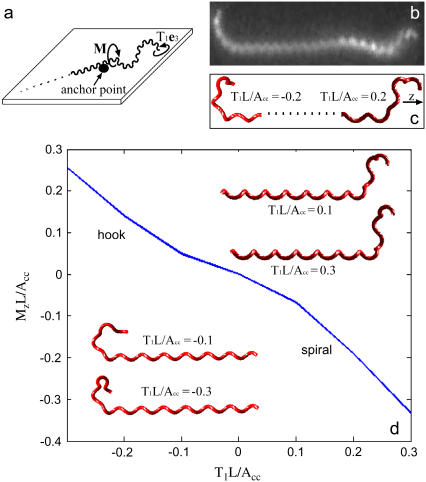
FIGURE 4

Open in a new tab

(a) Schematic of our steady shape calculation. The cell is assumed to be anchored near one end of the cell. This anchor point holds the cell fixed in position and applies a moment, M, to the cell. The flagellar motor applies a torque, T1 to the free end of the cell cylinder. (b) Dark field image of a translating L. illini cell with one hook-shaped end and one spiral-shaped end. Image courtesy of Stuart Goldstein. (c) Computed shape of the ends of a cell with Apf/Acc = 0.15 and T1L/Acc = 0.2 (left) and T1L/Acc = −0.2 (right). The swimming direction is along the z-axis. (d) Moment along the z-direction at the juncture between the cell end and the remainder of the cell required to hold the cell stationary, Mz, as a function of torque applied on the flagellum. The insets show the computed end shapes for representative values of T1. A helical portion of cell is drawn attached to the computed end shapes as a visual aid.

For negative applied torques, which corresponds to clockwise rotation of the flagellum, the model predicts that the cell end maintains a hook-shaped morphology. However, as the torque increases, the hook distorts by bending out of the original hook plane (see the insets to Fig. 4 d for T1L/Acc = −0.1 and T1L/Acc = −0.3). For positive values of T1, we found two solutions for the end morphology. The first solution is hooklike and is similar to the morphologies that are observed for clockwise rotation. The second solution resembles a left-handed superhelical structure (Fig. 4, c and d) and is qualitatively similar to the spiral-shaped ends of translating or tethered cells (Fig. 4, b and c).

To resolve which end shape would be observed for clockwise rotation, we solved the full dynamical problem over the entire cell length using a finite-difference, variable-order algorithm. We chose boundary conditions such that the total applied force at the ends was zero and the applied moments were T1Re3 and T1Le3 at the right and left ends, respectively. This method confirmed the steady-state calculation in that for counter-clockwise rotation of the flagella, the end was hook-shaped. Furthermore, for clockwise rotation of the flagellum, the end was spiral-shaped. One reason that the spiral shape may be favored is that it allows a greater percentage of the cell cylinder to lie closer to the rotational axis (the z-direction in Fig. 4 c), which produces less dissipation due to drag and would therefore be energetically favorable. This argument is similar in context to that posed by Levinthal and Crane (22) in the context of DNA transcription and by Goldstein et al. (23) for polymorphic transformations of bacterial flagella.

In Fig. 4 b, we show a dark field image of a translating L. illini cell with one hook-shaped end and one spiral-shaped end. Comparison to the shapes computed by the model for clockwise torque at the right end (T1L/Acc = −0.2) and counter-clockwise torque at the left end (T1L/Acc = 0.2, Fig. 4 c) is qualitatively similar. The model predicts that the spiral-shape during counter-clockwise rotation has the opposite handedness of the cell body, which is in agreement with the observation that L. illini has a right-handed cell cylinder and the spiral-shape is left-handed.

To hold the remainder of the cell stationary requires a moment to be applied at the juncture between the cell end and the remainder of the cell (Fig. 4 a). The rotation rate of the end about the swimming direction, which we will define as the z-direction (Fig. 4 c), should be roughly proportional to the z-component of this moment, Mz. The magnitude of the moment increases with increasing torque (Fig. 4 d). Interestingly, the model predicts that the hook shape requires a smaller moment than the spiral shape, which suggests that the rotational velocity of hook-shaped ends will be smaller than that for the spiral-shaped ends for tethered cells.

DISCUSSION

Here we have presented a model for the end morphology and dynamics of the Leptospiraceae. This model assumes that competition between the preferred shapes of the cell cylinder and the periplasmic flagellum determines the morphology of the ends of the bacterium. Since the PF is constrained to reside at the radius of the cell cylinder, both the PF and the CC must deform elastically. The minimum energy configuration in the absence of applied forces or torques is a hook shape. The model predicts that the bending modulus of the PF is ∼7 times smaller than that of the CC.

The Young's modulus of the cell wall of the Leptospiraceae has not been measured; however, the modulus of other bacteria has been. For example, optical trapping experiments estimated the Young's modulus of Bacillus subtilis to be 5.0 MPa (24) and atomic force microscopy has found the modulus for the cell wall of Myxococcus xanthus to be 1.3 MPa (25), 25.0 MPa for Escherichia coli (26), and 0.085–0.15 MPa for Magnetospirillum gryphiswaldense (27). The bending modulus of the cell can be estimated using the radius of the cell, a, and the thickness, t, of the cell wall as Acc = πEa3t. If we use a moderate value of the Young's modulus for the cell wall of 1.0 MPa and a thickness of 10 nm, we estimate Acc to be ∼2 × 10−23 N m2. Therefore, our model predicts the bending modulus of the PF to be ∼3 × 10−24 N m2. Estimates based on experiments using Salmonella flagellar filaments reported values ranging from 10−24 N m2 (28) to 10−22 N m2 (29). Kim and Powers reanalyzed the data from (29) using slenderbody theory and estimated a value of 3.2 × 10−24 N m2 for the flagellar bending modulus (30).

We showed that clockwise rotation of the PF driven by a torque applied by a rotary motor located at the end of the cell can maintain a hook shape. As well, rotation of the flagellum in a counter-clockwise direction can produce left-handed, spiral-shaped end morphology. These morphologies are a result of linear elastic deformation induced by the applied torque from the flagellar motor and the internalization of the PF inside the periplasmic space. Our model produces realistic cell shapes when the torque of the bacterial flagellar motor of the Leptospiraceae is between 0.1 and 0.3 Acc μm−1. Using the estimate for the bending modulus of the CC given above, we calculate a torque of 2000–6000 pN nm. Berry and Berg measured the stall torque of the flagellar motor of Escherichia coli to be ∼4500 pN nm (31). Therefore, our model predicts realistic cell shapes for reasonable values of the applied torque.

To test this model, the bending moduli of the PF and CC should be measured. One possible method would be to use an optical trap to apply forces to these structures. By measuring the end-to-end displacement as a function of forcing, the bending moduli can be estimated.

Acknowledgments

The authors thank N. W. Charon, R. E. Goldstein, and S. F. Goldstein for comments and useful discussions and T. R. Powers for discussions pertaining to the relationship between functional derivatives and the moment.

This work was supported by the National Institutes of Health (grant No. R01 GM072004).

APPENDIX A: GENERALIZED ELASTIC ROD THEORY

For composite filament problems like the ones presented in this article, it is useful to develop a generalized framework for handling the equilibrium and dynamic behavior of these complex filamentary systems.

The configuration of the centerline of a filamentary object can be described by its position, r(s), and the twist (angular rotation per length) about the centerline, Ω3. Equivalently, the configuration of the filament can be defined by a strain vector Ω. The rotation of an orthonormal material triad, (e1, e2, e3), is described by this strain vector as

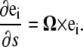graphic file with name M11.gif (A1)

For a linearly elastic rod, the restoring moment, M, is related to the strain vector,

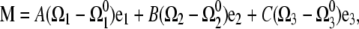graphic file with name M12.gif (A2)

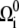with Inline graphic functions that define the equilibrium configuration of the rod, A and B the bending moduli, and C the twist modulus. In equilibrium, moment and force balance along the length of the filament lead to the Kirchoff rod equations (20),

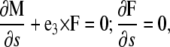graphic file with name M14.gif (A3)

where F is the force.

An equivalent representation of the physics defines a quadratic deformation energy of the filament,

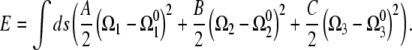graphic file with name M15.gif (A4)

The equilibrium configuration of the filament is given by the minimum of this energy functional, which is the same as the force per length,

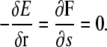graphic file with name M16.gif (A5)

Note that for this energy, the moment in Eq. A2 is equal to

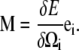graphic file with name M17.gif (A6)

For a composite filament, the configuration of the centerline can still be described using the vector, rcc, or the strain vector, Ω. However, depending on the constraints in the system, the form for the moment in terms of the Ω values is not obvious. It is often easier to write the energy for these systems. Typically, this energy will depend on Ω and its derivatives, in which case the functional derivative in Eq. A5 can be quite tedious to compute and difficult to solve for the equilibrium configuration. If a relation for the moment, such as Eq. A6, exists that satisfies Eq. A3, it can be much easier to solve for the equilibrium configurations of the system. In this section, we compute the generalized moment and show that this moment satisfies Eq. A3.

To begin we assume an energy that depends on Ω and its derivatives with respect to the arclength, s,

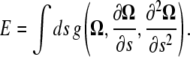graphic file with name M18.gif (A7)

To outline the calculation, we will assume that the energy does not depend on derivatives higher than first-order, as this exemplifies the approach and does not change the end result. Therefore, 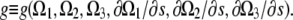Inline graphic A variation in the energy is

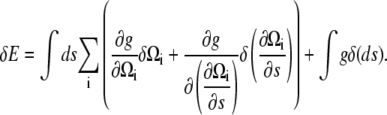graphic file with name M20.gif (A8)

Using that 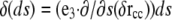Inline graphic(32), we can integrate by parts to get

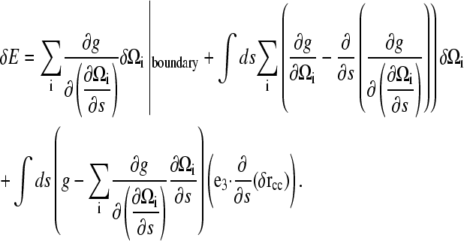graphic file with name M22.gif (A9)

In this equation, the first term is a surface term that, in the absence of applied forces and moments, should be zero. The second term describes how variations in the strain vector affect the energy.

We note that the bracketed piece of the second term is equal to the functional derivative of the energy with respect to Ωi and make the definition

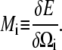graphic file with name M23.gif (A10)

Therefore,

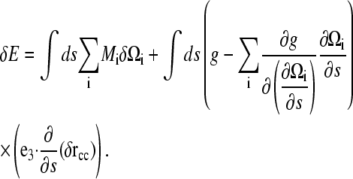graphic file with name M24.gif (A11)

The variations in Ωi were worked out in Goldstein et al. (32) and are

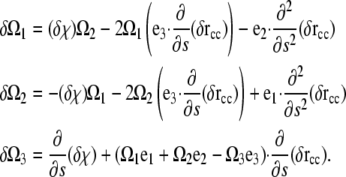graphic file with name M25.gif (A12)

Substituting Eq. A12 into Eq. A11 and integrating the second derivative pieces by parts once, we get

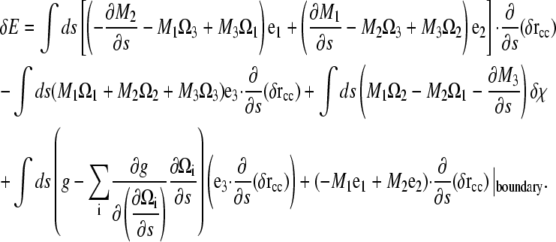graphic file with name M26.gif (A13)

Since the force per length is the functional derivative of the energy, we define the force, F, as the components of the integrand that multiply the derivative of δr with respect to arclength. Therefore,

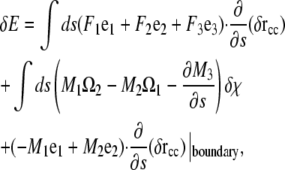graphic file with name M27.gif (A14)

where

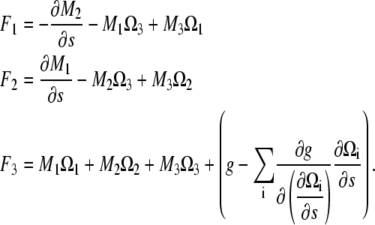graphic file with name M28.gif (A15)

Equation A15 can be rewritten using Eq. A1 and that the functional derivative of E with respect to χ and r is zero to recover Eq. A3. Therefore, the components of the moment along a filament with a general energy functional is given by Eq. A10.

APPENDIX B: DERIVATION OF THE DYNAMIC EQUATIONS FOR THE MORPHOLOGY OF THE LEPTOSPIRACEAE

For low Reynolds number motions, as occur with swimming bacteria, the restoring moments and forces are balanced by viscous drag from the fluid. For long, thin objects, slenderbody hydrodynamic theory (33) suggests that local drag coefficients can be defined for motion parallel to the long axis of the filament, 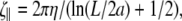Inline graphic motion perpendicular to the long axis, 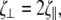Inline graphic and rotation about the centerline, 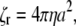Inline graphic where a is the radius, L is the length of the filament, and η is the viscosity of the fluid. If the flagellum rotates at velocity ωα, we assume that the drag force on the cell cylinder is −ζαωα. Balancing the drag moments and forces with the restorative moments and forces leads to the dynamic equations

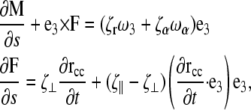graphic file with name M32.gif (B1)

with ω3 the rotational velocity of the filament about its axis. Likewise, we balance the drag on the flagellum against the elastic restoring moment that is calculated from the functional derivative of the energy with respect to α,

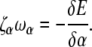graphic file with name M33.gif (B2)

The rotational velocity of the centerline, ω, is related to the rotation rate of the material orthonormal triad as

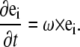graphic file with name M34.gif (B3)

At steady state, we expect that the bacterium is deformed and rotating, but with a fixed cell shape. Therefore, we expect that

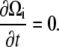graphic file with name M35.gif (B4)

for all i. Using Eq. B3, it is possible to show that Eq. B4 is equivalent to

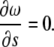graphic file with name M36.gif (B5)

By differentiating the second equation of Eq. B1 and using Eq. B3, we find that

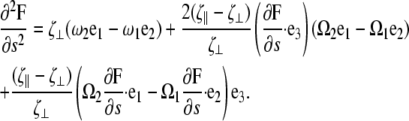graphic file with name M37.gif (B6)

Eqs. B1, B2, B5, and B6 form a closed system of first-order equations that can be solved for the steady-state dynamics of the morphology of the Leptospiraceae. We used MatLab function bvp4c to solve these equations with the following boundary conditions:

At s = 0, we assume that the velocity and angular velocity are zero and that the moments on the flagellum and CC are zero:

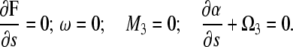graphic file with name M38.gif (B7)

At s = L, we assume that the force is equal to zero and that the moments on the PF and CC are equal to T1:

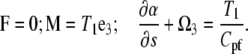graphic file with name M39.gif (B8)

For the static calculations, Eq. 7 was solved using the MatLab boundary value problem solver (bvp4c) with no external moment acting on the PF, which leads to the boundary condition, 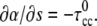Inline graphic For the dynamic calculations, we solved Eqs. 4 and 5 by turning the dynamic problem into a steady-state, boundary value problem. MatLab bvp4c was used to integrate the steady-state equations.

To measure the hook radius of curvature, we used a compass to draw the best fit-by-eye curve through the image shown in Fig. 2 a. To determine the hook radius of curvature from our simulations, we solved Eq. 7 and used that solution in Eq. 6. These Ω values were used to integrate the material frame to get the position of the centerline of the CC. The discrete points for the centerline were then fit to a circle of radius Rh using a least-squares minimization routine.

Editor: Alexander Mogliner.

References

  • 1.Berg, H. C., and L. Turner. 1979. Movement of microorganisms in viscous environments. Nature. 278:349–351. [DOI] [PubMed] [Google Scholar]
  • 2.Charon, N. W., and S. F. Goldstein. 2002. Genetics of motility and chemotaxis of a fascinating group of bacteria: the spirochetes. Annu. Rev. Genet. 36:47–73. [DOI] [PubMed] [Google Scholar]
  • 3.Hayashi, F., K. D. Smith, A. Ozinsky, T. R. Hawn, E. C. Yi, D. R. Goodlett, J. K. Eng, S. Akira, D. M. Underhill, and A. Aderem. 2001. The innate immune response to bacterial flagellin is mediated by toll-like receptor 5. Nature. 410:1099–1103. [DOI] [PubMed] [Google Scholar]
  • 4.West, A. P., A. A. Koblansky, and S. Ghosh. 2006. Recognition and signaling by toll-like receptors. Annu. Rev. Cell Dev. Biol. 22:409–437. [DOI] [PubMed] [Google Scholar]
  • 5.Bromley, D. B., and N. W. Charon. 1979. Axial filament involvement in the motility of Leptospira interrogans. J. Bacteriol. 137:1406–1412. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Holt, S. C. 1978. Anatomy and chemistry of spirochetes. Microbiol. Rev. 42:114–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Berg, H. C., D. B. Bromley, and N. W. Charon. 1978. Leptospiral Motility. Symp. Soc. Gen. Microbiol. 28:285–294. [Google Scholar]
  • 8.Nauman, R. K., S. C. Holt, and C. D. Cox. 1969. Purification, ultrastructure, and composition of axial filaments from Leptospira. J. Bacteriol. 98:264–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Brich-Andersen, A., H. Hovind-Hougen, and C. Borg-Petersen. 1973. Electron microscopy of Leptospira. 1. Leptospira strain Pomona. Acta. Pathol. Microbiol. Scand. Sect. B. 81:665–676. [DOI] [PubMed] [Google Scholar]
  • 10.Trueba, G. A., C. A. Bolin, and R. L. Zuerner. 1992. Characterization of the periplasmic flagellum proteins of Leptospira interrogans. J. Bacteriol. 174:4761–4768. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Goldstein, S. F., and N. W. Charon. 1988. Motility of the spirochete Leptospira. Cell Motil. Cytoskeleton. 9:101–110. [DOI] [PubMed] [Google Scholar]
  • 12.Goldstein, S. F., and N. W. Charon. 1990. Multiple-exposure photographic analysis of a motile spirochete. Proc. Natl. Acad. Sci. USA. 87:4895–4899. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Picardeau, M., A. Brenot, and I. Saint. 2001. First evidence for gene replacement in Leptospira spp. inactivation of L. biflexa flaB results in non-motile mutants deficient in endoflagella. Mol. Microbiol. 40:189–199. [DOI] [PubMed] [Google Scholar]
  • 14.Auran, N. E., R. C. Johnson, and D. M. Ritzi. 1972. Isolation of the outer sheath of Leptospira and its immunogenic properties in hamsters. Infect. Immunol. 6:968–975. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Noguchi, H. 1918. Morphological characteristics and nomenclature of Leptospira (Spirochaeta) icterohaemorrhagiae (Inada and Ido). J. Exp. Med. 27:575–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Li, C., M. A. Motaleb, M. Sal, S. F. Goldstein, and N. W. Charon. 2000. Spirochete periplasmic flagella and motility. J. Mol. Microbiol. Biotechnol. 2:345–354. [PubMed] [Google Scholar]
  • 17.Charon, N. W., G. R. Daughtry, R. S. McCuskey, and G. N. Franz. 1984. Microcinematographic analysis of tethered Leptospira illini. J. Bacteriol. 160:1067–1073. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Carleton, O., N. W. Charon, P. Allender, and S. O'Brien. 1979. Helix Handedness of Leptospira interrogans as determined by scanning electron microscopy. J. Bacteriol. 137:1413–1416. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Goldstein, S. F., K. F. Buttle, and N. W. Charon. 1996. Structural analysis of the Leptospiracae and Borrelia burgdorferi by high-voltage electron microscopy. J. Bacteriol. 178:6539–6545. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Landau, L. D., and E. M. Lifshitz. 1986. Theory of Elasticity. Butterworth-Heinemann, Oxford, UK.
  • 21.Namba, K., and F. Vonderviszt. 1997. Molecular architecture of bacterial flagellum. Q. Rev. Biophys. 30:1–65. [DOI] [PubMed] [Google Scholar]
  • 22.Levinthal, C., and H. R. Crane. 1956. On the unwinding of DNA. Proc. Natl. Acad. Sci. USA. 42:436–438. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Goldstein, R. E., A. Goriely, G. Huber, and C. W. Wolgemuth. 2000. Bistable helices. Phys. Rev. Lett. 84:1631–1634. [DOI] [PubMed] [Google Scholar]
  • 24.Mendelson, N. H., J. A. Sarlls, C. W. Wolgemuth, and R. E. Goldstein. 2000. Chiral self-propulsion of growing bacterial macrofibers near a surface. Phys. Rev. Lett. 84:1627–1630. [DOI] [PubMed] [Google Scholar]
  • 25.Pelling, A. E., Y. Li, W. Shi, and J. Gimzewski. 2005. Nanoscale visualization and characterization of Myxococcus xanthus cells with atomic force microscopy. Proc. Natl. Acad. Sci. USA. 102:6484–6489. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Yao, X., M. Jericho, D. Pink, and T. Beveridge. 1999. Thickness and elasticity of Gram-negative murein sacculi measured by atomic force microscopy. J. Bacteriol. 181:6865–6875. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Arnoldi, M., M. Fritz, E. Bauerlein, M. Radmacher, E. Sackmann, and A. Boulbitch. 2000. Bacterial turgor pressure can be measured by atomic force microscopy. Phys. Rev. E. 62:1034–1044. [DOI] [PubMed] [Google Scholar]
  • 28.Fujime, S., M. Maruyana, and S. Asakura. 1972. Flexural rigidity of bacterial flagella studied by quasielastic scattering of laser light. J. Mol. Biol. 68:347–359. [DOI] [PubMed] [Google Scholar]
  • 29.Hoshikawa, H., and R. Kamiya. 1985. Elastic properties of bacterial flagellar filaments. II. Determination of the modulus of rigidity. Biophys. Chem. 22:159–166. [DOI] [PubMed] [Google Scholar]
  • 30.Kim, M. J., and T. R. Powers. 2005. Deformation of a helical filament by flow and electric or magnetic fields. Phys. Rev. E. 71:021914. [DOI] [PubMed] [Google Scholar]
  • 31.Berry, R. M., and H. C. Berg. 1997. Absence of a barrier to backwards rotation of the bacterial flagellar motor demonstrated with optical tweezers. Proc. Natl. Acad. Sci. USA. 94:14433–14437. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Goldstein, R. E., T. R. Powers, and C. H. Wiggins. 1998. Viscous nonlinear dynamics of twist and writhe. Phys. Rev. Lett. 80:5232–5235. [Google Scholar]
  • 33.Keller, J., and S. Rubinow. 1976. Slender-body theory for slow viscous flow. J. Fluid Mech. 44:705–714. [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES