Sugar Transport across Lactose Permease Probed by Steered Molecular Dynamics

Abstract

Escherichia coli lactose permease (LacY) transports sugar across the inner membrane of the bacterium using the proton motive force to accumulate sugar in the cytosol. We have probed lactose conduction across LacY using steered molecular dynamics, permitting us to follow molecular and energetic details of lactose interaction with the lumen of LacY during its permeation. Lactose induces a widening of the narrowest parts of the channel during permeation, the widening being largest within the periplasmic half-channel. During permeation, the water-filled lumen of LacY only partially hydrates lactose, forcing it to interact with channel lining residues. Lactose forms a multitude of direct sugar-channel hydrogen bonds, predominantly with residues of the flexible N-domain, which is known to contribute a major part of LacY's affinity for lactose. In the periplasmic half-channel lactose predominantly interacts with hydrophobic channel lining residues, whereas in the cytoplasmic half-channel key protein-substrate interactions are mediated by ionic residues. A major energy barrier against transport is found within a tight segment of the periplasmic half-channel where sugar hydration is minimal and protein-sugar interaction maximal. Upon unbinding from the binding pocket, lactose undergoes a rotation to permeate either half-channel with its long axis aligned parallel to the channel axis. The results hint at the possibility of a transport mechanism, in which lactose permeates LacY through a narrow periplasmic half-channel and a wide cytoplasmic half-channel, the opening of which is controlled by changes in protonation states of key protein side groups.

INTRODUCTION

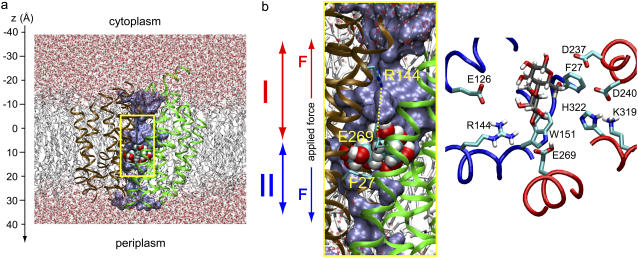
Escherichia coli lactose permease (LacY) (1) is a member of the major facilitator superfamiliy (MFS) (2) found in all life forms (3). LacY is composed of 12 transmembrane helices (I–XII) whereof I–VI and VII–XII constitute the N-domain and the C-domain, respectively (4–6). LacY utilizes the free energy stored in the cell's electrochemical proton gradient (Δμ_H+) to transport lactose (sugar) across the inner membrane (3,6–11). Under physiological conditions Δμ_H+ drives inwardly directed sugar transport; reversal of Δμ_H+ drives sugar transport outwardly. Diffusion of sugar down its gradient can regenerate Δμ_H+ ((3,4,6); see Fig. 2).

FIGURE 2.

Overview of E. coli lactose permease embedded in a fully hydrated POPE lipid bilayer. (a) (Side view) N- and C-domains of LacY are colored brown and green, respectively. Lactose is centrally located in the binding pocket. SMD pulling is bidirectional and departs from initial sugar positions. Pulling along these two respective directions, i.e., across cytoplasmic and periplasmic half-channels, is indicated by red and blue arrows, respectively. (b) Magnification of the LacY lumen with sugar located in the binding pocket (side view as in a). Key residues participating in sugar binding along with the sugar are shown in the right panel with fragments of the LacY N- and C-domains colored blue and red, respectively (top view). The water occupying the lumen is shown in a blue surface representation. Lactose is displayed in van der Waals representation; side chains of residues Glu-269, Arg-144, and Phe-27 are shown in stick representation.

Lactose/H⁺ symport supposedly involves large-scale conformational changes of LacY (3,5,6,12). LacY has been proposed to alternate between two conformational states, an “inward open” and an “outward open” state where the substrate is accessible from the cytoplasm and periplasm, respectively (3,5,6). The coupling between protein conformational changes between these two states, H⁺-transfer events, and lactose translocation is known in modest detail (3,6). A particularly challenging problem is how LacY controls alternating substrate accessibility from the cytoplasmic and periplasmic sides (3–6). Mainly, this problem arises since only one liganded intermediate of the proposed transport cycle has been solved structurally, namely the “inward open” conformation (3,5,6), whereas an “outward open” conformation has not yet been identified. Recently, the crystal structures of apo-LacY were reported at neutral and acidic pH (12,13).

According to a large body of experimental evidence, six residues are essential for lactose transport (3,6). The essential residues are Glu-126, Arg-144, Glu-269, Arg-302, His-322, and Glu-325 (3,6), all located in or near the central, hydrophilic binding cavity of LacY (see Fig. 2 b). These residues participate in substrate binding, proton transfer events, and the coupling of these processes (3,4). Mutation of Glu-325 to a neutral residue decouples the lactose/proton symport; active transport and proton translocation are blocked, but exchange, counterflow, and binding of lactose still occur (14). Mutagenesis experiments also indicate that Tyr-26, Phe-27, Phe-29, Asp-240, Leu-321, and His-322 either directly or indirectly mediate sugar recognition in LacY (15). Moreover, mutants of Met-23, Trp-151, Glu-257, Ala-295, and Glu-377, were found to play a role in sugar recognition and accumulation (16).

The molecular mechanism underlying lactose/H⁺ symport has been addressed in numerous biochemical and biophysical studies (2–5,12,13,17,18). The most prominent result of these studies is the 3.5-Å x-ray structure of LacY (5), in which a centrally located hydrophilic binding cavity holds a (hydrated) lactose analog: β-d-galactopyranosyl-1-thio-β-d-galatopyranoside (TDG). Due to the rather low 3.5-Å resolution, hydration of the lumen (see Fig. 1) of LacY is not resolved (5). The lumen is seen shielded from the periplasm, but exposed to the cytoplasm. The x-ray structure, therefore, represents an asymmetric conformation. The availability of the x-ray structure permits detailed computational studies (19), which can complement experimental data, e.g., by providing structural intermediates of the proposed transport cycle that have not yet been identified experimentally (5,6,19).

FIGURE 1.

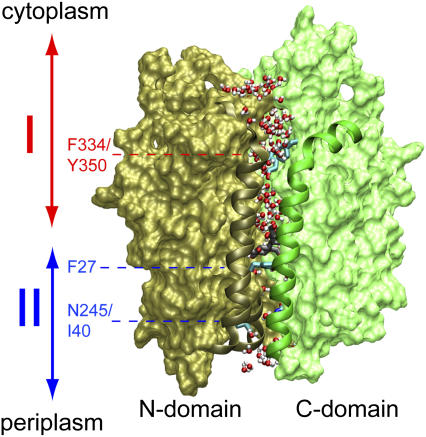
Overview of LacY. The structure shown corresponds to that of the inward closed conformation as obtained from our equilibrium MD simulations with Glu-269 and Glu-325 protonated and deprotonated, respectively (19). Before our SMD simulations, this structure was subjected to additional equilibration (see text). N- and C-domains are shown in brown and green, respectively. Residues 30–40 and 136–166 (N-domain; helix I and V, respectively) and 253–287 (C-domain; helix VIII) are presented as ribbons. Sugar in the centrally located, water-rich binding cavity is shown (without hydrogen atoms) in gray and red along with the side chain of Phe-27. The lumen of LacY is defined to start at the Phe-334/Tyr-350 constriction and end at the Ile-40/Asn-245 constriction. Water molecules at the vestibules, i.e., above Phe-334/Tyr-350 or below Ile-40/Asn-245, as well as within the lumen, are shown in red and white. Regions I (cytoplasmic half-channel) and II (periplasmic half-channel) are indicated by double arrows in red and blue, respectively.

Beginning from the “inward open” conformation, molecular dynamics (MD) simulations have demonstrated that sugar binding and protein conformational changes are intimately related to protonation states of two strictly conserved residues, Glu-269 and Glu-325 (19). Protonation of Glu-325 arrests the protein in an “inward open” conformation (19) in accordance with experiments (5). This conformation is stabilized by a salt bridge between Glu-269 and Arg-144. Deprotonation of Glu-325 and simultaneous protonation of Glu-269 causes partial closure of the cytoplasmic half-channel on a nanosecond timescale via breakage of the salt bridge between Glu-269 and Arg-144 owing to a large movement of the charged guanidinium group of the latter (see Fig. 2) and concurrent loss of two net charges in the intradomain cavity (19).

In contrast to the lactose transport in LacY, sugar molecules, such as long maltodextrin chains, cross the outer membrane of E. coli through porins relatively unhindered by means of facilitated, passive diffusion (20). Such porins, e.g., maltoporin, are believed to only undergo little or no conformational change during substrate conduction (20). The same applies to facilitated diffusion of linear polyols (small sugars) across aquaglyceroporins (21). Facilitated sugar diffusion, therefore, contrasts with the prevailing picture of lactose transport by LacY (3,6), although key mechanistic features are shared. Conduction of sugar by a membrane channel is known to be associated with a costly increase in energy owing to a large extent to significant dehydration of the substrate while passing the constriction formed by the membrane protein (20,22–24). To overcome this barrier, maltoporin, for instance, permits its substrate to move in consecutive register shifts while forming hydrogen bonds with ionic (titrable) residues lining the channel interior (20). In addition, the sugar forms hydrophobic interactions with aromatic residues that together constitute a so-called greasy slide (20,22,23). Facilitated diffusion of small, linear sugars across E. coli aquaglyceroporin GlpF occurs along channel lining carbonyl groups that together with water solvate the permeant (21).

To study the mechanism of lactose permeation across LacY we will employ MD simulations that resolve the conduction process in atomic level detail and, thereby, reveal the physical mechanisms underlying the channel's function. MD simulations have been applied successfully to the study of membrane channels as reviewed (25–27). However, a key limitation of the method is the short timescale covered, today typically 10–100 ns (19,28,29). By applying to a permeant external forces one can accelerate the conduction process enough to complete within the simulation time. The respective method, steered MD (SMD), has been reviewed (30–33). SMD had been applied initially to proteins and biomolecules with mechanical functions (34–36), in which case it proved successful in confirming and explaining observed mechanical properties of an immunoglobulin domain of titin (37), in guiding experimental studies on fibronectin (38), and in predicting (39) later observed (40,41) properties of ankyrin. SMD has been employed successfully to membrane channels (24,42–47) resolving conduction energetics and mechanisms. SMD permits one to identify structural determinants for lactose transport such as protein conformational changes induced by the permeant.

In the next section, we outline computational and analysis methods deployed in this study. We then present our results and conclusions.

METHODS

Modeling of lactose-liganded LacY embedded in a fully hydrated POPE lipid bilayer is described elsewhere (19). In that study, the cocrystallized substrate TDG was replaced by lactose through superposition of the heavy atoms in the two rings of the two sugar molecules (superimposed structures are shown in supplemental Fig. S1 a, Supplementary Material). Due to structural differences between the two sugar molecules, especially around the glycosidic linkage, this procedure resulted in a poor superposition of the glucose (GLC) ring, whereas the galactose (GAL) ring, which is important for sugar specificity (48), was well superimposed on TDG in the binding pocket (Fig. S1 a, Supplementary Material). Equilibrium molecular dynamics simulations starting from this initial configuration (19) clearly showed that the GLC ring of lactose is flexible in the binding pocket of LacY and undergoes significant conformational changes at room temperature, whereas the GAL ring experiences stronger confinement (19). The behavior of the two rings is illustrated in Fig. S1 b of Supplementary Material, where the structure of the sugar is shown for several snapshots taken from equilibrium simulations. As the conformation of the GLC ring significantly changes during the equilibrium simulations, and since all the simulations reported in this work started from those equilibrium simulations (19), it is unlikely that initial placement of the GLC ring affects the results of this work.

The simulated protonation state is denoted LacY(269^H/325⁻) where Glu-325 is deprotonated and Glu-269 protonated; the protonation state arises for the “inward closed” conformation of the protein (19) and is in all key residues identical to the simulation reported in Yin et al. (19). His-35, a noncritical residue located in the periplasmic vestibule (3,5,12), is also protonated in accord with pK_a calculations (19). Using a snapshot of the inward closed conformation taken after ∼6 ns (19), His-35 was protonated and the resulting system was minimized and equilibrated for another 2 ns (Θ(t) = 0 in Eqs. 1 and 2 below).

To probe lactose transport we deployed constant velocity (cv) SMD simulations ((32,49) cv-SMD), subjecting the lactose center of mass (c.o.m.) to the external force

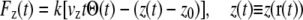(1)

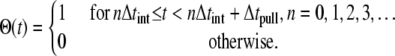(2)

The switching function Θ(t) in Eqs. 1 and 2 is adopted to diminish the nonequilibrium effect due to the applied force by alternating between pulling (pull) and equilibration (eq) intervals. Equilibration intervals permit, in particular, the protein degrees of freedom to better respond to the induced substrate permeation relative to a simulation scheme where such equilibration is not introduced (24). In Eq. 2 Δt_int ≡ Δt_pull + Δt_eq is the length of pulling and equilibration intervals. We chose Δt_int = 3 ns, Δt_pull = 2 ns.

The force in Eq. 1 is directed along the z axis, approximately aligned parallel to the channel axis (Fig. 2, a and b) and is defined positive for pulling along the +z-direction (periplasm direction); z(t) is the position of the lactose c.o.m. along z at time t, k = 300.15 pN/Å is the spring constant, and v_z is the speed of the moving constraint. We assumed a pulling speed v_z = 2 × 10⁻³ Å/ps and an initial position of the lactose c.o.m of z₀ ≈ 9 Å. This position coincides with the center of the lactose binding pocket inside LacY. From this position, we pulled lactose in two opposite (+/−z)-directions, i.e., the moving constraint and, consequently, lactose was displaced out of the binding pocket along the −z-direction (toward cytoplasm) as well as along the +z-direction (toward periplasm), by the applied force as shown in Fig. 2, a and b. The center of the binding cavity is schematically indicated in gray in Fig. 3 b.

FIGURE 3.

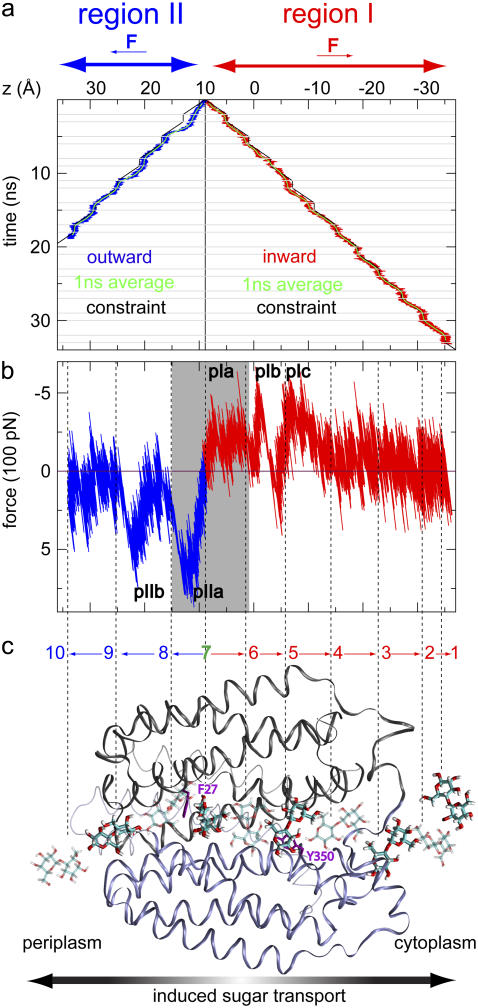
Induced sugar transport across LacY in SMD simulations. (a) Lactose trajectories resulting from an inwardly (− z) and outwardly (+ z) directed applied force, respectively (Methods section and Fig. 1). The initial position of lactose (z₀ ≈ 9 Å) is indicated by a solid black vertical line. The trajectory of the moving harmonic constraint and running averages (1 ns) of the lactose trajectories are shown for reference. Horizontal gray lines in panel a delineate alternation between pulling and equilibration segments, with respective lengths of 2 and 1 ns. Introduction of equilibration intervals implies that the nonequilibrium effect due to the applied force is discernible only during outwardly directed sugar displacement where the sugar and constraint trajectories are seen to slightly deviate initially. (b) Force-displacement profiles across regions I and II. Force peaks are labeled pI (a,b,c) and pII (a,b) for regions I and II, respectively. The gray shaded region illustrates the approximate center of the binding cavity. Dashed vertical lines connect to 10 representative lactose positions in panel c. The force peaks in Fig. 3 b are predominantly positive and negative across regions I and II, respectively. The sign change in the force between the two regions is due to the direction of the applied force, defined positive for pulling along + z. The largest force peaks occur for outwardly directed displacement of lactose as also reflected in the deviation between constraint and lactose trajectories in panel a. (c) Lactose conduction across LacY illustrated by 10 representative quasiequilibrium positions of lactose with the sugar displayed in either solid or transparent stick representation. These snapshots correspond to approximate separations in time by 5 ns. We denote (directional) sugar translocations between positions i and j as 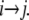Phe-27 and Tyr-350 are displayed in purple for reference.

Our simulations were conducted at constant temperature and pressure (NPT; T = 310 K, P = 1 atm) using Langevin dynamics coupling temperature and pressure to Langevin thermostat and barostat, respectively. Only nonsugar, nonhydrogen atoms were coupled to the Langevin thermostat; the simulation protocol was otherwise the same as reported in Yin et al. (19).

RESULTS AND DISCUSSION

Below we discuss conformational changes of LacY probed by inducing lactose translocation across the protein. We also present the forces required to shift lactose along the channel. Furthermore, we identify protein-lactose interactions during lactose translocation and examine the latter across LacY monitoring sugar hydration, energetics, and sugar orientation.

Protein conformational response

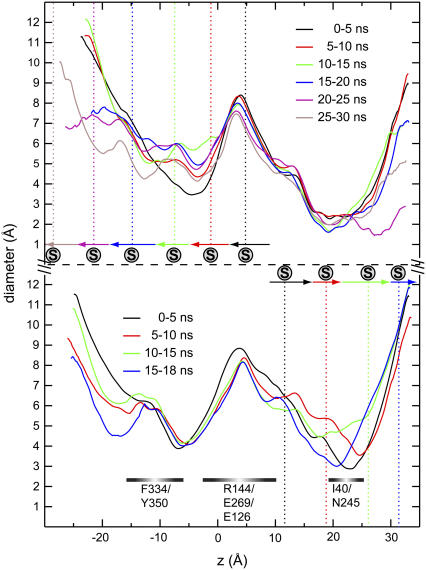
The most prominent protein conformational changes induced by SMD-enforced permeation of lactose is a widening of the narrowest channel segment in LacY. Correlation between (mean) sugar position and local widening of the channel can be discerned from Fig. 4. The cytoplasmic half-channel of LacY, referred to as region I (see Fig. 1), is manifestly wider than the periplasmic half-channel, referred to as region II (see Fig. 1) (19). Region I, in response to sugar permeation, widens by up to 50% across the narrow Phe-334/Tyr-350 constriction (Fig. 4, upper curves). The narrowest point of the channel, i.e., the Ile-40/Asn-245 constriction within the periplasmic half-channel, widens by up to 90% upon lactose passage (Fig. 4, lower panel; 5–10 ns and 10–15 ns windows). On the short simulated timescale we do not observe correlation between channel widening owing to sugar passage across one half-channel and concurrent closure of the other half-channel.

FIGURE 4.

Lumen diameters of LacY(269^H/325⁻) calculated using HOLE (57). The diameters represent mean values of 500 configurations separated by 10 ps and belonging to 5-ns time windows. Upper and lower panels present probing of protein conformational changes induced in response to sugar movement toward cyto- and periplasm, respectively. Mean sugar positions within each time window are delineated by vertical dashed lines. Horizontal arrows indicate overall sugar displacement within each time window according to Fig. 3.

Equilibrium MD simulations of LacY suggest that the N-domain is more flexible than the C-domain (19). This difference prevails in our SMD simulations. In- and outward pulling of lactose yield, respectively, for the N- and C-domains the following average root mean square deviation (RMSD) values of the C_α atoms calculated relative to the t = 0 structure and averaged from t = 1 ns to the end of the simulation: RMSD (N-domain) = (1.5 ± 0.1) Å versus RMSD (C-domain) = (1.1 ± 0.1) Å (region I) and RMSD (N-domain) = (1.7 ± 0.1) Å versus RMSD (C-domain) = (1.3 ± 0.2) Å (region II). Clearly, N-domain flexibility is larger whereas region II exhibits the highest RMSD value. Region II is more compact than region I and lactose consequently induces a larger conformational change in this narrower region in accord with the above induced changes in respective channel diameters of regions I and II. This asymmetry is likely explained by the hydrogen bonding interactions between sugar and channel (Table 1). The majority of intraluminal hydrogen bonding interactions occur between residues of the more flexible N-domain and lactose. Structural flexibility, here mainly provided by the N-domain, is typically required for ensuring a dynamically changing pattern of hydrogen bonding between channel and sugar (21).

TABLE 1.

Hydrogen bonding and hydrophobic interactions between sugar and channel lining

Region I				Region II
Hydrogen bonding interactions
Domain	Residue	z	Atom	Domain	Residue	z	Atom
C	Ser-346	−15.9	Hγ,O	C	Glu-269	0.2	Oε
C	Thr-338	−17.1	O	N	Phe-118	1.0	O
N	Asp-68	−18.0	Oδ	N	Met-23	1.8	Sδ
N	Lys-131	−19.0	Hζ	C	His-322	4.6	Nε
C	Val-343	−21.2	O	C	Asp-237	5.0	Oδ
N	Asn-199	−24.9	O	N	Tyr-26	6.6	O
C	Ala-417	−26.6	HN	N	Phe-27	6.9	O
N	Ala-200	−27.2	O	C	Asp-240	8.6	Oδ
N	Ala-198	−28.9	O	C	Lys-319	9.7	Hζ
N	Arg-134	−22.5	Hη	C	Gln-241	10.1	O,Oε
N	Glu-130	−16.2	Oε	N	Phe-30	11.5	HN,O
N	Glu-126	−9.1	Oε	C	Gln-242	14.9	Hε,Nε
N	Arg-144	−7.2	Hη	N	Pro-31	14.0	N
N	Pro-123	−7.7	O	C	Asn-245	18.2	Hδ,Nδ,Oδ
C	Cys-333	−7.6	Hγ,Sγ	N	Lys-42	19.9	Hζ
N	Cys-148	−3.4	Hγ,Sγ	N	Ile-40	19.9	O
C	Asn-272	−2.5	Hδ,Nδ,Oδ	C	Thr-248	20.2	Hγ
N	Asn-119	−1.1	Hδ	N	Asp-36	21.9	Oδ
C	Lys-358	−0.5	Hζ		–	–	–
Hydrophobic interactions
Domain	Residue	z		domain	residue	z
C	Phe-334	−12.8	–	N	Tyr-26	6.6	–
C	Tyr-350	−10.7	–	N	Phe-27	6.9	–
C	Phe-354	−5.7	–	N	Phe-49	10.1	–
N	Phe-118	1.0	–	N	Phe-30	11.5	–
N	Trp-151	1.9	–	C	Phe-261	12.6	–

The list is partitioned into regions I and II covering cytoplasmic and periplasmic half-channels, respectively. For hydrogen bonding interactions, all polar protein side-chain atoms were considered as donors/acceptors along with the amide nitrogen and oxygen atoms of the peptide backbone. For lactose, all hydroxyl groups were considered as donors/acceptors along with the oxygen atom of the 1,4-glycosidic linkage. A hydrogen bond was registered for a donor-acceptor distance ≤3 Å. For hydrophobic interactions distances between any atom of the aromatic ring of residues Phe, Trp, and Tyr and any nonhydrogen atom of sugar were used for assigning an interaction with the same distance cutoff as above. The mean center-of-mass of each residue is given by z (Å). Each residue is assigned to its respective domain (N or C).

Force profile

Lactose trajectories are presented in Fig. 3 a. The corresponding force acting on lactose as function of its position in regions I and II is shown in Fig. 3 b. Around the central binding cavity the force profile is asymmetric. One recognizes a broad region of considerable force starting with force peak pIa and ending with force peak pIb that accompanies inwardly directed unbinding, i.e., sugar transitions 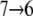and 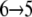in Fig. 3 c. Peak pIIa is associated with outwardly directed sugar unbinding and the displacement 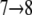(see Fig. 3 c). According to the magnitude of force peaks pIa, pIb, and pIIa, the maximal unbinding force required for inwardly directed sugar unbinding (pIa and pIb) is smaller than that required for outwardly directed sugar unbinding (pIIa). For a detailed discussion of sugar binding to the central cavity we refer to Yin et al. (19) as well as to Fig. 2 b.

The apparent asymmetry in the force-displacement profile suggests that lactose unbinding is more favorable toward the cytoplasm, at least for the assumed protonation state, i.e., LacY(269^H/325⁻). This is consistent with the inwardly directed lactose transport being the physiologically more relevant process ((4–6) c.f. Fig. 2). The asymmetry is also consistent with the fact that the wider cytoplasmic half-channel facilitates the inward conduction process by reducing friction between channel and protein mainly due to more complete sugar hydration than found across the more tightly packed periplasmic half-channel.

Force peak pIc originates from translocation, transition 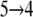in Fig. 3 c, across the constriction region of the cytoplasmic half-channel constituted by Phe-334 and Tyr-350 (19). By moving along a ladder of four titrable residues of alternating polarity, i.e., Glu-126, Arg-144, Glu-130, and Arg-134 (Table 1), lactose finds itself in an energetically favorable state while passing the constriction region. Across region I, force peaks are smaller in magnitude than across region II, since region I is manifestly wider than region II (19). Relative to region II, sugar hydration is more pronounced within region I as seen in Fig. 2 b. Direct protein-lactose interactions are consequently few and weaker. Interactions (friction) between channel and sugar are relatively strong across the narrower region II. The largest force peak in Fig. 3 b is pIIa with a value of F ≈ 800 pN. A second force peak of similar magnitude, pIIb, arises between sugar positions 8 and 9 in Fig. 3 c. This location coincides with the periplasmic half-channel's constriction region defined by Ile-40 (N-domain) and Asn-245 (C-domain; see also Table 1 and Fig. 4).

Passage across the Ile-40–Asn-245 constriction region involves several sugar-channel interactions. At the C-domain, Asn-245 (Hδ, Nδ, Oδ) and Thr-248 (Hγ) along with the long, mobile, and occasionally lumen-protruding side chain of Gln-242 interact with lactose. Hε and Nε of Gln-242 interact with lactose when the Gln-242 side chain is not buried between the interface of helix II of the N-domain and helices VII and XI of the C-domain. At the N-domain, residues Asp-36 (Oδ), Ile-40 (O), and Lys-42 (Hζ) interact with lactose, as Asp-36 and Lys-42 are both charged, they exhibit a particularly strong interaction. Noteworthy is also that the backbone O-atom of Ile-40 is exposed to the channel lumen and not engaged in α-helical hydrogen bonding, lending itself, therefore, as a hydrogen acceptor. Such inward-out orientation of backbone atoms is a motif controlling channel selectivity as found also in potassium channels and aquaporins (27). Hydrophobic interactions with the apolar Ile-40 side chain also contribute to the stabilization of lactose. A possible means of ensuring sufficient structural flexibility and sufficient sugar stabilization that together permit lactose to cross the tight periplasmic constriction, is achieved by having lactose strongly interact with residues Ile-40, Asp-36, and Lys-42 (Table 1). These are all part of the rather flexible N-domain and, moreover, located in the helix I-II connecting loop at, or adjacent to, the periplasmic constriction (Fig. 1).

Sugar hydration and interactions with the protein

As shown in Fig. 5 a, lactose undergoes dehydration upon entry into the LacY lumen. Relative to the bulk where ∼25 water molecules coordinate to lactose directly, only ∼5 water molecules hydrate lactose in the channel's vestibules. Hydration is much less (less than five water molecules per lactose) at the Ile-40/Asn-245 constriction. In the central binding cavity and within the wider cytoplasmic half-channel, hydration is slightly more extensive. The central binding cavity exhibits strong local variation in hydration reflecting multiple modes of channel-sugar interactions. Loss of hydration could result in a barrier against sugar entrance (20,24). However, dehydration of lactose is compensated by multiple stabilizing interactions with the channel lining (Table 1), which reduce the channel's resistance against sugar transport. As demonstrated below, no unfavorable, overall energy increase occurs at the channel's boundaries where dehydration and rehydration take place.

FIGURE 5.

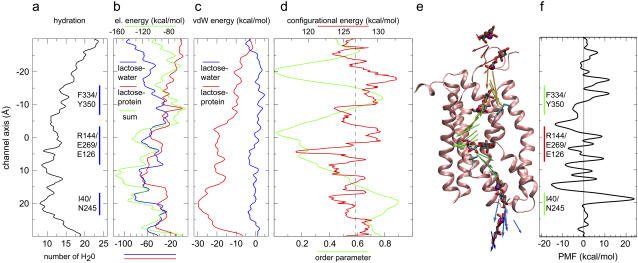
Lactose hydration and interaction energy across the channel (a–c). Lactose configurational energy and orientation (d–e) and potential of mean force (PMF ≡ G(z)) for sugar translocation across the inward closed conformation of LacY (f). (a) Hydration of lactose calculated as the number of water molecules within 3 Å of any sugar oxygen. The central binding region and the Phe-334/Tyr-350 and Ile-40/Asn-245 constrictions are delineated by vertical blue lines. (b) Lactose-protein and lactose-water electrostatic interaction energies and their sum. (c) Lactose-protein and lactose-water van der Waals interaction energies. (d) Configurational energy of lactose calculated as the sum of bond, angle, torsional, and nonbonded energies, and orientation of lactose in terms of the order parameter P_S·P_P. P_S and P_P are directors given by the principal axes associated with the smallest moments of inertia, i.e., sugar and protein long axes, respectively. LacY has its director aligned approximately parallel to the membrane normal. The order parameter equals +1 for parallel, −1 for antiparallel, and zero for perpendicular sugar orientation relative to the protein director. (e) Lactose director along with lactose depicted at selected positions. Lactose is displayed with the carbon atoms of the galactose and glucose rings colored in gray. C₅ of the glucose ring is presented as a purple sphere to guide the eye. The C-domain of the protein is represented in pink. For clarity, the N-domain of LacY is omitted. Residues Tyr-350 of the cytoplasmic constriction and Phe-27 at the border of the binding cavity and the periplasmic half-channel are shown for reference. The director is color coded such that the color scale progresses from red to blue with time, illustrating temporal evolution of an inwardly directed transport event. A movie underlining this figure is supplied in Supplementary Material. (f) PMF, free energy of lactose translocation as function of its position across LacY. We assumed a faster pulling speed permitting for the reconstruction (see Appendix). The energy values shown do not account for the energy decrease occurring during the relaxation intervals of the interrupted SMD simulations (see Eqs. 1 and 2).

Lactose-water electrostatic interaction energy, presented in Fig. 5 b, correlates with the hydration profiles in Fig. 5 a. This energy increases by up to 80 kcal/mol as lactose moves across the channel, reflecting a concurrent decrease in pore hydration and sugar hydration. An energy maximum is reached at the Ile-40/Asn-245 constriction where, as stated above, hydration is most sparse. The unfavorable lactose-water electrostatic interaction energy is compensated by favorable lactose-protein electrostatic interaction energy, which is minimal near the central binding cavity, namely around −70 kcal/mol at z ≈ 12 Å (Fig. 5 b). At this position, the combined lactose-protein and lactose-water interaction energies are also most favorable, namely, −120 kcal/mol.

The van der Waals energies shown in Fig. 5 c are significantly smaller than the electrostatic interaction energies, but nonetheless reach a minimum of −30 kcal/mol, again at the Ile-40/Asn-245 constriction where protein-sugar hydrophobic contacts are pronounced owing to a high density of aromatic residues (Table 1; the main contribution to the favorable van der Waals interaction is from Phe-30 and Phe-49 in the N-domain and Phe-261 in the C-domain). Apparently, this constriction has a hydrophobic gating function possibly preventing H⁺ flow from the periplasm. We note finally that the lactose-water van der Waals interaction remains small and practically constant across the entire channel.

Sugar orientation

A demand for large protein conformational changes occurring in conjunction with lactose transport seems to derive from lactose being a bulky molecule, in particular, since its size is effectively enlarged through hydration (3–6). However, we have found that lactose is favorably stabilized by pore water molecules within the channel, by hydrogen bonding interactions with channel lining residues, including ionic residues, and by hydrophobic interactions with (predominantly) aromatic channel lining residues. As a result, lactose is not accompanied by a bulky hydration layer during its translocation, putting less demand on protein conformational change. As a disaccharide, lactose has a shape that by itself is difficult to accommodate, regarding control of the sugar's orientation during passage through LacY.

In our simulations we find that lactose undergoes a change of its orientation upon unbinding from the central binding cavity. Fig. 5 d depicts, as a function of lactose position, the sugar configurational energy, i.e., the sum of bond, angle, torsional, and nonbounded energies. Fig. 5 d also depicts the sugar orientation, the latter represented as a director (order parameter) projected onto the protein principal axis. Fig. 5 e provides a visual representation of the director in panel d.

The order parameter profile in Fig. 5 d and the snapshots of the sugar director in Fig. 5 e reveal that the orientation of lactose relative to the protein varies significantly during translocation. Lactose exhibits minimal alignment along the protein long axis in the binding pocket of LacY, where the order parameter approaches zero (c.f. Fig. 5 d), implying that the sugar rings lie parallel to the membrane plane as illustrated in Fig. 5 e. In fact, this result also holds for the inward open conformation although the exact minimum for the order parameter along z varies (data not shown; in part this difference also reflects a sampling error). The observed sugar orientation and, consequently, confinement of the sugar's GAL and GLC rings, e.g., via steric interactions with Phe-27 and Trp-151, are consistent with the x-ray structure and fluorescence measurements of LacY. The side chains of the aromatic residues Phe-27 and Trp-151 within the LacY binding cavity confine, orient, and energetically stabilize lactose by means of offering stacking interactions with the rings of the permeating sugar (3,5,50,51).

To test if the pivoting route taken by lactose is due to pulling the sugar bidirectionally out of the binding pocket we performed a control simulation at 10 times higher speed. In this simulation unidirectional pulling was performed with lactose initially positioned outside the cytoplasmic outlet. This simulation led qualitatively to the same order parameter profile as in Fig. 5 d. A movie of the simulation is provided in Supplementary Material.

The orthogonal (to the membrane normal) sugar orientation seen in the central cavity may be linked to the different roles of the N- and C-domains of LacY; the N-domain, situated at one side of the cavity, has been proposed to mainly account for substrate specificity; the C-domain, located on the other side of the cavity, has been proposed to contribute mainly to substrate affinity (5,19). Hence, specificity and affinity of LacY for lactose arise mainly for one of the two sugar rings, respectively. This implies, however, that one sugar ring (GAL) will be more strongly bound, lending itself eventually as a pivot point during permeation. Fig. 5 e further reveals that lactose crosses LacY in a nearly rigid-body manner.

Apparently, lactose largely avoids sugar conformational changes that would unfavorably increase its self-energy and, thus, the energy of permeation. Across the entire channel, sugar configurational energy (Fig. 5 d) remains relatively constant, i.e., 126.8 ± 2.4 kcal/mol, averaged over the full channel. The configurational energy is positive overall due to a large positive electrostatic contribution whereas all bonded terms contribute on average −20.8 ± 2.3 kcal/mol. Lactose, accordingly, crosses LacY with some sugar conformational changes. The lactose configurational energy reaches its minimum within the binding cavity region at 118.2 kcal/mol, which is even lower than in bulk-like conditions at the channel outlets (|z| > 20 Å, Fig. 5 d). Interestingly, the configurational energy features also two local minima at the Phe-334/Tyr-350 and at the Ile-40/Asn-245 constrictions where lactose, albeit being most constrained conformationally due to the narrow channel diameter, nonetheless interacts favorably with the channel lining. Little or no increase in self-energy of lactose should favor lactose binding to LacY, which is noteworthy since LacY's affinity for lactose is modest (3–6).

Energetics of sugar translocation

We also calculated the potential of mean force (PMF), i.e., the free energy during lactose translocation starting with the inward closed conformation of LacY (see Appendix).

The PMF along the channel is presented in Fig. 5 f. The potential is asymmetric across the two half-channels, but reveals identical free energies outside the channel, in agreement with the fact that lactose is solvated in similar aqueous environments at both (cyto- and periplasmic) sides. Multiple local barriers and minima are featured within the lumen (−20 Å < z < 20 Å; see Fig. 1), which to some extent is indicative of several local binding sites with the reservation that limited sampling (number of trajectories N = 4) introduces an error. Owing to the applied constraints on the protein C_α atoms, which were required due to a relatively large pulling speed (see Fig. 5 and Appendix), and sampling error the PMF likely also exhibits too large barriers. Nonetheless, transitions between minima are associated with transient energy increases due to rupture of channel-sugar hydrogen bonding interactions and of hydrophobic contacts. The largest free energy barrier measuring approximately E_a ≈ 40 kcal/mol occurs, not surprisingly and consistent with Fig. 5, a–d, at the Ile-40/Asn-245 constriction within the tightly packed periplasmic half-channel (c.f. Fig. 1) where pore and sugar hydration is minimal and the friction between protein and lactose is maximal. The large friction due to numerous stabilizing interactions between lactose and residues within both domains of the protein translates into a minimum in the PMF at this constriction. Barriers within the cytoplasmic half-channel, in contrast, are smaller, reflecting that this half-channel remains, on the present timescale at least, open.

The free-energy barrier value, E_a, of 40 kcal/mol equals approximately the upper limit of the Arrhrenius activation energy determined experimentally by flux measurements of LacY incorporated into membrane vesicles. The observed values are 4.6 kcal/mol ≤ E_a ≤ 38.8 kcal/mol where lowest and highest values of E_a correspond to values above and below the main phase transition temperature of the vesicle, respectively (52). Our simulations were carried out above the main phase transition temperature of POPE, thus mimicking the fluid state of the bilayer. Although the experimental value refers to the complete transport process, our E_a refers to sugar translocation only, and, moreover, assumed a fixed protonation state of all key residues. The high barrier at the periplasmic constriction suggests that further opening of the periplasmic half-channel is likely. Possibly, this involves displacement of the TM helix I, which is disrupted at Pro-28 noting that opening of the periplasmic half-channel is hampered by the constraints imposed onto the protein C_α atoms.

Implications on transport mechanism

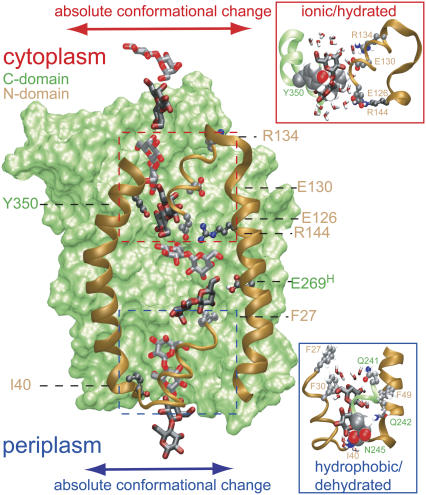
Our main findings from probing sugar conduction across LacY using SMD simulations are summarized in Fig. 6. During permeation lactose is stabilized by multiple interactions with residues lining the lumen of the protein. Sugar interactions with N-domain residues were more frequent than with C-domain residues (see Table 1) owing to a more flexible N-domain. Each half-channel of LacY features a tight constriction region defined by Phe-334/Tyr-350 and Ile-40/Asn-245 within the cytoplasmic and periplasmic half-channels, respectively. The latter gives rise to the, presumably, major barrier against transport (Fig. 5 f). In keeping with LacY preventing unwanted proton flow from the periplasm, hydrophobic interactions arise predominantly between lactose and hydrophobic residues lining the barely hydrated periplasmic half-channel. The main interactions of lactose across the water rich cytoplasmic half-channel, in contrast, involve predominantly ionic residues.

FIGURE 6.

Sugar permeation across LacY. Superimposed on LacY are eight snapshots, taken from simulation LacY(269^H/325⁻), of lactose shown alternately in light and dark. The C-domain is shown in a green surface representation; the N-domain is drawn only partially, for clarity, and is shown in brown ribbon representation. Key N-domain residues, shown in stick representation are Ile-40, Phe-27, Arg-144, Glu-126, Glu-130, and Arg-134. The latter four residues form an ionic ladder stabilizing lactose during its passage across the constriction within the cytoplasmic half-channel as defined by Phe-334 and Tyr-350 (see text). Passage across this region is shown in detail in the upper right inset with Phe-334 (almost hidden, not annotated) and Tyr-350 displayed in van der Waals representation. This region remains fairly hydrated during sugar passage. Phe-27 and Ile-40 of the N-domain interact with lactose within the binding cavity and within the tight periplasmic constriction, respectively. Passage across the latter, also defined by Asn-245, is shown in detail in the lower right inset with Ile-40 (almost hidden) and Asn-245 displayed in van der Waals representation. This region is poorly hydrated during sugar passage. Two key C-domain residues, shown in stick representation, are Tyr-350 and Glu-269 (protonated). Within the binding cavity, lactose engages in interactions with other key residues (Trp-151, Asp-237, Asp-240, His-322) omitted for visual clarity (see text, Fig. 2, and Table 1); within the cytoplasmic constriction region lactose engages in hydrophobic interactions with aromatic residues (Phe-30, Phe-49, Phe-261, all omitted for visual clarity, see text and Table 1). Absolute conformational changes of cytoplasmic and periplasmic half-channels are schematically illustrated by lateral arrows. The channel diameter widens in response to sugar passage across the latter half-channel (cf. Fig. 4).

Sugar passage across the two half-channels occurs with the permeant aligned with its long axis parallel to the channel axis, whereas within the centrally located binding cavity where multiple interactions with key residues occur, lactose aligns its long axis perpendicular to the channel axis (see Table 1 and Figs. 2 and 5 e). It's possible that sugar translocation across LacY does not require an extensive “flip-flop-like” motion of the protein as suggested earlier (3,6), but owing to the short simulation times, lack of sampling, and restriction of protonation states the evidence provided is not yet conclusive.

CONCLUSION

We have investigated transport across E. coli lactose permease LacY using steered molecular dynamics simulations. Via applied forces it was possible to follow the interaction between lactose and channel during lactose permeation. Protein and sugar conformational changes during transport were inspected along with energetic details of the transport process.

The water-filled lumen of LacY offers partial hydration of sugar during conduction. Compensation for pronounced sugar dehydration upon entrance of the channel lumen occurs via multiple sugar-channel interactions. Lactose permeates the channel essentially in an extended conformation. The sugar rings are aligned parallel to the channel axis during permeation across the two half-channels and are perpendicularly aligned when crossing the central binding cavity (Fig. 5 e).

Rather than undergoing a large symmetric alternation between inward and outward open conformational states as proposed in Abramson et al. (5), the steered molecular dynamics simulations suggest that protein conformational changes within the two halves of LacY could be possibly decoupled. Conformational changes within each half-channel, induced by the presence of the permeant, are found to be largest within the tighter periplasmic half-channel, widening of the channel involving movement of the kinked helix TMI. Recent site-directed alkylation studies indicate increased reactivity within the periplasmic half-channel upon uptake of sugar, which is indicative of protein conformational changes in this region being significant, yet is not specific for a particular nature of the underlying motion, e.g., hinge-like or peristaltic (53). Although our previous simulation results (19) demonstrated that alternation between an open and a partially closed cytoplasmic half-channel is controlled by changes of protonation states of residues Glu-269 and Glu-325 (19), it is not clear from this study if similar conformational changes of the periplasmic half-channel occur in response to sugar passage only or in response to changes in protonation states of key residues or by a combination of these two factors.

The function of LacY involves proton transfer between protein residues involving, possibly, also structurally bound water molecules, stepwise sugar translocation, and protein conformational changes. Unraveling the coupling of proton transfer, sugar translocation, and protein conformational changes in LacY's sugar/proton symport is challenging to both experimental and theoretical investigations. The conclusions of this study are based on a still limited number of simulations on timescales that are too short to capture full development of conformational changes of LacY. However, the simulations do provide a dynamical, atomic-detailed picture of molecular events that might be of relevance to the overall transport mechanism of LacY and help develop a more complete view of the fundamental process of active molecular transport across cellular membranes.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX: PMF RECONSTRUCTION

The Hamiltonian of our nonequilibrium cv-SMD system is

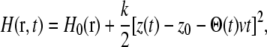(3)

where H₀(r) is the Hamiltonian without external force, z(t) is the position of the lactose c.o.m. across the channel, Θ(t) is given by Eq. 2, and 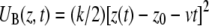is the biasing potential. Jarzynski's identity (55)

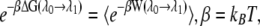(4)

where k_B is the Boltzmann constant, permits one to extract the equilibrium free energy difference controlled by the parameter λ_j = z₀ + vt_j by averaging (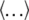) over multiple nonequilibrium cv-SMD simulations (24). The external work W in Eq. 4 is the work performed on lactose due to U_B(z, t) minus the instantaneous value of U_B(z, t)

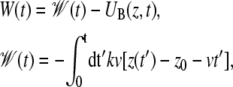(5)

i.e., work is performed to the system for Θ(t) = 1 only in Eq. 3. Within the stiff-spring approximation G(z) can be fairly accurately calculated from N trajectories using the second-order cumulant expansion (24,56)

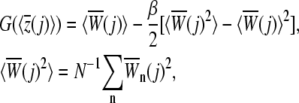(6)

with

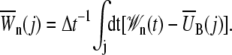(7)

In Eq. 7

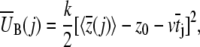(8)

is the mean bias within the jth time window of length Δt = 20 ps, and in Eq. 8 we define

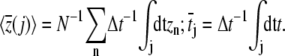(9)

In the simulations used for PMF reconstruction we assumed v_z = 2 × 10⁻² Å/ps with z₀ ≈ 9 Å, and z₀ ≈ 1 Å, respectively. Using a snapshot of the inward closed conformation taken after ∼6 ns (19) and equilibrated for additional 0.2 ns (Θ(t) = 0 in Eqs. 1 and 2), lactose was steered out of the binding pocket (see Fig. 1). Only the sections of the trajectory corresponding to a nonzero force contributed (Θ (t) = 1 in Eqs. 1 and 2). To prevent the protein from moving out of the bilayer harmonic constraints along z with k = 340 pN/Å were imposed onto all C_α atoms. The PMF was calculated as an average over n = 4 simulations (different initial random velocities). Sectional PMFs were merged together via fit to a Fourier series of K = 60 sine functions as where z_c is the cytoplasmic outlet at z = −30 Å and Δ_z = 60 Å is the length of the complete channel (24). This series expansion enforces that the PMF is identical at the two channel exits.