Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2007 Apr 6;93(1):11–20. doi: 10.1529/biophysj.106.100263

Stochastic Signal Processing and Transduction in Chemotactic Response of Eukaryotic Cells

Masahiro Ueda *, Tatsuo Shibata †
PMCID: PMC1914446  PMID: 17416630

Abstract

Single-molecule imaging analysis of chemotactic response in eukaryotic cells has revealed a stochastic nature in the input signals and the signal transduction processes. This leads to a fundamental question about the signaling processes: how does the signaling system operate under stochastic fluctuations or noise? Here, we report a stochastic model of chemotactic signaling in which noise and signal propagation along the transmembrane signaling pathway by chemoattractant receptors can be analyzed quantitatively. The results obtained from this analysis reveal that the second-messenger-production reactions by the receptors generate noisy signals that contain intrinsic noise inherently generated at this reaction and extrinsic noise propagated from the ligand-receptor binding. Such intrinsic and extrinsic noise limits the directional sensing ability of chemotactic cells, which may explain the dependence of chemotactic accuracy on chemical gradients that has been observed experimentally. Our analysis also reveals regulatory mechanisms for signal improvement in the stochastically operating signaling system by analyzing how the SNR of chemotactic signals can be improved on or deteriorated by the stochastic properties of receptors and second-messenger molecules. Theoretical consideration of noisy signal transduction by chemotactic signaling systems can further be applied to signaling systems in general.

INTRODUCTION

Living cells can sense and respond to environmental signals through dynamic signaling processes in the reaction networks of biomolecules. Because biomolecules operate stochastically under the strong influence of thermal fluctuations, living cells can be referred to as stochastically operating biomolecular computation systems. Recent progress in the area of single-molecule detection techniques has identified the stochastic nature of biomolecules in vitro and in living cells (1,2). For example, single ion channels have been observed to exhibit a random transition between open (“on”) and closed (“off”) states in an alternating manner (3). Such stochastic behavior has also been observed in catalytic reactions by single enzyme molecules and in steplike movements by single molecular motors (4–7). On-off fluctuations in individual molecules inevitably cause number fluctuations in the ensemble of the molecules, thus making intracellular signaling processes inherently noisy. This leads to a fundamental question about intracellular signaling processes in general: how does the signaling system operate reliably under thermal and stochastic fluctuations? To gain insight into how signals are received, processed, and transduced by stochastically operating molecules, we study the chemotactic signaling system of eukaryotic cells as a typical example of a stochastic computation system.

Chemotaxis is a fascinating phenomenon in which cells sense chemical gradients and move with directional preference toward or away from the source of the chemical cues. Eukaryotic cells can sense the differences in chemoattractant concentration across the cell body and respond by extending pseudopods directed up the chemical gradient (8–12). In Dictyostelium cells, extracellular cyclic adenosine 3′, 5′-monophosphate (cAMP) functions as a chemoattractant. Only 2% gradients can induce a biased movement of the cells toward the source of cAMP in a wide range from 10 pM to ∼10 μM (13–15). Because Dictyostelium cells are 10–20 μm in size and contain ∼80,000 receptors on the surface evenly, with an average Kd of ∼100 nM (16,17), receptor occupancy is estimated to be ∼16,000 molecules at the maximum efficiency of chemotaxis (25 nM), whereas the differences in receptor occupancy between the anterior and posterior halves are ∼130 with 2% gradients. Recently, the lowest gradient value where directed motion is observed was determined by using microfluidic devices (18). The difference in receptor occupancy was estimated to be only on the order of 10 molecules for gradients close to the lower threshold (∼10−3 nM/μm). Ligand binding to the receptors is a stochastic process, so receptor occupancy should fluctuate with time and space. Assuming a Poisson process, fluctuations in receptor occupancy are the square root of the averaged occupancy, and therefore ∼130, which is comparable to the spatial differences. Around the threshold stimulation (100 pM), occupancy and its fluctuations are ∼80 ± 9 molecules, whereas the differences are ∼1 to ∼8 molecules with 2% to ∼20% gradients. Although this estimation includes many uncertainties, it implies that the input signals for chemotaxis become noisy due to the fluctuations in ligand binding to the receptors. Such fluctuations in signal input have been observed directly by single-molecule imaging of the attractant bound to living Dictyostelium cells (19). Chemotactic signaling systems should amplify small changes in input signals. However, by the same system, small random changes (noise) in the input signal would be amplified also, resulting in the propagation of noise as well as signal. Thus, how chemotactic cells reliably obtain information regarding the gradient from such noisy input is a critical question for directional sensing in chemotaxis.

Stochastic signaling processes in living cells have been studied theoretically. Oosawa constructed a theory of spontaneous signal generation in living cells based on thermal fluctuations of biomolecules (20–22). Berg and Purcell have shown that chemoreception by receptors is limited by molecular counting noise (23). For the chemotaxis of amoeboid cells, Tranquillo and colleagues constructed a stochastic model in which the ligand-receptor binding reaction generates stochastically the intracellular messenger that is the critical regulator of the motile system to modulate turning frequency of cells. Based on kinetic fluctuations in ligand-receptor binding, the model explains well the characteristic features of leukocyte random motility and chemotaxis (24,25). Recently, generation and propagation of noise in intracellular processes have been studied in engineered transcriptional regulatory networks (26–29). Elowitz and colleagues have clearly shown experimentally that noise propagates along a cascade of gene expression. Paulsson unified the gene network experiments by analyzing the propagation of noise in gene networks from a theoretical point of view (30). Shibata and Fujimoto addressed how noise relates to the amplification of signals in intracellular signaling processes, which is summarized as the gain-fluctuation relation (31). The relation tells us that signal and noise propagation along the signaling cascade can be characterized by the gain and characteristic time of the signaling reactions, which can be applied generally to intracellular signaling reactions including Michaelis-Menten, allosteric, and push-pull reactions. Recent progress in imaging techniques to monitor directly intracellular signaling reactions makes it possible to determine stochastic properties of signaling molecules, and therefore a theoretical framework is required to evaluate quantitatively how the properties of signaling molecules affect cellular response.

Here we consider a simple but general model in which receptors receive ligands stochastically and the resulting active receptors generate second messengers stochastically. We applied the gain-fluctuation relation to this model, by which the signal/noise ratio (SNR) of chemotactic signals can be calculated based on the properties of the signaling molecules obtained experimentally. Analysis of the SNR reveals that directional sensing in eukaryotic chemotaxis is limited by receptor-generated stochastic noise, and also reveals how the stochastic nature of the receptor and second messengers affects the SNR of chemotactic signals, which suggests regulatory mechanisms for the noisy signal transduction in chemotactic cells. Our model provides a theoretical framework with experimental approaches to the chemotactic signaling system and can further be applied to stochastic signaling systems in general.

RESULTS AND DISCUSSION

Noisy signal inputs and propagation for chemotaxis in Dictyostelium cells

Single-molecule imaging of ligand binding to chemoattractant receptors in living Dictyostelium cells demonstrates that signal inputs fluctuate with time and space (Fig. 1 A)(19,32). The lifetime of ligand binding shows an exponential distribution, with time constants ranging between ∼1 and ∼3 s (Fig. 1 B). The time series of receptor occupancy exhibits fluctuations (Fig. 1 C) with exponential time correlations. These results demonstrate that ligand binding can be described basically as a Poisson process. This means that the chemotactic ligand binds to the receptor randomly and, hence, that input signals are noisy. Note that such fluctuations in input signal are not derived from an error of experimental measurements. The fluctuations are due to the stochastic nature of the ligand-binding process, which is accompanied inherently by the ligand-binding reaction.

FIGURE 1.

FIGURE 1

Open in a new tab

Fluctuations in signal inputs for chemotactic response. (A) Single-molecule imaging of a fluorescent-labeled cAMP (Cy3-cAMP) bound to the receptor in living Dictyostelium cells. Cy3-cAMP was added uniformly to Dictyostelium cells at 10 nM. The basal surface of the cells was observed by using total internal reflection fluorescence microscopy, as described previously (19,32). Individual white spots are single molecules of Cy3-cAMP bound to the receptors in living cells. Time, h:min:s. Scale bar, 5 μm. (B) Cumulative frequency histogram of lifetime of Cy3-cAMP spots. The lifetimes of individual Cy3-cAMP molecules were obtained by counting the time duration between the appearance and disappearance of the fluorescent spots. The line represents the fitting of data to a sum of two exponential functions, Inline graphic where a1, a2, k1, and k2 are fitting parameters. k1 and k2 are dissociation rates, the inverse of the average lifetime. The number of Cy3-cAMP spots analyzed was 1024. k1 = 1.0 and k2 = 0.13 s−1. a1 = 74.3% and a2 = 31.4%. (C) Time course of the number of Cy3-cAMP spots bound to the basal surface of the cells, showing the number fluctuations of signal inputs for chemotactic response.

We have developed a stochastic model that describes the signal and noise propagation along the transmembrane signaling pathway by receptors. As shown in Fig. 2 A, we assume that receptors receive ligands randomly as signal input, leading to the stochastic generation of intracellular messengers as output. The second output messengers then degrade with time. This scheme is representative of many signaling pathways. In the chemotactic signaling system of Dictyostelium cells, the first and subsequent reactions correspond to cAMP binding to the receptor and G-protein activation, respectively (10–12). The noise of the active receptors is the deviation from the average amount of active receptors, which can be quantified by Inline graphic where R* is the molecular number of active receptors per cell and Inline graphic is its average. Assuming that the receptors distribute uniformly on the surface of the cells, the noise, Inline graphic is given by the gain-fluctuation relation (31), as follows,

graphic file with name M5.gif (1)

where the gain, gR, quantifies the response of receptors, ΔR*, to small changes in ligand concentration, ΔL, which is defined as

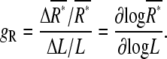graphic file with name M6.gif (2)

FIGURE 2.

FIGURE 2

Open in a new tab

Stochastic model of chemotactic signaling. (A) Signal transduction reactions by chemoattractant receptors. The ligand (L) binds to the inactive receptor (R), leading to the formation of an active receptor (R*), which produces the active second messenger (X*) from the inactive precursor (X). The active X* is switched off to the inactive state, X, in due time. These reactions can be described by Michaelis-Menten kinetics. (B) The cell is placed under a ligand-concentraion gradient. L, average concentration; ΔL, difference in ligand concentration between the anterior and posterior ends of the cell. 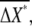The anterior and posterior halves sense Inline graphic and Inline graphic on average, respectively. The difference in receptor occupancy ΔR* is produced from ligand-concentration differences, which lead to the difference in second messenger, ΔX*, between the anterior and posterior halves. The differences ΔR* and ΔX* should include the noise Inline graphic and Inline graphic around average values Inline graphic and Inline graphic respectively.

From Eq. 2, it is clear that a reaction with higher gain is more sensitive to small changes in input signal, resulting in higher amplification of the signals. However, Eq. 1 tells us that the reaction with higher gain also generates larger noise, because noise is proportional to gR. That is, a higher gain is required for higher amplification of input signals, but it also inevitably and simultaneously increases noise. When the ligand-binding reaction is described by Inline graphic the gain, gR, decreases as the increase of ligand concentration, L (Fig. 3 A; see Eq. 9), and, hence, the relative noise, Inline graphic decreases (Fig. 3 C). Thus, chemotactic cells receive noisier signals at lower ligand concentrations.

FIGURE 3.

FIGURE 3

Open in a new tab

Relationship between gain and noise. (A) Active receptor concentration (R*; solid line) and gain (gR; dashed line) plotted as functions of ligand concentration. (B) Dependence of the gain gX on receptor occupancy. (C) Dependence of relative noise in R* on ligand concentration. (D) Dependence of relative noise in X* on ligand concentration. Extrinsic noise and intrinsic noise are represented by black dashed and solid lines, respectively. The total noise strength is represented by the red solid line. The parameter values used for the calculation are summarized in Table 1. (Inset) Log-log plot. Extrinsic noise contributes dominantly to the total noise in the lower ligand-concentration range, whereas intrinsic noise contributes dominantly in the higher ligand-concentration ranges.

The active receptor, R*, leads to the stochastic activation of intracellular messenger X to the active form X* as output. The noise of the active second-messenger concentration 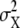Inline graphic is described by (30,31)

graphic file with name M16.gif (3)

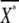where Inline graphic and gX are, respectively, the average number of active second messengers and the gain of the reaction, defined as Inline graphic τR and τX are the characteristic time constants of the ligand-binding reaction and second-messenger-production reaction, respectively, which are defined by the rate constants of the corresponding reactions (see Eq. 10).

The second term on the righthand side of Eq. 3 is the extrinsic noise (26), which describes how the noise of active receptor R* propagates into the noise of second-messenger concentration. When the time constant of the second-messenger production is faster than that of the active receptor (Inline graphic), the noise of the active receptor is propagated more efficiently into the noise of the second messenger, with a decrease in τX, because the term Inline graphic increases gradually and reaches unity as Inline graphic increases. In this case, the second-messenger-production reaction can follow rapid temporal changes of the active receptor. On the other hand, in the case of Inline graphic the second-messenger reaction cannot follow the noise of the active receptor. Instead, the noise of the active receptor is averaged temporally, and the extrinsic noise decreases. In the extreme case, the extrinsic noise is eliminated from the total noise by time-averaging effects. Thus, the relatively slower reaction is required in the second-messenger production to reduce the extrinsic noise generated by the ligand-binding reaction, whereas the relatively faster reaction causes the noise propagation.

Even if the amount of active receptor is constant without noise (σR = 0) or the extrinsic noise is almost neglected by the effect of temporal averaging in the second-messenger reaction, the second messenger should be accompanied by noise, because the active receptors activate stochastically the second messenger. Such intrinsically generated noise by the second-messenger-activation reaction itself is called intrinsic noise (26), which is given by the first term on the righthand side of Eq. 3. The intrinsic noise is included inevitably in the total noise of second messengers. Fig. 3 D shows the relative contributions of intrinsic and extrinsic noise to the total noise. The total noise, 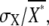Inline graphic increases with decreasing ligand concentration. Because extrinsic noise is proportional to the square of the gain, whereas intrinsic noise is proportional to the gain (Eq. 3), extrinsic noise contributes dominantly to the total noise in the lower ligand-concentration ranges, where the gain, gX, becomes relatively higher (Fig. 3 B). On the other hand, intrinsic noise contributes dominantly in the higher ligand-concentration ranges (Fig. 3 D, inset). Thus, the receptors generate noisier signals in the lower ligand-concentration range, which would take into account the inefficient chemotaxis in the corresponding ranges, as described in the next section.

Limitation of directional sensing by noise

To explain the mechanisms whereby cells sense chemical gradients, two representative mechanisms have been proposed: temporal sensing and spatial sensing mechanisms (8,9,23,33). In the temporal sensing mechanism, the movements of cells or their parts, such as pseudopods, are essential for gradient sensing, in which the spatial differences in chemoattractant concentration are converted into temporal changes through the movements. In the spatial sensing mechanism, cells detect the signals simultaneously at different points over their surfaces. As a result of comparison of the detected signals, the cells sense the direction of the chemical gradient. Dictyostelium cells can form positive or negative gradients of some signaling molecules, such as PI3-kinase and PTEN (tensin homology protein), inside the cell along the gradient of cAMP without cell movements and pseudopod extensions, indicating that the cells can sense the higher-concentration side of cAMP across the cell body without motion, which provides strong evidence that the origin of chemotactic signals is spatial differences in receptor occupancy (10–12). Thus, the cells do not necessarily require temporal sensing mechanisms for gradient sensing.

Devreotes and colleagues propose an alternative mechanism, the so-called local excitation global inhibition (LEGI) mechanism, in which temporal and spatial mechanisms are integrated to take into account the behavior of chemotactic cells (10,34,35). In the LEGI mechanism, receptor occupancy in a local area determines the local level of excitation, whereas the average level of receptor occupancy over the entire surface of the cell determines the level of inhibition in all regions of the cell. Although this mechanism does not assume direct comparison of the ligand concentration between different points over the cell surface, spatial differences of the ligand concentration are sensed through a comparison between the excitatory signals and the inhibitory signals at each of the local areas. Thus, chemotactic signals in the LEGI mechanism are derived from differences in receptor occupancy between the local region and the total surface of the cells. With regard to the origin of chemotactic signals, the LEGI mechanism can be thought of as an extension of the spatial sensing mechanism, which provides the molecular basis for the comparison of the spatial differences in receptor occupancy across the cell body. Although the temporal sensing mechanism may have a role for gradient sensing of chemotactic cells, the spatial sensing mechanism is essential, as described above. Here, we discuss the signal and noise propagation based on the spatial sensing mechanism, in which the chemotactic signals are the spatial differences in receptor occupancy across the cell body. We did not consider sensory adaptation in our model, because G-protein activation does not exhibit adaptation in Dictyostelium cells when ligand stimulation is applied continuously to cells (36).

We consider the differences in second-messenger concentration, ΔX*, between the higher- (anterior) and lower (posterior)-ligand-concentration regions of chemotactic cells placed under a chemical gradient. As shown in Fig. 2 B, the concentration difference in the ligand concentration, ΔL, may produce the difference in receptor occupancy, ΔR*, which may then lead to the difference in second-messenger concentration, ΔX*, between the anterior and posterior regions of chemotactic cells. 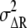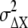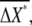The ΔR* and ΔX* should include the noise, Inline graphic and Inline graphic around the average values, Inline graphic and Inline graphic respectively.

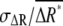To evaluate the effects of the noise on gradient sensing, we studied the SNR, defined as Inline graphic From Eq. 3, we obtain the following relation between Inline graphic and Inline graphic (see Appendix for derivation).

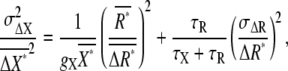graphic file with name M31.gif (4)

where the first and second terms on the righthand side are the intrinsic and extrinsic noise, respectively, of gradient sensing. The SNR, 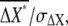Inline graphic is obtained by the inverse of the square root of Eq. 4.

Fig. 4 A shows dependence of the SNR, 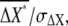Inline graphic on the average concentration of ligand. The parameter values to calculate the SNR for Dictyostelium cells are summarized in Table 1 (see Appendix and Eq. 11). We also performed stochastic numerical simulation showing agreement with our theory (Fig. 4 A). The SNR of chemotactic signals attains a maximum at the ligand concentration between the affinity of the receptor, Kd, and the EC50 concentration, where the G-protein activation reaches half-maximum. This optimal concentration value is dependent mainly on the receptor affinity Kd, and is relatively unaffected by the EC50 variation of G-protein activation (data not shown). In the lower-ligand-concentration range, the SNR is determined mainly by the contribution of the extrinsic noise, meaning that the fluctuations in active receptor dominantly affect the quality of the chemotactic signals. In the higher-ligand-concentration range, the SNR deteriorates with an increase in ligand concentration, because receptors are gradually saturated, making them unable to produce the large differences in second-messenger concentration between the anterior and posterior halves of cells, leading to an increase in intrinsic noise.

FIGURE 4.

FIGURE 4

Open in a new tab

SNR of chemotactic signals. (A) Dependence of the SNR on ligand concentation obtained theoretically by Eq. 4 (red line) and numerically (green diamonds). The cell is located without locomotion under a linear chemoattractant gradient of 2% along the anterior-posterior axis with the midpoint concentration L. The parameter values used for the calculation are summarized in Table 1. For the simulation, the spatial coordinate of the cell is discretized into small boxes appropriately, and the reactions take place in each box according to the Gillespie's algorithm (44). (B) Relative contributions of extrinsic (blue) and intrinsic (green) noises on the total SNR of chemotactic signals (red). (C) Numerical calculation of chemotactic signals. Time course of second-messenger concentration difference (ΔX*) between anterior and posterior halves of single cells. L = 0.01 μM. (D) A proportional relation between the SNR of chemotactic signals and γ, which represents the ratio between the total time durations with ΔX* > 0 and ΔX* < 0. Dashed line, 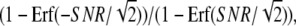Inline graphic where Erf(x) is the error function. (E) Comparison of the SNR with Fisher's experimental data for chemotactic accuracy of Dictyostelium cells (14). The SNR obtained theoretically (red line) was overlaid on the experimental data (red circles). (Adapted from Fig. 5 of Fisher et al. (14) with permission). The SNR was plotted on the same scale as in A.

TABLE 1.

Model parameters

Parameters Values
Φ Cell length 10 μm
ΔL Gradient 0.02L*
Rtotal Total receptor 80,000 molecules/cell†
KR Ligand affinity 0.18 μM†
koff Dissociation rate 1 s−1†
kon Association rate 5.6 s−1μM−1†
Xtotal Total second messenger 200,000 molecules/cell‡
EC50 § 0.01μM§
KX § 4210 molecules/cell§
kd X degradation rate 1.0 s−1‡
kp X production rate 1/4210 s−1(molecules/cell)−1
Open in a new tab

X represents G-protein, because the second reaction is G-protein activation in Dictyostelium cells.

*

The gradient is expressed as the concentration difference between the anterior and posterior ends of a cell. For calculation of the SNR, the concentration difference at the center of anterior and posterior regions was used, and the difference, ΔL, is 0.01L (13,14).

†

Receptor number, ligand affinity, and dissociation rate were obtained experimentally (Fig. 1) (16,17,19). Association rate was obtained from KR and koff.

‡

The values were inferred.

§

EC50 and KX are the concentration of cAMP and active receptor where the activation of the second messenger reaches half-maximum, respectively (36). KX was obtained from EC50, KR, and Rtotal, according to Eq. 8.

kp was determined by kp = kd/Kx.

We next examined the relationship between the SNR of chemotactic signals and the signaling accuracy. As shown in Fig. 4 C, the time series of ΔX* obtained by numerical calculation indicates that ΔX* can sometimes be negative. This means that the concentration gradients of second messengers can be reversed against ligand-concentration gradients by fluctuations in ligand binding and second-messenger production reactions. Because chemotaxis is expected to be more accurate when ΔX* > 0 is produced more frequently, the ratio between the total time durations with ΔX* > 0 and ΔX* < 0, γ, can be used as an index of chemotactic signaling accuracy. As shown in Fig. 4 D, the ratio γ increases in proportion to the SNR. Thus, when chemotactic signals have a higher SNR, ligand gradients are represented on the second-messenger gradient for a longer time, which would lead cells to exhibit chemotaxis more accurately.

The chemotactic accuracy of Dictyostelium cells has been measured experimentally by Fisher et al. (14). The dependence of chemotactic accuracy on ligand concentration exhibits a profile similar to our calculated SNR (Fig. 4, A and E). In the experiment, the cell's movements were biased toward the higher concentration of cAMP over a range of 10 pM to 10 μM, and chemotactic accuracy attained a maximum at 25 nM of cAMP concentration. This optimal value is almost the same as the concentration at which the SNR reaches the maximum (Fig. 4 E). The agreement between the SNR and chemotactic accuracy indicates that the ability of directional sensing is limited by the inherently generated stochastic noise during the transmembrane signaling of receptors. Note that Eq. 4 does not depend on a particular detail of the spatial sensing mechanism, and can be applied to other systems. In fact, similar dependence of chemotactic accuracy has been observed in mammalian leukocytes and neurons, although these cells exhibit chemotaxis at different ranges of ligand concentration (37,38). Such differences in the dependence of chemotactic accuracy on ligand concentration can be explained by cell-type-specific parameters, such as the ligand-binding affinity of receptor, Kd, and the EC50 concentration for second-messenger activation.

When the ligand concentration L is sufficiently small (L ≪ KR, KXR in Eq. 11), the SNR of the chemotactic signals changes in a manner of Inline graphic If the cell requires a signal exceeding a threshold SNR to detect chemical gradients, the cell will exhibit a threshold, ΔLthreshold, for each ligand concentration L for chemotaxis. Then, supposing that such threshold SNR is independent of ligand concentration L, we obtain the relation ΔLthreshold ∝ L0.5. The threshold gradient in a given concentration of ligands can be measured experimentally. In fact, Van Haastert (39) reported the relation between the average concentration of ligand and the corresponding threshold gradient at which 50% of the cells can respond in the chemotactic assay. He found that α for ΔLthreshold ∝ Lα was estimated to be 0.35, which largely agrees with our estimation. In the experiments, the relatively high background cAMP concentrations were used to reveal sensory adaptation processes. Then, the threshold relation is not simply applicable at experimental conditions. Sensory adaptation, which was not considered in our model, may contribute to the α value being lower than theoretical estimation. To further evaluate our model, similar experiments would be required at the lower background concentrations in shallow gradients.

According to Eq. 11, the SNR changes in proportion to ΔL at a given concentration of ligands, L. Fisher et al. also studied the dependence of chemotactic accuracy on ΔL at 25 nM cAMP (14). The accuracy was reduced almost linearly with a decrease of ΔL, vanishing at 10 pM/μm, which was a 0.3% to ∼0.6% gradient. From our formula, the SNR for the 0.3% gradient around 25 nM was estimated to be ∼0.07. Supposing that such a minimum SNR is a threshold for chemotaxis at any chemoattractant concentration, the ligand concentration required for chemotaxis at 2% gradient ranges from ∼200 pM to 1 μM (Fig. 4, A and E), which is narrower than the observed range of chemotaxis in experiments. Those mechanisms not considered in our model, such as the temporal sensing mechanism or sensory adaptation, may contribute to chemotaxis at the lowest and highest concentration ranges. The role of adaptation in the SNR of chemotactic signals will be discussed elsewhere.

Despite the qualitative agreement between the SNR of chemotactic signals at the receptor level and chemotactic accuracy, the quantitative relationship between the two remains to be clarified. The chemotactic signaling system of Dictyostelium cells and other cell types has many components between the receptors and motile apparatus to convert the signals from receptors into unidirectional cell movement. Devreotes and colleagues have revealed that one of the key reactions in the chemotactic signaling system is a distinctive localization of phosphatidylinositol 3,4,5-trisphosphates (PI(3,4,5)P3) on the membrane facing a higher concentration of cAMP (10–12). The PI(3,4,5)P3 localization takes place in an all-or-none manner, meaning that noisy input is processed and transduced to generate a clear signal reflecting the gradient direction of chemoattractants through the cascades upstream of PI(3,4,5)P3. It would be valuable to examine how the SNR of chemotactic signals at the receptor level is reflected in the dynamics of PI(3,4,5)P3 localization.

Improvement of the SNR of chemotactic signals

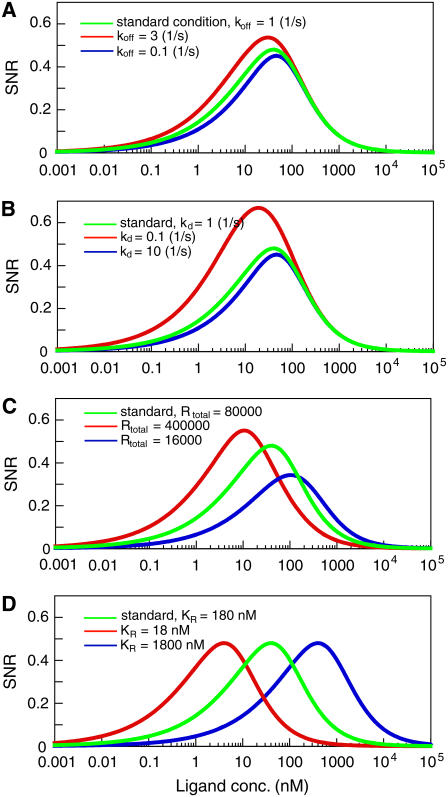
Our results suggest how the SNR of chemotactic signals is improved by the properties of the receptors and the downstream second messenger. First, the SNR can be improved with a decrease of τR, meaning that faster transitions between the ligand-binding (on) state and ligand-unbinding (off) state of the receptors can produce chemotactic signals with higher SNR (Fig. 5 A). When ligand concentration is increased, the ligand association rate (konL) to the receptor is accelerated, resulting in a decrease in the time constant, τR (Eq. 10). That is, an increase in ligand concentration results in better efficiency of chemotactic signals not only by increasing the average concentration of the active receptor but also by decreasing the characteristic time of fluctuations of the active receptor. Moreover, signal improvements are possible by increasing the on-rate (kon) and/or off-rate (koff). For example, when the potential barrier between the on-state and off-state of the receptor becomes lower, the cycling between the two states is accelerated by the acceleration of the on-rate (kon) and the off-rate (koff) resulting in a decrease in τR and, hence, improvement of the SNR of chemotactic signals. Ueda et al. (19) reported polarity in receptor kinetic states along the length of chemotactic cells, which suggests that the SNR is higher at the pseudopod region than at the tail region. Such polarity in the SNR of chemotactic signals may provide a basis for the polarity observed in the response of Dictyostelium cells (40).

FIGURE 5.

FIGURE 5

Open in a new tab

Signal improvements. (A) Receptor fluctuation-dependent signal improvements. The dissociation rates of a ligand ( koff) were changed: (blue line) 0.1 s−1; (green line) 1 s−1 (standard condition); (red line) 3 s−1. (B) Time-averaging effects. The SNR was improved by increasing the time constants of the second messenger. The degradation rates (kd) were changed and the corresponding SNR was calculated: (blue line) 10 s−1; (green line) 1 s−1; (red line) 0.1 s−1. (C) Dependency of the SNR on the expression levels of receptors. The receptor numbers per single cell are 16,000 (blue), 80,000 (green), and 400,000 (red) molecules/cell. (D) Effects of affinity modulation on the SNR. Ligand-binding affinity: 18 nM (red), 180 nM (green), and 1800 nM (blue).

Second, the SNR can be improved by increasing τX. Longer lifetime of the second messenger, which corresponds to slower degradation, causes noise reduction more effectively through time-averaging of the extrinsic noise (Fig. 5 B). This means that the regulatory mechanism for the degradation or the inactivation of second messengers has a pivotal role on the signal improvements for chemotaxis. In the case of G-protein, the hydrolysis rates of the bound GTP on the α-subunit and the reassociation rates with the βγ-subunit mostly determine the lifetimes of active G-proteins, and thus affect the SNR of chemotactic signals. This suggests that the GTPase-activating protein, such as regulators of G-protein signaling (RGS), can regulate the quality of the signal by modulating the inactivation rates of G-protein.

Third, an increase in gain gX can contribute to improved SNR. A high gain that is larger than unity can be obtained for reactions with some cooperativity or ultrasensitivity (31). Eq. 4 can be applied for such reactions. When the cells use cooperative or ultrasensitive reactions for second-messenger activation, chemotactic signals can be improved through reduction of the intrinsic noise.

Fourth, the SNR depends on the total amount of receptor expressed in cells (Fig. 5 C). The SNR is improved in the lower and higher concentration ranges of chemoattractant by increasing and decreasing receptor number, respectively. Receptor internalization can contribute to SNR improvements in the higher concentration ranges by decreasing membrane-bound receptors. Also, receptor affinity for the chemoattractant is an important factor in adjusting the concentration ranges in chemotaxis (Fig. 5 D). Modification in the affinity causes a shift in the dependence of SNR on chemoattractant concentration, which would be a basis for a wider-range response. It is well known that the cAMP receptors in Dictyostelium cells are phosphorylated with cAMP stimulation, leading to a three- to approximately sixfold decrease in ligand-binding affinity (41). According to our formula, such an affinity shift of receptors contributes to an SNR increase in the higher-ligand-concentration range, and thus extends the response range to higher ligand concentrations.

Our discussion on the minimum model of chemotactic signaling cascade can be generalized for a longer cascade including multistep reactions. In such a case, extrinsic noise would be amplified by the gain or reduced by time-averaging effects at each step. The gain depends on the type of reaction (31) and also on the concentration ranges of the reaction (e.g., Fig. 3, A and B). Time-averaging of the extrinsic noise depends on the time constants of the reaction at each step, which are usually determined by both the production and the degradation rates of the messenger molecules. Intrinsic noise would be added inevitably to the extrinsic noise at each step. When the time constants of the reactions become longer along the signaling cascade, the SNR of chemotactic signals would have a more improved effect at the lower reactions through time-averaging effects. In such a signaling system, the shallow gradient can be detected at downstream reactions of the cascade even if it does not generate effectively a clear signal at upstream reactions, suggesting that the downstream molecules have a pivotal role in the detection of a faint signal. Dictyostelium cells treated with a PI3-kinase inhibitor can exhibit chemotaxis, but it is restricted to the higher concentration range (42), suggesting that PI3-kinase and the PTEN system are required for detection of a faint signal in a noisy environment. Similar reasoning can be applied to parallel cascades with different time constants. Thus, our model can evaluate the quality of signals in the chemotactic signaling system, which can be further applied to stochastically operating signaling systems in general. To reveal how signal and noise are propagated in a stochastic signaling system, it is important to determine experimentally the gains and time constants of reactions along the signaling cascade. Noise propagation along longer signaling cascades will be discussed elsewhere.

Acknowledgments

We thank Paul R. Fisher for permission to use the experimental data reported in his published work (14) and Peter J. M. Van Haastert for valuable comments on his experimental data and our model. We also thank Toshio Yanagida for continuous encouragement and Peter Karagiannis for critical reading of the manuscript.

This study was supported by Leading Project of the Ministry of Education, Cultures, Sports, Science and Technology (MEXT), Japan.

APPENDIX: DERIVATION OF SNR OF CHEMOTACTIC SIGNALS

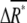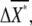We define chemotactic signals as the difference in the concentration of X*, ΔX*, between the anterior and posterior halves of chemotactic cells (Fig. 2 B). Since we are interested in chemotaxis in a shallow gradient, the difference ΔL is small enough so that we only consider linear terms with respect to the differences. The average differences, Inline graphic and Inline graphic between the anterior and posterior halves are defined as

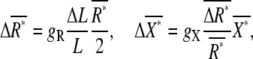graphic file with name M38.gif (5)

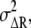where Inline graphic and Inline graphic are the average numbers of active receptor and the active second messenger, respectively, in the cell. The noise of the differences in active receptor, Inline graphic is approximately equal to the summation of the noise in the anterior and posterior regions, given by Inline graphic where the subscripts “anterior” and “posterior” indicate the regions of the cell. From Eq. 1, we find

graphic file with name M43.gif (6)

Similarly, the noise of chemotactic signals, 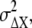Inline graphic is approximated by 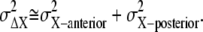Inline graphic Since the concentration gradient of ligand is so small, we may expect that the gain, gX, and the formed gradient of the active receptor are almost constant

graphic file with name M46.gif (7)

From Eqs. 5 and 7, the relative noise strength of chemotactic signals, 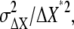Inline graphic is obtained in Eq. 4. The SNR of chemotactic signals is the square root of the inverse of the relative noise strength.

To calculate the parameters in Eq. 4 for Dictyostelium cells, we consider the simplest reaction scheme:

graphic file with name M48.gif

According to this scheme, the average number of active receptor, 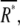Inline graphic and second messenger, Inline graphic are given by Michaelis-Menten kinetics,

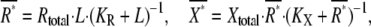graphic file with name M51.gif (8)

where Rtotal is the total molecular number of receptors per single cell, 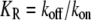Inline graphic the affinity for the ligand with association and dissociation rate constants kon and koff, Xtotal the total molecular number of second messenger per cell, 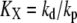Inline graphic the concentration of active receptor where the activation of the second messenger reaches half-maximum with production and degradation rates kp and kd of the second messenger. The gains of active receptor to the ligand concentration and the second messenger to the active receptor number are given by

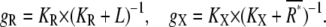graphic file with name M54.gif (9)

The time constants of the reactions are calculated by

graphic file with name M55.gif (10)

When Eqs. 5, 6, 8, and 9 are substituted into Eq. 4, the SNR is obtained as a function of L and ΔL by

graphic file with name M56.gif (11)

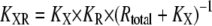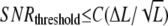Here, Inline graphic is the ligand concentration with which the activation of X reaches the half-maximum value, and Inline graphic According to Eq. 11, the SNR is proportional to Inline graphic when ligand concentration is much smaller than KR and KXR. 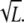Supposing that cells can sense the gradient if the SNR of chemotactic signals is larger than the threshold SNR, Inline graphic with constant C, and hence we have Inline graphic (SNRthreshold/C) for chemotaxis. Therefore, the minimum differences of ligand concentration for chemotaxis are proportional to the square root of L, ΔLthreshold ∝ Inline graphic

We should note that Eq. 1 may have an additional noise derived from the fluctuation of the ligand concentration in extracellular solution, which can be given by

graphic file with name M63.gif (12)

where D is the diffusion constant of the ligand and Φ is the cell size (23,43). Using D ≈ 103 μm2/s for cAMP and the other parameter values shown in Table 1 we find 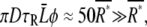Inline graphic indicating that the second term in Eq. 12, which is derived from the ligand concentration fluctuation in extracellular solution, is negligible.

Editor: Thomas Schmidt.

References

  • 1.Ishijima, A., and T. Yanagida. 2001. Single molecule nanobioscience. Trends Biochem. Sci. 26:438–444. [DOI] [PubMed] [Google Scholar]
  • 2.Sako, Y., and T. Yanagida. 2003. Single-molecule visualization in cell biology. Nat. Rev. Mol. Cell Biol. 4:SS1–SS5. [PubMed] [Google Scholar]
  • 3.Sakmann, B., and E. Neher. 1995. Single Channel Recording. Plenum, New York.
  • 4.Funatsu, T., Y. Harada, M. Tokunaga, K. Saito, and T. Yanagida. 1995. Imaging of single fluorescent molecules and individual ATP turnovers by single myosin molecules in aqueous solution. Nature. 374:555–559. [DOI] [PubMed] [Google Scholar]
  • 5.Lu, H. P., L. Xun, and X. S. Xie. 1998. Single-molecule enzymatic dynamics. Science. 282:1877–1882. [DOI] [PubMed] [Google Scholar]
  • 6.Kitamura, K., M. Tokunaga, A. H. Iwane, and T. Yanagida. 1999. A single myosin head moves along an actin filament with regular steps of ∼5.3 nm. Nature. 397:129–134. [DOI] [PubMed] [Google Scholar]
  • 7.Kinosita, K., Jr., K. Adachi, and H. Itoh. 2004. Rotation of F1-ATPase: how an ATP-driven molecular machine may work. Annu. Rev. Biophys. Biomol. Struct. 33:245–268. [DOI] [PubMed] [Google Scholar]
  • 8.Zigmond, S. H. 1974. Mechanisms of sensing chemical gradients by polymorphonuclear leukocytes. Nature. 249:450–452. [DOI] [PubMed] [Google Scholar]
  • 9.Devreotes, P. N., and S. H. Zigmond. 1988. Chemotaxis in eukaryotic cells: a focus on leukocytes and Dictyostelium. Annu. Rev. Cell Biol. 4:649–686. [DOI] [PubMed] [Google Scholar]
  • 10.Parent, C. A., and P. N. Devreotes. 1999. A cell's sense of direction. Science. 284:765–770. [DOI] [PubMed] [Google Scholar]
  • 11.Parent, C. A. 2004. Making all the right moves: chemotaxis in neutrophils and Dictyostelium. Curr. Opin. Cell Biol. 16:4–13. [DOI] [PubMed] [Google Scholar]
  • 12.Van Haastert, P. J., and P. N. Devreotes. 2004. Chemotaxis: signalling the way forward. Nat. Rev. Mol. Cell Biol. 5:626–634. [DOI] [PubMed] [Google Scholar]
  • 13.Mato, J. M., A. Losada, V. Nanjundiah, and T. M. Konijn. 1975. Signal input for a chemotactic response in the cellular slime mold Dictyostelium discoideum. Proc. Natl. Acad. Sci. USA. 72:4991–4993. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Fisher, P. R., R. Merkl, and G. Gerisch. 1989. Quantitative analysis of cell motility and chemotaxis in Dictyostelium discoideum by using an image processing system and a novel chemotaxis chamber providing stationary chemical gradients. J. Cell Biol. 108:973–984. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Van Haastert, P. J. M. 1997. Transduction of the chemotactic cAMP signal across the plasma membrane. In Dictyostelium. Y. Maeda, K. Inouye, and I. Takeuchi, editors. Universal Adacemy Press, Tokyo. 173–191.
  • 16.Janssens, P. M. W., and P. J. M. Van Haastert. 1987. Molecular basis of transmembrane signal transduction in Dictyostelium discoideum. Microbiol. Rev. 51:396–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Johnson, R. L., R. Gundersen, D. Hereld, G. S. Pitt, S. Tugendreich, C. L. Saxe, A. R. Kimmel, and P. N. Devreotes. 1992. G-protein-linked signaling pathways mediate development in Dictyostelium. Cold Spring Harb. Symp. Quant. Biol. 57:169–176. [DOI] [PubMed] [Google Scholar]
  • 18.Song, L., S. M. Nadkarni, H. U. Bödeker, C. Beta, A. Bae, C. Franck, W.-J. Rappel, W. F. Loomis, and E. Bodenschatz. 2006. Dictyostelium discoideum chemotaxis: threshold for directed motion. Eur. J. Cell Biol. 85:981–989. [DOI] [PubMed] [Google Scholar]
  • 19.Ueda, M., Y. Sako, T. Tanaka, P. Devreotes, and T. Yanagida. 2001. Single-molecule analysis of chemotactic signaling in Dictyostelium cells. Science. 294:864–867. [DOI] [PubMed] [Google Scholar]
  • 20.Oosawa, F. 1975. The effect of field fluctuation on a macromolecular system. J. Theor. Biol. 25:175–186. [DOI] [PubMed] [Google Scholar]
  • 21.Oosawa, F. 1990. Hierarchy of noise production in living cells. In White Noise Analysis. H. Hida, H. H. Kuo, J. Potthoff, and L. Streit, editors. World Scientific, Singapore. 315–329.
  • 22.Oosawa, F. 2001. Spontaneous signal generation in living cells. Bull. Math. Biol. 63:643–654. [DOI] [PubMed] [Google Scholar]
  • 23.Berg, H. C., and E. M. Purcell. 1977. Physics of chemoreception. Biophys. J. 20:193–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Tranquillo, R. T., D. A. Lauffenburger, and S. H. Zigmond. 1988. A stochastic model for leukocyte random motility and chemotaxis based on receptor binding fluctuations. J. Cell Biol. 106:303–309. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Tranquillo, R. T. 1990. Theories and models of gradient perception. In Biology of the Chemotactic Response. J. P. Armitage and J. M. Lackie, editors. Cambridge University Press, Cambridge, UK. 35–75.
  • 26.Elowitz, M. B., A. J. Levine, E. D. Siggia, and P. S. Swain. 2002. Stochastic gene expression in a single cell. Science. 297:1183–1186. [DOI] [PubMed] [Google Scholar]
  • 27.Rosenfeld, N., J. W. Young, U. Alon, P. S. Swain, and M. B. Elowitz. 2005. Gene regulation at the single-cell level. Science. 307:1962–1965. [DOI] [PubMed] [Google Scholar]
  • 28.Pedraza, J. M., and A. van Oudenaarden. 2005. Noise propagation in gene networks. Science. 307:1965–1969. [DOI] [PubMed] [Google Scholar]
  • 29.Hooshangi, S., S. Thiberge, and R. Weiss. 2005. Ultrasensitivity and noise propagation in a synthetic transcriptional cascade. Proc. Natl. Acad. Sci. USA. 102:3581–3586. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Paulsson, J. 2004. Summing up the noise in gene networks. Nature. 427:415–418. [DOI] [PubMed] [Google Scholar]
  • 31.Shibata, T., and K. Fujimoto. 2005. Noisy signal amplification in ultrasensitive signal transduction. Proc. Natl. Acad. Sci. USA. 102:331–336. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Ueda, M., Y. Miyanaga, and T. Yanagida. 2005. Single-molecule analysis of chemotactic signaling mediated by cAMP receptor on living cells. In Methods in Signal Transduction, Series 6. T. Haga, and S. Takeda, editors. CRC Press, Boca Raton, FL. 197–218.
  • 33.Gerisch, G., D. Hulser, D. Malchow, and U. Wick. 1975. Cell communication by periodic cyclic-AMP pulses. Philos. Trans. R. Soc. Lond. B Biol. Sci. 272:181–192. [DOI] [PubMed] [Google Scholar]
  • 34.Kutscher, B., P. N. Devreotes, and P. A. Iglesias. 2004. Local excitation, global inhibition mechanism for gradient sensing: an interactive applet. Sci. STKE. 2004:l3. [DOI] [PubMed] [Google Scholar]
  • 35.Ma, L., C. Janetopoulos, L. Yang, P. N. Devreotes, and P. A. Iglesias. 2004. Two complementary, local excitation, global inhibition mechanisms acting in parallel can explain the chemoattractant-induced regulation of PI(3,4,5)P3 response in Dictyostelium cells. Biophys. J. 87:3764–3774. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Janetopoulos, C., T. Jin, and P. Devreotes. 2001. Receptor-mediated activation of heterotrimeric G-proteins in living cells. Science. 291:2408–2411. [DOI] [PubMed] [Google Scholar]
  • 37.Zigmond, S. H. 1977. Ability of polymorphonuclear leukocytes to orient in gradients of chemotactic factors. J. Cell Biol. 75:606–616. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Rosoff, W. J., J. S. Urbach, M. A. Esrick, R. G. McAllister, L. J. Richards, and G. J. Goodhill. 2004. A new chemotaxis assay shows the extreme sensitivity of axons to molecular gradients. Nat. Neurosci. 7:678–682. [DOI] [PubMed] [Google Scholar]
  • 39.Van Haastert, P. J. 1983. Sensory adaptation of Dictyostelium discoideum cells to chemotactic signals. J. Cell Biol. 96:1559–1565. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Swanson, J. A., and D. L. Taylor. 1982. Local and spatially coordinated movements in Dictyostelium discoideum amoebae during chemotaxis. Cell. 28:225–232. [DOI] [PubMed] [Google Scholar]
  • 41.Xiao, Z., Y. Yao, Y. Long, and P. N. Devreotes. 1999. Desensitization of G-protein-coupled receptors. agonist-induced phosphorylation of the chemoattractant receptor cAR1 lowers its intrinsic affinity for cAMP. J. Biol. Chem. 274:1440–1448. [DOI] [PubMed] [Google Scholar]
  • 42.Postma, M., J. Roelofs, J. Goedhart, H. M. Loovers, A. J. Visser, and P. J. Van Haastert. 2004. Sensitization of Dictyostelium chemotaxis by phosphoinositide-3-kinase-mediated self-organizing signalling patches. J. Cell Sci. 117:2925–2935. [DOI] [PubMed] [Google Scholar]
  • 43.Bialek, W., and S. Setayeshgar. 2005. Physical limits to biochemical signaling. Proc. Natl. Acad. Sci. USA. 102:10040–10045. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Gillespie, D. T. 1977. Exact stochastic simulation of coupled chemical-reactions. J. Phys. Chem. 81:2340–2361. [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES