Choice in a Successive-Encounters Procedure and Hyperbolic Decay of Reinforcement

Abstract

Pigeons responded in a successive-encounters procedure that consisted of a search state, a choice state, and a handling state. The search state was either a fixed-interval or mixed-interval schedule presented on the center key of a three-key chamber. Upon completion of the search state, the choice state was presented, in which the center key was off and the two side keys were lit. A pigeon could either accept a delay followed by food (by pecking the right key) or reject this option and return to the search state (by pecking the left key). During the choice state, a red right key represented the long alternative (a long handling delay followed by food), and a green right key represented the short alternative (a short handling delay followed by food). In some conditions, both the short and long alternatives were fixed-time schedules, and in other conditions both were mixed-time schedules. Contrary to the predictions of both optimal foraging theory and delay-reduction theory, the percentage of trials on which pigeons accepted the long alternative depended on whether the search and handling schedules were fixed or mixed. They were more likely to accept the long alternative when the search states were fixed-interval rather than mixed-interval schedules, and more likely to reject the long alternative when the handling states were fixed-time rather than mixed-time schedules. This pattern of results was in qualitative agreement with the predictions of the hyperbolic-decay model, which states that the value of a reinforcer is inversely related to the delay between a choice response and reinforcer delivery.

Optimal foraging theory has been used to predict the conditions under which animals will accept or reject prey items they encounter when searching for food. If an animal encounters a large prey item with a short handling time (the time needed to capture and consume the prey), the animal should, of course, accept it. If, however, the prey item is small or the handling time is long, the animal may be better off rejecting the prey and waiting for the next one to come along. According to optimal foraging theory, the critical ratio is E/h, where E is the energy content of the prey and h is the handling time. If the E/h ratio for a particular prey item is greater than the average E/h ratio in the current environment, the prey item should always be accepted; if not, it should be rejected. A number of studies conducted in naturalistic settings have obtained results that were generally consistent with the predictions of optimal foraging theory, except that prey items were usually not accepted or rejected on an all-or-none basis (Goss-Custard, 1977; Krebs, Kacelnik, & Taylor, 1978).

Lea (1979) tested the predictions of optimal foraging theory using a laboratory analog to a foraging situation called the successive-encounters procedure, in which an animal periodically encounters one of two types of prey that have different handling times. An example from Lea's experiment will illustrate the predictions of optimal foraging theory for this type of situation. In one condition, each trial began with a fixed-interval (FI) 5-s schedule on a white center key (the search period). When the pigeon completed the FI schedule, the center key remained white, and a side key was lit either green or red (with equal probability), representing the availability of food after completion of another FI schedule that was either a short (FI 5 s, if the key was green) or long (FI 20 s, if the key was red). With either alternative, the pigeon could accept the reinforcer (by pecking the green or red key) or reject the reinforcer (by pecking the white key three times, which would return the pigeon to the search state and the beginning of a new FI 5-s schedule). For this example, optimal foraging theory states that the pigeon should always reject the long (red key) alternative, because a strategy of continually returning to the search state until the short (green key) alternative is presented would result in an average of one food delivery every 15 s (ignoring any differences between the scheduled and actual FI durations), which is shorter than the 20-s handling time for the long alternative. Optimal foraging theory predicts an indifference point if the search state is FI 7.5 s, because in that case the average time to food is 20 s whether the animal accepts the long alternative or returns to the search state. That is, if the long alternative is always rejected, it will take, on average, two returns to the search state to encounter the short alternative, because the probability of a short encounter is .5. The total of the two search states (each 7.5 s) plus the FI 5-s handling state of the short alternative is 20 s. The theory therefore predicts that the long alternative should always be rejected if the duration of the search state is less than 7.5 s, and it should always be accepted in the duration of the search state is greater than 7.5 s.

Lea (1979) found only partial support for the predictions of optimal foraging theory. As predicted by the theory, the pigeons were more likely to accept the long alternative as the duration of the search state increased. However, contrary to the predictions of the theory, acceptance of the long alternative was usually not all-or-none; instead, the percentage of acceptances increased gradually as the duration of the search state increased. Furthermore, the indifference points (the points at which the long alternative was accepted 50% of the time) occurred when the search period was much greater than the predicted 7.5 s. Other studies using the successive-encounters procedure have also found support for some predictions of optimal foraging theory but some discrepancies as well (e.g., Hanson & Green, 1989a, 1989b; Snyderman, 1983).

Abarca and Fantino (1982) were able to obtain better support for the predictions of optimal foraging theory by making a slight change in Lea's (1979) procedure. Instead of using FI 5-s and 20-s schedules as handling states for the short and long alternatives, Abarca and Fantino used variable-interval (VI) 5-s and 20-s schedules. Their pigeons tended to reject the long VI schedule when the search state was FI 4-s but to accept it when the search state was FI 10-s, which suggested that the indifference point was a search state of approximately 7.5 s, the value predicted by optimal foraging theory. Abarca and Fantino also showed that delay-reduction theory (Fantino, 1969; Squires & Fantino, 1971) makes the same prediction as optimal-foraging theory (an indifference point of 7.5 s) for this procedure. In later experiments with the successive-encounters procedure, Fantino and his colleagues (Abarca, Fantino, & Ito, 1985; Fantino & Preston, 1988) manipulated other variables, such as reinforcement percentage in the handling state and the probability of encountering the less favorable alternative, and they found that their results were in qualitative agreement with the predictions of both optimal foraging theory and delay-reduction theory.

Neither optimal foraging theory nor delay-reduction theory offers a good explanation of why the type of schedule used in the search state (FI or VI) should affect an animal's behavior. Lea (1979) suggested that both the principles of optimal foraging theory and other factors (e.g., a tendency to sample both alternatives, a preference for more immediate reinforcers, etc.) may need to be considered in order to account for behavior in the successive-encounters procedure. Abarca and Fantino (1982) noted that the behavioral differences seen with FI versus VI schedules in the successive-encounters procedure are similar to those found with concurrent-chains schedules. However, delay-reduction theory provides no explanation of why there should be such differences between FI and VI schedules, in either procedure.

One theory that may be able to account for these differences between FI and VI schedules in the successive-encounters procedure is the hyperbolic-decay model. Results from many experiments with both humans and nonhumans have shown that a reinforcer's strength or value decreases according to a hyperbolic function as its delay increases (e.g., Green, Fry, & Myerson, 1994; Mazur, 1987; Odum & Rainaud, 2003; Richards, Mitchell, de Wit, & Seiden, 1997). For choice procedures where the delay between a response and a reinforcer is variable, Mazur (1984, 1986) found that the following equation could make accurate predictions of pigeons' choices:

1

V is the value of an alternative that can deliver any one of n possible delays on a given trial, and P_i is the probability that a delay of D_i seconds will occur. A is a measure of the amount of reinforcement, and K is a parameter that determines how quickly value decreases with increasing delay. Equation 1 states that the total value of an alternative with variable delays can be obtained by taking a weighted mean, with the value of each possible delay weighted by its probability of occurrence in the schedule.

One advantage of Equation 1 is that it can readily account for the well documented preference for reinforcers delivered after variable delays rather than fixed delays. For instance, if a pigeon must choose between food after a fixed delay of 10 s and food after a variable delay that might be either 2 s or 18 s, the pigeon will show a strong preference for the variable alternative, even though the average delay to food is 10 s for both alternatives. The hyperbolic-decay model predicts this result because, according to Equation 1, the overall value of the variable alternative is greater (for all values of K greater than 0 and less than infinity). For example, according to Equation 1, if K  =  1 and A  =  100, the value (V) of a reinforcer delayed 10 s is 9.09, and the value of a reinforcer delayed either 2 s or 18 s is 19.30, so the model predicts a preference for the variable alternative. Furthermore, the model predicts that the variable alternative should be equally preferred to a reinforcer with a fixed delay of 4.18 s (because its value is also 19.30). Mazur (1984) gave the pigeons choices involving many different fixed and variable delays, and he found that Equation 1 could accurately predict the birds' indifference points.

The purpose of the present experiment was to determine whether the hyperbolic-decay model could be applied to the successive-encounters procedure, and whether it could account for differences in animals' choices when different combinations of fixed and variable schedules were used in the search states and the handling states. The experiment consisted of four phases. In Phase 1, pigeons received a series of conditions in which the search state was an FI schedule and the handling states for both the short and long alternatives were fixed-time (FT) schedules (i.e., fixed delays of 5 s and 20 s, respectively, followed by food). In Phase 2, the handling states were the same two FT schedules, but the search states were two-component mixed-interval (MI) schedules (in which the interval requirement was either a short or a long duration, with equal probability). In Phase 3, the search states were FI schedules, but handling states for both alternatives were mixed-time (MT) schedules (in which the delay to food was either short or long, with equal probability). For the short alternative, the two possible delays were 1 s and 9 s, and for the long alterative, they were 4 s and 36 s. Therefore, the average delays to food for these two alternatives were 5 s and 20 s, just as they were in Phases 1 and 2. Finally, in Phase 4, the search states were MI schedules and the handling states were MT schedules. In each phase, the duration of the search state was varied across conditions in order to estimate an indifference point—a search-state duration at which a pigeon was equally likely to accept or reject the long alternative.

More specific predictions of the hyperbolic-decay model will be presented later, but basically, the model predicts that animals will be more likely to reject the long alternative with MI search states than with FI search states, but that they will be more likely to accept the long alternative with MT handling states than with FT handling states. The model makes the first prediction because with MI search states, if the animal rejects the long alternative and returns to the search state there is a 50% chance that the next search state will be of short duration, whereas there is no such possibility with FI search states. The model makes the second prediction because with MT handling states, if the animal accepts the long alternative, there is a 50% chance that the delay to food will be short (4 s), whereas it is always 20 s with the FT handling states.

The predictions of both optimal foraging theory and delay-reduction theory for this experiment are straightforward. These theories do not make different predictions for different types of reinforcement schedules (although, as already noted, Abarca & Fantino, 1982, suggested that the predictions of delay-reduction theory may be more suited to VI handling schedules than FI handling schedules). Because the mean durations of the handling states were 5 s and 20 s for the two alternatives throughout this experiment, both optimal foraging theory and delay-reduction theory predict that the animals should accept the long alternative with search states of greater than 7.5 s and reject the long alternative with search states of less than 7.5 s.

Method

Subjects

The subjects were 4 male White Carneau pigeons (Palmetto Pigeon Plant, Sumter, South Carolina) maintained at approximately 80% of their free-feeding weights. All had previous experience with a variety of experimental procedures.

Apparatus

The experimental chamber was 30 cm long, 30 cm wide, and 31 cm high. The chamber had three response keys, each 2 cm in diameter, mounted in the front wall of the chamber, 24 cm above the floor and 8 cm apart, center to center. A force of approximately 0.15 N was required to operate each key. Behind each key was a 12-stimulus projector (Med Associates, St. Albans, VT) that could project different colors or shapes onto the key. A hopper below the center key and 2.5 cm above the floor provided controlled access to grain, and when grain was available, the hopper was illuminated with a 2-W white light. The chamber was enclosed in a sound-attenuating box containing a ventilation fan. All stimuli were controlled and responses recorded by a personal computer using MED-PC software.

Procedure

Experimental sessions usually were conducted 6 days a week. The experiment consisted of 18 conditions, each lasting for 12 sessions. Each session included a series of trials that consisted of a search phase, a choice phase (in which a reinforcer was either accepted or rejected), and, if the reinforcer was accepted, a handling phase (a delay followed by food).

Phase 1 (Conditions 1–5)

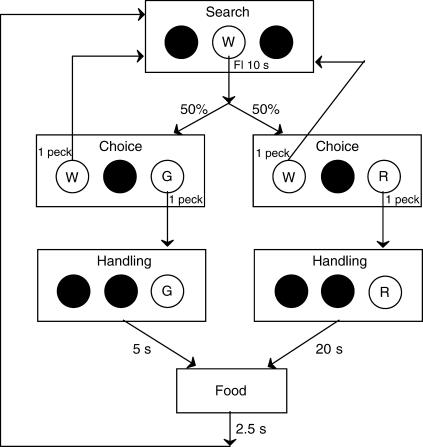
In this phase, the search state was an FI schedule, and the handling states were FT 5-s for the short alternative and FT 20-s for the long alternative. Figure 1 diagrams the procedure for Condition 1. Each trial began with the search state, in which the center key was white and an FI 10-s schedule in effect. Once the pigeon completed the FI requirement, the center key became dark, and the choice period began, with the left key white and the right key either green or red (with key color chosen randomly with the constraint that in every 20 trials, each color occurred 10 times). If the right key was green, this indicated that the short alternative (FT 5 s) was available. The pigeon could either accept the short alternative by pecking the green key or return to the search state by pecking the white key. If the green key was pecked, the left key became dark and the right key remained green for the 5-s handling period, which was followed by a 2.5-s food presentation. Only the white light above the food hopper was lit during all food presentations. After each food presentation, the white center key was turned on and the search state of the next trial began.

Fig 1. A diagram of the procedure in Condition 1.

If the right key was red during the choice period, this indicated that the long alternative (FT 20-s) was available, and the pigeon could accept this alternative by pecking the red key or return to the search state by pecking the white key. If the red key was pecked, the left key became dark and the right key remained red for the 20-s handling period, which was followed by a 2.5-s food presentation and then the start of the next trial.

During both the search state and the choice period, every effective peck on an illuminated key produced a feedback click. Pecks on the right key during the handling states did not produce feedback clicks, nor did pecks to dark keys. Sessions ended after 60 food presentations or 60 min, whichever came first.

In the other four conditions of Phase 1, the procedure was the same except that different FI schedules were used during the search states, and each FI schedule was associated with a different stimulus on the center and left keys (in place of the white keys that were used in Condition 1). For example, in Condition 4, the search state was an FI 12.5-s schedule. A vertical white line was projected on the center key during the search state and on the left key during the choice period. Table 1 shows the schedules and stimuli used in each condition of the experiment. The conditions in Phase 1 will be called FI–FT conditions, referring to the types of schedules used in the search and handling states, respectively.

Table 1.

Order of conditions. All durations are in seconds.

Condition	Search Stimulus	Search Intervals	Handling Delays
			Green	Red
1	White	10	5	20
2	X	5	5	20
3	Circle	7.5	5	20
4	Vertical line	12.5	5	20
5	Circle	7.5	5	20
6	X	0.5, 9.5	5	20
7	Vertical line	1.25, 23.75	5	20
8	Circle	0.75, 14.25	5	20
9	Square	2, 38	5	20
10	Triangle	3, 57	5	20
11	Circle	7.5	1, 9	4, 36
12	Horizontal line	2.5	1, 9	4, 36
13	Plus sign	0.5	1, 9	4, 36
14	X	5	1, 9	4, 36
15	Horizontal line	0.25, 4.75	1, 9	4, 36
16	Circle	0.75, 14.25	1, 9	4, 36
17	Plus sign	0.05, 0.95	1, 9	4, 36
18	X	0.5, 9.5	1, 9	4, 36

Phase 2 (Conditions 6–10)

The conditions in this phase will be called MI–FT conditions. The handling states continued to be fixed delays of 5 s and 20 s for the two alternatives, but the search states were two-component MI schedules instead of FI schedules. Each condition used a different MI schedule, and in each MI schedule the larger interval was 19 times as long as the smaller interval. For example, in Condition 9, the search state was MI 2 s 38 s. Each time the search state was entered, the interval requirement was either 2 s or 38 s, selected at random with the constraint that each interval occurred five times in every 10 entries into the search state. As shown in Table 1, each different MI schedule was associated with a different shape, which appeared on the center key during the search state and on the left key during the choice period. Notice that if an MI schedule had the mean duration as one of the FI schedules used in Phase 1 or Phase 3, then the same stimulus was used. For example, the search schedule in Condition 6 was MT 0.5 s 9.5 s, so the mean search interval was 5 s. The stimulus for the search state in this condition was an “X” on the center key, just as it was in Conditions 2 and 14, both of which had FI 5-s schedules as the search states.

Except for the change from FI to MI search states, the procedure was the same as in Phase 1.

Phase 3 (Conditions 11–14)

This phase used FI–MT conditions. The search states were FI schedules, but the handling states for both alternatives were two-component MT schedules. For the short (green) alternative, the handling state schedule was MT 1 s 9 s. Each time the green handling state was entered, the delay to food was either 1 s or 9 s, selected at random with the constraint that each delay occurred four times in every eight entries into the short handling state. For the long (red) alternative, the handling state schedule was MT 4 s 36 s. In all other respects, the procedure was the same as in Phase 1.

Phase 4 (Conditions 15–18)

This phase used MI–MT conditions. The MT schedules for the handling states were the same as those in Phase 3 (MI 1 s 9 s for the short alternative and MI 4 s 36 s for the long alternative). The search states were similar to those in used in Phase 2 (two-component MI schedules, with the longer interval always 19 times longer than the short interval). The mean durations of the four MI schedules used in these conditions matched those of the four FI schedules in Phase 3. The stimuli used on the center key during the search state and on the left key during the choice period were the same as those used for the corresponding FI schedules in Phase 3.

Results

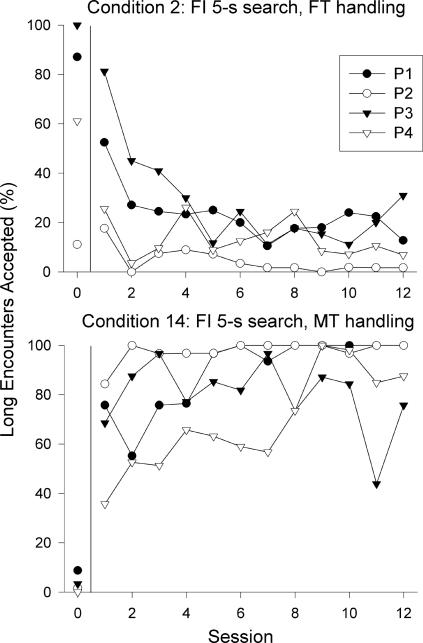
Each condition lasted for 12 sessions, and the pigeons' choices usually adapted rapidly at the start of each new condition. For two typical conditions, Figure 2 shows the percentage of long-alternative encounters that were accepted by each pigeon, plotted separately for each of the 12 sessions of these conditions. (The results from the last session of the preceding condition are shown as “Session 0” in the figure.) The pigeons' acceptance percentages changed rapidly in the first three or four sessions, and by the sixth session the percentages were comparatively stable. The results from the last six sessions of each condition were used in all subsequent data analyses.

Fig 2. For two representative conditions, the percentage of long encounters accepted in each of the 12 sessions is shown for each pigeon.

The session numbered “0” is the last session from the previous condition.

Most accounts of behavior in this situation would predict that a pigeon should always accept the short alternative when it is encountered, because rejecting it would always lead to a longer delay to food. Throughout the experiment, the pigeons did accept the short alternative on the vast majority of trials. Out of 72 cases (18 conditions for each of 4 pigeons), the acceptance percentage for the short alternative was 100% in 59 cases, and the percentage was below 95% in only two instances (78% for Pigeon P2 in Condition 8, and 84% for Pigeon P4 in Condition 18). Averaged across the experiment, the short alternative was accepted 99% of the time.

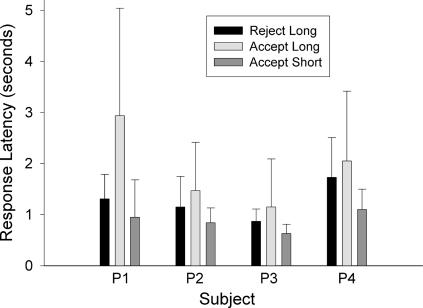
During the choice period, the pigeons typically responded quickly on one of the two side keys. For each pigeon, Figure 3 shows the response latencies for rejecting the long alternative, accepting the long alternative, and accepting the short alternative. Latencies for rejecting the short alternative are not shown because there were very few such cases. The latencies shown are medians averaged across the last six sessions from all 18 conditions. For all 4 pigeons, response latencies were longest when accepting the long alternative and shortest when accepting the short alternative. A repeated-measures analysis of variance found a significant effect of response type, F(2, 6)  =  6.99, p < .05. A Tukey HSD test showed that latencies for accepting the long alternative were significantly longer than for accepting the short alternative (p < .05). There were no other significant differences.

Fig 3. For each pigeon, median response latencies for rejecting the long alternative, accepting the long alternative, and accepting the short alternative are shown.

The data are averaged across the last six sessions of all 18 conditions, and the error bars are semi-interquartile ranges.

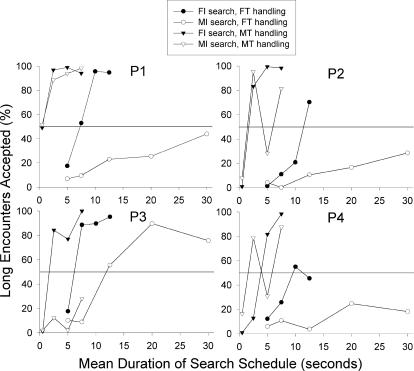
As explained in the Introduction, according to both optimal-foraging theory and delay-reduction theory, in this experiment the long alternative should be rejected if the search period is less than 7.5 s and accepted if the search period is greater than 7.5 s. However, according to the hyperbolic-decay model, acceptance of the long alternative should vary depending on whether the schedules in the search and handling states were fixed or variable. Figure 4 shows the percentage of long encounters accepted by each pigeon in each condition. (The data from Conditions 3 and 5, which had identical schedules, were combined.) As can be seen, the percentage of long encounters accepted varied substantially depending on what types of schedules were used in the search and handling states. Although there was some variability among subjects, overall, the pigeons were most likely to accept the long alternative in the FI–MT and MI–MT conditions, less likely in the FI–FT conditions, and least likely in the MI–FT conditions.

Fig 4. For each pigeon, the percentage of long encounters accepted is shown for each condition.

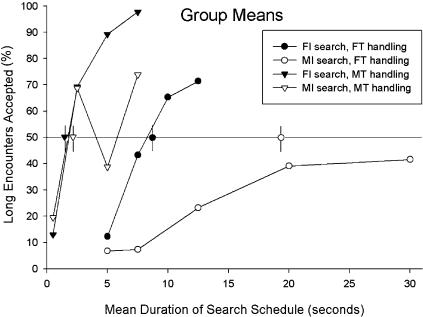
The group means are plotted in Figure 5, and these data are compared to predictions obtained from the hyperbolic-decay model (Equation 1) with K set to 1.0. The predictions are the symbols with vertical lines through them that are plotted on the 50% line, and they represent the points at which the model predicts that the animals should shift from rejection to acceptance of the long alternative. These predictions were obtained as follows: The basic assumption was that when the acceptance percentage was 50% for the long alternative, this was the point at which V_a, the value of accepting the long alternative, was equal to V_r, the value of rejecting the long alternative and returning to the search state. Equation 1 first was used to calculate V_a, and then to find the duration of the search state that led to the same value for V_r if the pigeon accepted the long alternative on 50% of the encounters.

Fig 5. Group means of the percentages of long encounters accepted are shown for each condition.

The symbols with vertical lines through them that are plotted on the 50% line are predictions of the hyperbolic decay model with K  =  1.0. They indicate the point at which the model predicts a shift from rejection to acceptance of the long alternative.

An example will show how Equation 1 was used to obtain these predictions for the FI–FT conditions. For this example, assume that all choice responses have a latency of 1 s, set K  =  1, and set A  =  1000 (the value of A has no effect on the predictions). Using Equation 1 to calculate V_a, the value of accepting the long alternative, is straightforward. Because the delay for the long alternative is 20 s, V_a  =  1000/(1+20)  =  47.6. The objective is now to find a search state duration at which V_r is also equal to 47.6, which will be the predicted indifference point. This calculation is more complex because there are many possible sequences of events that can follow a rejection response. Assume that the long and short alternatives occur with equal probability, that the short alternative is always accepted, and that the long alternative is accepted 50% of the time at the indifference point. Some of the possible sequences that can occur after a rejection response, and their probabilities, are: (1) a return to the search state followed by acceptance of short alternative, 50%; (2) a return to the search state followed by acceptance of the long alternative, 25%; (3) a return to the search state, another rejection of the long alternative, another search state, then acceptance of the short alternative, 12.5%; (4) a return to the search state, another rejection of the long alternative, another search state, then acceptance of the long alternative, 6.25%; and so on. Suppose that the search state duration is 8.8 s. If so, the total delays between the initial rejection response and food for these four sequences are (1) 14.8 s, (2) 29.8 s, (3) 24.6 s, and (4) 39.6 s. For example, the fourth sequence consists of two 8.8-s search states, two 1-s choice response latencies, and one 20-s handling state, for a total of 39.6 s.

For a given search state duration, a computer program used Equation 1 to calculate the values for all the different possible sequences of acceptance and rejection (up to a maximum of three consecutive rejections of the long alternative), multiply these values by their appropriate probabilities of occurrence, and then sum them to obtain the total value of V_r. The duration of the search state was varied systematically to find the duration at which V_r was approximately equal to V_a. For the FI–FT conditions, V_r is approximately 47.6 with a search state duration of 8.8 s, so this is the predicted indifference point. The same general procedure was used to obtain predictions for the other conditions, except that the calculations had to take into account more possible sequences because of the mixed schedules used in the search states, the handling states, or both.

The predictions shown in Figure 5 should be viewed as rough approximations rather than precise predictions, for several reasons. First, as already noted, all the predictions were based on choice response latencies of 1 s. Second, the predictions were based on programmed rather than obtained search interval durations. Third, the predictions were obtained with K equal to 1.0 (a value that has yielded good predictions for pigeons in other applications of Equation 1; see Mazur, 1984). With larger values of K, the predicted indifference points all shift to the right, and with smaller values of K they shift to the left, but the ordinal predictions for the four different combinations of schedules remain the same. As Figure 5 shows, a general prediction of the model is that the indifference points (50% acceptance of the long alternative) should occur with shortest search states in the FI–MT conditions, and with progressively longer search states in the MI–MT, FI–FT, and MI–FT conditions, respectively. This is what was found in the group means shown in Figure 5 (although the mean acceptance percentage never reached 50% in the MI–FT conditions).

To assess the reliability of these predictions at an ordinal level, the following analyses were conducted. First, for each pigeon, the results from the four phases were rank ordered, from the phase with the greatest likelihood of accepting the long alternative to the phase with the lowest likelihood. To obtain these rank orderings, pairwise comparisons were made among the four phases, using the acceptance percentages from all conditions in which the two phases had the same mean search-state durations. For example, the MI–MT and FI–FT phases both had conditions with mean search states of 5 s and 7.5 s, so the mean acceptance percentages from these conditions were compared to rank order these two phases. As can be seen in Figure 4, for these two search-state durations, the acceptance percentages were higher in the MI–MT conditions for 3 of the 4 pigeons, but lower for Pigeon P3. Therefore, 3 of the 4 pigeons supported the model's prediction that acceptance percentages would be higher in the MI–MT conditions than in the FI–FT conditions. Similar pairwise comparisons were made among all phases of the experiment. Across the four phases, there are six pairwise comparisons for each of the 4 pigeons, for a total of 24 comparisons. For 22 of the 24 comparisons, the predictions of the hyperbolic-decay model were supported at an ordinal level (p < .001, two-tailed binomial test). The rank orderings also were used in a Friedman's analysis of variance for ranks, which found a significant effect of phase, F(4, 4)  =  9.9, p < .01.

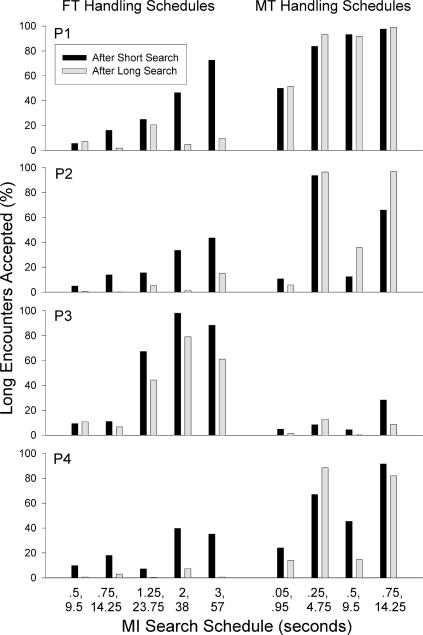
Additional analyses were conducted for the conditions with MI search states, to determine whether long encounter acceptance percentages varied depending on which component of the mixed schedule had just occurred. For the nine conditions with MI search states, Figure 6 shows the long encounter acceptance percentages for choices that followed either the short or long component of the MI schedule. The results from conditions with FT handling schedules are on the left, and those from conditions with MT handling schedules are on the right. With MT handling schedules, there were no systematic differences: In 8 of 16 cases, the long encounter acceptance percentage was higher after a short search interval, and in 8 cases it was higher after a long search interval. However, with FT handling schedules, the long encounter acceptance percentage was higher after a short search interval in 18 of 20 cases. In some instances, the difference in percentages was very large. For instance, with an MI 3-s 57-s search schedule, the acceptance percentage for Pigeon P1 was 73% after the 3-s component but only 10% after the 57-s component. All 4 pigeons showed this effect with the longer MI schedules. One possible explanation for this behavior is that, because the short and long search components were randomly selected with the constraint that every 10 search states include five short and five long intervals, there was a slightly greater chance that a short search interval would follow a long one. Averaged across the nine conditions with MI search schedules, when the long alternative was rejected after a short search interval, the next search interval was also short on 43.7% of the trials. When the long alternative was rejected after a long search interval, the next search interval was short on 55.3% of the trials. It is not clear whether this difference was responsible for the patterns of behavior shown in Figure 6, or why it occurred with FT but not MT handling states. However, this result shows that the pigeons' choices depended, not just on the average or global contingencies in this situation, but also on a more local event—the duration of the search state that had just occurred.

Fig 6. For the nine conditions that included MI search states, the percentage of long encounters accepted is shown for choices that followed either the short or the long component of the MI schedule.

Discussion

The predictions of both optimal foraging theory and delay-reduction theory for choices in a successive-encounters procedure are based on the assumption that animals will follow a strategy that minimizes the average time to food. For the present experiment, these theories predict that (1) the short alternative should be accepted whenever it is encountered, and (2) the long alternative should be rejected if the average duration of the search state is less than 7.5 s, and accepted if it is more than 7.5 s. The first of these predictions was supported, but the second was not. Figures 4 and 5 show that acceptance of the long alternative varied greatly as a function of the type of schedules (fixed or mixed) used in the search and handling states. In the FI–MT and MI–MT conditions, the pigeons tended to accept the long alternative with search states that were shorter than 7.5 s. In the FI–FT conditions, the switch from rejection to acceptance of the long alternative did occur at approximately 7.5 s. In the MI–FT conditions, the pigeons typically continued to reject the long alternative with search states that were much longer than 7.5 s.

The hyperbolic-decay model offers a simple explanation for this pattern of results. According to this model, the pigeons' choices in this procedure should depend on whether V_a, the value of accepting the long alternative, is greater or less than V_r, the value of rejecting the long alternative and returning to the search state. These values, in turn, depend on whether the search and handling schedules are fixed or variable. The model predicts that the animals should be more likely to accept the long alternative with MT rather than FT handling schedules because with MT handling schedules there is a 50% chance that food will be delivered after the short, 4-s delay. Figures 4 and 5 show that the results were consistent with this prediction—acceptance percentages of 50% were reached with much shorter search states in the FI–MT and MI–MT conditions than in the FI–FT and MI–FT conditions. In addition, the model predicts that the animals should be more likely to reject the long alternative with MI rather than FI search schedules because with MI search schedules there is a 50% chance that the next search state will be short. Consistent with this prediction, Figures 4 and 5 show a large difference between acceptance percentages in the FI–FT conditions and the MI–FT conditions. Differences between the FI–MT and MI–MT conditions were also in the predicted direction but smaller in size. However, as shown in Figure 5, Equation 1 predicts that the differences between these two types of conditions should be small. Overall, the differences in results among the four phases of the experiment were qualitatively consistent with the predictions of the hyperbolic-decay model.

As already explained, the predictions shown in Figure 5 should be viewed as approximations and not precise quantitative predictions because they are based on several simplifying assumptions. In fact, it may be difficult to derive precise quantitative predictions of the hyperbolic-decay model (or other mathematical models) for the successive-encounters procedure. The difficulty for the hyperbolic-decay model is that it assumes that value is a direct function of delay, and that one second of delay is equivalent to another. However, in the successive-encounters procedure, some of the time between a choice response and the eventual delivery of food may consist of a response-independent delay, some may consist of time spent responding on an FI or MI schedule, and some may consist of time spent switching from one key to another. There is no reason to assume that the periods of time spent in these different ways all have equivalent effects on reinforcer value. For instance, it is possible that the decay parameter, K, assumes one value for a simple delay period, another value for time spent responding on an FI schedule, and so on. Evidence supporting this possibility can be found in studies that showed that time spent in a response-independent delay is not equivalent to time spent responding on a ratio schedule, and that the strength of a reinforcer is decremented more by the latter than by the former (Crossman, Heaps, Nunes, & Alferink, 1974; Grossbard & Mazur, 1986; Mazur & Kralik, 1990). Despite these complexities, the qualitative agreement between the data and the predictions of the hyperbolic-decay model suggests that choice in the successive-encounters procedure is heavily dependent on the distribution of delays between response and reinforcement, just as it is in other choice procedures (e.g., Herrnstein, 1964; Mazur, 1984; Rider, 1983).

One prediction of the hyperbolic-decay model was not supported in this experiment. Although the model correctly predicted the differences observed with the different types of schedules, the model predicts that preference should be all-or-none in this situation. That is, the long alternative should always be rejected if V_r is greater than V_a, and always accepted if V_r is less than V_a. As already explained, both optimal foraging theory and delay-reduction theory also predict that preference should be all-or-none in this procedure. Whereas some of the individual functions in Figure 4 may approximate a step function that would indicate all-or-none preference, others show a gradual increase in the long encounters accepted as the duration of the search state increased. This type of gradual increase in acceptance percentages was also found in previous studies with the successive-encounters procedure (e.g., Abarca & Fantino, 1982; Abarca et al., 1985; Fantino & Preston, 1988; Hanson & Green, 1989a, 1989b; Lea, 1979).

There are many possible reasons why all-or-none preference has not usually been found in studies using the successive-encounters procedure. First, Lea (1979) proposed that there are advantages in occasionally sampling both alternatives, because without such monitoring an animal could never detect any change in the reinforcement contingencies for an alternative. Second, it is possible that in some of the studies, the animals' behavior was still in a state of transition, and if conditions were continued for more sessions, behavior approximating all-or-none preference eventually might have been observed. In the present experiment, all conditions lasted for 12 sessions, and no stability criteria were used. Although acceptance percentages usually appeared relatively stable after six or seven sessions, the possibility of further changes in behavior with more exposure cannot be ruled out. Third, the tendency to accept or reject an alternative might fluctuate over trials as a result of short-term events (such as the different acceptance percentages observed after short and long search states in some conditions of this experiment). There also may be some random variability associated with V_a and V_r, such that on one trial V_a may be slightly greater than V_r, and on a later, seemingly identical trial, V_r may be slightly greater than V_a. Finally, departures from all-or-none preference might be the result of “errors” on the part of the animal, due to failures of discrimination, failures of association, or accidental responses on the wrong key (cf. Davison & Jenkins, 1985; Jones & Davison, 1998). Whatever the reasons, all-or-none choice in this procedure has been the exception and not the rule.

One feature of the choice procedure used in this experiment differed from previous experiments with the successive-encounters procedure. In previous studies, the pigeons had to switch from a search key to a handling key to accept the alternative presented, but they could reject the alternative simply by continuing to peck on the search key. In the experiments of Lea (1979), Abarca and Fantino (1982), and Fantino and Preston (1988), the pigeons could reject an alternative by making three pecks on the search key, or accept the alternative by making one peck on the handling key. This asymmetry between the responses required to reject or accept the alternatives may have introduced a bias of unknown size and direction into the procedure. There might have been a bias toward rejection (because no switch to a different key was required) or toward acceptance (because only one peck was required for acceptance but three pecks for rejection). The procedure of the present experiment was designed to make the choice responses more symmetrical (1) by requiring the pigeon to switch to one of the side keys for either acceptance or rejection, and (2) by using the same response requirement—one peck—to accept or reject the alternative. Whether this change made the procedure more or less similar to foraging in a natural environment is debatable, but for evaluating the predictions of different mathematical models of choice, the symmetry of this choice procedure may have some advantages. Another difference from previous studies is that the handling states consisted of response-independent delays rather than response-dependent (FI or VI) schedules. It is not known whether this difference in the procedure had any effect, but it did ensure that the actual handling times were exactly the same as the scheduled times.

The results of this experiment suggest that it may be possible to use the same general approach that has been applied previously to choices between fixed and variable delays to reinforcement (Mazur, 1984) to explain how choices in a successive-encounters procedure depend on the types of schedules used in the search and handling states. The main principle is that because of the high values of reinforcers delivered after short delays, schedules with variable delays to food are preferred to those with fixed delays to food. In the successive encounters procedure, this principle manifests itself as follows: An animal is more likely to accept an alternative when its handling state is variable rather than fixed, and the animal is more likely to return to the search state when its duration is variable rather than fixed.