Elastic properties of ribosomal RNA building blocks: molecular dynamics of the GTPase-associated center rRNA

Abstract

Explicit solvent molecular dynamics (MD) was used to describe the intrinsic flexibility of the helix 42–44 portion of the 23S rRNA (abbreviated as Kt-42+rGAC; kink-turn 42 and GTPase-associated center rRNA). The bottom part of this molecule consists of alternating rigid and flexible segments. The first flexible segment (Hinge1) is the highly anharmonic kink of Kt-42. The second one (Hinge2) is localized at the junction between helix 42 and helices 43/44. The rigid segments are the two arms of helix 42 flanking the kink. The whole molecule ends up with compact helices 43/44 (Head) which appear to be modestly compressed towards the subunit in the Haloarcula marismortui X-ray structure. Overall, the helix 42–44 rRNA is constructed as a sophisticated intrinsically flexible anisotropic molecular limb. The leading flexibility modes include bending at the hinges and twisting. The Head shows visible internal conformational plasticity, stemming from an intricate set of base pairing patterns including dynamical triads and tetrads. In summary, we demonstrate how rRNA building blocks with contrasting intrinsic flexibilities can form larger architectures with highly specific patterns of preferred low-energy motions and geometries.

INTRODUCTION

The ribosome is a ribonucleoprotein machine that catalyzes protein synthesis (1,2). It consists of a small (30S in prokaryotes) and a large (50S) subunit (3–5). The ribosome dynamically interacts with tRNAs, mRNA and translation factors and shows large-scale dynamical movements (6,7).

There are three tRNA binding sites (A-aminoacyl, P-peptidyl and E-exit) localized across both subunits (8). The small subunit binds mRNA, mediates the codon—anticodon interaction between mRNA and tRNA and is responsible for proofreading of the codon–anticodon helix. The peptide bond is formed at the peptidyl transferase center located at the large subunit. After the reaction the A- and P-site tRNAs (and mRNA) translocate by one codon to the P- and E- sites. Finally the E-site deacylated tRNA leaves the ribosome and a new aminoacyl tRNA binds to the A-site (9,10).

There is a growing number of structural studies of subunits and the whole ribosome, such as cryo-electron microscopy (cryo-EM) (8,11–16) and X-ray crystallography studies (5,17–20). Cryo-EM (3,21) reveals conformational changes of particular parts of the ribosome during different phases of protein synthesis. Coarse-grained modeling (22,23) also provides crude estimates of the ribosome dynamics and correlation between motions of its most flexible parts (e.g. the L1 and L7/L12 stalks). These methods, however, do not provide atomic resolution insights. The X-ray studies (4,5) show basically static structural snapshots and some presumably flexible regions are often not resolved. Thus, many key structural and dynamical features of the ribosome remain unclear.

Translocation involves movement of tRNAs and mRNA through the central cavity between the subunits and is accompanied with large movements of the L1 stalk. Recent studies reveal also high mobility of the L7/L12 stalk (21, 24–27). Translocation is accompanied with conformational changes coupled by GTP hydrolysis (25) which is catalyzed by translation factor EF-G (in bacteria) and triggered by its interaction with the L7/L12 stalk domain. Translation factor EF-G interacts with the rRNA portion of GTPase-associated center (rGAC; helices 43 and 44) known also as the factor binding site. This causes EF-G-induced conformational changes in the ribosome (28–30).

Here we complement the preceding studies of the L7/L12 stalk dynamics by explicit solvent molecular dynamics (MD) simulations focused on the rGAC. MD simulations have often been used to provide qualitative information about the structure and dynamics of RNA molecules (31–43). MD simulations can be also used for fitting the low-resolution cryo-EM maps with the aim to provide better structural information. For example, recent study of L11-rGAC complex (i.e. the complete GAC) (44) focused on A1067 flipping and improved overlap of fitted MD structures with available cryo-EM maps. Thus, they found out possible structural candidates matching the functional L11-rGAC conformations captured by cryo-EM. It is obvious, that the MD simulation method is limited by the force field approximations and the short simulation time scale [for a review see (45)]. Nevertheless, the simulations are well poised to capture, e.g. qualitative differences in the basic intrinsic dynamical flexibility of various RNA segments and motifs (35–37). Due to the limited simulation time scale, the simulated rRNA segments remain in the ribosome-like geometries even for molecules that would unfold in solution experiments in the absence of the adjacent ribosomal parts. In simulations, before any unfolding, the molecule first extensively samples the conformational space around its ribosome-like geometry (35). Simulations thus suggest regions of easily accessible conformations that are available for the motions inside the ribosome. MD simulation captures also quasiharmonic and anharmonic contributions which often are of primary importance and are not included with methods like normal mode analysis (NMA) that are based on harmonic approximation. When qualitatively addressing the RNA flexibility, the outcome of simulations is less sensitive to force field approximations compared to majority of other MD applications often dealing with quite subtle structural details.

Recently, we have shown that rRNA kink-turns (K-turn; Kt) (46) show profound elbow-like intrinsic flexibilities around the ribosome-like geometries, without disruption of any single structural feature characteristic of a folded K-turn (47). The K-turn oscillatory dynamics is pivoting at the A-minor interaction (48) mediating the contact between the C- and NC-stems, is associated with a dynamical water insertion and the motion is very anharmonic (35). Anharmonic structural elements are well suited to passively mediate large motions due to their very wide and flat free energy minima. We speculated that Kt-42 of helix 42 of the large subunit could contribute to the dynamics of factor binding site (i.e. rGAC) (49) seen in experiments (6,7,50). Also other studies (38,51–53) revealed K-turn flexibility. In this work, we show that the GTPase-associated center rRNA contains a second flexible region formed by the helix 42—helix 43/44 junction. The direction of preferred motion at this junction roughly coincides with the direction of the elbow-like motion of the Kt-42 and both motions preferably shift the rGAC towards or outwards the body of the subunit. The two consecutive flexible elements create a highly versatile RNA limb characterized by a complex set of bending and twisting essential dynamical modes. In other words, MD technique shows that individual rRNA building blocks have contrasting intrinsic dynamical predispositions and consecutive rRNA segments can further create molecular structures with characteristic patterns of internal flexibilities (intrinsically preferred low-energy motions). We assume that the basic physico-chemical properties of the RNA motifs as characterized by MD method can often be maintained in the RNA assemblies, and thus are worth to analyze.

MATERIALS AND METHODS

Starting structure

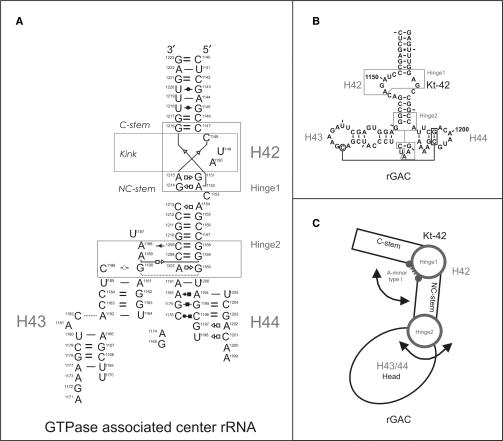
The starting geometry of helices 42–44 of Domain II of 23S rRNA of Haloarcula marismortui was taken from the X-ray structure of the 50S subunit of H. marismortui (PDB file 1JJ2) (5). Helix 42 forms the kink-turn motif (Kt-42) (46) while helices 43 and 44 form the GTPase-associated center rRNA (rGAC). The whole rRNA system named as Kt-42+rGAC was simulated as single-stranded RNA molecule containing 84 nucleotides (nt); residues 1140–1223 using H. marismortui numbering (Figure 1). The system can be roughly divided into two parts: Kt-42 with the attached stems (residues 1140–1157 and 1210–1223) and the rGAC (helices 43/44; residues 1158–1209, Figure 1C). The V-shaped Kt-42 contains the canonical stem (C-stem), internal loop (Kink) and non-canonical stem (NC-stem). The rGAC comprises a very complex pairing pattern described in detail in Figure 1A using the standard nomenclature (54). The starting structures of helices 42–44 of 23S rRNA of Escherichia coli were taken from PDB files 2AW4 and 2AWB (18) (residues 1036–1119 using E. coli numbering).

Figure 1.

Kt-42+rGAC rRNA system. (A) Base pairing in the simulated Kt-42+rGAC system (helices 42–44 from the 23S rRNA of H. marismortui) using standard nomenclature (54). The two flexible regions are marked as rectangles and the individual helices are marked as H42, H43 and H44. Strand connectivity is not highlighted to keep the figure readable. (B) Secondary structure of the Kt-42+rGAC. (C) Schematic representation of the Kt-42+rGAC showing its modularity with five consecutive segments (C-stem, Hinge1, NC-stem, Hinge2 and Head) with very distinct intrinsic mechanical properties and dynamics (see the text). Two flexible Hinges (circles) link three rigid segments (C-stem, NC-stem and Head). Arrows indicate the direction of preferred motions at both Hinges.

Molecular dynamics simulations

Simulations were carried out using the Sander module of AMBER-6.0 with the Cornell et al. (55) force field (30.5 ns of standard and 11 ns of control restrained MD—details available in Supplementary Data). The control MD simulations of E. coli (2 × 10 ns) were carried out using AMBER-8.0 (56). The RNA molecules were neutralized by Na⁺ monovalent cations, initially placed using the Xleap module of AMBER at the most negative solute positions. The counterions were displaced away from the solute to improve sampling [see (49) for justification] and these starting coordinates are available in Supplementary Data. Na⁺ radius was 1.868 Å and well depth 0.00277 kcal/mol (57). Solute molecules were solvated by a water box with periodic boundary conditions using ∼20 000 TIP3P water molecules. Prismatic water box was added around the rRNA to a depth of 16 Å (H. marismortui) and 17 Å (E. coli). The actual size of water box was ca. 112 × 76 × 88 ų for H. marismortui and 115 × 86 × 79 ų for E. coli systems. Due to large motion occurring in the first 5 ns of MD and the length of the simulated molecule (see ‘Results’ section), we monitored its position inside the box after every ns of simulation. No contacts with the periodic image structures occurred in the simulations. Equilibration was carried out in the following way. First, the RNA structures were kept rigid while only solvent molecules with counterions were allowed to move. Then the RNA structures were relaxed, the systems were heated gradually from 50 to 300 K and simulations were initiated under periodic boundary conditions. A 2 fs time step was used and the PME (particle mesh Ewald) (58) method was employed to calculate electrostatic interactions. Structures were visualized using VMD (59). Solute-solvent contacts were monitored over the entire trajectories using the Carnal and ptraj modules of AMBER. All cation binding sites with inner-shell occupancy >40% were analyzed. Histograms were calculated from the original MD data, with bin widths 0.1 Å and 1.0°.

Bending and displacement of rGAC pivoting at Hinge2 (Figure 1C) was quantified via angle between the rGAC and the Kt-42 NC-stem, defined using three centers of mass: the NC-stem of Kt-42 (residues 1152–1157 and 1210–1214), nucleotides involved in base triples forming the Hinge2 (residues 1158, 1159, 1208, 1209, 1188 and 1189) and the rest of rGAC (residues 1160–1187 and 1190–1207). Twisting and coupled shift of rGAC was described as virtual torsion angle formed by four centers of mass. The 1st one contains the C-stem of Kt-42 (residues 1142–1146 and 1217–1221). The 2nd one contains C = G pair of the type I A-minor interaction of Kt-42 (residues 1147 and 1216), the 3rd one contains its A/G pair (residues 1152 and 1214) and the 4th one comprises the rest of rGAC (residues 1161–1185 and 1191–1206). Analogous centers of mass were also defined for the E. coli structure.

Essential dynamics analysis

The essential dynamics analysis [EDA, known also as principle component analysis and related to quasiharmonic analysis (QHA)] was performed using trjconv, g_covar and g_anaeig modules of GROMACS (60). EDA filters out unessential motions (noise) and decomposes the overall motion into individual modes (directions of motions), which belong to individual eigenvectors with particular eigenvalues, derived by diagonalization of the covariation coordinate matrix from the atomistic MD trajectory (61,62). EDA, as applied in our study, is more general compared to related QHA which, after diagonalization, would approximate the free energy surface by harmonic modes (61,62). EDA thus reflects the full-scale motion sampled during the simulation including harmonic, quasiharmonic and anharmonic contributions. Nevertheless, the distributions along individual modes (cf. Supplementary Figure S2) seem to be reasonably well approximated by gaussian functions which would be assumed by QHA (63).

Elastic network mode analysis

The NMA, based on the harmonic approximation of potential energy surface around the minimum energy conformation, was performed using ElNemo (64) web server (http://igs-server.cnrs-mrs.fr/elnemo/index.html). It allows the analytic solution of the equations of motion by diagonalizing the Hessian matrix. The eigenvectors of this matrix are the normal modes, and the eigenvalues are the squares of associated frequencies. The macromolecule movement can then be represented as a superposition of normal modes, fluctuating around a minimum energy conformation (65). Instead of using the atomistic force field, the potential function is simplified with single-parameter ‘coarse grained’ Hookean potential (elastic network mode analysis—ENM) (66). We standardly used cut-off radius 12 Å, force constant 10 N/m and 1 nt as the block. Note that since the spring constant is arbitrary, ENM does not predict the absolute values of the fluctuations.

RESULTS

The Kt-42+rGAC rRNA is formed by alternating rigid and flexible segments

We carried out 31 ns MD simulation of the Kt-42+rGAC rRNA of H. marismortui. During the first 5 ns the molecule gradually changed its initial (X-ray) arrangement to a new stable geometry. The relaxation changes the initial position of helices 43/44 by ca. 25° with respect to helix 42 (Figure 2A). After the initial transition is completed, the overall RMSD fluctuates in the range of 5–11 Å and 1–5 Å versus the starting and averaged structures, respectively (Figure S1). This initial structural transition is pivoting around the junction between helices 42 and 43/44, specifically base triples G1158 = C1209/A1188 and G1159 = C1208/A1189. We suggest that this structural transition reflects the relaxation of the system in the absence of the adjacent ribosomal elements. The initial relaxation does not lead to any changes in base pairing or isostericity of the simulated molecule.

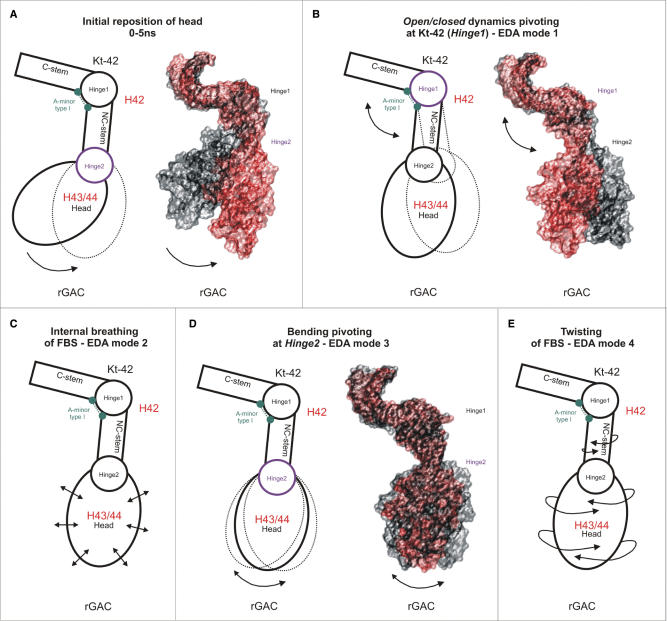
Figure 2.

Essential dynamics of Kt-42+rGAC rRNA system. Schematic (left) and surface (right) representations of the leading essential dynamics motions, double arrows indicate oscillations. (A) The initial displacement of the Head stemming from the rearrangement of Hinge2 (purple) observed during the first 5 ns of simulation and causing the permanent increase of the inter-helical angle by ca 25° (initial geometry in black, final in red). (B) Anisotropic anharmonic oscillation of rGAC pivoting at Kt-42 (Hinge1) (purple, EDA mode 1). (C) Internal breathing of rGAC (EDA mode 2) not contributing to the overall motion of rGAC and involving mainly the dynamics of non-canonical base pairs (see Supplementary Data). (D) Fluctuations of rGAC around Hinge2 (purple, EDA mode 3) characterized as anisotropic oscillatory bending of the duplex containing the upper part of helix 42 and helix 43. (E) Twisting of rGAC (EDA mode 4) stemming from twisting inherent to Kt-42 (35) and twisting in the Hinge2 region.

The simulated system consists of three rigid segments (one of them shows breathing, see subsequently) that are inter-linked by two flexible segments, leading to a double-elbow intrinsic dynamics (Figure 1C). The first flexible segment (Hinge1, Figure 1) includes nucleotides 1147–1152 and 1214–1216, i.e. the Kt-42. It shows anharmonic elbow-like oscillatory dynamics correlated with insertion of long-residency waters into its A-minor type I base pair (C1147 = G1216/A1152) between the C- and NC-stems. The Kt-42 dynamics is described elsewhere (35,49) while the present article is aimed at description of the rGAC helices 43/44, the junction between helices 42 and 43/44 and coupling of all motions. Hinge2 is localized at the junction between NC-stem of Kt-42 and helices 43/44 (residues 1158–1160, 1207–1209, 1186 and 1188–1190, Figure 1) and is responsible for the initial shift of the Head during the first 5 ns (Figure 2A). After the initial relaxation it shows substantial oscillations around its averaged geometry, preferably in direction back towards or further away from the starting structure but with a smaller amplitude (Figure 2D).

The most rigid segment is the C-stem of Kt-42 (1140–1146 and 1217–1223, with internal RMSD of ca. 1.0 Å). The other rigid segment is the NC-stem arm of Kt-42 (1153–1157 and 1210–1213) with RMSD 1.7 ± 0.5 Å. The compact helices 43/44 of the rGAC (1161–1185 and 1191–1206) do not contribute to the global motion but show internal breathing (see subsequently) with internal RMSD 1.9 ± 0.8 Å.

Essential dynamics analysis confirms presence of two independent flexible hinges

The EDA finds essential motions occurring during the simulation (61), disregarding the first 5 ns. The ratio of EDA eigenvalues of modes 1–4 is ca 1.0: 0.20: 0.18: 0.12 (plots of displacement along the individual eigenmodes are given in Supplementary Data, Figure S2). The first mode (ca. 60% of the overall motion) corresponds to the hinge-like oscillatory global motion of the upper part of the structure with respect to the C-stem at the base of helix 42 with a range ∼20 Å (Figure 2B) and pivoting around the Kt-42 (49). The second mode represents internal breathing of the compactly folded rGAC not associated with displacements of distant parts of the simulated system (Figure 2C). It can be described as reversible expansions and compactions of the Head within the range of ca. 5 Å (Figure S3). The third mode (Figure 2D) is oscillation around the relaxed geometry of the helix 42–helices 43/44 junction in direction of the initial structural rearrangement. Thus, the initial position of the Head in the H. marismortui crystal structure can be interpreted as a large amplitude deflection along the EDA mode 3. Interestingly, this direction roughly coincides with the preferred direction of the elbow-like motion of the Kt-42. Thus, the overall flexibility is highly anisotropic, with both hinges shifting the rGAC either towards or outwards the body of the subunit. The mode 3 oscillations produce movement of rGAC on a scale of ∼10 Å (displacement of U1170(P)) due to ∼10° oscillation of the angle between rGAC and Kt-42’s NC-stem (see ‘Materials and Methods’ section). The fourth mode represents twisting fluctuations of the rGAC with respect to the helix 42 (Figure 2E) due to combined twisting around the NC-stem of Kt-42 and the internal twisting of Kt-42. Note that although the Kt-42 is a genuine elbow-like element, it is also associated with non-negligible twisting components of its low-energy modes, cf. Figures S10–11 in Razga et al. (35). Mode 4 is associated with ∼13 Å range of U1170(P) atom fluctuations and ∼25° range of fluctuations of the fictive dihedral angle between the Head of rGAC and the C-stem of helix 42 (see subsequently).

Structure and dynamics of Hinge2

The junction between helix 42 and helix 43/44 comprises the bases localized at the border between the extended Kt-42 NC-stem and the rGAC, namely base triads G1158 = C1209/A1188 and G1159 = C1208/A1189 and tetrad A1207/G1160 … G1190/C1186 (Figures 1 and 3). This Hinge2 represents the pivoting point of the initial displacement of rGAC. Then it becomes the center of the directional (anisotropic) oscillations (Figure 2D) of the angle between the upper part of helix 42 and rGAC. The intrinsic Hinge2 bendability is not localized as in case of Kt-42, where the motion is pivoting around a single H-bond of the A-minor interaction (35). For Hinge2, the structural dynamics of the A-minor interaction, triad and tetrad (see Supplementary Data) are not coupled with either the initial displacement of rGAC or the subsequent EDA mode 3 dynamics.

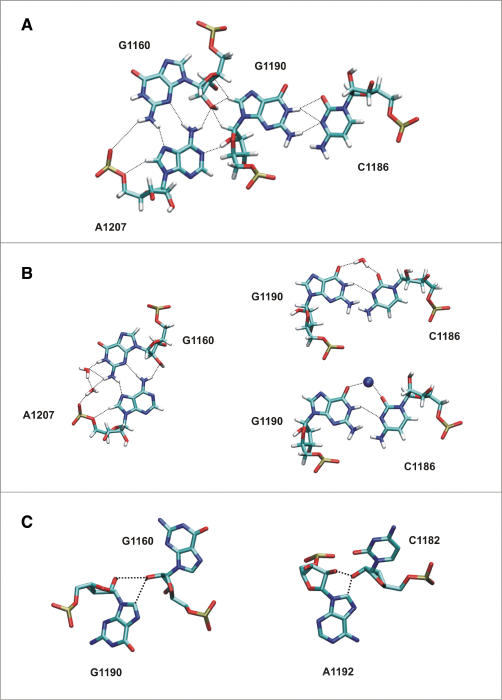
Figure 3.

Base tetrad A1207/G1160 … G1190/C1186 at the helix 42/rGAC junction. The overall X-ray geometry (A), the trans H/SE A1207/G1160 base pair with dynamical water insertion (B left), the trans WC/WC G1190/C1186 base pair assisted either by water or ion (B right) and the unusual G1190/G1160 base pair (X-ray structure, C left). A similar A1192/C1182 contact is shown (C right). Extended analysis of base pairing dynamics is given in Supplementary Data.

The movement of rGAC (the initial displacement and the EDA mode 3) correlates with change of major groove width of the RNA duplex formed by the upper part of helix 42 and bottom of rGAC. Spontaneous initial straightening of this rRNA duplex from its bent form (X-ray) to straight canonical-like form is indicated by increase of the following inter-phosphate distances: G1210(P)-A1152(P) from 9.5 Å (X-ray) to 16.0 Å (relaxed MD), C1209(P)-C1153(P) from 9.2 Å to 19.1 Å, C1208(P)-A1154(P) from 12.4 Å to 22.9 Å and A1207(P)-G1155(P) from 11.3 Å to 23.0 Å (Figure S4). The 11 ns restrained MD simulation confirms (see Supplementary Data) that motion around Hinge2 is fully independent of the dynamics of the triads in this region and the initial displacement of rGAC can be best described as a spontaneous straightening of an initially bent duplex to a straight conformation. Additionally, two free MD simulations of corresponding rRNA segment in E. coli structures reveal similar initial dynamical behavior of the Head position. Full details about the complex pairing patterns and rich local dynamics at Hinge2 are present in Supplementary Data.

Conservation and isostericity of Hinge2

We compared the sequence, base pairing and 3D-architecture of the Hinge2 region in crystal structures of large ribosomal subunits of H. marismortui, D. radiodurans, and E. coli (codes 1JJ2, 1NKW, 2AW4 and 2AWB). We also examined sequence alignments obtained from the latest release of the European Ribosomal Database (67) and isostericity analysis was carried out by Ribostral (68). The data show that the 3D-structure of this region is universally conserved in all organisms even if individual nucleotides are not the same. Full details are given in Supplementary Data.

Twisting motion of the rGAC with respect to helix 42

The X-ray study of 70S E. coli ribosome (18) reveals modest conformational changes in the position of the rGAC. The authors concluded that there is a twisting of the C-stem of Kt-42 with no structural change in the K-turn itself. However, we suggest that the two X-ray structures of E. coli (2AW4 and 2AWB) could within the limits of the resolution equally well reflect the dynamics of the A-minor interaction of the Kt-42. As shown earlier, the elbow-like flexibility of Kt-42 (Hinge1) involves also substantial twisting motions, see Supplementary Data in Razga et al. (35). Thus, some Kt-42 twisting can easily occur even without a visible elbow-like bending. The key inter-atomic distance C1043(O2′)-A1048(O2′) in the dynamical A-minor type I interaction of the Kt-42 is 2.6 and 3.8 Å in the 2AW4 and 2AWB structures while the corresponding C1147(O2′)-A1152(O2′) distance in H. marismortui structure (1JJ2) is 3.0 Å. The range of open/closed dynamics of this distance in simulations is 2.6–4.0 Å. The dynamical inter-phosphate distance C1043(P)-A1048(P) is 13.4 and 14.4 Å in 2AW4 and 2AWB structures. The corresponding C1147(P)-A1152(P) distance is 14.7 Å in H. marismortui and 13.6–16.7 Å in simulations. Thus, if these X-ray distances are accurate enough, they match the typical internal K-turn dynamics (35). Similarly, the virtual torsion angle describing the overall helix 42–44 twisting (see ‘Materials and Methods’ Section and Figures S5 and S6) is −59° and −83° in the 2AW4 and 2AWB E. coli structures and −67° in the H. marismortui crystal structure. MD reveals broad distribution of this angle with peaks around ca. −65° and −90° (Figure S6), similar to what is seen in the X-ray structures. In contrast, RMSD of 0.7 Å characterizes the base of the helix 42 containing the C-stem of Kt-42 for the two E. coli structures when residues 1036–1041 and 1114–1119 are overlaid. Comparing structures of E. coli and H. marismortui the helical properties of the base of helix 42 look different (RMSD = 1.15 Å). However, E. coli sequence contains two non-canonical cis WC/WC base pairs (A1039/G1116 and A1040/G1115) instead of the standard base pairs in the H. marismortui. This may contribute to different helical parameters and mechanical properties of this region (69), and thus detailed comparison of H. marismortui and E. coli C-stem regions is not straightforward. We, therefore, tentatively suggest that the modest X-ray variability of the rGAC positions can be reasonably explained as a combination of twisting around NC-stem of Kt-42 and twisting component of Kt-42 dynamics. It resembles the EDA mode 4 analyzed above, with participation of motion of the Head stemming from Hinge2.

Breathing of the rGAC

To investigate the substantial internal breathing of rGAC (helix 43/44, EDA mode 2) we carried out detailed analysis of the dynamics of all base pairs. The non-canonical interactions reveal considerable structural dynamics and primarily contribute to the internal breathing of the rGAC. Many rGAC non-Watson–Crick interactions are mediated by complex long-residency hydration sites and we also identified several sites with a substantial occupation by monovalent cations. We noticed a dynamical A1192 … C1182 interaction involving base-sugar A1192(C8)-C1182(O2′) H-bond, A1192(C2′)-C1182(O2) and A1192(C3′)-C1182(O2) contacts, and some sugar–sugar contacts (Figures 3C and S7). This interaction is seen as planar in the crystal structure but prefers a perpendicular orientation of bases in the simulation (Figure S8). An analogous tertiary contact is also seen in the Hinge2 between G1160 and G1190, with bifurcated H-bonds between O2′ of G1160 and O2′ and C8 of G1190. This interaction remains coplanar in the simulations. This base pairing pattern does not belong to any characterized types of base pairs according to Leontis et al. classification and may represent a new recurrent type of tertiary interactions. This is supported by structural motif search in available ribosome structures (70) which in addition reveals that this type of interaction is frequently found as a perpendicular contact in the ribosome. Full details about this interaction and about structural dynamics of all other interactions in the helix 43/44 area are given in Supplementary Data.

Length of the stems flanking Kt-42 is conserved

The motion of the two Hinges in the Kt42+rGAC region is highly anisotropic and actually both hinges have preferable motions in the direction towards and outwards the body of the subunit. Variation of the length in any of the stems of helix 42, on which the rGAC region is based, would considerably change the direction of flexibility. This is not likely to occur if the motions are of biological significance. We thus investigated the stem lengths of helix 42 in available sequence alignments (71), to see if they are conserved throughout evolution. The area studied corresponds to E. coli numbers 1030–1055 (5′ strand) and 1104–1124 (3′ strand). After filtering out repeated sequences and obvious alignment or sequencing errors, we ended up with an alignment that includes 34 archaeal, 751 bacterial and 154 eukaryal unique sequences. With the help of Ribostral (68) we found out that the length of helix 42 is completely conserved across all three domains. The only exception was found in about 15% of bacteria that have the 3′ strand longer by 3–5 nt compared to the remaining sequences. This increase in the 3′ strand length is not complemented by any change in the 5′ strand length, and occurs near the edges of the kink turn internal loop area (Figure S9). Therefore, the extra nucleotides do not seem to lengthen the helix, and could be probably bulged out near the internal loop area without causing any major change in the overall structure and flexibility.

If we compare the conservation of length of helix 42 to that of other large ribosomal subunit helices in the three domains of life, we conclude that helix 42 is among the ∼50% most conserved in length (Figure S10). Even more striking is that when the two organelles, mitochondria and chloroplasts, are considered, helix 42 is among ∼30% of the most length-conserved helices (Figure S10). The two organelles are under substantially different evolutionary pressure than members of the three domains of life, and thus the subunits are smaller in size, with some helices shortened or even missing. Helix 42 has, therefore, been suggested to be an integral part of a minimal functional ribosome (72).

Comparison with coarse-grained normal mode analysis

Coarse-grained methods were used earlier to evaluate the dynamics of ribosome (22,23). Such calculations typically perform a normal mode analysis (NMA) within the elastic network mode (ENM) approximation. ENM uses a simplified potential to create a network of harmonic springs that connects atoms or pseudoatoms within a given cut-off distance. It works well for, e.g. globular proteins where interatomic interactions are quite homogenous. It is less likely to work for something as specific and non-globular as the stalk elements of ribosome.

We performed the ENM NMA analysis on Kt-42+rGAC RNA system (starting from the X-ray structure) using ElNemo (64) web server (http://igs-server.cnrs-mrs.fr/elnemo/index.html) and analyzed the four lowest-frequency modes of Kt-42+rGAC. The NMA (NME) mode 1 with frequency (f) equal to 1 and collectivity (c) equal to 0.5467 (64) represents the bending motion with the origin in the Hinge2 area. This motion is similar to the initial displacement of the Head (observed during the first 5 ns) or EDA mode 3 (Figure 2A and D). The mode 2 (f = 1.65 and c = 0.6994) represents the overall twisting of the rGAC with respect to the helix 42, stemming from a combined twisting around the NC-stem of Kt-42 and the internal twisting of Kt-42, similar to our EDA mode 4 (Figure 2E). The mode 3 (f = 2.15 and c = 0.3350) represents mainly the internal twisting of Kt-42. The mode 4 (f = 3.16 and c = 0.1754) shows some breathing of the Kt-42’s C-stem and is already rather insignificant. In conclusion, the ENM ElNemo analysis captures only two out of four dominant motions of the Kt-42 + rGAC system observed in MD. Most importantly, the key elbow-like dynamics of the Kt-42 appears to be missed and also the breathing of the Head (EDA mode 2) is not observed.

Another assessment of the applicability of normal mode type of calculations applied to RNA can be found in the literature (63) and for additional information see also (73). Our ENM results are given in Supplementary Data. In conclusion, the atomistic simulations with explicit inclusion of solvent followed by EDA have no alternative for the present system, where we need to describe details of H-bonding dynamics including the dynamical water insertion. Further, we deal with a system, which has a very broad free energy minimum, and thus is anharmonic.

Comment on ions

The present simulations were carried out in presence of a net-neutralizing set of Na⁺ ions. This can be justified in the following way. The non-polarizable pair additive force field relies on a quite primitive approximation, representing the ions as simple van der Waals spheres with atom-centered point charges of +1 or + 2. Due to this crude approximation, the force field is unlikely to exactly mimic the ‘experimental’ ion conditions and it is quite justified to run the simulations using the net-neutralizing set of monovalent ions only. A meaningful description of divalent cations is fairly outside the applicability of the force field while sampling of divalent cations in simulations is terribly insufficient. Therefore, inclusion of divalent ions into nucleic acid simulations may cause artifacts and basically is not advised. Fortunately, the simulations are usually too short to exhibit instabilities stemming from inexact salt conditions. We have shown recently that the K-turn dynamics is independent of the type of ions used in simulation (49). Further discussion of the ion issue can be found in our recent papers (36,45,74).

DISCUSSION

We carried out 31 ns MD simulation on Kt-42+rGAC rRNA (complete rRNA helices 42–44 including kink turn 42 and GTPase-associated center rRNA), starting from the X-ray structure of the 50S subunit of H. marismortui (5). Simulation was supplemented by restrained control simulation, control simulations of helix 42–44 rRNA of E. coli X-ray structure, and sequence, isostericity and motif search analyses. The aim was to highlight the basic intrinsic dynamical flexibility of this rRNA segment in the ribosome-like geometry.

The simulation trajectory can be divided into two parts. During the first 5 ns, we observed a smooth initial rearrangement which changes the initial position of helices 43/44 by ca. 25° with respect to helix 42 (Figure 2A). This initial rearrangement brings no visible local changes in the base pairing and isostericity of the interactions. The structural transition is roughly pivoting around the junction between helix 42 and helices 43/44, specifically around the type II A-minor base triple G1158 = C1209/A1188 and its neighboring triad G1159 = C1208/A1189. It can be best described as straightening of rRNA duplex from its bent geometry (X-ray) to straight, canonical-like RNA. We suggest that some other component of the ribosome (this area is substantially disordered in the X-ray structures) may push the rGAC towards the large subunit. This simulation in any case clearly indicates that the junction between helices 42 and 43/44 is easily deformable. After the initial transition is completed, the simulated molecule shows no further structural development, but exhibits profound stochastic fluctuations revealing that this rRNA region possesses a unique internal flexibility.

The Kt-42+rGAC rRNA consists of three rather rigid (one of them internally ‘breathing’) segments linked by two flexible ones. The basically rigid segments are the C- and NC-stems of Kt-42 and the compact helices 43/44 of the rGAC. The first flexible segment (Hinge1) is the Kink region localized between C- and NC-stem of Kt-42. The Kt-42 shows anharmonic elbow-like oscillatory dynamics correlated with insertion of long-residency waters into its A-minor type I base pair between the C- and NC-stems (49). Hinge2 is localized at the junction between the NC-stem of Kt-42 and helices 43/44 (Figure 1). Bendability of this region is, however, not localized, in contrast to Kt-42. Hinge2 is responsible for the initial shift of the Head (helices 43 and 44) (Figure 2A). After the initial relaxation it shows substantial oscillations around its averaged geometry, preferably in direction towards or away from the starting structure but with smaller amplitude.

The intrinsic flexibility of the helix 42–44 23S rRNA segment is visualized by EDA filtering out unessential motions and noise. EDA (disregarding the initial displacement of the Head of the GTPase-associated center rRNA) reveals several leading motions. The first EDA mode represents ca. 60% of the overall motion and corresponds to the hinge-like oscillatory global motion of the GTPase-associated center rRNA with respect to the C-stem at the base of helix 42, stemming from the Kt-42. There are three additional modes that substantially contribute to the dynamics. The second mode represents internal breathing of the compactly folded rGAC. The third mode represents oscillations (around the relaxed geometry) of the rGAC at the junction between helix 42 and helices 43/44 (Figure 2D) in direction of the initial structural rearrangement. Thus, the initial position of the Head in the crystal structure can be interpreted as a large amplitude deflection along the EDA mode 3. Interestingly, this direction also coincides with the preferred direction of the elbow-like motion of the Kt-42. The Hinge2 dynamics does not stem from any specific oscillation of base pairs, triples or quadruples but correlates with changes of major groove width of the RNA duplex formed by the upper part of helix 42 and helix 43. The fourth mode represents twisting fluctuations of rGAC with respect to the helix 42 stemming from combined twisting around the NC-stem of Kt-42 and the internal twisting of Kt-42.

The simulation results were compared with NMA using the ENM approximation that is commonly used for coarse-grained modeling. As expected, the leading EDA modes 1–2 were missed by the ENM approach. Note that these include mainly the elbow-like dynamics of the Kt-42. The present system therefore requires full-scale atomistic explicit solvent simulation to be properly described.

The dynamics should be interpreted in the following way. The free MD simulation samples spontaneously the available space of low-energy geometries of the studied system. In other words all geometries that are significantly populated in such simulation are intrinsically very easily accessible for the studied RNA. The helix 42–44 region is thus an internally highly flexible (deformable) and anisotropic RNA modulus with preferred motions towards and outwards the 50S subunit, localized at two hinges and complemented by twisting motions.

The motion of the two Hinges in the Kt42+rGAC region is highly anisotropic. Variation of the length of stems of helix 42 would considerably change the direction of flexibility. This is not likely to occur if the motions are of biological significance. Indeed, we found that helix 42 length is entirely conserved and when mitochondria and chloroplasts are considered, helix 42 is among ∼30% of the most length-conserved helices (Figure S10). Although there are many conceivable structural and functional constraints that would require essential helices to be conserved in length, such as preservation of local or tertiary interactions (75), it is likely that helix 42 has the additional constraint of housing two important hinges whose movement would be asynchronized and re-directed, if helix length is changed. Base pair substitutions do occur in the helix 42 stems and may subtly modify the directionality of motions (69). The entire conservation of the length of both rigid arms flanking the Kt-42 indicates that the profound anharmonic and anisotropic double-elbow flexibility of the Kt-42+rGAC rRNA segment may be important in tRNA selection and translocation. For example, it may be involved in positioning the L7/L12 stalk with respect to the 50S ribosomal subunit. The flexible rRNA Kt-42+rGAC segment is in a close contact with the highly dynamical L7/L12 complex, whose exact position is yet to be determined. The Kt-42+rGAC rRNA segment flexibility is very different from the anisotropic spring-like stiffness of the tRNA (76), since the Kt-42 is a highly anharmonic element suitable to act as a passive and adjustable elbow to mediate motions of the surrounding structural elements.

Analysis of the sequence conservation and isostericity of the junction between the helix 42 and the rGAC shows that all observed base substitutions appear to fully keep conserved isosteric structure of this region. We, however, made two interesting observations. The second triple in the junction region (G1159 = C1208/A1189 in H. marismortui, G1066 = C1115/A1096 in D. radiodurans and G1055 = C1104/A1085 in E. coli) forms a typical A-minor interaction in the latter two species. In H. marismortui, however, the adenine is flipped to syn and forms a rather unexpected trans Hoogsteen (H)/Sugar edge (SE) interaction between A1189 and G1159 (Figure S11). Since the overall compactness of the triad is almost the same for both arrangements, both geometries are compatible with the sequence analysis. There is a tertiary contact in the adjacent tetrad between G1160 and G1190, with bifurcated H-bonds between O2′ of G1160 and O2′ and C8 of G1190. This is replaced by identical G … A contacts in both bacterial organisms while sequences belonging to the three domains are GA, AG, GG and AA. There is an almost identical base pair also in U1164–A1192/C1182 base triad between A1192 and C1182 (Figure 3C). This base pairing pattern does not belong to any characterized types of base pairs (54) and may represent a new recurrent type of tertiary interactions in ribosome, as supported by the structural motif search (70) (Figure S8, Table S1).

The compact region (Head) formed by helices 43 and 44 contains an intricate set of base pairing patterns including triads and tetrads. Many of these interactions are very dynamical, conferring a substantial structural plasticity to the shape of the rGAC. The Head shows visible inflation/deflation dynamics and also the local RNA structure on its surface is variable. The structural dynamics of this region is intimately associated with long-resideny hydration and cation binding sites (32,35,74). It forms a typical family C three-way junction with extensive interactions between the P1 and P3 stems and between J31 and the shallow groove of P2 (77). The ‘breathing’ described above originates in the dynamics of the P1/P3 inter-stem interactions and the bending is localized in the area of J31/P2 interactions.

The recent crystallographic study of 70S E. coli ribosome (18) indicates modest conformational changes in the position of the rGAC in two independent structures of the ribosome. The structural difference was attributed to twist of the C-stem region below the Kt-42 at the base of helix 42. However, we also found a 1.2 Å variability of the key inter-atomic distance C1043(O2′)-A1048(O2′) in the dynamical A-minor type I interaction of the Kt-42 (corresponding to the C1147(O2′)-A1152(O2′) distance in H. marismortui structures). This indicates that the crystal data could also by interpreted assuming the flexibility of the Kt-42, because its dynamics is pivoting around this inter-atomic distance. Since the K-turn low-energy conformational space has non-negligible twisting components, K-turn twisting motions could occur without any substantial bending, and can be combined with twisting motions of the Head of the rGAC (Figure 2E).

In summary, we demonstrate that rRNA building blocks posse contrasting intrinsic flexibilities (flexibility signatures) and can be combined to form larger architectures with complex patterns of preferred low-energy motions and geometries. MD simulation technique appears to be particularly suitable to capture the qualitative differences in intrinsic flexibilities of rRNA building blocks since it captures atomic resolution dynamics while the molecules do not unfold on the simulation time scale away from the ribosomal geometries. In contrast to, e.g. the NMA method the MD simulations include the key anharmonic contributions. We suggest that the basic intrinsic physico-chemical properties of the RNA motifs can in many cases be maintained in the RNA assemblies, and thus are worth to analyze.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.