Abstract
MRI was extended to the measurement of changes in oxidative metabolism in the normal human during functionally induced changes in cellular activity. A noninvasive MRI method that is model-independent calibrates the blood oxygen level dependent (BOLD) signal of functional MRI (fMRI) against perfusion-sensitive MRI, using carbon dioxide breathing as a physiological reference standard. This calibration procedure provides a regional measurement of the expected sensitivity of the fMRI BOLD signal to changes in the cellular activity of the brain. Maps of the BOLD signal calibration factor showed regional heterogeneity, indicating that the magnitude of functionally induced changes in the BOLD signal will be dependent on both the local change in blood flow and the local baseline physiology of the cerebral cortex. BOLD signal magnitude is shown to be reduced by 32% from its expected level by the action of oxygen metabolism. The calibrated fMRI technique was applied to stimulation of the human visual cortex with an alternating radial checkerboard pattern. With this stimulus oxygen consumption increased 16% whereas blood flow increased 45%. Although this result is consistent with previous findings of a significant difference between the increase in blood flow and oxygen consumption, it does indicate clearly that oxidative metabolism is a significant component of the metabolic response of the brain to functionally induced changes in cellular activity.
Keywords: hypercapnia, cerebrovascular reactivity
Functionally related changes in neuronal activity in the normal brain are reliably accompanied by changes in local cerebral blood flow (CBF) (1). The degree to which the cerebral metabolic rate for oxygen (CMRO2) also changes with activity-related increases and decreases in neuronal activity remains controversial. Although some reports show little or no task-induced increase in CMRO2 (2–4), others have shown varying degrees of coupling of oxidative metabolism to glucose consumption and blood flow (5–7), both of which increase dramatically with task activation (3, 4, 8). Some have suggested that the reason CBF changes more than CMRO2 during functionally related increases in neuronal activity (decreases have not been addressed) is to enhance the diffusion-limited delivery of oxygen to the tissue (9–11).
Current functional MRI (fMRI) methods rely on the fact that CBF changes more than CMRO2, producing localized changes in tissue oxygen content. These localized changes in tissue oxygen content change magnetic fields in a manner that can be detected with MRI. This signal has been termed the blood oxygen level dependent (BOLD) signal of fMRI (12, 13). The fMRI BOLD signal has been viewed as a reasonable marker of functionally related changes in neuronal activity. The magnitude of the BOLD signal, of course, is dependent on the relationship between changes, if any, in CMRO2 and the changes in CBF. The greater the increase in CMRO2 for any increase in CBF, the smaller the BOLD signal becomes and vice versa.
In this paper we examine the degree to which the relationship between CBF and CMRO2 varies across the brain because of variations in the functionally induced changes in CMRO2. The goal of our study was to calibrate the BOLD signal against CBF measured with MRI (12, 14) by using carbon dioxide breathing as a physiological means of manipulating CBF independent of CMRO2 (15, 16). Using this experimental framework, we were able to generate relatively assumption-free measurements of CMRO2 change during functionally related changes in neuronal activity and to compare these measurements between regions and between subjects.
THEORY
We assume that the BOLD effect behaves as a change in observed NMR transverse relaxation rate, ΔR*2, which is linearly dependent on the blood volume fraction fv (17–19) and dependent on magnetic susceptibility difference between blood and tissue, Δχ, raised to a power β. The susceptibility difference, which is proportional to blood deoxyhemoglobin (dHb), has a supralinear effect: a linear large vessel component is combined with small vessel contributions, which tend toward a quadratic effect on relaxivity according to the Luz-Meiboom model for diffusion-mediated exchange on the capillary scale (17–20). We performed Monte Carlo NMR simulations (18) using 2% venous and 2% capillary volume fractions, varying venous oxygen saturation from 60% to 95%; for these values, and our imaging parameters β = 1.5 fits the simulated ΔR*2 vs. Δχ curve.
Fick’s law describes conservation of oxygen delivery and oxygen uptake, stating the mass-balance principle that oxygen delivery is proportional both to blood flow (CBF) and to the arteriovenous oxygen difference (21). Because the arteriovenous difference is proportional to deoxygenated hemoglobin production, Fick’s law can be written in terms of dHb: dHb ∝ CMRO2/CBF. In terms of physiological variables, ΔR*2 between time 0 and t is then
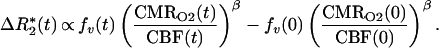 |
1 |
We define Bt, Ft, and Vt as the BOLD signal, CBF signal, and blood volume at time t normalized by ratio to a baseline period in the experimental paradigm. rCMRO2 is the CMRO2 relative to baseline. For small change in relaxivity (TEΔR*2 ≪ 1) the BOLD signal is Bt ≅ 1 − TEΔR*2(t). Substituting the above normalized variables into Eq. 1 and extracting the baseline values, we have
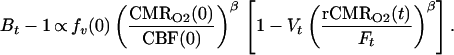 |
2 |
CBF is directly measurable by arterial spin tagging perfusion MRI; we selected the FAIR method (flow sensitive alternating inversion recovery) for this report (12, 14). We express blood volume changes in terms of CBF: V = Fα where α = 0.38 is taken from a previous study (22) and verified by using MRI contrast agents by Mandeville in our laboratory (not shown). We aggregate the baseline values from Eq. 2 and the proportionality constant relating BOLD signal change to dHb into a calibration parameter: M ∝ fv(0) (CMRO2(0)/CBF(0))β. For convenience, this relation is written as a proportionality; the addition of constants for magnetic susceptibility of dHb, susceptibility effects on transverse relaxation, and echo time dependence would complete the equality.
M is dependent on baseline tissue dHb content; it thus may vary between trials and between brain regions. M can be thought of as the baseline dHb concentration, scaled in terms of BOLD signal. Because BOLD signal is dependent on washout of this dHb, M is the BOLD signal headroom for blood flow-induced signal changes, assuming no concomitant metabolic change.
To estimate M, we calibrate against the physiological challenge of hypercapnia (subscript H), assuming there is no significant increase in metabolic rate over baseline during hypercapnia (15, 16). We then manipulate Eq. 2 to determine its implicit proportionality constant including baseline values:
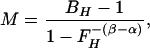 |
3 |
where BH and FH are BOLD and CBF ratios for CO2 breathing versus baseline. Because hypercapnia causes dramatic increase in blood flow, which washes out dHb, both BH and FH are expected to be greater than one, and because the exponent on FH is negative (−1.12 in our model), M must be positive. Because M is also the maximum BOLD signal change for the current baseline state, we also have M > B(t) − 1 for any activating stimulus.
With the experiment calibrated by determination of M, the normalized time courses of perfusion F(t) and BOLD fMRI B(t) can be used to compute dynamic oxidative metabolism maps (rCMRO2(t)) relative to baseline.
 |
4 |
Application of Eqs. 3 and 4 provides the desired measurement of BOLD sensitivity to CBF, and dynamics of the relative metabolic rate for oxygen.
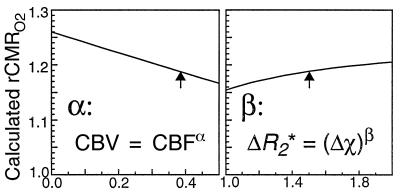
We finally consider the sensitivity of our results to the details of our model. We computed our average result as a function of the only undetermined parameters of the model, α and β, and plotted results in Fig. 1 as the parameters are varied for a given set of data. If blood volume does not change with blood flow, then our rCMRO2 estimates are at most 6% low (30% more change than predicted). If the susceptibility effect is linear (β = 1), then our rCMRO2 estimates are at most 4% high. In the small vessel limit of quadratic dependence, our estimates would be 2% low. Sensitivity of our model to these parameters is therefore small, on the order of our standard error of measurement for a single subject (see Table 1).
Figure 1.
Model dependency on design parameters. Ranges of calculated rCMRO2 were obtained by varying α and β through plausible values. The blood volume coupling exponent ∝ has been measured at 0.38 (22); Monte Carlo simulations show β ≅ 1.5 for our experiment. We used these values (arrows) for our analyses.
Table 1.
Oxidative metabolism averaged over regions of interest during 10 trials
| Subject | Voxels
|
Hypercapnia
|
Photic stimulation
|
||||
|---|---|---|---|---|---|---|---|
| Total 225 | BH | FH | M | BS | FS | rCMRO2 | |
| 1A | 23 | 1.020 ± 0.001 | 1.169 ± 0.001 | 0.11 ± 0.01 | 1.016 ± 0.001 | 1.35 ± 0.02 | 1.14 ± 0.01 |
| 1B | 25 | 1.009 ± 0.001 | 1.058 ± 0.008 | 0.09 ± 0.01 | 1.014 ± 0.001 | 1.40 ± 0.05 | 1.19 ± 0.03 |
| 2A | 12 | 1.025 ± 0.001 | 1.27± 0.05 | 0.06 ± 0.02 | 1.021 ± 0.001 | 1.55 ± 0.07 | 1.17 ± 0.04 |
| 2B | 27 | 1.024 ± 0.002 | 1.26 ± 0.03 | 0.08 ± 0.02 | 1.021 ± 0.001 | 1.46 ± 0.03 | 1.16 ± 0.02 |
| 3A | 32 | 1.0218 ± 0.007 | 1.15 ± 0.01 | 0.12 ± 0.01 | 1.0204 ± 0.0008 | 1.38 ± 0.03 | 1.16 ± 0.02 |
| 3B* | 28 | 1.0133 ± 0.0006 | 1.21 ± 0.01 | 0.06 ± 0.003 | 1.019 ± 0.001 | 1.54 ± 0.04 | 1.12 ± 0.02 |
| 4A | 27 | 1.014 ± 0.002 | 1.11 ± 0.02 | 0.06 ± 0.02 | 1.022 ± 0.002 | 1.47 ± 0.03 | 1.16 ± 0.03 |
| 4B* | 10 | 1.010 ± 0.002 | 1.08 ± 0.04 | 0.06 ± 0.02 | 1.005 ± 0.001 | 1.28 ± 0.04 | 1.18 ± 0.02 |
| 5A | 21 | 1.0222 ± 0.0004 | 1.17 ± 0.02 | 0.09 ± 0.01 | 1.016 ± 0.001 | 1.35 ± 0.04 | 1.15 ± 0.02 |
| 5B | 20 | 1.017 ± 0.001 | 1.29 ± 0.02 | 0.053 ± 0.005 | 1.022 ± 0.002 | 1.67 ± 0.06 | 1.13 ± 0.03 |
| Mean ± SE | 1.018 ± 0.002 | 1.18 ± 0.03 | 0.079 ± 0.007 | 1.017 ± 0.005 | 1.45 ± 0.04 | 1.16 ± 0.01 | |
| SD(exp) | 0.00572 | 0.0807 | 0.02355 | 0.005421 | 0.1173 | 0.02109 | |
| SD(sim) | 0.00073 | 0.0107 | 0.00550 | 0.000577 | 0.0273 | 0.02530 | |
| Var ratio | 61 | 57 | 18 | 88 | 18 | 0.7† | |
Least squares estimates ± standard errors in primary visual cortex. BH and FH, BOLD and CBF hypercapnia divided by baseline; BS and FS, BOLD and CBF photic stimulation divided by baseline; M, BOLD sensitivity calibration parameter; rCMRO2, change in cerebral metabolic rate for oxygen.
Long duration (5 min) stimulus paradigm; not averaged into Fig. 2.
rCMRO2 is the only estimate without measurable inter-trial variance compared with Monte Carlo simulated measurement noise, SD(sim) (α = 0.7). The remainder have significant variance over measurement noise (P < 0.001; F = 10 at α = 0.001, n1 = 9, n2 = 9).
METHODS
Volunteers‖ breathed gases delivered through a nonrebreathing face mask with bag (Baxter 1203) at 15 liters/min, attending to a projected image. During eight paired trials in five subjects, periods of baseline fixation dot stimulus were interleaved with images of a radial checkerboard pattern alternating at 12 Hz. After five 1-min periods of photic stimulation alternating with baseline, inhalation gas was changed from air to a mixture of 5:21:74 percent CO2/O2/N2 for 5 min. During the final 5 min, the subjects again breathed air and repeated the same stimulus as during the first 5 min. To test the response to longer duration stimuli, additional experiments were performed in two subjects with 5 min of visual stimulation and 4 min of CO2 breathing separated by 2 min of baseline condition. Physiological monitors recorded heart rate, respiratory rate, oxygen saturation, and end-tidal CO2.
Echo-planar MRI images (Advanced NMR/General Electric Signa 1.5 T) were collected through calcarine cortex by using 7-mm slice thickness and 3.1-mm square voxels from a 32-ms readout window. The following two pulse sequences were used: (A) BOLD asymmetric spin echo, TR = 2 s, TE = 70 ms, refocusing pulse advanced 25 ms from TE/2; (B) FAIR inversion recovery spin echo, TR = 3 s, TI = 1 s, TE = 45 ms, slice-selective initial inversion pulse thickness 14 mm alternating with a nonselective inversion pulse. Subtraction of nonselective from selective echoes produced the FAIR signal proportional to perfusion. The order of experiments (A) and (B) was randomized between trials.
By using image display and analysis suite xds developed by one of the authors (T.L.D.), regions of interest within primary visual cortex were selected to include areas responsive both to hypercapnia and to photic stimulation for both FAIR and BOLD experiments. Pixels with large baseline variances or large calculated variance in M were automatically excluded. Accounting manually for inter-experiment motion, the regions were then matched between experiments (A) and (B), and were identical for visual stimulation, hypercapnia, and baseline periods within each experiment. Temporal windows were chosen for summary analysis to include only time points after the stabilization of signal, typically from 10 s after stimulus change until the next stimulus change, and after 15 s in the poststimulation baseline state to minimize the effect of transient signal undershoot. For the visual stimulus analysis, the first 5 min of alternating stimulus and baseline was used; for the hypercapnia statistics, baseline points were taken between visual stimuli both before and after the CO2 breathing portion of the experiment.
Data for each subject were pooled into baseline, stimulated, and hypercapnia epochs for both pulse sequences. After removing drift in the BOLD signal with a quadratic fit to baseline points, ratios were computed for hypercapnia to baseline (CBF FH and BOLD BH) to calculate M using Eq. 3. Least-squares estimates of average stimulation and time courses of CMRO2 were computed by using Eq. 4, including second-order statistics for noise estimation (see Appendix). These calculations were compared with observed inter-trial variation to assess individual variation in BOLD sensitivity and metabolic and hemodynamic reactivity.
RESULTS
Breathing carbon dioxide-enriched air resulted in 5 ± 1 mmHg increases in end-tidal CO2 in all subjects, along with a small increase in respiratory rate but not heart rate or oxygen saturation. This level of hypercapnia elicited 18 ± 3% average ± SE increase in CBF, with concomitant BOLD signal increases of 1.8 ± 0.2% (Table 1). The average M within activating visual cortex, calculated separately for each trial, was 7.9 ± 0.7%. During photic stimulation CBF increased 45 ± 4% and BOLD signal increased 1.7 ± 0.5%. CMRO2 increases, calculated separately for each trial, averaged 16 ± 1% during photic stimulation. CMRO2 increased much less than CBF in all subjects; however, this moderate increase in CMRO2 limited the BOLD effect on average to 68% of its maximal value for the given perfusion increase.
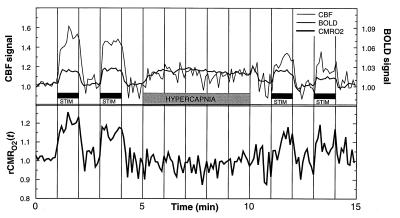
Cross-subject time course averaging for eight trials (Fig. 2) revealed BOLD and CBF signal responses that track the stimulation paradigm to within two image collection frames (12 s). The dynamic response of CMRO2 calculated from this average shows prompt tracking of metabolism to stimulus, increasing transiently by up to 20%, and prompt recovery during rest periods. Only the first 5 min was used for the photic stimulation averages shown in Table 1 to minimize the effects of subject motion in later time points. Additional experiments with 5-min stimulation periods (trials 3B and 4B in Table 1) showed no significant differences from those with short periods: there was no habituation effect or change in oxidative metabolism over time.
Figure 2.
BOLD and CBF time courses normalized to the hypercapnia signal change, averaged across eight trials. Compared with hypercapnia-induced signal change, the CBF signal outstrips the BOLD signal changes during photic stimulation. rCMRO2 time course calculated from the same data shows metabolic response within seconds of photic stimulation onset. No temporal smoothing was done: all time points (6-s resolution) were collected and calculated independently. Note that by analytic design the average rCMRO2 during the hypercapnia period and baseline periods are both set to 1.
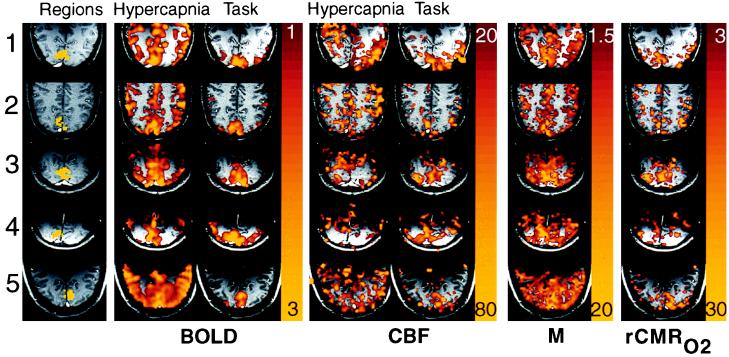
Maps of photic stimulation and hypercapnia normalized to baseline (Fig. 3) show general cortical signal increase during hypercapnia, and localized primary visual cortex signal increase during photic stimulation using both BOLD and FAIR methods. Positive signal change is required during the hypercapnia stimulus for a valid voxel estimate of M to be calculated (nonzero denominator in Eq. 3). Comparison of valid M estimates in visual to peripheral cortex shows increased M in visual cortex, implying increased BOLD signal sensitivity. Maps of rCMRO2 also show focally increased metabolic uptake in primary visual cortex.
Figure 3.
Maps from trial (A) of each subject from Table 1 show regional variations. The first column shows regions of interest in yellow superimposed on an anatomical image weighted for slow flow to highlight veins: note prominent sagittal sinuses. No venous structures were seen within the regions of interest. The second and third columns show BOLD hypercapnia and task activation responses as color overlays: colors represent signal increases from 1% (red) to 3% (yellow). The fourth and fifth columns show CBF hypercapnia and task activation increasing 20% to 80%, the calibration parameter M calculated from hypercapnia data alone is shown in color from 1.5% to 20%. The right-most column shows rCMRO2 for each subject, from 3% to 30%, calculated from M and task activation images. All subjects show a confluent patch of increased rCMRO2 averaging from 13% to 19% within visual cortex. Some peaks reach up to 30% increase in metabolism, corresponding to peaks of blood flow up to 70%.
Individual responses are tabulated in Table 1 with standard error estimates calculated from second-order statistics in the source images. Large variance is seen between trials in the BOLD responses and in the M calibration parameter. This discrepancy between expected and measured inter-trial variance is eliminated for rCMRO2, indicating much less variability for metabolic changes than for BOLD fMRI sensitivity and responsiveness.
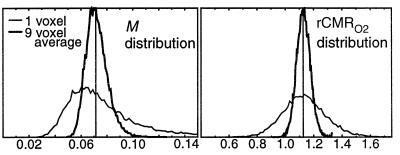
Simulations were performed to determine the effect of noise on model-based estimates. Fig. 4 shows how variance in the estimates is dramatically improved by a 3 × 3 voxel smoothing step at the beginning of analysis. We also see the effect of noise on bias in the estimation of M, caused by the largest noise source occupying the denominator of M, which self-corrects for rCMRO2.
Figure 4.
Noise propagation simulation results, from Monte Carlo simulation with means and second order noise characteristics taken to match single voxel or nine voxel averages from the primary data. (BOLD and FAIR baseline SNR 100:1, FAIR perfusion signal component 4%). Although the maximum likelihood for the M estimate is skewed toward lower values, the bias is self-correcting in the estimate for rCMRO2, which shows no noise bias.
DISCUSSION
The calibration of fMRI represents an extension of commonly used brain mapping techniques, allowing interpretation of activation signals in terms of the underlying physiology without requiring assumptions about the baseline metabolic state. Other work previously has developed theoretical relationships between perfusion and BOLD signal (12, 19, 23), but interpretation in terms of metabolism required the equivalent of estimating M from literature values.
Calibration Robustness.
The two design parameters for the model, relating blood flow to estimated blood volume changes, and relating dHb to transverse relaxation, are shown to have little effect on the results. This insensitivity is caused by the nature of the calibration step, which defines a baseline operating point around which only the small perturbations in physiology are detected. Because of this feature, the method is robust to inaccuracies in the design parameters, which also may vary spatially. We determine rCMRO2 independent from baseline physiology, enabling the noninvasive investigation of metabolic reactivity in diseased tissues and altered physiological states.
Of note, there are no a priori assumptions regarding resting blood volume fraction, resting capillary or venous oxygen saturation, blood flow, or metabolic rate for oxygen, as these are all accounted for in the single calibration step. The presence of large draining veins in an imaging voxel contributes excess noise in that voxel, which may require its exclusion from analysis, but would not bias the metabolism measurement according to our model.
We assume that the extracted oxygen is metabolized, rather than being transported out of the tissue. An alternative hypothesis has been advanced, of oxygen shunting by counter-current exchange between arteries and nearby veins. Shunting may be significant in muscle and skin (24), and may be important for dHb-dependent nitric oxide release in arterioles (25). However, counter-current oxygen exchange has been shown to have a negligible effect on brain hemoglobin saturation (26), perhaps because of reduced pairing of arteries and veins compared with muscle and other tissues. Direct coupling of brain capillary dHb to metabolism remains a reasonable assumption for our model.
Concern for flow effects on BOLD images is minimized by long repetition interval and use of the asymmetric spin echo pulse sequence. Pulsatile flow would shield some intravascular spins from NMR visibility. Our use of similar spin echo based pulse sequences between BOLD and CBF eliminates mismatches between visible spin populations.
Magnitude of Metabolism Changes.
Our observations are consistent with those advocating a partial coupling of blood flow to oxygen demand (5, 6, 9, 27) and difficult to reconcile against those declaring little or no oxidative metabolism change during task activation (2, 3). Diffusional limitation on oxygen delivery to brain has been proposed, requiring large CBF increases to support smaller CMRO2 increases (9, 10). Although not confirmatory, our results are consistent with this theory. Unexplained by this theory are local changes in glucose consumption, which, like CBF, exceed those of CMRO2 (3, 28, 29). Our results also differ from those claiming slow conversion to aerobic metabolism in the brain (7, 30, 31), but are consistent with MRI results showing no reduction in BOLD over time (32).
Interestingly, we show larger increases both in hemodynamic response (CBF increases 22% to 79%) and in metabolic response (CMRO2 increases 11% to 23%) than comparable positron emission tomography (PET) experiments. This finding may be secondary to partial volume effects in the PET experiments. Combined fMRI and PET experiments may help to sort out these technique-dependent magnitude differences. Different stimuli and different regions may produce widely varying changes in metabolism and blood flow; this possibility should be taken into account when comparing results.
Dynamics of Metabolism Changes.
Our method allows noninvasive, dynamic, continuous monitoring of oxidative metabolism changes with temporal resolution of several seconds. The oxidative metabolic changes are rapid and tightly coupled to stimulus onset and cessation (Fig. 2), concordant with optical spectroscopic measurements in animals (33, 34), which show highly localized relative deoxygenation in active columns beginning within hundreds of milliseconds. This early deoxygenation has been implicated as a mechanism of an early dip in BOLD signal that precedes the hemodynamic alterations in the first 2 sec of stimulation (35).
Care must be taken in examination of transient changes in oxidative metabolism when using our methods. The model as described assumes tight coupling of perfusion to blood volume, based on previous work performed at steady state. However, recent experiments in rats show that blood volume changes may lag BOLD effect changes with a 14-s time constant (36). Unless blood volume is measured separately, time course estimates that rely on tight flow-to-volume coupling may underestimate CMRO2 during the up-regulation and overestimate CMRO2 during down-regulation of CBF, such as during poststimulation undershoot of BOLD. When less than 14-s temporal resolution is needed, the model for blood volume change should include a delay component, easily implemented by filtering the CBF data once the human response is known. Alternatively, blood volume time course may be collected in a separate experiment by using an intravascular contrast agent (36).
Interpreting the Calibration Parameter.
In addition to CMRO2, we have measured the local sensitivity of BOLD to changes in CBF. The sensitivity parameter M—precisely the needed calibration parameter for CMRO2 estimation—is interpretable in its own right. Variations in M bear directly on variations in observed BOLD signal magnitude. These variations may be caused by differences in blood flow, venous volume, metabolic rate, or a combination of these.
BOLD sensitivity may be quite variable, both regionally and between subjects. In voxels dominated by veins, the baseline blood volume contribution to M is quite large; a threshold cutoff for M provides a ready method for exclusion of large vessels from regions of interest. Conversely, voxels with small M or poorly defined M (FH ≈ 1, Eq. 3) are rendered insensitive to BOLD because they have little reactive dHb-containing blood volume. Maps of the M parameter may be used to divide tissue into three groups: regions with large blood volume, expected to contain large veins and excludable from analysis; regions with reactive parenchyma sensitive to BOLD imaging and directly interpretable; and those that are insensitive to BOLD and must not be interpreted either as active or inactive.
Mapping M throughout the brain using a global stimulus such as hypercapnia will allow quantitative estimation of sensitivity to BOLD between physiologically disparate brain regions, such as primary somatosensory cortex, association cortex, higher level centers, deep gray matter and brainstem, which have widely varying microvascular anatomy. Calibration will be useful in comparing magnitudes between subjects and between physiological states, and is necessary to disambiguate cerebrovascular from cerebrometabolic reactivity. Apart from task-activation experiments, calibration of BOLD adds to our knowledge of physiology underlying fMRI, and may allow extension of brain mapping to comparison of activation magnitudes between brain regions that otherwise would be difficult to interpret.
Implications of the Calibration Parameter.
The observation of high M in primary visual cortex raises issues of magnitude and variability of BOLD signals. Primary visual cortex is known to be reliably responsive to task activation, with larger BOLD responses in brain parenchyma than any other known task activation experiment. Previously, we had attributed the robustness of visual activation to the large area subserving primary visual sensory input, the relatively small attentional modulation of visual activation, and the ease of repeatable stimulus presentation. Our data suggest another possibility: baseline tissue dHb. In our single slice experiments, the largest values for M (up to 16%) were found in visual cortex, with smaller M (3–5%) in surrounding pareital and occipital cortex (see Fig. 3). Why should visual cortex be unusually sensitive to BOLD? Likely this sensitivity is attributable to the microvascular anatomy of this region, which is known to contain a disproportionate concentration of venules (37).
Between-subject differences in signal change have been puzzling to the fMRI community, with some subjects showing 1% BOLD signal changes and others repeatedly demonstrating 5% or greater signal changes within brain parenchyma (data not shown). Why are some subjects strong activators? An explanation is provided by variability of M out of proportion to noise and much larger than variability in CBF or CMRO2. It is the baseline tissue dHb concentration that determines the sensitivity of BOLD contrast; the changes in blood flow and oxidative metabolism between subjects may be, in fact, relatively invariant.
Limitations and Future Work.
The chief limitation of this technique is methodological: subjects are required to wear a mask and additional minutes of imaging are required to obtain the calibration data, placing limitations on study design. If subject physiological state (e.g., caffeine and dietary intake) is regulated and volumetric image re-registration can be done, then calibration may be possible during a separate session. However, the requirement for collecting perfusion and BOLD-weighted data persists. We have implemented a hybrid pulse sequence, combining the elements of our methods (A) and (B), which has the potential of measuring CMRO2 in a single trial. Calibrated fMRI will be most useful when physiological interpretation is desired, such as during assessment of drug responses, and for evaluating response in tissues that are physiologically distinct, such as midbrain and brainstem.
Improved signal-to-noise ratio in perfusion images would aid CMRO2 measurement. Our current method estimates CMRO2 changes in 0.6-cc volumes (similar to PET resolution) averaged over several time points or several subjects. Possible improvements include continuous inversion arterial spin tagging, increased field strength, increased imaging time, and improved receiver coils.
We quantify relative rather than absolute changes in metabolism. Absolute quantification would require knowledge of baseline metabolism, whereas calibration of M determines only the baseline MRI effect of dHb; percent saturation is not obtained because oxyhemoglobin is not visible. Administration of an intravascular contrast agent along with arterial sampling has the potential of fixing the constant terms of M separately from the blood volume, blood flow, and metabolic rate, and may allow more complete quantification of metabolic changes.
Our approach promises to provide insights to understanding activity-linked metabolism in the human brain. Additionally, the methods provide a bridge between previous steady-state physiological measurements using PET and dynamic measurements of transient hemodynamic-linked phenomena observed with fMRI. The interpretation of dynamic physiology provided by application of this calibration technique is essential to the application of fMRI to diseased tissues, for which the physiological baseline is unknown and may vary through the course of an experiment.
Future application to delineate metabolic behavior unique to specific processing streams such as magnocellular versus parvocellular visual cortex, higher order centers, deep gray matter structures, and regions of reported negative activation, all will provide noninvasive physiological windows on the relationship of metabolism to brain function.
Acknowledgments
We thank Drs. Peter Bandettini and Marcus Raichle for helpful discussions regarding hypercapnia and for help in manuscript preparation, Dr. John Marota for advice regarding inhalation gas delivery, Drs. Joseph Mandeville, Jack Belliveau, and Gary Engelhardt for useful discussions, and Terrance Campbell, RT for technical support.
ABBREVIATIONS
- CMRO2
cerebral metabolic rate for oxygen
- rCMRO2
CMRO2 relative to baseline period
- PET
positron emission tomography
- CBF
cerebral blood flow
- fMRI
functional MRI
- BOLD
blood oxygen level dependent
- FAIR
flow sensitive alternating inversion recovery
- dHb
deoxyhemoglobin
ERROR ANALYSIS
Noise in the input ratio images for hypercapnia normalization (BOLD BH and CBF FH) and time courses (BOLD Bt and CBF Ft) produces uncertainty in the estimates of M and CMRO2. We show the effect of noise for the case when relative blood volume is approximated as Ftα and the additive source image noise is wide-sense stationary. Covariance in the data arises from reuse of the baseline points between BH and Bt and between FH and Ft, and in the case of a combined FAIR/BOLD pulse sequence (see Discussion), in the BOLD data that form half of the FAIR image pairs.
In the case of our experiment, with identical baseline points between FH and Ft, we define h, t, b as independent samples with variances σh2, σt2, σb2, such that FH = h/b and Ft = t/b. The covariances then are σFH2 = (b2σh2 + h2σb2)/b4, σFt2 = (b2σt2 + t2σb2)/b4, and σFHFt2 = σb2ht/b4. The variance in the estimate for M is then
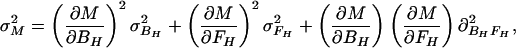 |
5 |
where the partial derivatives are
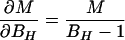 |
and
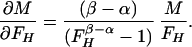 |
Let R stand for rCMRO2; its expected variance is
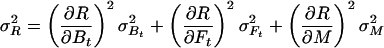 |
6 |
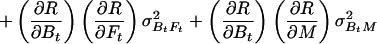 |
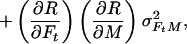 |
where
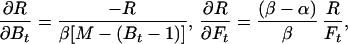 |
and
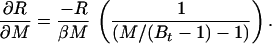 |
The above statistics σM and σR allow estimation of variance for a given experimental design.
Footnotes
Written informed consent was obtained according to protocol approved by the Massachusetts General Hospital subcommittee on human subjects.
References
- 1.Raichle M E. In: Handbook of Physiology: The Nervous System V. Plum F, editor. Bethesda, MD: Am. Physiol. Soc.; 1987. pp. 643–674. [Google Scholar]
- 2.Fox P T, Raichle M E. Proc Natl Acad Sci USA. 1986;83:1140–1144. doi: 10.1073/pnas.83.4.1140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fox P T, Raichle M E, Mintun M A, Dence C. Science. 1988;241:462–464. doi: 10.1126/science.3260686. [DOI] [PubMed] [Google Scholar]
- 4.Madsen P L, Hasselbalch S G, Hagemann L P, Olsen K S, Buelow J, Holm S, Wildschiodtz G, Paulson O B, Lassen N A. J Cereb Blood Flow Metab. 1995;15:485–491. doi: 10.1038/jcbfm.1995.60. [DOI] [PubMed] [Google Scholar]
- 5.Roland P E, Eriksson L, Stone-Elander S, Widen L. J Neurosci. 1987;7:2373–2389. [PMC free article] [PubMed] [Google Scholar]
- 6.Seitz R J, Roland P E. Acta Neurol Scand. 1992;86:60–67. doi: 10.1111/j.1600-0404.1992.tb08055.x. [DOI] [PubMed] [Google Scholar]
- 7.Hyder F, Chase J R, Behar K L, Mason G F, Siddeek M, Rothman D L, Shulman R G. Proc Natl Acad Sci USA. 1996;93:7612–7617. doi: 10.1073/pnas.93.15.7612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chen W, Novotny E J, Zhu X-H, Rothman D L, Shulman R G. Proc Natl Acad Sci USA. 1993;90:9896–9900. doi: 10.1073/pnas.90.21.9896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gjedde A, Ohta S, Hiroto K, Meyer E. In: Brain Work and Mental Activity 31. Lassen N A, Ingvar D H, Raichle M E, Friberg D, editors. Copenhagen: Munksgaard; 1991. pp. 177–184. [Google Scholar]
- 10.Buxton R B, Frank L R. J Cereb Blood Flow Metab. 1996;17:64–72. doi: 10.1097/00004647-199701000-00009. [DOI] [PubMed] [Google Scholar]
- 11.Cooper R, Crow H J, Walter W G, Winter A L. Brain Res. 1966;3:174–191. doi: 10.1016/0006-8993(66)90075-8. [DOI] [PubMed] [Google Scholar]
- 12.Kwong K K, Belliveau J W, Chesler D A, Goldberg I E, Weisskoff R M, Poncelet B P, Kennedy D N, Hoppel B E, Cohen M S, Turner R. Proc Natl Acad Sci USA. 1992;89:5675–5679. doi: 10.1073/pnas.89.12.5675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ogawa S, Lee T M, Kay A R, Tank D W. Proc Natl Acad Sci USA. 1990;87:9868–9872. doi: 10.1073/pnas.87.24.9868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kim S-G. Magn Reson Med. 1995;34:293–301. doi: 10.1002/mrm.1910340303. [DOI] [PubMed] [Google Scholar]
- 15.Horvath I, Sandor N T, Ruttner Z, McLaughlin A C. J Cereb Blood Flow Metab. 1994;14:503–509. doi: 10.1038/jcbfm.1994.62. [DOI] [PubMed] [Google Scholar]
- 16.Yang S-P, Krasney J A. J Cereb Blood Flow Metab. 1995;15:115–123. doi: 10.1038/jcbfm.1995.13. [DOI] [PubMed] [Google Scholar]
- 17.Yablonskiy D A, Haacke E M. Magn Reson Med. 1994;32:749–763. doi: 10.1002/mrm.1910320610. [DOI] [PubMed] [Google Scholar]
- 18.Boxerman J L, Hamberg L M, Rosen B R, Weisskoff R M. Magn Reson Med. 1995;34:555–566. doi: 10.1002/mrm.1910340412. [DOI] [PubMed] [Google Scholar]
- 19.Ogawa S, Menon R, Tank D, Kim S, Merkle H, Ellermann J, Ugurbil K. Biophys J. 1993;64:803–812. doi: 10.1016/S0006-3495(93)81441-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Luz Z, Meiboom S. J Chem Phys. 1963;39:366–370. [Google Scholar]
- 21.Guyton A C. Textbook of Medical Physiology. New York: Saunders; 1986. [Google Scholar]
- 22.Grubb R L, Raichle M E, Eichling J O, Ter-Pogossian M M. Stroke. 1974;5:630–639. doi: 10.1161/01.str.5.5.630. [DOI] [PubMed] [Google Scholar]
- 23.Kim S-G, Ugurbil K. Magn Reson Med. 1997;38:59–65. doi: 10.1002/mrm.1910380110. [DOI] [PubMed] [Google Scholar]
- 24.Torres Filho I P, Kerger H, Intaglietta M. Microvasc Res. 1996;51:202–212. doi: 10.1006/mvre.1996.0021. [DOI] [PubMed] [Google Scholar]
- 25.Stamler J S, Jia L, Eu J P, McMahon T J, Demchenko I T, Bonaventura J, Gernert K, Piantadosi C A. Science. 1997;276:2034–2036. doi: 10.1126/science.276.5321.2034. [DOI] [PubMed] [Google Scholar]
- 26.Sharan M, Jones J, Koehler R C, Traystman R J, Popel A S. Ann Biomed Eng. 1989;17:13–38. doi: 10.1007/BF02364271. [DOI] [PubMed] [Google Scholar]
- 27.Katayama Y, Tsubokawa T, Hirayama T, Kido G, Tsukiyama T, Iio M. J Cereb Blood Flow Metab. 1986;6:637–641. doi: 10.1038/jcbfm.1986.118. [DOI] [PubMed] [Google Scholar]
- 28.Ueki M, Linn F, Hossmann K-A. J Cereb Blood Flow Metab. 1988;8:486–494. doi: 10.1038/jcbfm.1988.89. [DOI] [PubMed] [Google Scholar]
- 29.Woolsey T A, Rovainen C M, Cox S B, Henegar M H, Liang G E, Liu D, Moskalenko Y E, Sin J, Wei L. Cereb Cortex. 1997;6:647–660. doi: 10.1093/cercor/6.5.647. [DOI] [PubMed] [Google Scholar]
- 30.Frahm J, Krueger G, Merboldt K-D, Kleinschmidt A. Magn Reson Med. 1996;35:143–148. doi: 10.1002/mrm.1910350202. [DOI] [PubMed] [Google Scholar]
- 31.Hathout G M, Kerlew K A T, So G J K, Hamilton D R, Zhang J X, et al. J Magn Reson Imag. 1994;4:537–543. doi: 10.1002/jmri.1880040405. [DOI] [PubMed] [Google Scholar]
- 32.Bandettini P A, Kwong K K, Davis T L, Tootell R B H, Wong E C, Fox P T, Belliveau J W, Weisskoff R M, Rosen B R. Hum Brain Mapp. 1997;5:93–109. [PubMed] [Google Scholar]
- 33.Frostig R D, Lieke E E, Tso D Y, Grinvald A. Proc Natl Acad Sci USA. 1990;87:6082–6086. doi: 10.1073/pnas.87.16.6082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Malonek D, Grinvald A. Science. 1996;272:551–554. doi: 10.1126/science.272.5261.551. [DOI] [PubMed] [Google Scholar]
- 35.Hennig J, Janz C, Speck O, Ernst T. Int J Imaging Systems Technol. 1995;6:203–208. [Google Scholar]
- 36.Mandeville, J. B., Marota, J. A., Kosofsky, B. E., Keltner, J., Weissleder, R., Rosen, B. R. & Weisskoff, R. M. (1998) Magn. Reson. Med., in press. [DOI] [PubMed]
- 37.Marinkovic R, Cvejin B, Markovic L, Budimlija Z. Med Pregl. 1995;48:7–9. [PubMed] [Google Scholar]