The purpose of this section is to provide some of the background material and definitions needed to assist readers in their understanding of the mechanical effects of ultrasonic fields. It provides a brief overview of ultrasonic propagation and describes many of the possible mechanisms for inducing biological effects. The terms used throughout many of the subsequent sections in this issue of the journal are defined in an effort to clarify their meaning and use.
Any process that can produce a biological effect without a significant degree of heating, e.g., one producing an increase of less than about 1°C above normal physiological temperature, is a nonthermal mechanism. As defined in this work, any nonthermal mechanism is considered to produce an effect by mechanical actions or processes, or by reactive chemicals produced subsequent to a mechanical process, e.g., inertial cavitation. Thus, a nonthermal mechanism may be thought of as equivalent to a mechanical mechanism—the phrase being understood to include consequences directly attributable to that primary mechanical mechanism.
There are two general classes of such mechanisms, cavitational and noncavitational, that may arise during exposure of a biological material to ultrasound. As may be inferred from the designations, these mechanisms generally occur in the presence and absence, respectively, of gas bodies.
As used in this document, the term “gas body” refers to any volume of gas or vapor that is nearly or completely surrounded by a liquid, e.g., blood, or a solid, e.g., tissue, or both. Thus, gas bodies include all of the following: (1) naturally occurring microbubbles; (2) the gas in the lung, bowel, or other organ; and (3) injected microbubble ultrasound contrast agents.
It is important to note that the mere presence of gas bodies at the site of an observed bioeffect does not guarantee a cavitational mechanism, cf. the discussion of lung damage in Sections 4 and 5. Similarly, the absence of obvious gas bodies does not ensure the lack of a contributory cavitational effect. Before addressing the various specific forms these general mechanisms may take, it will prove useful to describe acoustic output and field parameters that may influence the thresholds for, and extent of, any mechanical effects produced. Definitions of specific terms are found at the end of this section.
2.1 Acoustic Output and Field Parameters
Sound may be defined as an alteration in pressure, stress, particle displacement, or particle velocity that is propagated in an elastic medium (e.g., water or tissue), or the superposition of such propagated alterations (Beranek, 1988). Ultrasound refers to sound in which the frequency of alteration is greater than the audible range in human beings, i.e., greater than about 20 kHz. Such propagated alterations, or waves, may be either longitudinal (compressional), for which the particle motion is parallel to the direction of propagation, or transverse, for which the particle motion is perpendicular to the direction of propagation. Only longitudinal (compressional) waves are treated here. Transverse, e.g., shear, waves are rarely generated in tissues other than bone and in bone are attenuated very rapidly (Frizzell et al, 1976). The characterizing parameters (pressure, stress, etc.) are related to one another by different mathematical expressions for different wave types (planar, spherically converging, etc.) (Nyborg, 1978). The elastic media of interest in this work may be water, other aqueous or nonaqueous fluids, cells suspended in aqueous fluids, tissues or various combinations of these materials.
2.1.1 Continuous Wave
Imagine a long duration, i.e., continuous, mono-frequency acoustic wave (CW) traveling in an elastic medium. The acoustic pressure of this wave, i.e., the difference between the total and hydrostatic pressures in the medium, will oscillate in the direction of propagation as illustrated in Figure 2-1; an equivalent figure may be drawn to represent the pressure over a period of time at a fixed location. Figure 2-1 may be used to illustrate several concepts. For example, the acoustic wavelength, λ, is the distance between any two consecutive, equivalent points, e.g., two pressure maxima, on the curve. If the abscissa were time rather than space, the same definition could be applied to acoustic period, i.e., to the duration between two consecutive, equivalent pressures. In addition, the inverse of the period is the frequency, f, or the rate of repetition of complete cycles, of the wave. Positive acoustic pressures are those for which the total pressure is greater than the hydrostatic pressure, while negative acoustic pressures imply that the total pressure is less than the hydrostatic pressure. The positive and negative acoustic pressure amplitudes, p+ and p−, respectively, are simply the maximum values of those differences (Fig. 2-1). Note that the compressional and rarefactional pressure amplitudes, pc and pr, respectively, are identical to p+ and p−, and may be used interchangeably with those terms.
Figure 2-1.
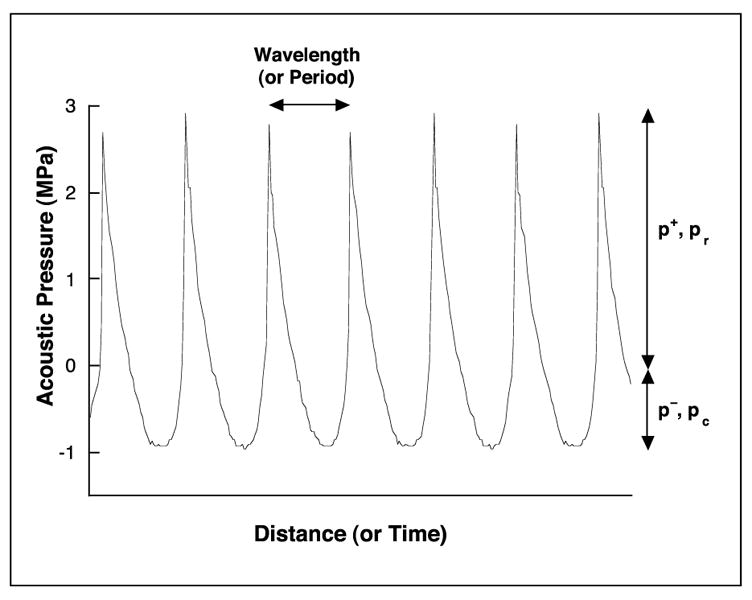
The measured acoustic pressure of a wave traveling in the positive x direction. The curve shows the acoustic pressure as it varies in time at a fixed position or, equivalently, the variation in pressure with position at a fixed time. The wave exhibits distortion due to nonlinear propagation in water, resulting in the generation of harmonics of the transmitted frequency and an asymmetric waveform, i.e., a waveform with p+ > p−.
2.1.2 Pulsed Wave
Although some applications of medical ultrasound, e.g., CW Doppler, employ continuous wave exposures as illustrated in Figure 2-1, most diagnostic ultrasound techniques, e.g., B-mode or color Doppler imaging, utilize short pulses of acoustic waves (Fig. 2-2). Additional parameters are required in order to characterize pulsed waves. For example, the effective temporal duration of a pulse is referred to as the pulse length, while the time from the beginning of one pulse to the beginning of the next is the pulse repetition period (PRP). The rate at which equivalent pulses are emitted is the pulse repetition frequency (PRF); 1/PRP = PRF. A pulsed wave also contains a broader range of frequencies than does a continuous wave but may be characterized by the average frequency of its Fourier (frequency) series representation, the so-called center frequency.
Figure 2-2.
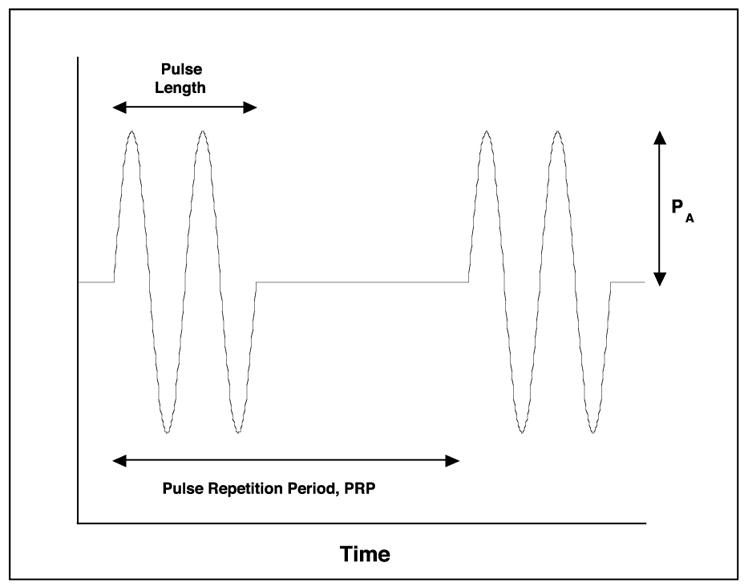
A series of two idealized acoustic pulses of pressure amplitude PA, plotted as a function of time, t. The curve shows the acoustic pressure as it varies in time at a fixed position. It is important to realize that measurements of actual acoustic pulses often show the effects of nonlinear distortion depicted in Figure 2-1.
2.1.3 Traveling, Standing, and Stationary Waves
As noted above, most medical applications of ultrasound utilize pulsed rather than continuous wave fields. Generally, either type of exposure involves the propagation of acoustic energy outward from the ultrasound probe. This propagation is said to consist of traveling waves. However, if an acoustic wave should impinge upon a strongly reflective surface, e.g., bone, the wave reflected back toward the probe will interfere with itself to form a standing wave. This wave consists of a spatially periodic array of pressure maxima and minima. The presence of such an array may produce unexpected effects in in vitro or in vivo exposures. A stationary wave, a useful abstraction, is a standing wave formed by a perfect reflector in which the acoustic pressure is exactly zero at the minima.
2.2 Cavitational Mechanisms
The gas bodies required for this general class of mechanisms fall into one of three categories. They may be present naturally in the body, e.g., in the lung or intestine, they may be produced from pre-existing cavitation nuclei within the body by the passage of an acoustic wave of sufficient intensity, e.g., in the kidney during shock wave lithotripsy, or they may be produced by an external process and subsequently may be introduced into the body, e.g., by intravenous injection of ultrasound contrast agents. As used in this work, the term “gas body” is used to represent any physically contiguous collection of gas molecules without restriction on size or shape and which may be acted upon by the acoustic field. Thus both the lung as a whole and the individual microbubbles constituting an ultrasound contrast agent, as well as anything in between, are considered gas bodies.
A bubble in a sound field is acted upon by acoustic stress at its surface. Because a bubble is composed of highly compressible gas, this stress, i.e., the time-varying acoustic pressure, produces oscillations in the bubble volume. The amplitude of the radial oscillations is proportional to the acoustic pressure amplitude at low pressures, as shown in the theoretical plot of Figure 2-3 for a 4 μm diameter air bubble in blood plasma exposed to a 2 MHz sound wave with a pressure amplitude of 0.01 MPa. However, with relatively modest increases in pressure amplitude, the volume response may increase rapidly, as shown in the theoretical plot of Figure 2-4 for a 4 μm bubble exposed to a sinusoidal 2 MHz wave at 0.5 MPa. The rapid increase in radial response with the amplitude of the acoustic field is particularly strong for small bubbles, i.e., those of less than linear resonance size (the bubble size exhibiting the largest radial response for low driving pressures at the acoustic frequency of interest, e.g., ~3.9 μm at 2 MHz) (Fig. 2-5). The mechanisms by which a bubble may affect nearby biological material are dependent on the magnitude of its response to the acoustic field. Essentially all bubbles produce acoustic radiation forces and microstreaming, while only the more strongly affected will exhibit the violent responses, e.g., shock wave generation or free radical production, characteristic of inertial cavitation. Descriptions of these effects follow.
Figure 2-3.
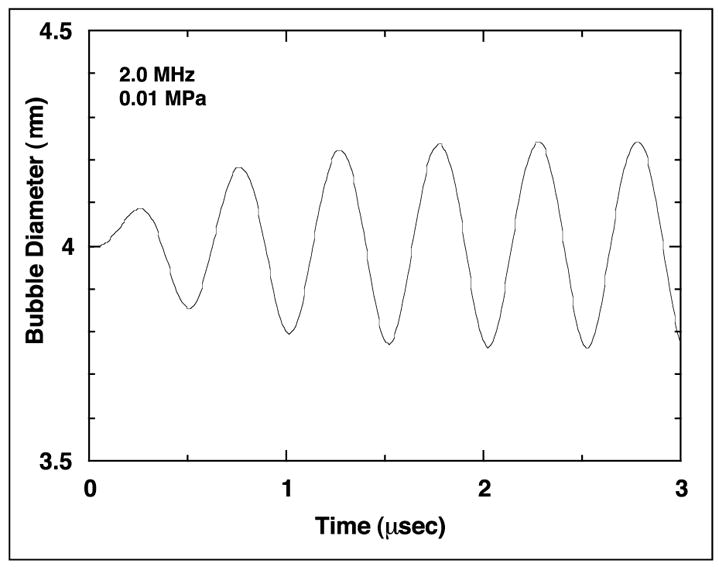
Bubble diameter as a function of time for a 4 μm diameter air bubble in blood plasma exposed to a 2.0 MHz acoustic wave with an amplitude of 0.01 MPa.
Figure 2-4.
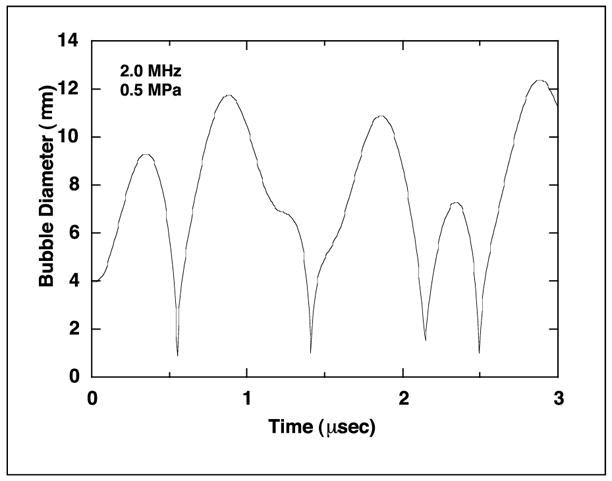
Bubble diameter as a function of time for a 4 μm diameter air bubble in blood plasma exposed to a 2.0 MHz acoustic wave with an amplitude of 0.5 MPa.
Figure 2-5.
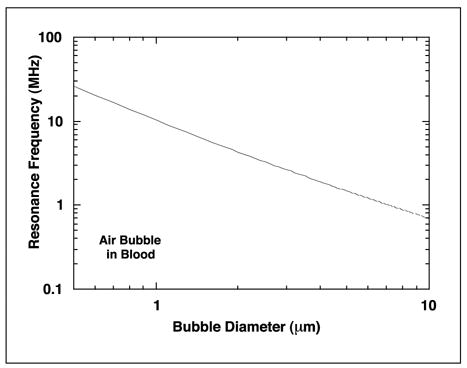
Equilibrium bubble diameter at linear resonance as a function of acoustic frequency for air bubbles in blood plasma.
2.2.1 Radiation Forces
A bubble in a sound field experiences not only the time-varying acoustic pressure p, but also the gradient, i.e., the spatial variation, of the pressure ∇p. Conceptually, since the pressure is greater on one side of the bubble than on the other, it is clear that the bubble will tend to move in response to the acoustic field and that the magnitude of the driving force will depend on the bubble size, or volume V. The bubbles of interest are often much smaller than the acoustic wavelength, i.e., smaller than a few tens of micrometers for frequencies above 1 MHz. For such bubbles, the instantaneous force on the bubble is indeed found to be –V∇p, while the time-average force is just <–V∇p>. For low amplitude acoustic fields, both the bubble’s pulsations and the sound waves themselves oscillate sinusoidally, and the time-average of the product of two such quantities can be shown to be the product of their respective amplitudes and the cosine of the phase difference between them. For higher amplitude pulsations, the force must be computed numerically.
In a traveling acoustic wave, the amplitude of the sound wave may be considered constant, while the phase of the wave changes with location. The pulsation amplitude of a bubble in a traveling wave field varies with bubble radius, being greatest for resonant bubbles and less for either larger or smaller ones, while the phase varies from 0 to π as the radius increases from much below to much above resonance size. A formal analysis shows that the radiation force due to a traveling wave is in the direction of propagation of the wave for a bubble of any size but that the magnitude of the force is dependent on the bubble radius.
In a stationary acoustic wave, the amplitude of the sound wave varies with location, while the phase is constant within any half-wavelength-thick region between successive planes having zero acoustic pressure. The pulsation amplitude of a bubble in a stationary wave varies not only with bubble radius but also with location. The phase difference between ∇p and V varies from ~π for bubbles smaller than resonance size to π/2 for resonant bubbles to ~0 for larger bubbles. The net result is that small bubbles, i.e., those of less than resonance size, are forced in the direction of pressure maxima, while larger bubbles move toward pressure minima; bubbles of resonance size experience no net force in a stationary wave field. Also, because a bubble’s pulsation amplitude increases with increasing acoustic pressure, the acoustic force on a small bubble increases as it approaches a pressure maximum, although the force at the maximum itself is 0 since ∇p = 0. Interestingly, the force on a large bubble decreases as it approaches a pressure minimum and is again 0 at the minimum because ∇p = 0. Thus smaller bubbles are held more tightly at the maxima than large bubbles are at the minima.
Bubbles in either traveling or stationary waves scatter a part of the acoustic energy affecting them. If a second bubble happens to be near the first, this scattered wave will exert a force on the second bubble; the second bubble also exerts a force on the first. If the two bubbles are both smaller or larger than resonance size, the net force will be attractive, and the bubbles will move toward one another. This force is responsible for one of the possible mechanisms whereby bubbles in a sound field may grow because if the two bubbles touch, they may coalesce into a single, larger bubble. If one of the bubbles is larger than resonance size and the other is smaller, then the smaller will be attracted to the larger when the two are relatively close together but will be repelled for larger separations (Coakley and Nyborg, 1978).
The acoustic wave scattered by a bubble may also affect small particles, e.g., biological cells, that happen to be near the bubble. For particles denser than the suspending medium, which includes most cases of biological interest, the direction of the force is toward the bubble, while the magnitude of the force decreases as the fifth power of the distance from the center of the bubble. Oscillating bubbles will tend to attract nearby particles or cells, thus collecting them into small, highly concentrated groups where they may be easily damaged or destroyed by the pulsating bubble. However, the oscillation of a bubble may be reduced by material accumulating on its surface.
2.2.2 Microstreaming
Oscillating bubbles in a sound field, especially if they are located on a solid surface (Nyborg, 1965), produce a small scale (hence “micro”), vigorous circulatory motion in the surrounding fluid. Such fluid motion is called microstreaming. Oscillating bubbles that are being pushed by the acoustic force produced by the action of a traveling wave also may produce shearing flow in the surrounding fluid, but this motion is noncirculatory. In all cases, because the velocity of the fluid flowing around the bubble is greatest near the bubble surface and since the fluid velocity decreases as distance from the bubble increases, a gradient exists in the fluid flow field around the bubble. When a cell is carried by the streaming flow into a region of strong fluid velocity gradients, the fluid will exert greater force on the side of the cell near the bubble and less force on the side farther away. This unequal distribution of forces on the exterior of the cell results in shearing stresses or forces that tend to distort and tear the cellular membrane. Because cells exhibit viscoelasticity, some minimum time is required for a given level of shear stress to disrupt a membrane, while the cell-bubble contact time during which cells in suspension are exposed to high stresses has been shown to be relatively short. Thus, more than one exposure to a high stress field may be required for microstreaming to produce significant damage in a biological cell.
2.2.3 Shock Waves
As indicated above, a bubble exposed to relatively low amplitude pressure waves will oscillate linearly, and a plot of radius versus time will be a simple sinusoid centered about the bubble’s equilibrium radius (Fig. 2-3). On the other hand, exposure to a sufficiently high acoustic pressure will induce higher amplitude, nonlinear oscillations in the bubble volume. A plot of bubble radius versus time for nonlinear oscillations is characterized by high amplitude, long duration (i.e., greater than half of an acoustic period) excursions above the equilibrium radius separated by relatively brief intervals below it (Fig. 2-4). As the bubble contracts from a radial maximum to the subsequent minimum, the motion of the surrounding fluid may attain such a large momentum that the rising pressure within the bubble, which easily counteracts this momentum at low acoustic intensities and thus produces a balanced (sinusoidal) oscillation, cannot resist the in-rushing liquid. The bubble’s radius very rapidly becomes extremely small, i.e., the bubble collapses. This is termed an “inertial collapse” because the motion is dominated by the inertia of the liquid.
During an inertial collapse, the speed of the gas-liquid interface may be very high, in some cases becoming supersonic in both the gas (~330 m/s) and the liquid (~1500 m/s). Such supersonic motion produces shock waves both within the bubble and in the surrounding fluid. The external shock will propagate outwardly as a spherically diverging wave. A biological cell or tissue exposed to the shock will briefly experience very large stresses. It is plausible to imagine that these stresses may damage the exposed biological materials by disrupting their structural integrity, although unlike the case for shear stress described above, there is no firm evidence for these events.
2.2.4 Free Radicals
When a bubble undergoes inertial collapse, there is a brief time (on the order of nanoseconds in duration) near the radial minimum during which the pressure within the bubble may rise to hundreds or thousands of megapascal, and the temperature may reach thousands of kelvin. In addition to various atmospheric gases, e.g., nitrogen, oxygen, and argon, the interior of a bubble contains water vapor. The existence of high temperatures in such a medium may lead to the formation of chemically reactive free radicals, such as H• and OH•, by the dissociation of water (Verral and Sehgal, 1988). Although these free radicals would be very damaging to any biological tissue they should encounter, they tend to have extremely short lifetimes in vivo (~10−9 s, equivalent to a mean free path of ~0.5 μm (Henglein and Kormann, 1985; Henglein, 1987). However, hydrogen peroxide, H2O2, which may be produced by recombination of the appropriate free radicals, is another product of cavitational activity. This molecule is long-lived and has been shown to induce single strand breaks in DNA in vitro (DL Miller et al, 1991c). One may speculate that any of the long-lived chemical species produced by the action of the sound wave, e.g., H2O2, may injure biological cells or tissues in the vicinity of a collapsing bubble. Damage may result from a direct action of a sonochemical on a biological molecule such as DNA, thus entailing the potential for a genetic effect, or an indirect action involving the production of potentially toxic secondary chemicals, e.g., radical adducts. However, intensive investigations in vitro have shown that it is very difficult to induce genetic mutations in intact cells even for exposure levels far above those permitted in diagnostic ultrasound examinations (Doida et al, 1990).
2.2.5 Microjets
The foregoing descriptions of the mechanisms by which bubble-mediated ultrasound bioeffects occur are based on theoretical investigations that assume the bubble remains spherically symmetrical throughout its motion. While this assumption is valuable in that it allows detailed investigations of various aspects of cavitational activity, bubbles in the relatively strong acoustic fields common to biomedical ultrasound probably do not remain completely spherical. At frequencies in the lower ultrasonic range, the acoustic pressure threshold for the generation of surface waves on the bubbles can be less than 0.1 MPa (Coakley and Nyborg, 1978), and the amplitude of the waves increases with the acoustic driving pressure. At high amplitudes, surface waves become distorted such that microbubbles or liquid jets are formed. The generation of microbubbles is important because they may act as nuclei, or “seeds,” from which additional biologically damaging cavitation bubbles may develop. Small liquid jets, called micro-jets, may also produce significant biological effects.
When a bubble located on or near a solid boundary is exposed to an acoustic wave, it expands and contracts in response to the time-varying pressure as would any other bubble. In this case, however, while the fluid opposite the boundary is free to flow toward the bubble’s center, the solid surface restricts the motion of fluid on that side of the bubble. This asymmetry distorts the bubble interface in such a way that an invagination of fluid forms on the side of the bubble opposite the boundary. As the acoustic pressure is increased, this distortion is magnified until the liquid flows completely through the bubble and strikes the solid boundary. Such events are known to be very violent, being able to pit brass plates and even pierce aluminum foils (Coleman et al, 1987). Although the relevance of microjet activity to ultrasound bioeffects research remains to be determined, a recent report by Kodama and Takayama (1998) has shown, by in vitro experiments, that microjets formed from existing bubbles by lithotripter shock waves will be directed toward nearby compliant surfaces, such as liver, and that considerable tissue damage may result.
2.3 Noncavitational Mechanisms
There are several examples of ultrasound bioeffects produced not only in the absence of excess heating but apparently also without cavitation bubbles or other gas bodies in the exposed sample. In such cases, the mechanism of action is sometimes found to be in the form of radiation force or torque or of acoustic streaming.
2.3.1 Radiation Force
A traveling acoustic wave carries energy and momentum outward from its source. If the wave impinges on an object that absorbs the energy in the wave completely, the interaction becomes manifest as a force on the object. The magnitude of the force is W/c, the ratio of the acoustic power to the speed of sound in the liquid. If the object absorbs a fraction of the total energy, the force is proportionately less. Certain biological tissues, e.g., lung, tend to reflect much of the incident energy. In the case of complete reflection, the force is 2W/c. The force is greater for strongly reflecting tissues because the net change in the momentum of the wave is twice as great as for complete absorption. Biological tissue responds to an acoustic force by distorting (bending) in the direction of the incident sound wave. Tissues having low physical strength may lose their mechanical integrity, i.e., may be torn or otherwise disrupted, if this distortion is of sufficient magnitude.
For small particles in a sound field, such as individual biological cells, the radiation force is proportional to the particle volume as well as the density and compressibility contrasts between the particle and the surrounding fluid (Nyborg, 1978). Theoretical calculations for cells in a stationary wave indicate that the cells will be forced to pressure minima. This effect has been observed experimentally in the circulatory systems of chicken embryos exposed to CW ultrasound. The red cells in large vessels formed bands separated by evenly spaced regions of clear plasma. When the sound was turned off, the bands dispersed, and blood flow continued normally (Dyson et al, 1971).
Dalecki et al (1995a) showed that tactile response is elicited by applying repeated pulses of focused ultrasound to the human finger or upper forearm. PRFs in the range 50–1000 Hz and pulse durations of 0.1 to 100 ms were employed. The mechanism was shown to be acoustic radiation force exerted on the tissue.
In addition, Dalecki et al (1993a) have shown that pulses of ultrasound may affect both cardiac rhythm and aortic pressure when applied to the hearts of frogs. The authors used single 5 ms long pulses of 1.2 or 3.7-MHz ultrasound and found a threshold peak positive pressure of 5–10 MPa. While the mechanism responsible for disruption of cardiac rhythm remains unclear, changes in aortic pressure are induced by acoustic radiation force (Dalecki et al, 1997g).
2.3.2 Radiation Torque
When a sound wave impinges on a suspended object, a twisting action may be exerted by a phenomenon related to radiation force, the so-called radiation torque. The torque will cause a freely suspended, spherically symmetrical body to rotate, while an asymmetrical object will tend to assume a preferred orientation. In arrangements where observations are made through an optical microscope during ultrasound exposure, it has been found that intracellular particles are caused to rotate, with speed and direction depending on details of the acoustic field (Harvey and Loomis, 1928; Wilson et al, 1966). Radiation torque on a disc-like particle causes it to seek an orientation with its axis parallel to the oscillatory velocity in the sound field. Trenchard (1987) has employed this orientation tendency in a technique for assaying platelet viability. Radiation torques also may be produced in nonuniform acoustic fields, such as those produced when a traveling wave impinges on a boundary obliquely and is reflected.
2.3.3 Acoustic Streaming
The small-scale acoustic microstreaming produced by oscillating gas bubbles was described in the subsection on microstreaming. A fluid may also be set into circulatory motion simply by the passage of a sound wave through the medium. The flow results from a transfer of momentum to the liquid because it absorbs a portion of the energy of the acoustic field. The rate of flow is proportional to the acoustic power and the absorption coefficient α and is inversely proportional to the coefficient of shear viscosity of the liquid η.
The stirring action produced by acoustic streaming may be important in any situation for which a sound wave passes through a volume of liquid, e.g., in the bladder, large blood vessels, or the heart. Starritt et al (1989) investigated the streaming produced in a water tank by ultrasound beams. Commercial diagnostic equipment produced flow rates up to 14 cm/s when operated in pulsed Doppler mode but only up to about 1 cm/s in imaging modes; M-modes produced intermediate speeds of about 5 cm/s. Under similar operating conditions, the flow rates in many biological fluids, e.g., amniotic fluid or urine, will have approximately these values, but for others they may be much greater than in water because the ratio α/η is higher. For example, in blood at 37°C the value of α/η is approximately 30 times higher than in water (Nyborg, 1997). Flow rates may also be greater than predicted by linear theory under conditions promoting nonlinear propagation, e.g., high acoustic intensities in liquids with low linear attenuation coefficients such as amniotic fluid because the total energy absorption may increase by orders of magnitude (Dalecki et al, 1991).
2.4 Terms
Acoustic cavitation
The mechanical response of one or more cavities to a sound field; cavitation may be inertial or noninertial.
Acoustic pressure
The excess of the instantaneous pressure at a point in a sound field over the pressure in the absence of the sound field.
Acoustic pressure amplitude
For a field, either pulsed or continuous, in which the acoustic pressure varies sinusoidally with time, one half of the maximum value of the peak to peak excursions of the acoustic pressure PA (Fig. 2-2). For nonlinearly distorted acoustic waves, the amplitude is a function of time and space, the peak positive and negative acoustic pressure amplitudes, p+ and p−, respectively, are not equal, and the pressure amplitude is not easy to define unambiguously (Fig. 2-1).
Acoustic radiation force
Time-averaged force on an object produced by a sound field.
Acoustic radiation torque
Time-averaged torque on an object produced by a sound field.
Acoustic streaming
Time-averaged flow of a liquid or gas produced by a sound field.
Attenuation
The decline in the acoustic pressure amplitude of a sound field with propagation distance due to conversion of acoustic into thermal energy by viscous and other effects.
Bubble
A cavity that is completely surrounded by a liquid or solid.
Cavitation nucleus
A small body, usually a cavity, that can serve as a site for acoustic cavitation; not necessarily a stabilized gas body.
Cavity
A volume filled with gas or vapor, or both.
Center frequency
The arithmetic average fc, of the frequencies f1 and f2, determining the bandwidth of an acoustic wave, where f1 and f2, are the most widely separated frequencies at which the acoustic pressure is 71 percent (–3 dB) of its maximum value.
Collapse
A rapid decrease in volume of a cavity that, in an aqueous medium, may lead to production of shock waves, free radicals, or sonoluminescence.
Derated pressure
The reduced value obtained when the acoustic pressure measured in water is adjusted downward by a derating factor designed to account for the average attenuation of the acoustic wave as it travels from its source through tissue to a location of interest. The Output Display Standard (AIUM/NEMA, 1992b) uses a derating factor of 0.3 dB/cm-MHz.
Encapsulated bubble
A cavity in which the gas and liquid phases are separated by a thin shell of insoluble solid or liquid material.
Fundamental frequency
For a continuous periodic acoustic wave, the rate at which the wave repeats its pressure oscillation. For a wave derived by distorting or modulating (i.e., pulsing) a continuous periodic wave, the fundamental frequency of the latter.
Gas body
A general term used to represent any physically continuous collection of gas or vapor molecules without restriction on size or shape. Examples include the lung as a whole or in part, bowel gas, and the microbubbles used as ultrasound contrast agents.
Gas body activation
A subcategory of noninertial cavitation involving the mechanical response of stabilized gas bodies to a sound field.
Harmonic
A spectral component whose frequency is n times that of the fundamental frequency, where n is a positive nonzero integer.
Inertial cavitation
A class of acoustic cavitation involving growth and collapse of one or more cavities; previously denoted “transient cavitation.”
Mechanical Index (MI)
A quantity defined by the Output Display Standard as the derated peak rarefactional pressure (in MPa) at the location of the maximum pulse intensity integral (effectively the focus) divided by the square root of the center frequency (in MHz). The MI is a measure of the likelihood of occurrence of a clinically significant nonthermal bioeffect during a diagnostic examination.
Noninertial cavitation
A class of cavitation in which a violent collapse does not occur. Its physical effects include acoustically induced translational motion of bubbles, bubble growth by rectified diffusion or coalescence, continuous heat production, radiation forces on neighboring particles, and microstreaming.
Sonochemicals
Chemical species requiring the occurrence of inertial cavitation for their production, e.g., free radicals and the products of their reactions, which may include relatively long-lived radical adducts.
Sonoluminescence
The production of light by inertial cavitation.
Stable cavitation
Cavitation in which the bubble or stabilized gas body involved oscillates about its equilibrium radius for an extended period of time; it may be inertial or noninertial.
Stabilized gas body
A gas-filled cavity that is stabilized against dissolution by structures that partially or completely surround it.
Subharmonic
A spectral component whose frequency is 1/n times that of the fundamental frequency, where n is a positive nonzero integer.


