Abstract
We developed a stochastic version of the Impact = Population·Affluence·Technology (IPAT) model to estimate the effects of population, affluence, and technology on national CO2 emissions. Our results suggest that, for population, there are diseconomies of scale for the largest nations that are not consistent with the assumption of direct proportionality (log–linear effects) common to most previous research. In contrast, the effects of affluence on CO2 emissions appear to reach a maximum at about $10,000 in per- capita gross domestic product and to decline at higher levels of affluence. These results confirm the general value of the IPAT model as a starting point for understanding the anthropogenic driving forces of global change and suggest that population and economic growth anticipated over the next decade will exacerbate greenhouse gas emissions.
It is certain that the atmospheric concentrations of greenhouse gases (GHGs) are increasing (1, 2). These growing concentrations threaten to produce disruptive changes in global climate. There is widespread scientific agreement that the increased concentrations are the consequence of human activities around the globe. Among these anthropogenic factors, the principal ones (often called “driving forces”) are (i) population, (ii) economic activity, (iii) technology, (iv) political and economic institutions, and (v) attitudes and beliefs (3). These forces usually are assumed to drive not just GHG emissions but all anthropogenic environmental change.
Despite agreement about the list of forces that affect anthropogenic GHG emissions, we have little understanding of the relative importance of each driving force. Thus, our basic knowledge of the biosphere and our ability to choose appropriate policy responses will remain significantly incomplete until we better understand the human dimensions of the system (3–5). Our goals here are to suggest an approach for analyzing anthropogenic environmental changes and to apply that approach to anthropogenic emissions of the principal GHG: CO2.
To organize our analysis, we adopted the Impact = Population·Affluence·Technology (IPAT) framework first proposed in the early 1970s (6) as part of an ongoing debate on the driving forces of environmental change (7–11). It still finds wide use as an orienting perspective (12–20). The framework incorporates key features of human dimensions of environmental change into a model as follows:
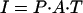 |
1 |
where I is environmental impact, P is population, and A is affluence or economic activity per person. T is the environmental impact per unit of economic activity, which is determined by the technology used for the production of goods and services and by the social organization and culture that determine how the technology is mobilized. The model is simple, systematic, and robust: simple because it incorporates key anthropogenic driving forces with parsimony; systematic because it specifies the mathematical relationship between the driving forces and their impacts; and robust because it is applicable to a wide variety of impacts (including GHG emissions). Written as Eq. 1, the model is usually applied as an accounting or difference equation. Data on I, P, and A are used to solve for T, with the relative impact of P, A, and T on I determined by their changes over time (13).
Remarkably little effort has gone toward disciplining the model with empirical analysis since the original papers describing it were first published. Although there have been attempts to assess the validity of the model, they have typically relied on qualitative assessments, field study demonstrations, or projections rather than on an assessment of the model’s overall fit to an appropriate data base (13, 21–23, §).¶ This was our main task here. We reformulated the model slightly and applied the reformulation to the anthropogenic sources of CO2 emissions. Our reformulation assumes a stochastic version of Eq. 1:
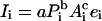 |
2 |
Here, I, P, and A remain, respectively, environmental impact, population, and affluence, but we have added the subscript “i” to emphasize that these quantities vary across observational units. The quantities a, b, c, and e can be estimated by applying standard statistical techniques. The coefficients b and c determine the net effect of population and affluence on impact, and a is a constant that scales the model. Technology is modeled as a residual term. The technology term actually incorporates not only technology as it is usually conceived but also social organization, institutions, culture, and all other factors affecting human impact on the environment other than population and affluence (13). Like the original formulation, this stochastic model aggregates these myriad effects into a single multiplier.‖
For ease of expression in Eq. 2, we have written b and c as constants. This form suggests that the effects of population and affluence are constant in proportions (linear in logarithms). In fact, the original formulation implies that a = b = c = 1. But the effects of driving forces may not be strictly proportional. As the original papers describing the IPAT framework emphasized, there may be thresholds and other nonproportional effects (8, 9, 11, 29, 30). Our stochastic formulation accommodates such effects if we substitute more complex functions for the coefficients b and c . Estimating such functions allows us to identify levels of affluence or population that produce threshold, accelerating, or other complex effects. Thus, the stochastic version of the IPAT model can be used to identify diminishing or increasing impacts due to increases in population or in affluence and thereby capture an important feature of the IPAT framework.
We focused on estimation of effects on CO2 because it is among the most important drivers of radiative forcing and because sound data are available on CO2 emissions for a variety of nations.** Our unit of analysis was the nation–state because it is the principal collective actor in generating environmental impacts and in developing policies in response to them. Thus, our measure of environmental impact (I) was industrial CO2 emissions (in millions of metric tons of carbon per year) for the 111 nations for which data are available (33). We used population size for P and gross domestic product per capita (gdp) for A (33, 34).‡‡ The nations included in our analysis are listed in Table 1. We chose data for 1989 because it is the most recent year for which all relevant data are available.
Table 1.
Technology multiplier for national CO2 emissions
| Identifier | Nation | Technology multiplier* | Identifier | Nation | Technology multiplier* |
| 1 | Algeria | 0.87 | 57 | Libya | 1.22 |
| 2 | Angola | 0.81 | 58 | Madagascar | 0.84 |
| 3 | Argentina | 1.54 | 59 | Malawi | 1.06 |
| 4 | Australia | 1.60 | 60 | Malaysia | 0.93 |
| 5 | Austria | 0.77 | 61 | Mali | 0.37 |
| 6 | Bangladesh | 0.84 | 62 | Mauritania | 5.36 |
| 7 | Belgium | 1.07 | 63 | Mauritius | 0.47 |
| 8 | Benin | 0.90 | 64 | Mexico | 0.70 |
| 9 | Bhutan | 0.47 | 66 | Mozambique | 2.07 |
| 10 | Bolivia | 1.62 | 65 | Morocco | 1.02 |
| 11 | Botswana | 0.46 | 67 | Nepal | 0.62 |
| 12 | Brazil | 0.24 | 68 | Netherland | 0.85 |
| 13 | Bulgaria | 5.75 | 69 | New Zealand | 0.81 |
| 14 | Burkina Faso | 0.56 | 70 | Nicaragua | 0.76 |
| 15 | Burundi | 0.58 | 71 | Niger | 1.24 |
| 16 | Cameroon | 0.59 | 72 | Nigeria | 3.78 |
| 17 | Canada | 1.75 | 73 | Norway | 1.55 |
| 18 | Central African Republic | 0.41 | 74 | Oman | 0.93 |
| 19 | Chad | 0.56 | 75 | Pakistan | 1.78 |
| 20 | Chile | 0.97 | 76 | Panama | 0.48 |
| 21 | China | 1.74 | 77 | Papua New Guinea | 0.76 |
| 22 | Colombia | 1.09 | 78 | Paraguay | 0.47 |
| 23 | Congo | 0.85 | 79 | Peru | 0.62 |
| 24 | Costa Rica | 0.37 | 80 | Phillippines | 0.81 |
| 25 | Cote d’Ivoire | 1.55 | 81 | Poland | 4.11 |
| 26 | Czechoslovakia | 2.94 | 82 | Portugal | 0.63 |
| 27 | Denmark | 1.07 | 83 | Rwanda | 0.27 |
| 28 | Dominican Republic | 1.16 | 84 | Saudi Arabia | 1.58 |
| 29 | Ecuador | 1.59 | 85 | Senegal | 0.99 |
| 30 | Egypt | 2.62 | 86 | Sierra Leone | 2.01 |
| 31 | El Salvador | 0.40 | 87 | Singapore | 1.36 |
| 32 | Ethiopia | 0.68 | 88 | Somalia | 2.19 |
| 33 | Finland | 1.33 | 89 | South Africa | 2.11 |
| 34 | France | 0.50 | 90 | Spain | 0.41 |
| 35 | Gabon | 1.40 | 91 | Sri Lanka | 1.05 |
| 36 | Germany | 0.85 | 92 | Sweden | 0.86 |
| 37 | Ghana | 1.33 | 93 | Switzerland | 0.98 |
| 38 | Greece | 1.22 | 94 | Syrian Arab Republic | 2.75 |
| 39 | Guatemala | 0.56 | 95 | Tanzania | 1.47 |
| 40 | Guinea | 0.63 | 96 | Thailand | 0.78 |
| 41 | Haiti | 0.59 | 97 | Togo | 0.92 |
| 42 | Honduras | 0.58 | 98 | Trinidad | 2.96 |
| 43 | Hungary | 1.56 | 99 | Tunisia | 1.66 |
| 44 | India | 1.14 | 100 | Turkey | 1.19 |
| 45 | Indonesia | 1.05 | 101 | Uganda | 0.32 |
| 46 | Iran | 0.56 | 102 | United Arab Emirates | 3.72 |
| 47 | Ireland | 0.86 | 103 | United Kingdom | 0.70 |
| 48 | Israel | 0.76 | 104 | United States | 0.95 |
| 49 | Italy | 0.50 | 105 | Uruguay | 0.51 |
| 50 | Jamaica | 1.08 | 106 | Union of Soviet Socialist | 0.62 |
| 51 | Japan | 0.62 | Republics† | ||
| 52 | Jordan | 2.74 | 107 | Venezuela | 1.49 |
| 53 | Kenya | 1.36 | 108 | Yugoslavia | 1.14 |
| 54 | Korea, South | 0.56 | 109 | Zaire | 0.70 |
| 55 | Kuwait | 1.57 | 110 | Zambia | 0.83 |
| 56 | Lao People’s Republic | 1.22 | 111 | Zimbabwe | 4.87 |
The technology multiplier is the antilog of the residual from the log–polynomial regression reported in Table 2.
Data from 1989.
To allow for nonlinearities, we first estimated a general additive model in which the effects of log population and log gdp on log CO2 emissions were fitted with a nonparametric regression procedure, loess (35, 36). This method is a form of multiple regression that makes no a priori assumptions about the functional forms that link P and A to I. The loess procedure used does not estimate a specific function linking P and A to I, so we developed these functions using models with polynomial terms in the log of population and affluence that were then compared with the loess model. A polynomial that was quadratic in the log of population and cubic in the log of gdp provided an adequate parametric match to the nonparametric fit (F = 0.99, df = 3.1, P < 0.42).††
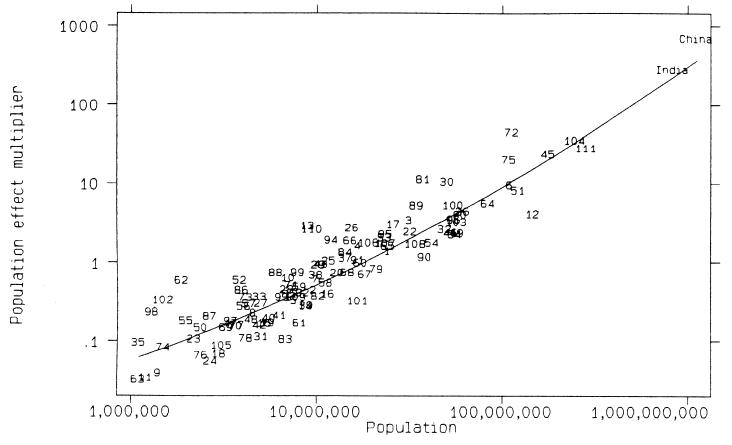
The effects of population and affluence multipliers are displayed in Figs. 1 and 2, with coefficient estimates in Table 2. The quadratic term for log of population size is statistically significant, but an examination of Fig. 1 and other standard diagnostics suggests that this is because the two nations with the largest population, China and India, have substantial influence on our estimates. (These data points are in the upper right corner of Fig. 1.) When we dropped these two nations and reestimated the log–polynomial model, the quadratic term in log population lost its significance (b = 0.024, t = 0.8, P > 0.4). When we deleted China and India from the original data set and estimated a model that was linear in the log of population, the coefficients for the linear, quadratic, and cubic affluence terms were nearly identical to those reported in Table 2. These results weaken the argument that population has little effect (12), or even a beneficial effect (39), on the environment because they show a significant and nonlinear effect. The results also lend support to ongoing concern with population growth as a driving force of environmental impacts (14, 40).
Figure 1.
Effects of population on CO2 emissions. Solid line indicates the effect of population size relative to the geometric mean of population across nations (12.3 million). Population effects calculated at the geometric mean of gross domestic product ($1476). Data points are plotted using identification numbers from Table 1. Countries are plotted at the point corresponding to the expected population effect multiplied by the residual displayed in Table 1.
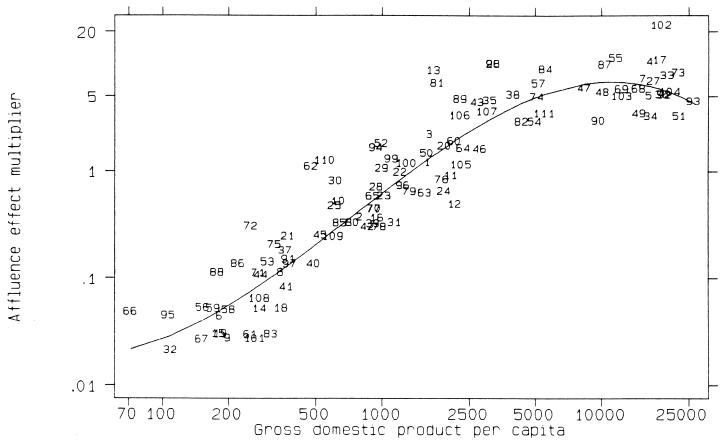
Figure 2.
Effects of affluence on CO2 emissions. Solid line indicates the effect of gross domestic product per capita relative to the geometric mean of gdp across nations ($1476). Affluence effects calculated at the geometric mean of population (12.3 million). Data points are plotted using identification numbers from Table 1. Countries are plotted at the point corresponding to the expected gdp effect multiplied by the residual displayed in Table 1.
Table 2.
Effects of population and affluence on 1989 CO2 emissions of 111 nations
| Log–polynomial model
|
Log–linear model
|
|||
|---|---|---|---|---|
| Coefficient | SE | Coefficient | SE | |
| Population | ||||
| Linear | 1.123 | 0.058 | 1.149 | 0.060 |
| Quadratic | 0.063 | 0.026 | ||
| Affluence | ||||
| Linear | 1.484 | 0.105 | 1.084 | 0.047 |
| Quadratic | −0.152 | 0.026 | ||
| Cubic | −0.070 | 0.020 | ||
| Intercept | 16.854 | 0.101 | 16.545 | 0.073 |
| Coefficient of determination | 0.931 | 0.891 | ||
Fig. 2 and Table 2 indicate that the effects of affluence on CO2 emissions level off and even decline somewhat at the very highest levels of gdp. We suspect that this shift is the result of two structural changes: (i) a shift to a service-based economy and (ii) the ability of the more affluent economies to invest in energy efficiency. Unfortunately, this decline in impact only occurs when per capita affluence is above ≈$10,000.§§ Seventy-five percent of the 111 nations in our sample have gdps below $5000. Thus, our results suggest that, for the overwhelming majority of nations, economic growth that can be anticipated for the next quarter century or so will produce increasing, rather than declining, CO2 emissions. Reductions in CO2 emissions will not occur in the normal course of development and will have to come from targeted efforts to shift toward less carbon-intensive technologies and activities. We will return to this point later.
Table 1 lists the technology multiplier (the antilog of the residual term) for all nations for which the relevant data are available. Again, it is important to remember that this term (labeled “technology” in keeping with previous applications of the IPAT model) includes not just physical infrastructure but also social and economic organization, culture, and all factors whose effects are not captured by population and affluence. The technology multiplier varies across nations by more than 1 order of magnitude. A deeper understanding of the effects of social and economic structure and institutions and of culture on GHGs can be advanced by careful analysis of these multipliers. Of particular interest are nations with unusually large multipliers and substantial impact, such as Bulgaria, Mauritania, Zimbabwe, or Poland. Also of interest are those affluent nations with relatively small multipliers and thus minimal impact on the climate system compared with their size, such as Brazil, Spain, France, and Italy.
Bulgaria, Mauritania, Zimbabwe, and Poland all have multipliers greater than 4, indicating that they emit far more CO2 than would be expected from their size and level of affluence. Bulgaria and Poland have economies based on heavy industry, and, because their energy costs were subsidized by the Soviet Union, they have lacked economic incentives for energy efficiency. Thus, their economies have consumed very substantial amounts of fossil fuels relative to their levels of affluence. Both Mauritania and Zimbabwe have an unusually large industrial sector for nations with relatively low levels of affluence. In addition, Zimbabwe is a fossil fuel producer.
Among industrial nations, France, Italy, and Spain have multipliers of 0.5 or less, indicating that they emit approximately one-half the CO2 that would be expected as a result of their populations and gdps. This is the result of a variety of factors affecting their energy production and consumption. Among them are France’s substantial reliance on nuclear power, Italy’s use of natural gas and imported electricity, and Spain’s substantial use of nuclear and hydroelectric power and its relatively low level of automobile ownership. And, of course, all three nations are favored by climates milder than those of most other industrial nations. Brazil has the lowest multiplier of any nation. This may be a result of its extensive use of hydroelectric power as well as its emphasis on liquid fuels.
We used the estimated coefficients of our model to project global CO2 emissions for the year 2025. In one scenario, we assumed that national technological multipliers will not change over time. In the second scenario, we assumed an increase in efficiency (and thus a decrease in the technology multiplier) of 1% per year. In both cases, we used the United Nations medium case scenario for population projections and assumed a 2% annual real growth in gdp (33). The first scenario, with no technological progress, implied global CO2 emissions in 2025 of 4.3 × 1010 metric tons, a 95% increase over 1991 emissions. A 1% per year increase in carbon efficiency would mean an increase of only 36%—to 3.0 × 1010 metric tons. To achieve a goal of stable emissions at 1991 levels in the face of economic and population growth, our model suggested that efficiency increases would need to average about 1.8% per year from 1990 to 2025. Although such increases are feasible, they will not occur without strenuous efforts.
When we estimated our model without polynomial terms, the coefficients for both population and affluence were close to, but slightly greater than, 1, which, as noted above, is the value assumed in the original IPAT formulation.¶¶ Our basic results appear consistent with the original IPAT framework and with recent applications of it to the related problem of energy consumption (41). This further attests to the robustness and utility of the approach. That we found all of the driving forces—population, affluence, and technology—to have important effects on CO2 emissions is consistent with views that recognize the importance of, and interactions among, these forces. Our results show that the impacts of population are roughly proportional to its size across the range of population sizes that will characterize most nations over the next few decades. This contradicts the views of those who are complacent about population growth. Even so, because of demographic inertia, successful efforts to slow population growth will be realized in the long term rather than the short term (42). Economic growth in itself does not offer a solution to environmental problems. Our results indicate that, when affluence approaches about $10,000 in gdp, CO2 emissions tend to fall below a strict proportionality. But growth to this level of affluence is not a realistic expectation for most nations over the next 2 or 3 decades. On the other hand, significant improvements in CO2 efficiencies are possible and have the potential to reduce emissions substantially.
Acknowledgments
We thank W. Catton, R. Dunlap, A. Ford, E. Franz, W. Freudenburg, L. Hamilton, L. Kalof, and P. Stern for their comments. This work was supported in part by National Science Foundation Grants SES-9109928 and SES-9311593, by the Dean of the College of Liberal Arts at Washington State University, and by the International Institute of George Mason University.
Footnotes
Abbreviations: IPAT, Impact = Population·Affluence·Technology; GHGs, greenhouse gases; gdp, gross domestic product per capita
Kolsrud, G. & Torrey, B. B. Presented at the Annual Meeting of the Population Association of America, Washington, DC, March 21–23, 1991.
Recent economic analyses of environmental impacts use a stochastic model similar to ours (24–27). But they assume that the impacts of population are strictly proportional, and our approach is to treat the form of the relationship as an hypothesis. Preston (28) decomposes the variance/covariance structure of the IPAT model but does not further explore IPAT as the basis of a stochastic model.
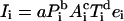 |
Standard accounts suggest that more than half of radiative forcing can be attributed to CO2. We focused on industrial emissions because data on cement and biogenic emissions are much less reliable. Data on other GHGs also are less reliable than the industrial CO2 data. Current estimates of CH4 (methane) emissions are uncertain to at least a factor of 2 and do not take account of biomass burning, which may contribute perhaps one-fifth of the total anthropogenic emissions (31). Data on chlorofluorocarbons are reported as an aggregate for the European Community nations, which are among the highest chlorofluorocarbon producers and consumers (32). Nitrous oxide emissions are available only for a handful of nations. For these reasons, we limited our analysis to industrial emissions of CO2.
Data on gdp for the USSR (Union of Soviet Socialist Republics) in 1989 were not available, so we used a value interpolated from 1991 reports. Deleting the USSR from the analysis did not significantly change the results.
The results reported are for ordinary least squares, with SE based on 500 replications of case-based bootstrap resampling, which are preferable to normal theory SE in this context (37, 38). To reduce colinearity among polynomial terms, we centered the population and gdp variables by using deviations from the mean of the logs instead of raw values for the linear in log terms and in generating the polynomial terms. In such models, the intercept represents the expected value for a country with population and affluence equal to the geometric mean on those variables, which, for this data set, were 12.3 million and $1476, respectively. We also computed estimates of the log–polynomial model using least median of squares, least trimmed squares, and a robust regression that uses Huber estimates followed by biweighted least squares. These techniques are robust with regard to outliers in residuals and in carriers (37, 38). The robust estimates yield substantively identical results to the more familiar, ordinary least squares reported here.
Most economic analyses of economic growth and environment, which do not allow for nonproportional effects of population, suggest that impact declines somewhere between $1000 and $10,000 in gdp (24, 27). The exception is the analysis of Holtz–Eakin and Selden (25), whose analysis of CO2 emissions implies a turning point of over $35,000 per capita.
For population, the coefficient is 1.149 (normal theory SE = 0.055), and for gdp it is 1.084 (normal theory SE = 0.050). The intercept for this model is 16.545 (normal theory SE = 0.077), and the coefficient of determination is 0.891. For consistency, we used centered values of population and gdp.
References
- 1.Houghton J T, Jenkins G J, Ephraums J J. Climate Change: The IPCC Assessment. Cambridge, U.K.: Cambridge Univ. Press; 1990. [Google Scholar]
- 2.Intergovernmental Panel on Climate Change. Climate Change: The IPCC Response Strategies. Washington, DC: Island; 1991. [Google Scholar]
- 3.Stern P C, Young O R, Druckman D. Global Environmental Change: Understanding the Human Dimensions. Washington, DC: Natl. Acad. Press; 1992. [Google Scholar]
- 4.Dowlatabadi H, Morgan M G. Science. 1993;259:1813. doi: 10.1126/science.259.5103.1813. , 1932. [DOI] [PubMed] [Google Scholar]
- 5.Stern P C. Science. 1993;260:1897–1899. doi: 10.1126/science.260.5116.1897. [DOI] [PubMed] [Google Scholar]
- 6.Ehrlich P R, Holdren J P. Bull At Sci. 1972;28:16. , 18–27. [Google Scholar]
- 7.Commoner B. In: Population, Resources and the Environment. Ridker R G, editor. Washington, DC: Government Printing Office; 1972. pp. 339–363. [Google Scholar]
- 8.Commoner B. Bull At Sci. 1972;28:17. , 42–56. [Google Scholar]
- 9.Ehrlich P R, Holdren J P. Science. 1971;171:1212–1217. doi: 10.1126/science.171.3977.1212. [DOI] [PubMed] [Google Scholar]
- 10.Ehrlich P R, Holdren J P. In: Population, Resources and the Environment. Ridker R G, editor. Washington, DC: Government Printing Office; 1972. pp. 365–377. [Google Scholar]
- 11.Holdren J P, Ehrlich P R. Am Sci. 1974;62:282–292. [PubMed] [Google Scholar]
- 12.Commoner B. Making Peace with the Planet. New York: The New Press; 1992. [Google Scholar]
- 13.Dietz T, Rosa E A. Hum Ecol Rev. 1994;1:277–300. [Google Scholar]
- 14.Ehrlich P R, Ehrlich A H. The Population Explosion. New York: Simon & Schuster; 1990. [Google Scholar]
- 15.Goodland R, Daly H, Kellenberg J. Futures. 1994;26:146–155. [Google Scholar]
- 16.Green C P. Popul Rep. 1992;10:1–31. [Google Scholar]
- 17.Harrison P. The Third Revolution. London: Penguin; 1993. [Google Scholar]
- 18.Harrison P. Hum Ecol Rev. 1995;1:265–276. [Google Scholar]
- 19.Keyfitz N. Popul Ind. 1991;57:5–22. [PubMed] [Google Scholar]
- 20.United Nations Fund for Population Activities. Population, Resources and the Environment: The Critical Challenges. New York: United Nations Fund for Population Activities; 1991. [Google Scholar]
- 21.Bongaarts J. Popul Dev Rev. 1992;18:299–319. [Google Scholar]
- 22.Davis K, Bernstram M S. Resources, Environment and Population. New York: Oxford Univ. Press; 1991. [Google Scholar]
- 23.Mazur A. Popul Environ. 1994;15:371–378. [Google Scholar]
- 24.Grossman G, Krueger A. Q J Econ. 1995;110:353–377. [Google Scholar]
- 25.Holtz-Eakin D, Selden T M. J Publ Econ. 1995;57:85–101. [Google Scholar]
- 26.Selden T M, Song D. J Environ Econ Manage. 1994;27:147–162. [Google Scholar]
- 27.Shafik N. Oxf Econ Papers. 1994;46:757–773. [Google Scholar]
- 28.Preston S H. Popul Res Policy Rev. 1996;15:95–108. [Google Scholar]
- 29.Ehrlich P R, Holdren J P. Sat Rev. 1970;27:42. [Google Scholar]
- 30.Ehrlich P R, Holdren J P. Sat Rev. 1970;31:52. [Google Scholar]
- 31.Cicerone R J, Oremland R S. Global Biogeochem Cycles. 1988;2:229–327. [Google Scholar]
- 32.Benedick R E. Ozone Diplomacy. Cambridge, MA: Harvard Univ. Press; 1991. [Google Scholar]
- 33.World Resources Institute. World Resource 1992–93. New York: Oxford Univ. Press; 1992. [Google Scholar]
- 34.World Bank. World Development Report. Washington, DC: World Bank; 1984. [Google Scholar]
- 35.Hardle W. Applied Nonparametric Regression. Cambridge, U.K.: Cambridge Univ. Press; 1990. [Google Scholar]
- 36.Hastie T J, Tibshirani R J. General Additive Models. London: Chapman & Hall; 1991. [Google Scholar]
- 37.Dietz T, Frey R S, Kalof L. Am Sociol Rev. 1987;52:380–390. [Google Scholar]
- 38.Dietz T, Kalof L, Frey R S. Rural Sociol. 1991;56:461–474. [Google Scholar]
- 39.Simon J L. The Ultimate Resource. Princeton: Princeton Univ. Press; 1981. [Google Scholar]
- 40.The Royal Society and the National Academy of Sciences. Popul Dev Rev. 1992;18:375–390. [Google Scholar]
- 41.Holdren J. Popul Environ. 1991;12:231–255. [Google Scholar]
- 42.Bongaarts J. Science. 1994;263:771–776. doi: 10.1126/science.8303293. [DOI] [PubMed] [Google Scholar]