Microscopic Diffusion and Hydrodynamic Interactions of Hemoglobin in Red Blood Cells

Abstract

The cytoplasm of red blood cells is congested with the oxygen storage protein hemoglobin occupying a quarter of the cell volume. The high protein concentration leads to a reduced mobility; the self-diffusion coefficient of hemoglobin in blood cells is six times lower than in dilute solution. This effect is generally assigned to excluded volume effects in crowded media. However, the collective or gradient diffusion coefficient of hemoglobin is only weakly dependent on concentration, suggesting the compensation of osmotic and friction forces. This would exclude hydrodynamic interactions, which are of dynamic origin and do not contribute to the osmotic pressure. Hydrodynamic coupling between protein molecules is dominant at short time- and length scales before direct interactions are fully established. Employing neutron spin-echo-spectroscopy, we study hemoglobin diffusion on a nanosecond timescale and protein displacements on the scale of a few nanometers. A time- and wave-vector dependent diffusion coefficient is found, suggesting the crossover of self- and collective diffusion. Moreover, a wave-vector dependent friction function is derived, which is a characteristic feature of hydrodynamic interactions. The wave-vector and concentration dependence of the long-time self-diffusion coefficient of hemoglobin agree qualitatively with theoretical results on hydrodynamics in hard spheres suspensions. Quantitative agreement requires us to adjust the volume fraction by including part of the hydration shell: Proteins exhibit a larger surface/volume ratio compared to standard colloids of much larger size. It is concluded that hydrodynamic and not direct interactions dominate long-range molecular transport at high concentration.

INTRODUCTION

Biological processes often depend on diffusive transport of macromolecules within cells and tissue. In the heterogeneous environment of the cytoplasm, one has to discriminate between fixed obstacles and protein interactions affecting passive transport. The latter has been termed crowding, since excluded volume effects play a dominant role (1–4). In the following we investigate, on a mesoscopic scale, how diffusion of a single protein in a biological cell is modified by interactions at high concentration: Hemoglobin, the main component of red blood cells (92%), assumes a concentration of 330 mg/ml under physiological conditions, corresponding to a volume fraction of Φ = 0.25 (5). With an average center-to-center distance of 7 nm and a protein diameter of 6 nm, the molecules interact within their sphere of rotation, as was already noted by Perutz (6). The rotational diffusion coefficient of hemoglobin in red blood cells (RBCs) is a factor-of-two lower than in dilute solution (7). However, the translational diffusion coefficient is diminished by a factor of five according to field gradient NMR- and fluorescence recovery experiments (8,9). An even larger reduction (1/10) is found in the diffusivity of myoglobin, which is the oxygen carrier in striated muscle cells (10). Tracer diffusion experiments with hemoglobin and myoglobin by Wittenberg et al. (11) yield a roughly exponential decrease with concentration, which is attributed to obstruction effects by excluded volume interactions. Hemoglobin diffusion presumably facilitates the exchange of oxygen across the erythrocyte surface in the lung (11), but the magnitude of the effect is still debated (12).

The red blood cell is not an easy object for optical inspection, because of the high absorption coefficient of the heme group. Dynamic light scattering experiments in the visible range yield information about the RBC surface and the fluctuations of the cell membrane, but cannot penetrate into the cell interior (13). This may be possible in the near future with FCS versions of two-photon fluorescence excitation in the IR (14,15). NMR and optical techniques record displacements on a scale of several hundred nanometers. The molecular interactions in RBCs are established, however, on a length scale of a few nanometers—the mean distance between hemoglobin molecules. This range can be studied using energy-resolved neutron scattering methods, in particular spin-echo spectroscopy, which allows recording the time evolution of protein diffusion on the relevant spatial scale. With this technique we address the question whether hemoglobin diffusion can be understood based on concepts developed for nearly uncharged colloidal particles (16,17): Molecular liquids interact by direct forces, van der Waals and electrostatic; whereas, for a colloid, hydrodynamic interactions, which are mediated by the solvent, play an important role. Each molecule moves in the flow field induced by the motion of its neighbors. The different types of interactions can be sorted out by measurements of the short- and long-time diffusion coefficients at various length scales. The latter is selected by varying the wave-vector of the scattering experiment: Hydrodynamic interactions dominate at short times, and their propagation occurs with the speed of sound, while direct forces are established during the structural relaxation time of the colloidal solution, τ_D. This requires diffusion across the center-to-center distance d: τ_D ≈ d²/6D. One distinguishing property of proteins is their small size, with diameters of a few nanometers, in contrast to several hundred nanometers of a standard colloid. Whether the solvent can be treated equivalently as a continuum for large and small colloids and within what range of size remains to be established. The theoretical interpretation of diffusion in colloidal suspensions in the presence of direct and hydrodynamic interactions has reached a certain degree of refinement: For self-diffusion it has been shown that direct interactions are relatively unimportant compared to hydrodynamic interactions. Approximate short- and long-time diffusion coefficients as a function of volume fraction and wave-vector have been derived, which agree reasonably well with experimental data taken with standard colloids (16–19). In contrast, for collective diffusion, direct interactions play an important role (20). In the following we investigate whether these concepts can be applied on a mesoscopic scale to concentrated protein solutions and, in particular, to hemoglobin diffusion inside RBCs.

THEORETICAL CONCEPTS

We assume a binary solution of an aqueous solvent and a solute of protein molecules. Macromolecular diffusion thus results in concentration fluctuations, which modulates the local density. The basic experimental quantity to be determined with neutron spin-echo spectroscopy is the intermediate scattering function, S(q,τ), which records the correlations of intermolecular density fluctuations due to relative protein displacements r_i-r_j (21),

(1)

where q is the scattering vector, q = 4π/(λ)sin(θ/2), λ is the wavelength of the incident neutrons, and Θ is the scattering angle. With q, one selects a particular length scale d = 2π/q, and τ denotes the time shift. N is the total number of particles. The brackets 〈…〉 imply ensemble averaging over initial positions of the particles. Assuming spherical particles without internal degrees of freedom, the displacements in Eq. 1 exhibit a Gauss distribution at long times. The Gauss average of Eq. 1 yields

(2)

S(q, 0) denotes the static structure factor. D_c is the collective or gradient diffusion coefficient defined by Fick's law. A phenomenological interpretation of D_c can be obtained from linear irreversible thermodynamics in combination with the Einstein equation. The latter relates a molar mobility (the Onsager coefficient) to a molecular friction coefficient f_c (22),

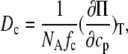(3)

where N_A is the Avogadro number and c_p is the molar concentration of the macromolecule. The osmotic compressibility κ_os = ∂ c_p/∂Π acts as a driving force: A low compressibility enhances the rate of restoring locally a uniform concentration. In dilute solutions the osmotic pressure varies linearly with concentration: Π = RT · c_p, which, if inserted into Eq. 3, yields the familiar Einstein equation: D_c = k_BT/f_c.

The compressibility decreases with increasing concentration, implying faster collective diffusion. In parallel, enhanced particle interactions increase the collective friction coefficient, which compensates for the osmotic effect. In concentrated solutions exhibiting strong particle interactions, the molecular displacements can deviate from a Gauss distribution, involving a time- and q-dependent diffusion coefficient D(q,τ) in Eq. 2 (23–25). The short-time value reflects molecular motions of particles in a static environment, while long-time diffusion involves an adjustment due to structural relaxation on the scale of the interaction time τ_D. The correlation function S(q,τ) of strongly interacting systems is thus inherently heterogeneous in time.

Following Ackerson (24), we express D(q,τ) as the ratio of a so-called hydrodynamic function H(q,τ) and a static susceptibility, the interparticle structure factor S(q),

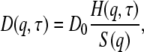(4)

where D₀ denotes the free particle diffusion coefficient at infinite dilution, D₀ = k_BT/f₀, and f₀ is the coefficient of the protein-solvent friction.

The inverse of the hydrodynamic function is the friction factor, f_c/f₀ = H(q,τ)⁻¹, resulting from direct and hydrodynamic interactions between protein molecules. At short times, τ ≪ τ_D, only hydrodynamic interactions are involved. In the limiting case of low q-values and long times, Eq. 4 turns into the collective or gradient diffusion coefficient D_c of Eq. 3. The low-q structure factor is thus given by S(q → 0,Φ) = RT κ_os, which allows deriving the osmotic compressibility from scattering experiments at low scattering vectors. The self-diffusion coefficient D_s in contrast is independent of κ_os and involves only the self-friction coefficient f_s:

(5)

The long-time self-diffusion coefficient is equivalent to the tracer diffusion coefficient ≡ D_t. Its short-time value, 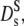can be measured with neutron spectroscopy, since the generalized collective diffusion coefficient D(q,τ) in Eq. 4 tends to 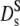at q ≥ q_max, above the structure factor maximum, where S(q) approaches unity (23).

Experimental values of the collective and the tracer diffusion coefficients of hemoglobin and myoglobin versus the protein volume fraction Φ are displayed in Fig. 1. The self-diffusion coefficient of hemoglobin in red blood cells, as determined with NMR (8), fits well into the concentration series. It is striking that D_t and D_c diverge with increasing volume fraction (29): While D_c decreases only slightly in a linear fashion, a roughly exponential decrease with volume fraction is found for the tracer diffusion coefficient. The fit to D_t ≈ D₀ · exp(−Φ/Φ₀) yields Φ₀ = 0.15. Experimental values of κ_os(Φ), represented by the solid line in Fig. 1, also decrease exponentially with the volume fraction yielding Φ₀ = 0.12. According to Eq. 3, D_c ∝ should thus increase exponentially with the volume fraction. Instead, a slight decrease is observed, which implies that osmotic and friction effects nearly compensate each other in Eq. 3, yielding f_c(Φ) · κ_os ≈ constant. Indeed, the osmotic compressibility declines in parallel with the tracer diffusion coefficient, which depends exclusively on f_s. The slight difference may reflect a nonequivalence of self- and collective friction. However, κ_os is a thermodynamic susceptibility that depends on excluded volume and other direct interactions, but not on hydrodynamic forces. The experimental values of κ_os for hemoglobin and myoglobin, displayed in Fig. 1 (solid line), are well represented by theoretical results of the virial expansion of S(q) assuming a suspension of hard spheres (29,30). Although the compensation between friction and osmotic effects holds up to intermediate volume fractions (Φ < 0.3), where both quantities vary by more than a factor of 10, there is no theoretical basis for such a relationship, which would exclude hydrodynamic interactions.

FIGURE 1.

Normalized long-time diffusion coefficients D(Φ)/D₀: (triangles) collective diffusion coefficient D_c of hemoglobin in solution (light scattering), (dash-dotted line) fit to D_c/D₀ = 1+ B₁ · Φ with B₁ = −0.76. Tracer diffusions coefficients, D_t, of hemoglobin in solution (small open squares) (29,37) and in red blood cells (NMR): large open square (8), and of myoglobin in solution (solid circles) (11,37), (dash-dotted line) fit of D_t to an exponential function with Φ₀ = 0.15, (solid line) exponential fit to the osmotic compressibility, κ_os, of hemoglobin and myoglobin yielding Φ₀ = 0.12 (29,30).

MATERIALS AND METHODS

Sample preparation

Human blood samples, drawn by venipuncture from an adult male, were used immediately. Three types of D₂O-buffer solutions were prepared. Buffer A was a modified physiological sodium salt solution with the following ingredients (per liter): 9.0 g NaCl, 17.16 mg adenine, 26.22 mg inosine, 2.5 g albumin (fraction V), 10 ml vitamins (Nr. 273; Seromed Biochrom, Berlin, Germany) and 10 ml penicillin/streptomycin (Nr. A22129; Seromed Biochrom) adjusted to pD 7.4. Buffer B serves as the anti-coagulant and contains (per liter): 16 g Na-citrate, 25 g glucose, 17.1 mg adenine, 26.2 mg inosine, 2.5 g albumin, 10 ml vitamin E, and 10 ml Pen/Strep adjusted to pD 7.4 by citric acid. Buffer C, composed of 4 units of buffer A plus 1 unit of B, is the final buffer to dilute the RBCs at the standard osmolarity of 300 mOsm. The pD of 7.4 is close to the isoelectric point of hemoglobin. The preparation proceeds as follows: 4 units (by volume) of blood are mixed with one unit of buffer B. The resulting solution is then centrifuged for 5 min at 2000 g. After removal of the plasma and “buffy coat”, the cells are washed five times with buffer C and centrifuged. The number of exchangeable hydrogens is then reduced by a factor of 100. The RBCs were inspected with a microscope to ensure the absence of significant deviations from their normal shape. For the neutron scattering experiments, the RBCs were centrifuged for 5 min at 2000 g and the concentrated solution was filled in a quartz-glass cell with 0.5 mm in thickness. The experiments were performed within 24 h after preparation. Human hemoglobin A samples were prepared by lysis of erythrocyte suspensions and purified by DEAE-cellulose chromatography. The concentrated samples were freeze-dried and resuspended in buffer C at the desired concentration (21 mM) before the experiment. The viscosity of buffer C was measured using a Schott capillary viscosimeter: η(D₂O)/η(H₂O) = 1.243 (±0.05) at 20°C and η(D₂O, 37°C)/η(D₂O, 20°C) = 0.6686 (±0.0004). The factor converting the diffusion coefficient from buffer C (D₂O) at 37°C to water at 20°C is then 0.79 (±0.005).

Neutron scattering experiments

Protein-internal motions and diffusion have been studied by neutron time-of-flight and back-scattering spectroscopy (26,27). The neutron spin echo experiments with hemoglobin (28) were performed at the Orphée reactor of the Laboratoire Léon Brillouin (France) and the European high flux reactor of the Institut Laue Langevin. We employed the spin echo spectrometer G1bis at the LLB and IN15 at the Institut Laue Langevin. On G1bis we measured the intermediate scattering function S(q,τ) using an incident wavelength λ₀ = 10.3 Å and a spread Δλ/λ ∼0.15 within a wave-vector range q ≃ 0.05–0.3 Å⁻¹. Accessible spin echo times range from τ ≃ 27 ps to 20 ns. On IN15 two wavelengths were employed to cover the maximal wave vector range with appropriate spin echo times (λ = 9 Å and λ = 15 Å, q ≃ 0.02–0.13 Å⁻¹, τ ≃ 190 ps to 190 ns).

In the relevant q-range (0.01 ≤ q ≤ 0.25 Å⁻¹) the distance between atomic scattering centers (≈1 Å) is much smaller than 2π/q ≈ 25 Å. By coherent neutron scattering, one thus probes the scattering length density contrast between solute and the solvent (here D₂O for optimal contrast). The signal, the scattered intensity, is thus proportional to Δρ², the squared difference in scattering length density between solute and the solvent. As a result, one probes the density fluctuations induced by relative motions of protein molecules in the D₂O-solvent. The scattering function is dominated by hemoglobin but contains minor contributions (a few percent) from the cell membrane. Moreover, since the molecules are almost spherical and the molecular scattering density distribution is homogeneous at the low q-values, translational and not rotational displacements dominate the scattering function.

RESULTS

Time- and wave-vector dependent diffusion

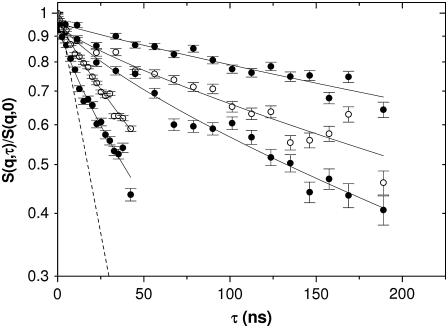
Fig. 2 displays the normalized intermediate scattering function S(q,τ)/S(q) of hemoglobin in RBCs at several wave-vectors. The fits to a single exponential decay on a logarithmic timescale are also shown. The decay rates increase with the wave-vector as expected for translational diffusion. The exponential fit emphasizes the overall or long-time decay of the correlation function. The resulting long-time diffusion coefficient D^L(q) is displayed in Fig. 4 (top). However, due to the large q-values or short length scales probed, as compared to light scattering, the short-time regime may still apply. To emphasize the short-time behavior, a plot of ln[S(q,τ)] versus τ is shown in Fig. 3. A straight line (exponential decay) accounts for the data at the lower q-values; however, deviations become significant at high q, which is indicated by the dashed line. The initial slope yields the effective short-time diffusion coefficient D^S(q) = −1/(q²S(q)) (dS/dτ)_τ→0. For Gauss displacement distributions one expects the diffusion coefficient to be constant. In contrast, we observe a q- and time-dependent coefficient D(q,τ). Fig. 4 (top) shows the long-time value derived from an exponential fit to the data: D(q) increases with decreasing wave-vector, while above q = 0.1 Å⁻¹, a plateau is reached. According to Eq. 4, D(q) is composed of two q-dependent functions: the intermolecular structure factor S(q) and the hydrodynamic function H(q). We first investigate the effect of the structure factor on D(q).

FIGURE 2.

Normalized intermediate scattering functions S(q,τ)/S(q,0) of hemoglobin in RBCs on a log-timescale, measured with the neutron spin-echo-spectrometer IN 15 (Institut Laue-Langevin in Grenoble) at several wave-vectors q; (lines) fits of the data to a single exponential function as described in the text.

FIGURE 4.

(Top) Generalized diffusion coefficient D(q,τ) (Eq. 4) of hemoglobin in RBCs at 37°C in D₂O-buffer C; the line is drawn to guide the eye. (Middle) Interparticle structure factor S(q) of hemoglobin in RBCs, MSA calculations adjusted from Krueger et al. (5,32). (Bottom) Theoretical short-time hydrodynamic function of a hard-sphere colloid H(q) at Φ = 0.25 adjusted from Beenakker and Mazur (16), experimental H(q) = D(q)/D₀ · S(q); the solid line through data is the prediction H(q)/2.1 adjusted to fit the experimental data.

FIGURE 3.

Semilogarithmic plot ln[S(q,τ)/S(q,0)] of the intermediate scattering function shown in Fig. 2 at the same wave-vectors q = 0.03, 0.04, 0.05, 0.1, and 0.12 Å⁻¹. The lines are fits of the data to a single exponential function. The dashed line at q = 0.12 Å⁻¹ refers to the fast component reflecting short-time diffusion.

In previous work, we determined the structure factors of myoglobin and hemoglobin solutions from low-angle neutron scattering data (31). Applying the mean spherical approximation (MSA) with a hard sphere potential as input, reasonable fits to the data could be achieved. The contribution of electrostatic interactions was estimated to be small. This is reasonable, since the measurements were performed near the isoelectric point of the protein. The structure factor of red blood cells was analyzed earlier by Krueger et al. (5,32) using contrast variation methods. This allows our discriminating between membrane and protein scattering contributions to the structure factor. According to this work, it is not possible to eliminate the membrane scattering completely by contrast variation, because the respective scattering length density is inhomogeneous: The membrane is composed of lipid bilayers and a variety of membrane proteins. However, due to the small size of hemoglobin with respect to the cell dimension and its high relative bulk concentration, Krueger et al. were able to verify that the scattering contributions due to membrane and hemoglobin are mostly wave-vector separated. The data were refined in the relevant wave-vector range q ≥ 0.06 Å⁻¹ using the mean spherical approximation (MSA) method (33,34) and the result at Φ = 0.25 is displayed in Fig. 4 (middle). The structure factor exhibits a broad maximum in the q-range of interest to our diffusion measurement (Fig. 4, top): The diffusion coefficient decreases where the structure factor shows a corresponding increase. This result is qualitatively in accordance with Eq. 4, since D(q) ∝ 1/S(q). Above q_max, where the structure factor approaches unity, D(q) tends to a constant value. This regime allows us to extract a self-diffusion coefficient D_s(q), since correlations diminish with S(q) → 1. In contrast, at q-values below the structure factor maximum, coherent effects dominate, yielding D_c(q), the collective diffusion coefficient. The steplike increase in D(q) in Fig. 4 (top) thus reflects the crossover from self- to collective diffusion. This mechanism closes the gap observed between D_c and D_t in Fig. 1. The gap exists not only on a macroscopic but also on a microscopic scale and is related to the properties of the q-dependent osmotic compressibility. The limiting value of D_c(q → 0), observed with light scattering in Fig. 1, is not reached here because of a restricted experimental q-range. If the q-dependence of D(q) could be attributed entirely to S(q), there would be no room for hydrodynamic interactions. This is not the case, as will be demonstrated in the next section.

The hydrodynamic function H(q)

From Eq. 4 we derive the hydrodynamic function, since independent experimental information on D(q) and S(q) is available in Fig. 4 (top and middle). Interestingly, H(q) is not constant, as shown in Fig. 4 (bottom, data points), but displays a broad maximum in phase with the structure factor S(q). A wave-vector-dependent friction function was observed previously with concentrated myoglobin solutions (31). This indicates that the hydrodynamic function and the static structure factor are correlated as proposed by hydrodynamic theories: Beenakker and Mazur have calculated the short-time self-diffusion coefficient 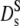of a concentrated suspension of hard spheres taking into account the hydrodynamic interactions between an arbitrary number of spheres (16). Direct interactions can be ignored at short times for τ ≪ τ_D. They derive a wave-vector dependent function H(q), oscillating in phase with the structure factor. Their result, adjusted for size and volume fraction of hemoglobin in RBCs, is displayed as the upper solid line in Fig. 4 (bottom). The theoretical result exhibits a similar q-dependence, but the absolute values are larger than the experimental data. This implies that the theory underestimates the magnitude of the hydrodynamic friction ∝ H(q)⁻¹. Adjusting the theoretical result by a constant factor (2.1) fits the data in the respective q-range quite well.

Short- and long-time diffusion

The discrepancy in the magnitude of H(q) is somewhat surprising, since the theory agrees quite well with experimental data on short-time self-diffusion coefficients of standard uncharged colloids at comparable concentrations (16,35). A likely origin of the discrepancy could be a difference in the relevant timescale: The diffusion coefficients in Fig. 4 (top) reflect the overall decay in S(q,τ) and therefore represent rather the long-time self-diffusion coefficient than D^S. Moreover, with neutron scattering we investigate much higher q-values than with light scattering.

Our experimental estimate of the self-diffusion coefficient of hemoglobin in RBCs is derived from the plateau in D(q) at high q in Fig. 4 (top), where S(q) → 1. Corrected to buffer C (H₂O) at 37°C, we obtain 1.75 (±0.2) · 10⁻⁷ cm²/s for RBCs and 2.5 (±0.2) · 10⁻⁷ cm²/s for hemoglobin at Φ = 0.25. Corrected to 20°C and water, the coefficient in RBCs is 1.1 · 10⁻⁷ cm²/s, a factor 6.2 lower than in dilute solution.

The normalized values D_s/D₀ of hemoglobin in RBCs and in solution assuming D₀(37°C, D₂O) = 8.61 · 10⁻⁷ cm²/s are displayed in Fig. 5. Also shown is the self-diffusion coefficient of myoglobin (solid circles) measured in the same q-range with neutron spin-echo spectroscopy (31). The comparison with the data in Fig. 1 demonstrates that the self-diffusion coefficients measured at q ≥ q_max are nearly identical with the long-range tracer diffusion coefficient of hemoglobin and myoglobin. Both quantities exhibit essentially the same exponential decay with the volume fraction.

FIGURE 5.

Normalized relative diffusion coefficients D(Φ)/D₀: (open triangles) D_c, collective diffusion coefficient of hemoglobin in solution (dynamic light scattering) from Fig. 1, neutron scattering results at q = 0.12 Å⁻¹: (open circles) suggested long-time diffusion coefficient of hemoglobin in blood cells and of hemoglobin in solution (open diamonds) at Φ = 0.25. (Open squares) Short-time diffusion coefficient 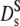of hemoglobin in RBCs from Fig. 3. (Solid circles) 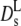of myoglobin in solution (31) and (dash-dotted line) exponential fit to D_t (Fig. 1) yielding Φ₀ = 0.15, (dashed line) theoretical short-time self-diffusion coefficient, 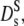for hard sphere suspensions (16,17,35), and (solid line) theoretical long-time self-diffusion coefficient, 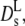for hard sphere suspensions (17).

The D_s values of hemoglobin in RBCs and of hemoglobin in solution at the same volume fraction coincide within experimental error and fit quite well into the concentration series.

The dashed line in Fig. 5 represents the calculated short-time diffusion coefficient for a suspension of hard spheres, 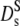(Φ) by Beenakker and Mazur (16,35). The experimental data are significantly lower at all concentrations than the theoretical prediction. At Φ = 0.25 the discrepancy amounts to a factor of two, which is the adjustment factor used in Fig. 4 (bottom). However, the data agree quite well with long-time tracer diffusion coefficients of hemoglobin and myoglobin at the same concentration. This suggests that the self-diffusion coefficient determined from the overall decay of the intermediate scattering function in Fig. 2 should be interpreted as a long-time value 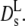Due to memory effects by structural relaxation, the long-time diffusion coefficient is generally lower than the short-time value. The short-time self-diffusion coefficient can be estimated from the initial decay of the correlation function in Fig. 3. The corresponding short-time coefficient, indicated by an open square in Fig. 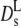5, at q = 0.12 Å⁻¹, is above but still lower than the theoretical value. Possibly even higher q-values than those employed here need to be considered.

DISCUSSION

Comparison with hard sphere colloidal suspensions

The calculation of the short-time diffusion coefficient at high concentrations involves a consideration of many-body hydrodynamic interactions (16). At short times the configuration of particles remains essentially fixed. For the long-time diffusion coefficient memory, effects due to configurational relaxation have to be included. This leads to slowing down of particles motions: The long-time diffusion coefficient is thus generally lower than at short times. A complete solution to the latter problem, providing the full range nonexponential correlation functions versus volume fraction, is not available. Early calculations by Medina-Noyola were based on a decoupling approximation: The molecules perform short-time diffusion under the influence of hydrodynamic interactions, while the obstruction effect at later times is assumed to be independent of the short-time trajectories. Thus only D₀ is renormalized by hydrodynamic interactions (36), while the obstruction effect is derived from the static structure factor. The model predicts a significant difference between short- and long-time diffusion due to direct interactions. The model agrees with experimental data at high volume fractions (≥0.3) in the presence of strong direct forces. Later Tokuyama and Oppenheim developed a more systematic theory of concentrated hard-sphere suspensions, where both direct and hydrodynamic interactions are present (17,35). The volume fraction dependence of short- and long-time diffusion coefficients are calculated from a unifying point of view. Both the short- and long-range hydrodynamic interactions are shown to play an important role in both coefficients, while the direct interactions are drastically reduced by the hydrodynamic coupling. Their 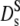(Φ) coincides essentially with the results of Beenakker-Mazur (16,35) shown in Fig. 5. The new feature is the calculation of a long-time diffusion coefficient 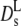(Φ), which is represented by the full line in Fig. 5. The theory predicts experimental data of uncharged colloids at intermediate and high volume fraction quite well (17,18). Moreover, it is reasonably well approximated by an exponential function with Φ₀ = 0.19 at low and intermediate volume fractions. Our experimental values of 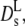derived from the long-time decay of S(q,τ) of myoglobin and hemoglobin solutions, are conspicuously lower than those predicted for hard sphere colloidal suspensions. The difference may point to further attractive interactions, slowing down self-diffusion, since also the collective diffusion coefficient D_c (Fig. 5) decreases (instead of increasing) with concentration. Nevertheless, the calculated 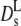accounts much better for the protein diffusion coefficients than the short-time values 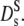This comparison supports our previous conclusion that the long-time limit of the self-diffusion coefficient is achieved, at least above Φ = 0.2, despite the mesoscopic q- and time-range covered by our experiment. How is this possible?

The largest q-value (0.125 Å⁻¹ in Fig. 4, top) corresponds to a spatial scale of 50 Å, which is close to the center-to-center distance d ≈ 70 Å between hemoglobin molecules at Φ = 0.25. For the respective correlation time we find τ ≈ 60 ns. Within this range, taking the value of the short-time diffusion coefficient, (Φ = 0.25) ≈ 0.5 D₀ (Fig. 5), as an upper limit, an average displacement of 40 Å is derived. In addition, accounting for the diameter of hemoglobin, σ = 56 Å, a much smaller displacement of d* = d − σ = 14 Å could lead to a collision. Thus deviations from the short-time behavior are expected for correlation times exceeding ∼10 ns. It is thus plausible that the data in Fig. 4 (top) refer to the long-time regime of self-diffusion.

This interpretation of long-time diffusion is not easily reconciled with the q-dependence observed for H(q) in Fig. 4 (bottom), which agrees with calculations in the short-time diffusion regime (16). However, Segre and Pusey found with hard sphere colloidal suspensions, that (q) and (q), while differing significantly in magnitude, exhibit nearly the same q-dependence (19). Thus the dynamical function H(q), observed with hemoglobin in Fig. 4 (bottom), can be interpreted in terms of long-time self-diffusion, which is dominated by hydrodynamic interactions. Moreover, the factor that had to be chosen in Fig. 4 (bottom) to superimpose experimental H(q) data and those calculated for short-time diffusion, ≈2.1, is close to the theoretical ratio of the short- and long-time diffusion coefficient at Φ = 0.25 (17). Moreover, the fast initial decay of the correlation function observed at the highest q-value in Fig. 3 supports the existence of short-time diffusion.

Effect of the protein hydration shell

While the experimental values for the long-time self-diffusion coefficient of colloidal suspensions agree quite well with theoretical predictions at intermediate and high concentrations (17,18), consistently lower values are observed for hemoglobin and other proteins. As mentioned above, this discrepancy could indicate transient protein clusters due to attractive forces. For this reason we have performed extensive SANS studies of concentrated myoglobin solutions (31). The MSA analysis of the scattering curves was, however, consistent with hard-sphere monomers. For hemoglobin, a small fraction of oligomers had to be assumed to explain the scattering curves (5,32). Figs. 1 and 5 show that myoglobin and hemoglobin, as well as other proteins (37), exhibit nearly the same exponential decrease in the self-diffusion coefficient with volume fraction. Moreover, the diffusion coefficient is only weakly dependent on the molecular weight (D ∝ M^−1/3), thus cluster formation as the major cause of the decline in D_s(Φ) can be excluded. Strong electrostatic interactions can also reduce the self-diffusion coefficient (38). However, close to the isoelectric point, the average charge of hemoglobin is small (5,31). Is there an alternative explanation?

According to Alpert and Phillies, the hydration shell of the macromolecule has to be included in the volume fraction to improve agreement with hydrodynamic calculations (39,40). Moreover, Phillies derives a stretched exponential decay of D_s(Φ) as the signature of hydrodynamic interactions between particles based on heuristic arguments (41). Up to this point it was assumed that the volume fraction can be calculated from the dry protein volume in a manner similar to a large colloid. With decreasing particle size, the surface gains relevance and may affect the dynamic properties. Proteins in general are surrounded by a thin layer of interfacial water. Due to the larger surface/volume ratio of protein molecules with respect to a conventional colloid, the weight fraction of the hydration shell, ∼0.3 g/g protein, is significant. The interfacial water moves with the protein (stick condition) and thus contributes to the hydrodynamic volume v_h. The volume fraction discussed above refers to the bare protein and was calculated from the dry specific volume, v_d = 0.75 cc/g (42) using Φ = c_p · v_d, where c_p denotes the concentration in g/cc. Thus the 330 mg/ml of hemoglobin in RBCs yield a volume fraction of 0.247. The protein specific volume is a thermodynamic quantity, which does not include the hydration shell. Fitting the intermolecular structure factor S(q) of protein solutions to a hard sphere model (MSA) yields the dry- and not the hydrodynamic volume as the relevant size parameter (5,32). The hydration shell, however, contributes to protein friction and the hydrodynamic function H(q): The hard-sphere radius of hemoglobin determined from the static structure factor by scattering experiments is 28 (±1) Å (5), while the hydrodynamic radius determined from diffusion measurements amounts to 31 Å. The diffusion coefficient, which involves the ratio of H(q)/S(q) thus depends on both the dry- and the hydrodynamic volume. Dry and hydrodynamic volume are related by Tanford (42): v_h = v_d + δ · v_s. Here v_s denotes the specific volume of the solvent and δ denotes the fraction of solvent contributing effectively to the protein volume. The volume fraction is now an adjustable parameter depending on 0 ≤ δ ≤ 1. For hemoglobin at c_p = 330 mg/ml, one has Φ_d = 0.25, which we have used above, while the hydrated volume fraction is Φ_h = 0.36, assuming δ = 0.35. With the conventional definition of the volume fraction Φ = 4/3π n_p R³, one obtains, inserting the radius of the equivalent sphere (R = 28 Å), Φ_d = 0.27, while with the hydrodynamic radius R_H = 31 (±0.05) Å one obtains Φ_h = 0.366. Therefore the discrepancy observed between theoretical and experimental values of the long-time diffusion coefficient of colloidal protein solutions could be relieved by introducing a renormalized volume fraction, which takes the hydration shell into account. As mentioned above, the concentration dependence of theoretical and experimental values can be approximated by an exponential decay assuming a characteristic volume fraction Φ₀. For hemoglobin and myoglobin, one obtains Φ₀ = 0.15 (±0.01), while the calculated long-time diffusion coefficient is approximated by Φ₀ = 0.189. The renormalization factor would thus amount to 1.26. Attributing the discrepancy totally to this effect would yield an effective specific volume of 0.945 cc/g instead of 0.75 cc/g in the dry case. The dynamic effective volume fraction of hemoglobin in RBCs is then 0.32. This shift is indicated by an arrow in Fig. 4 and indeed improves the agreement with the calculated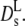

CONCLUSIONS

We have shown that protein diffusion at high concentration and inside erythrocytes can be understood based on concepts developed for colloidal suspensions with particles of much larger size. The main difference is that the effective volume fraction of proteins includes the interfacial water due to the large surface/volume ratio. In crowded environments, excluded volume interactions determine the interprotein structure factor. However, the interprotein friction and the long-time self-diffusion coefficient are controlled mainly by hydrodynamic interactions. This conclusion is based essentially on the observed q-dependence of the self-diffusion coefficient, which is a characteristic feature of hydrodynamic interactions. The concentration dependence of D_s alone would not prove the point, since, for instance, the same trend could be reproduced by Brownian dynamics simulations of proteins assuming Lennard-Jones and screened electrostatic interactions without hydrodynamic coupling (43). A second argument concerns the compensation between osmotic and friction effects, discussed above in the context of Fig. 1. It gives rise to a nearly concentration-independent collective diffusion coefficient. This property, D_c(Φ) ≈ constant, was derived for hard sphere colloids at short times, where hydrodynamic interactions prevail (16). Moreover, the friction factor H(q) varies in phase with the structure factor S(q) even at long times. This result establishes the missing link between osmotic and friction effects. It also provides a rational for the puzzling observation, derived from dynamic light scattering, that H(q → 0) of globular proteins decreases with the volume fraction at intermediate concentrations (20). According to calculations of Tokuyama and Oppenheim, long-range hydrodynamic forces play an important role at long times, while excluded volume interactions are drastically reduced (17). Thus a new mechanism of long-range communication in addition to electrostatic coupling between protein molecules in cells and tissue is proposed.