Force-Response Considerations in Ciliary Mechanosensation

Abstract

Considerable experimental evidence indicates that the primary, nonmotile cilium is a mechanosensory organelle in several epithelial cell types. As the relationship between cellular responses and nature and magnitude of applied forces is not well understood, we have investigated the effects of exposure of monolayers of renal collecting duct chief cells to orbital shaking and quantified the forces incident on cilia. An exposure of 24 h of these cells to orbital shaking resulted in a decrease of amiloride-sensitive sodium current by ∼60% and ciliary length by ∼30%. The sensitivity of the sodium current to shaking was dependent on intact cilia. The drag force on cilia due to induced fluid flow during orbital shaking was estimated at maximally 5.2 × 10⁻³ pN at 2 Hz, ∼4 times that of thermal noise. The major structural feature of cilia contributing to their sensitivity appears to be ciliary length. As more than half of the total drag force is exerted on the ciliary cap, one function of the slender stalk may be to expose the cap to greater drag force. Regardless, the findings indicate that the cilium is a mechanosensory organelle with a sensitivity much lower than previously recognized.

INTRODUCTION

Many types of epithelial cells in an organism grow a single nonmotile cilium on their free surface. This organelle protrudes several microns above the surface, is encased by the cell membrane, and is composed of a central axoneme containing nine microtubule doublets. Although its existence and microscopic structure has been known for more than four decades, its functions are not well explored. Its functions have come under intense investigation with the demonstration that, in humans, defects in the cilium and its cellular anchor, the basal body, are associated with several human pathophysiological phenotypes, including Kartagener syndrome, polycystic kidney disease, nephronophthisis, Bardet-Biedl syndrome, and Meckel-Gruber syndrome.

Several different types of observations indicate that the primary cilium of renal and other epithelial cells can function as a mechanosensory organelle (1–5). Given that the cilium cantilevers out into the extracellular milieu, this is a reasonable hypothesis. However, it immediately begs the question about types and magnitudes of forces that can be sensed. In most of the published experiments, acute forces were applied in the form of physical bending of cilia or forced fluid flow over a monolayer of epithelial cells. Cellular read-outs under these conditions were increases in cytosolic Ca²⁺ and decreases in stimulated cAMP levels. In other, more recent experiments (6,7), gentler forces in the form of orbital shaking were applied overnight to epithelial monolayers. In one type of experiment using shaking (6), trafficking of the angiotensin receptor type 1 to the apical surface was enhanced, suggesting the possibility that ciliary mechanosensation plays a role in flow-dependent enhancement of proximal tubular salt and fluid reabsorption. In another type of experiment, ciliary mechanosensation by mild shaking effected retention of the transcription factor STAT6 in the cilium and prevention of translocation to the nucleus (7), thus suggesting, together with other data, that the cilium serves as sensor for orienting cell division along the tubular axis (8).

The fluid-mechanical forces experienced by cells during mild orbital shaking must be very small because it is difficult to detect macroscopic fluid flow under these conditions. Nevertheless, cells must be able to sense the minute forces to generate observed changes in cellular structure and metabolism. We present evidence that cellular regulation of amiloride-sensitive sodium current (= current via the epithelial sodium channel (ENaC)) by mild orbital shaking is dependent on an intact cilium. To provide for a rational understanding of the relationship between the magnitude of applied force during mild orbital shaking and cellular response, we have quantified estimates of possible forces that cells and cilia experience using a model system of differentiated collecting duct cells grown in cell culture on permeable support. The ENaC current in these differentiated collecting duct cells was used as read-out because it can be quantified repeatedly in the same monolayer, i.e., before and after manipulations. Interestingly, the measurements and theoretical considerations indicate that the forces experienced by cilia under orbital shaking are maximally three times that of thermal noise, i.e., ∼5 fN and therewith much lower than the previously reported force of 78 fN (9). Interestingly, such low force over a relatively long time (>12 h) results in an altered cellular state with decreased steady-state ENaC current and ciliary length (this report) and altered STAT6 and angiotensin receptor trafficking (6,7). A review of fluid inertial forces used in published experiments reveals that ciliary length is one feature that can make cilia very sensitive to fluid flow.

Theoretical considerations

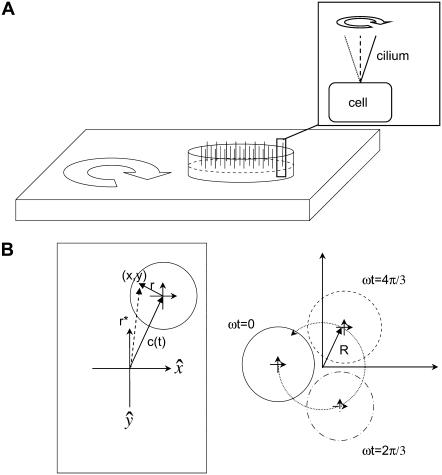
The experimental geometry for orbital shaking is shown in Fig. 1. A confluent monolayer containing ciliated cells is placed atop an orbital shaker platform, which then executes orbital motion of constant throw (R) and user-controlled frequency (ω). A crucial distinction exists between orbital motion and rotational motion, in that in orbital motion there is no center of rotation; that is, neighboring points maintain a constant relative orientation with respect to each other. The orbital movement and the relationship of neighboring points during the movement are illustrated in Fig. 1 B. The cells, including cilia, undergo a pure translation at velocity ωR around a closed circular path. Because there is no net rotation of the fluid body, the conservation of vorticity demands that no angular momentum be introduced via the motion of the dish. At the low frequencies used in the study (≤5 Hz), there is very little mixing of the fluid.

FIGURE 1.

Geometry of orbital shaking and buoyancy forces. (A) Shaker table with filter insert containing a confluent monolayer of cells each with a single apical primary cilium (inset). The cilium pivots around its cellular anchoring point. (B) Movement of a point (x,y) on an orbital shaker relative to the laboratory frame defined by directions 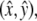which are fixed. (Left frame) The vector r*(t) = x(t),y(t) is composed of a vector to the center of the monolayer c(t) and the time-independent vector r from the center of the monolayer to the point (x,y). (Right frame) Illustration of the movement of all points on the monolayer in the laboratory frame (coordinates): ω = shaking frequency, t = time, R = orbital throw. The circles represent the position as a function of time. The crossed arrows in the center indicate the orientation of the monolayer, showing that 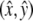remain constant in both the laboratory and monolayer frame (absence of rotation around the monolayer center).

There are three types of mechanical forces due to the shaking, which are readily identified: 1), shear stress on the apical membrane due to fluid movement relative to cells, 2), drag force on the cilium due to fluid movement, and 3), buoyancy induced by centripetal forces and density differences between the cilium and apical fluid and often referred to as “body force” because this force is distributed throughout the volume of the cilium.

The section below summarizes the major concepts and equations used for a quantitative analysis of flow-induced forces on cilia and cells, based on Lamb (10).

The shear stress (τ) at the apical surface of the monolayer is defined by

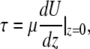(1)

whereby U = fluid velocity, μ = viscosity, and z = direction orthogonal to the monolayer (z = 0).

The drag force on a cilium can be calculated from fluid velocity transverse to the cilium assuming the cilium to be a rigid cylinder capped by a hemisphere. That may be an oversimplification, but the resulting calculation represents a maximal drag force. For a sphere of radius a, the drag force (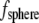) is

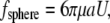(2)

whereby the symbols have the same meaning as in Eq. 1 and a = radius of the cylinder.

The drag force on the cylinder cap 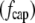is simply that on a hemisphere:

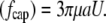(3)

Calculating the drag force per unit length against a cylinder of radius a 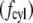is considerably more complex, but was solved by Oseen (10) and is given by

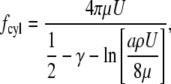(4)

where γ is Euler's constant (0.577…) and ρ = the density of the fluid. Equation 4 can be simplified by using the Reynolds number

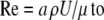(5)

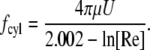(6)

The total drag force on a cilium is the sum of 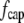and 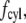the latter integrated over the length of the cilium.

It is useful to recall the physical meaning of the Reynolds number. It is the inertial force/viscous force ratio experienced by the fluid. The inertial force is responsible for shear and drag forces on surfaces in contact with the fluid. For biological experiments with physiological salt solutions, the inertial force can be varied experimentally by changing fluid velocity.

The buoyancy force comes about because the tip of each nonmotile cilium is pointing “up” and will, in general, execute a slight circular path with respect to its point of cellular attachment during orbital shaking (see inset of Fig. 1 A). Even if the monolayer and the fluid co-move (or if the cilium is free to pivot and is freely advected by the fluid), there will be a resultant force on the cilium, which can be derived as follows: In the frame of the monolayer, that is, using coordinates that co-move with the monolayer, the velocity field is exactly zero. The acceleration felt by the monolayer results simply from the motion of the monolayer with respect to the stationary laboratory frame. Any point (x,y) on the monolayer moves along a path in the laboratory frame described by

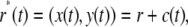(7)

whereby r* = vector to point (x,y), r is the vector from the center of the monolayer to the point of interest, and c(t) is the vector from the laboratory origin to the center of the monolayer (see Fig. 1 B).

Thus, the acceleration at any point on the monolayer is

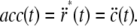(8)

For orbital motion with throw R and 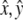as unit vectors, the acceleration becomes

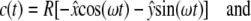(9)

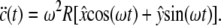(10)

Because this acceleration field arises purely due to relative motion between the monolayer frame and laboratory frame, the resultant force is sometimes called “fictitious” and is exemplified by centripetal acceleration. The force density 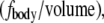averaged over time, is simply equal to

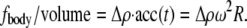(11)

The total force on a cilium is then the force density integrated over the volume of the cilium. For comparison, it is useful to calculate the random thermal noise of ciliary movements

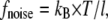(12)

whereby 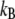is the Boltzmann constant, T is the temperature, and l is the length of the cilium.

Calculations of the shear and drag forces require information on the fluid velocity profile between wall and cilia tips, in addition to fluid density and viscosity and ciliary geometry, whereas those for the buoyancy force require additional information about the density difference between cilium and fluid.

METHODS

Cell culture

Experiments were carried out with a mouse cell line derived from the cortical collecting duct (mCD 1296 (d)) of a heterozygous offspring of the Immortomouse (Charles River Laboratories, Wilmington, MA). The Immortomouse carries as transgene a temperature-sensitive SV40 large T antigen under the control of an interferon-γ response element. Cells were maintained on collagen-coated Millicell-CM inserts (inner diameter 10 mm, permeable support area 0.6 cm²; Millipore, Billerica, MA) to promote a polarized epithelial phenotype. Cells were grown to confluence at 33°C, 5% CO₂ and then maintained at 39°C, 5% CO₂ to enhance differentiation. The growth medium consisted of the following (final concentrations): Dulbecco's modified Eagle medium w/o glucose and Ham's F12 at a 1:1 ratio, 5 mM glucose, 5 μg/ml transferrin, 5 μg/ml insulin, 10 ng/ml epithelial growth factor (EGF), 4 μg/ml dexamethasone, 15 mM HEPES, 0.06% NaHCO₃, 2 mM L-glutamine, 10 ng/ml mouse interferon-γ, 50 μM ascorbic acid 2-phosphate, 20 nM selenium, 5% fetal bovine serum (FBS). For differentiation, FBS, insulin, and interferon-γ were omitted from the apical medium and insulin, EGF, and interferon-γ from the basal medium. The apical amount of medium was restricted to 100 μl per filter insert (10 mm) so that the apical fluid thickness is ∼1270 μm (neglecting curvature of the air-media interface near the contact line). Cells were incubated in differentiation conditions for at least 48 h before any shaking or chloral hydrate treatment (see below). All monolayers were routinely monitored for electrical resistance and transepithelial potential (see below).

Chloral hydrate treatment protocol

Addition of chloral hydrate to the apical media will effectively remove the primary cilium (11). A total of 4 mM chloral hydrate was added to the apical media of the cells for 68 h and then removed, using the protocol in Mickey and Howard (19). Monolayers were only shaken after termination of the chloral hydrate treatment and replacement with differentiation medium.

Electrophysiology protocol

Transepithelial voltage and resistance measurements were performed using an Endohm chamber (World Precision Instruments, Sarasota, FL) connected to an epithelial voltage clamp (model 558C-5, Bioengineering, University of Iowa) and the output recorded with a strip-chart recorder. Data analysis was carried out using the strip chart recorder output. The transepithelial voltage was constantly read out. The resistance was calculated every 20 s from the voltage change produced by a short, bipolar 2-μA current pulse and corrected for fluid and electrode resistance measured in the absence of a monolayer. The current pulse was sufficiently long to ensure steady-state (DC) conditions. Cells were placed in the Endohm chamber for no more than 3 min, during which time the transepithelial voltage remained constant. The transepithelial voltage and resistance were converted to short-circuit current equivalent (Isc_eq) assuming an ohmic relationship. More than 95% of Isc_eq was inhibited by 10 μM apical amiloride and thus is considered to be proportional to the activity of ENaC in the apical plasma membrane.

Immunocytochemistry

Fixation and immunocytochemistry were performed using standard techniques. The cells were briefly fixed in 4% paraformaldehyde and counterstained with wheat germ agglutinin-AlexaFluor 594 for 15 min. After rinsing, the monolayers were fixed again with 4% paraformaldehyde, permeabilized for 10 min with a solution of 0.1% Triton-X and 0.5% saponin in a blocking buffer containing 5% donkey serum, 5% goat serum, 1% bovine serum albumin (BSA), and 5% FBS. The monolayers were then stained with a monoclonal mouse antibody against acetylated α-tubulin (Invitrogen, Carlsbad, CA) followed by an anti-mouse antibody labeled with AlexaFluor 488 (Invitrogen). The stained filter was cut out of the culture insert and transferred to a microscope slide, monolayer side up. The filter was mounted in VectaShield (Vector Labs, Burlingame, CA) with 4′,6-diamidino-2-phenylindole (DAPI). A No. 1½ coverslip was placed on top of the monolayer—if needed, small spacers were used to prevent the coverslip from compressing the monolayer. The slides were then sealed with nail polish and stored for imaging.

Microscopy protocol

Image stacks were acquired with a Zeiss 200M Axiovert inverted microscope, with a DG4 switchable fluorescent light source (Sutter Instrument, Novato, CA) and a 12-bit CoolSnap HQ camera (Roper Scientific, Tucson, AZ) under control of MetaMorph v 6.2 (Molecular Devices, Sunnyvale, CA). Images were deconvolved using Huygens Essential (Scientific Volume Imaging, Hilversum, The Netherlands) blind deconvolution software running in a 64-bit Linux environment. Cell counting images were obtained with a 40× numerical aperture 1.3 fluar lens, whereas image stacks for deconvolution were obtained with a 100× numerical aperture 1.3 neofluar lens. Typical exposure times for individual frames were 200 ms, and bleaching was minimal.

Orbital motion protocol

Cells were subjected to orbital motion by placing 12-well plates with differentiated monolayers on culture inserts on top of a shaker table (MTS 2/4, IKA, Wilmington, NC), which was placed within a standard laboratory incubator. Control monolayers without shaking were maintained in the same incubator. The rates of shaking were measured with a stopwatch. Monolayers were generally subjected to orbital motion at a fixed frequency for 24 h. Electrophysiological measurements or fixation for immunocytochemistry were carried out on cells immediately after removal from the orbital shaker, i.e., within ∼2 min.

Particle tracking protocol

We are interested in microscopic details to the flow, but the induced flow could not be imaged on a microscope due to the macroscopic orbital movement, constraints on what would fit on the microscope, and the fact that 10-mm-diameter wells are too small to admit a high numerical aperture microscope objective, which is required to both resolve the advected particles and limit the thickness of the observation plane. We therefore attached a long working distance dipping objective directly to a small camera; this allowed us to place the imaging system atop the orbital shaker and effectively subtract out the unrelated macroscopic motion.

A water immersion dipping objective lens (Leica U-V-I 63X, numerical aperture = 0.90, 2.2-mm working distance; Leica Microsystems, Wetzlar, Germany) was attached directly to a digital camera (Point Grey Research, Vancouver, British Columbia, Canada), which is capable of capturing digital video at 15 frames per s. The camera and lens were placed on the orbital shaker and used to image phosphate-buffered saline (PBS) seeded with polystytrene microspheres (5.5-μm diameter, Bangs Labs, Fishers, IN), partially filling a 6-well plate (BD Biosciences, San Jose, CA). One hundred frames of video were acquired at a time and analyzed in Metamorph. The particle height from the bottom surface was determined by the use of a micrometer (Mitutoyo, Aurora, IL), which controlled the height of the microscope objective with respect to the plate.

Using a high numerical aperture lens to establish a narrow plane of focus far from the lens surface and measuring the flow at multiple locations and depths are sufficient checks to ensure that our flow measurements are repeatable and are in qualitative agreement with preliminary observations using ink drops (data not shown).

Even though our particles are larger than those generally used for particle imaging velocimetry (PIV), the induced flow velocities are so slow that there is no fluid slip over the surface of our spheres. The Reynolds numbers for the spheres are on the order of 4 × 10⁻⁵, indicating that our spheres are indeed faithfully following the flow pattern and not displaying inertial effects different than the cilia.

Viscosity measurement protocol

The dynamic viscosity of apical media was measured with a Cannon-Fenske Routine Viscometer (Induchem Lab Glass, Roselle, NJ) with the apparatus and media equilibrated to 37°C. The density of the media was measured by weighing a controlled volume (100 μl Dummond Wiretrol disposable micropipette, Dummond Scientific Company, Broomall, PA). In both cases, the apparatus was calibrated by measurements on double distilled water to ensure accuracy.

Statistical analysis

Statistical analysis was done by Student's t-test, two-tailed heteroscedastic, as appropriate. Values of p < 0.01 are considered significant.

RESULTS

Choice of experimental system

To investigate the relationship between the forces generated by slow orbital shaking and cellular responses, we chose a mouse collecting duct (mCD) cell line that had been generated in the laboratory by microdissection of cortical collecting duct tubules from the kidney of a heterozygous Immortomouse. This transgenic mouse contains a gene for a temperature-sensitive SV40 large T-antigen, which confers potential immortalization on all cells. SV40 large T antigen is active at the permissive temperature of 33°C, allowing continued cell division, but not at the mouse body temperature of 39°C. The resulting cell line consists of principal cells that form confluent, electrically resistant monolayers on permeable support, i.e., filter inserts, such as Millicell-CM. The cell line retains differentiated characteristics important for this study, namely well-developed primary cilia (see Fig. 2) and sodium reabsorption via the apical ENaC. This current can be measured repeatedly under sterile conditions for each monolayer, i.e., allowing serial measurements of this property, e.g., before and after exposure to shaking.

FIGURE 2.

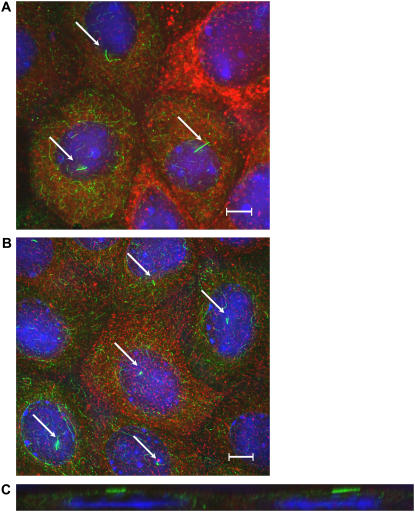
Comparison of ciliary length between nonshaken (A) and shaken (B) monolayers of mCD cells. (A and B) En face images of cells stained with an antibody for acetylated α-tubulin (green) and counterstained with wheat germ agglutinin for apical surface glycoproteins (red) and DAPI for nucleic acids (blue). The primary cilia (indicated by arrows) are clearly visible. Images have been deconvolved. Scale bar is 5 μm. (C) x-z slice of a showing primary cilia lying against the apical surface.

Sodium absorption via ENaC is a well-understood process that is described by the classical and, by now, textbook Ussing model of sodium absorption: Sodium entry at the apical membrane is by electrodiffusion through the ENaC channel and exit is by active transport via Na,K-ATPase in the basolateral plasma membrane. Due to the presence of potassium channels in the basolateral plasma membrane, transepithelial sodium absorption by this process is completely electrogenic and can be quantified by measuring the short-circuit current (Isc) with identical electrolyte solutions on both sides of the epithelium. The current flow through ENaC is conveniently quantified by sensitivity of Isc to 10 μM of apical amiloride, a well-understood diuretic drug. Similarly, calculation of Isc_eq from transepithelial potential and resistance provides a quantitative measure of ENaC activity. As under the conditions of this study, both Isc and Isc_eq are more than 95% inhibitable by 10 μM amiloride, the terms Isc (or Isc_eq) and ENaC current or activity are used interchangeably in this article.

Collecting duct cells had previously been shown to respond to mechanical stimulation mediated by cilia: 1), Nauli et al. (12) showed in similar mouse CD cells that they respond to acute changes in apical fluid flow with an increase in cytosolic calcium, which is eliminated by an abnormal ciliary protein (polycystin 1); and 2), Praetorius and Spring (5) and Low et al. (7) had shown in the canine CD cell line MDCK that these cells respond to acute mechanical stimulation with elevated calcium in a cilium-dependent manner and retain Stat 6 in the cilia when exposed overnight to low frequency orbital shaking. The mCD cell line used in this study has the advantage over MDCK cells of expressing ENaC activity.

For this study, mCD cells were expanded to form confluent monolayers and then maintained under differentiation conditions to allow for expression of the cilium and ENaC activity. Then matched differentiated monolayers were exposed for 24 h to no or low frequency orbital shaking and cellular responses quantified in terms of amiloride-sensitive Isc_eq and ciliary length. In addition, the fluid movement induced by gentle orbital shaking for this type of geometry was measured using particle image velocimetry and this information used to generate upper limits for the forces acting on cellular surface and cilia.

Cilium length decreases with orbital shaking

Fig. 2, A and B, shows control (unshaken) and chronically shaken (24 h) mCD cells stained for acetylated α-tubulin, and counterstained for apical surface glycoproteins with wheat germ agglutinin and for nucleic acids. Because cilia contain a high density of microtubules with acetylated α-tubulin, they stain extremely well and stand out against the rest of the microtubule network. Although living cells present the cilia normal to the monolayer surface, the effect of fixation in paraformaldehyde is to cause the cilia to lie against the apical surface of the cells. This is shown in Fig. 2 C, which is an x-z slice of Fig. 2 A.

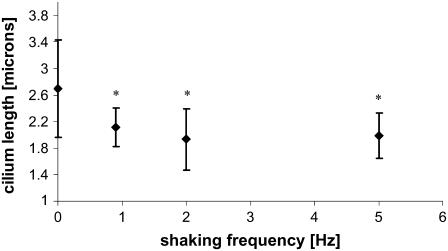
The cilium length was measured directly from images, such as in Fig. 2 C, using MetaMorph to determine the length of a traced line. Strictly speaking, the length of acetylated α-tubulin in the ciliary axoneme was measured and used as an index of cilium length. Fig. 3 presents measured cilia lengths of cells subjected for 24 h to shaking frequencies of 0.9–5 Hz. There is a significant decrease in the lengths of the cilia with shaking, but no statistical difference exists between the different shaken populations. The images used for length measurements were taken in various regions around the monolayer to assess whether cilium length would vary with position in the monolayer: No variation in cilium length with position was observed. The finding that cilium length did not depend on shaking frequency above 0.9 Hz could mean that the cellular response was saturated even at the lowest force employed in this study.

FIGURE 3.

Effect of shaking on cilia length. mCD cell monolayers were incubated without or with shaking for 24 h at the indicated frequency. The ciliary length was measured from images acquired after fixation and staining as in Fig. 2. Asterisks indicate a p < 0.01 compared to unshaken monolayers.

Cells initially subjected to orbital shaking for 24 h and then incubated without shaking for an additional 24-h period possessed cilium lengths identical to those cells that had never been shaken, indicating that the cellular response to shaking is reversible. Furthermore, cilium length in unshaken monolayers was not time dependent, at least during the period of examination in this study.

Transepithelial ENaC current decreases with orbital shaking

Once mCD cells have achieved confluence and are placed in differentiation conditions at 39°C, actvive ENaC channels can be found in apical membrane as measured by Isc_eq. Typically, this current fully develops after 1 week of incubation in differentiation conditions and survives, with regular media changes, for up to 3 weeks. Monolayer resistance was typically 1–2 kΩ × cm² so that even small changes in Isc_eq could be measured with high accuracy. Because different batches of monolayers exhibited variability in Isc_eq, control and test monolayers from the same batch were always paired. In addition, due to time series measurements before and after shaking, each monolayer also served as its own control.

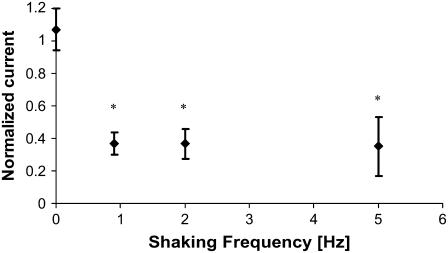
Fig. 4 presents the effect of shaking mCD cells on ENaC current. The shaken monolayers have significantly reduced ENaC current. The decrease is ∼60%, and the degree of reduction is constant over the whole range of the employed shaking frequencies. It should be emphasized that the shaken monolayers recovered after the termination of shaking and were not distinguishable from unshaken monolayers 24 h later, at least in terms of ENaC current. The order of shaking did not matter, for example, cells shaken for 24 h first at 5 Hz and then 24 h at 0.9 Hz behaved identically to cells shaken first at 0.9 Hz and then 5 Hz. (data not shown). These data indicate that the response to mechanical stimulation is fully reversible.

FIGURE 4.

Effect of shaking on the magnitude of ENaC activity, measured as amiloride-sensitive Isc_eq. mCD cell monolayers were incubated with or without shaking for 24 h at the indicated frequency. Isc_eq was measured immediately after termination of shaking and normalized relative to Isc_eq of unshaken monolayers. The absolute value for the control short-circuit current I_sc is ∼10 μA/cm², with a standard deviation of ∼1 μA/cm². Number of unshaken control monolayers = 20; number of shaken monolayers = 16 at each frequency. Asterisks indicate a p < 0.01 compared to unshaken monolayers. The effect of shaking on ENaC current is already maximal at the lowest frequency tested. The same experiment was performed with monolayers exhibiting higher I_sc, ∼50 μA/cm², with the same results (data not shown).

Loss of the primary cilium is associated with an ENaC current unresponsive to shaking

The ciliary length and Isc_eq measurements clearly showed that cells can sense the mechanical force that is exerted by gentle orbital shaking. To assess whether the cilium is involved in the sensing, the Isc_eq response to shaking was measured after media manipulations that result in resorption of cilia. If the primary cilium is not integral to the sensory pathway, we would expect that deciliated cells would continue to show a decrease of ENaC activity with shaking. If the cilium is instead part of the sensory pathway, we would expect this response to be abolished by deciliation and to reappear as the cilium regrows.

The addition of 4 mM chloral hydrate apically for several days results in the resorption of the primary cilium. This manipulation has been used previously to assess the involvement of the cilium in mechanosensation (5,13). Recent experiments with cholangiocytes indicate that the conclusion about ciliary involvement in mechanosensation is the same whether chloral hydrate treatment or molecular biological manipulations are used to diminish or abolish cilium expression. Although chloral hydrate treatment certainly has more effects on cells than just resorption of cilia, it is not fatal to the cells and does not disrupt the actin network or the integrity of the monolayer, as measured, e.g., by monolayer resistance. The resistance of monolayers immediately before treatment averaged 1.9 kΩ × cm², whereas immediately posttreatment the resistance was measured to be 1.4 kΩ × cm². The microtubule networks fully recover after cessation of treatment. Thus, chloral hydrate represents one method that allows assessing a role of primary cilia in sensation or response. We therefore deciliated confluent mCD monolayers by chloral hydrate treatment and then compared the electrophysiological response to shaking as a function of time after removal of chloral hydrate when the cilium regrows. This type of experiment is possible even though chloral hydrate completely abolishes ENaC current because the ENaC current completely recovers within 24 h after removal of chloral hydrate, whereas the regrowth of the cilium takes considerably longer.

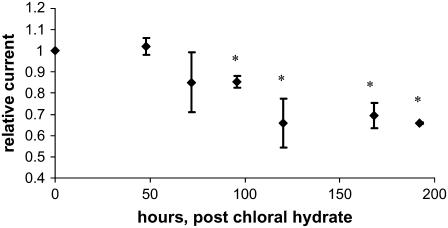
Fig. 5 presents data on the time required for chloral hydrate-pretreated monolayers to recover a mechanosensory state. It plots the Isc_eq ratio of shaken over unshaken monolayers as a function of time. An orbital frequency of 0.9 Hz was chosen as it represents the lower bound of applied force accessible with the current shaker. We verified with imaging of immunostained cells that chloral hydrate treatment abolished the primary cilium (images not shown). Initially, although the cells lack cilia, the monolayers were unresponsive to the applied force, i.e., Isc_eq was the same with and without shaking. All monolayers resumed the pretreatment ENaC current of unshaken monolayers within 24 h of the removal of chloral hydrate. The monolayers that were not subjected to shaking maintained this level of current without change for an additional 168 h. The monolayers that were subjected to orbital shaking maintained this level of current for ∼48 h, at which point the ENaC current began to drop concurrently with the regrowth of cilia.

FIGURE 5.

Recovery of sensitivity of Isc_eq to shaking after treatment with chloral hydrate. Monolayers were treated with 4 mM chloral hydrate for 4 days. After removal of chloral hydrate, some monolayers were placed on the orbital shaker at a frequency of 0.9 Hz and the others served as unshaken controls. Relative current is defined as the ratio of Isc_eq from shaken monolayers to those from unshaken monolayers. Amiloride-sensitive Isc_eq of the unshaken control monolayers recovers to the prechloral hydrate state within 24 h. The response of Isc_eq to shaking recovers with a time constant of ∼100 h. The absolute value for the control short-circuit current I_sc was ∼10 μA/cm², with a standard deviation of ∼1 μA/cm². The resistance of the shaken and unshaken monolayers averaged 1.5 ± 0.6 kΩ/cm² and 1.2 ± 0.4 kΩ/cm², respectively. The number of unshaken monolayers = 5, the number of shaken monolayers = 10. Asterisks indicate a p < 0.01 compared to unshaken monolayers.

As cilia regrow, the cells regained their ability to sense fluid flow, as shown by the decrease in the Isc_eq ratio over time. The time constant for this process is ∼100 h. Our data are in agreement with those of Praetorius and Spring (11), which indicated the primary cilium grows back after 96–120 h after cessation of chloral hydrate treatment.

The chloral hydrate treated monolayers shown in Fig. 5 asymptote to an Isc_eq ratio of ∼0.7. This value is larger than ∼0.4 for untreated monolayers shown in Fig. 4. The reason is currently not known. One possibility could be that there is a difference in microtubule network configuration when microtubules form (or reform) in absence or presence of an applied force. In the experiment in Fig. 4, cilia and the microtubule network formed without exposure to mechanical forces and the cellular response to force was only measured after the cilia had fully formed. In the experiment in Fig. 5, cilia and microtubule network regrew/reformed in the presence of a mechanical force due to shaking. Another possibility is that the mechanotransduction mechanism acquires a different setpoint when it forms in the presence or absence of a stimulus. In any event, these data clearly demonstrate that the presence of an intact primary cilium is required to sense applied fluid flow, at least in terms of ENaC current.

Magnitude of induced fluid flow due to orbital shaking

The fluid flow induced by gentle orbital shaking, particularly when the fluid layer above the cells is only ∼1 mm, constitutes a complex problem. To the best of our knowledge, neither an analytical nor a modeling solution of the flow field is available in the literature. An initial macroscopic analysis of very thin fluid layers during shaking using ink particles showed only azimuthal oscillatory movements that gradually rectified in the direction of rotation. Therefore, we performed particle tracking in situ.

The size of the polystyrene spheres (diameter 5.5 μm) was chosen to balance buoyancy effects and Brownian motion. A camera with a water immersion dipping objective was placed on the orbital shaker and used to image the fluorescent particles in a thin layer of PBS (for more details see Methods). An example of a tracked particle is shown in Fig. 6. During the measurement interval, the particles remained within the focal plane of the objective lens (0.6 μm). Measurements were obtained for both 0.9 Hz and 2 Hz orbital motion, with images taken at the bottom surface (0 μm height) and several different heights above the surface. Several locations were measured to check whether there was radial dependence on the flow pattern, but none was observed.

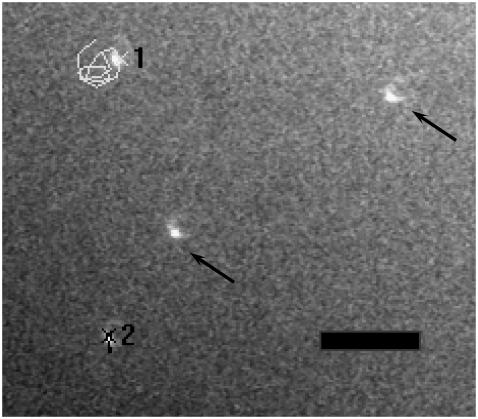
FIGURE 6.

Fluid flow measurements by particle image velocimetry. The figure shows a sample frame of a particle-tracking movie. Only partial track is shown for clarity. Particle “1” is located ∼5 μm from the bottom surface; particle “2” is attached to bottom surface. Scale bar is 25 μm. Arrows indicate other spheres in the field of view. Note that the illumination is from the side, not from below.

The detailed motion of the particles was noisy, most likely due to high frequency jitter from the shaker mechanism and sliding friction over the support block. For example, Fig. 6 shows that a sphere does not execute a precise circular path. However, the paths were approximately circular, with an orbital motion approximately twice that of the shaker motion.

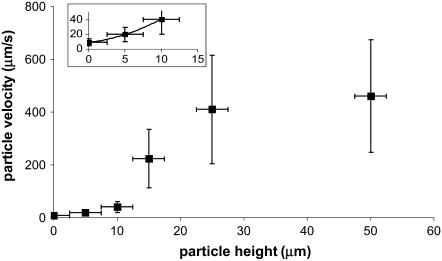
The signal/noise ratio of the data at 2 Hz was sufficiently high for a quantitative analysis of induced fluid velocity. Fig. 7 shows these data. There was some relative motion between the camera and test plate, evidenced by particle tracking images and the fact that our best-fit line does not pass through the origin. This motion does not affect the final results as this residual velocity was subtracted out. Knowing the velocity profile allows us to calculate the applied drag force on the cilium (see Discussion and Analysis). One point to note is that even though the fluid velocity is considerable in the bulk region, close to the bottom surface the velocity is very low. We thus measured a time-averaged velocity (U) profile within the heights of the cilia as

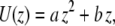(13)

with 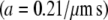and 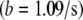and z indicating the height above the apical stationary surface.

FIGURE 7.

Measured particle velocities for 2 Hz orbital shaking as a function of height from the bottom surface. Inset is the region near the bottom surface and shows a quadratic fit.

DISCUSSION AND ANALYSIS

Cellular responses to an applied force

The results present two types of cellular responses to chronic, low frequency orbital shaking, which had not been reported before, to our knowledge: decreased ENaC current and decreased ciliary length. Cilia are clearly required for either sensing or translating the mechanical stimulus in the case of ENaC current. The molecular nature of the sensing and signaling pathways is currently not known. For the effect on ENaC, a potential signaling pathway could involve elevation of cytosolic calcium and activation of MAP kinase ERK1/2; this kinase is activated by mechanical stimulation in other cell types (14) and ERK1/2 activation downregulates ENaC activity in collecting duct cells (15).

Regulation of ciliary length is currently not well understood. The rod outer segment, a modified cilium, actively replaces itself at a rate of ∼1 μm per day (16). This replacement is mediated by shedding of the tip portion of the rod outer segment and import of new material from the cell body. Phagocytosis and digestion of shed parts by an overlying pigment epithelium cleans up the environment. Alternatively, ciliary material is retrieved back into the cell body. Evidence has been accumulating that flagellar length is a regulated process (17), and so it is possible that the primary cilium is subject to a similar type of regulatory pathway. Given that the measured flexural rigidity of microtubules is ∼0.2 GPa (2 × 10⁹ dyn/cm²) (18,19) and the cilium itself is ∼2 × 10⁶ dyn/cm² (20), it is difficult to imagine how the low shear levels applied to the cilium during shaking (see below) would directly result in tip shedding. Rather, it seems more likely that cells can regulate the length of cilia in response to a stimulus via changes in intraflagellar transport. As will be shown below, drag forces on cilia are proportional to ciliary length for a given fluid flow (more precisely, for a given inertial force at the cilium tip). Therefore, length regulation could be used as a variable gain for mechanosensation.

Applied force calculation

The main thrust of this section is to establish an upper limit on the force applied to a cilium during low frequency orbital shaking. We chose orbital rotation amplitudes and rates similar to those used in Kolb et al. (6) and Low et al. (7) so that our force calculations would be applicable to the previously published experiments. Knowledge of the limits of applied forces is important for exploring the physiological roles of cilia in mechanosensation and ciliary pathophysiology in human disease, such as polycystic kidney disease. The calculations were restricted to limit estimates because, as indicated above, no mathematical or modeling solution of the flow field is currently available for the type of geometry present in orbital shaking. We also need to emphasize that the elastic interaction between a cilium and the apical fluid is the subject of much research and a definitive picture has yet to emerge. We assume here, given the smallness of the applied forces, that the cilia do not move. If the cilia either flex or deflect in response to an applied force, then the applied force is even smaller than we calculate here, and so we consider our calculations to provide a maximal value.

The geometry of orbital shaking is shown in Fig. 1 and was discussed in the Theoretical considerations section. At least three different types of mechanical forces due to fluid movement or density differences can be envisioned: Shear on the surface and ciliary membrane, drag on cilium, and buoyancy on cilium. The equations given in the Theoretical considerations will be used in this section to calculate the forces on cilia of mCD cells exposed to orbital shaking of 2 Hz, the frequency at which the fluid velocity was measured. The shaker table has a throw of 3 mm (R = 3 mm). Calculations are carried out for cilia before shaking with a measured length of 2.7 μm (Fig. 3) and a diameter of 0.2 μm.

Buoyancy force

Even if monolayer and fluid co-move (or if the cilium is free to pivot and is freely advected by the fluid), there will be a resultant force on the cilium due to centripetal acceleration. The force density, averaged over time, is given by Eq. 11. The total force on a given body is then the force density integrated over the volume of the body. Estimating the cilium contents as 20% protein (1.4 g/cm³), 5% carbohydrates (1.6 g/cm³), 75% lipids/water (1.0 g/cm³) gives an averaged uniform cilium density = 1.11 g/cm³. For mCD cilia (length 2.7 μm, radius 0.1 μm) shaken at 2 Hz, the buoyancy force amounts to 1.1 × 10⁻⁴ fN. For comparison, the force due to thermal noise (Eq. 12) is 1.6 fN. Thus, it seems unlikely that the only force acting on a cilium is centripetal and that there must be some additional force applied by induced fluid flow.

Drag force

To simplify the calculation, the cilium is considered as rigid cylinder capped by a hemisphere without bending or flexing in response to the flow. Thus, our calculations represent a maximal drag force. The total drag force for cap and cylinder are given by Eqs. 4 and 6, respectively. The velocity profile normal to the cell surface is obtained from the measured values summarized in Eq. 13. The drag force on the cap for the measured ciliary dimensions (length 2.7 μm, radius 0.1 μm), fluid viscosity (μ = 0.637 ± 0.012 cP), and fluid velocity at 2 Hz (Eq. 13) amounts to f_cap = 2.5 fN. The drag on the cylinder is obtained by integrating the force along the length of the cilium, using the velocity U from Eq. 13. The force is f_cyl = 2.7 fN, resulting in a total drag force of f_total = 5.2 fN.

There are several remarkable findings with these calculations: 1), the total force is only ∼3-fold above the thermal noise of 1.6 fN; 2), >50% of the drag force is on the tip of the cilium; and 3), the force is much lower than the 78 fN force that was acutely applied in Liu et al. (21) and yielded a cellular response in the form of increased cytosolic calcium, and it is also lower than the 10 fN that was acutely applied without an observable cellular response (21). Considering that cells had already responded at lower shaking frequencies than the 2 Hz used for the calculations and that the cellular response in terms of decreased ENaC activity was already maximal at 0.9 Hz, our data indicate that mCD cells are sensitive to very low amplitude disturbances. However, it is important to keep in mind that the low force was applied chronically.

Shear stress on apical surface

Fluid flow is also associated with shear stress on the apical cell surface, which can be calculated according to Eq. 1. From Eq. 13, we get 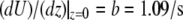so that the apical shear stress 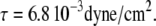The measured cellular cross-sectional area for mCD cells is ∼4.2 μm² (from Fig. 2). If this area is assumed as effective apical surface area, then the shear force on the entire cytoskeleton per cell is ∼2.9 fN. This shear force can be compared to a drag force of ∼5.2 fN located entirely at the ilium. A similar calculation for the shear force at the tip of the cilium reveals a negligible shear force of 0.093 fN (taking into account dU/dz at the cilium tip (Eq. 13) and assuming the surface of a hemisphere).

Comparison with previous experiments

There exists an extensive body of data concerning mechanosensation in primary cilia. Unfortunately, various authors provide different measures of the fluid flow or forces involved so that useful comparisons cannot be done without considerable efforts in estimating the applied forces. For example, one article (20) approximated the velocity profile along the cilium either as a linear function of height or as constant over the height, whereas others (5,13) simply provide macroscopic flow parameters and do not calculate a drag force at all. Others calculate the drag force using an “effective medium” treatment (9,21). In no case did any previous drag calculation take into account the tip of the cilium.

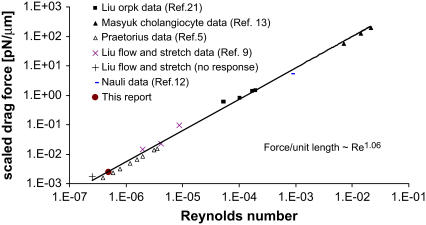
To explore sensitivity of ciliary mechanosensation, the Reynolds numbers for the fluid at the cilium tip were calculated from published experiments and are plotted against the total drag force on the cilium normalized per unit length (Fig. 8). For those experiments in which the fluid velocity had not been measured at the level of cilia, Poisseuille-type flow was assumed and the radial fluid velocity profile calculated from the volumetric perfusion flow rate and the physical dimensions of the tubule, channel, or duct preparations. The Reynolds number (Eq. 5) is the ratio of inertial to viscous forces of the fluid, and, because the viscous force against a cilium (= fluid viscosity/cilium radius) is essentially identical in all experiments, the Reynolds number is proportional to the inertial force (or momentum density) of the fluid acting on cilia. Fig. 8 reveals that the applied inertial forces in previous and current experiments varied in magnitude by ∼5 orders. This range reflects differences in the fluid velocity among the published experiments. Cellular responses are seen down to Reynolds numbers of 4 × 10⁻⁷. Interestingly, differences in force level to elicit a cellular response (elevated cytosolic calcium) are observed between MDCK (5) and rabbit renal cortical collecting duct chief cells (9). No response was observed at a Reynolds number of 3 × 10⁻⁷ in rabbit cortical collecting duct cells when the total drag force was ∼4.3 fN (ciliary length = 2.5 μm), whereas MDCK responded down to 4 × 10⁻⁷ for a total drag force of ∼12 fN (ciliary length = 8 μm). This indicates that a cellular response is dependent on the total force acting on a cilium.

FIGURE 8.

Range of inertial force at cilium tip and drag force in published experiments. The log-log plot shows microscopic Reynolds numbers at cilium tip against the total drag force on the cilium normalized for length (scaled drag force). The Reynolds number is as defined in Eq. 5, assuming viscosity and density of water at the appropriate temperature. If the velocity was not directly measured, it was calculated assuming Poiseuille flow within the tubule or channel. The drag force includes the contributions from both cilium cap and cylinder, i.e., sum of 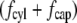(Eqs. 3 and 6 with 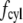integrated over the length of the cilium). The scaled ciliary drag force = 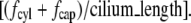The data are from published experiments as indicated by the reference. (+) An experiment in which no cellular response (elevation of cytosolic calcium) was observed. In that experiment, the matched positive controls with a cellular response (elevated cytosolic calcium) are designated by the symbol “×”.

Fig. 8 also reveals why cilia may be so sensitive to mechanosensation: The scaled drag force versus Reynolds number collapses to one line under the different experimental conditions, indicating that the total drag force on a cilium is proportional to the cilium length for a given fluid inertial force at its tip. The drag force is also proportional to the fluid velocity at the cilium tip, and this velocity increases linearly with distance from the wall for Poiseuille flow and ciliary lengths much smaller than tubule diameter (see Appendix for derivation and limits). Therefore, the total drag force is proportional close to (cilium length)². Furthermore, the thermal noise for ciliary movements is inversely proportional to ciliary length (Eq. 12), so that the ratio (total drag force)/(thermal noise) is proportional to (cilium length)³. In other words, increasing ciliary length increases the signal/noise ratio by length close to the power of 3. These considerations provide a rationale for why cells would develop slender projections on their surface to sample fluid mechanical forces.

As discussed earlier, at least half of the drag force on cilia is exerted on the cap. Thus the long stalk of cilia can be seen as a structure to increase the sensitivity of ciliary mechanosensation by moving the cap into a region of greater fluid velocity and hence exposure to a greater drag force.

CONCLUSION

The primary finding of interest here is that the cells respond to levels of an applied force that is of the same order of magnitude as thermal noise. The calculated drag force on the cilium at a shaking frequency of 2 Hz is much greater than the centripetal buoyancy force on the cilium and slightly greater than the calculated shear force on the entire cellular cytoskeleton. Under chronic conditions, cells may be able to sense even lower force levels, as a maximal cellular response in terms of a decreased ENaC current was already seen with the lowest applied shaking frequency of 0.9 Hz. The drag force on the ciliary cap by fluid flow amounts to slightly more than half of the total force, and the total drag force in all published surveyed experiments on epithelia is shown to be proportional to cilium length. These findings indicate that cilia can sense very low force levels whereby ciliary length appears as a key parameter determining the drag force experienced for a given fluid volume flow (or Reynolds number at the cilium tip). These considerations suggest that cells may adjust the length of cilia to change their sensitivity.

APPENDIX: SCALING RESULTS

In a tube or channel with radius R, the Poiseuille flow profile is given by

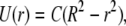(A1)

where U(r) = fluid velocity at point r and r runs from the center to the wall. C is a constant for a given set of conditions (maximal velocity, fluid viscosity, and density, R). Changing coordinates to z that run from the wall to the tip of the cilium (assuming a position normal to the wall and without bending), z = R − r, we have

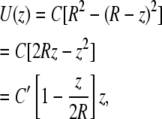(A2)

where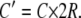

For ciliary heights much less than the tubule diameter (z M 2R), the term in brackets is ∼1, and so the velocity at the tip is linearly proportional to the length. For longer cilia, the velocity increases sublinearly.