Dynamics of Magnetotactic Bacteria in a Rotating Magnetic Field

Abstract

The dynamics of the motile magnetotactic bacterium Magnetospirillum gryphiswaldense in a rotating magnetic field is investigated experimentally and analyzed by a theoretical model. These elongated bacteria are propelled by single flagella at each bacterial end and contain a magnetic filament formed by a linear assembly of ∼40 ferromagnetic nanoparticles. The movements of the bacteria in suspension are analyzed by consideration of the orientation of their magnetic dipoles in the field, the hydrodynamic resistance of the bacteria, and the propulsive force of the flagella. Several novel features found in experiments include a velocity reversal during motion in the rotating field and an interesting diffusive wandering of the trajectory curvature centers. A new method to measure the magnetic moment of an individual bacterium is proposed based on the theory developed.

INTRODUCTION

Most bacteria respond by active motility to the vast range of environmental signals like concentrations of nutrients, toxins, oxygen levels, pH, osmolarity, intensity, and frequency of the light, magnetic field, etc. (1). It is a challenge to describe an integral behavior of bacterial population through individual active motions of the single cells and to find the relationship in the behavior of individuals with the characteristics of the population. Study of the individual movements of single cells is an obligatory prerequisite for such an approach, and magnetotactic bacteria may serve as a convenient model taking into consideration the possibility to control the magnetic field as one of the major factors influencing their motion.

Since their discovery in the early 1970s (2), magnetotactic bacteria have been intensively studied for more than 30 years. These bacteria assemble linear arrays of nanometer-scaled ferromagnetic particles called magnetosomes that are synthesized in the periplasmic space and internalized in the cytoplasm where chains of magnetosomes are stabilized by interaction with filaments analogous to eukaryotic cytoskeletal filaments (3–5). Orientation along the earth's magnetic field lines is thought to enable these bacteria to navigate to environments with suitably low oxygen concentrations. Recently the genes that encode the biochemical machinery responsible for synthesis of magnetosomes and their alignment into chains along the filamentary cytoskeleton-like structures of the bacteria have been partially identified and sequenced (6,7).

One of the well-characterized magnetotactic microorganisms is microaerophilic alphaproteobacterium Magnetospirillum gryphiswaldense, which contains crystals of magnetite Fe₃O₄. For this bacterium, a cultivation protocol in an oxystat fermentor has been elaborated, allowing one to study the physiology of magnetosome biomineralization (8) or to produce magnetite nanoparticles for possible nanotechnology applications (for review, see (9)).

Magnetotactic bacteria provide their motility through flagella, the nanoengine that is the key factor for the magnetotaxis (10). They respond to a number of environmental signals, where the responses to the oxygen concentration or oxygen gradient were described in the literature (11–13). There is the difference in the morphology of flagella between species, i.e., magnetotactic spirilla usually have two distal flagella, whereas magnetic cocci, the most abundant morphotypes in nature, have bundles of flagella (2).

Important information about the motion of magnetotactic bacteria can be obtained from the study of their behavior in time-dependent magnetic fields. The U-shaped trajectories of bacteria resulting from switching the direction of the magnetic field have been used to measure their magnetic properties (14). Rotating magnetic fields can be used to determine the critical frequency below which a rotation of single magnetic bacterium is synchronized with the field (15,16). This allows measurement of the ratio of the magnetic moment of the bacterium to its rotational drag coefficient.

In the previous study (17), the dynamics of magnetotactic bacteria under the action of a rotating magnetic field was theoretically investigated, and different trajectories with rather peculiar shapes were predicted depending on the frequency of the rotating field.

Here we report the results of experimental observations of the motion of the magnetotactic bacterium M. gryphiswaldense in rotating magnetic fields with different strengths and frequencies and interpret these motions in the framework of existing models (17) for an active magnetic particle. Although in general the behavior of the bacteria corresponds to what is expected from the theoretical model, several unanticipated phenomena were found in a rotating field, namely 1), a reversal of bacterium motion in a rotating field; 2), the possible escape into the third dimension out of the plane of a rotating field; and 3), a rotational Brownian motion around the steady state in a rotating field, as well as other features. For their interpretation, corresponding models are proposed.

THEORETICAL MODELS

The simplest model that might be proposed for a magnetotactic bacterium is a rigid magnetic dipole 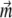coupled to the direction of its long axis 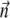along which the self-propelling motion of a bacterium occurs. The angular velocity of the bacterium 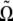is found from the viscous and magnetic torque balance, and the equation of the motion for its long axis reads

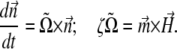(1)

Here ζ is the rotational drag coefficient of the bacterium. Applying Eq. 1 to a field 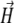rotating in the x,y plane with angular frequency ω (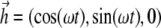( 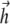is the unit vector along the field direction), gives

(2)

Here 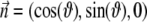and it is assumed that motion of the long axis takes place in the plane of a rotating field. If a lag β = ωt − ϑ of the bacterium axis (with the respect to the field direction) is introduced, then, from Eq. 2, follows

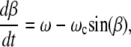(3)

where ω_c = mH/ζ is the critical frequency below which synchronous motion of the bacterium and the field takes place. If ω < ω_c, Eq. 3 has a steady solution with β determined by sin(β) = ω/ω_c. If ω > ω_c, Eq. 3 has only a periodic solution:

(4)

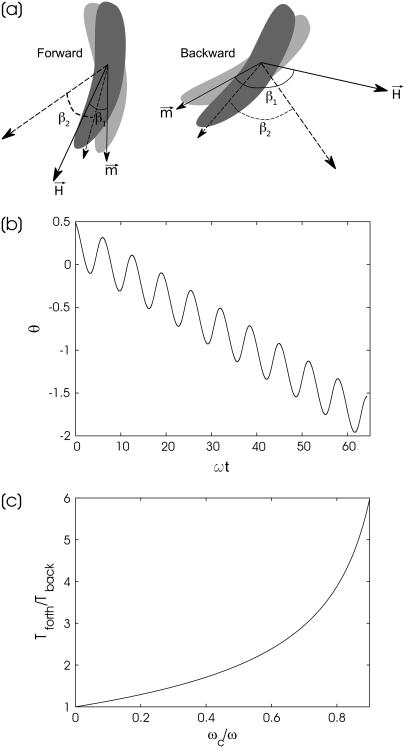
Angular velocity of the bacterium is ω_c sin(β). Since β changes with time in the asynchronous regime, a characteristic back-and-forth motion of the magnetic dipole takes place, as shown schematically in Fig. 1 a. Corresponding to its change of orientation, angle ϑ is illustrated in Fig. 1 b.

FIGURE 1.

Angular motion of bacterium. (a) Sketch of the relative motion of a long axis of a bacterium and a rotating field at ω > ω_c. (b) Back-and-forth motion of long axis of a bacterium quantified by measurement of the angle between the bacterial axis and a reference direction for a period consisting of multiple rotations of the field (ω_c/ω = 0.25). (c) Ratio of times that the bacterium rotates forward T_forth and backward T_back as a function of the ratio of a critical rotation frequency and the field rotational frequency ω_c/ω.

The time interval during which the magnetic moment and the field rotate in the same direction is followed by a shorter time interval when the magnetic moment and the field rotate in opposite directions. The ratio of the time intervals for forward (0 ≤ β ≤ π) and backward (π ≤ β ≤ 2π) motion as a function of ω_c/ω (calculated according to the relation T_forth/T_back = (1 + a)/(1 − a), where 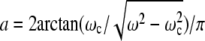), is shown in Fig. 1 c. This dependence is used in the next section to determine the critical frequency of a bacterium with one end attached to the microscope cover glass. It should be remarked that Eq. 4 is well supported by experimental observations of the motion of ferromagnetic particles under the action of a rotating field, which has interesting biological applications (18).

In the simplest model, the velocity of a bacterium is assumed to be in the direction of its long axis. Since the bacterium is not axisymmetric, there should be a velocity component perpendicular to its long axis but since a bacterium rotates during its motion this does not contribute to the overall shape of the trajectory. As the result, the trajectory of the bacterium is found from the equations

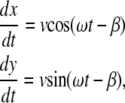(5)

where β is given by the solution of Eq. 3. Since the velocity of a bacterium v is along the tangent to the trajectory, it is easy to derive its curvature

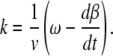(6)

In a steady case of a synchronous motion dβ/dt = 0, and for the curvature we have

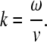(7)

This result can be easily obtained as the ratio of the perimeter of a circle along which a bacterium moves in the synchronous regime and the period of the field. Equation 7 shows that the radius of a circle diminishes with the frequency of the rotating field, as it should, since in a constant field the trajectory of a bacterium is a straight line. The linear dependence of the curvature of the trajectory on the frequency allows us to directly determine the velocity of a bacterium's motion, as illustrated in the next section.

Although reversals of bacterium velocity, as experimental observations show, is not a frequent event nevertheless it can happen. At each such reversal, the center of the circle along which a bacterium moves makes a finite displacement. Since these reversals can take place at random times, the reversals lead to a curious diffusion of the particle trajectory curvature center. Assuming that the reversal of the bacterium is a random Poisson process with a probability of reversal per unit time interval given by λ exp(−λt), the derivation of the corresponding diffusion coefficient is straightforward. The result reads as

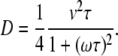(8)

Here τ = 1/λ is a characteristic time of the reversal event. In the case ω = 0, Eq. 8 coincides with the expression given in Berg (19) for the diffusion coefficient of a bacterium such as Escherichia coli in two dimensions. Experimental observation of the described diffusion process is discussed in the next section. Confirmation of the frequency dependence of the diffusion coefficient given by Eq. 8 remains a challenge for future experimental work.

Another issue that should be discussed here is the influence of rotational Brownian fluctuations. The fluctuations of the bacterium orientations around the steady state in a rotating field allow us to determine the magnetic moment of the bacterium as shown in the next section. The Boltzmann principle for the distribution of the bacterium orientation angle around the steady state P reads

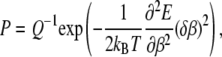where 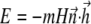is the energy of a bacterium in a rigid dipole approximation when dipole interactions fix the magnetic moment along the long axis of a bacterium. As a result, the mean quadratic angular fluctuation is

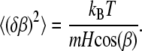(9)

In an asynchronous regime, it follows from Eqs. 3 and 6 that

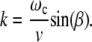(10)

Thus in this regime there are parts of a trajectory with a negative curvature. A change of the sign of the curvature in this case reflects the back-and-forth motion of the magnetic moment of a bacterium. This is shown for the case 2T_o = 25 T_f in Fig. 2. Here 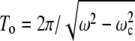is the period of the orientational motion and T_f = 2π/ω. We note that, during part of the trajectory, the magnetic moment and field move toward each other. At a given condition, the periods of orientational motion and a field are commensurate, and the trajectory of the bacterium is a closed curve. In the general case when the ratio of periods is an irrational number, a bacterium covers a definite region of space by an unclosed curve but contains parts of a trajectory with a negative curvature. Experimental observation of paths with negative curvature is described in the next section.

FIGURE 2.

Negative curvature during backward motion of the long axis of a bacterium under conditions where the period of orientational motion T_o is greater than the period of the rotating field T_f (2T_o = 25T_f). Dashed arrows are along the field direction, solid arrows are along the direction of the long axis of the bacterium.

The theoretical models described so far are based on the assumption that the motion of the bacterium takes place in the plane of the rotating field. This should happen if the magnetic moment of the bacterium is rigidly connected with its axis. This is true if the external field is much weaker than the internal anisotropy field, which holds the magnetic moment along the preferred axis of the bacterium. In the case of a chain of magnetosomes, the anisotropy field arises from the magnetodipolar interaction. Considering a chain of magnetosomes as a cylinder of infinite length, its energy E_a can be estimated as

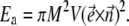Here 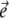is the unit vector along the direction of the magnetic moment of the magnetosomes, which is assumed to be the same for all magnetosomes, V is the total volume of the magnetosomes, and M is their saturation magnetization. As a result, the energy of the chain of magnetosomes in an external field reads

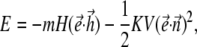(11)

where K = 2πM² is an effective anisotropy constant of the chain of magnetosomes. The equation of the rotational motion of a bacterium in this case reads

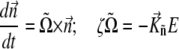(12)

at the condition of equilibrium with respect to orientation of the magnetic moment in a bacterium

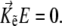(13)

Here 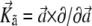is the operator for infinitesimal rotations. This model for the description of single domain particles of magnetic colloids was introduced in the late 1960s in Caroli and Pincus (20). It was found then that at 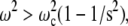the set of equations possess a steady solution when the axis of the particle 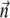(here the long axis of the bacterium) processes around the normal to the plane of a rotating field with its inclination γ given by the relation

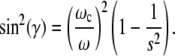(14)

Here s = KV/mH is the ratio of the internal anisotropy field and the external field, and in the case of a chain of magnetosomes, can be estimated as 2πM/H. Since the magnetosomes of M. gryphiswaldense contain Fe₃O₄ with M = 500 G, then this ratio for an external field H = 10–20 Oe is large. Nevertheless, the solution of Eqs. 12 and 13 shows that at ω > ω_c, a bacterium eventually should escape in the third dimension perpendicular to the plane of the rotating field. The characteristic features of this escape may be found by numerical solution of Eq. 12 with constraint Eq. 13, which makes the problem rather difficult. An efficient approach for the numerical solution of Eqs. 12 and 13 is proposed in Cēbers, A., T. Cirulis, and O. Lietuvietis, unpublished. According to this report, the constraint Eq. 13 is put in the form

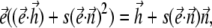(15)

which shows that vectors 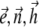are in the same plane. Equation 15 allows us to obtain a fourth-order polynomial equation for 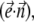which is solved together with ODE for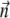

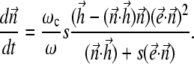(16)

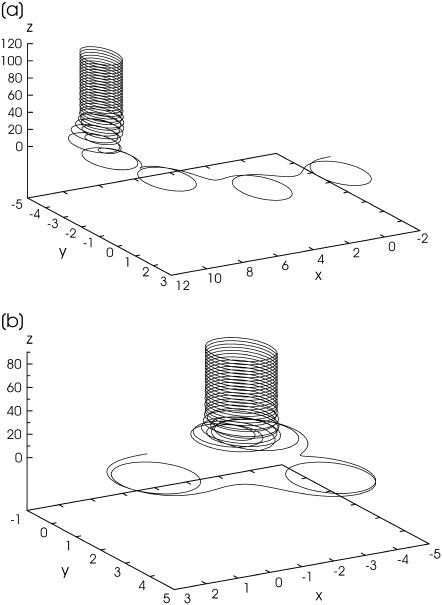
Numerical solution of Eq. 16 confirms that at 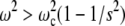the characteristic features of the bacterium motion in the asynchronous regime, shown in Fig. 2, may be observed as transients. This is illustrated by three-dimensional trajectories of the bacterium shown in Fig. 3 a (sin(γ) = 0.85; s = 10) and Fig. 3 b (sin(γ) = 0.9; s = 10)). In real experiments, the observation of three-dimensional trajectories of the bacterium is a challenge for future work. Some indications of the possible transition to the three-dimensional regime of the bacterium motion at rather large frequency of the rotating field are given in the next section.

FIGURE 3.

Simulated three-dimensional motion of bacterium. In these simulations, the bacteria execute several loops in the x,y plane in which the field rotates and then escape into the third dimension out of the plane of the rotating field as they continue to move in circular trajectories. (a) sin(ϑ) = 0.85; s = 10; (b) sin(ϑ) = 0.9; s = 10.

EXPERIMENTAL METHODS

Cultures of M. gryphiswaldense were generously provided by D. Schuler and cultivated in standard medium according to Heyen and Schuler (8). All chemicals of analytical grade were purchased from Sigma (St. Louis, MO). Cultivation of M. gryphiswaldense was carried out under microaerobic conditions in 15-ml tubes sealed by butyl rubber stoppers and saturated with a 1:99 oxygen/nitrogen mix (AGA, Riga, Latvia) before autoclaving. The culture was inoculated using 2-ml sterile syringes by injection through the stopper. Initial cell density after inoculation was ∼10⁶ cells/ml, and the culture was incubated for 48 h at 25°C without agitation.

Samples for phase-contrast microscopy were taken by sterile 2-ml syringe and placed between two glass slides separated by 0.028-mm-thick double-stick tape with an aperture cut in the center. An AC magnetic field surrounding the field of view was created by four water-cooled coils with a variable power supply giving a rotating field of 0–20 Oe in a frequency range 0–5 Hz. The trajectories at room temperature were captured by a Zeiss Universal microscope (Carl Zeiss, Oberkochen, Germany) and a JAI CV-S3200 video camera (JAI, Copenhagen, Denmark) scanning at a rate of 25 frames per second. Tracking of trajectories from video frames was carried out by adapting the MatLab code (22) for our system.

Samples for electron microscopy were adsorbed on carbon-formvar copper grids and stained with 1 percent uranyl acetate aqueous solution (pH 4.5). The grids were examined by a JEM-100C electron microscope (JEOL, Tokyo, Japan) at an accelerating voltage of 80 kV.

EXPERIMENTAL RESULTS

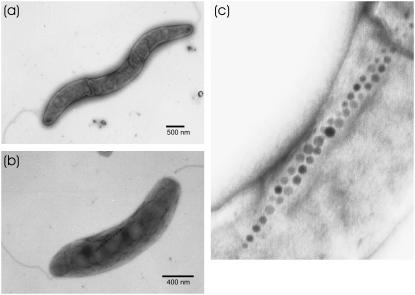
Electronmicrographs of magnetotactic bacterium are shown in Fig. 4, a–c. These images show distinctly that the bacteria have two flagella and contain a chain of magnetosomes. Due to delayed cytokinesis the bacterium frequently has an elongated helical shape as may be seen by a comparison of Fig. 4, a and b, but even when elongated it contains linear arrays of magnetosomes. Fig. 4 a shows an interesting example of two single filaments aligned next to each other, presumably before cell division. The alignment of the magnetic moments is evidently parallel, as judged by the half-staggered arrangement of the individual magnetosomes.

FIGURE 4.

Electronmicrographs of M. gryphiswaldense. Due to delayed cytokinesis a bacterium can have an elongated helicoidal shape (a) as well as the slightly curved shape of the single bacterium shown in panel b. Half-staggered chains of magnetosomes and two flagella can be distinctly seen in panel a. Electronmicrograph of M. gryphiswaldense with single chain of magnetosomes, in which two flagella can be distinctly seen (b). Enlarged view of the region with doubled number of magnetosome chains (c).

How the magnetic particle chains are split between bacteria during the cell division is not yet known. Experimental evidence occasionally obtained by observing the bacterium motion in a rotating magnetic field shows that, immediately after division, both daughter cells continue to rotate in rotating field; one cell possesses both an active flagella and magnetosomes, since it moves along the circular trajectory. At the same time, the second daughter cell rotates in a fixed place, indicating the absence of active motion (or flagella) but the presence of magnetosomes. This observation shows that during cell division the magnetic material is divided between the cells. This explanation is supported by Fig. 4 c, showing two magnetosome chains that are already duplicated but not segregated before the division of bacterium. Most probably, the number of magnetosome chains is doubled before the division event.

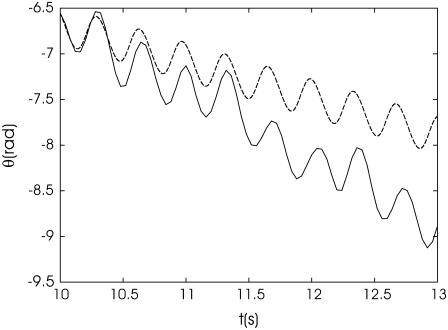
In most samples, some of the bacteria are attached to the cover glass of microscope, and these provide the possibility to observe the back-and-forth orientational motion of a bacterium in a rotating field. An example of the experimentally determined dynamics of the long axis of a bacterium is given in Fig. 5 (the field H = 14 Oe with frequency ν = 3 Hz is rotating clockwise). The ratio of the forth-and-back motion times for data shown in Fig. 5 is ∼1.30. Fitting this ratio to the data in Fig. 1 c gives ω_c/ω = 0.205. A theoretical curve calculated for this value of ω_c/ω = 0.205 and frequency ν = 3 Hz is shown in Fig. 5 by dashed line. It shows deviation from the experimental curve. Since the mean quadratic deviation in time interval 3 s of orientation angle calculated according to the rotational diffusion coefficient of a bacterium 7.8 × 10⁻³ s⁻¹ is 0.21, then, presumably, the thermal fluctuations are not responsible for disagreement of the experimental and theoretical data.

FIGURE 5.

Orientation angle of a long axis of a bacterium during its back-and-forth motion. The value θ is the angle between the long axis of the bacterium and the horizontal axis of the image. The magnetic field rotates clockwise. Theoretical dependence of θ at ω_c/ω = 0.205 is shown by the dashed line. H = 14 Oe; ν = 3 Hz.

If the magnetic moment of the bacterium is known, the ratio of ω_c/ω can be used to calculate the drag coefficient of the bacterium and its rotational diffusion coefficient. For a bacterium with a magnetic moment of 1.3 × 10⁻¹² emu, corresponding to 40 magnetosomes with magnetite cores of size 50 nm, the rotational drag coefficient of the bacterium with an attached end is 4.74 × 10⁻¹² erg/s, a value larger than the rotational drag coefficient of 2.4 × 10⁻¹² erg/s for an ellipsoid with long and short axes 4 μm and 0.5 μm, respectively, in water. This difference is reasonable, since the bacterium is attached to the cover glass and its rotational drag coefficient accounts for both the motion of its center of mass and its interaction with the glass surface. It should be remarked here that, during the event shown in Fig. 5, an untethered nonmotile cell was rotating with the frequency of a rotating field, as should be expected since the critical frequency of the untethered cell is larger due to the smaller rotational drag coefficient in comparison with a tethered cell.

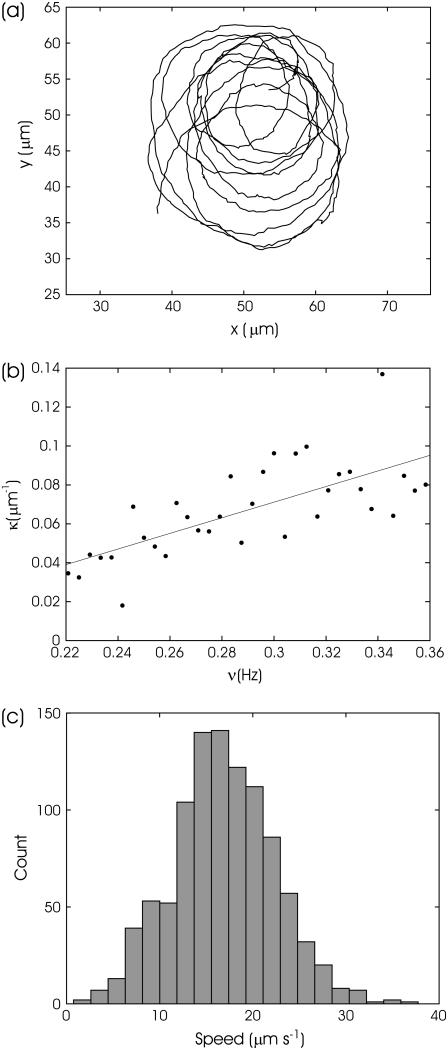
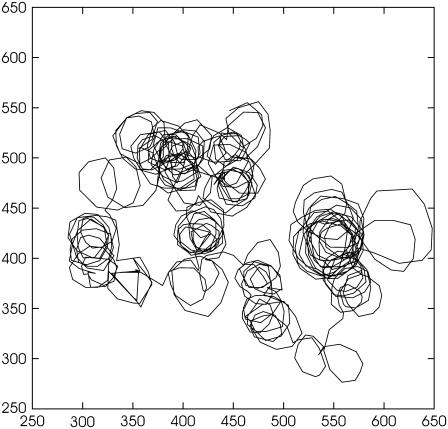
To determine how the motion of a bacterium depends on the parameters of the rotating field, single bacteria were followed as the frequency of the rotating field was slowly altered. Fig. 6 a shows the tracked trajectory of a bacterium for 40 s in a rotating 14 Oe field as its frequency changes from 0.2 to 0.367 Hz. The dependence of the trajectory curvature on the field rotation frequency is obtained after fitting the data by smoothing splines and is shown in Fig. 6 b. Despite their somewhat noisy character, the data clearly show an increase of curvature with an increase in the frequency of the rotating field. A linear fit of the data in Fig. 6 b for the velocity of the bacterium gives 15.6 μm s⁻¹, a value that is close to the value 16.9 ± 5.3 μm s⁻¹ obtained by directly tracking the displacement of the bacterium between frames. A histogram of the velocity distribution for the trajectory shown in Fig. 6 a is given in Fig. 6 c. Since its width corresponds to the error in determining the displacement of a bacterium between video frames, 4.5 μm s⁻¹, there is no evidence in this case for a significant change in velocity of the bacterium during the time interval shown. Velocity reversal events are not observed for the trajectory shown in Fig. 6 a.

FIGURE 6.

Tracking of bacterium motion. (a) Trajectory of magnetotactic bacterium in a rotating field. H = 14 Oe. The frequency at the start of the measurement is ν = 0.2 Hz and ν = 0.367 Hz at the end, slowly increasing at a rate of 0.0042 Hz/s. (b) Dependence of trajectory curvature on the frequency of the rotating field. (c) Histogram of the bacterium velocity distribution obtained by tracking its displacement between video frames. The width of the distribution is close to 1 pixel error at the tracking position of the bacterium 4.5 μm s⁻¹.

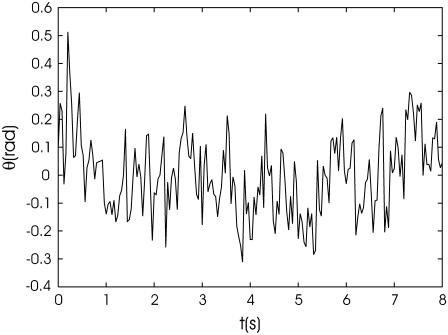
Tracking of the orientation of the bacterium during its motion along the circular trajectories shown in Fig. 6 a allows us to determine the contribution of thermal fluctuations to its orientation in a rotating magnetic field. A linear fit of the time dependence of the bacterium orientation angle for an 8-s-long time interval when the frequency is 0.2 Hz gives ϑ = 1.35t + const, which is close to the expected value of ϑ = 1.26t + const for a synchronous regime of motion. Extracting this regular variation of the orientation angle from the tracked orientations of the bacterium, we obtain the data shown in Fig. 7. The error of orientation angle determined by MatLab routine (22) is estimated as Δd/L, where Δd is error in bacterium width ∼1 pixel but L is the bacterium length of ∼20 pixels. An estimate of the mean quadratic deviation 〈(δϑ)²〉 for the data shown in Fig. 7 gives 0.14. This value is considerably larger than the error estimated above. The 〈(δϑ)²〉 value agrees with the expectation according to Eq. 8 if m cos(β) = 2.04 × 10⁻¹⁴ emu. For a reasonable value of the magnetic moment of a bacterium m = 10⁻¹³ emu, this result gives cos(β) = 0.2. Since the direction of the magnetic field is not registered in the present experiments, we were not able to determine the value of the angle β directly.

FIGURE 7.

Fluctuations of the orientation of a bacterium around its steady state in a rotating magnetic field.

If the direction of a magnetic field is known, then a measurement of the orientational fluctuations of a magnetotactic bacterium is a novel method to determine the magnetic properties of the single bacterium. For this, a rotating sample in a constant field may be used or the direction of the magnetic field should be fixed electronically. In this case the magnetic moment can be directly determined from the measured orientation of the bacterium with the respect to the field by using Eq. 8. A great advantage of this approach is that, in this case, knowledge of the rotational drag coefficient is not necessary.

We should remark here that, at present, different methods for the measurement of the magnetic moments of the magnetotactic bacteria have been proposed. Due to the finite orientational time of a bacterium at a field polarity change, the bacterium makes a characteristic U-shape trajectory (14,23). Its parameters allow one to determine the ratio of the magnetic moment of a bacterium to its rotational drag coefficient. By this method the magnetic moment m = 6.1 × 10⁻¹³ emu of the M. magnetotacticum (23) and magnetotactic cocci 2.4–54 × 10⁻¹² (14) have been determined. We should draw the reader's attention to the interesting and not frequently referenced article by van Kampen (24), in which the characteristic time of U-turn is calculated by a singular perturbation theory.

In Kalmijn (25), the magnetic field strength dependence of the migration velocity along the field lines caused by orientational thermal fluctuations of a bacterium is used for the measurement of its magnetic moment. The values of m found for freshwater magnetic bacteria are 6–7 × 10⁻¹³ emu.

Among the other methods used to determine the magnetic moment of a single bacterium, magnetic atomic force microscopy should be mentioned (26)—which, for vibroid cells of the strain MV-1 (27), gives m = 4 × 10⁻¹³ emu.

Several methods use the ensemble of magnetic bacteria to extract the properties of a single bacterium, light scattering (28), and superconducting quantum interference device microscopy (29). The latter method is based on measurements of magnetic field fluctuations generated by an ensemble of magnetic bacteria and the dependence of the orientation relaxation time of a bacterium on the magnetic field strength, an effect that is well known from studies of magnetic colloids (for general review see (30)). This method determines a value of magnetic moment of M. magnetotacticum of 3 × 10⁻¹³ emu (29). This value is close to that determined earlier for A. magnetotacticum 2.2–2.7 × 10⁻¹³ by light scattering (28).

We are not aware of magnetic moment measurements of M. gryphiswaldense, except indirect estimates based on the number of magnetosomes in the cell, which may be as large as 60 (31). A similar estimate for M. magnetotacticum m = 10⁻¹² emu is given in Lee et al. (32). Application of the method described here for the measurement of the magnetic moments of an individual M. gryphiswaldense bacterium will be considered in future work.

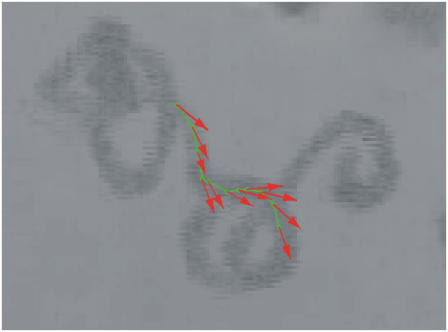
As illustrated above, an essential feature of the asynchronous regime is the existence of paths with a negative curvature. Fig. 8 shows an observation of such an event during a 4.5-s-long trajectory in a rotating field H = 10 Oe with frequency ν = 0.8 Hz. This event allows us to estimate the upper bound of the magnetic moment of the bacterium, if for the rotational drag coefficient we take its value for an ellipsoid with long and short semiaxes 4 μm and 0.5 μm, respectively, to be 2.4 × 10⁻¹² erg/s. We get m < 1.2 × 10⁻¹² emu, which is in reasonable agreement with data referenced above.

FIGURE 8.

Path with a negative curvature in a rotating field. A bacterium's long axis direction is along the red arrow. The magnetic field rotates clockwise. On a part of the trajectory with a negative curvature, the long axis and magnetic field rotate in opposite directions. H = 10 Oe and ν = 0.8 Hz.

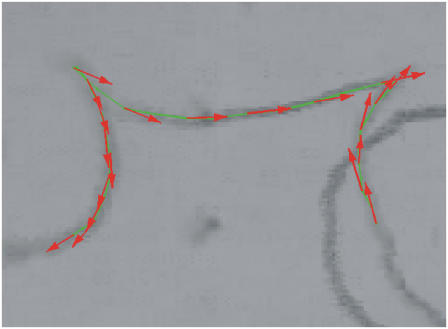
Although reversals of bacterium motion seem to be quite rare events, as suggested by the data in Fig. 6, such reversals are occasionally observed in our samples. One such event is shown in Fig. 9 (H = 10 Oe;ν = 0.65 Hz). Tracking the orientation of the long axis of the bacterium and its position allows us to demonstrate that the bacterium changes direction of its motion at particular times corresponding to abrupt switches of the trajectory curvature center. Indeed, although at this moment both the long axis and magnetic moment aligned along it continue to follow the direction of magnetic field, the trajectory forms cusps. This finding may be explained only by an abrupt change in the direction of the velocity of the bacterium with respect to its magnetic moment, i.e., a bacterium with two flagellar motors reverses. It is essential to remark that after reversal, the speed of the bacterium changes significantly as seen in Fig. 10 where the distribution of bacterium velocities is shown for several reversal events. At each reversal the velocity switches between lower and higher mean values that can also be detected by the change in the curvature of the trajectory at each reversal.

FIGURE 9.

Reversals in a rotating magnetic field. H = 10 Oe and ν = 0.45 Hz. The field rotates clockwise. Two reversal events can be seen. Although the long axis of the bacterium continues to rotate clockwise at the both vertices of the trajectory, due to the reversal of the motion of the bacterium, the trajectory has cusps. An increase in the curvature radius of the trajectory after reversal can also be noticed.

FIGURE 10.

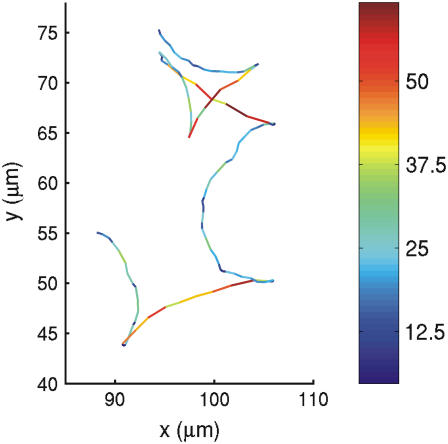
Bacterial velocity distribution at reversals. Consecutive changes from lower to higher and higher to lower speeds can be noticed at reversal events. H = 10 Oe and ν = 0.4 Hz. The trajectories shown at the left are color-coded for speed as quantified by the calibration scale at the right. Numbers correspond to the values of velocity in μm/s.

Theoretically, two mechanisms are possible to explain the phenomenon. One is that the bacterium may use one of two flagella to move forward and the second to move backward. The second hypothesis is that the flagellar engines may change their direction of the rotation causing the reversal of the movement direction of the bacterium. At this stage, it is worthwhile to make some guesses about the reasons for this phenomenon, considering the knowledge accumulated on magnetotactic behavior of the bacteria. Reversals of two magnetotactic bacteria, namely 1), marine coccus MC-1, which has two flagellar bundles; and 2), M. magnetotacticum were observed (12). Two different models, to explain the bacterial band formation in an oxygen gradient and its behavior at a change of polarity of the field, have been proposed. According to the first one, the cocci switch their rotary motors at two critical oxygen concentrations, whereas the second model supposes that spirilla use the oxygen gradient sensor to switch the engine with some delay. A number of motional effects were observed for other magnetotactic prokaryotes caused by oxygen gradients, and/or redox potential (13,33,34). Particularly, very specific reversals of multicell prokaryotic organism, MMP, with significant acceleration during backward movement were observed when it reached an extreme oxygen concentration (33). All these circumstances are characterized by the nonuniform environment, e.g., gradients of oxygen/redox potential etc.

Since in our experimental conditions bacteria were placed in a uniform environment we believe that the reversals are not caused by any significant gradient of the putative signal. Therefore, one may propose that random back-and-forth orientational “investigational” motions may be helpful for these bacteria in certain physiological conditions to look for additional niches for successful colonization.

The mechanisms of the reversal movement are unclear. Some ways to solve the problem one can find in Berg (35), where polymorphic transformations of flagella were studied for E. coli. It was shown that at the change of the direction of rotation the flagella underwent transformation from left-handed helices rotating counterclockwise (normal waveform) to right-handed helices rotating clockwise. Since the direction of the propelling force at this transformation remains the same, this mechanism cannot be responsible for the observed velocity variation at the reversal. However, the fact that flagella can rotate in opposite directions motivates the analogous study of magnetotactic bacteria.

Nevertheless, since the change of the direction and value of velocity at a reversal of the rotary motor is observed for monotrichous bacteria (36) we may assume that the variation of speed at reversal could be connected with some change of flagellar helix pitch at the change of the rotation direction. This possibility is suggested by the results of Kim and Powers (37) where the mechanical deformation of a helix subjected to rotational flow is considered. Since the sign of helix deformation in rotational flow depends on its handedness (37), this hypothesis at least qualitatively corresponds to observations. Nevertheless, we should mention unpublished data by H. Berg referenced in Kim and Powers (37), which show that this effect is not sufficient to explain the experimental data. Thus, we conclude that the observed change in speed at reversals of magnetotactic bacterium is open for further theoretical and experimental investigations. For this purpose, the known methods of labeling flagella by fluorescent dyes (35) may be useful.

Velocity reversals of the bacterium lead to a diffusion process of the curvature center around which a bacterium moves in a rotating field. This is illustrated in Fig. 11 by a 200-s-long run of a bacterium in a rotating field with a strength H = 10 Oe and frequency slowly increasing from 0.47 to 0.62 Hz. To diminish the amount of the data, only each fifth frame has been tracked in the case of the trajectory shown in Fig. 11. We explicitly see that a reversal of the bacterium motor leads to the diffusive wandering of the centers of the circles.

FIGURE 11.

Wandering of the centers of circular trajectories due to reversals in a rotating magnetic field. H = 10 Oe, and frequency slowly increases from 0.47 Hz to 0.62 Hz during 200-s-long time interval. Coordinates of bacterium are shown in pixels. 18 pixels = 3.2 μm.

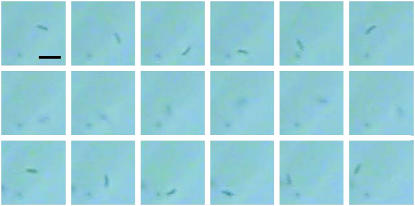
Qualitatively the escape of a bacterium out of the plane of a rotating field is shown in Fig. 12. The bacterium continues to move along a circular trajectory after it escapes from the focal plane of the microscope, as predicted by the theoretical model and illustrated in Fig. 3.

FIGURE 12.

Three-dimensional motion of the magnetotactic bacterium. In the first row, bacterium motion for 1-s time intervals is shown. In the second row, a bacterium escaped the focal plane and is hardly visible for a time interval of 1 s. Adjusting of the microscope focus shows the motion along a circular trajectory in the other plane for a 1-s-long time interval. The scale bar in the first frame corresponds to 4 μm. The field strength is 14 Oe, and the frequency ν = 0.8 Hz.

CONCLUDING REMARKS

Despite a quite-long history of study of magnetotactic bacteria, their physical properties are not yet fully defined. Existing approaches mainly give qualitative information about their magnetic and hydrodynamic properties. Here we show that studies of the motion of magnetotactic bacteria in rotating fields can provide rich information about their properties. It is even possible to determine the magnetic moment of a single bacterium by studying its thermal fluctuations in a rotating field. A rotating field also provides the possibility to quantify the process of a reversal in direction of the motion of a bacterium that has not yet been carried out. The physics of magnetotactic bacterium motion in a rotating field is rather rich and includes such phenomena as the escape of a bacterium in the third dimension out of the plane of a rotating field, a reversal-dependent diffusion process of the trajectory curvature center, and other novel features. Their investigation is a challenge for the future experimental work.

It is interesting to remark that trajectories similar to those of magnetotactic bacteria have also been observed in the case of nonmagnetic Listeria monocytogenes (38), due to the torque acting on the bacterium from the propelling actin comet (39). Quantitative studies of these trajectories may reveal those mechanisms of torque generation that are not yet clear.