Depth-Resolved Measurement of Transient Structural Changes during Action Potential Propagation

Abstract

We report noncontact optical measurement of fast transient structural changes in the crustacean nerve during action potential propagation without the need for exogenous chemicals or reflection coatings. The technique, spectral domain optical coherence tomography, provides real-time cross-sectional images of the nerve with micron-scale resolution to select a specific region for functional assessment and interferometric phase sensitivity for subnanometer-scale motion detection. Noncontact optical measurements demonstrate nanometer-scale transient movement on a 1-ms timescale associated with action potential propagation in crayfish and lobster nerves.

INTRODUCTION

Optical detection of neural action potentials (APs) has attracted attention since the early 1950s; its noncontact and noninvasive nature without the need of contrast agents would allow application in a wide range of neurobiological studies where other methods are not feasible. Noninvasive detection of neural activity is important for early detection of neural diseases, including assessment of human retinal nerve functionality in vivo because nerve cell death is irreversible. Intracellular or extracellular electrodes can measure change in membrane potential during AP propagation but inaccessibility or potential damage to nerve fibers is a disadvantage. Signs of neural activity that can be detected optically include changes in absorption, optical rotation, retardation, fluorescence, light scattering, and volume changes (1). Many studies have been reported on optical instrumentations, yet a single noninvasive/noncontact device that can measure individual AP propagation in a clinical setting has remained elusive. This is due to the invasive nature of measurements or the transmission-mode geometry.

Here we present a method that provides a cross-sectional image of neural tissue and allows reflection-mode measurement of transient changes simultaneously over many depth positions in the nerve with subnanometer axial resolution and submillisecond time resolution at a predetermined location in the cross-sectional image.

There are a number of intrinsic optical contrast mechanisms associated with transient structural changes during AP propagation that can be detected with a time resolution in the millisecond range. In 1968, Cohen et al. demonstrated light scattering and birefringence changes during neural activity with nerve bundles from walking legs of crabs and squid giant axons (2). In the same year, Tasaki et al. reported fluorescence, turbidity, and birefringence changes with nerve trunks from the legs of lobsters and spider crabs and with squid fin nerve (3). The transient optical changes also occur in the electric organ of Electrophorus electricus (4) and the olfactory nerve of pike (5). Biochemical and structural changes contributing to these optical signals in the functioning nerve may include molecular reorientations in the membrane, influx and outflux of ions, and change in axon diameter.

The transient structural changes accompanying AP propagation are still not well understood, but the mechanical changes such as swelling and shrinkage of neural structures during activity can be detected optically. Volume changes due to stimulation of unmyelinated axons in cuttlefish (6) or crab or lobster leg nerves (7) were investigated using optical instrumentation over 50 years ago. A rapid change in diameter of a crayfish giant axon was measured by laser interferometry in the presence of nanometer-diameter gold particles on the axon (8). Measured phase change indicated a 1.8-nm contraction of the axon surface over a period of 1 ms followed by a slow swelling. Also, using gold particles to enhance reflection from the axonal surface, a fiber sensor measuring change in back-reflected light intensity yielded a 0.5-nm swelling of the squid giant axon over a 1-ms period (9). The rapid mechanical changes were reported in the garfish olfactory nerve using a stylus device fastened to a piezoceramic bender (10,11). The swelling signal and AP reached a maximum nearly simultaneously (11). Measurement of rapid changes in hydrostatic pressure in a watertight chamber demonstrated a volume expansion in which shortening and swelling events during neural activity did not compensate each other (10). Also, an optical lever placed on a lobster nerve and a knife edge was used to report 0.1–0.8-nm swelling of the lobster nerve (12). All of these reports indicate structural changes in the functioning nerve.

Traditional or time-domain optical coherence tomography (OCT) may noninvasively detect slow (few seconds to few minutes) changes in neural reflectivity (13) and scattering (14), but this OCT system was insensitive to fast (ms) and small (nm) changes accompanied by the AP propagation. Recently, noncontact measurements of transient surface displacement associated with AP propagation have been reported from nerve bundles dissected from crayfish (15) and lobster (16) legs using differential phase interferometry. In these measurements, nanometer-scale surface displacements were recorded from a single point.

Recent developments in OCT technology, especially the emergence of spectral domain OCT (SD-OCT) has led to vastly superior sensitivity (17) and phase stability (18–20). SD-OCT provides simultaneous intensity and interferometric phase information. The intensity of interference yields real-time high resolution (2–10 μm) structural images that can be used to select a particular region of interest in neural tissue for functional interrogation. Because of the superior phase stability, subnanometer-range optical path length change is detectable with 34 μs temporal resolution. Therefore, SD-OCT technology has the time resolution and phase sensitivity to measure the transient structural changes that are directly related to AP propagation at all depth points. Based on these attractive features of SD-OCT, we report transient surface displacements associated with AP propagation at multiple points along a full depth profile. If the transient structural changes during excitation indicate functional and dysfunctional neural regions selectively, the optical method can be used to study the neural mechanisms, especially in a laboratory setting, and may lead to early detection of neural diseases in the future.

MATERIALS AND METHODS

System description

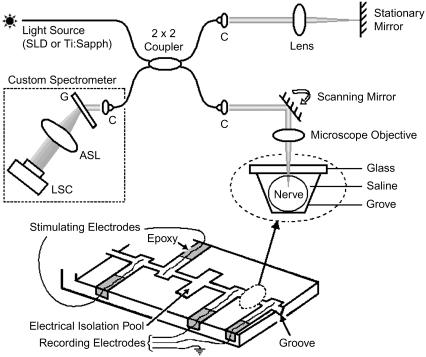
OCT is a noninvasive optical technique to create cross-sectional images of biological tissue with a few micrometers of resolution up to a depth of 1–2 mm. It is similar to ultrasound imaging except that back-scattered light is used rather than acoustic waves. In conventional or time-domain OCT (21) the reference arm length of a Michelson interferometer is rapidly scanned to create a depth profile of a sample. An alternative to scanning the reference arm is measuring the spectrum at the detection arm of the Michelson interferometer by means of a spectrometer (22–24). The spectrometer disperses the detection arm light by a grating and measures the optical spectrum by a charge-coupled device (CCD) line scan camera. In SD-OCT, no mechanical scanning of the reference arm is required, contributing significantly to the phase stability (18–20). Depth information is obtained by a Fourier transform of the spectrum. A schematic of a fiber-based SD-OCT system with a nerve chamber in its sample arm is shown in Fig. 1.

FIGURE 1.

Schematic of a fiber-based SD-OCT setup and a nerve chamber in its sample arm. The optical setup measures nerve movement relative to a stationary glass-saline interface. Nerve is positioned in a 20-mm-long and 1-mm-wide groove. Electrical stimulation and recording electrodes are made of platinum. Cross-sectional images can be acquired by scanning the beam over the sample laterally; however, the beam is stationary during the actual measurement. ASL, three element air-spaced lens; C, light collimator; G, transmission grating; LSC, line scan camera; SLD, superluminescent diode; Ti:Sapph, mode-locked titanium sapphire laser. Inset shows the optical read out.

We used broadband light sources such as a superluminescent diode or a mode-lock Ti:Sapph laser to obtain high axial resolution (∼6 μm and 2.5 μm in tissue, respectively). In the sample arm, the 1/e² diameter of the collimated beam was ∼3.4 mm and the numerical aperture of the microscope objective was ∼0.4. The lateral resolution determined by the sample path optics was ∼4 μm. In the detection arm, our custom-built spectrometer with a 60-mm focal length achromatic collimating lens, 1200 lines/mm transmission grating (Wasatch Photonics, Logan, UT), and a 100-mm focal length air-spaced imaging lens projected the optical spectrum onto a CCD line scan camera consisting of 2048 pixels, each 10 μm × 10 μm in size (Basler Vision Technologies, Ahrensburg, Germany).

The nerve chamber is made of plexiglass. To stimulate and record AP electrically, platinum electrodes are placed into the pools of the nerve chamber and fixed with epoxy. The groove, in which the nerve is positioned, is ∼20 mm long and 1 mm wide. A microscope glass is glued on top of the groove between the two recording electrodes, so that the nerve movement compared to this stationary glass-saline interface can be measured differentially.

Detection

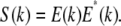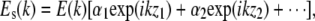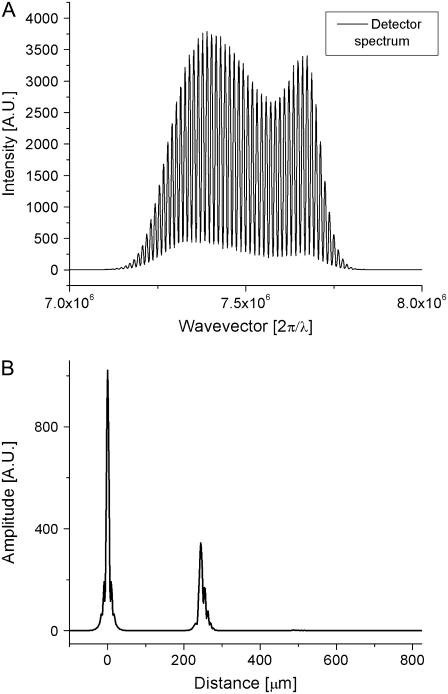
The interference pattern at the spectrometer in the detection arm of SD-OCT can be described as follows: the field returning from the reference arm as a function of wave vector k is given by E(k), with the source spectrum S(k) given by The field returning from the sample arm after the reflection from the sample is given by where E(k) is the field strength incident on the sample, and α₁ and α₂ are the square root of the reflectivities at locations z₁ and z₂, respectively. The intensity at the detector as a function of wave vector k is given by the interference of sample and reference arm light, 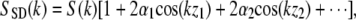where α₁ and α₂ were assumed to be ≪1. As is apparent from this equation, spatial information is encoded on top of the source spectrum by a modulation 2α cos(kz). A Fourier transform of S_SD(k) results in a peak at zero (the Fourier transform of the source spectrum) and the spatial reflectivity information of the sample (peaks at the spatial locations z₁, z₂, etc.). As an example, a reflector was placed in the sample arm of an interferometer, and the spectrum was measured at the detection arm. The resulting spectrum is shown in Fig. 2 A, and the Fourier transform of this spectrum, showing the spatial information, is shown in Fig. 2 B.

FIGURE 2.

Description of SD-OCT measurement to locate depth-resolved structures. (A) Optical spectrum at the detection arm of the interferometer, showing a strong modulation on the spectrum due to a single reflective surface in the sample arm. (B) Fourier transform of the optical spectrum, giving the spatial information in the sample arm. The peak at zero is a Fourier transform of the source spectrum; the peak at 240 μm is the reflective object causing modulations on the spectrum. The width of the peaks corresponds to axial resolution, which is inversely proportional to the bandwidth of the light source spectrum.

A Fourier transform of the real spectrum S_SD(k) results in a complex function 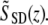The reflectivity profile in Fig. 2 B is given by 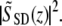The phase φ(z) at every location along the depth profile can be calculated by a four-quadrant inverse tangent of imaginary and real parts of 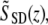where φ(z) ∈ [−π, π]. To eliminate common mode noise in the interferometer, the phase of a particular point at a location z is subtracted from the phase of a reference surface (glass-saline interface). The phase difference Δφ(z) is directly related to a small path length change Δp(z) due to displacement within the nerve during the activity by 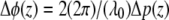with λ₀ the center wavelength of the source. In principle, optical path length change Δp(z) may arise from changes in the refractive index and/or physical dimension of the sample, since the optical path length is the product of refractive index and physical length. Because i), the top surface of crayfish nerve resulted in nanometer-range displacements (8,15), and ii), optical path length change between two fixed surfaces placed below and above the nerve were not detectable at 10–20 picometer resolution (15), our nanometer-range optical path length changes are not attributed to refractive index changes but to physical displacements within the nerve during AP propagation.

Sensitivity

To determine the minimal displacement that can be measured, a glass slide was placed in the sample arm of the SD-OCT system. The front surface of the glass slide acted as a reference surface, and the back surface of the glass slide acted as the location where the phase difference Δφ(z) or displacement Δp(z) was measured. Ideally, the displacement Δp(z) should be zero. The measurements were taken every 35 μs over 21 s with a signal/noise ratio (SNR) of ∼100.4 dB. Standard deviation of the measurement demonstrated an extraordinary accuracy of 25 picometer (20). The phase sensitivity is an explicit function of SNR, the phase variance is related to the SNR by the following equation (25,26): 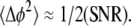The predicted precision based on the SNR is 0.4 picometer. The difference between the theory and the measurement can easily be accounted for by vibrations present in the glass slide. In nerve experiments, SNR decrease in tissue and motion artifacts may require signal averaging to observe nanometer-range transient structural changes associated with AP propagation.

RESULTS

Nerves are extracted from the front walking legs (cheliped) of crayfish (Carolina Biological Supply, Burlington, NC) under a dissection microscope. An extracellular solution of 205 mM NaCl, 5.3 mM KCl, 13.5 mM CaCl₂·2H₂O, and 2.45 mM MgCl₂·6H₂O with pH adjusted to 7.4 with NaOH is used to bathe the crayfish nerve during and after dissection. Tying both ends of the nerve bundle with sutures prevents leakage of the axoplasm and assists with positioning. After placing the nerve in the groove, slots housing the electrodes are electrically isolated from each other by petroleum jelly. An isolated pulse stimulator (Model 2100, A-M Systems, Sequim, WA) is used to generate and apply 50-μs duration adjustable electric current pulses to the nerve. Typically, nerves that exhibit signal propagation for stimuli of 1 mA or less were deemed viable. A differential amplifier (Model 1800, Microelectrode AC Amplifier, A-M Systems) connected to the recording electrodes measures the AP with its low- and high-pass cutoff frequencies set to 10 Hz and 10 kHz, respectively. The AP is displayed on an oscilloscope screen to monitor the repeatability of each response. Multiple responses are averaged to increase the SNR. The time interval between the individual current pulses was 270 ms (3.7 stimuli/s). The entire system, including the SD-OCT system and the electrical stimulation and recording equipment, is controlled by a single computer to insure simultaneous recording of the optical and electrical signals.

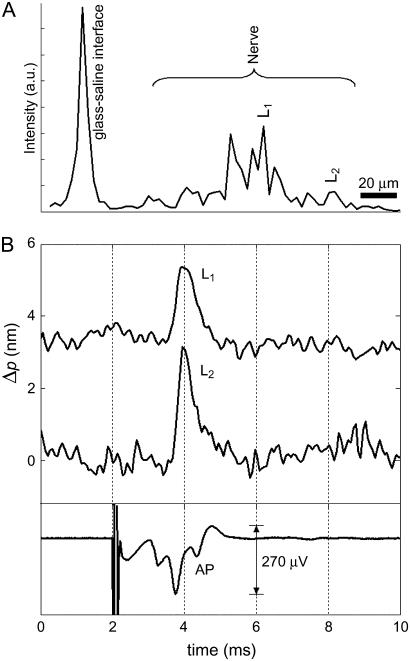
Fig. 3 demonstrates optical detection of AP propagation in a crayfish leg nerve. Fig. 3 A shows a single depth profile of the backscattered light intensity. The glass-saline interface, which acts as a reference in our measurement, and multiple neural surfaces underneath are visible. Among the depth locations showing displacement, two locations are selected within the crayfish nerve, L₁ within the focused spot and L₂ giving the largest displacement. Optical path length changes as a result of transient displacement during AP propagation at location L₁ and L₂, and the compound electrical AP are plotted as a function of time in Fig. 3 B. Stimulus pulses (1 mA, 50 μs) are presented at 2 ms and produced a localized artifact followed by a complex compound AP in the electrical signal. At point L₁ and point L₂, 2- and 3-nm optical path length changes during the AP propagation are measured, respectively. Optical path length change divided by the refractive index of the media (∼1.33) gives magnitudes of the actual displacement, which are 1.5 nm for point L₁ and 2.25 nm for point L₂. The transient increase in optical signal represents a displacement toward the reference glass surface. The duration of the transient signal is ∼1–2 ms and consistent with AP arrival to the optical measurement area. To reduce noise, 50 displacement profiles are averaged. Electrical AP is also averaged for comparison. Both electrical and optical signals have a 5-kHz bandwidth. Standard deviations of the noise in the first 2 ms of the optical signals (Fig. 3 B) are 0.19 nm and 0.3 nm for the locations L₁ and L₂, respectively. The higher noise level for location L₂ can be attributed to the lower SNR as shown in the depth profile (Fig. 3 A). In this measurement, a superluminescent diode (Superlum Diodes, Moscow, Russia) with 50-nm bandwidth centered at 840 nm resulted in 6-μm axial resolution for the structural profile. The diameter of the sample beam at focus was ∼4 μm (Rayleigh range: ∼15 μm), and the optical power on the nerve did not exceed 1 mW.

FIGURE 3.

Optical detection of AP propagation in a crayfish leg nerve. (A) Depth profile showing the glass-saline interface and multiple surfaces within the nerve. Labels L₁ and L₂ indicate two locations inside the crayfish nerve. (B) Optical path length changes due to transient displacement during AP propagation at locations L₁ and L₂ and corresponding compound AP recorded differentially with respect to ground by a pair of platinum electrodes that are placed before and after the optical read-out area. Transient increase in optical signal represents a displacement toward the reference glass surface. Stimulus (1 mA, 50 μs) is presented at 2 ms and caused a localized artifact in the electrical measurement. Fifty responses are averaged in each trace.

We repeat the same experiment with the nerve bundles dissected from walking legs of locally obtained lobsters. In this case, an extracellular solution of 462 mM NaCl, 16 mM KCl, 26 mM CaCl₂·2H₂O, 8 mM MgCl₂·6H₂O, 10 mM D-glucose, and 10 mM HEPES, with its pH adjusted to 7.4 with NaOH is prepared for the lobster nerve. By using a Ti-Sapph laser (Integral OCT, FemtoLasers, Vienna, Austria), which has ∼120-nm bandwidth around 820 nm, the axial resolution for structural imaging is improved to ∼2.5 μm in tissue. The lateral resolution (∼4 μm), Rayleigh range (∼15 μm), and the optical power on the nerve (∼1 mW) were similar to the previous experiment.

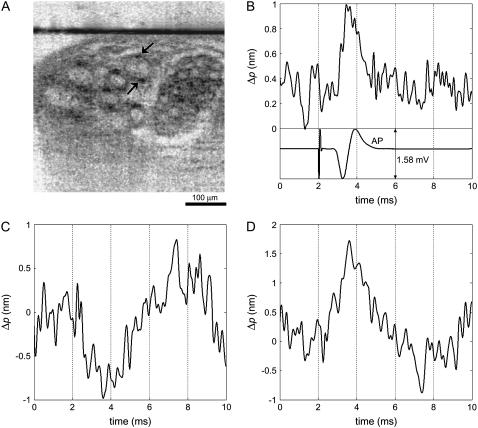
Before functional interrogation, a cross-sectional image (lateral position versus depth) was obtained by scanning the SD-OCT beam laterally across the width of the lobster nerve. After identifying a nerve fiber bundle in real time, the SD-OCT beam was positioned at a selected lateral position near the center of a fiber bundle. Fig. 4 A shows the cross-sectional image of the lobster nerve, which consists of several nerve fibers in different sizes. The arrows indicate the points of interest, and the horizontal line corresponds to the stationary glass-saline interface. Phase difference between these two surface reflections removes the common mode noise and allows measurement of nanometer-scale displacement of the neural surface.

FIGURE 4.

Optical detection of AP propagation in a lobster leg nerve. (A) Cross-sectional SD-OCT image shows several nerve fibers. Horizontal line corresponds to the glass-saline interface. (B) Optical path length change due to transient displacement of the location indicated by the upper arrow during AP and corresponding compound AP recorded differentially with respect to ground by a pair of platinum electrodes that are placed before and after the optical read-out area. Optical signal represents a transient displacement toward the reference glass surface and suggests movement of the top surface of nerve fiber in swelling direction. Stimulus (300 μA, 50 μs) is presented at 2 ms and caused a localized artifact in the electrical measurement. (C) Optical path length change of a depth location indicated by the lower arrow represents a displacement during AP propagation that is away from the reference glass. (D) Optical path length increase measured between the two points indicated by the arrows shows that a reference glass may not be necessary for the measurement. One hundred responses are averaged in each trace.

Fig. 4 B shows the electrical and optical measurements at the time of stimulation. Stimulus pulses (300 μA, 50 μs) applied at a rate of 3.7 stimuli/s are presented at 2 ms and resulted in a localized artifact in the electrical measurement. The negative and positive peaks of the electrical signal indicate AP arrival at the first and second recording electrodes, respectively. Therefore, AP is expected to reach the optical measurement area around the zero-crossing of the electrical signal. The optical measurement in Fig. 4 B demonstrates 0.7-nm fast transient change in optical path length, which corresponds to ∼0.5-nm actual displacement of the top surface of the nerve fiber indicated by the upper arrow in Fig. 4 A. The transient displacement is toward the reference glass surface. Fig. 4 B clearly shows that the onset and duration of the transient displacement is highly correlated with the electrical AP. Fig. 4 C shows the optical path length change of the depth location (bottom surface of the nerve fiber), indicated by the lower arrow in Fig. 4 A. The signal, during AP propagation, represents a similar transient displacement comparable to Fig. 4 B but in the opposite direction. The differential phase measurement of these two locations in the nerve can be obtained without needing the reference glass surface. Fig. 4 D shows the resulting optical path length increase between these two locations. Therefore, the simultaneous measurements from the top and bottom surface of a nerve fiber in the lobster nerve suggest an ∼1-nm swelling in 1 or 2 ms duration during AP propagation. One hundred displacement profiles are averaged to improve the SNR. Standard deviations of the noise in the first 2 ms of the optical signals are 0.16 nm, 0.19 nm, and 0.23 nm for Fig. 4, B–D, respectively. Electrical and optical signals have a 5-kHz bandwidth.

DISCUSSION

The time course of the optical measurement is similar to the time course of nanometer-range surface displacements recorded from a medial giant axon of crayfish (8) and squid giant axon (9). This suggests that the SD-OCT signal at a particular depth, due to high axial and lateral resolution, may originate from one or a few axons. Magnitude and duration of our crayfish and lobster nerve displacements are similar to an earlier report (15) that uses the same preparation with crayfish nerve. Our lobster nerve result, which shows ∼0.5-nm displacements of top and bottom surfaces in 1 or 2 ms duration, is recorded from a structure within the nerve and may not be comparable to a different lobster nerve preparation (16) that reports ∼5-nm swelling of top surface over 10 ms from a longer and maybe slightly thicker nerve sample.

Since electrical and optical signals are different signatures of neural activity, comparison of these signals may be difficult. In our experiments the electrical signal is a compound AP produced by many axons (∼1–50 μm in diameter). Nevertheless, the electrical and optical signals appeared simultaneously. Squid giant axon may be the best model to compare timing of the electrical and optical signals for a single axon.

Many studies reported in the literature measure relative light intensity change (ΔI/I) with an apparatus consisting of two crossed polarizers, whereas the nerve under study is placed between these components typically at 45° to the incident polarization state (2,3). Measured intensity change during AP propagation can be interpreted as a retardation change 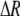in the nerve (27), with 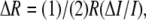which is usually attributed to a birefringence change (1–5,27). Birefringence, the difference in index of refraction for light polarized parallel and perpendicular to a particular optic axis, is an optical property shared by many biological structures including neural tissue. Since retardation (R) is the product of birefringence and sample thickness, the change in sample thickness should also contribute to a retardation change ΔR (15). In fact, if the birefringence of squid giant axon (27) (6.6 × 10⁻⁵) is assumed unchanged during AP propagation, 1-nm thickness change in squid giant axon diameter would alter the retardation by 0.066 picometer. This value is three times smaller than 0.2-picometer retardation change measured for squid giant axon (2,4) and 8.5 times smaller than 0.56-picometer retardation change measured at the edge of the axon (27). Retardation change solely due to a thickness change may be too small to explain the change in transmitted light intensity; however, thickness change is also expected to affect the light-scattering properties and correspondingly alter the detected light intensity. The transient thickness change of the nerve fibers may be a major contributor to the intrinsic signals of neural activity.

Cross-polarized light intensity has been measured in a reflection-mode geometry, and a theoretical model based on geometrical optics has been proposed recently (28). In the model, the cross-polarized baseline intensity and the transient intensity change are attributed to light reflection from axonal fibers and a change in the scattering properties due to axonal swelling during AP propagation, respectively. Although recent reports indicate the role of transient swelling, more study is required to understand the optical signals and the mechanisms of neural activity. Both swelling (15,16) and sometimes shrinkage (8,15) of the nerve fibers during activity have been reported using interferometry; therefore, it is possible that swelling or shrinkage may occur under different circumstances. Also, by understanding the mechanisms behind the transient structural changes, one could optimize the detection or enhance the magnitude of such optical signals.

SD-OCT technology is useful for measuring the transient structural changes that are directly related to neural activity at all depth points. Recent developments in SD-OCT technology provided a big step toward clinical applications for both functional and structural imaging. Intensity measurements such as in slow reflectivity changes in light-activated retina (29–31) can also be studied at particular depths in neural tissue. Although the small magnitude of swelling and motion artifacts pose a challenge in a clinical setting, the potential of differential measurements between locations in the nerve could minimize axial motion artifacts, and further development of active feedback lateral tracking mechanisms demonstrated for in vivo retinal imaging (32,33) might provide the necessary lateral stability.