Mixing of Exciton and Charge-Transfer States in Photosystem II Reaction Centers: Modeling of Stark Spectra with Modified Redfield Theory

Abstract

We propose an exciton model for the Photosystem II reaction center (RC) based on a quantitative simultaneous fit of the absorption, linear dichroism, circular dichroism, steady-state fluorescence, triplet-minus-singlet, and Stark spectra together with the spectra of pheophytin-modified RCs, and so-called RC5 complexes that lack one of the peripheral chlorophylls. In this model, the excited state manifold includes a primary charge-transfer (CT) state that is supposed to be strongly mixed with the pure exciton states. We generalize the exciton theory of Stark spectra by 1), taking into account the coupling to a CT state (whose static dipole cannot be treated as a small parameter in contrast to usual excited states); and 2), expressing the line shape functions in terms of the modified Redfield approach (the same as used for modeling of the linear responses). This allows a consistent modeling of the whole set of experimental data using a unified physical picture. We show that the fluorescence and Stark spectra are extremely sensitive to the assignment of the primary CT state, its energy, and coupling to the excited states. The best fit of the data is obtained supposing that the initial charge separation occurs within the special-pair P_D1P_D2. Additionally, the scheme with primary electron transfer from the accessory chlorophyll to pheophytin gave a reasonable quantitative fit. We show that the effectiveness of these two pathways is strongly dependent on the realization of the energetic disorder. Supposing a mixed scheme of primary charge separation with a disorder-controlled competition of the two channels, we can explain the coexistence of fast sub-ps and slow ps components of the Phe-anion formation as revealed by different ultrafast spectroscopic techniques.

INTRODUCTION

The D1/D2/Cytb₅₅₉ reaction center of Photosystem II (PSII-RC) performs the initial charge separation in oxygenic photosynthesis (1–4). According to the x-ray structure (5–8) the PSII-RC comprises eight chlorins and two carotenes participating in excitation energy and electron transfer. Four chlorophyll (Chl) and two pheophytin (Phe) molecules are arranged in two branches associated to the D1 and D2 proteins, respectively, and located in the central part of the complex. The D1 branch is known to be active in charge separation (2). Two additional Chls are bound at the periphery of the complex at distances of ∼24 Å from the core pigments. The energy transfer and primary steps of charge separation in this complex have been studied by a multitude of spectroscopic techniques, such as visible pump-probe (9–19), visible pump-IR probe (20), low-temperature fluorescence (21), time-resolved fluorescence (18,22), photon echo (23), hole-burning (24,25), and Stark spectroscopy (26).

The first attempt to explain the spectra and kinetics in the PSII-RC was performed using the so-called multimer model (27,28), where the transition energies of the six core pigments (P_D1, P_D2, Chl_D1, Chl_D2, Phe_D1, and Phe_D2) were taken to be equal, giving rise to delocalized exciton states. The Redfield relaxation theory was then used to model the dynamics within the excited state manifold and its spectral signatures, such as pump-probe (28,29) and photon echo responses (23). Each of these studies was restricted to the fitting of just one type of spectrum, and no attempt was made to extend it to other measured data.

A simultaneous fit of all available linear spectra together with nonlinear (pump-probe) kinetics was performed for the first time by Renger and Marcus (30). They obtained a reasonable unified picture of the spectra and dynamics of the PSII-RC at 77 K, but the multimer model (with equal site energies) used in this study did not give a good quantitative fit of the spectral shapes. In a later study of Renger and co-workers (31) the multimer model was replaced by a more realistic model where site energies were extracted from a simultaneous evolutionary-based fit of the linear spectra. The line shapes of the exciton states were obtained using the modified Redfield theory. The model allowed a quantitative fit of the 5 K absorption (OD), linear dichroism (LD), circular dichroism (CD), and fluorescence (FL) spectra and the temperature dependence of OD in the 6–277 K range. These site energies were verified by calculations of the absorption difference spectra for RCs with 1), modified Phe_D2; 2), modified Phe_D1 and Phe_D2; 3), reduced Phe_D1; 4), absorption of so-called RC5 complexes that lack one of the peripheral Chls; and 5), triplet-minus-singlet (T-S) spectra at 10 and 277 K assuming a thermal distribution of the triplet state between P_D1 and Chl_D1. The thus obtained site energies differ from those of the multimer model. In particular, the accessory Chl_D1 was suggested to be the red-most pigment which may act as the primary donor, in agreement with the original suggestion of van Brederode et al. (32,33) and the results obtained from site-specific mutagenesis on the ligands for P_D1 and P_D2 (34).

This approach was further extended 1), by taking into account a mixing of the excited states with charge-transfer states; and 2), by including into the fit the transient absorption (TA) and FL kinetics reflecting the interplay between energy transfer among the eight pigments and the primary steps of charge separation (35). In our previous article (35) we tried to extract the site energies (and energies of the first radical pairs) from a simultaneous fit of the room temperature OD, LD, CD, and FL spectra together with the TA and FL kinetics upon different excitation wavelengths using the modified Redfield theory. This modeling suggested that the sequence of electron transfer events starts from a state with charge separation within the special pair P_D1P_D2. The mixing of this state with the excited states of the six core pigments results in a charge-transfer intermediate that lies below the pure exciton states, has significant dipole strength, and can be reached via fast relaxation from the excited states.

We also found that the fit of the room temperature spectra is not unique, i.e., there are at least four different sets of site (and radical pair) energies that yield a quantitative fit of the OD, CD, LD, and FL spectra (35). This uncertainty is connected with a significant broadening of spectral lines at room temperature hiding the fine structure of the exciton spectra. In this article, we extend our model by including into the fit the low-temperature data, i.e., OD, CD, LD, and FL, together with the spectra of the Phe-modified RCs, RC5 complexes, and T-S spectra. This has led to an unambiguous assignment of the site energies. To determine precisely the energies and couplings for the primary charge-transfer state, we also model the Stark spectrum. The theory of the Stark response is developed using the density matrix approach based on the one- and two-exciton states and their mixing with charge-transfer states. Generalization of the theory to the case of strong exciton-phonon coupling (within the framework of the modified Redfield theory) allows a modeling of the Stark spectra with the same physical picture as used in the modeling of other spectra.

We conclude that, in the PSII-RC at room temperature, at least two pathways for primary charge separation coexist—the relative contribution of which fully depends on the realization of the disorder. In the first, ultrafast charge separation occurs between Chl_D1 and Pheo_D1, as observed in ultrafast Vis-pump-mid-IR-probe experiments followed by electron transfer from P_D1 (20), while the second path involves ultrafast formation of the intraspecial pair charge transfer state 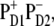followed by slow formation of the Pheo_D1-anion.

The model

We consider an isolated PSII-RC complex consisting of eight pigments, arranged in the D1 and D2 subunits with pseudo-C2 symmetry, i.e., two chlorophylls of the special pair P, two accessory chlorophylls, two pheophytins, and two additional chlorophylls (denoted as Chlz). We will number them as 1-P_D1, 2-P_D2, 3-Chl_D1, 4-Chl_D2, 5-Phe_D1, 6-Phe_D2, 7-Chlz_D1, and 8-Chlz_D2, where the active branch corresponds to the D1 subunit.

Coupling between the excited and charge-transfer (CT) states initiates primary charge separation. The latter includes formation of the initial CT state and after electron transfer steps resulting in the formation of the second and third CT states. In a previous article (35) we have modeled this sequence of CT states (referred to as radical pairs RP₁, RP₂, and RP₃) by a decreasing order of their energies, where the first (highest) state lies close to the lowest excited state, in agreement with earlier models (1,36). As a consequence, the excited and CT states will become mixed and the highest CT state becomes dipole-allowed, borrowing some dipole strength from the excited-state manifold, thereby changing the absorption and fluorescence profiles. Mixing with CT states, however, increases the static dipole moment for the lowest exciton states, thus changing the Stark spectrum. In the following we will neglect the mixing of the excited states with the second and third CT states, because this has only a minor effect on the steady-state linear and Stark spectra. Thus, in this study the excited-state manifold consists of the electronically excited sites 1–8 and one CT state.

The one-exciton Hamiltonian and the two-exciton Hamiltonian (needed to model the Stark response) are constructed as in our previous model (35). The linear spectra are calculated using the modified Redfield theory as described elsewhere (35). Expressions needed to calculate the Stark spectra within the same framework (i.e., including strong pigment-pigment interactions and coupling to the CT state) are given in the Appendix. The effective Q_y transition dipoles of Chl and Phe are 4 and 3 Debye, respectively (35,37). The Q_y static dipole of Chl is taken to be 1.8 Debye (26). The Q_y static dipole of Phe is supposed to be smaller in proportion to the Phe transition dipole, i.e., 1.35 Debye. We suppose that the static dipoles have the same directions as the transition dipoles.

The coupling between the excited and CT states is supposed to be 35 cm⁻¹ (35). The static dipole of the CT state is taken to be 30 Debye. Notice that this value cannot be estimated without a detailed knowledge of how charge is separated between the macrocycles of the two pigments involved. For example, approximating the charge distribution within the special pair by point charges at the centers of P_D1 and P_D2, we obtain a static dipole of 42 Debye. However, due to overlap of macrocycles, the true value is expected to be smaller.

The site inhomogeneity (diagonal disorder) is 80 cm⁻¹ (full width half-maximum of a Gaussian distribution) for the excited states and assumed to be 2.3 times bigger for the CT state.

The electron-phonon spectral density C(ω) for the sites n = 1–8 includes an overdamped Brownian oscillator (with a coupling strength of λ₀ = 70 cm⁻¹ and damping constant of γ₀ = 40 cm⁻¹) and 48 underdamped high-frequency modes (with the same parameters as in our previous model (35)). For the CT state, the coupling λ₀ and couplings for 48 modes are increased by a factor of 1.6 (the choice of this scaling factor is discussed below; see Coupling of the CT States to Vibrations).

RESULTS

Simultaneous fit of the 4–10 K spectra: extraction of the site energies

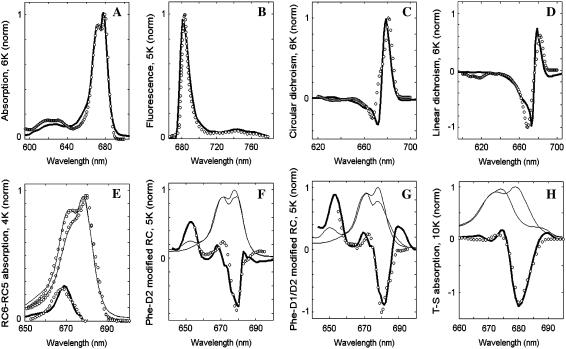
We start with modeling of all the low-temperature (4–10 K) spectra. At this stage we consider the site energies as free parameters that should be determined from the fit of the data. The best fit obtained by an evolutionary-strategy based search (using a genetic algorithm) is shown in Fig. 1.

FIGURE 1.

Simultaneous fit of the low-temperature spectra of isolated PSII-RC. Open circles show the experimental data, solid lines (including thick lines in panels A–H and thin lines in E–H) represent calculated spectra. (A, C, and D) Modeling of the 6 K OD, CD, and LD spectra (38,39). (B) Modeling of the nonselective FL profile at 5 K (40). (E) Modeling of the 4 K absorption spectra for normal 6-chlorophyll RC (RC6) and for modified RC lacking one of the peripheral Chlzs (RC5). The calculated RC6, RC5, and difference RC6-RC5 spectra are shown together with the measured ones (41). (F and G) Modeling of absorption changes induced by modification of Phe_D2 (F) or both Phe_D2 and Phe_D1 (G) at 5 K (39). Thin solid lines show absorption spectra calculated for normal and modified RCs (the latter have bleachings near 680 nm and absorption peak near 650 nm due to blue-shift of the modified Phes). (H) Modeling of the triplet minus singlet (T-S) spectra measured at 10 K (39). The calculated T-S spectrum (thick line) is obtained as a difference between the ground-state absorption (thin line) and absorption without contribution of the Chl_D1 (thin line), implying localization of the triplet state at Chl_D1 at 10 K.

The main absorption band in the 660–690 nm region is determined by the Q_y transitions of the eight pigments. The subbands at 670 and 680 nm appear due to different site energies of the pigments (in combination with the exciton splitting and phonon-induced reorganization shifts). The broad absorption at 620 nm is determined by coupling of the Q_y transitions to high-frequency vibrations (note that Q_x transitions are not included into our model). The low-temperature FL has its main peak at 680 nm and displays a broad vibrational wing with a maximum at 740 nm.

We note that the fit of the linear (4–10 K) spectra (OD, CD, LD, and FL) is not unique, i.e., there are several models with different site energies that allow a good simultaneous fit of these four spectra. To this end we have extended the fit by modeling also the spectra obtained for Phe-modified RCs, RC5 complexes, and T-S spectra. This allows a precise determination of the energies of some particular pigments, thus making a determination of the other site energies easier. For example, the difference between RC6 and RC5 absorption (Fig. 1 E) indicates that the monomeric peripheral Chlzs must have an absorption peak near 670 nm. The spectra of Phe-modified RCs (Fig. 1, F and D) suggest that both Phe_D2 and Phe_D1 contribute to the exciton states that determine the 680-nm absorption peak. The triplet-minus-singlet (T-S) spectrum depends on the energies of the sites that carry the triplet excitation. It is well established that the triplet state at low temperature is localized on the accessory Chl_D1 (34,42–44). Thus, the T-S bleaching at 680 nm (Fig. 1 H) suggests that Chl_D1 contributes to this spectral region.

The fit of the low-temperature spectra shown in Fig. 1 allowed a precise determination of the site energies of all the eight pigments (see below). Introduction of a coupling between the excited and the CT state produces relatively small changes in the absorption-type spectra (OD, CD, LD), but has a dramatic effect on the FL profile, from which we can determine the energy of the CT state. Its value (obtained from the low-temperature fit) can be further adjusted from the fit of the 77 K spectra. The 77 K data includes the Stark spectrum, which is sensitive not only to the energy but also to the configuration of the CT state, thus allowing a comparative study of possible pathways for primary charge separation (see below).

Fitting of linear and Stark spectra at 77 K: adjustment of the radical pair parameters

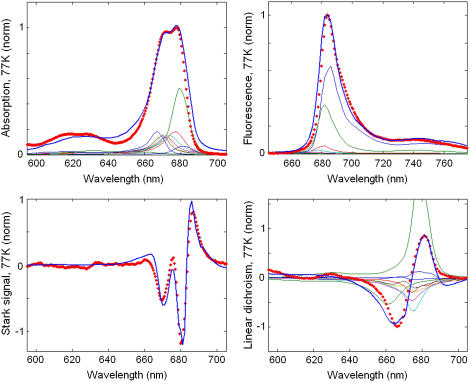
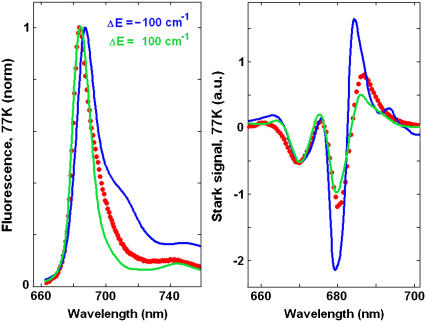
The fit of the 77 K data shown in Fig. 2 has been done with the same parameters as the low-temperature fit in Fig. 1. The lowest state in our model (with an absorption peak near 682 nm) corresponds to a charge-transfer state. The best fit was obtained supposing that this state corresponds to a charge separation within the special pair, i.e., 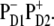This state becomes weakly allowed, borrowing some dipole strength due to mixing with the pure exciton states. The next state (peaking at 680 nm) is a superradiant exciton state determined by a coherent superposition of the pigments of the active branch (specifically Chl_D1 and Phe_D1) and two chlorophylls of the special pair. On the one hand, it is important that the FL spectrum is mostly determined by contributions from these two lowest states, which means that the FL profile will be extremely sensitive to the precise energy of the CT state. On the other hand, the presence of the CT state with a huge static dipole significantly affects the Stark spectrum near 680 nm. Fig. 3 illustrates how the calculated FL and Stark spectra change upon a shift of the CT energy by 100 cm⁻¹ to the red or blue from its optimal position. To explain these features we have to study in more detail the exciton structure and the character of the CT-excited state mixing.

FIGURE 2.

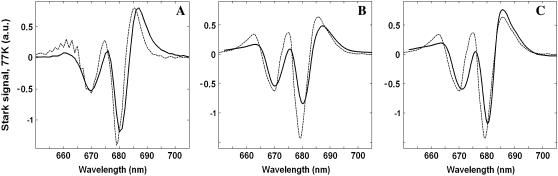
Simultaneous fit of the 77 K spectra of isolated PSII-RC. Points show the experimental data, including OD, FL, and LD spectra (45) and Stark spectrum (26). Solid lines are calculated spectra, where the linear spectra, i.e., OD, FL, and LD are shown together with contributions from the individual exciton states (thin lines). The calculated spectra correspond to a primary charge separation within the special pair, i.e., CT =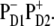

FIGURE 3.

The 77 K FL and Stark spectra calculated with a shift of the CT state by 100 cm⁻¹ to higher (green line) or lower (blue line) energies from its optimal position shown in Fig. 2. Points show the experimental data.

Structure of the exciton states

Site energies and eigenstate energies

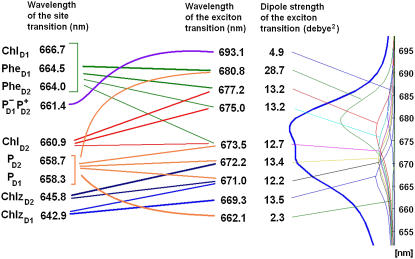
The site energies extracted from the simultaneous fit of the low-temperature and 77 K data (Figs. 1 and 2) are given in Fig. 4. The excitonic interactions between the pigments produce the exciton eigenstates with the energies shifted from the energies of noninteracting sites. These eigenstates are further red-shifted due to reorganization effects corresponding to interaction of the collective electronic excitations with the phonons and intramolecular vibrations. The reorganization shift depends on the delocalization of the exciton states (being proportional to the participation ratio (35,46). Finally, slow conformational motions perturb the site energies, inducing disorder of the exciton states and disorder of the reorganization shift values (47). Thus, the energies of excitonic transitions are determined by the combined action of exciton shifts and reorganization shifts.

FIGURE 4.

(Left column) Wavelengths corresponding to the unperturbed site energies (without including a reorganization shift) of eight pigments and the first charge-transfer intermediate 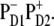(Middle column) Wavelengths of the zero-phonon lines of the exciton eigenstates (averaged over disorder). Lines between left and middle columns indicate participation of the pigments in the exciton states. Numbers (from 4.9 to 28.7 Debye²) near the wavelengths correspond to the dipole strength of the exciton states (averaged over disorder). (Right column) Absorption spectrum (the same as shown in Fig. 2) with the individual exciton components.

The spectral lines of these transitions exhibit homogeneous broadening (including phonon-induced broadening of the main absorption peak together with the appearance of vibrational wings) and inhomogeneous broadening due to disorder. The position of the main peak of each exciton component can be roughly characterized by the position of its zero-phonon line (ZPL) averaged over disorder. Notice that the ZPL energies are generally significantly different from the site energies (see Fig. 4). The red shift of the ZPL is the biggest for localized states (25–26 nm for the peripheral Chlzs and 32 nm for 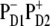) due to their large reorganization energies. For the collective exciton states, the reorganization shift is reduced by delocalization and generally can be comparable with the exciton splitting value. In the special pair (with the biggest pigment-pigment coupling) the excitonic blue shift of the high energy level is slightly less than the reorganization red-shift, giving rise to the higher exciton state peaking at 662 nm, i.e., 3–4 nm red-shifted from the original electronic transitions of the P_D1 and P_D2 sites. The position of a higher exciton state with a different orientation was experimentally observed at 667 nm by singlet-minus-triplet absorbance difference spectroscopy (48), which is reasonably close to the value indicated by our modeling. The lower energy component is red-shifted by ∼14–15 nm due to the combined action of the exciton shift and the reorganization shift. The superradiant state at 680 nm (which is the lowest state of the Chl_D1-Phe_D1-P_D1-P_D2 cluster) exhibits a similar red shift of ∼14–16 nm with respect to the Chl_D1 and Phe_D1 site energies. The right panel of Fig. 4 illustrates how the different exciton states contribute to the absorption spectrum.

Generally the absorption maximum corresponding to a certain exciton component is blue-shifted from the averaged ZPL position. This shift is typically not big (not more than 1–2 nm) for the various exciton states, and is determined by the coupling to low-frequency phonons. However, for the lowest CT state with an averaged ZPL position at 691 nm the absorption maximum is shifted to 682 nm (Fig. 4). Such a shift reflects a much stronger mixing of the exciton states (and more pronounced borrowing of their dipole strength) in realizations with blue-shifted CT states (see below). Note that this additional absorption component at 682 nm resembles the 683-nm state experimentally observed in low-temperature spectra of the PSII-RC and discussed in many articles (see (1)). In particular, it was shown that both the 680- and 683-nm states have similar vibrational fine structures. Our present analysis allows an assignment of this additional red state as the CT state borrowing dipole strength from the 680-nm transition.

Density matrices of the exciton states

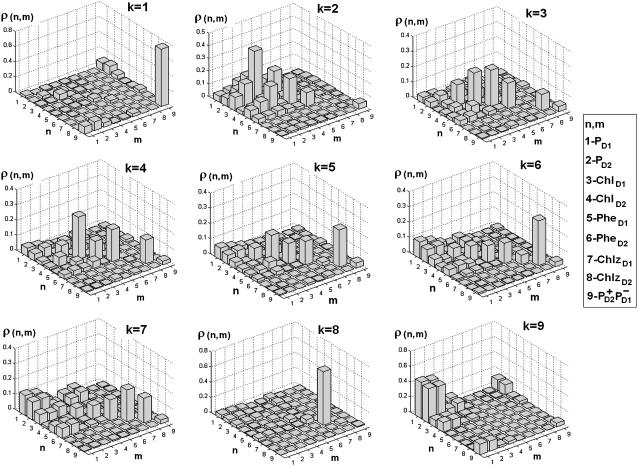
The participation of the pigments in the various exciton states can be characterized in a more quantitative way by the density matrices ρ in the site representation calculated for each exciton state as shown in Fig. 5. Diagonal ρ(n,n) and off-diagonal elements ρ(n,m) correspond to the site populations and intersite coherences, respectively.

FIGURE 5.

Density matrix for the exciton states from k = 1 to k = 9 averaged over disorder. Bars show the density matrix elements ρ(n,m) in the site representation, where n and m number the eight pigments and CT state in the following order: 1-P_D1; 2-P_D2; 3-Chl_D1; 4-Chl_D2; 5-Phe_D1; 6-Phe_D2; 7-Chlz_D1; 8-Chlz_D2; and 9-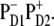

In the lowest k = 1 state only the CT state is populated. Coherences ρ(9,1), ρ(9,2), and ρ(9,3) reflect the coupling of this state with the sites P_D1, P_D2, and Chl_D1. Although 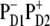state is not connected directly with the accessory Chl, the ρ(9,3) element still appears due to coupling between the special pair and Chl_D1. Thus, the primary transition from the excited state to the charge-separated state can occur from the special pair and also from accessory Chl_D1.

The lowest exciton state k = 2 is the best candidate for the state that initiates primary charge separation because of 1), the participation of pigments 1, 2, 3, and 5 in this state; 2), the small energy gap between this state and the k = 1 CT state; and 3), the predominant population of this state after equilibration within the six core pigments. Feature 1 determines the strong coupling between the k = 2 state and the CT state with different charge-separated configurations (including the 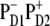configuration shown in Fig. 5, but also other possible configurations like 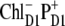or ). Taken together, features 1 and 2 determine the effective mixing of the CT and the k = 2 state, producing a fast electron transfer channel, which is (due to 3) dominating at low and also at high temperature. Notice the pronounced coherences between the pigments 1, 2, 3, and 5 in the k = 2 state. This confirms that the state that initiates charge separation is truly a multimeric state, in line with earlier suggestions (27).

The next three states (k = 3–5) contain a noncoherent mixture of the sites 3–8 (notice, however, some sizable local coherences ρ(4,6), ρ(3,5), and ρ(4,2)).

In the states k = 5–7 there is a coherent mixing of the P_D1 and P_D2 sites with the other core pigments. The contribution of P_D1 and P_D2 to these states originates from the lowest exciton level of the special pair peaking at 671–673 nm. The higher level of the special pair determines the k = 9 state peaking at 662 nm.

The peripheral Chlzs contribute to the states k = 6–8 near 669–672 nm depending on the realization of the disorder. Notice that Chlz_D2 has a lower energy than Chlz_D1 in our model. Correspondingly, Chlz_D2 is always noncoherently mixed with other pigments (as shown by diagonal distribution of the density matrixes for k = 6 and 7) in contrast to Chlz_D1. Thus, the state k = 8 corresponds to a pure Chlz_D1 excitation that is only weakly superimposed with excitations of other pigments (that are lower in energy) and with the high exciton state of the special pair (that is higher in energy).

Participation ratio and dipole strength of the exciton transitions

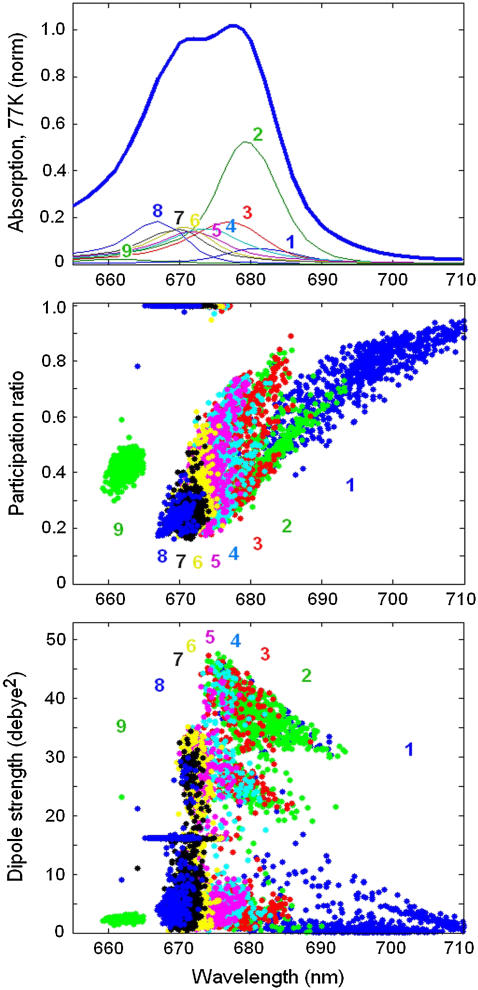
In Figs. 4 and 5 we show the parameters of the exciton states averaged over disorder. To study the spread of these parameters in different realizations we have calculated the participation ratio (PR) and dipole strength of the exciton states for 2500 realizations of the disorder as shown in Fig. 6.

FIGURE 6.

Participation ratio (PR) and dipole strength of the exciton states as a function of the ZPL position calculated for 2500 realizations of the disorder. (Top panel) OD spectrum averaged over disorder (the same as in Fig. 2). The exciton components from k = 1 to k = 9 are labeled by numbers from 1 to 9 and shown by different colors. (Middle panel) PR values for 2500 realizations. PR values for different exciton states are shown by the same colors and have the same labels as exciton components of the OD spectrum. (Bottom panel) The same as in middle panel, but for the dipole strength of the exciton levels.

Excitation of monomeric Chlzs produces localized states (with PR = 1 and monomeric dipole strength of 16 Debye²) that are clearly distinguishable in the region between 665 and 675 nm.

The exciton states of the six core pigments (between 660 and 685 nm) are delocalized over 1.5–5 sites (PR = 0.75–0.2) depending on the realization of the disorder. Redistribution of the dipole strength between the exciton states produces a spread of its value from zero (for almost forbidden states) to 32–45 Debye² (for the states with a superradiance of 2–2.8).

For most of the realizations, the superradiant lowest exciton state (k = 2) is characterized by PR values varying between 0.25 at 675 nm and 0.65 at 690 nm. These realizations form a separated branch in the PR distribution (shown in middle panel of Fig. 6). A second branch also appears with higher PR values in this state, i.e., from 0.4 at 675 nm to 0.85 at 685 nm appearing in more rare realizations. The first branch is determined by multimeric excited states delocalized over pigments 1, 2, 3, and 5 with predominant population of pigment 3 (accessory Chl_D1). In the dipole strength distribution (shown in the bottom panel of Fig. 6) these states are grouped within a separated area between 675 and 690 nm and dipole strength of 32–45 Debye². The second branch contains the states with an unusually big contribution from pigments 4, 5, or 6 producing two additional groups of states, one with the dipole strengths between 1–6 and the other with 20–26 Debye², respectively (see bottom panel of Fig. 6). Note that, in some realizations, the CT (k = 1) and superradiant exciton state (k = 2) have a reversed order of their energies, i.e., the CT state is higher in energy, whereas the excitonic state is the lowest. In these realizations the excitonic state is typically localized on pigment 3 (accessory Chl_D1). These realizations also contribute to the second branch.

The higher exciton levels of the multimeric state are rather delocalized (PR = 0.2 = 0.25) and weakly allowed (2–7 Debye² in most cases). They are noncoherently mixed with the localized Chlz excitations in the region near 670 nm (k = 6–8).

The higher exciton level of the special pair always corresponds to the high k = 9 level near 662 nm. This state is weakly allowed and has a dipole strength of ∼2 Debye².

The CT state (k = 1) is characterized by a very broad distribution of the ZPL positions (in the 680–720 nm region). The red-shifted realizations are localized and almost forbidden. The realizations with higher energies are characterized by a stronger mixing between the CT and excited states. Due to such mixing the CT state borrows more dipole strength. The integrated dipole strength of the lowest state is 4.9 Debye², i.e., 0.3 of the dipole strength of monomeric Chl a.

Recently it was found that charge separation in PSII core complexes at low temperatures can be initiated by illumination far to the red from the main absorption region, i.e., in the 690–730-nm region (49). Spectra in the 690–730 nm region were described supposing the presence of the CP47 trap state absorbing at 689 nm with a dipole strength of 1 Chl a, and an additional state with broad absorption at ∼705 nm with a dipole strength of ∼0.15 Chl a. This component then determines the conspicuous red tail observed in the absorption of PSII cores in the 700–730 nm region. Two possible assignments of this red state have been suggested, i.e., the lowest exciton level of the PSII-RC, or a CT state corresponding to a charge separation within the RC special pair (49).

It is interesting to note that the broad red tail of the absorption described by Hughes et al. (49) has almost the same parameters as predicted by our model. Thus, we have the absorption component near 682 determined by realizations where the CT state is strongly mixed with the exciton states. Far to the red from this peak we find a broad absorption due to realizations where the CT states are only weakly allowed due to their weak mixing with the lowest exciton state. This component determines the red tail of the absorption in the 690–720-nm region. The integrated dipole strength of this broad component is ∼0.08–0.13 Chl a in our model, i.e., comparable with the value of 0.15 ± 0.05 Chl a estimated by Hughes et al. (49). (This dipole strength of the red tail should be not confused with the total dipole strength of the whole CT state, which is 0.3 Chl a in our model.) It should be noticed that the low-energy state found by Hughes et al. (49) was reported to be homogeneously broadened, based on the lack of hole-burning activity. This is in contradiction with our model that predicts inhomogeneous broadening of the lowest CT state. We will discuss this feature later (see Homogeneous versus Inhomogeneous Broadening of the CT States).

Our modeling allows an assignment of the red component of the absorption as the CT state mixed with the excited-state manifold. The character of how this CT state contributes to the absorption is basically the same for all possible configurations of the initial charge separation. Thus, the same distribution of PR and dipole strength as shown in Fig. 6 for 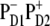can be obtained with other CT configurations (for example, 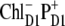or 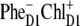). To specify the origin of the CT state, a simultaneous fit of the absorption, FL, and Stark spectra is needed (see below).

Origin of primary charge-separated state: comparing different schemes

Lowest exciton state and charge separation pathways

We have seen that the lowest excited state from which the charge separation is initiated consists of a coherent superposition of four pigments, i.e., Chl_D1, Phe_D1, P_D1, and P_D2. Participation of these sites in the multimeric exciton state is not uniform: on the average, the excitation is predominantly localized at Chl_D1, the population of Phe_D1 is ∼2 times less, the population of the special pair is even smaller (Fig. 7). But note there is a strong coherence between these four sites, which means that some CT state coupled with any of these four pigments will be effectively mixed with the whole set of exciton state (the amount of mixing depending on the size of the energy gap between the excitonic and CT state). Thus, the primary electron transfer toward Phe can, in principle, start from P_D2, P_D1, or Chl_D1, producing the first charge-separated configuration 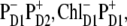or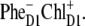

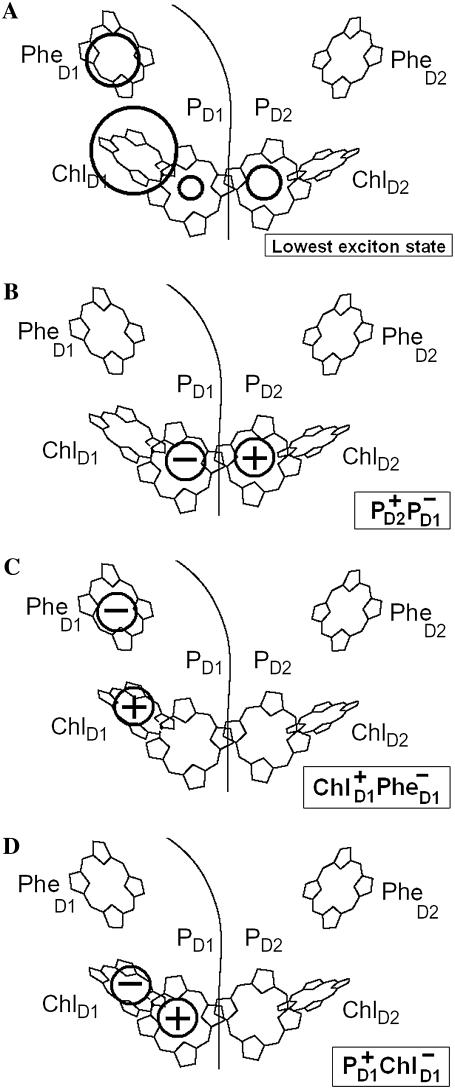
FIGURE 7.

The structure of the lowest exciton state that initiates charge separation, and possible configurations of the first CT state. (A) Circles show the pigments that are coherently mixed in a lowest exciton state. The area under the circle is proportional to population of the corresponding site. (B–D) Circles show a localization of the electron and hole in the CT states (i.e., 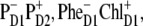and 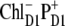) that can be coupled to the lowest exciton state.

The predominant population of Chl_D1 is a strong argument for considering this pigment as the primary electron donor producing the charge transfer state 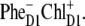However, the special pair is characterized by a bigger overlap of the electronic wavefunctions of the two pigments, thus creating a better coupling between the excited states of P_D1 and P_D2 and the 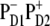charge transfer state. It is clear that these two factors compete and this competition between them will be strongly dependent on the realization of the disorder producing different participations of the pigments (P_D2, P_D1, and Chl_D1) in the lowest state as well as different energy gaps between the excited and the corresponding CT state. For instance, we have seen that in some realizations the excitation can be strongly localized at Chl_D1; moreover, this localized state can be even lower in energy than the 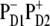charge transfer state. Obviously, in such realizations even in the presence of mixing between the excited states and the 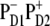intermediate, the charge transfer will be started from Chl_D1 with the formation of the 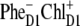radical pair. However, in delocalized multimeric realizations the 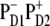state is much better connected with the whole excited-state manifold, and thus can play the role of the initial CT state.

Thus, the pathways of charge separation in PSII-RC are strongly disorder-controlled. We remind the reader that, in our model, the disorder values are 80 and 184 cm⁻¹ for the excited and primary CT state, respectively. Both values are much bigger than the coupling between the excited and CT states (i.e., ∼35 cm⁻¹). In the presence of the two alternative charge separation pathways, a particular realization of the disorder can destroy one of them and create good conditions for the other. Consequently, the measured kinetics (averaged over disorder) will contain a superposition of components corresponding to different pathways. As a result, various experimental methods sensitive to different aspects of the electron transfer can produce a large spread of the estimated time constants of primary charge separation (see Discussion).

Different CT configurations and Stark spectrum

Now we switch to modeling of the Stark and FL spectra using the charge transfer schemes with different CT states discussed above. We have found that the character of the mixing between the CT and exciton states (and the degree to which this influences the Stark and FL spectra) is essentially dependent on the CT configuration. An example of a simultaneous fit of the Stark and FL profiles (in the case of 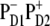state) has been shown in Fig. 3, where we saw that such a fit is very sensitive to a variation of the energy of 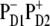state. Checking out other possible CT states (i.e., 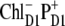and 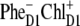) we have found a very similar behavior. For all these configurations we have varied the energy of the CT state to obtain its optimal value. The best simultaneous fits corresponding to this optimal CT energy are shown in Fig. 8 for the three CT configurations.

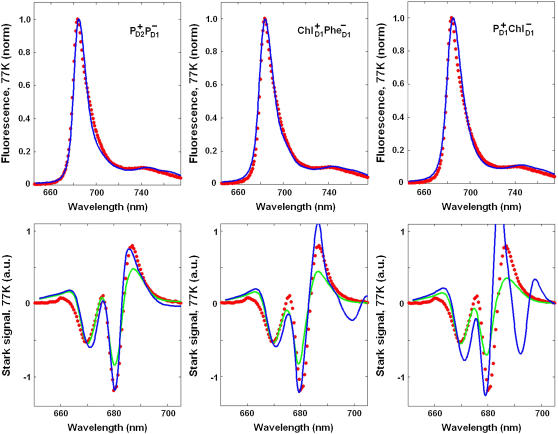
FIGURE 8.

The best fit of the 77 K FL and Stark spectra obtained with different CT states, i.e., 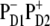(left), 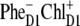(middle), and 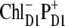(right). Points correspond to experimental data; calculation is shown by solid lines. The Stark signal is calculated with the CT static dipole of 30 D (blue) and 0 (green).

For all CT configurations there is no problem to obtain a good fit of FL, because the latter depends only on the CT energy, being almost insensitive to the character of mixing between the CT and exciton states. In contrast, the Stark spectrum depends both on the energy and the nature (configuration) of the CT state involved. The amplitude of the Stark signal for any exciton state is proportional to the product of transition and static dipoles for this state (see Appendix). The spectral shape corresponding to the k^th excited state is given by the imaginary part of the third power of the complex lineshape function L_kg (see Appendix). This gives a line shape in a form of the second derivative of the absorption profile for each exciton component. When static dipoles are not much different for the different exciton states, the Stark spectrum of the whole complex will roughly be similar to the second derivative of the OD spectrum. However, the presence of additional states with bigger static dipoles will produce anomalous Stark components in the corresponding spectral region. Typically, the mixing with a CT state changes the amplitudes of the Stark peaks and produces additional peaks on the red side. In Fig. 8, we compare Stark spectra with and without contribution of the static dipole of the CT state.

In case of the configuration, the CT is mixed with the P_D1 and P_D2 sites. These sites on their turn are mixed with other pigments, thus participating in many exciton states (see Fig. 5). As a result, we obtain a more or less uniform coupling of this CT with many exciton states producing a moderate contribution of the CT state to the red part of the Stark spectrum. In this case the calculated Stark spectrum is in good agreement with the measured one (Fig. 8, left).

The 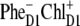configuration is coupled with Phe_D1 and Chl_D1, participating predominantly to the lowest exciton state. As a consequence, the coupling of this CT with the exciton states is more nonuniform in this case. As a result, the influence of this CT state on the Stark amplitudes in the red is more pronounced: the 685-nm peak becomes too intense as compared with the measured data, and also an additional peak at 700 nm (not present in the measured spectra) appears (Fig. 8, middle). Such an additional peak cannot be accounted for by just a second-derivative type contribution from some red-shifted state with an enhanced static dipole. In fact, the distribution of both transition and static dipoles at ∼700 nm is rather monotonous, i.e., without any resonant peaks. Restricting to the type I contributions to the Stark signal (see (50)) one could expect an increase in the Stark amplitude for the whole spectral region from 680 nm to longer wavelengths. Such an increase, originally suggested by Frese et al. (26), is confirmed by our modeling as shown in Fig. 8 (compare the curves with and without the CT static dipole). However, in addition to the type I we also have the type II contributions, reflecting transitions within the one-exciton manifold. For example, an overlap of the wavefunctions for the k′ = 1 and k = 2 states produces the d_k′k element (Eq. 15) that can create a significant Stark amplitude in the k′ = 1 spectral region even if the k′ = 1 state is dipole-forbidden (see the first term in Eq. 19 with k″ = k). Due to such contributions we can find additional Stark peaks in the regions far from the main absorption peaks, where the second derivative is close to zero (i.e., >690 nm in our case).

In the case of 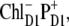we find an even stronger increase of the 685-nm peak and an additional peak at 692 nm. The mixing of this CT configuration with P_D1 also produces an increase of the Stark amplitudes near 670 nm. No satisfactory fit can be obtained in this case (Fig. 8, right).

Stark spectrum and the second derivative of the absorption

In Liptay's phenomenological theory of the Stark effect (58), where the excitonic contributions are ignored, the shape of the Stark spectrum is determined mostly by the second derivative of the absorption spectrum (SDS). That is why in experimental articles the Stark spectrum is usually compared with the SDS. In studies of the PSII-RC (26) it was shown that the long-wavelengths peaks of the Stark spectrum (at wavelengths longer than 675 nm) exhibit a red-shift with respect to the SDS. It was supposed that this phenomenon reflects a mixing with CT states, although at that time no attempt was made to support this by modeling.

This study is based on a theory where excitonic contributions to the Stark signal are included explicitly. Due to these excitonic contributions, the Stark spectrum generally should not match the SDS; in particular, some shift with respect to the SDS peaks is possible.

Fig. 9 shows deviations of the Stark spectrum from SDS as they appear in experiment (26) and in our modeling. The 675-, 680-, and 685-nm peaks of the measured Stark spectrum are ∼2 nm red-shifted from the corresponding peaks of SDS (Fig. 9 A). We have shown that these features can be reproduced without including a coupling to CT states (Fig. 9 B). Thus we conclude that the observed red shift of the Stark peaks with respect to the SDS is mostly determined by the excitonic contributions. However, the amplitudes of the purely excitonic Stark peaks are smaller than those observed in the experiment (compare Fig. 9, A and B). Switching on the coupling to CT state does not significantly shift the main peaks, but increases their amplitudes, allowing a better fit (Fig. 9 C). One thing that is not well reproduced is the difference between the Stark and SDS at wavelength longer than 685 nm. In the presence of the CT state the Stark signal increases mostly near 685 nm, thus reducing the red shift of the 687-nm peak. We assign it to limitation of our model that supposes a simplified character of mixing between the excited and CT states (see Discussion).

FIGURE 9.

Comparison of the Stark spectrum and the second derivative of the absorption spectrum (SDS). (A) The Stark spectrum (solid line) and SDS (dotted line) measured at 77 K (26). (B and C) The calculated Stark spectra (solid line) and SDS corresponding to calculated OD (dotted line). The calculated data is obtained with the 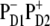configuration of the CT state. The Stark signal is calculated with the CT static dipole of 30 D (C) and 0 (B).

DISCUSSION

Comparison with previous models

It is useful to compare our present model with the models previously published by us (35) and by Renger and co-authors (31). In both these studies the spectra of PSII-RC have been explained at a quantitative level using the modified Redfield approach. The site energies extracted from the fit of the data are listed in Table 1.

TABLE 1.

Unperturbed transition energies of the pigments (n = 1–8) and first CT state (n = 9) for the present model and models proposed earlier (Models A–D proposed by Novoderezhkin et al. (35) and the model of Raszewski et al. (31))

n	1	2	3	4	5	6	7	8	9
Pigment	PD1	PD2	ChlD1	ChlD2	PheD1	PheD2	ChlzD1	ChlzD2	CT
Novoderezhkin et al. (35), Model A	15130	15165	15095	15110	15175	15280	15435	15430	15095
Novoderezhkin et al. (35), Model B	15110	15425	15090	15330	15190	15290	15420	15470	15165
Novoderezhkin et al. (35), Model C	15210	15210	15019	15233	15091	15151	15461	15438	15110
Novoderezhkin et al. (35), Model D	15300	15105	15030	15130	15100	15100	15425	15420	15100
This study	15190	15180	15000	15130	15050	15060	15555	15485	15120
Raszewski et al. (31)	15215	15215	14950	15192	15081	15015

Transition energies are given in cm⁻¹, and do not include the reorganization energy shift. The energies of six core pigments obtained by Raszewski et al. (31) are increased by 200 cm⁻¹ (see the text).

First, we wish to compare the site energies determined from the low-temperature fit of the linear and Stark spectra (the present study) and those obtained from the fit of the linear spectra and nonlinear TA and FL kinetics at room temperature (35). We remind the reader that the modeling based on the room-temperature data resulted in four possible configurations (Models A–D) obtained from the fit of four linear spectra (OD, LD, CD, and FL). The fit of these spectra is not unique because they are determined by a strong superposition of significantly broadened exciton components. In this study, we include into the fit the low-temperature spectra for normal and modified RCs, making the unambiguous determination of the site energies possible.

The present model is close to the Model C from our previous study. The major difference is the 90–100 cm⁻¹ red shift of the 4–6 (Chl_D2-Phe_D2) dimer and the 45–95 cm⁻¹ blue shift of the peripheral Chlzs in the present model. However, the energies of the pigments participating in the lowest exciton states (P_D1, P_D2, Chl_D1, and Phe_D1) and the CT state energy are almost the same. We remind the reader that Model C also gave a good fit of the TA and FL kinetics in the 0.5–100 ps scale, whereas the fast dynamics during 0–0.5 ps (reflecting the exciton relaxation) was not well reproduced.

In the previous study, we gave some preference to Model B that allowed a quantitative explanation of dynamical features including the fast component of the TA. However, that model predicted site energies that are in not in agreement with those obtained in the present study, which have been determined in a much more reliable way.

It is interesting to note that all previous models (Models A–D) yielded almost the same energy for the first CT state, which is also in agreement with the present study. Note that in our previous modeling the CT state energy was adjusted from the fit of the TA/FL kinetics, whereas in the present study we extract its value from the simultaneous fit of the FL and Stark profiles. For a further verification, the current model should be applied for interpretation of the TA/FL kinetics (work in progress).

The model of Raszewski et al. (31) is very close to the Model C from our previous article (35) and to our present model. This is not surprising, because Raszewski et al. used the same low-temperature spectra for normal and modified RCs as we did here. However, they did not include in their modeling the mixing of the excited and CT states, and also restricted themselves to a simple form of the spectral density of exciton-phonon coupling (containing only low-frequency modes). As a result, the model cannot reproduce the vibrational wing of the spectra determined by the high-frequency modes. Furthermore, it should be noted that the coupling to high-frequency modes (in Chl a/b-protein complexes like LHCII, PSII, and PSI) induces much bigger reorganization shifts than the coupling to low-frequency phonons (35,37). That is why the difference between the energies of the pure electronic transitions and the energies of the real states, i.e., dressed with phonons/vibrations, is much more pronounced in our modeling than obtained by Raszewski et al. (31). Due to such differences, the site energies (not including the reorganization shifts) should be taken different in our models, to account for the real (measured) spectral position of the exciton states. This difference cannot be compensated by a simple uniform shift of all the site energies, because the reorganization shift is different for the different exciton states (being proportional to their PR values). In particular, the difference between the site energies for the monomeric and coupled pigments is bigger in our model than in models with lower reorganization values. For example, the difference between the site energies for the peripheral Chlzs (with PR = 1) in our model and in the model of Raszewski et al. (31) is ∼500 cm⁻¹, which is equal to the reorganization shift induced by high-frequency modes. The same difference for the core pigments (with the averaged PR value of 0.4) is ∼200 cm⁻¹. In Table 1 we show the site energies of PSII-RC-core pigments obtained by Raszewski et al. (31) increased by 200 cm⁻¹. The thus-corrected energies are in agreement with our model (and with Model C). Some differences may be connected with the roughness of such a correction taking the average PR value.

Ab initio calculations and reorganization effects

Recently the site energies for PSII-RC have been calculated ab initio by Ivashin and Larsson (51). The calculated wavelengths of the Q_y states are in the 560–580 nm range, i.e., ∼100 nm blue-shifted with respect to the measured values. This difference has been attributed to reorganization effects that were supposed to shift uniformly the entire spectrum. Note that this is a rather questionable point, because in an excitonically coupled system, reorganization effects produce essentially nonuniform shifting of the eigenstates. According to this calculation the red-most are P_D2 (582 nm) and Chl_D2 (581 nm) pigments, whereas P_D1 (573 nm), Chl_D1 (567 nm), and both Phe_D1 (565 nm) and Phe_D2 (572 nm) are on the blue. The relative values of these site energies would be very similar to the Model B (Table 1) after exchange of the active and inactive branch. Clearly, such a configuration can explain the OD and LD spectra (due to D1-D2 symmetry), but is in contradiction with the data for modified RCs (Phe-modified, for example).

Mixing between the exciton and CT states: limitations of the modified Redfield theory

The Stark theory used in our modeling is developed on the basis of purely electronic states, i.e., the mixing of the excited states as well as the mixing between the excited and CT states is supposed to be independent of nuclear coordinates. It is known, however, that in photosynthetic RCs the CT states can be strongly shifted along one or several special nuclear coordinates (52,53). In this case, the lowest exciton state and the first (nearest in energy) CT state should be represented by two potential surfaces with different displacements along effective nuclear coordinates, thus reflecting stronger coupling to phonons for the CT state. In such picture the mixing of the two surfaces near their crossing point will produce some borrowing of the transition dipole strength from the exciton state (making the CT state weakly allowed), and borrowing of the static dipole from the CT state (increasing the amplitude of the Stark signal in the long-wavelength region). This mixing will also induce the transfer from the exciton to the CT state (and the back transfer). Relaxation along nuclear coordinates within the exciton and CT potentials causes a dynamic localization of the excitation/CT-state near the bottom of the corresponding surfaces (note that these regions are only weakly perturbed by the exciton-CT coupling in the case of relatively large displacements between the two states).

The Förster theory allows a calculation of the transfer rates supposing complete localization of the two states without taking into account the mixing of their wavefunctions (thus, excluding all spectral consequences of such mixing, like the red wing of OD, broadening of the FL profile, and the increase of the Stark amplitude). This is valid in the case of big relative displacements of the two potential surfaces and weak coupling between the states. In this approach it is possible to calculate the transfer rates without considering the dynamics of the nuclear coordinates (although arbitrarily strong coupling to all phonon modes is included explicitly).

In the modified Redfield theory the coupling between the two states is supposed to be independent of the nuclear coordinates, giving rise to a uniform mixing of the two potential surfaces. The theory allows the calculation of the relaxation rates between the mixed eigenstates as well as the spectral features induced by such mixing. Arbitrarily strong exciton-phonon coupling (at least its diagonal part) is described by the spectral density function, but the nuclear degrees of freedom are not included as system coordinates. This approach is valid if the reorganization energy associated with the relative displacements of the two states along the nuclear coordinates is smaller than their coupling. Otherwise the degree of mixing will be overestimated, especially in the case of a small energy gap between the two states.

Extrapolation between these two limiting cases (localized and strongly mixed, described by the Förster and modified Redfield theories, respectively) is possible by explicitly including the dynamics along one (maximum two) nuclear coordinates (53,54,60). Due to the limited number of phonon/vibrational modes this approach cannot give a realistic lineshape, making a quantitative modeling of the spectra impossible.

In this article, we consider the mixing between the exciton and CT state as manifested by its contribution to the linear (OD, LD, CD, FL) and nonlinear (Stark) spectra of the PSII-RC. First, we have found that the measured spectra cannot be reproduced when neglecting the exciton-CT mixing. The simplest way to include this mixing is the modified Redfield approach that enables us to reproduce the data at a quantitative level. This approach does not include the dynamic localization, but it gives the same results as the localized (Förster) theory in the case of big energy gaps (that breaks the mixing of the states) (61). Thus, on the one hand, we may expect that the long-wavelength (>690 nm) part of the spectra (determined by realizations of the disorder with a large red shift of the CT state) will not be affected by the Redfield theory artifacts. But on the other hand, the mixing of the exciton and CT states is overestimated (due to use of the Redfield approach) for realizations for which the CT is close to the lowest exciton level, i.e., in the 680–690-nm region. In this region, we can find some realizations with an equal distribution of the dipole strength between the exciton and CT states (see Fig. 6, bottom panel). This redistribution of the dipole strength within the same spectral region does not affect the OD and FL spectra, but can increase the Stark signal in this region due to overestimated borrowing of the static dipole by the exciton states. To estimate how realistic the resulting picture is, one should compare it with a more advanced model where the mixing of the exciton and CT states depends on the vibrational coordinates. This complicated task (connected with serious numerical problems even for a limited number of nuclear modes) is beyond the scope of our present study.

Coupling of the CT states to vibrations

A general property of the mixed exciton-CT states is an enhanced (and strongly temperature-dependent) homogeneous broadening due to much stronger (compared to neutral excited states) coupling of the CT states to phonons. The apparent broadening is determined by a product of two factors: 1), phonon coupling for the CT state; and 2), the degree of the exciton-CT mixing. The strong coupling of the mixed exciton-CT states to vibrations is evidenced by the temperature-dependent OD spectrum of bacterial RCs (as discussed by Renger (62)). The temperature dependence of the spectral shape for the PSII-RC is not as prominent as in bacterial RCs (31,35). This implies that the exciton-CT mixing for PSII-RC is less than in bacterial RC (supposing that the CT states in these two RCs are characterized by comparable values of the phonon coupling). However, the presence of such a mixing in the case of the PSII-RC is well discernible, for example in the temperature dependence of the FL profile (this dependence can only be explained as resulting from some weakly allowed transition below the lowest exciton state). To reproduce the experimental spectra by our model we increased the coupling of the CT states to vibrations (compared to the neutral excited states) by a factor of 1.6. It should be noted that this value is not an exact estimate of the coupling strength for the CT, but some effective value needed to reproduce the data within the limits of the modified Redfield approach. Bearing in mind that modified Redfield theory overestimates the degree of mixing (by taking it to be independent on vibrational coordinates), we may suppose that the real coupling to vibrations for the CT state is larger. If instead of uniform mixing (used in the modified Redfield) we consider a mixing at the crossing point between the two potentials (representing the exciton and CT state), a much-bigger-than-1.6 scaling factor will be needed to produce the same contribution of the exciton-CT mixing to the spectra. However, when using such values in the modified Redfield approach, the spectra (especially FL profile) become unrealistically broad.

Homogeneous versus inhomogeneous broadening of the CT states

A huge static dipole of the CT states suggests an increased value of both homogeneous and inhomogeneous broadening as a result of much stronger coupling to nuclear motion including fast vibrations and slow conformations producing random quasi-static shifts of the transition energies. Large homogeneous and inhomogeneous broadening was observed in hole-burning studies of bacterial RCs (63,64) and the PSI primary donor P700 (64). The absence of narrow holes for the P700 band of PSI was interpreted as a result of an increased Huang-Rhys factor for low-frequency modes up to S = 4–6 due to mixing of the exciton and CT states. Direct calculation shows that an increase in the Huang-Rhys factor reduces the relative amplitude of the zero-phonon line (ZPL) in the hole-burning spectrum, making it almost unobservable at S = 4–6 (64). Such strong coupling to phonons would produce strong homogeneous broadening that is comparable or even exceeds the inhomogeneous width. In recent studies of PSII-cores, the lack of hole-burning activity in the 705–730-nm region was interpreted as an evidence for predominant homogeneous broadening of the CT state associated with the special pair of RC (49).

Here we note that the modeling of Hayes et al. (64) was done within the Condon approximation, i.e., supposing that the transition dipole of the mixed exciton-CT does not depend on the nuclear coordinates, which is only true if the exciton and CT states have the same displacements along the nuclear coordinates thus producing uniform mixing of their vibronic states. In a more realistic picture (where the exciton and CT states have different displacements along the nuclear coordinates) the coupling will be strong only near the crossing point between the potential surfaces. If the CT surface is lower in energy than the lowest exciton state, then the effective coupling (and appreciable borrowing of the dipole strength from the exciton state) will correspond to higher vibrational levels of the CT state, whereas its lowest vibrational state will be only weakly affected. Consequently, the zero-phonon transition of the CT state will remain almost invisible, thus leading to the disappearance of the ZPL even for moderate phonon coupling (i.e., for Huang-Rhys factors <S = 4). This simple example illustrates that the absence of sharp and intense ZPLs in a hole-burning experiment does not necessarily imply very large S-values accompanied by increase of homogeneous broadening. For that reason the conclusion that the spectral profile associated to the CT state of the PSII-RC is predominantly homogeneously broadened (49) remains questionable.

In our previous analysis (35) the ratio of homogeneous versus inhomogeneous broadening for the CT states of the PSII-RC was determined from a fit of the experimental data. It was concluded that a simultaneous fit of the TA and FL kinetics is only possible in the case of predominant inhomogeneous broadening of the CT transitions. The same conclusion was drawn before based on modeling of experimental kinetics by Barter et al. (29). By modeling the Stark spectrum and using very similar parameters as in previous work (35) we obtain the inhomogeneously broadened CT state as illustrated by distribution of ZPLs shown in Fig. 6.

Charge transfer pathways and timescales

The simultaneous fit of absorption (OD, LD, and CD), fluorescence, and Stark spectra allowed us to adjust the parameters of the excited and primary charge-separated state in the PSII RC. Including the Stark spectra into the fit allowed, for the first time to our knowledge, a precise determination of the energy of the highest CT state and the degree of its mixing with the excited states. Such a fit also enabled us to unravel the origin of the primary donor. We conclude that two schemes for charge separation are possible, depending on the realization of the disorder: In the first, charge separation starts with formation of 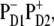while in the second, 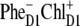is the first charge-separated state.

Our modeling is carried out assuming strong coupling of the initial CT state with the exciton states, as we have seen that this feature is necessary to explain the shapes of the FL and Stark profiles. This also implies that such a strongly coupled CT intermediate must be very quickly populated via relaxation from the exciton states, or even directly populated upon long-wavelength excitation. Therefore, fast dynamics is expected in the spectral regions corresponding to a bleaching of the pigments involved in this initial CT state.

In the scheme where charge separation is started from the 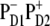state (strongly mixed with the exciton states) this state is populated within 500 fs with a fastest component of <100 fs (35). The following electron transfer to Chl_D1 and Phe_D1 is much slower. The physical modeling of the PSII-RC, assuming 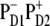is the first charge-separated intermediate (based on quantitative fit of linear and nonlinear spectral responses at room temperature), predicts picosecond dynamics of transient absorption with fastest components of ∼7.5 ps in the Phe-anion absorption band at 460 nm and 12 ps in the Phe Q_x absorption band at 545 nm (35).

If, however, the initial CT state is 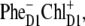the kinetics at 460 and 545 nm will be fast, reflecting sub-ps dynamics of 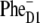formation.

In visible pump-probe experiment, the dynamics of the Phe Q_x band bleaching at 545 nm is superimposed with a time-dependent background due to excited-state absorption. Extraction of the bleaching from the background showed that 40% of the bleaching signal is formed instantaneously, i.e., within the pump pulse (which was ∼200-fs long), whereas the remaining part of the bleaching is developing with time constants of 9 and 54 ps (16). Recent pump-probe data (19) gave the 543-nm kinetics with the time constants of 2–4 ps, 7–11 ps (minor component), and 30–50 ps. In the 460-nm dynamics ∼50% of the signal is determined by a fast component hidden under the instrument response and the remaining part is formed with the time constants of 7 and 48 ps (16). It is difficult to estimate how large the contribution from the background to the 460-nm kinetics is.

Thus, the slow picosecond dynamics in the 460–545-nm region provides direct evidence for a 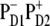configuration of the primary CT state. However, the instantaneous bleach due to initial population of Phe molecules must be ∼20% in the 545-nm kinetics (according to our present model with the 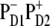configuration) and close to 0% in the 460-nm kinetics. This estimation suggests that ∼20–50% of the 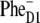formation is determined by fast sub-ps (including very fast sub-100 fs) components. This is only possible if Phe in a significant fraction of the realizations is involved in the initial CT state that is strongly coupled to the exciton states.

Recently the primary charge separation was studied using visible-pump-mid-IR-probe spectroscopy and it was concluded that, after 681-nm excitation at room temperature, the initially formed radical pair contained a significant fraction of 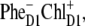which on a timescale of ∼6 ps led to the formation of 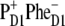(20). In addition much slower charge-separation components were present, which had already been identified in earlier fluorescence experiments (55). Groot et al. (20) suggested that, possibly, the slow phase of charge separation reflected PSII RCs, where Chl_D1 could not operate as the primary electron donor due to unfavorable energetics, and consequently that P_D1 took over, but with a much slower rate. Interestingly, the slow charge-separating states also seemed to correlate with a more blue emission spectrum, intuitively supporting this idea of disorder-controlled pathways.

These arguments support our conclusion that the pathways of charge separation in PSII-RC are strongly disorder-controlled, i.e., charge separation is initiated from 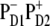or 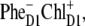depending on realization of the disorder. In such a scheme, both fast (sub-ps) and slow (from few picoseconds to dozens of picoseconds) components should be present in the Phe Q_x and 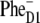kinetics. In this respect it would be highly relevant to analyze the wavelength dependence of the visible-pump-mid-IR probe kinetics on the basis of the model proposed here.

CONCLUSIONS

We propose an exciton model of PSII-RC based on a quantitative simultaneous fit of all the available spectroscopic data, including those obtained for chemically modified PSII-RCs. In this model the excited state manifold includes a primary CT state that is supposed to be strongly mixed with the pure exciton states. We show that fluorescence and Stark spectra are extremely sensitive to the assignment of the primary CT state, its energy, and coupling to the excited states. The best fit of the data is obtained supposing the initial charge separation within special pair. The scheme with primary electron transfer from the accessory Chl to Phe also gave a reasonable quantitative fit. We reason that these two pathways compete, and that the relative effectiveness of these two pathways is strongly dependent on realization of the energetic disorder. Supposing a mixed scheme of primary charge separation with a disorder-controlled competition of the two channels we can explain a coexistence of fast sub-ps and slow ps components of a Phe-anion formation as observed in many time-resolved experiments.

APPENDIX: STARK SPECTRA OF MOLECULAR AGGREGATES

Stark spectroscopy is a powerful tool for studying the excited and charge-transfer states in diverse systems from isolated molecules to complicated molecular aggregates in biological systems (56,57). The simplest interpretation can be done using Liptay's theory based on a perturbed eigenstate approach (58). This theory does not include contributions from the excitonic interaction between chromophores. In many cases, the exciton couplings cannot be ignored; more general exciton theory should be used. Somsen et al. (50) developed the theory where exciton couplings were included explicitly, and performed a detailed comparison of this theory and Liptay's approach. They calculated the Stark signal using both Green function and the sum-over-state approaches within the limits of a modified rotating-wave approximation (modified RWA). Their version of the modified RWA implies a retaining of resonant terms containing both permanent (static) and transition dipoles together with the first-order off-resonant terms that do not include permanent dipoles. This approximation is valid in the case of exciton-coupled molecules, where permanent dipoles are much smaller than the transition dipole moments. However, this is not the case if exciton states are mixed with the charge-transfer (CT) states (carrying huge static dipoles).

Here we calculate a Stark response using the sum-over-state method in the basis of the exciton states (including mixed exciton-CT states). In our approach we use an extended version of the modified RWA, taking into account all the pathways with all possible combinations of the transition and static dipoles, but containing no more than one off-resonant contribution. First, we derive the Stark signal using the density matrix equation with the standard Redfield relaxation tensor. Then we generalize the result by using the modified Redfield theory.

The density matrix approach (standard Redfield theory)

We consider an aggregate containing N excited states (that can be S₀→S₁ excitations and charge-transfer states). Two-exciton manifold consists of N(N+1)/2 states including excitations of molecular pairs (or molecular excitation plus charge transfer state) and double-excited states (S₂) of one molecule (or excited state of a charge-transfer complex). The system Hamiltonian in the eigenstate basis is

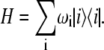(1)

where index i takes values g (ground state), k, k′,… (for N one-exciton states), q, q′,… (for N(N+1)/2 two-exciton states), and ω_i are the energies of the corresponding states. The interaction with an optical and static field is described by

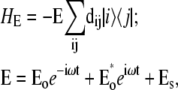(2)

where d_ij is dipole moment for the j→i transition. The absorption and Stark spectra are

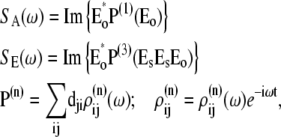(3)

where P⁽ⁿ⁾ denotes the nonlinear (n^th order) polarization amplitude expressed through the amplitudes of the reduced density matrix. The density matrix is given by the Liouville equation with the Redfield relaxation operator describing a system-bath interaction:

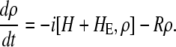(4)

Expansion in eigenstates allows us to obtain the n^th order amplitudes as

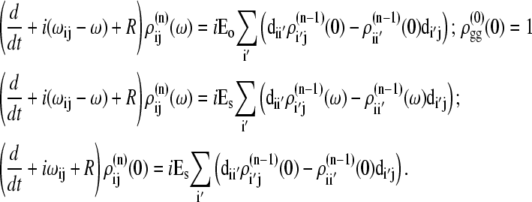(5)

Here, ω_ij = ω_i−ω_j, R is a fourth-rank relaxation tensor. For the steady-state absorption spectrum we get

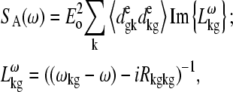(6)

where d^e denotes a projection of the dipole moment on E_o. The angular brackets indicate an averaging over orientations of the aggregate with respect to the fields (for random orientations 〈…〉 = 1/3|d_kg|²). We suppose that the ground-to-excited state coherence transfers (given by the R_kgk′g elements) are negligible (secular approximation). This gives us a Lorentzian lineshape. The linewidth R_kgkg includes the relaxation-induced broadening and pure dephasing. Both these values can be expressed through the exciton wavefunctions and the spectral density of exciton-phonon coupling (59). A homogeneously broadened spectrum given by Eq. 6 should be averaged over realizations of the static disorder.

The Stark response is a sum of many different pathways shown in Fig. 10. We use a modified RWA retaining all the pathways containing no more than one off-resonant contribution, i.e., 14 pathways shown in Fig. 10. In Fig. 10, diagram 1 corresponds to the pure RWA limit, giving the Stark signal

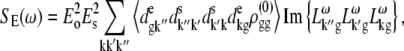(7)

where d^s denotes a projection of the dipole moment on E_s. Transitions within the one-exciton band are possible due to difference between the ground-and excited-state permanent dipoles. If the optical frequency is in resonance with the one-exciton transitions, i.e., ω−ω_kg ≪ Ω, where Ω ≈ ω_kg ≈ ω (implying that the exciton splitting ω_k'k is small compared with Ω), then all the three lineshape functions L in Eq. 7 will be resonant. Fig. 10, diagrams 2–6, give contributions

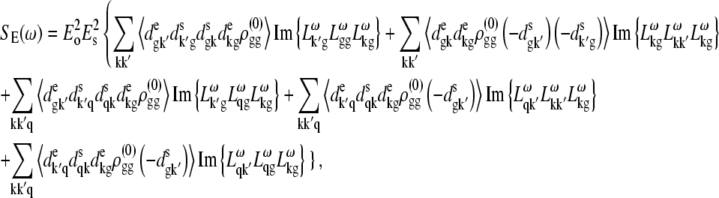(8)

containing only transitions dipoles and one off-resonant factor, i.e.,

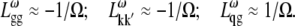(9)

FIGURE 10.

Contributions to the Stark signal due to transitions between the ground state (g), one-exciton (k), and two-exciton states (q) induced by interactions with an optical (open arrows) and static (solid arrows) fields. Diagram 1 corresponds to a pure RWA, diagrams 2–6 and 9–14 correspond to a modified RWA with one off-resonant interaction depending on transition dipoles, and diagrams 7 and 8 contain one off-resonant interaction that depends on permanent dipole.

Notice that in Fig. 10, diagrams 3 and 5, the second interaction creates the one-exciton populations ρ_kk (and coherences) ρ_kk′ oscillating with the optical frequency Ω ≈ ω. The population and coherence transfers between the second and third interaction are negligible, being determined by nonsecular terms. For example, the transfer of population ρ_kk(Ω) (through the k→k″ relaxation pathway) will create population ρ_k″k″(Ω) ∼ (R_k″k″kk/Ω)ρ_kk(Ω). This is in contrast with effective transfers between nonoscillating ρ_kk(0) populations created via resonant interactions (for example, in the pump-probe scheme). Thus, the relaxation dynamics is not included in Fig. 10, diagrams 3 and 5. In Fig. 10, diagrams 4 and 6, we also do not include a transfer between the ground-to-two exciton coherences ρ_qg (given by the R_qgq′g elements).

In the case when difference permanent dipoles are much less than transition dipoles, the off-resonant contributions in Eq. 8 can be comparable with the resonant term given by Eq. 7. Combination of these two types of terms is known as the modified RWA (50). Notice that two last terms in Eq. 8 corresponding to Fig. 10, diagrams 5 and 6, are cancelled according to Eq. 9.

The next two contributions (Fig. 10, diagrams 7 and 8) contain one off-resonant factor and permanent dipoles,

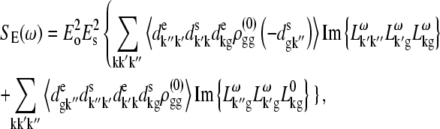(10)

with

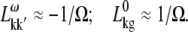(11)

Finally, Fig. 10, diagrams 9–14, give canceling contributions. Notice that Fig. 10, diagrams 9 and 10, are presented by one diagram, where the static field acts on the same levels but from different sides of the density matrix. The corresponding second-order density matrix amplitudes are cancelled:

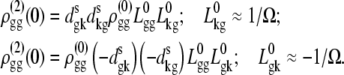(12)

Similarly, for Fig. 10, diagrams 11 and 12 (as well as for diagrams 13 and 14),

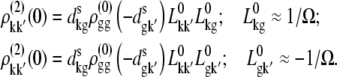(13)

Combining Eqs. 8–11, we obtain the Stark signal in a form

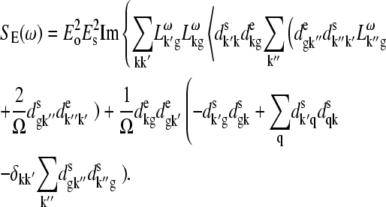(14)

Equation 14 contains five terms: the first one (with the product of the three line functions) containing only resonant contributions and two permanent dipole moments; the second term with one off-resonant contribution (proportional to /Ω) and two permanent dipoles; and the group of three terms with one off-resonant contribution and without permanent dipoles. If we neglect the second term (which is relatively weak in a purely exciton system, i.e., without mixing with charge-transfer states), then Eq. 14 becomes identical to the expression of Somsen et al. (50).

The dipole moments in Eq. 14 can be expressed through the S₀→S₁ (d_n) and S₁→S₂ (d_nn) transition dipoles and the difference between the S₁ and S₀ permanent dipoles (Δd_n) for the n^th excited state. Here, index n numbers the three-level molecules and the charge-transfer states. In the latter case, d_nn corresponds to D⁺A⁻ →(D⁺A⁻)* transition that can be dipole-allowed, whereas the D⁺A⁻ state itself is forbidden, i.e., d_n = 0. The permanent dipole Δd_n of the D⁺A⁻ state can be much higher than that of the molecular excited state S₁. In the eigenstate basis we get

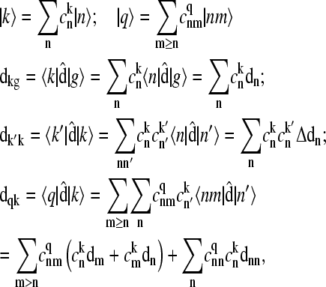(15)

where the dipole moments and wavefunction amplitudes and 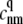are taken to be real. Using normalization rules for the wavefunctions,

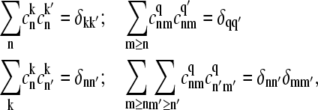(16)

we rewrite Eq. 14 in more compact form as

(17)

In the case of random orientation of the aggregates, the averaging rules (for parallel, perpendicular, and magic-angle orientations of the optical and static fields) are

(18)

For example, the magic-angle Stark signal is given by

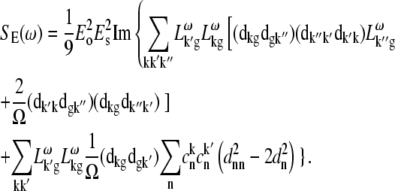(19)

The modified Redfield theory

In the modified Redfield approach, the lineshape functions (given by Eq. 6 in the standard Redfield theory) should be replaced by

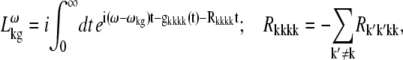(20)

where ω_kg corresponds to the first moment of the absorption and g_kkkk is the line-broadening function the k^th state. The relaxation-induced broadening of the k^th state is given by a sum of the k→k′ relaxation rates. The modified Redfield tensor and line-broadening functions are given by (46)

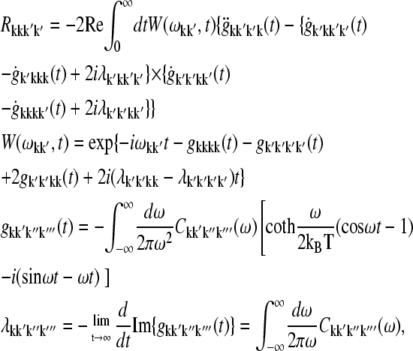(21)

where ω_{kk′ =} ω_kg−ω_k′g, C_{kk′k″k‴}(ω) is the matrix of the spectral densities (in the eigenstate—i.e., exciton—representation), which determines the line-broadening functions in Eqs. 20 and 21, and reflects strong coupling of one-exciton states to a manifold of nuclear modes.