Dynamical Control of the Shape and Size of Stereocilia and Microvilli

Abstract

We discuss theoretically the shape of actin-based protrusions such as stereocilia or microvilli that have important functions in many biological systems. These linear protrusions are dynamical structures continuously renewed by treadmilling: actin polymerizes at the tip of the cilium and depolymerizes in its bulk. They also often have a well-controlled length such as in the hair bundles of the inner ear cells where they appear in a graded staircase structure. Recent experimental results by another group of researchers show that the treadmilling velocity of the hair cell stereocilia is proportional to their length. We use generic arguments to describe the physics of stereocilia taking into account the effect of many individual proteins at a coarse-grained level by a few phenomenological parameters. At the tip of the cilium, we find that actin polymerization induces an effective pressure. Below the tip, the shape of the cilium is determined by depolymerization: Agreement with the observed shape requires that depolymerization occurs at least in two steps. Under these conditions, we calculate the cilium shape and provide physical grounds for the proportionality between treadmilling velocity and cilium length. We also calculate the penetration of the stereocilium in the actin cortical layer.

INTRODUCTION

Actin-based protrusions play an important role in cell biology (1,2). They extend either in a planarlike fashion as in lamellipodia or linearly as in filopodia (3), microvilli (4), or stereocilia (5–7). In both cases, the actin polymerization/depolymerization process controls the protrusion dynamics. Assembly takes place at or very near the plasma membrane and disassembly occurs deeper in the cell.

Whereas the actin network in lamellipodia is significantly branched and can be remodeled under the action of molecular motors such as myosin II (8), it is composed of tightly bundled parallel filaments in the linear protrusions (3). Ciliated structures are ubiquitous in epithelial tissues and their physiological function can vary considerably from cell type to cell type (1,2). Examples are the brush-border ciliated cells of the intestine or the stereocilia of inner ear cells.

Stereocilia present two remarkable features (5–7): they can be as long as 100 μm and they are assembled in groups of 50–100, called a hair-bundle. In a given hair-bundle, a stereocilium length can range from a few microns to 100 μm. One can thus compare stereocilia of different lengths in the same cell. Furthermore, the scale is large enough that accurate dynamical studies can be performed. It has been clearly shown that:

• The polymerization process takes place at the tip of the cilia (9).

• In a given cell, the steady-state cilium length is proportional to the actin polymerization rate, i.e., to the treadmilling velocity; in other words, irrespective of their length, cilia are renewed in a given time, typically two days (10). Note that, between different cells such as cells of the organ of Corti and cells of the vestibule, this time can be different.

• In a given cell, thick cilia are longer than thin ones (11,12).

• Biopolymer cables, called tip-links, connect adjacent cilia and deform the tip of the smallest cilia in a characteristic way: tallest cilia which are not deformed by tip-links are oblate or quasi-spherical, whereas smaller ones which are deformed are prolate or pointed, the tip being tilted in the direction of the cable (13,14).

• The base of the cilia, which is tapered, extends significantly into the cell cortex (15).

To avoid any confusion, in the following, we call fascicle the parallel network of actin filaments and bundle the group of cilia in hair cells.

These experimental observations raise the following questions:

• Why is the treadmilling velocity proportional to the length?

• What is the relationship between cilium diameter and length?

• What does determine the root and emerging part of the cilium?

• Can the observation of the shape of a cilium provide information on the nature and intensity of the forces involved in the process?

It would be ideal to answer those questions starting from a molecular level. This is, however, too complex a task: the number of proteins present in a cilium is by far too large and their structures by far too complex to allow for a detailed description. For instance, at the tip of a cilium an electron dense region has been observed, called the tip-complex, in which all proteins have not yet been identified (10). Even the outer membrane embracing a cilium cannot be described in all of its details. We thus have to adopt some level of coarse-graining.

We describe the membrane as a flexible surface under tension, a procedure that is well accepted now (16). The actin filaments are cross-linked in stereocilia by proteins such as espin (11). We consider here the actin fascicle as a solid body made of close-packed filaments that all move at the same treadmilling velocity. The filaments polymerize at their barbed end located at the cilium tip and depolymerize statistically in the bulk of the fascicle (1,10). The depolymerization is hindered by binding proteins such as espin or possibly by specific minus end capping proteins. On the sides of the cilium, the fascicle/membrane interaction can be characterized by a standard interaction energy per unit area.

At the tip, the actin-growing front is interacting with the membrane: we write generic dynamical equations showing that the polymerization process generates an effective pressure, which depends on the difference between the “would-be” polymerization rate in a stress-free situation and the actual polymerization rate. This formulation is model-free in the sense that the parameters involved could be measured in independent experiments. Alternatively the parameters could be extracted from molecular theories such as the polymerization-ratchet model (17,18), or a model describing the role of formins (19). For stereocilia, the polymerization process is known to depend on the presence of myosin XV (20,21), via a mechanism yet to be understood and the role of the tip complex is essentially unknown. For these reasons, we concentrate in this manuscript on those results, which do not depend on molecular details. This is in particular the case for the cilia shape and the forces involved. Recently, a theoretical description of filopodia has been proposed in which the interaction of the polymerizing filaments with the membrane is described by a ratchet model (22). This description is useful as it stresses the necessity of a certain degree of bundling to obtain long enough filopodia. The obtained shapes are, however, valid only if the fascicle radius is much smaller than the natural radius of membrane tubes pulled by a point force in the absence of actin. Furthermore, neither the lateral fascicle-membrane interaction nor depolymerization is considered. In a cilium, the diameter is significantly larger than the natural tube radius; the fascicle-membrane interaction and depolymerization are essential features of the cilium dynamics.

Our article is organized as follows. In Shape of the Tip, we discuss the shape of the tip of a cilium both in the absence and in the presence of tip links. In particular, we obtain a general relation between polymerization rate and cilium radius. In Shape of the Stem, we describe the depolymerization in the fascicle and deduce the shape of the associated stem. Membrane Shape is devoted to the shape of the membrane surrounding the cilium. In Partition between Emerged and Immersed Parts of the Fascicle, we study the interaction of the cilium with the cortical actin layer and the partition of the cilium between an emerged and an immersed part. In the Discussion, we extract from the experimentally observed shapes the typical forces involved in cilia and discuss the role of specific proteins such as espin, myosin XV, or myosin VI.

SHAPE OF THE TIP

Oblate shape of the tip in the absence of tip-link

The polymerization process at the tip of the cilia is complex, and involves, in general, regulation by several proteins. A good example is given by proteins of the formin family (23,24), which build complexes with the barbed ends of the actin filaments: they regulate the actin critical concentration and are very sensitive to forces of approximately picoNewtons; their activity requires ATP hydrolysis. In the case of stereocilia, the role of myosin XV has been evidenced (21): this motor could simply push the membrane to help provide space for the addition of new monomers (20). PicoNewton forces are again large enough to severely modify the polymerization rate. More generally, other proteins such as ezrin are known to regulate the polymerization process (25,26).

In view of the complexity of the phenomena involved at a molecular level, it is useful to develop a model free formulation. We first write generic equations valid for “weak forces,” and then extend our results to account for strong nonlinearities in Appendix A.

The physics of the tip growth is governed by the existence of two physically coupled surfaces: the plasma membrane and the actin polymerization front. The plasma membrane represented in Fig. 1 is characterized by its shape and normal velocity, which depend on its effective tension, its curvature modulus, and the forces that the polymerizing front exerts on the membrane. The polymerizing front in turn is also characterized by its shape and velocity along the actin axis and the force that the membrane exerts on the front. According to Newton's third law, the force exerted by the membrane on the front is equal and opposite to the force exerted by the front on the membrane.

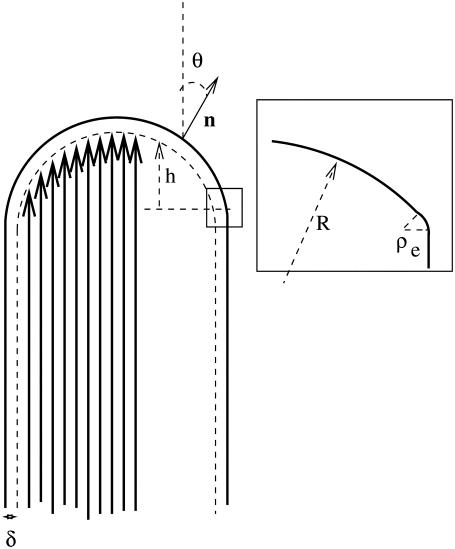
FIGURE 1.

Geometry of the tip of the cilium: the actin filaments are parallel to the vertical axis and their barbed end is in the direction of the arrow. The polymerization front is represented by a dashed line at a distance δ from the membrane (continuous line). The inset shows the crossover to the stem region with an edge of radius of curvature ρ_e.

We parameterize the membrane shape by a vector r(x) (where x is a two-dimensional vector giving the coordinates in the plane perpendicular to the stereocilium) and the front by the local height along the direction parallel to the cilium axis, h(x) as defined on Fig. 1.

At linear order in the force, the coupled dynamical equations for the motion of the two fronts read

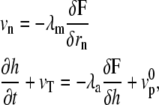(1)

where v_n is the velocity normal to the membrane, r_n the local coordinate along the normal n to the membrane, and 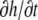the velocity of the actin front in the z direction; both velocities are defined in the cell rest frame.

These equations describe the average shape of the membrane-actin front interface. Both the polymerization front and the membrane are fluctuating. Equation 1 should thus include generalized fluctuating forces. In this work, we omit them since we only consider the average behavior.

The dynamical equations involve two positive dissipative coefficients λ_m and λ_a. A more general formulation would also include cross-terms, but this would lead to the same results with a slight difference in the definition of the pressure defined below. Both λ_m and λ_a can, in principle, be measured experimentally. Indeed, λ_m is a mobility coefficient relating the membrane velocity to an applied force and λ_a describes the force dependence of the polymerization rate due to the membrane. The dynamic equations automatically satisfy the local force balance.

The treadmilling velocity v_T is the velocity of the actin monomers counted as positive toward the base of the cilium; the polymerization velocity 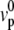is the polymerization velocity for a flat unperturbed actin front at the equilibrium distance δ₀ from the membrane (δ₀ is defined more precisely below).

The total free energy of the system ℱ is a functional of both the membrane position r(x) and the front height h(x). We write it as 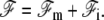The membrane free energy 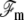at a distance δ₀ from the fascicle front involves a tension contribution, a curvature contribution, and a pressure term:

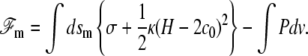(2)

Here, ds_m is the surface element parallel to the membrane. The energy per unit area σ of the membrane in interaction with the front at a distance δ₀ depends both on the number of phospholipids per unit area, and on the interaction energy of that membrane with the actin fascicle, in particular via linking proteins. As a result, σ depends, in principle, on the angle θ between the membrane normal and the fascicle axis. The value κ is the membrane curvature modulus, H the total local curvature, and c₀ a spontaneous curvature that exists when the membrane is asymmetrical. P is the hydrostatic pressure difference between the inside and the outside of the cilium. Note that the only difference with the standard Helfrich free energy of membranes is in the θ dependence of the tension σ.

The interaction energy between the membrane and the fascicle front 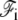can be expanded in powers of the perpendicular distance δ between the tip of the actin filaments and the membrane. To lowest order, we write:

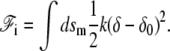(3)

Here, k is a spring constant per unit area, and δ₀ the membrane-front average distance at thermal equilibrium. Both k and δ₀ depend on the membrane characteristics and on the nature of the linking proteins between the membrane and the fascicle front. They provide a coarse-grained description of the tip complex and its interaction with the membrane. The equilibrium distance δ₀ might, in general, depend on the angle θ between the membrane normal n and the cilium axis 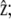in a first approximation, we ignore this orientational dependence. The membrane-front distance is 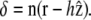The detailed calculation of the derivatives of the interaction free energy is given in Appendix A and leads to

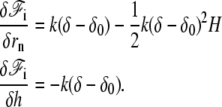(4)

At steady state (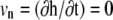), the shape equation of the membrane is then obtained from Eq. 1:

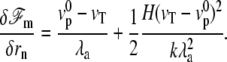(5)

This equation is formally equivalent to the equilibrium equation of a membrane submitted to an effective hydrostatic pressure difference and effective tension:

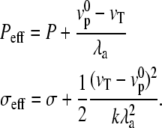(6)

We show in Appendix A that this result is general and that even for the full nonlinear problem the effect of treadmilling can be recast in the form of an effective pressure and an effective membrane tension.

Note that the shape Eq. 5 implies that, for any treadmilling velocity v_T, there is, in general, a unique solution for the membrane shape (16). Equation 5 implies also a global force balance 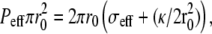where r₀ is the fascicle radius at the edge of the tip where θ = π/2 and the effective tension σ_eff is calculated for an angle θ = π/2. The global force balance determines the effective pressure, i.e., the difference between the treadmilling velocity and the bare polymerization velocity for a given fascicle radius r₀. In the limit where there is no pressure difference P = 0, we find, in a linear approximation,

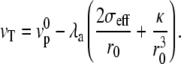(7)

We have neglected here the treadmilling contribution to the tension, which is of higher order. This relation imposes that thicker cilia have a larger treadmilling velocity at constant polymerization velocity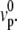

The shape of the tip may be described by three regimes:

• Large tips (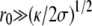). One can distinguish two regions as shown on Fig. 1: the central region essentially spherical with a radius R = 2σ_eff(θ = 0)/P_eff and the edges with two principal radii of curvature, a small radius of curvature 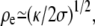and a large one equal to r₀.

• Small tips (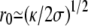). The central region disappears and the tip is almost spherical with a radius (κ/2σ)^1/2.

• Small fascicles (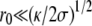). This case is discussed in Atilgan et al. (22) and has been observed with microtubules bundles in vesicles (27). The fascicle acts as a point force on the membrane, and the results of Derényi et al. (28) hold. This regime only exists if the membrane does not adhere to the filaments which is possible if the energy of the nonadhering membrane is smaller than that of the adhering one, 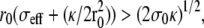where σ₀ is the tension of the nonadhering membrane.

Prolate shape of the tip in the presence of tip-link

As already mentioned, in a hair cell, the hair-bundle has a graded array of stereocilia. The stereocilia in one row all have the same size and are connected to larger stereocilia in the next row by tip-links. It has been shown that the larger stereocilium exerts a point force on the smaller ones via the tip-link. A point force f in the direction of the tip must therefore be included in Eq. 2. In the presence of this force the shape of the stereocilium is no longer rotationally symmetric and one must rely on numerical methods to find it. We used the Surface Evolver program (29) in the same way as in Derényi et al. (28). We give examples of the obtained shape on Fig. 2. Fig. 2 a corresponds to no force and no polymerization pressure; Fig. 2 b corresponds to no force and finite polymerization pressure; and Fig. 2 c corresponds to a finite polymerization pressure and a finite force.

FIGURE 2.

Shape of the tip of a stereocilium. (a) Shape with no polymerization pressure and no force; membrane tension σ = 5 10⁻⁵ N/m, bending modulus κ = 10 kT. Note the flat region in the center, corresponding to the absence of polymerization pressure. (b) Shape with a polymerization pressure P_eff = 9 10³ Pa and no force; membrane tension σ = 5 10⁻⁵ N/m, bending modulus κ = 10 kT. Note the curvature difference between the central region and the edges as described in the text. (c) Shape with a polymerization pressure P_eff = 6 10³ Pa with an external force of ∼20 pN; σ = 5 10⁻⁵ N/m, bending modulus κ = 45 kT. Note the prolate shape due to the tip-link pulling force.

The set of dynamical expressions in Eq. 1 describes the tip shape due to the polymerization kinetics. It can no longer be used below the location z = 0, where the membrane tangent is parallel to the cilium axis. From there on, no polymerization occurs, but instead a statistical depolymerization takes place. We describe this process, which controls the shape of what we call the stem, in the following section.

SHAPE OF THE STEM

The actin fascicle being solidly held together by binding proteins such as filamin and espin, it can be considered as incompressible to a very good approximation. This allows us to discuss the shape of the fascicle independently of that of the membrane in this part of the cilium.

For the discussion of the stem shape of a long cilium, we can ignore the tip curvature and suppose that all filaments have their barbed ends in the same plane. The radius of the cilium in this plane is the radius r₀ at the base of the tip. If the surface density of actin barbed ends perpendicular to the fascicle axis is c_s, the number of actin filaments is 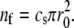Actin filaments polymerize at their barbed ends with a polymerization rate k_p and depolymerize at their pointed end located inside the fascicle at a rate k_d. The treadmilling velocity is v_T = k_pa, where a is the size of an actin monomer.

In physiological conditions, it is likely that actin filaments pointed ends are capped by various capping proteins when they are formed. We consider here one of these capping proteins and assume that it controls the depolymerization, which is possible only if the filament is uncapped. The uncapping rate of the pointed ends is k_u. For simplicity, we ignore here recapping events and we suppose that once a filament is uncapped it depolymerizes at its pointed end. A full calculation including recapping events leads to similar results. Bundling proteins can also prevent depolymerization and can be treated in essentially the same way.

We first study the distribution of the pointed ends in the fascicle. There are capped pointed ends and uncapped pointed ends. We call p^c(n) the probability to find a capped pointed end of an actin filament containing n monomers, and p^u(n) the probability to find an uncapped pointed end of a filament containing n monomers. The master equation for these two probabilities (30):

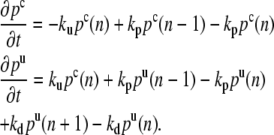(8)

When an uncapped pointed end depolymerizes, the size of the corresponding filament decreases and the filament disappears when all monomers have depolymerized. Therefore p^u(n = 0) = 0. In a steady state, statistically, the loss of filaments is balanced by the appearance of new filaments. The formation of new filaments occurs by a nucleation process, the minimal seed for growth being of the order of three or four monomers. There is a finite flux of new actin filaments in the fascicle and the probability p^c is finite close to the polymerization plane. This probability is defined for a number of monomers larger than the seed size. A steady state of the fascicle then exists with filaments of different lengths having been created at different times.

The steady-state solution of the master equation with these boundary conditions is

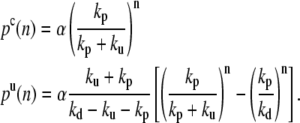(9)

The constant α is fixed by the normalization below. Note that the distribution of endpoints decreases to zero when n is large only if k_d > k_p, which we assume below.

The distance z between a fascicle section and the tip of the fascicle can be labeled by the number of monomers m = z/a between this section and the barbed end of the actin filament. The number of actin filaments in section m is related to the total probability of finding a pointed end in the fascicle p^e(n) = p^c(n) + p^u(n) by 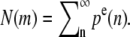Imposing the total number of barbed ends at z = 0, we find

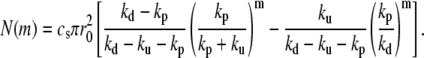(10)

The incompressibility of the actin fascicle then directly gives the shape of the fascicle. The radius r at a distance z from the plane of the polymerizing barbed ends is deduced from the relation N(m) = c_sπr²(z):

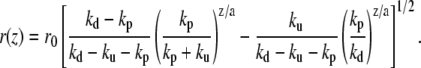(11)

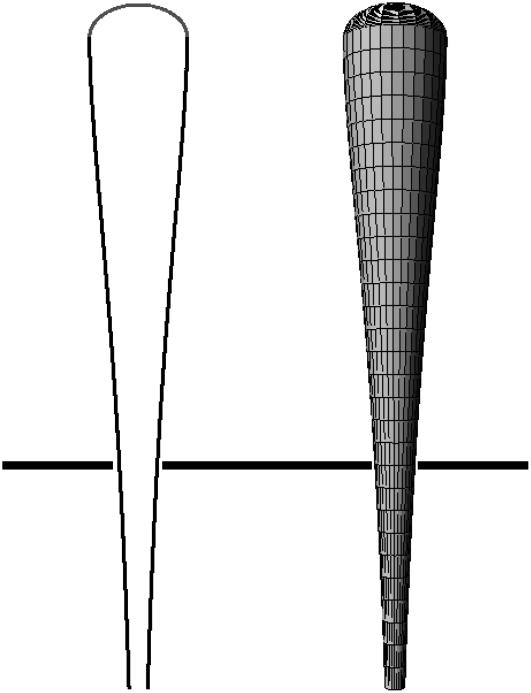
We show, in Fig. 3, a typical fascicle stem shape calculated from this equation.

FIGURE 3.

Two-dimensional shape and three-dimensional reconstruction of a cilium calculated from Eq. 11. The tip has been added. The parameters are k_u/k_p = 0.05 and (k_d − k_p)/k_p = 0.055. These values have been chosen to reproduce the experimental shapes of Fig. 6 of Rzadzinska et al. (10).

The weight average length of the actin filaments can be calculated from the monomer distribution

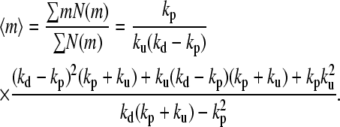(12)

We consider, in the following, the limit where depolymerization is faster than polymerization and where uncapping is the slowest event 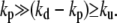In this case, at large distances the radius of the cilium decreases exponentially as 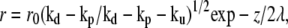where 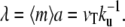The length of the fascicle can be defined by imposing that the fascicle radius must be larger than a monomer size and is given by

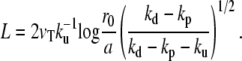(13)

We here recover the law found experimentally by Rzadzinska al. (10), stating that the treadmilling velocity in a stereocilium is proportional to the fascicle length. The ratio between the length and the velocity defines a timescale governing the length of the filaments. This time is the detachment time 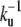of the capping protein from the actin filaments pointed ends required for depolymerization.

In the vicinity of the tip, the profile is almost perfectly cylindrical and the curvature is oriented toward the cilium inside. If k_d − k_p and k_u are not very close (as in Fig. 3), the shape is similar to the experimental shapes observed in Rzadzinska et al. (10) in the situation where the Myosin XV have been knocked out. Normal fascicles containing Myosin XV have a more cylindrical shape (15). In our model the shape gets closer to a cylinder if 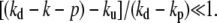Our model can also be extended by assuming that not only one capping protein is involved before depolymerization but that several capping proteins must unbind in a sequential order. Depolymerization could also occur preferentially on the surface of the fascicle in contact to the membrane. These improved models are not presented here for simplicity, although they would lead to more cylindrical shapes that are closer to the experimental ones.

MEMBRANE SHAPE

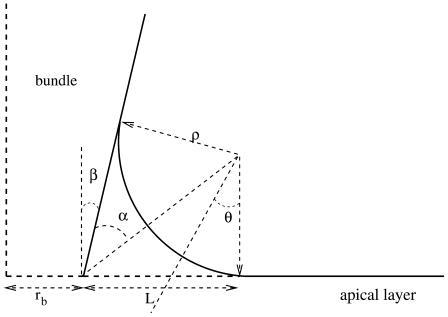
In the discussion of the tip, we have already discussed the membrane shape. In this section, we consider the membrane along the stem and its connection to the apical side of the actin cortex (Fig. 4).

FIGURE 4.

Membrane shape in the vicinity of the apical layer. The membrane adheres to the fascicle on the left and to the apical layer on the right. There is no adhesion in the intermediate transition region.

We distinguish three domains.

The stem domain

The membrane is bound to the fascicle via connecting proteins. There is only one equilibrium equation: 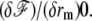In practice, the spring constant k and the distance δ₀ might differ from the one used in the tip discussion. However, since δ₀ is a molecular length, for all practical purposes in this regime the shape is the same as that of the fascicle. The argument is particularly simple in the limit of “slow” shape variation 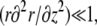but holds quite generally. In this regime, the equilibrium equation yields

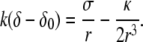(14)

This leads to 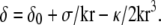Since (σ/k)^1/2 and (κ/k)^1/4 are both microscopic lengths of order δ₀ and r is a mesoscopic length, we obtain 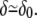For exactly the same reason, once δ is replaced by its equilibrium value, the free energy to be used is to a good approximation,

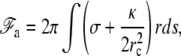(15)

where ds is the arc length element along the cilium contour, and r(s) is the shape of the cilium given by the solution of Eq. 11. The local radius of curvature of the cilium is r_c = r/cos β, where β is the local angle between the tangent to the cilium and the vertical axis. The integral runs over the portion of the fascicle on which the membrane adheres. As already mentioned, the tension appearing in Eq. 15, contains both the intrinsic tension of the membrane σ₀ and the fascicle-membrane adhesion energy γ, σ = σ₀ − γ.

Region connected to the apical cortex

The arguments used in the preceding paragraph can also be used for the membrane adhering to the apical cortex with the proviso that δ₀, γ, and k take on different values which we denote with primes. The membrane is thus flat, at a distance δ′₀ from the apical cortex, and the energy reads

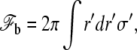(16)

where σ′ = σ₀ − γ′ and where the sum runs over the region where the membrane adheres to the cortex.

Transition region

In the transition region, the membrane adheres to neither the fascicle nor the cortex. The detailed calculation of its shape is fairly heavy, but to a good approximation, it is a portion of torus that is tangent to both stem and apical membrane, and of radii of curvature −ρ and r/sin θ, as shown in Fig. 4. The free energy of the cilium reads

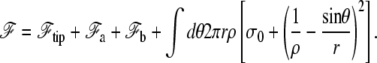(17)

The value 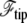is the free energy of the cilium tip. The last integral of Eq. 17 runs over the nonadhering region of the membrane, r depends on θ and in our approximation, ρ is constant. The membrane geometry is displayed in Fig. 4 and the details of the calculations are given in Appendix B.

Because the treadmilling timescales are, in all circumstances, very slow compared to membrane response times, the value of ρ is the value which minimizes the free energy 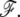Note that 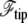disappears from this minimization procedure (Appendix B) since it does not depend on ρ.

One can identify two simple limiting regimes. If the radius at the base r_b is larger than ρ, the radius of curvature in the nonadhering region is

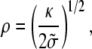(18)

where

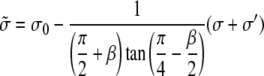(19)

is an effective tension of the membrane. The radius ρ of the transition region is independent of the radius at the base r_b. The extent of the transition region is of the same order of magnitude as the diameter of phospholipid tubes pulled by point forces (28), typically several tens of nanometers.

In the opposite limit where r_b ≪ ρ, we obtain a similar result with a different effective tension as

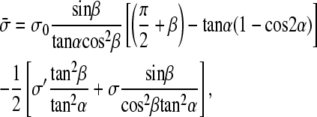(20)

where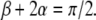

PARTITION BETWEEN EMERGED AND IMMERSED PARTS OF THE FASCICLE

In this discussion we have not yet specified what determines the length L_o of the cilium sticking out of the apical membrane (and equivalently the length L_i penetrating the apical actin cortex of the cuticular plate). Because treadmilling timescales are very long compared to the membrane timescales, we can totally ignore any friction terms due to interactions between the membrane and the fascicle. The force f_m exerted by the membrane on the fascicle is due to the fact that a change in the length L_o of the emerging part changes the total free energy of the membrane keeping the fascicle shape constant. It is calculated by proper differentiation of the membrane free energy as a function of L_o, 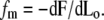The explicit calculation is given in Appendix B. In the limit where the radius at the apical level r_b is much larger than the radius of curvature of the transition region ρ, the force reads

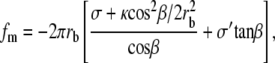(21)

where, as in the previous paragraph, σ and σ′ are the membrane tensions in the stem region and in the apical region, respectively. Note that, for most practical purposes, the term due to the bending energy is small, the fascicle is very elongated, and 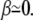In this limit, the contribution to the membrane force of the membrane adhering to the apical surface is negligible. The fascicle radius at the apical surface is given by the shape of the stem obtained in the previous section. We use here the simplest approximation r_b = r₀ exp − (L − L_i)/2λ, where r₀ is the radius at the tip and L = 2λ log(r₀/a) is the total length of the fascicle, and 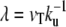as defined in Shape of the Stem.

The membrane force is balanced by the force on the fascicle due the cortical actin layer. As the treadmilling velocity is very slow, the interaction between the cortex and the fascicle can be described as a viscous friction force proportional to the treadmilling velocity v_T. Images of the fascicle root obtained by electron microscopy show that the fascicle remains tightly assembled; it can thus be considered as a solid penetrating the apical layer that we describe here as a liquid of viscosity η. This is licit as long as the cross-linking protein binding time (of the order of minutes) is small compared to the treadmilling time (of the order of one day). As in most of the electron micrographs, we assume here that the penetration depth L_i of the fascicle is smaller that the cortical layer thickness w. The hydrodynamic friction force on an elongated body is given by

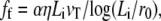(22)

where α is a numerical prefactor of ∼2π (31).

Equating the two forces, we obtain an equation for the penetration depth in the cortical layer

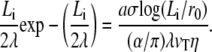(23)

If 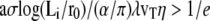where log e = 1, Eq. 23 does not have any solution and the fascicle is completely immersed in the apical layer. This occurs if the membrane tension is too large or if the viscosity is too small.

If 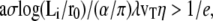Eq. 23 has two solutions, a solution smaller than 2λ and a solution larger than 2λ. Only the first solution is physical as it decreases with the viscosity.

When 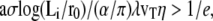there is a discontinuous transition between a totally immersed fascicle and a fascicle with a finite penetration depth L_i = 2λ. Note that a typical value of the fascicle size is 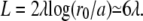The largest value of the penetration depth is L_i = 2λ. We therefore expect that the fraction of the fascicle immersed in the cortical layer is smaller than one-third.

The hydrodynamic value of the friction force is a good description of the interaction between the fascicle and the apical layer provided that the actin cortical layer behaves as a simple liquid and that there is a no-slip boundary condition at the fascicle surface. The boundary condition at the fascicle surface strongly depends on the proteins linking the fascicle to the apical layer. The no-slip boundary condition requires a stronger or equal binding between the fascicle and the apical layer than between actin filaments in the apical layer. If this binding is too weak, there is a finite slip at the surface of the fascicle. The finite slip is associated to a friction force of the form f_s = ξA_iv_T, where ξ is a friction constant per unit area and A_i is the immersed area of the fascicle which must be added to the hydrodynamic friction force. The results are identical provided that the tension σ is replaced by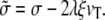

DISCUSSION

Our analysis provides a robust framework for understanding the essential geometric features of cilia and buds generated by actin polymerization. Typically, cilia have a tip, a cylindrical part, and a tapered tail.

In the absence of any external force such as the one exerted by the tip-links in hair-bundles, the tip is oblate. Its exact shape depends on many parameters: membrane tension, adhesion to the cytoskeleton, membrane curvature modulus, effective pressure P_eff. The effective pressure itself depends on the difference between the polymerization velocity which would be observed in the absence of external force and the treadmilling velocity. Although many parameters are involved, only two length scales are relevant for the shape of the tip: σ_eff/P_eff and (κ/σ)^1/2. In many practical cases, the tip radius r₀ is larger than (κ/σ)^1/2 and the curvature at the tip is equal to P_eff/2σ_eff. If we take as reasonable values σ_eff = 10⁻⁴ N/m and a radius of curvature ≃200 nm as suggested by Figs. 4 a or 6 a of Rzadzinska et al. (10), we find an effective pressure P_eff = 9 10³ Pa. This corresponds to a total upward force exerted by the filaments on the membrane 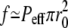= 500 pN. A typical fascicle comprises a few hundred filaments that lead to a force per filament of ∼1 pN.

We further show that each tip-link exerts a localized tensile force, orthogonal to the membrane, of the order of a fraction of the force required to pull an infinite tube from the membrane f_tube = 2π(2κσ_eff)^1/2. The curvature in the vicinity of the tip-link is given by 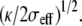Assuming σ_eff = 10⁻⁴ N/m and analyzing the shape of the stereocilium tip of Fig. 6 b of Rzadzinska et al. (10), we infer 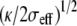= 40 nm and κ = 40 kT = 1.6 10⁻¹⁹ J and we estimate the tip-link force f_tip as a fraction of 36 pN. The numerical analysis of Fig. 2 confirms this result. The value of the bending modulus is typical for plasma membranes (16) and the tip-link force is consistent with the direct measurement of Hudspeth et al. (32).

The actual shape of the cylindrical section results from the fact that depolymerization can only take place after a suitable event has occurred. For the sake of simplicity we have considered here that this event is the uncapping of the pointed end of actin filaments. In real life, actin monomers forming the filament must also hydrolyze to an ADP form (1,33), and bundling proteins prevent depolymerization as well. Whereas in vitro studies suggest that hydrolysis is fast on the timescales considered here, the bundling proteins have clearly a stabilizing influence: the reason is that if they bind to the filament, they lower the free energy and thus stabilize the filament. Depolymerization beyond a cross-link requires the unbinding of the cross-linking protein. The longest of all these times determines the length of the cilium, once multiplied by the treadmilling velocity.

One of our important results is the law proposed in Rzadzinska et al. (10) that, in a given cell (i.e.: for identical biochemical conditions), the length of the cilium is proportional to the treadmilling velocity. A word of caution is needed here: these results are valid provided that the slowest processes correspond to the unbinding events. In the opposite limit, the cilium length is proportional to av_T/(v_d − v_T) and grows faster than linear with the treadmilling velocity.

Although our description is coarse-grained, we can still discuss the role of specific proteins controlling shape and dynamics of stereocilia such as espin (11). Overexpression of espin increases significantly the time 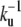that ctin filaments have to wait before depolymerization may have a chance to start. It thus increases significantly the length of the cylindrical part of the cilium, without changing the depolymerization rate k_d as observed experimentally (10,34). Overexpressing other strongly binding proteins and pointed-end capping proteins should lead to similar observations.

A component of the stereocilia that we did not discuss so far are minus-end directed Myosin VI motors, located along the membrane close to the base of the cilium (35). They exert forces that contribute to the global force balance and which tend to push the fascicle out of the cell body, opposite to the membrane force. The force due to Myosin VI (36) is given by the force per motor properly projected onto the fascicle axis, multiplied by the linear motor density and the perimeter of the base. This force is formally equivalent to the tension force, and all the results can be used provided that one replaces σ by σ − nf where f is the force exerted by one motor along the axis and n the motor density at the base of the cilium. Note that f is essentially the Myosin VI stall force. As a result, overexpression of myosin VI should increase the emerging part of the cilium, and inhibition decrease it. Myosin VI has another important role: it prevents the cilia from fusing. This last observation can be understood by considering the membrane-mediated interaction between cilia discussed in Derényi et al. (28).

The overall shape and size of the cilia depend on another parameter not discussed so far: the cilium radius at the tip. Equation 7 implies that thicker actin fascicles have a larger treadmilling velocity than thinner ones (everything else being kept equal). In turn, thick fascicles should be longer. These predictions are in direct agreement with the observation that, in hair cells, longer actin fascicles are thicker. The electron micrographs of Rzadzinska et al. (10) and Lin et al. (20) show a clear correlation between actin fascicle diameter and length at least for the cells of the organ of Corti. The observation that espin overexpression leads to longer and thicker filaments is compatible with our predictions (11); however, as we have already pointed out, even at constant radius and constant treadmilling velocity, cilia should be longer since the uncapping rate k_u should decrease. This observation is thus not a proof of validity of Eq. 7 unless the espin density does not change. We postpone for future work the discussion of factors determining the cilium radius. The angular dependence of the polymerization rate, spontaneous curvature of the membrane, and global availability of actin nucleators and monomers could play a role as well.

Finally, in practically all regimes discussed, the length of the cilia depends on many parameters that cannot be precisely controlled. It should then fluctuate, as discussed in Gov et al. (37). In many cases, the length fluctuations are compatible with the cilia functionality. However, in stereocilia, one could expect the length to be well defined over very long timescales as length codes for frequency (13,38): this is most likely not the case, in view of the large number of parameters to be controlled over a life span. One of the roles of the large number of cilia in a hair-bundle could be to precisely reduce the effect of independent fluctuations between cilia.

APPENDIX A: NONLINEAR EFFECTS AT THE TIP

In this Appendix, we give the details on the derivation of the tip free energy, and we show that the results recasting the effect of treadmilling, in terms of an effective pressure and an effective tension, are general and do not depend on the linear approximation used in the text.

Tip free energy: linear theory

Within the linear approximation, the free energy of the tip is given by Eqs. 2 and 3. The interaction free energy depends on the local distance δ between the membrane and the polymerization front. This distance is written as a function of the membrane and front coordinates as

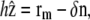(24)

where 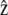is the unit vector along the cilium axis, and n the unit vector normal to the membrane. Differentiating this relation, we obtain 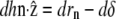where r_n is the displacement perpendicular to the membrane. The differential of the interaction free energy is

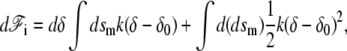(25)

where we have taken into account the fact that when the membrane is deformed, the surface element ds_m changes. To calculate this variation we use the Monge gauge ds_m = ds g^1/2 where ds is the surface element along the base of the cilium perpendicular to the cilium axis and g is the determinant of the metric tensor. When the surface is displaced in the perpendicular direction by dr_n, the change in g is dg = −2gHdr_n, where H is the total curvature. This leads to d(ds_m) = − ds_mdr_nH. Using this result and Eq. 24, we find the differential of the interaction free energy

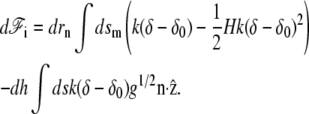(26)

The derivatives given in Eq. 4 are obtained by noting that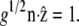

Nonlinear theory

In a nonlinear theory, the dynamic equations of the membrane in a steady state are written

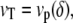(27)

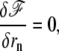(28)

where the polymerization velocity v_p is a nonlinear function of the distance δ between the membrane and the polymerization front. Inverting the first of these equations gives δ as a function of the treadmilling velocity. In a general nonlinear theory the interaction free energy is written as

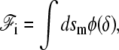(29)

where φ is a nonlinear function of δ which is minimum for δ = δ₀. Its differential reads 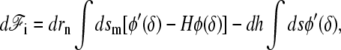where we denote, by a prime (′), the derivation with respect to δ. Using the same arguments as in the linear case, this leads to an effective pressure and an effective tension

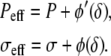(30)

APPENDIX B: MEMBRANE SHAPE

In this Appendix, we give a more detailed derivation of the membrane properties and of the connection of the membrane to the apical layer. The geometry is detailed on Fig. 4. As explained in the main text, the membrane free energy includes both tension and curvature contributions. We divide the membrane into three regions: the membrane in contact with the stem with a free energy 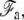the membrane connected to the apical layer with a free energy 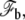and the transition regions in-between where the membrane does not adhere. The free energy of the membrane connected to the fascicle is

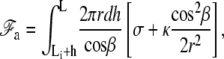(31)

where h denotes the vertical position of the point where the membrane detaches from the stem and h_max is the vertical position of the tip of the stereocilium. The free energy of the membrane connected to the apical layer is

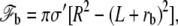(32)

where R is the radius of the apical surface considered as a circle around the cilium and r_b is the radius of the membrane at the level of the apical layer. The free energy of the transition region is

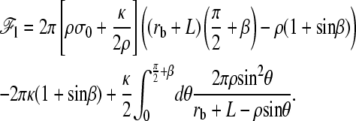(33)

The equilibrium value of the radius of curvature in the transition region ρ is obtained by minimization of the total free energy 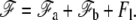We first consider the case where the radius at the base r_b is larger than ρ in the transition region (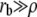). The explicit differentiation with respect to ρ of the total free energy leads to

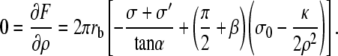(34)

The equilibrium radius of curvature is then 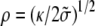with an effective tension given by Eq. 19. In this limit, the force exerted by the membrane on the fascicle is given by 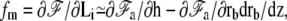where in the last equation we have used the fact that 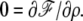This directly leads to Eq. 21 in the text. In the opposite limit where 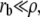the minimization of the free energy leads to

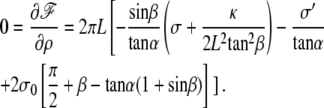(35)

This directly leads to Eq. 20.