Abstract
Massively parallel all-atom, explicit solvent molecular dynamics simulations were used to explore the formation and existence of local structure in two small alpha-helical proteins, the villin headpiece and the helical fragment B of protein A. We report on the existence of transient helices and combinations of helices in the unfolded ensemble, and on the order of formation of helices, which appears to largely agree with previous experimental results. Transient local structure is observed even in the absence of overall native structure. We also calculate sets of residue-residue pairs that are statistically predictive of the formation of given local structures in our simulations.
Keywords: molecular dynamics, simulation, protein folding, alpha helix, distributed computing
1. Introduction
Recent years have seen great advances in both experimental and computational methods for studying protein folding. Molecular dynamics simulation is among the techniques that have been at the vanguard of this wave of progress. In the years since Duan and Kollman’s (1998) landmark supercomputer trajectory for the villin headpiece, small peptides and proteins have been folded with molecular dynamics and initial comparisons with experiment made (Zagrovic et al., 2002; García and Onuchic, 2003; Snow et al., 2004; Rhee et al., 2004).
The use of model systems has been central to our progress in elucidating protein folding. Of particular utility have been proteins whose sizes and folding time scales are accessible to experiment and computation both. As noted, villin has been one of these systems. Zagrovic et al. (2002) reported folding the 36-residue protein in implicit solvent using massively parallel simulation. We have recently achieved this with explicit solvent (Jayachandran et al., 2006). Recent experiments have shed some light on the existence of structure in the denatured state of villin (Tang et al., 2004; Brewer et al., 2005). The B domain of protein A has been another important target for both experiment (Bai et al., 1997; Myers and Oas, 2001; Vu et al., 2004; Sato et al., 2004) and computation—ranging from weighted histogram analysis and use of minimalist or simplified models to high temperature unfolding and replica exchange (Olszeski et al., 1996; Guo et al., 1997; Alonso and Daggett, 2000; Berriz and Shakhnovich, 2001; Favrin et al., 2002; Ghosh et al., 2002; Linhananta and Zhou, 2002; García and Onuchic, 2003). Great interest exists in the manner in which local structure elements within the protein, sometimes termed “foldons” (Panchenko et al., 1997), may form independently.
As protein folding is a stochastic process, we believe that it is important to examine it statistically, with ensembles of trajectories. The combination of unbiased molecular dynamics with detailed simulation models and massive parallelism allows us to make quantitative measurements, of kinetics for example. While we have previously focused on trajectories that reach the folded state, we can also use it to examine the unfolded ensemble and transient local structure.
In this work, we will examine the existence of native-like local structure elements, and combinations of elements, in simulation ensembles of our two target proteins; the structure elements considered correspond to the helical segments of the proteins. We consider whether the elements can form independently or require other structure, an analysis made possible by the size of the ensembles obtained. We then consider the order in which the structural elements form. Finally, we apply statistical techniques to identify interresidue distances that correlate with local structure formation and examine their relative variabilities. The power of molecular dynamics is the detailed (high space and time resolution) view of dynamics that it can present, allowing observations and calculations inaccessible to experiment. We emphasize, though, that all results to be presented are for the given simulation model used—as with any simulation, it is valid beyond that only insofar as the model is valid, making comparison with available experimental observations vital.
2. Simulations
We previously simulated tens of thousands of trajectories of the 36-residue C terminal domain of the villin headpiece with molecular dynamics (Jayachandran et al., 2006) and now have also obtained several thousand trajectories of the larger 10-55 helical fragment B of protein A (which we will refer to simply as “Protein A”). Conformations were sampled at a 100 ps frequency in all simulations. Villin trajectories were generally 25 ns long while Protein A trajectories generally reached 35 ns. All of the analyses we describe later make use of sets of trajectories rather than individual trajectories. Also, any consideration of dynamics within trajectories is over times that are short compared to the trajectories. Therefore, the analysis techniques are relatively insensitive to the exact lengths of trajectories. The villin data set is discussed thoroughly in Jayachandran et al. (2006), in regards to methodology, native state data, and folding trajectories. (Two simulation models were used in that work—the ensemble obtained using reaction field is the one utilized here.) The Protein A simulations are described below.
2.1. Molecular dynamics details
All simulations were conducted with the Folding@Home distributed computing project, utilizing processors around the world (Shirts and Pande, 2000). Single precision GROMACS 3.1.4 (van der Spoel et al., 2005), adapted to the distributed environment, was used. The details of the Protein A molecular dynamics were as follows. The sequence used was the same as that used in García and Onuchic (2003), with N-acetyl and C-amino caps, and we follow the same numbering scheme as in that work, with our Gln 2 corresponding to Gln 10 in the Protein Data Bank (PDB) structure 1BDB (Gouda et al., 1992). The protein was solvated in approximately 5000 TIP3P water molecules (Jorgensen et al., 1983) in a cubic box, approximately 160 nm3, with periodic boundary conditions. Protein parameters were from the García-Sanbonmatsu modified version of AMBER94 (Cornell et al., 1995; García and Sanbonmatsu, 2002).
A 2 fs time step was used with a 20 fs neighbor list update frequency. Berendsen temperature and pressure coupling were used, with time constants of 0.1 and 1 ps, respectively (Berendsen et al., 1984). The temperature was 300 K and the pressure was 1.01 bar. Simulations with Berendsen controls have previously yielded accurate protein folding rates despite the method’s unphysical scaling of kinetic energies (Rhee et al., 2004; Jayachandran et al., 2006). The LINCS algorithm was used to constrain all bonds (Hess et al., 1997). The van der Waals neighbor list went up to 8 Å, with van der Waals interactions smoothed from 6 Å and an external dielectric of 80. The Coulombic neighbor list went up to 10 Å. Generalized reaction field was enabled in GROMACS for long range electrostatics (Tironi et al., 1995).
2.2. Starting structures, stability, and kinetics
For Protein A, 2129 trajectories started from the native structure each reached a length of 35 ns. Considering the conformations at that time point, 98% were within 2 Å alpha carbon distance root mean square deviation (DRMSD) of the native 1BDB, and this was taken to indicate that the native structure is stable within the simulation model. Henceforth, the “DRMSD” of a conformation will refer its alpha carbon DRMSD relative the native PDB, unless otherwise qualified.
One hundred trajectories were started from each of 49 unfolded structures. These initial structures were randomly chosen from a set of conformations that García and Onuchic (2003) identified from their replica exchange simulations as sampling the unfolded state. Among the 49 initial conformations, the lowest DRMSD with the native PDB was 3.3 Å. Only one other initial conformation was under 4.2 Å DRMSD (at 3.8 Å) and the mean DRMSD over all starting conformations was 5.9±1.4 Å.
Of the 4900 trajectories started from the 49 initial conformations, 10 reached a DRMSD below 2 Å. Table 1 shows statistics on the number of trajectories to reach other DRMSD values. We see that certain initial conformations have more trajectories reaching low DRMSD on the simulation timescale than others. For example, 5 of the 10 trajectories to reach a DRMSD of 2 Å started from the same conformation, the one which had the lowest initial DRMSD. The lowest DRMSD reached by any trajectory was 1.5 Å.
Table 1.
The number of Protein A trajectories that reached various DRMSDs with the native PDB conformation and the representation of starting conformations among those trajectories.
| Target DRMSD (Å) | Trajs. reaching target | Starting confs. among among trajs. reaching target | Median trajs. reaching target from a single starting conf. (among starting confs. with any trajs. reaching target) |
|---|---|---|---|
| 2 | 10 | 5 | 1 |
| 3 | 181 | 27 | 2 |
| 4 | 1013 | 47 | 16 |
Taking DRMSD<2Å as a very rough definition of the “folded” state and computing the maximum likelihood folding rate (Zagrovic and Pande, 2003; Jayachandran et al., 2006) for the data yields a result of 10±3.3 μs. The rate estimated excluding data from simulations started from t he two lowest DRMSD initial conformations, described above, agrees within error, at 11±5.6 μs. The TIP3P solvent model used is known to have an anomalous diffusion constant (Jorgensen et al., 1983), estimated to be 0.33 (Jayachandran et al., 2006) of true water. If we assume that this impacts the folding rate of a protein linearly, then an approximate correction would be to divide the above rates by 0.33. Deviation from the experimental full B domain rate measurement of approximately 10 μs (Myers and Oas, 2001; Vu et al., 2004; Sato et al., 2004) is likely due to limitations of our models, systematic error from the native state definition, and possibly the truncation of the protein.
Vu et al. (2004) proposed that Protein A folding includes a rapidly formed intermediate state, achieved in 90 ns, characterized by the presence of nascent helices. It is unclear how to translate this into a quantitative single-molecule based definition for our simulations, which we could then use to compute a rate to the putative intermediate. However, we note that if we roughly approximate the state definition as all three individual helix DRMSDs under 2 Å, then the rate estimated (by the same method as above and including the anomalous diffusion correction) is 270 ns, on the same order as the experimental value.
3. Results
We will first discuss the existence of native-like elements in the unfolded ensemble. Then, we will discuss the order of formation of elements. Finally, we will present a calculation of the particular limited local structures (residue pairs) that are most predictive of the formation of given structural elements over various short time scales.
In the analyses below, we will define the three helices in villin as residues Asp 5 to Val 11, Arg 16 to Asn 21, and Leu 24 to Glu 33. For Protein A, the three helices are taken to be Gln 2 to Ile 9, Glu 17 to Asp 29, and Ser 34 to Asp 46. Where a binary decision is required on whether or not a substructure is native-like (as in the transition diagrams below), we make the judgment by whether or not the substructure is within a given DRMSD of the corresponding substructure in the native conformation as defined by the PDB structure. The DRMSD thresholds were chosen based on the flexibility seen in simulations of the native state (Jayachandran et al., 2006), which demonstrate the native well within the simulation model. For villin, the DRMSD threshold for all three helical segments was 0.8 Å (Jayachandran et al., 2006). For Protein A, the thresholds were taken to be 0.8, 1.3, and 0.7 Å for each of the three helices respectively.
We also tested alternative Protein A local structure criteria. In particular, this alternative definition judged a given segment defined above to be structured if at least 75% of residues within the segment were identified as helical by the DSSP program (Kabsch and Sander, 1983). DSSP distinguishes between 3/10, alpha, and pi helices. We found little difference to arise from which of these were included in the helical definition. For 99.5% of Protein A conformations sampled, a definition requiring 75% of residues in a segment be classified as alpha helical yielded an identical judgment on which segments were helical and which were not as a definition that counted residues identified as either alpha or pi helical. For 99.6% of conformations sampled, a criterion permitting all three types of helical assignments yielded an identical judgment as one counting only residues classified as alpha or pi helical. Comparing to the DRMSD criteria, the alpha/pi helical DSSP criteria and the DRMSD criteria yielded an identical judgment on which segments were structured and which were not for 81.7% of conformations sampled. We find DRMSD to be more intuitive than DSSP classifications in conveying the degree of structure. Therefore, we primarily use DRMSD rather than DSSP in the analysis below (even for binary decisions on whether a segment is structured, in the interest of consistency). The DSSP criteria (alpha or pi) are used in certain Protein A analyses as a check of sensitivity to the specific criteria. For villin, we do not present results with alternate criteria here, but rates and other analyses using several different structural criteria were presented in Jayachandran et al. (2006). The ends of the villin chain are frayed, meaning that native-like structure does not necessarily imply helical DSSP structure at the end residues.
3.1. Helices in the unfolded ensemble
For the unfolded ensembles sampled, we computed joint distributions of helix DRMSDs relative the native PDBs. One can see that all combinations of low DRMSD helices are represented, and that certain combinations are more probable than others. For two pairs of helices (1 versus 2 and 2 versus 3) in villin, we see relatively two-state distributions: helix 1 and helix 3 are each most likely to have low DRMSD only with helix 2 in existence (Fig. 1a-b). The finding relates to the somewhat distinct experimental observation of Tang et al. (2004) that each of the three helices do not form when individually isolated from the rest of the amino acid sequence, but that some structure does form in the first two helices even if helix 3 is removed from the sequence. We see four distinct favored populations when plotting the DRMSD of helix 1 versus the DRMSD of helix 3 (Fig. 1c). Populations for all combinations of those two helices exist: both exist, neither exist, or one or the other exists.
Fig. 1.
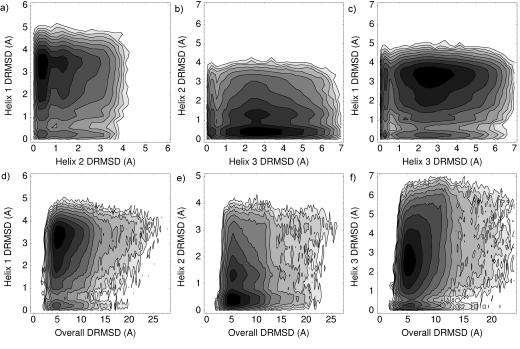
Logarithmic density plots for the DRMSDs observed in the unfolded ensemble of villin. a) Helix 1 DRMSD versus helix 2 DRMSD. b) 2 versus 3. c) 1 versus 3. d) 1 versus overall structure. e) 2 versus overall. f) 3 versus overall.
We also see that each of the three villin helices can form even in the absence of overall native structure (Fig. 1d-f). It appears, however, that each of the helices is most likely to exist only when the overall structure is somewhat native-like. This is also in agreement with Tang et al.’s (2004) conclusion—based on their experimental observation that individual secondary structure elements do not fold in isolation—that long range contacts play a key role in overall folding.
For Protein A, we see low DRMSD populations for each of the helices independent of the DRMSD of the other helices (Fig. 2a-c). Experimentally, Bai et al. (1997) found that only helix 3 was stable, that too marginally so, when isolated. Combined with the observations here, this suggests that long range contacts are important but can form even with participating elements not completely folded. Unlike for villin, we see a large spread in the populations of each helix in terms of their overall native character (Fig. 2d-f)—each of the helix population plots exhibits a low DRMSD state even when the overall structure is highly nonnative. This agrees with the diffusion collision model of the protein’s secondary structure elements forming independently (Karplus and Weaver, 1994; Myers and Oas, 2001; Islam et al., 2002).
Fig. 2.
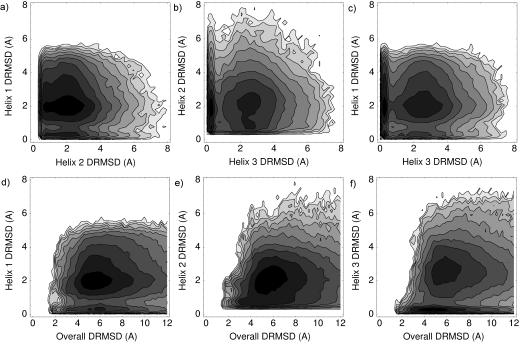
Logarithmic density plots for the DRMSDs observed in the unfolded ensemble of Protein A. The plots are ordered as in Fig. 1.
The average existence time of the transient structured segments is listed in Table 2. For Protein A, times are listed using both the DRMSD and DSSP criteria and show agreement quantitatively and in qualitative ordering. All lifetimes are very short, on the nanosecond scale. Generally, combinations of helices appeared to be structured for equal or less time as any individual constituent of the combination. The second helix had the longest individual lifetime for villin and the third helix had the longest lifetime for Protein A. This agrees with experimental findings about the relative individual helix stabilities in each protein, discussed earlier.
Table 2.
The average lifetimes (ns) of each transient helix or helix combination.
| H1 | H2 | H3 | H1+H2 | H2+H3 | H1+H3 | H1+H2+H3 | |
|---|---|---|---|---|---|---|---|
| Villin | 1.0 ± 1.9 | 2.2 ± 3.3 | 1.2 ± 2.7 | 0.9 ± 1.5 | 1.0 ± 2.1 | 1.4 ± 2.7 | 1.3 ± 2.2 |
| Protein A | 1.5 ± 2.8 | 1.3 ± 2.7 | 3.7 ± 6.8 | 1.0 ± 1.5 | 1.2 ± 2.4 | 1.6 ± 3.1 | 0.9 ± 1.4 |
| Protein A (DSSP) | 1.1 ± 1.6 | 0.9 ± 1.7 | 1.9 ± 3.5 | 0.6 ± 0.8 | 1.0 ± 1.7 | 1.0 ± 1.4 | 0.6 ± 0.8 |
3.2. Helix formation order
Considering those trajectories that formed more than one helix, we constructed transition diagrams showing the order of formation of the helices (Fig. 3). We computed the fraction of conformations of a given helix configuration that were observed to transition to each other configuration. We also computed the fraction of conformations of each helix configuration that transitioned from each other configuration. In both these calculations, we required a trajectory to retain a given helix configuration for at least 1 ns to consider it to have transitioned to that configuration, to reduce noisy fluctuations above and below the helix DRMSD thresholds.
Fig. 3.
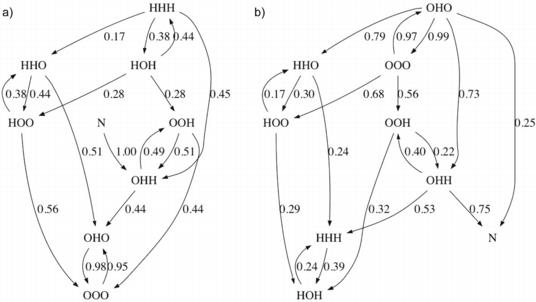
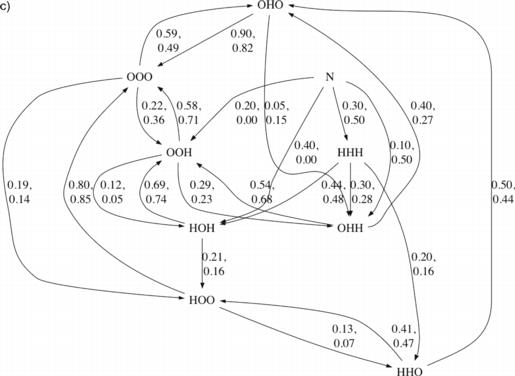
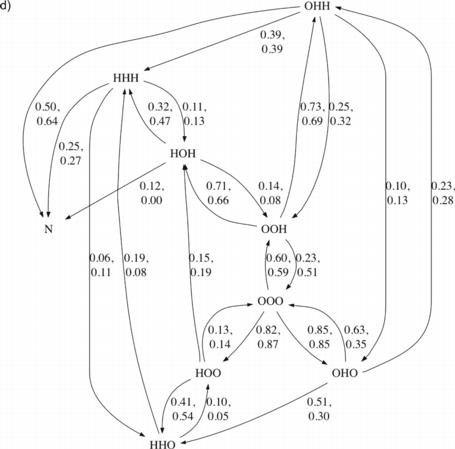
Transition diagrams for villin and Protein A. For each protein, one diagram is shown where each edge is labeled by the fraction of conformations in its source state that were observed to transition directly to its target state (outgoing normalized) and one diagram is shown where each edge is labeled by the fraction of conformations in its target state that were observed to transition directly from its source state (incoming normalized). For Protein A, two fractions are listed per edge—the first corresponds to the DRMSD criteria for helices and the second to the DSSP criteria. N indicates a state defined by DRMSD<2Å. For clarity, edges where both criteria’s fractions are under 0.1 are not shown. a) Villin, outgoing normalized. b) Villin, incoming normalized. c) Protein A, outgoing normalized. d) Protein A, incoming normalized.
For villin, we observed the middle helix forming first 95% of the time (Fig. 3a). It was also most often lost before any additional helices reached low DRMSD, agreeing with the short lifetimes computed for the transient local structure. When either helix 1 or helix 3 was present alone, then helix 2 was seen to additionally form next 38% and 51% of the time, respectively. All low overall DRMSD structures that unfolded were observed to maintain the second two helices longer than the first. All trajectories that reached low overall DRMSD did so from states that contained the middle helix; the third helix was also present 75% of the time (Fig. 3b).
For Protein A, like for villin, we observed the middle helix most commonly (approximately 60% of time) transiently forming first (Fig. 3c). The other two helices roughly evenly divided the remaining first helix transitions. If the third helix existed in isolation, it was observed to be lost in under 60% of cases and to gain the second helix in nearly 30% of cases. If either the first or second helix existed in isolation, it was most often lost—in 80% and 90% of cases, respectively—before any additional helices formed. Indeed, for each helix combination in Protein A, the majority of observed transitions involved loss of a helix rather than gain of an additional one. The less frequent helix gain events chained together constitute folding in our diagram. Similar results were found when considering the DSSP criteria for helices as the DRMSD criteria (Fig. 3c), with the only qualitative difference arising in relation to the low DRMSD state (N), where fractions were based on the fewest observations.
When a state with the second two helices only was reached, approximately 70% of the time the third helix had existed first and was then joined by the second (Fig. 3d). This observation was independent of the helix criteria used. The state with a low overall DRMSD was reached 75% of the time from a state where the second two helices were present, utilizing the DRMSD criteria. This figure was 91% if utilizing the DSSP criteria. Sato et al. (2004) concluded that the transition state for Protein A, late in the folding process, includes a well formed second helix, agreeing with our simulation result. There is also support from the results of García and Onuchic (2003), who inferred from free energy diagrams that the final stages of folding involved formation of helix 1 and its interactions with helix 2, and packing of an already formed helix 3 into the bundle.
3.3. Interresidue distances
We now move away from discussion of time ordering of helix formation to a statistical analysis of which residue-residue interactions best predict given helix formations in our data set, ahead of their formation by various times. A given residue-residue distance being predictive does not mean that the interaction between the two residues is itself necessarily strong, but that the distance is at least correlated with significant interactions. Beyond simply identifying the specific residue pairs, we can assess how much those local structures differ between when they precede a helix formation and they do not, and how much (or little) variation there is within those structures when a helix is going to be formed.
To identify interresidue distances predictive of a given helix forming in a given amount time (“precedence time”), we did the following. First, we computed all residue-residue alpha carbon distances for each sampled conformation, obtaining vectors of length 630 for villin and 1035 for Protein A. Then, for each trajectory, we identified the first sampled conformation having the helix of interest. If this conformation was at least the precedence time into the trajectory, then we put the conformation preceding it by the precedence time into a positive set of conformations. If the trajectory never formed the given helix of interest, then we put the conformation preceding the end of the trajectory by the precedence time into a negative set of conformations.
We now had a positive set and a negative set of conformations, each conformation associated with a vector of feature values (interresidue distances). The sizes of the sets ranged from several hundred to several thousand members. We performed forward selection, as implemented in PCP 2.0 (Buturovic, 2005; Buturovic, 2006), using 250 randomly selected elements of each set (this makes the calculation more tractable). Forward selection is a standard, heuristic feature selection technique that identifies a subset of the features in a high dimensional space that together well explains class membership (in our case, whether a conformation is in the positive or negative set). It operates by starting with an empty set of features and then repeatedly adding the feature that optimizes a given criterion, until the set has the desired number of features. We selected feature sets of cardinality two and used as the criterion the cross validation error rate of the nearest neighbor (Euclidean distance) classifier constructed using the selected features. For an identified feature pair, we tested the accuracy of a nearest neighbor classifier that considered just those two dimensions of the feature vectors. The accuracy was taken to be the fraction of conformations in the overall positive and negative sets that the classifier properly classified as positive or negative.
We repeated the above computation for a range of precedence times. For villin, as the middle helix tends to form very early in the trajectory and is present in nearly 70% of all conformations sampled, we conducted the analysis only for the first and third helices. For Protein A, we conducted it for all three helices. Table 3 shows the identified residue pairs, sizes of the positive and negative sets, and prediction accuracy rates for villin. Unsurprisingly, the prediction accuracy rates decrease with increased precedence time— it is harder to predict whether a helix will form the further ahead we try to make the prediction. The table also shows the mean partial DRMSD between members of the negative set and the mean of positive set. By “partial DRMSD,” we mean the root mean square deviation between two distances vectors that each include only the two interresidue distances selected. By the “mean of the positive set,” we signify the distances vector where each element i is the mean of i among all vectors within the positive set (Zagrovic et al., 2002). The mean partial DRMSD reported thus gives a sense of how much the positive set differs from the negative set in regards to the positioning of the predictive residue pairs identified. Table 4 shows the same information for Protein A.
Table 3.
For various precedence times, information on identified helix-predictive residue pairs for villin.a
| 200 ps | 1000 ps | 2000 ps | 5000 ps | |
|---|---|---|---|---|
| H1 | Asp5-Ala10, Phe8-Val11; 9468, 454; 84%; 0.28±0.10 Å | Ser4-Leu30, Glu6-Val11; 9468, 454; 70%; 0.55±0.25 Å | Glu6-Ala10, Glu6-Gln27; 9468, 454; 68%; 0.50±0.22 Å | Met2-Leu22, Ser4-Asn29; 9466, 450; 58%; 0.74±0.28 Å |
| H3 | Trp25-Asn29, Asn29-Lys32; 9380, 542; 84%; 0.30±0.12 Å | Asp5-Phe37, Gln27-Lys31; 9380, 542; 70%; 0.54±0.25 Å | Lys26-Leu30, Lys26-Lys31; 9380, 541; 66%; 0.28±0.15 Å | Ala20-Lys32, Leu24-Leu30; 9378, 536; 61%; 0.38±0.21 Å |
Each table cell lists the residue-residue pairs, the cardinalities of the negative and positive sets, the predictive accuracy of a nearest neighbor classifier based only on the two distances, and the mean partial DRMSD between members of the negative set and the mean of the positive set.
Table 4.
Information on identified predictive residue pairs for Protein A (formatted as in Table 3).
| 200 ps | 1000 ps | 2000 ps | 5000 ps | |
|---|---|---|---|---|
| H1 | Gln2-Phe6, Gln3-Ile9; 4257, 643; 78%; 0.30±0.14 Å | Gln3-Phe6, Ala5-Lys42; 4257, 642; 65%; 0.49±0.28 Å | Gln3-Tyr7, Leu27-Lys28; 4257, 626; 58%; 0.17±0.10 Å | Gln2-Leu10, Asn4-Hid11; 4253, 581; 57%; 0.33±0.18 Å |
| H2 | Glu18-Lys28, Ile24-Leu27; 3164, 1136; 79%; 0.30±0.17 Å | Leu15-Ser32, Phe23-Leu27; 3164, 867; 70%; 0.45±0.23 Å | Gln19-Lys28, Ile24-Leu27; 3164, 780; 68%; 0.26±0.15 Å | Phe23-Lys28, Ala35-Leu44; 3162, 629; 63%; 0.27±0.18 Å |
| H3 | Asp30-Lys43, Ala39-Leu44; 3699, 601; 83%; 0.43±0.24 Å | Leu27-Leu44, Ala39-Leu44; 3699, 568; 76%; 0.53±0.28 Å | Ala35-Leu38, Ala39-Lys43; 3699, 533; 76%; 0.25±0.13 Å | Asn36-Lys42, Glu40-Asn45; 3696, 446; 72%; 0.30±0.16 Å |
Residue pairs in Tables 2 and 3 are italicized if in the native PDB the center of mass of the pair’s first member, or one of its immediate neighbor residues in sequence, is within 6 Å of the center of mass of the pair’s second member or one of its immediate neighbor residues. For villin, most of the residue pairs identified as predictive of a given helix through a precedence time of 2 ns are native contacts according to the preceding definition. Val 11 (Val 50 in the overall villin sequence) is identified as involved in key distances for the first helix on short precedence times and is a key residue in stabilizing villin overall (McKnight et al., 1996; McKnight et al., 1997; Tang et al., 2004). For Protein A, 50% of the interresidue distances identified correspond to native contacts (in general, one of the two identified distances per helix/precedence time combination). We note that the residue pairs identified are those that are observed to be most statistically significant within the obtained data set, which is why there is variation in the identified residue pairs with precedence time—all those residue pairs play a role, or have correlation with important interactions, in reality.
Besides examining the difference between the negative and positive sets with mean partial DRMSDs, we also examined how much variation there was within each set. In particular, we computed the standard deviation for each of the two identified predictive features (interresidue distances), across each of the two sets, and then calculated the ratio of the maximum of the two feature standard deviations from the negative set to the maximum of the two feature standard deviations from the positive set (Fig. 4). This ratio conveys how much more or less variability there is in the predictive residue distances ahead of helix formation versus ahead of no helix formation. One can see that, for all helices of villin and Protein A, the ratio was around 2 for a precedence time of 200 ps. This means that there is less position variability in the predictive residue pairs preceding helix formation than is available to them. For longer times, the difference disappeared, except for helix 3 of Protein A, where a reduction in variability remained even at 5 ns.
Fig. 4.
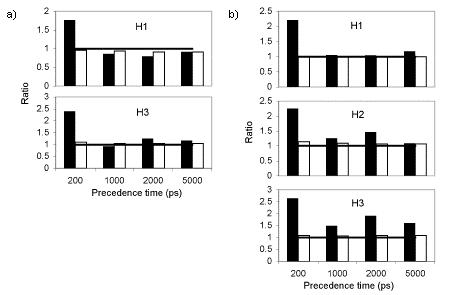
For various precedence times and helices, the ratio of the maximum standard deviation over the negative set in a predictive feature to the maximum standard deviation over the positive set in a predictive feature (black) and the ratio of the mean over all feature standard deviations for the negative set to that quantity for the positive set (white). Ratios above 1 (at which a horizontal line is drawn as a guide) indicate greater variability in the negative set than in the positive set. a) For villin. b) For Protein A.
Finally, we can also consider how much the positive and negative sets compare in internal variation for their overall structures, not just for the predictive residues. We computed the standard deviation in each residue-residue distance, for the negative and positive sets, and computed the mean of those standard deviations for each set. We then calculated the ratio of those two means (Fig. 4). One can see that there is not the difference between the negative and positive sets that was seen when considering just the selected predictive residues previously—the ratio is close to 1 in all cases. Even though the predictive residue pairs were less variable preceding formation of a helix, residue-residue distances over the entire structure appears just as variable whether or not a helix is to form. This supports the previous analyses that particular helices could form or not whether or not the protein was native-like overall.
4. Conclusion
Large ensembles of unbiased molecular dynamics trajectories for villin and Protein A were obtained and analyzed in regards to local structure formation. For villin, we saw that helices could form when the overall structure was nonnative, but were most likely to form when there was overall structure. The first helix and third helix usually formed only if the second one was present. The second helix had the longest lifetime and was required to be formed to complete folding. For Protein A, each helix could (and frequently did) transiently exist even when the overall structure was nonnative and regardless of whether any other helix was present. Experimental results suggest the third helix to form first. We observed the middle helix to be the most likely to transiently form first, but the third helix to be the most likely to lead to addition of another helix, rather than loss of the existing one, when alone. The folded state was most often reached from one with the second and third helical segments already native-like.
We performed a statistical calculation of which sets of residue-residue distances were predictive of the formation of given helices over various time periods. We saw that the key distances usually but not always involved residues within or near the given helix of interest. We also observed that the helix-correlated-distances were more restricted shortly before a structural element formed than otherwise, and that for the third helix of Protein A, this difference in relative position variability persisted to several ns ahead of formation. Interresidue distances overall in villin and Protein A did not exhibit this difference.
With increases in computational power, simulations with detailed models are becoming more and more accessible. Larger proteins are being pursued, as are longer time scales. This should allow for more comparisons to be made with experiment, and thus allow for more grounds for vital refinement of simulation methods. With large scale simulation comes large amounts of data. Statistical analyses will be crucial, especially given that folding, and molecular processes in general, involve variability. Together, powerful ways of generating data and methods for analyzing it should make possible new insights into the mysteries of protein motion and function.
Acknowledgments
This work was made possible by Folding@Home participants around the world. This material is based upon work supported by the National Science Foundation under Grant No. 0317072 and MCB 0543769 and the National Institutes of Health under grant GM62868.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alonso DO, Daggett V. Staphylococcal protein A: unfolding pathways, unfolded states, and differences between the B and E domains. Proc. Natl. Acad. Sci. USA. 2000;97(1):133–138. doi: 10.1073/pnas.97.1.133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bai Y, Karimi A, Dyson HJ, Wright PP. Absence of a stable intermediate on the folding pathway of protein A. Protein Sci. 1997;6:1449–1457. doi: 10.1002/pro.5560060709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berendsen HJC, Postma JPM, van Gunsteren WF, Dinola A, Haak JR. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984;81(8):3684–3690. [Google Scholar]
- Berriz GF, Shakhnovich EI. Characterization of the folding kinetics of a three-helix bundle protein via a minimalist Langevin model. J. Mol. Biol. 2001;310(3):673–685. doi: 10.1006/jmbi.2001.4792. [DOI] [PubMed] [Google Scholar]
- Brewer SH, Vu DM, Tang Y, Li Y, Franzen S, Raleigh DP, Dyer RB. Effect of modulating unfolded state structure on the folding kinetics of the villin headpiece subdomain. Proc. Natl. Acad. Sci. USA. 2005;102(46):16662–16667. doi: 10.1073/pnas.0505432102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buturovic LJ. PCP - Pattern Classification Program. Version 2.0. 2005. [Google Scholar]
- Buturovic LJ. PCP: a program for supervised classification of gene expression profiles. Bioinformatics. 2006;22(2):245–247. doi: 10.1093/bioinformatics/bti760. [DOI] [PubMed] [Google Scholar]
- Cornell WD, Cieplak P, Barly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]
- Duan Y, Kollman PA. Pathways to a protein folding intermediate observed in a 1-microsecond simulation in aqueous solution. Science. 1998;282(5389):740–744. doi: 10.1126/science.282.5389.740. [DOI] [PubMed] [Google Scholar]
- Favrin G, Irback A, Wallin S. Exploring the folding free energy surface of a three-helix bundle protein. Proteins. 2002;47(2):99–105. doi: 10.1002/prot.10072. [DOI] [PubMed] [Google Scholar]
- García AE, Sanbonmatsu KY. Alpha-helical stabilization by side chain shielding of backbone hydrogen bonds. Proc. Natl. Acad. Sci. USA. 2002;99(5):2782–2787. doi: 10.1073/pnas.042496899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García AE, Onuchic J. Folding a protein in a computer: An atomic description of the folding/unfolding of protein A. Proc. Natl. Acad. Sci. USA. 2003;100(24):13898–13903. doi: 10.1073/pnas.2335541100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh A, Elber R, Scheraga HA. An atomically detailed study of the folding pathways of protein A with the stochastic difference equation. Proc. Natl. Acad. Sci. USA. 2002;99(16):10394–10398. doi: 10.1073/pnas.142288099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gouda H, Torigoe H, Saito A, Sato M, Arata Y, Shimada I. Three-Dimensional Solution Structure of the B Domain of Staphylococcal Protein A: Comparisons of the Solution and Crystal Structures. Biochemistry. 1992;31:9665–9672. doi: 10.1021/bi00155a020. [DOI] [PubMed] [Google Scholar]
- Guo Z, Boczko EM, Brooks CL., III Exploring the folding free energy surface of a three-helix bundle protein. Proc. Natl. Acad. Sci. USA. 1997;94(19):10161–10166. doi: 10.1073/pnas.94.19.10161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hess B, Bekker H, Berendsen HJC, Fraaije JGEM. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997;18(12):1463–1472. [Google Scholar]
- Islam SA, Karplus M, Weaver DL. Application of the diffusion-collision model to the folding of three-helix bundle proteins. J. Mol. Biol. 2002;318:199–215. doi: 10.1016/S0022-2836(02)00029-3. [DOI] [PubMed] [Google Scholar]
- Jayachandran G, Vishal V, Pande VS. Using massively parallel simulation and Markovian models to study protein folding: Examining the dynamics of the villin headpiece. J. Chem. Phys. 2006;124(15) doi: 10.1063/1.2186317. [DOI] [PubMed] [Google Scholar]
- Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79(2):926–935. [Google Scholar]
- Kabsch W, Sander C. Dictionary of Protein Secondary Structure: Pattern Recognition of Hydrogen-Bonded and Geometrical Features. Biopolymers. 1983;22(12):2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
- Karplus M, Weaver DL. Protein folding dynamics: the diffusion-collision model and experimental data. Protein Sci. 1994;3:650–668. doi: 10.1002/pro.5560030413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linhananta A, Zhou Y. The role of sidechain packing and native contact interactions in folding: Discontinuous molecular dynamics folding simulations of an all-atom Go model of fragment B of Staphylococcal protein A. J. Chem. Phys. 2002;117(19):8983–8995. [Google Scholar]
- McKnight CJ, Doering DS, Matsudaira PT, Kim PS. A thermostable 35-residue subdomain within villin headpiece. J. Mol. Biol. 1996;260:126–134. doi: 10.1006/jmbi.1996.0387. [DOI] [PubMed] [Google Scholar]
- McKnight CJ, Matsudaira PT, Kim PS. NMR structure of the 35-residue villin headpiece subdomain. Nat. Struct. Biol. 1997;4:180–184. doi: 10.1038/nsb0397-180. [DOI] [PubMed] [Google Scholar]
- Myers JK, Oas TG. Preorganized secondary structure as an important determinant of fast protein folding. Nat. Struct. Biol. 2001;8:552–558. doi: 10.1038/88626. [DOI] [PubMed] [Google Scholar]
- Olszewski KA,A,K,J,S. Folding simulations and computer redesign of protein A three-helix bundle motifs. Proteins. 1996;25(3):286–299. doi: 10.1002/(SICI)1097-0134(199607)25:3<286::AID-PROT2>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- Panchenko AR, Luthey-Schulten Z, Cole R, Wolynes PG. The foldon universe: a survey of structural similarity and self-recognition of independently folding units. J. Mol. Bio. 1997;272(1):95–105. doi: 10.1006/jmbi.1997.1205. [DOI] [PubMed] [Google Scholar]
- Rhee YM, Sorin EJ, Jayachandran G, Lindahl E, Pande VS. Simulations of the role of water in the protein-folding mechanism. Proc. Natl. Acad. Sci. USA. 2004;101(17):6456–6461. doi: 10.1073/pnas.0307898101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato S, Religa TL, Daggett V, Fersht AR. Testing protein-folding simulations by experiment: B domain of protein A. Proc. Natl. Acad. Sci. USA. 2004;101(18):6952–6956. doi: 10.1073/pnas.0401396101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shirts MR, Pande VS. Screen savers of the world, Unite! Science. 2000;290:1903–1904. doi: 10.1126/science.290.5498.1903. [DOI] [PubMed] [Google Scholar]
- Snow CD, Qiu L, Du D, Gai F, Hagen SJ, Pande VS. Trp zipper folding kinetics by molecular dynamics and temperature-jump spectroscopy. PNAS. 2004;101(12):4077–4082. doi: 10.1073/pnas.0305260101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spoel DVD, Lindahl E, Hess B, Groenhof G, Mark AE, Berendsen HJ. GROMACS: fast, flexible, and free. J. Comp. Chem. 2005;26(16):1701–1718. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- Tang Y, Rigotti DJ, Fairman R, Raleigh DP. Peptide Models Provide Evidence for Signficant Structure in the Denatured State of a Rapidly Folding Protein: The Villin Headpiece Subdomain. Biochemistry. 2004;43(11):3264–3272. doi: 10.1021/bi035652p. [DOI] [PubMed] [Google Scholar]
- Tironi IG, Sperb R, Smith PE, van Gunsteren WF. A generalized reaction field method for molecular dynamics simulations. J. Chem. Phys. 1995;102(13):5451–5459. [Google Scholar]
- Vu DM, Myers JK, Oas TG, Dyer RB. Probing the Folding and Unfolding Dynamics of Secondary and Tertiary Structures in a Three-Helix Bundle Protein. Biochemistry. 2004;43(12):3582–3589. doi: 10.1021/bi036203s. [DOI] [PubMed] [Google Scholar]
- Zagrovic B, Snow CD, Khaliq S, Shirts MR, Pande VS. Native-like Mean Structure in the Unfolded Ensemble of Small Proteins. J. Mol. Biol. 2002;323:153–164. doi: 10.1016/s0022-2836(02)00888-4. [DOI] [PubMed] [Google Scholar]
- Zagrovic B, Snow CD, Shirts MR, Pande VS. Simulation of Folding of a Small Alpha-helical Protein in Atomistic Detail using Worldwide-distributed Computing. J. Mol. Biol. 2002;323:927–937. doi: 10.1016/s0022-2836(02)00997-x. [DOI] [PubMed] [Google Scholar]
- Zagrovic B, Pande VS. Solvent Viscosity Dependence of the Folding Rate of a Small Protein: Distributed Computing Study. J. Comput. Chem. 2003;24:1432–1436. doi: 10.1002/jcc.10297. [DOI] [PubMed] [Google Scholar]


