Coevolution of robustness, epistasis, and recombination favors asexual reproduction

Abstract

The prevalence of sexual reproduction remains one of the most perplexing phenomena in evolutionary biology. The deterministic mutation hypothesis postulates that sexual reproduction will be advantageous under synergistic epistasis, a condition in which mutations cause a greater reduction in fitness when combined than would be expected from their individual effects. The inverse condition, antagonistic epistasis, correspondingly is predicted to favor asexual reproduction. To assess this hypothesis, we introduce a finite population evolutionary process that combines a recombination modifier formalism with a gene-regulatory network model. We demonstrate that when reproductive mode and epistasis are allowed to coevolve, asexual reproduction outcompetes sexual reproduction. In addition, no correlation is found between the level of synergistic epistasis and the fixation time of the asexual mode. However, a significant correlation is found between the level of antagonistic epistasis and asexual mode fixation time. This asymmetry can be explained by the greater reduction in fitness imposed by sexual reproduction as compared with asexual reproduction. Our findings present evidence and suggest plausible explanations that challenge both the deterministic mutation hypothesis and recent arguments asserting the importance of emergent synergistic epistasis in the maintenance of sexual reproduction.

A widely accepted explanation for overcoming the 2-fold cost of sexual reproduction (1, 2) suggests that the concomitant benefits of creating genetic variation enhances the effectiveness of natural selection in weeding out deleterious mutations and maintaining advantageous ones. Sexual reproduction produces variation by bringing together such mutations, creating novel genotypes more rapidly via recombination, whereas an asexual population must wait for such genotypes to arise through successive mutations. Several theories have been put forward suggesting scenarios that favor the evolution of sexual reproduction (3–10). One of these, the deterministic mutation hypothesis (11), postulates that sexual reproduction will be advantageous under conditions of synergistic epistasis, where deleterious mutations have a greater effect on fitness reduction if they occur together than expected by their individual effects (in contrast to antagonistic epistasis, under which said effect would be smaller). To distinguish among different forms of epistasis, previous studies (12–14) have used a power model in which the mean effect of n deleterious mutations on fitness, W_n, follows log[w_n] = −αn^β, where α and β are constants and the magnitude and sign of 1 − β determines whether epistasis is synergistic (β > 1) or antagonistic (β < 1) (11). Thus, sexual reproduction in the presence of synergistic epistasis is conjectured to accelerate the removal of deleterious mutations by means of natural selection. Therefore, the ability of natural selection to weed out deleterious mutations depends on several factors but crucially on the recombination rate and the level of epistatic interaction among loci (10), factors that might themselves be subject to selection.

The relevance of epistasis to sexual reproduction can also be explained by its role in the buildup and maintenance of linkage disequilibrium among the loci at mutation-selection balance. Under multiplicative selection, where each mutant locus contributes multiplicatively to fitness irrespective of other loci, there will be no linkage disequilibrium at mutation-selection balance (15). In the absence of linkage disequilibrium, further randomization of haplotypes no longer can occur, and the recombination rate plays no further role (1, 2). However, Eshel and Feldman (16) showed that in the presence of epistasis (a departure from multiplicative fitness), nonzero linkage disequilibrium is maintained. Furthermore, Feldman et al. (15) showed that epistasis ensures the maintenance of linkage disequilibrium at mutation-selection balance, and that the sign of the linkage disequilibrium follows that of epistasis; that is, synergistic epistasis (β > 1) will result in negative disequilibrium (8, 14, 17), and antagonistic epistasis will result in positive disequilibrium. In a subsequent study (10), it was found that antagonistic epistasis indeed prevents the invasion of a modifier that increases recombination, whereas under synergistic epistasis it is favored. However, there exists a critical value of recombination between the modifier and the major genes (genes directly contributing to fitness) beyond which the modifier reducing recombination becomes favored (10). In this way, epistasis allows selection to act indirectly on recombination.

Previous studies (10, 15, 16) addressed the fate of sexual reproduction in the presence or absence of epistasis, rather than the evolution of epistasis itself. One hypothesis concerning the evolutionary fate of epistasis posits that the evolution of phenotypic modularity reduces interaction among genes contributing to different phenotypes, therefore reducing epistasis. In a recent study (18), this hypothesis was addressed by using the modifier allele formalism, such that the dynamics of a modifier affecting the level of epistasis between two major gene loci was analyzed. It was concluded that under well specified conditions, a modifier allele that increases epistasis among the major loci invades. It was argued that such an invasion is enabled by the possibility that fitness might be a locally increasing function of the level of epistasis.

More recently, Azevedo et al. (19) compared sexual and asexual reproduction in the context of gene-regulatory networks (20). First, they demonstrated that sexually reproducing populations evolve greater robustness (21–23) than comparable asexual populations, independent of stabilizing selection (20). Second, the authors (19) showed that synergistic epistasis evolves under sexual reproduction, whereas antagonistic epistasis evolved under asexual reproduction, suggesting that sexual reproduction evolves genetic properties that propagate its own maintenance. In a similar study, Misevic et al. (24) compared sexual and asexual reproductive modes in the context of digital organisms, and they also found that sexual reproduction led to greater robustness, together with reduced (although still positive) epistasis. However, these two studies did not explicitly verify the outcome suggested by the deterministic-mutation hypothesis (11), that sex will be favored when put in competition in a mixed, sexual and asexual, population under the condition of synergistic epistasis. Specifically, the model does not consider the coevolution of recombination rate and epistasis. Here we study the coevolutionary fate of these genetic parameters: (i) epistasis, by allowing its spontaneous emergence in the course of evolution as an intrinsic property of the gene-regulatory networks, and (ii) recombination, by following the evolutionary dynamics of a modifier locus that explicitly alters the rate of recombination (4–7, 15, 25, 26).

Results

Results presented here are based on a model (20) (see Methods) that, although abstract, is sufficiently complex to capture essential features of gene-regulatory networks in development. We extend the model by associating a diallelic (R, r) recombination modifier gene with each genotype. As in previous studies (20), evolutionary simulation proceeded by selecting parental genotypes at random from the population to form a zygotic (transient diploid) stage. Reproductive mode depended, however, on the parental modifier alleles. Homozygotes rr and RR reproduced asexually and sexually, respectively. For heterozygotes, cases in which R was either dominant or recessive were tested. Under sexual reproduction, each offspring inherits one of the two parental modifier alleles at random (under asexual reproduction, offspring are clones and therefore inherit the parental modifier). Each offspring then was mutated such that the nonzero elements of the W matrix were altered at a mean mutation rate of μ = 0.1 per genotype per generation (although no mutations were allowed in the modifier gene). A homogeneous initial population was created from a single founder genotype, with the single requirement that the founder be nonlethal (i.e., have stable expression dynamics). To assess the relevance of epistasis, the population evolved initially for a fixed number of generations (2,500) in either sexual (resulting in synergistic epistasis) or asexual (resulting in antagonistic epistasis) reproduction (19). After this initial phase, the recombination modifier alleles were introduced at random into the population with equal probability (p_R = p_r = 0.5 for R and r alleles). After the introduction of the modifier allele, successive generations were produced until one or other of the modifier alleles (R or r) reaches fixation. The evolutionary simulations were repeated for 1,000 different founder populations, and the total number of wins (fixation) for each allele R or r was recorded.

Table 1 summarizes the number of trials (out of 1,000) in which asexually reproducing individuals reach fixation in the final population. In each case, the networks [with n = 10, and connectivity, c = 0.75 (20)] were evolved under different conditions. As can be seen, assuming that the recombination modifier locus is itself neutral, the recombination reduction modifier wins overwhelmingly [see Table 1 and supporting information (SI) Table 2]. This result is contrary to the hypothesis that synergistic epistasis will favor sexual reproduction (10, 11, 19). However, although recombination reduction is significantly favored after the sexual initial phase, it is less pronounced than after the asexual initial phase (comparison of the two cases reveals χ² = 99.9, P < 10⁻¹⁵ when the modifier is dominant and χ² = 58.9, P < 10⁻¹³ when it is recessive). There also is a significant difference between dominant and recessive modes (asexual initial phase: χ² = 84.7, P < 10⁻¹⁵; sexual initial phase: χ² = 45.5, P < 10⁻¹⁰). The existence of these differences suggests that epistasis nonetheless may play a role in the evolution of sexual reproduction.

Table 1.

Summary of simulation results showing the number of cases that the modifier reducing recombination fixes in 1,000 trials

Initial phase	Recombination model	r allele fixations in 1,000 trials
Asexual	Dominant	990
Asexual	Recessive	892
Sexual	Dominant	878
Sexual	Recessive	761

All four results are significantly higher than neutral (binomial test, P < 10⁻¹⁶ in all cases). Tests were performed for combinations of asexual/sexual initial phases and dominant/recessive recombination models.

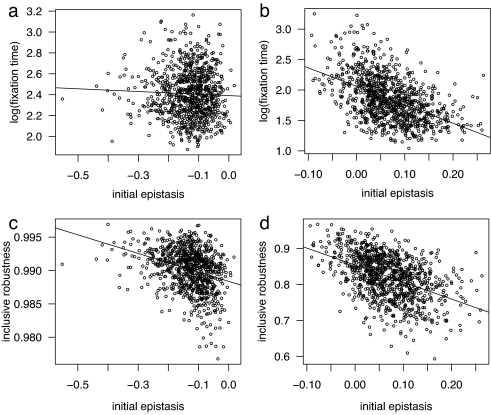
To further elucidate the role of epistasis, we study its effect on fixation time. Fig. 1 a and b shows the relationship between the fixation time of the r allele (leading to asexual reproduction) and initial epistasis level. After the sexual initial phase, no correlation is found between epistasis level and the fixation time, suggesting that the strength of synergistic epistasis plays no role (Fig. 1a and SI Fig. 2). In contrast, following an asexual initial phase, after which antagonistic epistasis emerges, a significant negative correlation between the strength of epistasis and fixation time is observed (Fig. 1b). In addition to the observed qualitative difference between synergistic and antagonistic epistasis in relation to fixation time (asexual win), a quantitative difference is observed. Mean fixation time (measured in generations) after the sexual initial phase is 297, compared with 110 after the asexual initial phase when the modifier is dominant and 578 and 390, respectively, in the recessive case. (Welch's two-sample t test was performed on the log-transformed time to fixation data. Time difference between sexual and asexual initial phase was statistically different, P < 10⁻¹⁶, when the modifier was dominant and P < 10⁻¹⁶ when it was recessive). As one would expect, changes in reproduction mode, as a consequence of the introduction and eventual fixation of the recombination modifier, cause changes in epistasis level. For example, after the sexual initial phase, asexual wins (dominant mode) exhibit a positive shift in epistasis level (initial median epistasis = −0.122, median epistasis at fixation = −0.043, significant difference by Welch's two-sample t test, P < 10⁻¹⁶). After fixation, further evolution brings the epistasis level to coincide with that appropriate for the reproductive mode.

Fig. 1.

Comparison of sexual and asexual initial phases for cases where the modifier allele (r) reducing recombination fixes (dominant mode). (a and b) After the sexual initial phase, epistasis and fixation time are uncorrelated (r = −0.040, R² = 0.002) (a), whereas for the asexual initial phase, they are negatively correlated (r = −0.490, R² = 0.240) (b). (c and d) In both cases, epistasis and inclusive robustness (see Methods) are negatively correlated: sexual initial phase (r = −0.320, R² = 0.102) (c) and asexual initial phase (r = −0.466, R² = 0.217) (d).

These observations suggest that, after an asexual initial phase, the appearance of recombination load in a population where it previously was absent confers a strong advantage to asexually reproducing individuals. By comparison, after the sexual initial phase, individuals experience little or no recombination load, resulting in a smaller advantage to asexually reproducing individuals. To quantify the effect of recombination load, we define “inclusive robustness” (see Methods), which measures effective fitness taking into account both reproduction and mutation. We use this measure to compare the populations before and after the introduction of the modifier. After the asexual initial phase, a significant reduction in inclusive robustness is observed (in dominant mode, 0.989 → 0.822; in recessive mode, 0.989 → 0.934; both P < 10⁻¹⁶, Welch's t test). After the sexual initial phase, the introduction of the recombination modifier transforms some individuals to asexually reproduce. In turn, average recombination load is lowered resulting in a slight, although significant, increase in inclusive robustness (in dominant mode, 0.988 → 0.990; in recessive mode, 0.988 → 0.995; both P < 10⁻¹⁶, Welch's t test). Fig. 1 c and d further shows the relationship between epistasis and inclusive robustness. In both cases, there exists a significant correlation; however, the asexual initial phase results in a stronger correlation.

Previous results indicate that selection pressure is reduced when the product of mutation rate and population size is small (19). Under these conditions, we expect a concomitant reduction in selection on the recombination modifier. Indeed, tests with lower mutation rate resulted in near neutral evolution of the modifier (μ = 1/M = 0.002; see SI Table 3).

To test the robustness of all reported results with respect to variations in the recombination rate, we checked the case in which the recombination levels were 0.01 and 0.5 (previously 0 and 1) for the two homozygotes, rr and RR, respectively (the heterozygotes, rR having the level, low or high, appropriate to the dominance mode), and found no qualitative difference in the results (see SI Table 4). Note that previously, in recessive mode, r genotypes formed a reproductively isolated group, and this test breaks the reproductive isolation. Previous research suggests (10), when the modifier is tightly linked to any of the fitness-affecting genes, a synergistic epistasis fitness regime favors increased recombination. This case is tested by implementing a segregation model for sexual reproduction in which a single crossover point k ∈ {1, …, N − 1} is chosen, and offspring inherit rows 1 … k together with the modifier allele, i.e., complete linkage from one parent and rows k + 1, …, N from the other. Here, too, the modifier reducing recombination prevailed overwhelmingly under all conditions (see SI Tables 2 and 5).

Although our results overwhelmingly favor asexual reproduction, in a small number of cases, the population fixated on sexual reproduction. We investigated the possibility that these trials did so because of particular characteristics of the network architecture. To test this, we selected five networks (of the 1,000 previously tested) for which the modifier increasing recombination succeeded. Each of these five networks were used as founders for 1,000 evolutionary runs each. In all cases, no qualitative difference was found with the previous random founder results (for each of the five networks, of 1,000 trials, reduction modifier wins were as follows: 798, 866, 898, 902, and 925; P < 10⁻¹⁶ for all cases; initial phase sexual, dominant modifier mode). Although this result indicates that architecture may play no role, further, more detailed investigation is required.

Discussion

Throughout many previous studies dealing with the evolution of recombination in response to epistatic mutations, a broad variety of models and assumptions have been adopted: models that assume the accumulation of deleterious mutations (8, 17), more general multilocus models where the modifier is assumed to have a weak effect (3), and, finally, three locus models with a modifier of recombination that assume nothing regarding fitness interaction or the effect of the neutral modifier locus (10, 15, 18). All of these models nonetheless did reach a common conclusion, namely, that when epistasis is antagonistic, decreased recombination rates are favored, whereas under synergistic epistasis, it is only with tight linkage between the modifier locus and the main gene that a modifier for increased recombination is favored.

Previous research (6, 7, 10, 15) suggests some potential explanations for the results observed here. First, Otto and Feldman (10) emphasized the importance of epistatic variation within individuals [here we use a population-wide epistasis measure (19)] in determining recombination modifier fate. In particular, high variation in epistasis among loci can cause selection against recombination even when mean epistasis is negative. To address this issue, we quantify intra-individual epistatic variation and relate this value to the outcome, i.e., which modifier reached fixation. We proceed by choosing a random genotype from the population immediately after the initial phase and choosing from it random pairs of nonzero interactions from different genes (w_ab, w_cd with a ≠ c). By repeatedly mutating these interactions (i.e., assigning values from a standard normal distribution), first independently and then together, we obtain three proportions (of stable mutants in n_p = 100 trials): Z(w_ab), Z(w_cd), and Z(w_ab,w_cd). Epistasis between w_ab and w_cd is e = Z(w_ab,w_cd) − Z(w_ab), Z(w_cd). Note that this measure is only an approximation to epistasis as defined by Otto and Feldman (10) because interaction pairs do not act independently in our model. Having measured epistasis, e, for n_r = 100 random pairs of weights, we calculate the dispersion (standard deviation), σ_e, for epistasis within a single individual. We then use logistic regression to classify the observed outcome (asexual or sexual win) by using σ_e as the independent variable. To compensate for frequency differences (asexual wins are more frequent), we performed 100 repeated regressions with equal size (100) samples from each outcome to obtain a mean rate for correct classification (note that random classification would achieve a 50% rate). From previous results (10), we would expect larger epistatic variation (larger σ_e) to be associated with asexual wins. However, we find no such association because mean classification rates consistently were poor (sexual initial phase/dominant: 52%; sexual initial phase/recessive: 53%; SD ≈ 3% in both cases). To verify that no bias was introduced as a consequence of using the proportions Z(w_ab), Z(w_cd), and Z(w_ab,w_cd), which could be hiding some variation, we repeated the analysis by using n_p = 1 and n_r = 10,000, obtaining equivalent results (52% in both cases).

Second, previous research also has shown (16, 27) that breaking apart negative linkage disequilibrium (and negative epistasis) increases the genetic variance in fitness, providing an advantage to a modifier increasing recombination. Direct measurement of linkage disequilibrium in this model is difficult because robustness induces a high level of neutral polymorphism. Classical population genetics models predict that the sign of linkage disequilibrium coincides with that of epistasis at mutation-selection balance. Thus, synergistic epistasis will result in negative linkage disequilibrium, whereas antagonistic epistasis results in positive linkage disequilibrium (15). At the same time, the sign of linkage disequilibrium can be assessed by using the variation in fitness of the recombined (V_r) vs. nonrecombined (V_n) offspring: under synergistic epistasis, the recombined offspring are expected to have higher variance in fitness (compared with the nonrecombined), whereas under antagonistic epistasis, the opposite is expected (16, 27). However, our results show higher variance in recombining offspring under both synergistic and antagonistic epistasis. Not only is the difference (V_r − V_n) positive under antagonistic epistasis (where the classical model predicts it should be negative), but it also is even greater in magnitude than under synergistic epistasis (see SI Table 6). Adopting an alternative approach, we still can estimate the actual changes in fitness dispersion and attempt to relate these to the modifier outcome. We proceed by modifying the inclusive robustness measure (see Methods) such that reproduction/mutation trials are repeated 100 times for the same random pair of individuals to obtain a proportion Y of stable mutants. In turn, M = 500 random pairs were tested to obtain a distribution for Y. We focus on the critical period immediately after the introduction of the modifier and obtain the Y distributions for two postintroduction generations, immediately after introduction and 10 generations later (at t = 2,500 and t = 2,510). In all cases, we found significantly different dispersion parameters (Ansari-Bradley, P < 0.05) between the two distributions. We further calculate the ratio, r_Y, of the two dispersion estimates, thus obtaining an estimated change in fitness dispersion (in particular, if r_Y 1, then fitness dispersion has increased). We again used the logistic regression method to obtain a mean rate for correct classification of outcome, now using r_Y as the independent variable. Based on previous results, we might expect that, after the sexual initial phase (negative epistasis, presumably negative linkage disequilibrium) increases in fitness variance should be associated with a sexual win. However, despite finding a wide range of r_Y values (both >1 and <1), we again find no association with outcome (sexual initial phase/dominant: 54%; sexual initial phase/recessive: 52%; SD ≈3% in both cases).

Third, previous results also have suggested that higher recombination will be favored only if negative epistasis is confined to a certain range [see Otto and Gerstein (28)]. In particular, epistasis should be small relative to selection. We addressed this possibility by again using the logistic regression method as a classifier for outcome, now using (population-level) epistasis, β, as the independent variable. We found no association because mean classification rates were again consistently poor (sexual initial phase/dominant: 53%; sexual initial phase/recessive: 53%; SD ≈3% in both cases). To exclude the possibility that the sexual wins might be occurring with a certain subrange for β, we calculated the proportion of sexual wins within each quartile for β and found no significant differences between any of the groups (Kruskal-Wallis, P > 0.05 for both sexual initial phase/dominant and sexual initial phase/recessive). As an alternative approach, we used quadratic discriminant analysis (instead of logistic regression), because of its capacity for nonmonotonic classification, but again obtained poor classification rates (sexual initial phase/dominant: 54%; sexual initial phase/recessive: 53%; SD ≈3% in both cases).

In all three cases described above, the differences with previous results presumably have arisen as a consequence of the more complex genotype/phenotype map we are dealing with here, illustrating how results from classical population genetics may be of limited utility for this class of model.

To conclude, although our results show that epistasis does not determine recombination modifier fate, it clearly is relevant to the process (see Fig. 1b). At the same time, the fate of epistasis is determined by the prevailing reproductive mode. For example, a population exhibiting synergistic epistasis (expected after a sexual initial phase) will evolve toward antagonistic epistasis if the reproductive mode becomes asexual (i.e., if the asexual modifier reaches fixation). These findings illustrate the coevolution of genetic parameters such as epistasis and recombination. Coevolution should be understood here in the looser sense of coinciding dynamics rather than strict codependence. Previous studies have been limited in that they failed to consider the coevolution of epistasis and recombination but rather have contemplated each factor in isolation, a shortcoming that may lead to erroneous conclusions. At the same time, previous studies (29) have empirically validated concepts such as the Fisher–Muller hypothesis (that sexually reproducing individuals will respond more rapidly to selection than asexual ones will) (30, 31). Regarding the coevolutionary process addressed here, the increasing amount of high-throughput data on epistatic interactions (32–34) soon will make it possible to test such theoretical predictions experimentally.

Methods

Broadly, we extend the modeling framework of Siegal and Bergman (20) to include a modifier of recombination. It is worth noting that in the model of Siegal and Bergman (20), selection has two aspects: first, a requirement for dynamic stability, and second, a fitness measure defined in terms of similarity to an optimum expression pattern. Because robustness evolves regardless of stabilizing selection (the relative importance of the fitness measure was adjustable), the authors concluded that the requirement for dynamic stability was the most salient phenotypic feature for the evolution of robustness. Azevedo et al. (19) used the model to investigate whether negative epistasis coevolved with robustness. In these circumstances, it is reasonable to ignore stabilizing selection (similarity to optimum expression) and use dynamic stability exclusively. However, because dynamic stability is a binary (stable/unstable) value, robustness and epistasis were defined as population-level measures, based on proportions of stable mutants for random mutations. Following Azevedo et al. (19), we create synergistic and antagonistic epistasis in sexual and asexual populations, respectively, by using the same parameter settings and similarly adopting population-level measures such as epistasis and introducing inclusive robustness. However, we also verify our findings by using individual-level measurements (see Discussion). At neither level (population nor individual), however, were such measures helpful in predicting the modifier outcome (sexual or asexual win).

Consider a finite population of M = 500 randomly mating individuals, each modeled as an interaction network of n = 10 genes. These interactions are represented by an N × N matrix, W, whose elements, w_ij, denote the effect on gene i of the product of gene j. Each network defines a dynamical system, with state vector S(t) = (s₁(t), …, s_N(t)) representing the expression levels of each gene at time t. The dynamics of S(t) are modeled by the set of nonlinear coupled difference equations

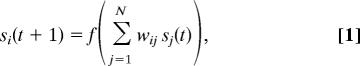where

is a sigmoidal function. The initial state, S(0), is constant for each simulation, and is set by randomly choosing each s_i = −1 or +1. We define development as the process of iterating Eq. 1 a fixed number of times or until equilibrium. The equilibrium steady state, Ŝ, is reached when a measure analogous to a variance,

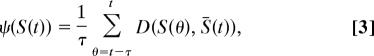is smaller than ε = 10⁻⁴, where

is the average of expression levels in the time interval (t − τ, …, t), and τ = 10.

All M individuals in the starting population are identical and are a copy of a randomly generated founder individual. The founder W matrix is a nonsymmetric random [Erdös-Rényi (35)] graph, constructed by assigning nonzero elements with probability P(w_ij ≠ 0) = c (the connectivity). Nonzero elements are assigned values from a standard normal distribution (w_ij = Normal (0, 1)). Connectivity was set to c = 0.75 for these experiments. Each w_ij value is drawn independently from the standard normal distribution. The founder is required to have a steady state.

Subsequent generations are produced by random pairing of individuals. Sexual reproduction assumes segregation among unlinked genes (i.e., offspring are created by randomly selecting rows of the W interaction matrix from each parent with equal probability). Results using a single-point segregation model (one recombination event among segregating genes) also were evaluated giving qualitatively equivalent results (see Results and SI Table 2). Asexual reproduction constitutes cloning one of the chosen parents (assuming complete linkage). Note that there exists no cost for sexual reproduction. Our model is haploid in that each individual has a single copy of each gene (represented as the ith row of the matrix W), and under sexual reproduction we have a transient diploid stage during which recombination occurs. In this model, all nonzero elements of row i of the W interaction matrix represent the set of upstream cis-regulatory elements of gene i and as such are considered to be in complete linkage to one another and to gene i. Thus, each row of W, comprising the gene and its cis-regulatory element, is represented by a single locus and consequently is transmitted as a unit.

After an initial phase of either sexual or asexual reproduction, the modifier is introduced (allele r or R is assigned with equal probability), and reproductive mode becomes dependent on the parental modifier alleles. Homozygotes rr and RR reproduce asexually and sexually, respectively. For heterozygotes, cases in which R is either dominant (Rr reproduce sexually) or recessive (Rr reproduce asexually) are tested.

Reproduction is followed in each case by mutation (replacement with an independent random number from the standard normal distribution) of each nonzero entry with probability μ/(cN²). An offspring is chosen to be included as a member of the population if it reaches developmental equilibrium. The life cycle therefore consists of reproduction–mutation-selection. Reproduction in sexual mode involves random pairing with segregation, whereas in asexual mode one parent is cloned (together with modifier). After mutation, we proceed with selection based on dynamic stability, such that unstable offspring are removed from the population (see also SI Fig. 3).

Dynamics in the model occurs at two timescales: at the individual level, the interaction network (W matrix) determines the gene-expression dynamics, whereas at the evolutionary level, reproductive mode together with fitness determine the dynamics of the composition of the population, that is, the elements of the W matrix within each individual.

Measurements

It is worth reiterating that, because we are investigating coevolution of robustness, epistasis, and reproductive mode, we have chosen to focus exclusively on developmental stability. Individual fitness in this model is binary (1 if stable, 0 if unstable); thus, an appropriate method for estimating mean fitness involves repeatedly measuring stability (after perturbations such as mutation and reproduction) and measuring the proportion of stable/unstable observations. Measuring fitness in this way lends itself to calculating previously proposed definitions for epistasis, robustness (11, 20), and inclusive robustness (see below) better than would be possible by using the binary fitness directly. Note that reproductive success depends exclusively on stability/instability and that the above measurements, which are emergent properties, have no direct effect on this success. In cases with continuous-valued fitness, as in Siegal and Bergman (20), there clearly is no need for an a priori estimate of mean fitness via iteration, and alternative ways of estimating the above parameters would be preferable.

Epistasis is calculated as 1 − β, where β is estimated by exposing each individual in the population to a maximum of n = 5 successive mutations. The proportion of stable mutants in 100 trials, W̄_n, is measured for each value of n ∈ {1, …, 5}. A generalized linear model with complementary log–log link and binomial error structure, log[−log[W̄_n]] = log[α] + β log[n], is used to model W̄_n for each individual, and β is estimated by using maximum likelihood (19). Median β values for each population are used.

Robustness is measured as the proportion of stable individuals as a result of perturbation. We define perturbation as the mutation of exactly one nonzero w_ij element by replacing it with an independently drawn random number from the standard normal distribution. Each individual's stability is averaged over 10 perturbations and then averaged over all 500 individuals in the population.

Inclusive robustness measures stability taking into account reproduction in addition to mutation. For each population of size M = 500, we measure the proportion of stable offspring in 100 × M reproduction/mutation trials. Each trial involves selecting two individuals at random from the population, producing an offspring according to the parental modifier alleles (and the dominance mode), applying mutation, then checking for stability. In an asexually reproducing population, inclusive robustness is equivalent to 1 − λ where λ is the mutation load. In this model, because no stabilizing selection is in effect, inclusive robustness is equivalent to the population mean fitness.