Protein hydration in solution: Experimental observation by x-ray and neutron scattering

Abstract

The structure of the protein–solvent interface is the subject of controversy in theoretical studies and requires direct experimental characterization. Three proteins with known atomic resolution crystal structure (lysozyme, Escherichia coli thioredoxin reductase, and protein R1 of E. coli ribonucleotide reductase) were investigated in parallel by x-ray and neutron scattering in H₂O and D₂O solutions. The analysis of the protein–solvent interface is based on the significantly different contrasts for the protein and for the hydration shell. The results point to the existence of a first hydration shell with an average density ≈10% larger than that of the bulk solvent in the conditions studied. Comparisons with the results of other studies suggest that this may be a general property of aqueous interfaces.

Hydration, ion binding, and hydrophobic effects are major factors in the stabilization of the tertiary and quaternary structure as well as in the interactions between macromolecules. Despite their importance, macromolecule–solvent interactions are understood inadequately because of the considerable difficulty associated with their experimental study (for a review, see ref. 1). Detailed hydration mechanisms and their effects on solubility even for nearly ideal interfaces are the subject of conflicting models. In some cases, the density of the first layer is predicted to be higher than that of bulk water, in others ice-like structures with a lower density are proposed. The very complex surfaces of biological macromolecules and their hydration and solvation are the most poorly defined parts of structures obtained by crystallography or NMR because they are often disordered or dynamically averaged.

Because of favorable contrast conditions, neutron diffraction and scattering experiments combined with x-ray results are very useful for the study of protein–solvent or nucleic acid–solvent interactions at various levels of resolution. Water and small solutes have been located at close to atomic resolution in single crystal work on small proteins (2, 3) and fiber diffraction experiments on DNA (4). Solution scattering experiments provide low resolution information, which also can be interpreted in terms of thermodynamic concepts (5) and continues to provide information on the hydration and solvation of proteins and tRNA (5, 6) as a function of solvent composition.

Comparisons between experimental x-ray solution scattering (SAXS) curves and those evaluated from crystallographic structures have been used widely to verify the structural similarity between macromolecules in crystals and in solution (see, e.g., refs. 7–9). It is well established that the experimental SAXS patterns from proteins cannot be adequately described without accounting for hydration effects, and different ways of doing this have been implemented (10–13).

Recently, the program crysol was developed (14), which takes the hydration into account by surrounding the macromolecule in solution by a border layer of variable scattering density. The latter may differ from that of the bulk solvent and is adjusted to fit the experimental solution scattering curve. Analysis of the SAXS data from proteins with known atomic structure (lysozyme, hexokinase, enolpyruvyltransferase, reverse transcriptase, aspartate transcarbamylase, ribonucleotide reductase, pyruvate decarboxylase, etc.) indicated that inclusion of the hydration shell significantly improved the agreement between the experimental and calculated x-ray scattering curves. The scattering density in the border layer was typically 1.05–1.25 times that of the bulk, suggesting that the hydration shell around proteins is denser than the bulk solvent.

A higher density in the hydration shell was predicted from molecular dynamic simulations (15), found for insulin molecules in the crystal by using solvent density refinement (16) and also was observed directly in a high resolution crystallographic study of mannose-binding protein A (17). According to Perkins (18), the volume occupied by a bound water molecule is ≈20% smaller than that of a free water, which also contributes to a higher density in the shell. In contrast, any ordering of a strongly directional molecule like water that leads to the formation of an extended ice-like structure would decrease the water density around the protein (ref. 19 and references therein). A strong argument against a hydration shell around proteins of mean density different from that of bulk solvent is that this would lead to a solvent-dependent, partial-specific volume for the protein. Measured protein volumes, however, are fairly independent of solvent and are in close agreement with those predicted from the amino acid composition (20). Richards (21) argued that, because of the heterogeneous nature of the protein surface, the hydration shell could have, locally, a higher or lower density than the bulk. He suggested that packing around hydrophobic groups would lead to lower density whereas electrostriction around charged groups would lead to higher density. Because approximately half of the protein surface is polar and half is nonpolar, the effect of density fluctuations would cancel out yielding a mean shell density close to that of the bulk. The packing efficiencies at the protein–water interface in 22 high resolution crystal structures were examined by Gerstein and Chothia (22). The authors reconcile a hydration shell of mean density ≈20% higher than the bulk with a looser packing of surface residues. The volume decrease due to the shell is compensated by an increase in the volume of the atoms at the protein surface. In this context, direct measurements of the mean density of the hydration shell of proteins in solution is of great interest.

SAXS solution studies alone would not provide unequivocal proof of the higher density in the hydration shell because a similar effect on the scattering curves could result from higher mobility or disorder of the surface side chains in solution compared with their average structure in the crystal, which would increase the apparent particle size. Below, the contributions of the protein and of the hydration shell to the scattering are separated by using the different contrast conditions provided by small angle neutron scattering (SANS).

MATERIALS AND METHODS

Sample Preparation.

For x-ray measurements, chicken egg white lysozyme (EC 3.2.1.17) (Merck) samples at 5, 10, and 20 mg/ml were prepared by dilution from the stock solutions at ≈50 mg/ml in 40 mM Na acetate (pH 3.8) in H₂O or in D₂O. For measurements at higher ionic strength, the buffer also contained 150 mM NaCl. Protein concentration was determined spectrophotometrically by using the absorbance A₂₈₀^1% = 26.4 for 1 cm. Buffers were degassed, and dithiotreitol was added to 10 mM concentration to both the sample and buffer. For neutron measurements, the lyophilized lysozyme powder (Sigma) was dissolved in 150 mM NaCl and 40 mM Na acetate buffer (pH 4.25). Samples in D₂O were obtained by dialysis against 40 mM Na acetate buffer (pH 4.25) in D₂O. Salt was not added to the D₂O solution to reduce the tendency of the protein to aggregate in these conditions. Sample concentrations were measured by using an absorbance of A₂₈₀^1% = 24.7 for 1 cm. Concentrations of 5, 20, 48 and mg/ml and 4, 18, and 51 mg/ml were measured in H₂O and in D₂O, respectively.

Recombinant Escherichia coli thioredoxin reductase (TR) was purified from E. coli as described (23). The buffers contained 0.5–1.0 mM ethylene diamine tetraacetic acid to maintain enzyme activity. Specific activity of TR was 78 units/mg (23). Protein R1 of E. coli ribonucleotide reductase (R1) was purified from E. coli strain C600/pLSH1 (24) as described (25) with an additional final step in the purification procedure: fast protein liquid chromatography on a MonoQ10 ion exchange column (Pharmacia) in a shallow gradient of NaCl. The procedure yielded essentially pure and active R1. Buffers used for R1 solutions always contained 11 mM MgCl₂ needed for enzyme activity and 10 mM dithiotreitol. The specific activity of R1 was 700 units/mg (26). Samples of TR and R1 in D₂O were prepared by gel filtration in spin columns as described (25). The estimated H₂O content did not exceed 0.5%. pH was measured by glass electrode and was not corrected for D₂O. Protein solutions were frozen and kept at −80°C. Protein concentrations were determined spectrophotometrically by using absorptions of A₄₆₀ = 11300 M⁻¹⋅cm⁻¹ and A₂₈₀^1% = 1.67 for 1 cm (TR) and A₂₈₀ − A₃₁₀ = 180000 M⁻¹⋅cm⁻¹ (R1).

For TR, the SAXS measurements were performed at 3, 5, and 10 mg/ml; SANS measurements in H₂O were performed at 3.5, 7, and 15 mg/ml and in D₂O at 3, 6, and 12 mg/ml. For R1, the SAXS measurements were performed at 5, 10, and 20 mg/ml. After thawing the R1 samples for the neutron, measurements displayed clear signs of aggregation and were centrifuged, yielding final concentrations of 4 and 19 mg/ml in H₂O and 1 and 2 mg/ml in D₂O.

Scattering Experiments and Data Treatment.

The synchrotron radiation SAXS data were collected following standard procedures on the X33 camera of the European Molecular Biology Laboratory on the storage ring DORIS III of the Deutsches Elektronen Synchrotron by using multiwire proportional chambers with delay line readout (27, 28). The scattering patterns measured at different sample detector distances covered the range of momentum transfer 0.38 < s < 5 nm⁻¹ for lysozyme, 0.2 < s < 3 nm⁻¹ for TR, and 0.17 < s < 5 nm⁻¹ for R1. The data were normalized to the intensity of the incident beam, corrected for the detector response, the scattering of the buffer was subtracted, and the difference curves were scaled for concentration. All procedures involved statistical error propagation by using the program sapoko (D.S. and M.H.J.K., unpublished work). Normalized high and low concentration curves were spliced and merged in the overlapping region to yield the final x-ray data sets.

Neutron scattering experiments were performed by using the D-22 instrument at the Institute Laue Langevin, Grenoble, France, with λ = 0.6 nm and Δλ/λ = 0.1. The lysozyme and the high concentration TR samples were measured at a sample detector distance of 1.8 m covering the range of momentum transfer 0.24 < s < 4.8 nm⁻¹. For the low concentration TR and for the R1 samples, a sample detector distance of 4 m was used to cover the range 0.12 < s < 2.4 nm⁻¹. The data were radially averaged, corrected for detector dead time, normalized to the intensity of the incident beam, and divided by the scattering of pure water. The scattering from the buffer, empty cuvette, and other sources was subtracted by using conventional procedures (29). The difference curves were scaled for concentration and sample transmission. Initial portions of the scattering curves were extrapolated to infinite dilution by using standard methods (30). The experimental curves from TR solutions at low and high concentrations were merged as described above for the x-ray data.

Evaluation of Solution Scattering Patterns.

The scattering intensity from a dilute monodisperse solution is an isotropic function proportional to the scattering from a single particle averaged over all orientations (30), and the experimental curves are obtained by subtracting the solvent scattering from that of the solution. The particle is defined by a boundary determining a region where the scattering density differs from that of the bulk solvent. It may thus (and does) differ from the particle in a crystal. To evaluate the solution scattering pattern from a given crystal structure, both the scattering from the excluded particle volume (filled with bulk solvent with a constant scattering length density ρ_s) and that from the hydration shell should be taken into account. The scattering intensity from the molecule defined in the crystal structure surrounded by a hydration layer with a scattering density ρ_b is expressed as

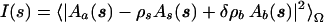1

where A_a(s) is the scattering amplitude from the particle in vacuo evaluated from the atomic coordinates, A_s(s) and A_b(s) are, respectively, the scattering amplitudes from the excluded volume and the hydration layer, both with unit density, and δρ_b = ρ_b − ρ_s is the contrast of the border layer. Here, s = (s, Ω) where s = 4π sinθ/λ denotes the momentum transfer, 2θ is the scattering angle, λ is the radiation wavelength, and <>_Ω stands for the average over the solid angle Ω in reciprocal space.

The SAXS curves from the crystallographic models were evaluated by using the program crysol (14). The program evaluates the amplitudes A_a(s) from the atomic structure factors and A_s(s) by using dummy Gaussian spheres placed at the atomic positions. The particle envelope is represented by an angular function connecting the center of mass with the most distant atom along each direction. The hydration shell that yields A_b(s) is approximated by a 0.3 nm-thick concentric border layer placed 0.2 nm outside the envelope to model the density profile of the first solvation shell. Two parameters, the excluded volume of the particle V and the electron density in the layer ρ_b, are varied to minimize the discrepancy

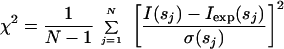2

where N is the number of experimental points, and I_exp(s) and σ(s) denote the experimental intensity and its SD, respectively. The excluded volume is varied around the value predicted from the molecular mass by changing the average displaced volume per dummy atom to account for an uncertainty in its partial specific volume.

The SANS curves were evaluated by using the program cryson, a modified version of crysol (D.S., unpublished work). The main differences between the two programs are that (i) the neutron scattering lengths of atoms and atomic groups are used to evaluate A_a(s); (ii) in solutions with D₂O fraction 0 < Y < 1, it is assumed that all hydrogens in hydrophilic (NH, NH₂, NH₃, OH, SH) groups are replaced by deuteriums with probability Y, and those belonging to the main chain NH groups with probability 0.9Y (31); (iii) to take the instrumental distortions into account, the calculated curve is smeared appropriately by using the resolution function (32); (iv) to correct for an uncertainty in the subtraction of the incoherent background, a constant—fixed or included as a free parameter in the fitting procedure—can be added to or subtracted from the experimental data. Variations in the exchange probability of the NH groups, e.g., by taking 0.8Y or 1.0Y instead of 0.9Y, influence the results only marginally.

The atomic coordinates of lysozyme, TR, and R1 are those from the crystallographic models in the Brookhaven Protein Data Bank (33), entries 6lyz (34), 1tde (35), and 1z1z (36), respectively.

Calculation of the Invariants.

The values of the forward scattering and the radii of gyration for individual experimental scattering curves were evaluated by using the Guinier approximation

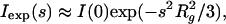3

which is valid in the range sR_g < 1.3 (30) and by the indirect transform program gnom (37). The extrapolated forward scattering value allows one to estimate the molecular mass of the solute after appropriate normalization for both SAXS and SANS measurements. SAXS data were calibrated against the scattering from a protein with known molecular weight (BSA); for SANS data, water scattering was used as a reference (38).

RESULTS

Hydration Effects in SAXS and SANS.

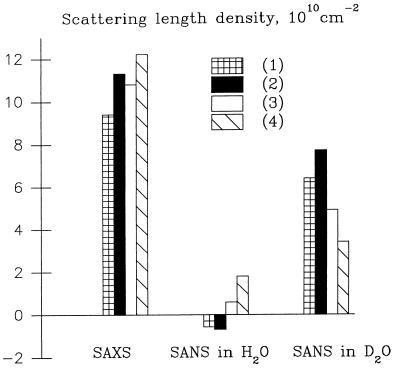
The difference between the two first terms in Eq. 1 is proportional to the particle contrast Δρ = ρ_p − ρ_s where ρ_p is the average scattering density of the particle, and the third term is proportional to the contrast in the hydration layer δρ_b. The net calculated intensity thus depends mainly on the relation between Δρ and δρ_b. Let us consider this relation for x-ray scattering from proteins in an aqueous solution (Fig. 1). The relative difference between ρ_p and ρ_s is small (≈30%), and an increase of 10–20% in ρ_b would affect significantly the observed scattering curve, making the particle look larger because both δρ_b and Δρ would be positive. Mobility of the side chains on the protein surface would lead to the same effect because the scattering density in the protein–solvent interface would lie between ρ_p and ρ_s.

Figure 1.

Relationship among the scattering densities of the bulk solvent, protein, and protein–solvent interface for x-rays and neutrons in H₂O and D₂O. (1) Bulk solvent, (2) a shell with density 20% above that of the bulk solvent, (3) mobility of the side chains on the protein surface; scattering density in the interface is drawn in the middle between those of protein and of bulk; (4) protein. Scattering density of protein in D₂O is larger than that in H₂O because of H/D exchange.

The situation is different for neutron scattering in H₂O/D₂O mixtures (Fig. 1). In H₂O, proteins still have a positive contrast, but the scattering length density of water is slightly negative. The neutron scattering length of deuterium is much higher than that of hydrogen, and the scattering length density of D₂O is higher than that of protein (negative contrast). A 10–20% denser hydration shell would in both cases reduce the apparent size of the particle; contrary to SAXS, the signs of δρ_b and Δρ would be opposite. Moreover, because the ratios  ρ_s/Δρ  for SANS are smaller than for SAXS, the effect is expected to be smaller, especially in H₂O. Mobility of the side chains would in both cases lead to the same effect as in the x-ray case and with approximately the same magnitude.

Parallel SAXS and SANS experiments on proteins with known crystallographic structure provide therefore a direct way to establish the origin of the denser border layer necessary to obtain a good fit with x-ray scattering data. If the fit to the SANS data recorded in H₂O and in D₂O requires a “larger” particle compared with the crystallographic structure (δρ_b/Δρ > 0) and if the magnitude of the effect is approximately the same as for x-rays, this shell should be attributed to the mobility of the protein surface. If the particle appears somewhat smaller in D₂O and practically unchanged in H₂O and δρ_b/Δρ < 0, the higher density is caused by the solvent. The density of the hydration shell relative to that of the bulk solvent can be estimated by the ratio (ρ_s + δρ_b) /ρ_s independently of the type of radiation used.

SAXS Results.

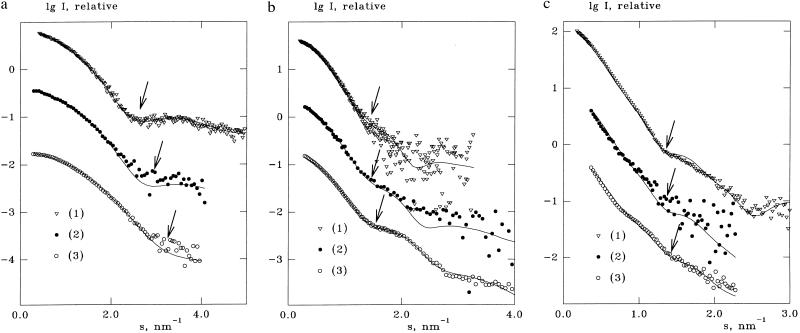
The experimental x-ray scattering curves from lysozyme, TR, and R1 are presented in Fig. 2 along with the best fits evaluated from the atomic structures accounting for the border layer. Extrapolated values of the forward scattering yielded molecular weights coinciding with the known values within experimental error, thus indicating the absence of aggregation. Parameters calculated from the atomic coordinates and from the SAXS data are summarized in Table 1. The radii of gyration of the atomic structure are evaluated without solvation shell (i.e., at δρ_b = 0); the excluded volumes were obtained from crysol by fitting the x-ray data. In all cases, the border layer required to fit the experimental data has positive contrast so that the relative density in the hydration shell varies from 1.03 to 1.2. If the hydration shell is omitted (δρ_b = 0), calculated radii of gyration are systematically smaller than the experimental ones, and the overall fit to the experimental data denoted as χ₀ is worsened (Table 1).

Figure 2.

Fit to the experimental data by crysol and cryson for lysozyme (a), TR (b), and R1 (c). Symbols represent the experimental curves; solid lines represent the best fits calculated from the atomic models with the hydration shell. Fits (1)–(3) correspond to x-rays, neutrons in H₂O, and neutrons in D₂O, respectively. Arrows indicate the onset of the first shoulder for each curve.

Table 1.

Parameters of proteins, hydration layers, and the fits to the experimental curves

	Lysozyme	Thioredoxine reductase	Ribonucleotide reductase R1
Molecular mass, kDa	14.5	68	160
Excluded volume, nm3	17.4	80.6	202.6
X-ray parameters
Rg atomic structure, nm	1.407	2.732	3.845
Rg experimental, nm	1.54 ± 0.02	2.82 ± 0.04	4.22 ± 0.04
δρb, e/nm3	25	60	10
χ, best fit	0.48	0.78	1.90
χ0, best fit at δρb = 0	0.78	1.39	2.00
Relative shell density	1.07	1.18	1.03
Neutron parameters in H2O
Rg atomic structure, nm	1.392 [1.395]*	2.734	3.864
Rg experimental, nm	1.38 ± 0.02	2.74 ± 0.05	–
δρb, 1010 cm−2	−0.06 [−0.06]	−0.11	−0.10
χ, best fit	1.7 [1.7]	1.8	1.6
χ0, best fit at δρb = 0	1.8 [1.8]	2.0	1.7
Relative shell density	1.11 [1.11]	1.20	1.18
Neutron parameters in D2O
Rg atomic structure, nm	1.420 [1.372]	2.741	3.859
Rg experimental, nm	1.24 ± 0.02	2.66 ± 0.03	–
δρb, 1010 cm−2	0.40 [0.36]	0.58	0.96
χ, best fit	2.2 [2.2]	1.8	2.8
χ0, best fit at δρb = 0	2.7 [2.6]	3.0	3.9
Relative shell density	1.06 [1.05]	1.09	1.15
Average relative density	1.08 ± 0.02	1.16 ± 0.05	1.12 ± 0.06

^*Values in brackets are evaluated from the neutron diffraction model of lysozyme. 

SANS Results.

The neutron radii of gyration of lysozyme and TR in H₂O extrapolated to zero concentration coincide with those calculated from the atomic structure, whereas the values in D₂O are smaller (Table 1). For both lysozyme and TR, absolute calibration of the normalized forward scattering values yielded molecular weights in good agreement with the theoretical ones. The samples of R1, especially in D₂O, displayed aggregation, and a reliable estimate of R_g was impossible (for this reason, initial portions of the scattering curves from R1 were discarded in further analyses).

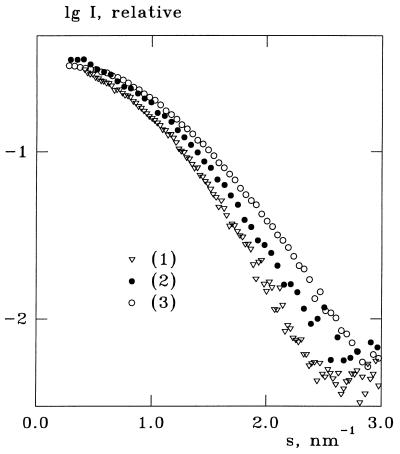
As seen from a visual comparison of the experimental x-ray and neutron scattering curves in Fig. 2, the onset of the first shoulder (indicated by an arrow for each curve) shifts toward higher angles when going from SAXS to SANS in H₂O and even further to SANS in D₂O. This effect is more clearly illustrated in the normalized lysozyme curves in Fig. 3 and means that the particle apparently “shrinks.” This qualitative observation is confirmed by the analysis by using cryson in Table 1 and Fig. 2. The excluded volumes of the proteins in the fitting procedure were kept within 5% difference of the values in Table 1. For all samples, the contrasts in the solvation shell yielding the best fit were negative for the H₂O data and positive for the D₂O data. Absolute values of δρ_b for H₂O solvents were smaller than those in D₂O, and the relative densities of the solvation shells were in the range of 1.06–1.2.

Figure 3.

Initial portions of the experimental curves from lysozyme (notations are as in Fig. 2) normalized to the same value of the forward scattering I(0).

Lysozyme at Different Ionic Strength.

As different ionic strength conditions were used for SANS measurements of lysozyme in H₂O and in D₂O, additional SAXS measurements were performed in these buffers. Four concentration series were measured, in buffers with 0 and 150 mM NaCl, both in H₂O and in D₂O, and the radii of gyration are presented in Fig. 4 along with those for SANS. In SAXS measurements, no difference was observed between samples in H₂O and D₂O buffers. Although solutions without salt display a stronger concentration dependence of R_g, the extrapolation of the SAXS results to zero concentration yields practically the same value (Table 1), which also agrees with the value 1.55 ± 0.05 nm found in an extensive study (39). The R_g of lysozyme found by SANS in D₂O correlates well with the value 1.25 nm reported in Niimura et al. (40). The results in Fig. 4 confirm that the observed effect is due to the hydration shell and not to a change of the solubility of the protein in different buffers.

Figure 4.

Radius of gyration of lysozyme as function of concentration for different solvents: SANS in H₂O, 150 mM NaCl (1); SANS in D₂O, no salt (2); SAXS in H₂O and in D₂O, 150 mM NaCl (3); SAXS in H₂O and in D₂O, no salt (4).

DISCUSSION

The proteins studied in the present work differ significantly in molecular weight and have different quaternary structures (lysozyme is a monomer, TR and R1 are homodimers). For all of them, inclusion of a hydration shell improves the fit to the experimental SAXS data, although the resulting contrast in the layer differs noticeably, leading to relative shell densities ranging from 1.03 for the R1 to 1.18 for the TR. The use of the border layer improves the fits to the SANS data as well, and the signs and magnitudes of the contrast in the layer are compatible with a denser hydration shell but not with a change in mobility of the side chains on the protein surface (Fig. 1). It should be stressed that our conclusions are based not simply on the analyses of the observed radii of gyration that may be subject to concentration effects but rather result from fitting procedures involving the entire scattering patterns.

The smallest improvement of the fit after including the border layer was observed for SANS in H₂O. This result is compatible with the hypothesis that the hydration shell has almost zero scattering density and is incompatible with disordering of the side chains. It also suggests that the observed effect is caused by the packing of the water molecules and not by counterion condensation (because the ions have essentially positive scattering lengths, the latter would lead to an effect similar to the disordering of the side chains). The effect in D₂O is larger than in H₂O but is still smaller than for x-rays. The estimates of the relative density in the hydration shell from SANS in Table 1 are generally in good agreement with those from SAXS. The largest discrepancy, observed for R1, has several causes. First, the best fit to the SAXS data of R1 displays some systematic deviations near the first shoulder (Fig. 2c), indicating that the structures in the crystal and in the solution may be different, which has been observed in other multidomain proteins (see, e.g., ref. 41). This difference may account for an exceptionally low value of the shell density for x-rays. Initial portions on the SANS curves from R1 had to be discarded because of aggregation (see Materials and Methods), limiting the accuracy of their quantitative analysis.

The search for the optimum fitting parameters performed by crysol and cryson does not provide error estimates, and this fact raises questions regarding the statistical significance of the shell contrasts. The latter can be assessed by considering the improvement of the fit after including the border layer

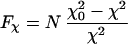4

(“test of additional term”), which obeys the F statistics (42). Even for the smallest F_χ = 9.8 obtained for lysozyme in H₂O (Table 1, n = 82), the probability that the reduction in χ is statistically significant exceeds 0.997. This proves that the densities in the border layer are significantly different from the bulk. Average values of the relative shell densities for the three proteins and their SD are presented in Table 1.

Most of the atomic models deposited in the Protein Data Bank are determined with x-rays and do not contain information about hydrogens. In cryson, these atoms are taken into account by using effective scattering factors of hydrogen-containing atomic groups (CH_n, NH_n, OH, and SH; see ref. 14). For the structures determined by neutron crystallography, positions and degrees of H/D exchange of individual hydrogen atoms are available, thus allowing more accurate calculations. The model of lysozyme of Mason and coworkers (43) was used to verify whether the observed differences between the SANS patterns in H₂O and in D₂O originate from the scattering of the internal particle inhomogeneities at different contrasts or from H/D exchange. For this, cryson was modified to explicitly take into account the hydrogen atoms and their degrees of exchange with deuterium; the results obtained for lysozyme are presented in Table 1 in brackets. From the difference in the calculated radii of gyration in D₂O it follows that the distribution of the exchangeable hydrogens in the neutron diffraction model is slightly different from the homogeneous exchange distribution assumed by default in cryson (see Materials and Methods). The fitting parameters for the hydration shell remain, however, practically the same as for the model without hydrogens, and this result confirms the higher density in the shell.

It is also interesting to compare the parameters of the hydrogen-containing model of lysozyme from neutron crystallography with the results of earlier contrast variation studies. At sufficiently high contrasts (i.e., both for H₂O and for D₂O solutions), the radius of gyration is expressed as (44)

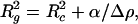5

where R_c is the radius of gyration of the particle at infinite contrast and α is a dimensionless constant describing whether the regions of higher scattering density are closer to the particle center or to its periphery. The contrasts of lysozyme in H₂O and in D₂O (2.46 × 10¹⁰ cm⁻² and −3.55 × 10¹⁰ cm⁻², respectively) are evaluated from its atomic composition, and the difference between the radii of gyration in the two solvents R_c^H₂O − R_c^D₂O depends on the sign and magnitude of α. The values R_c = 1.38 nm and α = 3.5 × 10⁻⁵ reported in an extensive contrast variation study of lysozyme (45) yield R_c^H₂O − R_c^D₂O = 0.1 nm. Those evaluated from the model (43) are R_c = 1.38 nm, α = 1.0 × 10⁻⁵ and R_c^H₂O − R_c^D₂O = 0.023 nm. The experimental value of α (45) can therefore not be accounted for by the atomic structure alone and largely reflects the contribution of the hydration shell.

As shown by Svergun et al. (14) the results of the fitting procedure do not depend much on the actual value of the thickness of the border layer d provided the product d×δρ_b remains constant. The value of d = 0.3 nm represents the most ordered first solvation shell only and neglects the other shells. This representation agrees well with the solvent density profiles as functions of the distance from the protein surface observed in x-ray diffraction studies (16, 17). The contrasts of the border layer reported in this study describe the average density in the first solvation shell. The actual thickness of the layer of solvent surrounding a protein that differs in its composition from the bulk depends on the composition of the latter, and the effects can be quite large, as shown by neutron scattering studies of apoferritin in H₂O and D₂O solutions containing various small molecules (46). The approach presented above should allow reinvestigation of these phenomena in more detail.

The focus here was primarily on the differences between bulk and hydration water, and the proteins were studied in solvents with relatively low salt concentration. At higher salt concentrations, it also should be possible to use the above approach to investigate the counterion distribution near the protein surface because significant effects of counterion condensation in the scattering from polyelectrolytes already have been observed (47).

A denser water layer in the first hydration shell also has been observed by x-ray scattering at electrode–electrolyte interfaces (48). In this case, ordering extended over 3–4 layers with only the first one displaying a density nearly twice that of the bulk. The similarity between the results obtained on such very different systems points to the general fundamental phenomena involved in the formation of aqueous interfaces.

CONCLUSIONS

The present work provides experimental evidence for the existence of a first hydration shell with a significantly higher density than that of the bulk solvent surrounding proteins in solution. Combined use of x-rays and neutrons was shown earlier to be a powerful tool to investigate the structure of bound solvent in the crystal (see, e.g., ref. 49). Our results extend this approach to the study of hydration phenomena in solutions.