The Evolution of Condition-Dependent Sex in the Face of High Costs

Abstract

Facultatively sexual organisms often engage in sex more often when in poor condition. We show that such condition-dependent sex carries evolutionary advantages and can explain the evolution of sexual reproduction even when sex entails high costs. Specifically, we show that alleles promoting individuals of low fitness to have sex more often than individuals of high fitness spread through a population. Such alleles are more likely to segregate out of bad genetic backgrounds and onto good genetic backgrounds, where they tend to remain. This “abandon-ship” mechanism provides a plausible model for the evolution and maintenance of facultative sex.

THE evolution of sex has long been a puzzle to evolutionary biologists (Michod and Levin 1988; Feldman et al. 1996; Barton and Charlesworth 1998; Otto and Lenormand 2002). Sexual reproduction tends to break up favorable genetic associations generated by selection (Altenberg and Feldman 1987). Even if sex were entirely cost free, evolution would not always favor increased rates of recombination, requiring synergistic epistasis (Feldman et al. 1980; Kondrashov 1988; Barton 1995), frequent environmental changes (Charlesworth 1976; Barton 1995), or random genetic drift in the presence of recurrent selection (Felsenstein 1974; Otto and Barton 1997; Otto and Barton 2001; Keightley and Otto 2006). To complicate matters, sexual reproduction is often very costly: producing males can, in the absence of paternal care, double the cost of reproduction. In addition, sexual organisms have to find and court a partner and then mate, thus wasting time and energy and exposing themselves to predation, disease transmission, and potential conflicts between the sexes. Despite all of the above, sexual reproduction is common among eukaryotes.

The majority of studies on the evolution of sex focus either on the evolution of recombination rates (see reviews by Feldman et al. 1996; Barton and Charlesworth 1998; Otto and Lenormand 2002) or on the long-term consequences of sex to the mean fitness and competitive ability of a population (e.g., Muller 1964; Kimura and Maruyama 1966; Kondrashov 1988; Howard and Lively 1994; Peck et al. 1997; Chasnov 2000; Agrawal and Chasnov 2001; Hadany and Feldman 2005). Fully understanding the evolution and maintenance of sex, however, requires that we consider populations capable of both sexual and asexual reproduction and investigate when increased investment in sexual reproduction can evolve. Facultative sex is common among plants, fungi, protists, and other organisms (Bell 1982) and is likely to be the mode of reproduction among the first sexual eukaryotes (Dacks and Roger 1999).

In this article, we consider how investment in sexual function evolves within facultatively sexual species if the tendency to reproduce sexually is condition dependent. Recent studies have found that alleles increasing the likelihood of reproducing sexually (independent of condition) can increase in frequency due to the advantages of segregation, as long as some inbreeding occurs within a population and dominance levels lie within specified regions (Dolgin and Otto 2003; Otto 2003).

These studies have assumed, however, that facultatively sexual species undergo sex at a constant rate. In reality, the frequency of sex generally depends on the condition of an individual, a pattern found broadly across both facultatively sexual prokaryotes and eukaryotes (Bell 1982). Individuals that are starved undergo sex at higher rates in a wide variety of organisms, including bacteria (Dubnau 1991; Redfield 1993; Jarmer et al. 2002; Foster 2005), yeast (Kassir et al. 1988; Mai and Breeden 2000), Chlamydomonas reinhardtii (Harris 1989), and daphnia (in combination with photoperiod and density cues; Kleiven et al. 1992). Cells with DNA damage have also been shown to undergo sex at higher rates in viruses (Bernstein 1987), bacteria (Wojciechowski et al. 1989), and yeast (Bernstein and Johns 1989). In soil microfungi, sex is more common under stressful environmental conditions associated with drought severity and high salinity (Grishkan et al. 2003). In four of five plant studies reviewed by van Kleunen et al. (2001), there was relatively greater allocation to sexual than to vegetative reproduction at high density (competitive stress). While in many of these examples the switch to sex coincides with the production of a more resistant or more dispersive stage in the life cycle (e.g., spores, seeds), this is not necessarily the case. For example, sex in the nematode, Strongyloides ratti, is induced in response to a host immune response (Gemmill et al. 1997; West et al. 2001), without involving a resistant or a dispersive stage. In summary, the majority of evidence suggests that facultatively sexual organisms are more likely to engage in sex when their condition is poor.

The premise of this article is that individuals experience different levels of stress, depending on their degree of adaptation to the current environment. As long as this premise holds, we can ask how the rate of sex should evolve as a function of an individual's level of stress. Specifically, we assume that an individual is able to assess its condition and to alter its reproductive mode in response. We do not assume that an individual is able to assess its fitness relative to others in the population.

Models of condition-dependent sex were introduced by Redfield (1988), who found that mean fitness in bacteria can be increased substantially when the less fit members of a population undergo transformation while the more fit individuals reproduce asexually. Moreover, in a haploid population subject to deleterious mutations or to environmental changes, modifier alleles inducing higher rates of recombination in unfit genotypes than in fit genotypes can spread by breaking away from less favorable genetic backgrounds and becoming associated with fitter alleles (Gessler and Xu 2000; Hadany and Beker 2003b). This has been called the “abandon-ship mechanism” (Agrawal et al. 2005). With more than one selected locus, such modifiers can result in increased average fitness (Hadany and Beker 2003b), even when the fitness landscape is rugged (Hadany and Beker 2003a). Considering modifiers that affect only recombination, however, we subsequently showed that fitness-associated recombination is much less likely to evolve in diploids, because diploid fitness is not a good indicator of whether the chromosome on which a recombination modifier resides is better or worse than the homologous chromosome (Agrawal et al. 2005). Yet diploid fitness is a good indicator of whether the genome within which a gene resides is well matched to current conditions. Thus, if a gene alters the frequency of sexual vs. asexual reproduction, then the abandon-ship mechanism might well apply to diploids as well as to haploids and favor more sex in low fitness genotypes than in high fitness genotypes. Here we investigate the evolution of fitness-associated sex. We explicitly incorporate costs of sex, which have been absent in previous models of condition-dependent sex.

We consider the fate of alleles at a “modifier” locus M that affects the likelihood of sexual reproduction in a fitness-associated way. Specifically, the condition of an individual alters its probability of reproducing sexually or asexually. In the text, we focus on a diploid population, extending the results to haploids in appendix a. We find that condition-dependent sex can evolve under a very wide parameter range and that sex, at least in some individuals, is favored even in the face of substantial costs.

MODEL

The simplest model that incorporates the advantages of fitness-associated sex (FAS) and diploidy involves two loci, a modifier locus M and a fitness locus A with nonoverlapping generations. This model is analytically tractable and allows us to gauge the relative advantages of uniform sex vs. FAS. We use this basic model to examine the conditions under which a modifier allele that causes FAS can invade a resident population, which may have a sexual, an asexual, or a mixed mating system. We start by assuming that sex involves random mating without a cost of sex and that a population is at a mutation–selection balance at the A locus. To this basic model, we then add a cost of sex and, finally, compare the results at mutation–selection balance to the case of the spread of a beneficial allele.

The basic model is similar to that described in Otto (2003), except for the fact that the mode of reproduction of an individual depends on its fitness as well as on its modifier genotype. The main goal is to determine what modifier alleles can invade a population, to predict how these alleles affect the evolution of facultative sex, and to identify the long-term evolutionarily stable state (ESS) (Maynard Smith 1982).

We begin by censusing the frequency of each genotype among the juveniles, before selection, and then follow these genotypes through selection, reproduction, and mutation. We let x_ij equal the frequency of juveniles that carry haplotypes i and j, where the label (i or j) specifies the haplotype:

We assume that all loci are autosomal, that an offspring's fitness does not depend on the sexual strategy of its parent, that there is no selection at the haploid or gametic stage, and that there is no parental imprinting. Consequently, x_ij = x_ji, and we keep track of x_ij for j ≥ i, only. Thus, for example, the frequency of MA/MA individuals is x₁₁ but the frequency of MA/Ma individuals is 2x₁₂. At this point, selection occurs depending on the genotype at the A locus, with viabilities equal to W_AA, W_Aa, and W_aa. Letting be the frequency after selection of adults carrying haplotypes i and j, then

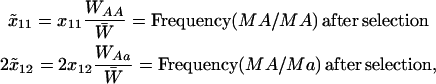(1)

etc., where

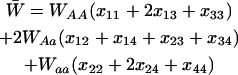is the mean viability due to selection at the A locus. When considering deleterious alleles at a mutation–selection balance, we set

(2)

where s is the selection coefficient (0 < s ≤ 1) and h is the dominance coefficient of the mutant allele a (0 ≤ h ≤ 1).

At this stage, reproduction occurs. The probability that an individual reproduces sexually, σ_ij, depends on its genotype at the modifier locus as well as on its condition (Table 1). This condition is assumed to be dependent on the effects of the A locus; that is, we assume that a mutation that decreases fitness also affects an organism's perceived condition. This does not require that an individual be able to assess the condition of other individuals (that is, σ_ij is held constant regardless of the genotype frequencies in the rest of the population). If an individual of genotype ij does not reproduce sexually, which occurs with probability 1 − σ_ij, then it contributes directly to the frequency of genotype ij in the next stage (x′_ij). Note that the average amount of sex, 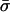, will depend on the average level of stress experienced in the current environment. Relative to this background level of sex, an individual assesses its condition and undergoes more or less sex.

TABLE 1.

Mating table

Frequency of sex	MA	Ma	mA	ma
MA	σ11	σ12	σ13	σ14
Ma		σ22	σ23 = σ14	σ24
mA			σ33	σ34
ma				σ44

A modifier of sex (M) alters the probability that a diploid individual reproduces sexually in a manner that depends on the absolute fitness of the individual. We assume that the modifier has the same effect in trans double heterozygotes, Ma/mA, as in cis double heterozygotes, MA/ma (σ₂₃ = σ₁₄), because both have fitness W_Aa. Similarly, we assume that the frequency of sex in individuals of genotype ij is the same as in those of genotype ji.

If the individual reproduces sexually, it contributes gametes to a gamete pool, with recombination between the M and the A loci occurring at rate r. Within this gamete pool, the frequency of haplotype i is given by y_i. Specifically, the frequencies of MA, Ma, mA, and ma gametes are

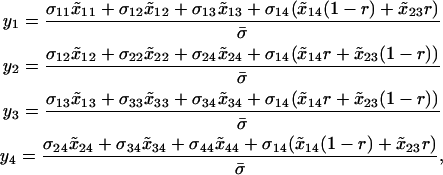(3)

respectively, where 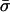is the average allocation of the diploid population to sexual reproduction, which equals the sum of the numerators in (3). We assume here that sexual reproduction cannot be “forced” on an individual and in particular not on an asexual individual.

We assume that the sexual reproduction is costly and that the total cost of sex, C, is distributed across L selected loci scattered throughout a genome. If we modeled an entire genome (as in the simulations described below), the classical “twofold cost of sex” would imply that sexuals contribute half the number of offspring to the next generation as asexuals (e.g., because sexuals divide resources between male and female function, but the number of offspring depends only on female investment). Even if the total cost of sex is large, the per-locus cost of sex, c, is likely to be small. To incorporate a per-locus cost of sex, we multiply the overall contribution to the juveniles of the next generation through sexual reproduction, , by a factor (1 − c). Because we model only one selected locus, A, we assume that c ≪ 1 (on the order of the total cost of sex, C, divided by L). After reproduction, the total frequency of MA/MA offspring is

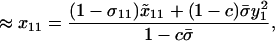(4a)

where the first term in the numerator corresponds to asexually produced offspring and the second term to sexually produced offspring. The denominator is the mean number of offspring produced, which is reduced by the cost of sex. Similarly, the frequency of MA/Ma offspring (including both 12 and 21 genotypes) equals

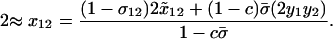(4b)

We assume that mutations occur during reproduction and that they do not affect the reproductive decisions of the parental generation. Mutations from allele A to a occur at rate μ, regardless of the mode of reproduction. Because our focus is on the mutation–selection balance at which allele A is nearly fixed, we ignore reverse mutations, which will be vanishingly rare when allele a is rare. Thus, after mutation, we have the frequencies of the diploid genotypes in the next generation:

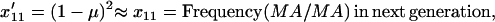(5a)

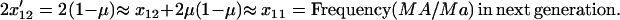(5b)

Recursion equations (5c)–(5j) for the remaining eight diploid genotypes were derived similarly (available upon request). Mathematica 5.0 (Wolfram 1991) packages that were used to derive the subsequent results are available upon request.

RESULTS

To examine the evolution of fitness-associated sex, we first consider populations at mutation–selection balance at locus A. We then describe analogous results for nonequilibrium populations. Finally, we describe multilocus stochastic simulations exploring the evolution of FAS in the presence of genomewide mutations within populations of finite size.

Mutation–selection balance:

When allele M is fixed, the population reaches a mutation–selection balance at locus A with

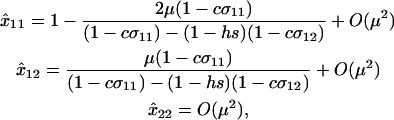(6)

which reduces to the familiar result, 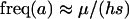, when there is no cost of sex. Equation 6 is a valid equilibrium as long as: (a) the mutation rate is low relative to selection, (b) the overall fitness of AA homozygotes including the cost of sex is higher than that of Aa heterozygotes [i.e., 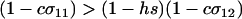], and (c) all genotypes are facultatively sexual or all are asexual (the system approaches a different equilibrium, at which heterozygotes are extremely rare, when AA individuals are asexual but other genotypes are not: σ₁₁ = 0 with σ₁₂ > 0). The terms in (6) can also be calculated explicitly (available upon request).

Mean fitness at mutation–selection balance:

Although we are primarily interested in knowing when FAS can evolve and to what degree, it is instructive to first consider the mean fitness effects of different strategies, as one might expect that FAS can invade only when it increases mean fitness. As we will show, this is not the case. Accounting for the deleterious impact of mutations and the costs of sex, the mean fitness of a population at mutation–selection balance is given by

(7)

Mean fitness is a decreasing function of the frequency of sex among AA individuals [] because of the cost of sex incurred by this abundant class of individuals. By considering terms of in (6) and (7), it is possible to show that mean fitness may increase or decrease as a function of sex among the less fit individuals, depending on how the frequency of sex relates to fitness.

First, we consider mean fitness in the absence of a cost of sex. By examining the terms, it is possible to show that the mean fitness increases with the frequency of sex among Aa individuals (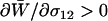). Essentially, the production of AA and aa offspring increases whenever heterozygotes engage in sex more often, resulting in an excess of homozygosity (that is, 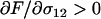, where F is Wright's inbreeding coefficient). This excess homozygosity reveals variation in fitness (by reducing masking in heterozygotes), improves the efficiency of selection, and results in increased average fitness. Conversely, mean fitness decreases when aa individuals engage in sex more often (). This is because an increased frequency of sex in aa homozygotes makes it more likely that they will cross with AA homozygotes and produce heterozygous offspring (i.e., 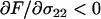), masking the deleterious alleles and making selection less efficient. These considerations suggest that, in the absence of a cost of sex, the mean fitness of a population would be highest when only heterozygotes engage in sex (“FAS_HetOnly”; 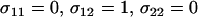). Although this claim is based on Equation 6, which assumes that AA individuals engage in some amount of sex (), it was confirmed numerically by evaluating the equilibrium of Equation 5 exactly and calculating the mean fitness across all possible values of σ₁₁, σ₁₂, and σ₂₂ between 0 and 1 in increments of (1/10) for all combinations of 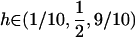and s .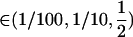

Additional factors influence mean fitness when sex is costly. Most importantly, fitness is reduced by a factor 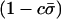due to the costs of sex. As a consequence, the fitness of a population is maximized when the fittest members of a population (AA individuals) never reproduce sexually. Nevertheless, mean fitness can be improved when less fit individuals engage in sexual reproduction, even when sex is costly (Figure 1). Indeed, when the cost of sex is paid by less fit individuals, the costs aid in the elimination of deleterious mutations. Consequently, FAS causes the mean viability, 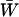, to rise with increasing costs of sex (Figure 1A), with the highest mean viability often produced when the fittest individuals reproduce asexually and all other individuals reproduce sexually (“FAS_Extreme”; 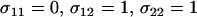). Yet, because the costs of sex reduce mean fitness, the overall mean fitness, 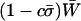, is highest when only heterozygotes engage in sex (FAS_HetOnly; Figure 1B). Numerical calculation of mean fitness revealed that FAS_HetOnly is the most fit strategy across all parameter combinations explored in the previous paragraph along with .

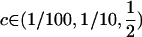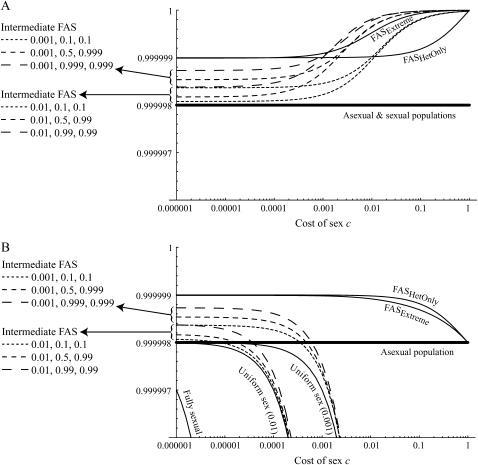
Figure 1.—

Mean fitness effects of FAS. The equilibrium of Equation 5 was determined numerically for μ = 10⁻⁶, s = 0.01, and h = 0.1 and used to calculate (A) the mean viability 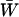(not including fitness cost of sex) and (B) the mean fitness 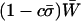(including fitness cost of sex) as a function of the per-locus cost of sex, c. Several sexual strategies were explored, including fully asexual, uniformly sexual ( 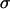fixed for all genotypes at 0.001, 0.01, or 1), FAS_Extreme (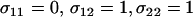), FAS_HetOnly (), and various intermediate FAS strategies. These FAS strategies always had a higher mean viability, 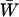, than asexual or uniformly sexual populations (the latter are nearly identical in mean viability). However, FAS strategies had a higher overall mean fitness, 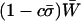, than an asexual population only when the cost of sex was weak and/or no sex occurred in the most fit AA individuals (FAS_Extreme and FAS_HetOnly). Recall that c is the cost of sex per locus, so that values within the range of 10⁻⁵ and 10⁻³ are most plausible. Qualitatively similar results are observed for smaller or larger values of h.

While the FAS_HetOnly and FAS_Extreme strategies have high fitness, they require perfect information about the condition of an individual, with no sex occurring in the most fit AA genotype. Figure 1 shows, however, that imperfect FAS strategies can also lead to a higher mean fitness than either asexual populations or uniformly sexual populations as long as the cost of sex per locus is relatively weak.

An interesting case is the family of strategies, FAS_linear, that reproduce sexually in direct proportion to the strength of selection (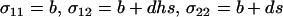, where b and d represent the baseline level of sex and the sensitivity to selection, respectively). Here, we consider only FAS_linear strategies that have different degrees of sensitivity, d, to selection. When selection is weak (s ≪ b), the effect of increasing the sensitivity, d, on the mean fitness of a FAS_linear population is

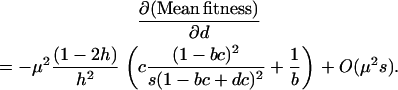This effect is weak (of the order 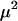), so that a population exhibiting a FAS_linear strategy has nearly the same fitness as a population engaging in uniform sex at the baseline rate b (indistinguishable from “uniform sex” curves in Figure 1B). Nevertheless, there is a small effect on the mean fitness of a population whose sign depends on . When selection is additive (h = ½), homozygotes and heterozygotes are, on average, equally likely to engage in sex, and FAS causes no change in the inbreeding coefficient, F, or mean fitness [to 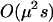]. As most deleterious mutations are partially recessive, we expect a FAS_linear strategy with a single fitness locus to disproportionately increase the amount of sex in the least fit aa individuals (assuming h < ½, d > 0, and ). In this case, a FAS_linear strategy leads to a decline in homozygosity, reducing the efficiency of selection and mean fitness.

Invasion of a new modifier allele:

At mutation–selection balance, we introduce a new modifier allele, m, which alters the pattern of sexual reproduction (see Table 1). Using a local stability analysis, we determine whether the m allele is able to rise in frequency while rare by calculating the leading eigenvalue, 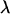. Whenever the leading eigenvalue is greater than one, the newly introduced m allele will spread within the population.

No cost of sex:

To begin, we consider the case where there is no cost of sex (c = 0). The leading eigenvalue obtained from a local stability analysis of Equations 1–5 near the mutation–selection balance equilibrium (6) equals

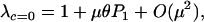(8)

where 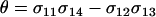measures the effects of the new modifier allele on the frequency of sex and where P₁ is a positive factor equal to

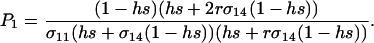The new modifier is able to invade whenever the leading eigenvalue is greater than one in magnitude, which requires that θ be positive. Consequently, the new modifier allele invades only if it causes the less fit Aa individuals to engage in sex more often than the more fit AA individuals, at least in comparison to the resident modifier (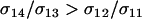). Furthermore, the strength of indirect selection on the modifier (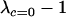) is proportional to the mutation rate, μ, which can become substantial when summed over multiple loci at mutation–selection balance (see simulation section).

The fact that the rate of recombination between the modifier and fitness loci affects the leading eigenvalue indicates that genetic associations between the two loci accumulate. This might, at first, seem surprising, given that common sources of genetic associations, like epistasis, are absent. FAS itself generates genetic associations, however, by altering the array of haplotypes entering the gamete pool. To guide intuition, consider the extreme case where the resident genotype, MM, induces random mating, while the new modifier allele, m, causes AA individuals to reproduce asexually (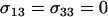, all other ). In this case, the gamete pool lacks gametes from mA/mA and MA/mA individuals, causing an underrepresentation of mA gametes relative to the component allele frequencies. Consequently, among the double heterozygotes of the next generation, mA/Ma becomes less common than MA/ma (we focus on the double heterozygotes, because these are the individuals in which recombination has an influence).

With an excess of cis double heterozygotes, recombination causes the m allele to “abandon ship” and jump from a poor genetic background (linked to allele a) to a better genetic background. This explains why looser linkage increases the rate of spread of FAS alleles (increasing P₁ in Equation 8). While the above heuristic argument is based on an extreme example, the logic holds generally. Indeed, even if genetic associations are initially absent, the two double heterozygotes differ in frequency in the next generation by an amount [dropping terms and assuming that m is rare]. Thus, modifier alleles, m, that induce FAS (θ > 0) cause an excess of cis double heterozygotes; recombination then acts to uncouple m from the less fit a allele, facilitating the spread of FAS modifiers.

While the speed with which a FAS modifier invades rises with the rate of recombination, recombination is not necessary for a FAS modifier to spread when rare in a diploid population. Even if r = 0, P₁ remains positive, and FAS modifier alleles are favored. In the absence of recombination, segregation of chromosomes via sex still facilitates the movement of a modifier allele m away from less fit alleles in the genotypes mA/Ma, mA/ma, ma/Ma, or ma/ma but a modifier residing in an ma/MA genotype can only move away by recombination. The equation for P₁ also provides insight about the relative contribution of segregation and recombination to the spread of fitness-associated sex. When 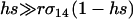, the rate of recombination has little influence on the leading eigenvalue, and the main advantage of FAS is the ability of a modifier to segregate away from deleterious alleles carried on the homologous chromosome. By contrast, when 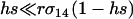, recombination also allows a modifier to recombine away from deleterious alleles carried on the same chromosome, and the rate of spread of the modifier is nearly double that observed when segregation acts alone. (In a haploid population, however, segregation is irrelevant, and recombination must be present for FAS to invade when rare. See appendix a.)

From the stability analysis we can also gain insight into the long-term evolution of condition-dependent sex after a series of different modifier alleles have appeared. To do so, we must assume that new alleles arise rarely at the modifier locus and that these modifiers rise to fixation whenever they encode a favorable sexual strategy with 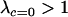. These assumptions are consistent with the quasi-linkage equilibrium analysis described later and numerical simulations (available upon request), as long as all individuals engage in some amount of sex and the reproductive strategy of Mm individuals is in between that of MM and mm individuals (specifically, a linear combination of the reproductive strategies of MM and mm). According to Equation 8, only modifier alleles that increase the ratio (frequency of sex of Aa heterozygotes)/(frequency of sex of AA homozygotes) will invade. The process of appearance and fixation of modifier alleles will then recur until this ratio reaches the maximum value that is biologically plausible, given constraints on the ability of an organism to assess its condition.

Whether mean fitness is increased or decreased during this process depends on how modifiers affect the frequency of sex among the least fit aa individuals. Increasing sex in this genotypic class does not, to leading order in 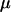, affect the invasion of a modifier allele but it does decrease mean fitness. Modifier alleles that cause 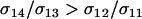spread because of the advantage that the modifier allele gains from escaping from bad genetic backgrounds (the most common of which is Aa); this process is blind to the long-term consequences to the mean fitness of a population, which depends on the frequency of sex in all of the genotypes. In particular, FAS_linear strategies that increase the amount of sex in less fit individuals (higher d) are able to invade, despite the fact that, once fixed, the mean fitness of the population would be reduced when h < ½.

Adding costs of sex:

We next consider the influence of a cost of sex. In the text, we assume that the per-locus cost of sex is weak relative to the strength of viability selection acting directly on locus A. Specifically, we assume that AA individuals are always more fit than Aa individuals, regardless of the modifier genotype, which is guaranteed only if 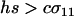. In appendix b, we describe the more complicated results that can arise if viability selection at locus A can be overwhelmed by the cost of sex.

When the per-locus cost of sex is large relative to the mutation rate (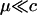), modifiers that reduce the frequency of sex are at an inherent advantage. A rare modifier allele, m, will invade a population near the mutation–selection balance equilibrium (6) only when 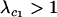, where

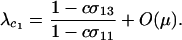(9)

Accordingly, the modifier invades only if the fittest AA individuals engage in sex less often when they carry allele m than when they do not (i.e., ).

In light of Equation 9, let us again consider the long-term evolution of condition-dependent sex when costs are present. As before, we assume that new modifier alleles arise occasionally and that these alleles fix whenever they encode a favorable sexual strategy with (consistent with the quasi-linkage equilibrium analysis described later and numerical simulations, as long as the resident population is not fully asexual). According to Equation 9, the process of invasion and fixation of modifier alleles will recur until σ₁₁ reaches its smallest possible value, given constraints on the reproductive system of the species. At or near this point in evolutionary time, modifier alleles that have little effect on the frequency of sex among AA genotypes might still spread because of their effect on the frequency of sex among less fit genotypes. To assess this possibility, we assume that and consider the next order term in the leading eigenvalue,

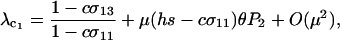(10a)

where again 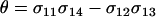measures the fitness-associated effects of the modifier and P₂ is

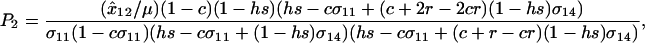which is positive under the assumption that .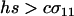

According to Equation 10a, the ability of a rare modifier to invade depends on the balance of two forces: direct selection acting to reduce the cost of sex among AA individuals and indirect selection arising from fitness-associated sex (the term proportional to θ). Under the assumption that the per-locus cost of sex is weak relative to viability selection (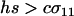), the new modifier allele is favored by reducing sex generally and/or by causing the less fit Aa individuals to engage in sex more often than AA individuals, at least in comparison to the resident modifier allele (θ > 0 or, equivalently, 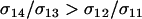). The invasion results for this case are summarized in Figure 2 and correspond qualitatively to the results with no cost of sex.

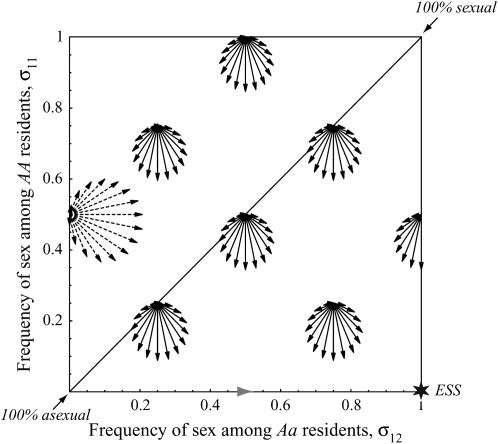
Figure 2.—

Evolutionarily favored transitions. According to Equation 10a, reproductive strategies are predicted to evolve in the directions shown. The axes represent the amount of sex among resident MMAA (vertical) and MMAa (horizontal) individuals (uniformly sexual populations lie on the diagonal). The direction of each arrow indicates the effect of a new modifier allele on the reproductive strategies of Mm individuals. The length of each arrow is proportional to the rate at which the modifier spreads. (The dashed arrows were reduced by 80% for clarity). Only modifier alleles that are able to invade are shown. Two types of evolutionary transitions toward FAS are favored: The system is strongly driven down toward no sex among AA individuals and more weakly to the right toward more sex among Aa individuals (assuming 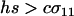). The results are consistent with a numerical calculation of the eigenvalues [also used to derive the shaded arrowhead on the bottom, where equilibrium (6) and Equation 10 do not apply]. Over evolutionary time, the system is driven toward an ESS (star), where AA individuals are asexual and Aa individuals are fully sexual or as close as is biologically feasible. r = ½, hs = 0.001, c = 0.0001.

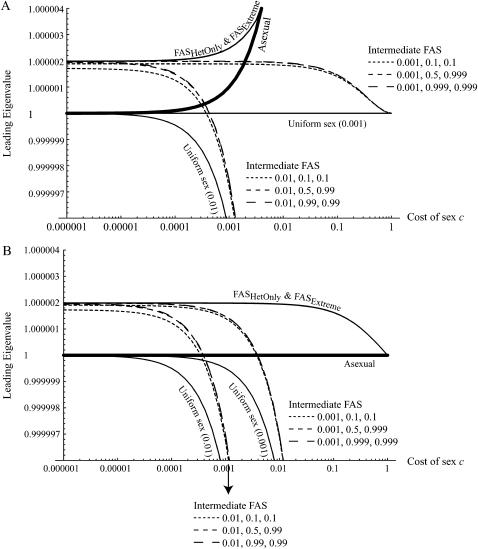
Figure 3A confirms that sexual populations are prone to invasion by FAS mutants (curves greater than λ = 1). Perfect FAS alleles that engage in sex only in less fit individuals (FAS_HetOnly and FAS_Extreme) are able to invade regardless of the cost of sex. Similarly, imperfect FAS alleles that arise in a sexually reproducing population and increase only the tendency of the less fit individuals to reproduce sexually are able to invade regardless of the cost of sex. For example, FAS_linear strategies with an increased sensitivity to selection, d, are always able to invade (not shown). Imperfect FAS alleles that increase the tendency for sexual reproduction in all genotypes (but more so in the less fit) are able to invade when the cost of sex per locus is sufficiently small (left-hand side of Figure 3) and in some cases even when they eventually reduce average fitness (compare Figures 1 and 3). Numerical simulations confirm that in sexual populations, modifiers that can invade rise to fixation (assuming weak and additive modifiers), regardless of the ultimate effect on mean fitness.

Figure 3.—

Invasion of FAS modifier alleles. The leading eigenvalue from a local stability analysis was calculated numerically for μ = 10⁻⁶, s = 0.01, h = 0.1, and r = ½ and plotted against the per-locus cost of sex (Equation 10 yields identical results). Whenever the leading eigenvalue is greater than one, the new modifier allele is able to invade. (A) The new modifier is introduced into a uniformly sexual resident population with 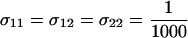. (B) The new modifier is introduced into an asexual resident population with 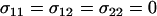. Several modifier strategies were explored, each assuming that the modifier acted additively, with mm homozygotes inducing complete asexuality, uniform sexuality (0.001 or 0.01 of the time), FAS_Extreme (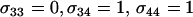), FAS_HetOnly (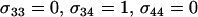), or intermediate FAS. FAS modifier alleles were able to invade sexual and asexual populations when the costs of sex were small. With higher costs of sex, FAS alleles were able to invade as long as the frequency of sex among AA individuals remained small. Recall that c is the cost of sex per locus, so that values within the range of 10⁻⁵ and 10⁻³ are most plausible.

The above considerations suggest that over the long term (that is, after a series of modifier alleles arise and occasionally fix), facultatively sexual organisms will evolve to minimize the amount of sex in individuals of high fitness while maximizing the amount of sex in individuals of low fitness, within the realm of possible modifiers that can arise. We next consider whether FAS can evolve within initially asexual populations.

Initially asexual populations:

In a fully asexual population (σ₁₁ = σ₁₂ = σ₂₂ = 0), Equation 10a simplifies to

(10b)

where P₃ is a positive factor equal to

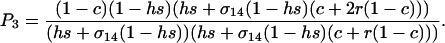Equation 10b indicates that an asexual population can be invaded by an m allele inducing sex as long as Aa individuals engage in more sex than AA individuals (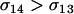) and the per-locus cost of sex experienced by the AA genotype is weak ().

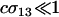Figure 3B confirms that asexual populations are also prone to invasion by FAS mutants (curves greater than λ = 1), even when sex is costly. Again, perfect FAS alleles that engage in sex only in less fit individuals (FAS_HetOnly and FAS_Extreme) are always able to invade. Imperfect FAS alleles that increase the tendency for sexual reproduction in all genotypes (but more so in the less fit) are able to invade when the cost of sex per locus is sufficiently small (left-hand side of Figure 3B). For intermediate levels of the cost of sex, imperfect FAS strategies can invade that would eventually reduce average fitness (compare Figures 1B and 3B, e.g., at c = 0.0002 for strategies inducing sex 1% of the time in AA individuals). In such cases, the strategies invade when rare, but they do not spread to fixation. Such strategies increase when rare because sex among Mm individuals allows the m allele to move away from low fitness genotypes (abandoning ship). Eventually, however, if sex occurs only among Mm and mm individuals, heterozygosity at the modifier locus declines until the population becomes composed entirely of MM and mm individuals. As these are now reproductively isolated subgroups, the mean fitness of the two strategies governs their fates, and the m allele is eventually outcompeted because of the lower equilibrium mean fitness of its carriers.

Evolutionary stable strategy:

Our results indicate that a population should evolve toward a state where the fittest genotype undergoes as little sex as possible while less fit genotypes are sexual (see Figure 2). Although mean fitness considerations indicate that FAS_HetOnly (σ₁₁ = 0, σ₁₂ = 1, σ₂₂ = 0) is the optimal strategy, numerical analyses indicate that FAS_HetOnly is subject to invasion by FAS_Extreme (σ₁₁ = 0, σ₁₂ = 1, σ₂₂ = 1). Even though a strategy that allows aa individuals to engage in sex lowers mean fitness in the long run, a modifier that engages in more sex in both Aa and aa individuals is more likely to escape from low fitness genetic backgrounds and is therefore more likely to be evolutionarily successful.

To confirm that FAS_Extreme represents the evolutionary stable strategy (ESS) (Maynard Smith 1982), we conducted a numerical analysis using the deterministic recursions (1)–(5). For each parameter combination we started with a certain reproductive strategy, M, fixed within the population and iterated the recursions until an equilibrium was reached (where the difference between the frequency of AA in one generation and the next was <10⁻⁷ in 100 consecutive generations). Then a new strategy, m, was introduced by converting 5% of the MM genotypes to Mm. We monitored the population until the frequency of the new m allele either increased above 0.5, in which case we concluded that the m allele had invaded, or decreased below 0.0025, in which case we concluded that invasion had not occurred. If the frequency of the mutant did not change at all over a period of 100 generations, the simulation was stopped. This occurred only in the controls, where the invading strategy was identical to the resident. If the simulation continued for over 100,000 generations without reaching any of the thresholds the simulation was stopped, and the direction of change was noted. This occurred only in some of the cases without a cost of sex (c = 0). Throughout, we assumed that the modifier allele has additive effects on the frequency of sex.

Several simulations were performed to confirm the analyses reported in previous sections (available upon request). Here we report only those simulations where the resident population was FAS_Extreme. Into this resident population, we examined whether modifier alleles could spread, exploring every combination of the following parameter values: σ₃₄ and σ₄₄ (the frequency of sex in mmAa and mmaa individuals, respectively) from 0.0 to 1.0, c from 0.0 to 0.9, and h and s from 0.01 to 1.0, all in steps of 0.01, along with r = 0.0 or 0.5, and μ = 10⁻⁵. We found that FAS_Extreme was stable against invasion by any other strategy considered, including FAS_HetOnly. We must caution against overinterpreting this result, however. While FAS_Extreme is evolutionarily stable, it seems highly unlikely that modifier alleles will ever arise that are able to assess perfectly the condition of their carrier. The extent to which FAS is able to evolve (i.e., the types of modifier alleles that are possible) remains an open empirical question.

Spread of beneficial alleles:

The above analysis is predicated on a population being near mutation–selection balance. Here we show that qualitatively similar results are obtained in populations that are subject to directional selection, with allele A spreading through a population due to directional selection. The recursion equations were subjected to a quasi-linkage equilibrium (QLE) analysis (Barton and Turelli 1991; Barton 1995), which approximates the dynamics using a separation of timescales, where associations among alleles are assumed to reach steady state over a fast timescale, while changes in allele frequencies occur over a slow timescale. Specifically, the QLE approximation assumes that sex and recombination are sufficiently frequent within the population relative to the strength of selection that linkage disequilibrium and departures from Hardy–Weinberg equilibrate at levels predicted on the basis of the current allele frequencies (see Appendix in Agrawal et al. 2005). To simplify the presentation of the results, we focus on the case where the A allele is at high frequency; similar results are observed when allele A is rare. Unfortunately, presentation of the more general case is complicated by the large number of parameters if each genotype is allowed to undergo sex at a different rate.

Assuming that the modifier has only a small effect on the probability of sex and that selection is weak relative to the rate of sex and recombination, the modifier allele m changes in frequency at a rate

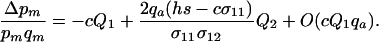(11)

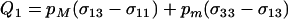measures the average effect of modifier allele m on the frequency of sex in the most common genotype, AA; when sex is costly, this first term always favors modifier alleles that reduce the frequency of sex. The second term in (11) describes selection that arises when the modifier changes the relative rates at which Aa and AA genotypes have sex, with 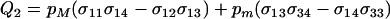. This second term contributes to the spread of the modifier only when cQ₁ is small.

The predictions from (11) are qualitatively the same as those observed at mutation–selection balance. When , the new modifier allele is favored by reducing sex in the majority of individuals and/or by causing the less fit Aa individuals to engage in sex more often than the fitter AA individuals (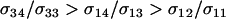). When 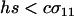(as in appendix b), however, the new modifier allele is favored by causing the less fit Aa individuals to engage in sex less often than the fitter AA individuals (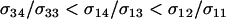). This reversal again occurs because the reduction in the frequency and costs of sex among Aa heterozygotes is enough to favor modifier alleles that preferentially remain associated with heterozygotes at the A locus. Fixation of such a modifier would not be stable in the long term, however, and the population would eventually be invaded by a modifier allele that reduced the frequency of sex among AA individuals, assuming such a modifier arises.

Stochastic simulations with multiple loci:

To allow selection to act on multiple loci and to determine whether the results are robust to the presence of random genetic drift, we studied a set of stochastic simulations using a long genome consisting of 10,000 fitness loci and a finite population consisting of N = 2000 diploid individuals. Two possible alleles segregated at each fitness locus, “1” (wild type) or “0” (deleterious mutant), and we explicitly tracked which chromosomes were carried by each individual within the population. Bidirectional mutation occurred at rate 0.05/genome/generation. The fitness of an individual was determined by the overall number of deleterious alleles it carried, n, regardless of their location and whether the carrier was homozygous or heterozygous. Specifically, the fitness of the individual was set to 0.98ⁿ, which assumes that fitnesses are multiplicative across loci. At the modifier locus, a resident allele, M, coded for a uniform rate of sex (US with σ_u = σ₁₁ = σ₁₂ = σ₂₂) and allele m coded for FAS. Individuals homozygous for allele m reproduced sexually with probability σ_poor if their condition was poor, specifically if their fitness was below a threshold w*, and reproduced sexually with probability σ_good if their fitness was above it, where σ_good < σ_poor. Individuals heterozygous at the modifier locus reproduced sexually with a probability given by the average of MM and mm homozygotes. As in the analytical model, we assumed that sexual reproduction could not be forced on an individual.

Each offspring generation was constructed from the parental generation in the following way. The overall contribution to the juveniles of the next generation through sexual reproduction was proportional to the average allocation to sex, 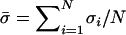, multiplied by a factor (1 − C), where σ_i is the tendency of individual i to reproduce sexually and C is the total cost of sex, which was set to 0.5 in the simulations. The overall contribution through asexual reproduction was proportional to the average allocation to asexuality, . The probability that a random juvenile in the next generation is produced sexually is thus

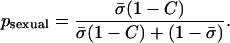For a sexually produced offspring, a mother was chosen at random with a probability proportional to her sexual tendency σ_i; this mother then produced a gamete by meiosis. A father was similarly chosen at random in proportion to his sexual tendency, and he produced a gamete by meiosis. The sexual tendency of an offspring was determined by the modifier alleles it inherited from both parents and by its fitness, determined by the alleles at all other loci. We also considered inbreeding by allowing the second gamete to be produced by the mother at rate f = 0.05. Inbreeding had little qualitative effect on the evolution of fitness-associated sex (in contrast to the sensitivity of the results to inbreeding when the frequency of sex does not depend on condition; Otto 2003), and these simulation results are not reported. If the offspring was produced asexually, a mother was chosen at random with a probability proportional to her asexual tendency (1 − σ_i), and the offspring genome was a copy of the maternal genome. Once produced, the offspring underwent mutation and selection until N surviving offspring were obtained. We considered two possible types of genomes. In the first case (segregation plus recombination), the genome was composed of five chromosomes, each of them segregating at random, with a single crossover occurring at a random location on each chromosome each generation. In the second case (segregation only), the genome contained a single completely linked chromosome (with 10,000 loci), allowing segregation but not recombination.

Evolution of FAS:

In each simulation, a population was initialized with allele M fixed and left to stabilize for 500 generations. At this point, 20% of the population was converted into Mm heterozygotes, and the simulation was run until either of the modifier alleles was eliminated from the population. Had the mutation been neutral, we would expect the rare m allele to take over the population in 10% of the runs.

We compared the frequency of invasion of various reproductive strategies; we also considered resistance to back invasion whenever a new reproductive strategy became fixed. In addition to an asexual strategy, we considered the following uniform sexual strategies: σ_u = 0.001, 0.01, 0.015, 0.02, 0.05, 0.1, 1.0. A FAS allele with σ_good = 0.01 and σ_poor = 1.0 using a fitness threshold of w* = 0.95 was also investigated. This parameter choice models a facultatively sexual organism that reproduces asexually most of the time and switches to sexual reproduction when experiencing significant stress. Note that this version of FAS is imperfect, as even the best genotype reproduces sexually “by mistake” 1% of the time. In Figure 4, we present the uniform sexual strategy that performed best vs. the FAS strategy in each competition, thus overestimating the success of a population engaging in a uniform rate of sex. As an additional control, we considered a modifier allele that has uniform sex at a changing rate, where each generation the rate is determined as the average level of sexual reproduction that would have occurred if the population had been reproducing by FAS given the current genotype frequencies at the modifier and selected loci. This unrealistic strategy (termed FAS-like US) provides a partial control for the possibility that FAS alleles might spread because they change the average frequency of sex. Weaker, but still significant, results in the same direction were obtained with lower frequencies of sex among the less fit individuals (σ_poor = 0.5, 0.1, results not shown).

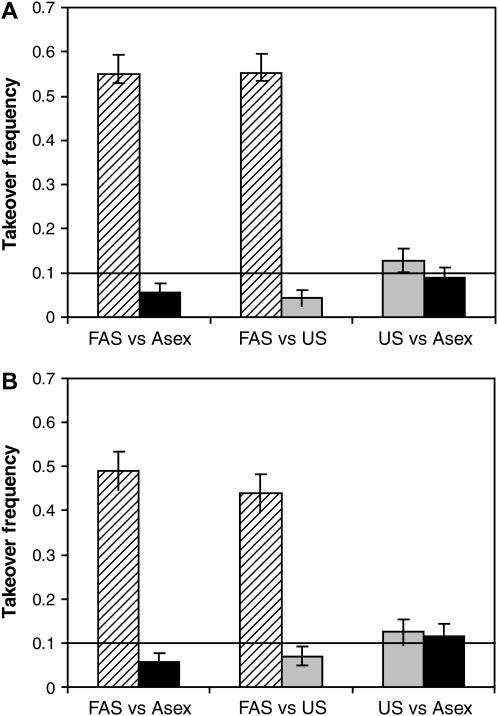
Figure 4.—

Invasion of modifier alleles with multiple fitness loci. Each column shows the takeover frequency of a certain modifier appearing within a population with a different modifier: Fitness-associated sex (FAS with σ_good = 0.01, σ_poor = 1.0) spreads to fixation in an asexual population (left, hatched bar), asexuality spreads in a FAS population (left, solid bar), FAS spreads in a uniformly sexual (US) population (middle, hatched bar), US spreads in a FAS population (middle, shaded bar), US spreads in an asexual population (right, shaded bar), and asexuality spreads in a US population (right, solid bar). In each case the introduced modifier started at 10% frequency, and the expected fixation rate of a neutral mutation is represented by the 0.1 line. (A) Sexual reproduction involves both segregation and recombination, where the genome is divided into five chromosomes with a single crossover on each; (B) sexual reproduction involves segregation without recombination (a single chromosome with r = 0). In each case, seven uniform strategies were tested: σ_u = 0.001, 0.01, 0.015, 0.02, 0.05, 0.1, and 1. The US strategy shown is the one that performed best against FAS (σ_u = 0.01 in A and σ_u = 0.015 in B). Parameters: C = ½, N = 2000, w* = 0.95, genomewide mutation rate = 0.05, with 1000 replicate simulations per bar (95% confidence intervals shown).

We found that FAS fixed within populations reproducing asexually significantly more often than a neutral allele (10%), despite a twofold cost of sex. FAS populations were also stable against back invasions by asexual mutants (such mutants succeeded in significantly <10% of the runs, see Figure 4). In contrast, none of the uniform sexual strategies invaded asexual populations or were stable to back invasion in comparison with a neutral allele. For part of the parameter range, however, invasion rates were close to 10%, and a weak advantage to uniform sex (as predicted by Otto 2003) cannot be ruled out (see Figure 4, columns 5 and 6). FAS also had a clear advantage against any of the uniformly sexual strategies studied: FAS mutants invaded and fixed within US populations and were stable against back mutations (Figure 4, columns 3 and 4). It should be emphasized that the FAS alleles studied induced sex in all individuals, even the most fit (σ_good = 0.01), demonstrating that fitness-associated sex can evolve even in the face of errors in an individual's ability to assess whether it is in good or poor condition (see also Gessler and Xu 2000). When comparing these simulations to our analytical results, it must be remembered that the cost of sex in Figure 3 is the amount “paid” by a single locus, c. In the simulations, we consider only the total cost of sex, C, which is distributed over L = 10,000 loci. Assuming that , our analysis and simulations both predict that intermediate FAS strategies can invade, despite the fact that they cause all individuals to engage in some amount of sex. Interestingly, the simulations that incorporated both recombination and segregation (Figure 4B) were nearly identical to the ones with only segregation (Figure 4A). This suggests that segregation is the primary force driving the evolution of sex in the multilocus model.

Effect on mean fitness:

To study the long-term fitness effects of each strategy, we monitored the average fitness of the population for 4000 generations (with 10,000 fitness loci and a twofold cost of sex). The simulations were initialized at the mutation–selection balance expected in a fully sexual population [i.e., with a deleterious mutant frequency = ]; monitoring then began after a 100-generation burn-in period.

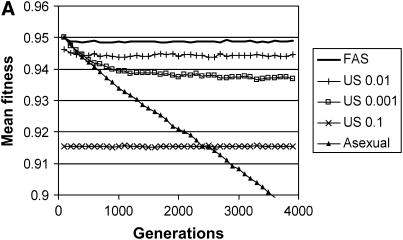
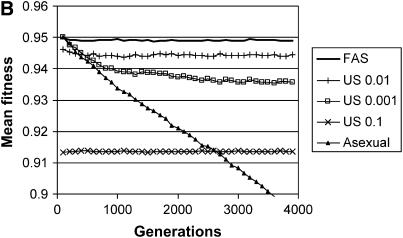
For the parameters considered, FAS was better than any uniform modifier in terms of average population fitness (Figure 5). The advantage of FAS over asexual populations can be easily understood in the parameter range studied: The asexual populations suffered from drift, and despite the reversibility of the mutation process, their average fitness deteriorated in comparison with any of the sexual strategies and reached a much lower mutation–selection–drift equilibrium. More interesting is the advantage of the FAS strategy over the best of the uniform modifier alleles (σ_u = 0.01). With FAS, the average frequency of sexual reproduction was higher, and thus a higher fraction of the population paid the cost. Nevertheless, FAS populations were more fit than the uniformly sexual populations for the parameters explored. It is, however, possible to fine tune the parameters in the simulations to find conditions where FAS reduces the mean fitness of a population compared to a uniform sexual population. Altogether, both the stochastic simulations (Figures 4 and 5) and the deterministic analysis (Figures 1 and 3) agree that FAS evolves under a wide parameter range and often results in increased mean fitness.

Figure 5.—

Long-term effects on mean fitness with multiple fitness loci. The mean fitness of the population is plotted as a function of time for four types of populations, each homogeneous for a different modifier: FAS (w* = 0.95, σ_good = 0.01, σ_poor = 1.0) and four uniform modifiers (σ_u = 0.0, 0.001, 0.01, 0.1). (A) Sexual reproduction involves both segregation and recombination, where the genome is divided into five chromosomes with a single crossover on each; (B) sexual reproduction involves segregation without recombination (a single chromosome with r = 0). Parameters: c = 0.5, N = 2000, genome mutation rate = 0.05, with each point representing an average of 100 runs. Mean fitness includes a twofold cost of sex, C = ½. Additional simulations with σ_u = 0.005, 0.015, 0.02, 0.05, and 1.0 are not plotted, but all these strategies resulted in significantly lower average fitness in comparison with σ_u = 0.01.

DISCUSSION

In this article we study the evolution of costly sexual reproduction, where facultative sex occurs at a rate that depends on an individual's fitness. When starting from an asexual population, we found that modifiers inducing sexual reproduction by the less fit genotypes are able to invade, even in the presence of a cost of sex. When starting from a sexually reproducing population, we again found that FAS could evolve, through an increased frequency of sex in less fit individuals and/or a decreased frequency of sex in more fit individuals, as long as the cost of sex that must be paid by a single locus is not too high (see Figure 2). According to our numerical analysis, extreme FAS, where the fittest individuals are asexual and all other individuals reproduce sexually, is an evolutionarily stable strategy in the model with one fitness locus, even when considering high per-locus costs of sex (including twofold). This strategy results in a higher mean fitness in comparison with any uniform level of sex. Among the imperfect FAS strategies that can invade, many, though not all, also raise mean fitness. Consistent results were obtained using analytical two-locus models and stochastic simulations of individuals with long genomes.

Previous studies on haploids have shown that fitness-associated recombination can readily evolve (Gessler and Xu 2000; Hadany and Beker 2003b) and would often result in increased average fitness (Hadany and Beker 2003a,b). Although some results on fitness-associated sex were obtained, costs of sex were not previously considered. In appendix a, we show that fitness-associated sex evolves in haploids in a very similar manner to diploids. In particular, as long as there is some sex within the population and costs of sex (per locus) are not too high, modifier alleles causing higher rates of sex in less fit individuals increase in frequency. Thus, in both haploids and diploids, we predict that less fit individuals should engage more readily in sexual reproduction.

These results suggest a possible mechanism for the first steps in the evolution of sex, when the molecular machinery was probably more error prone and therefore more costly. Within an asexual population, an allele inducing sex in less fit individuals would have been favored despite the costs of sex. This would allow the mechanism of sexual reproduction time to evolve and become more accurate. This is consistent with phylogenetic results suggesting that the first sexual lineages were facultative sexuals (Dacks and Roger 1999).

An important prediction of the current model is that in those organisms that are capable of reproducing either sexually or asexually sexual reproduction should occur more often when the organism has indications of low fitness, such as stress or starvation. This phenomenon has been documented in various organisms (see references in Introduction). Most of the examples describe a population switching from asexual to sexual reproduction under stress, but it seems likely that some individuals, especially those in good condition, might not switch or might undergo less of a switch in reproductive allocation. For example, only a fraction of cells sporulate when nitrogen starved in the budding yeast Saccharomyces cerevisiae, suggesting that cells that are better at extracting nitrogen and growing in their current environment might be less prone to sexual reproduction. More empirical data are needed to determine the extent of variation within populations in the probability of becoming sexual under stress and how this probability relates to fitness.

This work is far from ending the debate regarding the evolution of sex. In particular, our results turn the evolution of obligatory sex into an even greater riddle. Under our model, FAS is always able to invade obligatory sex. Our results suggest that the hardest question should be how obligatory sex evolves and is maintained—not only against asexuality or partial sexuality, but also against fitness-associated sex. The answer is likely to lie in factors that are not included in our model, such as environmental changes, epistasis, sexual selection, the difficulty to accurately evaluate one's fitness, or the possible cost of being able to reproduce both sexually and asexually. Finally, if obligatory sexuals can modify their rate of outcrossing so that the less fit individuals are more likely to mate with unrelated individuals (for example, by fitness-associated migration or mate choice), then obligatory sex might still gain many of the advantages of fitness-associated sex documented here.

APPENDIX A

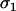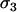A haploid model of FAS with costly sex was derived in the same manner as the diploid model considered in the text. Haploid individuals invested in haploid gametes with probability (MA), (Ma), (mA), and (ma) and otherwise reproduced asexually. All other assumptions (e.g., random mating) were the same as in the text. With unidirectional mutation from A to a, the equilibrium frequency of a is exactly

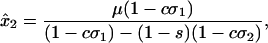(A1)

and the mean fitness is exactly . Reducing the frequency of sex in A individuals thus increases mean fitness, because of the decreased cost of sex. (With bidirectional mutation, reducing the frequency of sex in a individuals also increases mean fitness.) To leading order, the spread of a modifier allele is governed by two eigenvalues:

(A2a)

(A2b)

Invasion is assured if . If while 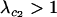, the invasion of the modifier causes the relative fitness of the a allele to rise above that of the A allele because carriers of allele a pay less of a cost of sex, destabilizing the mutation–selection balance (as in appendix b). Thus, assuming that equilibrium (A1) remains valid, invasion is determined by the magnitude of . Equation A2a predicts that the strongest force acting on the modifier favors a decreased frequency of sex among A individuals. Modifiers that have little effect on the frequency of sex in A individuals [ 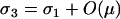] can also invade if , where

(A3)

where measures the effect of the modifier and P_H is

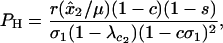which is positive [assuming the mutation–selection equilibrium remains vali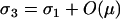d, , and 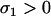]. Comparing Equation A3 for a haploid model and Equation 10a for a diploid model demonstrates that in both cases, FAS modifiers 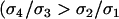) are favored as long as the per-locus costs of sex are not too severe (); otherwise anti-FAS modifiers are favored. One slight difference from the diploid model is that P_H = 0 in the absence of recombination, because it is then impossible for the modifier to abandon ship in the haploid case (segregation away from deleterious mutations is still possible in the diploid case). If M-bearing individuals are asexual, FAS would not evolve in the one-locus haploid case, but it could evolve with multiple selected loci, because of the indirect effect on disequilibria among selected loci (Hadany and Beker 2003b; Agrawal et al. 2005). As in the diploid model, FAS modifiers that do invade may (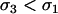) or may not (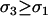) increase fitness.

APPENDIX B

In the text, we focus on cases where the per-locus cost of sex, c, is small relative to the strength of selection experienced at the A locus such that 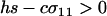. As described here, more complicated outcomes are possible when viability selection at a locus is so weak that it can be overwhelmed by the cost of sex.

When 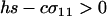, only the eigenvalue given by (10a) can be greater than one. When 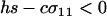, there is a second potential eigenvalue that can be greater than one:

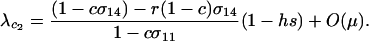A modifier allele m is able to invade a population near the equilibrium (6) if 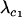and/or 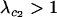. It is technically possible for to be >1 even though ≤ 1. Because the maximum value of 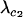is , this scenario is possible only if the resident AA individuals suffer a high cost of sex per locus relative to viability selection (). In addition, the modifier allele must cause Aa individuals to engage in sex substantially less often than the resident AA individuals. 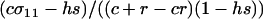Specifically, must be less than , which is <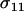. If a modifier allele that causes 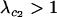while 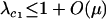were to appear, however, its invasion would destabilize the mutation–selection balance equilibrium (6) because Aa individuals are more fit than AA individuals among Mm carriers under these conditions. We consider this scenario to be implausible, because the invasion of such modifiers causes less viable genotypes to become the most fit via benefits of undergoing less sex. Even if such a modifier were to appear and spread to fixation, we conjecture that the population would be susceptible to invasion by subsequent modifier alleles that drive down the frequency of sex among AA individuals, until the a allele reverts to being deleterious. For example, a modifier causing complete asexuality would invade as it increases average fitness without mixing with the original population.

Even if determines invasion, an additional complication arises when 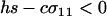. Recall that Equation 10a was derived under the assumption that 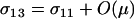. In this case, 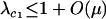, and must be <1 if we assume that equilibrium (6) is not destabilized. Consequently, 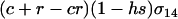must be greater than , which ensures that P₂ remains positive. Because Equation 10a involves P₂ multiplied by (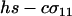), modifier alleles can invade when rare when 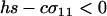if they cause carriers who are less fit to engage in less sex (). We call such modifier alleles “anti-FAS.” An anti-FAS allele m tends to “remain on sinking ships” and becomes associated with Aa genotypes, yet it invades because the reduction in the cost of sex among Aa individuals makes up for the fact that Aa individuals are inherently less fit. The anti-FAS strategy is unlikely to persist over long periods of evolutionary time, however, because populations exhibiting this strategy at the mutation–selection balance given by (6) can always be invaded by alleles reducing the probability of sex in AA individuals (Equation 9). Once the fittest class of individuals undergoes sex rarely enough that , only modifiers that increase the probability of sex in Aa individuals (or further decrease the probability of sex in AA individuals) can invade. Entirely analogous results are observed in the model of fitness-associated sex in a haploid population (appendix a).