Bayesian Mapping of Genomewide Interacting Quantitative Trait Loci for Ordinal Traits

Abstract

Development of statistical methods and software for mapping interacting QTL has been the focus of much recent research. We previously developed a Bayesian model selection framework, based on the composite model space approach, for mapping multiple epistatic QTL affecting continuous traits. In this study we extend the composite model space approach to complex ordinal traits in experimental crosses. We jointly model main and epistatic effects of QTL and environmental factors on the basis of the ordinal probit model (also called threshold model) that assumes a latent continuous trait underlies the generation of the ordinal phenotypes through a set of unknown thresholds. A data augmentation approach is developed to jointly generate the latent data and the thresholds. The proposed ordinal probit model, combined with the composite model space framework for continuous traits, offers a convenient way for genomewide interacting QTL analysis of ordinal traits. We illustrate the proposed method by detecting new QTL and epistatic effects for an ordinal trait, dead fetuses, in a F₂ intercross of mice. Utility and flexibility of the method are also demonstrated using a simulated data set. Our method has been implemented in the freely available package R/qtlbim, which greatly facilitates the general usage of the Bayesian methodology for genomewide interacting QTL analysis for continuous, binary, and ordinal traits in experimental crosses.

MOST complex traits are influenced by interacting networks of multiple genetic (QTL) and environmental factors. Recently several statistical methods and software have been developed to map multiple interacting QTL for continuous traits (Kao et al. 1999; Carlborg et al. 2000; Reifsnyder et al. 2000; Bogdan et al. 2004; Yi et al. 2005; Baierl et al. 2006). However, many complex traits in humans and other organisms are measured in an ordinal manner. For example, many diseases are scored in several ordered categories on the basis of the magnitude of the disease symptom. Although the phenotypes of these characters are discrete, their inheritance is determined by many factors, including multiple genes and environmental components (Lynch and Walsh 1998). Theoretically, the statistical methods for continuous traits are not optimal for ordinal traits because the normality assumption is violated (Johnson and Albert 1999; Gelman et al. 2003). Therefore, mapping QTL for ordinal traits requires new methods.

The probit model is commonly used to analyze discrete binary and ordinal data (Albert and Chib 1993; Johnson and Albert 1999). An important way for the statistical inference and interpretation of the probit model is to postulate the existence of a latent (unobserved) continuous variable associated with each response through a series of unknown thresholds (Albert and Chib 1993; Johnson and Albert 1999). In quantitative genetics, the latent presentation of the probit model is called the threshold model, which has been widely used to analyze the genetic architecture of binary and ordinal traits (Wright 1934; Lynch and Walsh 1998). Under the threshold model, one can treat the latent variable as an unobservable quantitative trait, and genes controlling ordinal traits can be treated as quantitative trait loci and handled using a QTL mapping approach.

A number of statistical methods have been developed to identify QTL for binary or ordinal traits in experimental crosses based on the threshold model of single QTL (Hackett and Weller 1995; Xu and Atchley 1996; Rao and Xu 1998; Xu et al. 2003, 2005). Recently, several methods have been proposed to simultaneously identify multiple QTL for ordinal traits (Coffman et al. 2005; Li et al. 2006). The method of Li et al. (2006) is based on multiple-interval mapping (MIM) of Kao et al. (1999) that fits a multiple-QTL model including epistasis and simultaneously searches for the number, positions, and interaction of QTL using a non-Bayesian model selection procedure and criterion.

Several studies have extended Bayesian methods of mapping multiple QTL for continuous traits to binary traits on the basis of the threshold model of multiple QTL. Yi and Xu (2000) first developed a Bayesian method via a reversible-jump Markov chain Monte Carlo (MCMC) algorithm to map multiple QTL for binary traits. The method of Yi and Xu (2000) is based on the idea of data augmentation, allowing an easy way to extend the existing Bayesian mapping methods to binary traits. Recently, Yi et al. (2004) extended the Bayesian mapping method via a reversible-jump MCMC algorithm to map multiple nonepistatic QTL for ordinal traits. However, Bayesian methods of mapping interacting QTL for ordinal traits are lacking. Even for continuous traits, identification of genomewide interacting QTL has been a formidable challenge, mainly due to numerous possible variables associated with hundreds or thousands of genomic loci that lead to a huge number of possible models.

In this study we propose a Bayesian model selection approach of genomewide interacting QTL for ordinal traits in experimental crosses. We first develop a Bayesian ordinal probit model (threshold model) for multiple interacting QTL, on the basis of the composite model space framework proposed by Yi et al. (2005). Our ordinal probit model simultaneously considers main and epistatic effects of QTL and environmental factors. We then use the composite model space framework to develop an efficient MCMC algorithm for identifying interacting QTL for ordinal traits. The composite model space approach was proposed by Yi (2004) for mapping multiple nonepistatic QTL and extended by Yi et al. (2005) to epistatic QTL mapping for continuous traits. The key advantage of the composite model space approach is that it provides a convenient way to reasonably reduce the model space and to construct efficient algorithms for exploring the complicated posterior distribution. Utility and flexibility of the method are demonstrated using real and simulated data sets.

BAYESIAN MODELING OF ORDINAL TRAITS

Ordinal data modeling via latent variables:

Assume that we observe an ordinal phenotype in a mapping population. The property of ordinal data is that there exists a clear ordering of the response categories, but no underlying interval scale between them (Johnson and Albert 1999). For example, it is usual to record disease severity using an ordinal character system that assesses the extent of the disease. Although one may record the ordinal categories as (arbitrarily) numeric values, it does not always make sense to do so. Even if numeric scores are used, it is not appropriate to apply the statistical methods for continuous data to ordinal data because the normality assumption is violated.

The ordinal probit model is commonly used to analyze ordinal data (Albert and Chib 1993; Johnson and Albert 1999). Let w_i be the ordinal phenotype and x_i the relevant explanatory variables for the ith individual in an experimental cross of sample size n. For notational convenience, we code the ordinal data as the integers 1, 2, ⋯, J, with J the number of categories. Under the ordinal probit model, the data distribution takes the form

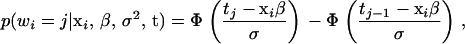(1)

where 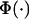is the standardized normal distribution function, β represents the overall mean and regression coefficients, σ² is the residual variance, and 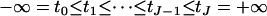are unknown thresholds.

An important idea for interpreting and computing the ordinal probit model involves reexpressing model (1) in terms of unobserved (latent) continuous data (Albert and Chib 1993). Let y_i represent the latent variable that underlies the generation of the ordinal response for the ith individual. The ordinal probit model is equivalent to the following model on latent data y_i,

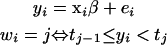(2)

with e_i, i = 1, ⋯, n, independently normal with mean zero and variance σ².

The advantage of the latent parameterization for the probit model is that it offers a convenient framework for MCMC simulation. Conditional on the parameters (β, σ², t) and the observed data, the distribution of y_i follows a truncated normal distribution that can be easily sampled. Conditional on the latent y_i's, the model is a normal linear regression and thus the posterior distribution of the model parameters (β, σ²) can be computed using standard results for normal linear models (Albert and Chib 1993; Johnson and Albert 1999; Yi et al. 2004).

Model (1), or (2), is overparameterized. There are usually two ways to impose restrictions on the parameters that can ensure identifiability. The first is to set t₁ = 0 and σ² = 1, so that there are J − 2 unknown thresholds (Albert and Chib 1993). An alternative approach, which we use here, is to set t₁ = 0 and t_J−1 = 1, leaving σ² as a parameter (Chen and Dey 2000; Yi et al. 2004). This latter approach has several attractive features, notably that threshold values are between 0 and 1.

Ordinal probit model of multiple interacting QTL:

In this section, we describe ordinal probit models of interacting QTL by extending the genomewide interacting QTL model for continuous traits developed by Yi et al. (2005). We approximate positions for all possible QTL using a partition of the entire genome into roughly equally spaced loci, including all observed markers and additional loci, or pseudomarkers (Sen and Churchill 2001), between flanking markers. We calculate the probabilities of genotypes at these preset loci given the observed marker data as priors of QTL genotypes in our Bayesian framework.

We place an upper bound on the number of QTL included in the model. This upper bound is larger than the number of detectable QTL with high probability for a given data set. Even with a moderate number of the upper bound, there are many possible genetic effects when considering interactions, but most are negligible and can be excluded. We use an unobserved vector of binary variables γ to indicate which main and epistatic effects across the possible loci are included in (γ_j = 1) or excluded from (γ_j = 0) the model. The indicator vector γ determines the number of included QTL and the activity of the associated genetic effects. We denote the positions of the included QTL by λ. The vector (γ, λ) thus determines the genetic architecture, the number and position of QTL, and their gene action. The goal of our Bayesian approach is to infer the posterior distribution of (γ, λ) and estimate the associated genetic effects.

We simultaneously model main and epistatic effects of QTL and environmental variables (covariates). We include those (continuous or discrete) covariates that may be important in understanding the effect of genotype on phenotype in the model (e.g., sex, family indicators, and some other traits correlated to the phenotype under study). Including relevant covariates can account for systematic or confounding effects that cannot be controlled experimentally. We use Cockerham's genetic model to construct main effects and epistasis, although other models are possible (Kao and Zeng 2002; Zeng et al. 2005), and apply conventional methods used in hierarchical linear models to construct environmental effects (e.g., Lynch and Walsh 1998; Gelman et al. 2003).

Suppose all genotypes are known across the genome. We can imagine a large design matrix D including all possible effects given the upper bound on the number of QTL. However, given any particular γ, we need focus only on a reduced matrix DΓ = X, identified by the genetic architecture (technically, Γ is a matrix containing only those columns of the identity matrix for which γ = 1). We partition the design matrix into environmental, main, and epistatic effects, X = [X_E: X_G: X_GG], and express the phenotype y as

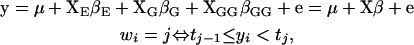(3)

where w_i 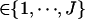, i = 1, ⋯, n, is the observed ordinal phenotype in a mapping population of n individuals, y = (y₁, ⋯, y_n) is the unobserved continuous data, 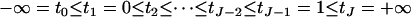are the thresholds, μ = (μ, ⋯, μ)^T is the vector of overall mean μ, β_E represents the vector of environmental effects, β_G and β_GG represent the vectors of selected main effects and epistatic effects, respectively, and e is the vector of independent normal errors with mean zero and variance σ². To simplify notation, we organize all effects into β and all design matrices into X.

Prior distributions:

We organize the unknowns in the above model into two sets, the parameters that also appear in the corresponding model for continuous traits and the additional parameters. The first set of unknowns includes the indicators γ, positions of QTL λ, QTL genotypes g, regression coefficients β, overall mean μ, and residual variance σ² (Yi et al. 2005). The QTL genotypes, g, determine the design matrices X_G and X_GG. The additional unknowns include the latent continuous data y = (y₁, ⋯, y_n) and the thresholds t = (t₂, ⋯, t_J−2).

For the parameters (γ, λ, g, μ, σ²), we use the priors proposed in Yi et al. (2005). Priors on environmental effects in β_E are assigned uniform distributions or normal distributions with mean 0 and unknown variances, labeled fixed or random effects from the non-Bayesian tradition, respectively (Gelman et al. 2003). For the unknown variances, we use conjugate priors, scaled inverse-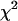. We take uniform prior on the unknown thresholds 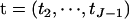; i.e., 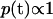, with the constraint .

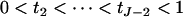Hierarchical priors on genetic effects:

We here suggest new priors on genetic effects (β_G, β_GG) that can restrict their values in a reasonable region and thus induce increased posterior probability on more promising models. We want effect priors that are invariant to the scales of the phenotype and the contrasts in model (3). This can be accomplished by hierarchical models in which the priors have empirical hyperpriors depending on the proportion of liability variance explained by the effect. We partition the genetic effects into batches, corresponding to different types of effects, e.g., additive, dominance, additive–additive interactions, etc. Effects in the same batch k, β_kj, follow the same prior, 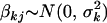. The prior variance 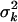is random with an inverse-χ² hyperprior, 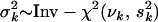. The degrees of freedom ν_k and scale hyperparameters s_k² are chosen to control the prior expected mean and the prior confidence region of the proportion of the liability variance explained by β_kj. The proportion of the liability variance explained by β_kj is then 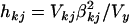, with V_kj the sample variance for the column of X associated with effect β_kj and V_y the total liability variance. The prior expectations are 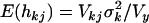and 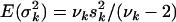. Setting 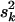= (ν_k − 2)/ν_k · E(h_kj)V_y/V_kj yields E(h_kj) as the prior expectation of variance explained by β_kj. E(h_kj) can be set small (say 0.05–0.2) to reflect any prior knowledge about genetic architecture. The prior degrees of freedom ν_k control the skew of the prior for 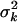, with larger values recommended (here ν_k = 6) to tightly center the prior around 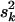(see Chipman 2004).

MCMC SAMPLING

Given the prior distributions of all unknowns and the observed data, the joint posterior density can be expressed as

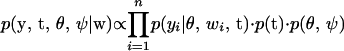(4)

with w = (w₁, ⋯, w_n) the observed ordinal data, θ = (γ, λ, g, β μ, σ²), and ψ represents all variance parameters for β. For notational convenience, we suppress the dependence on marker data and covariates here and in subsequent notation.

From model (3), the conditional distribution of the latent variable y_i follows a truncated normal distribution; i.e.,

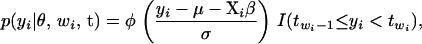(5)

where 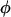denotes the standard normal density, X_i is the ith row of X, and 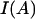is an indicator function for event A.

The latent parameterization for the ordinal probit model of multiple interacting QTL allows a convenient sampling approach for simulating from the joint posterior of the unknowns (θ, ψ, y, t). Conditional on the latent data y_i's, model (3) becomes the multiple-interacting-QTL model for continuous traits [the first line in model (3)] and thus the first set of unknowns θ can be updated using the sampling methods for continuous traits described in Yi et al. (2005). All elements of ψ can be sampled from independent inverse-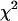 distributions (Gelman et al. 2003). Therefore, we need only an additional step to update the additional unknowns y and t. As described below, y and t can be jointly sampled from the joint conditional posterior p(y, t | θ, w).

We factor the joint conditional posterior of (y, t) into the product

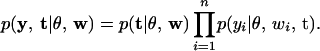(6)

This factorization suggests that we can first draw the threshold values t from p(t | θ, w) and then draw y_i from p(y_i | θ, w_i, t), i = 1, ⋯, n. The distribution p(y_i | θ, w_i, t) is the normal distribution 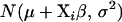truncated to the region 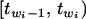. This truncated normal distribution can be sampled using the inverse transformation method (Yi et al. 2004). The first term in (6) can be obtained as

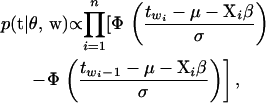(7)

where 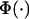is the standardized normal distribution function. A Metropolis–Hastings step is used to sample from this conditional posterior distribution. To update t_j, j = 2, ⋯, J − 2, we first sample a new threshold 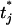uniformly from the interval [max(t_j−1, t_j − d), min(t_j+1, t_j + d)], where d is a predetermined tuning parameter, and t_j−1, t_j, and t_j+1 are the values. The proposal 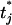is then accepted with probability min{1, r}, where

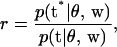(8)

where t are the current values of the thresholds and t* represents all elements of t except t_j is replaced by .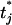

The MCMC algorithm described above is used to simulate a Markov chain from the joint posterior, called the posterior sample, (y, t, θ, ψ)⁽¹⁾, (y, t, θ, ψ)⁽²⁾, ⋯, which converges to the joint posterior p(y, t, θ, ψ | w) (Chipman et al. 2001). The posterior sample can be used to infer the genetic architecture of the ordinal trait, including the number and locations of QTL and their main and epistatic effects. The idea is that larger effects should tend to appear more often and early in a sample from the Markov chain, making them easier to identify. Our basic principle for posterior inference is to use all the saved iterations of the Markov chain, corresponding to model averaging, which assesses characteristics of the genetic architecture by averaging over possible models weighted by their posterior probabilities. Model averaging accounts for model uncertainty and hence provides more robust inference compared to a single “best” model approach (Raftery et al. 1997; Ball 2001; Sillanpää and Corander 2002).

We can use various methods to graphically and numerically summarize and interpret the posterior samples. The posterior inclusion probability for each locus is estimated as its frequency in the posterior samples. Each locus may be included in the model through its main effects and/or interactions with other loci (epistasis). The larger the effect size is for a locus, the more frequently the locus is sampled. Taking the prior probability into consideration, we use Bayes factors (BF) to show evidence for inclusion against exclusion of a locus. The Bayes factor for a locus is defined as the ratio of the posterior odds to the prior odds for inclusion against exclusion of the locus (Kass and Raftery 1995). Traditionally, a BF threshold of 3, or 2 log_e(BF) = 2.1, supports a claim of significance (Kass and Raftery 1995). We can separately estimate the posterior inclusion probability and corresponding Bayes factors of main effects and epistasis.

IMPLEMENTATION IN R/QTLBIM

We have implemented the methods proposed herein in the freely available package R/qtlbim (Yandell et al. 2007). R/qtlbim is an extensible, interactive environment for Bayesian analysis of multiple interacting QTL for continuous, binary, and ordinal traits in experimental crosses. It is built on the widely used R/qtl package (Broman et al. 2003) and includes all its advantages for extensibility. In R/qtlbim, the computationally intensive MCMC algorithms are written in C, with data manipulation and graphics in R. The algorithms for ordinal traits use the same C functions for continuous traits to update the first set of unknowns θ, with additional functions for jointly updating the latent data y and the thresholds t.

R/qtlbim provides tools to monitor mixing behavior and convergence of the simulated Markov chain, either by examining trace plots of the sample values of scalar quantities of interest, such as the numbers of QTL and epistatic effects, or by using formal diagnostic methods provided in the package R/coda (Plummer et al. 2004). The posterior summaries for ordinal traits are the same as those for continuous traits, because all the parameters of interest are included in the set of unknowns θ. R/qtlbim provides extensive informative graphical and numerical summaries of the MCMC output to infer and interpret key aspects of the genetic architecture (Yandell et al. 2007).

MAPPING INTERACTING QTL FOR FETUSES IN MICE

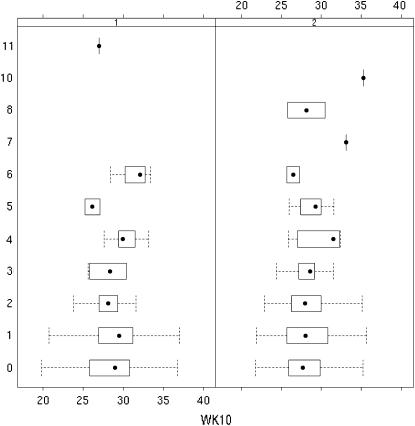
We illustrate our method by reanalyzing a reproductive trait from a QTL study done by Rocha et. al (2004). Ten-week-old F₂ females, of a cross between a high-growth M16i line and the low-body-weight L6 line, were exposed to unrelated F₁ males (B6C3F1/J) until a copulatory plug was detected. Both M16i and L6 mice were inbred lines. Pregnant females (n = 439) were subsequently euthanized at day 16 of gestation to obtain dead fetuses (DF) and several other reproductive phenotypes. Body weights at 10 weeks of age (WK10) were also measured. WK10 was significantly correlated with DF. These F₂ female mice encompass two consecutive replicates consisting of 217 and 222 mice, respectively, and 65 full-sib families/litters ranging from 1 to 11 mice. A total of 63 fully informative microsatellite markers spanning 19 autosomes were genotyped. The marker linkage map covered 1257.8 cM (Kosambi) with an average spacing of 30 cM. The observed DF took integral values ranging from 0 to 11 (Figure 1). We discarded 5 mice having >6 (7, 8, 10, and 11) dead fetuses that may be outliers.

Figure 1.—

Boxplots for week 10 weight by number of dead fetuses per replicate in the F₂ mice.

In spite of their conformity to an ordinal character, this F₂ data set was previously analyzed in Rocha et al. (2004), using standard composite-interval mapping (Zeng 1994) treating DF as continuous traits. The previous analysis first performed an ad hoc square-root transformation for the ordinal trait DF and then used residuals as a new phenotype obtained by linearly adjusting the effects of replicates and family. Rocha et al. (2004) reported a single significant (LOD = 4.4) QTL on chromosome 2 (position 41.6 cM) for DF.

DF is the natural phenotype of interest to exhibit the effectiveness of our proposed method in handling ordinal traits. In our Bayesian analysis, our model included WK10 and replicates as fixed continuous and discrete covariates, respectively, and family indicators as a random categorical covariate. We permitted the inclusion of epistatic effects in the model. We used Cockerham's genetic model to construct genetic effects, in which the additive and dominance contrasts are defined as (−1, 0, 1) and (−0.5, 0.5, −0.5) for the three genotypes, LL, ML, and MM, where L and M represent the L6 and M16i alleles, respectively. Each chromosome was partitioned into a 1-cM grid of putative QTL locations, resulting in 1257 possible loci across the entire genome.

The prior expected number of main-effect QTL was set at l_m = 1, the number of significant QTL detected in the previous analysis (Rocha et al. 2004), and the prior expected number of all QTL was taken to be l₀ = 4, allowing for some additional epistatic QTL with weak main effects. An upper bound on the number of QTL was set to 10 (= 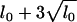, see Yi et al. 2005). To check posterior sensitivity to these prespecified values, we reran the algorithm with several other values of l_m and l₀ and obtained essentially identical results.

We performed the MCMC algorithm using our software R/qtlbim (Yandell et al. 2007). For all our analyses, the MCMC algorithm ran for 2 × 10⁵ iterations after discarding the first 1000 iterations as burn-in to ensure proper mixing of the Markov chain. To eliminate serial correlation, the chain was thinned by considering one in every 40 samples, rendering 5000 samples from the joint posterior distribution. Any result mentioned henceforth was based on these posterior samples. To assess convergence and mixing behavior, we ran three parallel MCMC sequences with starting points randomly generated from the priors and used the potential scale reduction factor 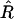to monitor the posterior samples (Gelman and Rubin 1992; Gelman et al. 2003; Plummer et al. 2004). For several scalar estimands (e.g., the numbers of QTL and epistatic effects and the total genetic variance), 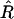fell below 1.1 quickly, indicating that the chains mixed well and converged rapidly.

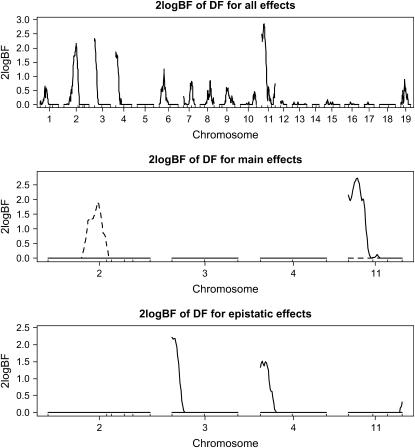
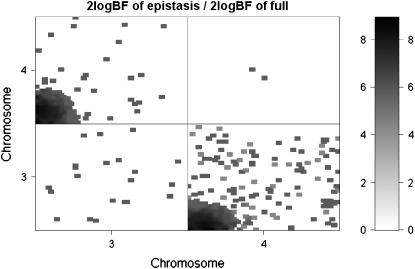
The profiles of Bayes factors, 2 log_eBF, across the genome broken down by genotypic effects showed evidence of QTL activity on chromosomes 2, 3, 4, and 11 (i.e., 2 log_eBF > 2.1) (see Figure 2, top). Chromosomes 2 (50.2 cM) and 11 (10.1 cM) showed evidence of QTL detected mainly through their dominance and additive effects (see Figure 2, middle), respectively, while chromosomes 3 (0.0 cM) and 4 (0.0 cM) showed evidence of mostly additive–additive epistatic effects (see Figure 2, bottom), where the values in parentheses were the posterior modes of positions. Rocha et al. (2004) detected a significant QTL only on chromosome 2, which agrees with our results. The estimated heritabilities of QTL on chromosomes 2, 3, 4, and 11 were 2.2, 4.1, 3.8, and 2.4%, respectively, and consisted of mainly dominance, additive–additive (between chromosomes 3 and 4), and additive components, respectively. Having evidence of epistatic QTL on chromosomes 3 and 4, we showed two-dimensional profiles for Bayes factor and heritability only on them as depicted in Figure 3. The graphs suggested that QTL on chromosome 3 interacted with QTL on chromosome 4, with 2 log_eBF being ∼2.3. The heritability of this epistatic interaction was estimated to 4%.

Figure 2.—

Real F₂ data analysis with the ordinal probit model: one-dimensional profiles of Bayes factors (rescaled as 2 log_eBF and negative values are truncated as zero). (Top) For all combined effects (additive, dominance, and epistatic effects); (middle) for main effects on the selected chromosomes (solid and dashed lines represent additive and dominance effects, respectively); (bottom) for epistatic interactions on the selected chromosomes (solid lines represent additive–additive interactions and other epistatic effects were not detected). On the x-axis, outer tick marks represent chromosomes and inner tick marks represent markers.

Figure 3.—

Real F₂ data analysis with the ordinal probit model: two-dimensional profiles of Bayes factors (rescaled as 2 log_eBF and negative values are truncated as zero). Top triangle shows Bayes factor of epistasis only; bottom triangle shows Bayes factor comparing full model with epistasis to no QTL.

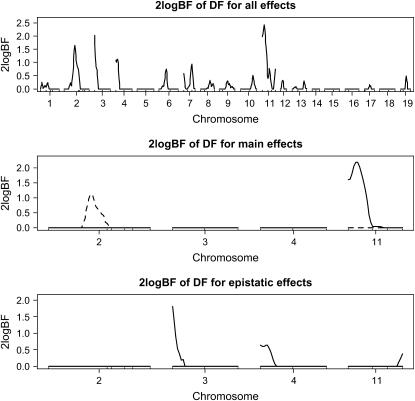
To investigate whether or not ordinal phenotypes can be analyzed by methods for continuous traits, we performed Bayesian multiple-QTL mapping by treating the ordinal phenotype DF or some transformation (e.g., a square-root transformation) as a continuous trait. Figure 4 displays the genomewide profile of Bayes factors, comparing the model with and without the locus for the analysis. This analysis detected evidence of QTL in the same chromosomal regions as those in the above analysis based on the ordinal probit model. Compared with the above result, however, the Bayes factors in Figure 4 were much lower, indicating that the proposed ordinal probit model is more powerful and appropriate for multiple-QTL mapping on ordinal traits.

Figure 4.—

Real F₂ data analysis by treating the ordinal trait DF as a continuous trait: one-dimensional profiles of Bayes factors (rescaled as 2 log_eBF and negative values are truncated as zero). (Top) For all combined effects (additive, dominance, and epistatic effects); (middle) for main effects on the selected chromosomes (solid and dashed lines represent additive and dominance effects, respectively); (bottom) for epistatic interactions on the selected chromosomes (solid lines represent additive–additive interactions and other epistatic effects were not detected). On the x-axis, outer tick marks represent chromosomes and inner tick marks represent markers.

SIMULATION STUDIES

The proposed method has been evaluated by analyzing simulated data sets with different combinations of various factors (e.g., sample size, heritabilites, the number and proportions of categories, and complexity of genetic architecture). For the purpose of simplicity, we here demonstrated only a simulated F₂ cross containing 500 individuals and 20 chromosomes. This simulation study was to evaluate the ability of the proposed method for mapping complex multiple epistatic QTL. Each chromosome was 100 (Haldane) cM in length and had 11 markers randomly spaced. A small amount (3%) of marker genotypes were missing at random. We simulated one binary fixed covariate, one categorical random covariate, and eight QTL, including three pairs of epistatic loci, to control a continuous trait (Table 1). Among the eight simulated QTL, five had main effects while the other three had no main effects but did have epistatic effects. The fixed and random covariates explained 3 and 4% of the phenotypic variance, respectively. The overall mean and residual variance were 10 and 1, respectively. The continuous phenotype was categorized into a four-category ordinal trait with the observed proportions of 30, 30, 20, and 20% for four categories, respectively. Our goal was to recover the simulated genetic architecture by analyzing the ordinal phenotype on the basis of the proposed method. For the purpose of comparison, we performed two additional analyses: We analyzed the simulated continuous phenotype to see how much information is lost by the categorization, and we used the methods for continuous traits to directly analyze the ordinal phenotype (coded as 0, 1, 2, 3).

TABLE 1.

F₂ simulation with eight QTL and two covariates

QTL	Chromosome	Position	Main effect	QTL 2	Epistasis
1	1	15	a = 0.5 (0.05)
2	1	45	a = 0.4 (0.03) d = 0.7 (0.05)
3	3	12	a = −0.5 (0.05)
4	5	15	a = 0.5 (0.05) d = −0.5 (0.02)
5	7	15	a = 0.4 (0.03)
5	7	15		4	aa = −0.7 (0.04)
6	10	15		8	ad = 1.0 (0.05)
7	12	35		3	da = 0.8 (0.03)
8	19	15

Effects were supplied while heritabilities in parentheses were estimated from a simulated sample of 500 individuals. The effects a, d, aa, ad, and da represent additive, dominance, additive–additive, additive–dominance and dominance–additive effects, respectively. QTL 2 refers to a QTL number.

For all analyses, the prior expected number of main-effect QTL was set at l_m = 3, and the prior expected number of all QTL (l₀) was taken to be 6. The upper bound on the number of QTL was then 13 (see Yi et al. 2005). To check posterior sensitivity to these prespecified values, we analyzed the data with several other values of l_m and l₀ and obtained essentially identical results. We ran the MCMC algorithm for 12 × 10⁴ after discarding the first 1000 iterations as burn-in. The chain was thinned by considering one in every 40 samples, rendering 3000 samples from the joint posterior distribution. The saved posterior samples were used to make inference about the genetic architecture.

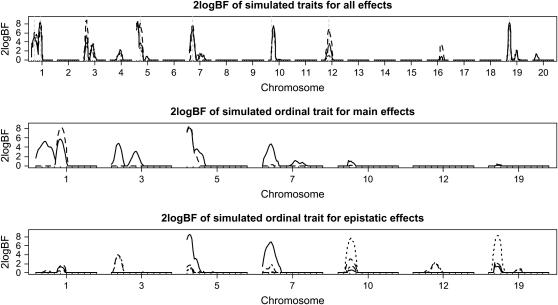
The top section of Figure 5 displays the one-dimensional profiles of Bayes factors comparing the model with and without the locus. For the first two analyses, all the simulated QTL were detected (i.e., 2 log_eBF > 2.1) and most of the simulated QTL positions were estimated close to the true values. The third analysis, which ignored the property of ordinal traits, missed the weakest QTL on chromosome 12. For chromosome 3, all three analyses detected two peaks, probably resulting from the random error of the simulated data. Among the three analyses, the analysis with the underlying continuous phenotype had the highest Bayes factors for all the detected QTL, followed by the ordinal probit model analysis. As expected, the analysis treating the ordinal phenotype as a continuous trait produced the lowest Bayes factors.

Figure 5.—

Simulated F₂ data analyses: one-dimensional profiles of Bayes factors (rescaled as 2 log_eBF and negative values are truncated as zero). (Top) For all combined effects (additive, dominance, and epistatic effects) for all three analyses: solid, dashed, and dotted lines represent analyses with the ordinal probit model, the continuous trait, and the model treating the ordinal phenotype as a continuous trait, respectively. Vertical shaded dashed lines show true location of QTL. (Middle) For main effects on the selected chromosomes (solid and dashed lines represent additive and dominance effects, respectively). (Bottom) For epistatic interactions on the selected chromosomes (solid, dotted, and dashed lines represent additive–additive, additive–dominance, and dominance–additive interactions, respectively). On the x-axis, outer tick marks represent chromosomes and inner tick marks represent markers.

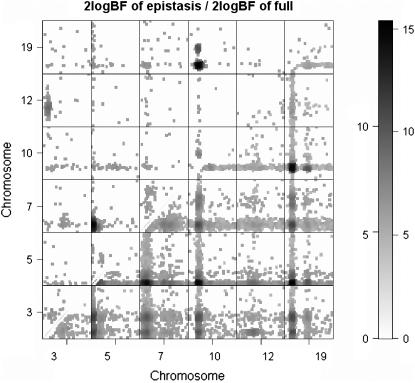
For the ordinal probit model analysis, the middle and bottom sections of Figure 5 depict the profiles of Bayes factors for each of the effects comparing models with and without the effect, for the chromosomes with evidence of QTL. These profiles show that our analysis recovered the true genetic effects that influenced the variation of the simulated trait. The estimates of main and epistatic effects for the detected QTL were also close to the true values (not shown here). To investigate which pairs of loci interacted, Figure 6 displays a two-dimensional profile of Bayes factors on the selected chromosomes showing evidence of epistatic QTL. Once again, our analysis recovered the true pattern of epistatic interactions.

Figure 6.—

Simulated F₂ data analysis with the ordinal probit model: two-dimensional profiles of Bayes factors (rescaled as 2 log_eBF and negative values are truncated as zero) on selected chromosomes. Bayes factor of epistasis only is shown above the diagonal; Bayes factor comparing full model with epistasis to no QTL is shown below the diagonal.

DISCUSSION

Yi (2004) proposed a unified Bayesian model selection framework to identify multiple QTL for complex traits in experimental designs, based upon a composite space representation of the problem. The composite model space approach places a global constraint on the number of detectable QTL and employs latent binary variables to indicate which effects of putative QTL are included in or excluded from the model. The key feature of the composite model space framework is that it provides a convenient framework to reasonably reduce the model space and to construct efficient MCMC algorithms. Yi et al. (2005) extended the composite model space approach to genomewide epistatic QTL analysis for continuous traits and developed efficient MCMC algorithms to explore the posterior distribution.

In this study, we extend the composite model space approach to detect multiple interacting QTL for ordinal traits on the basis of a threshold model. Although the threshold model has been widely used in QTL mapping for binary and ordinal traits, few studies address the problem of interacting QTL. Even for continuous traits, it is not a trivial task to extend the existing methods of noninteracting QTL to genomewide interacting-QTL analysis, mainly due to the dramatic increase in the size of model space. Recently, Li et al. (2006) developed a non-Bayesian method for mapping multiple epistatic QTL for ordinal traits on the basis of the MIM method of Kao et al. (1999) and the threshold model. Our method is Bayesian implemented via MCMC algorithms whereas MIM uses a maximum-likelihood method to estimate the parameters and a stepwise search procedure to build the model. One of the advantages of the Bayesian approach is that it can simultaneously address both model and parameter uncertainty (Raftery et al. 1997; Chipman et al. 2001).

Our ordinal probit model simultaneously fits all unknown elements that can potentially influence phenotypic variation, including arbitrary covariates, main effects of multiple QTL, and gene–gene interactions. We have developed an efficient and easily implemented MCMC algorithm for exploring the posterior of unknowns in the ordinal probit model. The key idea of our method is that conditional on the latent continuous data, the model becomes the multiple-interacting QTL model for continuous traits and thus the MCMC steps for searching for QTL in Yi et al. (2005) can be used. Using the real data sets illustrated in this article and extensive simulations (not shown here), the proposed MCMC algorithm was shown to mix rapidly, thus ensuring that high-probability models are visited frequently and quickly. The method described herein has been implemented in the package qtlbim for the open-source R environment. Our Bayesian methods developed in this study and other studies, along with the freely available package qtlbim, will greatly facilitate the general usage of the Bayesian methodology for genomewide interacting QTL analysis for continuous, binary, and ordinal traits in experimental crosses (Yandell et al. 2007).

Several issues deserve further investigation. Correlated ordinal and continuous traits are encountered in many QTL studies. Joint analysis of multivariate traits can usually improve statistical power in the detection of QTL and can provide formal procedures to investigate the genetic mechanisms such as pleiotropy and close linkage (Jiang and Zeng 1995). The data augmentation approach described herein may be especially attractive for joint analysis of multiple continuous and ordinal traits, where calculating the likelihood can be difficult. Our future plans also include extensions to experimental crosses derived from multiple inbred lines and outbred populations. More flexible and powerful models for genomewide interacting-QTL analysis are planned. We are also investigating ways to interpret epistasis detected on the basis of the ordinal probit model and to check the fit of inferred QTL models to data and prior assumptions.