Skip to main content
PMC home page
Genetics logoLink to Genetics
. 2007 Jul;176(3):1625–1633. doi: 10.1534/genetics.107.071639

Single-Locus Polymorphism in a Heterogeneous Two-Deme Model

Bastiaan Star 1,1, Rick J Stoffels 1, Hamish G Spencer 1
PMCID: PMC1931554  PMID: 17483422

Abstract

Environmental heterogeneity has long been considered a likely explanation for the high levels of genetic variation found in most natural populations: selection in a spatially heterogeneous environment can maintain more variation. While this theoretical result has been extensively studied in models with limited parameters (e.g., two alleles, fixed gene flow, and particular selection schemes), the effect of spatial heterogeneity is poorly understood for models with a wider range of parameters (e.g., multiple alleles, different levels of gene flow, and more general selection schemes). We have compared the volume of fitness space that maintains variation in a single-deme model to the volume in a two-deme model for multiple alleles, random selection schemes, and various levels of migration. Furthermore, equilibrium allele-frequency vectors were examined to see if particular patterns of variation are more prevalent than first expected. The two-deme model maintains variation for substantially larger volumes of fitness space with lower heterozygote fitness than the single-deme model. This result implies that selection schemes in the two-deme model can have a wider range of fitness patterns while still maintaining variation. The equilibrium allele-frequency patterns emerging from the two-deme model are more variable and strongly influenced by gene flow.

SPATIAL environmental heterogeneity has been considered a likely explanation of the high levels of genetic variation first observed in the 1960s (Kassen 2002). A heterogeneous environment can selectively maintain more variation within populations according to classical population genetic theory (Levene 1953; Felsenstein 1976; Karlin 1982; Hedrick 1986; Futuyma and Moreno 1988), and these predictions are supported by recent experimental studies (Gurganus et al. 1998; Travisano and Rainey 2000; Vieira et al. 2000; Weinig and Schmitt 2004). Selection in heterogeneous environments is further used to explain patterns of genetic variation in subdivided wild populations (Schmidt et al. 2000; Johannesson et al. 2004; Hanski and Saccheri 2006). The classical heuristic example for a protected polymorphism due to spatial heterogeneity is the two-allele situation, whereby one allele is considered most fit in one deme, but not as fit in a second deme where the other allele is the most fit. This situation can lead to a migration–selection equilibrium of the two alleles, resulting in more variation being maintained between and within demes.

It is well known that the potential to selectively maintain more genetic variation is influenced by the relative levels of fitness differences and gene flow between the demes (Endler 1973; Kawecki 2000; Lenormand 2002). This potential is greater when the amount of gene flow is limited and fitness differences are substantial between the habitats (Smith and Hoekstra 1980). Nevertheless, most studies on the maintenance of genetic variation in heterogeneous environments are limited in the range of parameters used in their examples (e.g., two alleles, fixed gene flow, and particular selection schemes) (Smith 1970; Eyland 1971; Bulmer 1972; Smith and Hoekstra 1980; Karlin 1982; Nagylaki and Lou 2001). Therefore, we still do not know how effective spatial heterogeneity is in maintaining genetic variation for a wider range of parameters (e.g., multiple alleles and more general selection schemes) in even a simple two-deme model.

One way of quantifying the ability of spatial variation in selection coefficients to maintain polymorphism is by comparing the volume of fitness space that maintains polymorphism in a one-deme system (Lewontin et al. 1978) to the corresponding volume of a multiple-deme system. Here we present a simulation study that explores the region of constant-viability fitness space that leads to a polymorphism for multiple alleles at a single locus with various levels of migration between two demes. We further analyze these fitness matrices to understand what fitness structures are necessary to successfully maintain variation. Moreover, we also examine the equilibrium allele-frequency vectors to see if particular allele frequency distributions characterize heterogeneous selection pressures.

MODEL

We consider a single, diploid autosomal locus under constant viability selection in two demes that are connected by migration. Generations are discrete and we ignore the random effects of drift. The frequency of the ith allele (i = 1, 2,…, n), Ai in the dth deme (d Inline graphic{1, 2}), after selection is given by

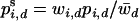graphic file with name M2.gif (1)

in which 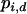Inline graphic is the current frequency of Ai in the dth deme, 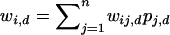Inline graphic is the current marginal fitness of Ai in the dth deme, 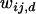Inline graphic is the fitness of the AiAj genotypes in the dth deme, and 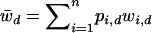Inline graphic is the current mean fitness of the dth deme. Migration takes place after selection with a proportion, m, of the frequency vector pi,d being divided over each deme, giving the new frequency of Ai in deme d,

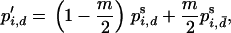graphic file with name M7.gif (2)

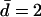where Inline graphic if d = 1 and vice versa. Selection acts locally and this is therefore a soft-selection model. The above equations are iterated until equilibrium, defined to be 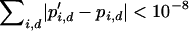Inline graphic or until an allele is considered lost, defined to be 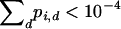Inline graphic for some i.

Simulations were run for two to five alleles and seven different migration rates (m 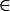Inline graphic{0, 0.01, 0.05, 0.1, 0.2, 0.5, 1.0}). Following Lewontin et al. (1978), fitnesses for each deme were separately drawn from the uniform distribution on [0, 1]. For each combination of n and m, 105 random fitness sets were evaluated by iterating Equations 1 and 2, starting with a single initial allele-frequency vector that was randomly chosen using the “broken-stick” method (Marks and Spencer 1991). The total proportion of simulations leading to a fully polymorphic equilibrium, what we call the potential to maintain variation, was then compared to the single-deme model from Lewontin et al. (1978).

In contrast to a fitness set for a single deme, a fitness set for a multiple-deme system can lead to multiple equilibria, which may or may not be polymorphic (Karlin 1982). The particular equilibrium to which such a fitness sets leads depends on the initial allele-frequency vector. To investigate these kinds of fitness sets, numerous new simulations were run in which each single fitness set was evaluated with 250 random initial allele frequencies. Fitness sets that led to the maintenance of all alleles for all initial allele frequency vectors were defined as type I fitness sets. Those that led to the maintenance of all alleles for <250 of the vectors were defined as type II fitness sets. To understand the properties of these two types of fitness sets, for each type we retained 1000 fitness sets for n = 2500 sets for n = 3 and 250 sets for n = 4 and 5. Several measures were recorded, including the proportion of all fitness sets that were type I and the proportion that were type II. For type II sets we also recorded the proportion of initial vectors that resulted in polymorphism. For each sampled fitness set, the fitness set itself and its fully polymorphic equilibrium allele-frequency vector(s) were stored for later analyses. To investigate the extent of balancing selection and disruptive selection in the two-deme model, the fitness data were analyzed for heterozygote advantage and the correlation of heterozygote fitness values between demes. All final polymorphic equilibrium allele-frequency vectors were analyzed for levels of skew of allele frequencies and the Ewens–Watterson test (Ewens 1972; Watterson 1978) was used to investigate if these patterns deviate detectably from the neutral hypothesis.

RESULTS AND ANALYSIS

Potential to maintain variation:

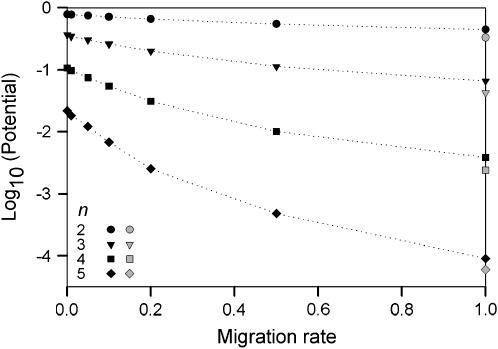
The proportion of simulations maintaining all alleles (i.e., the potential) decreases dramatically as the number of initial alleles increases and as the migration rate increases (Figure 1). When comparing the two-deme model to Lewontin's single-deme model (Lewontin et al. 1978), the overall proportions are low in both models, yet a significantly higher proportion (χ2-test for proportions) of fitness sets lead to full polymorphism in our two-deme model than in the single-deme model for all but one (n = 5 and m = 1.0) parameter setting. The increased potential is especially apparent for low levels of gene flow and five alleles when it is then up to two orders of magnitude higher. This effect is most easily explained for a situation with no gene flow. Here, different combinations of alleles maintained in separate demes can make up the total number of alleles. For example, five alleles can be maintained by having two alleles in one deme and three different ones in the other or by having three alleles in both demes. Even ignoring the potentially different combinations of alleles, the probability of maintaining two and three alleles in two demes alone is considerably higher than the probability of maintaining five alleles in one deme (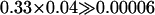Inline graphic; Lewontin et al. 1978). Therefore fitness sets with more alleles benefit relatively more from a heterogeneous selection regime than those with a lower number of alleles.

Figure 1.—

Figure 1.—

Open in a new tab

Logged potential maintaining all initial alleles as a function of migration rate. The shaded symbols reflect the proportions found in a single deme by Lewontin et al. (1978).

As gene flow increases, the effects of both selection and migration blend in a complex manner and the outcome of the simulation is not always intuitively clear. The main effect of increased gene flow is the averaging over the two demes of the fitness values for alleles, and a larger proportion of simulations will tend to become fixed for alleles with the highest mean fitness. This averaging effect of gene flow decreases the overall proportion of simulations that maintain variation. Yet, in simulations with completely averaged levels of gene flow (m = 1.0), fitness sets can occasionally maintain variation even while their averaged fitness matrix leads to directional selection. This behavior occurs because we are modeling soft selection, with relative viabilities and fixed population sizes per deme (Karlin 1982). A soft-selection model with high gene flow is, in contrast to a hard-selection model with high gene flow, not equivalent to a randomly mating population and maintains variation for a wider range of viabilities (Christiansen 1975). Furthermore, the proportion of simulations maintaining variation for m = 1.0 in our two-deme model is remarkably similar to the proportion found in a single-deme model with sex-dependent viabilities (Marks and Ptak 2000).

Proportion of type I and type II fitness sets:

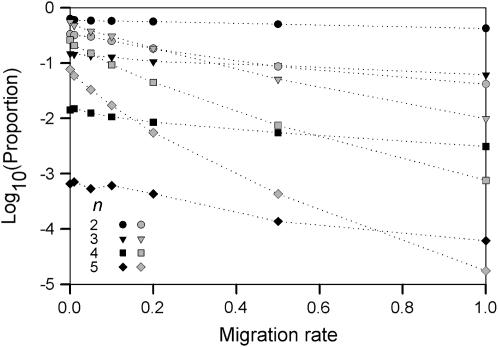
Due to the dependence on initial allele-frequency vectors, the proportion of type II fitness sets (i.e., those that maintain all alleles only for some initial allele-frequency vectors) decreases faster with increasing gene flow than the proportion of type I fitness sets (Figure 2). Convergence of type II fitness sets to polymorphic equilibrium depends on the skew of initial allele frequencies and increased migration reduces this skew by averaging the allele frequencies. For example, a fitness set for two alleles with underdominance in one deme and directional selection in the other deme will lead to polymorphism in the absence of migration if the initial allele frequency in the deme with underdominance is skewed toward the allele that is selected against in the other deme. With higher migration, however, fewer initial allele frequencies preserve this skew and fixation becomes more likely. In contrast to a type II fitness set, a type I fitness set will lead to polymorphism regardless of the initial allele-frequency vector. Thus, while increased gene flow has an overall effect on the average fitness of the alleles, the proportion of type I fitness sets is less influenced by gene flow than the proportion of type II fitness sets as convergence occurs for a wider range of allele frequencies.

Figure 2.—

Figure 2.—

Open in a new tab

Logged proportion of type I (solid symbols) and type II (shaded symbols) fitness sets leading to polymorphism as a function of migration rate.

Proportion of frequency vectors leading to equilibrium:

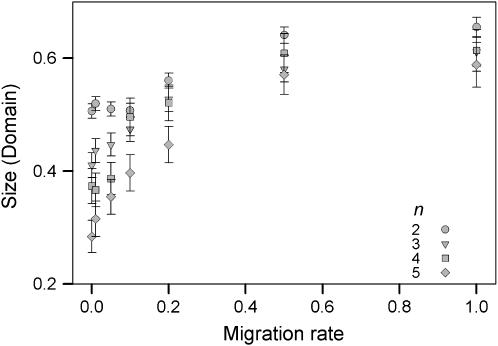
The proportion of initial allele-frequency vectors leading to fully polymorphic equilibrium for type II fitness sets is a measure of the size of the domain of attraction for a particular equilibrium. For a two-allele scenario without migration, the average size of the domain of attraction is ∼0.5, which indicates that on average 50% of the initial allele-frequency vectors will iterate to a fully polymorphic equilibrium (Figure 3). The size of the domain of attraction decreases with higher numbers of alleles for lower levels of gene flow and it increases for all numbers of alleles for higher levels of gene flow. Thus, while the proportion of type II fitness sets themselves decreases with an increasing migration rate, this reduction in potential to maintain variation is partially negated by an increased domain of attraction for the fitness sets that do maintain all alleles. Essentially only those type II fitness sets with large enough domains of attraction are sufficiently robust enough to continue to maintain full polymorphism under greater levels of migration.

Figure 3.—

Figure 3.—

Open in a new tab

Average size of the domain of attraction for type II fitness sets as a function of migration rate. The error bars are 95% confidence intervals.

Heterozygote advantage:

Balancing selection is more likely to maintain large numbers of alleles in a single-deme model if the difference between heterozygotes and homozygotes is sufficiently large (Lewontin et al. 1978). The probability that randomly generated fitness sets comply with these requirements decreases as the number of alleles increases. To compare levels of heterozygote advantage in the two-deme model to those in the single-deme model, average heterozygote advantage values were calculated for all fitness sets that maintain variation. Average heterozygote advantage per fitness set is defined as 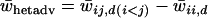Inline graphic, where the averaging is over all fitnesses from both demes. Calculating average heterozygote advantage using fitness values from one of the demes instead of from both demes produced similar results and these data are not shown below.

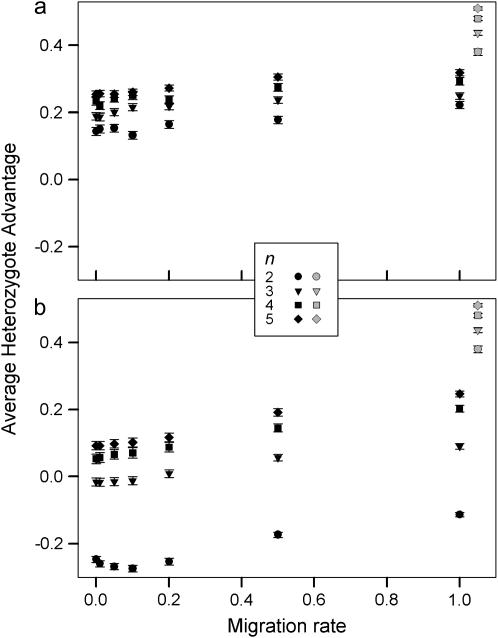
The average heterozygote advantage data were analyzed using ANOVA with the number of alleles, migration rate, and type of fitness sets as factors and 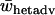Inline graphic as a response variable. Data from a single-deme model were included in the analysis as a separate group with a unique migration rate and type. Average heterozygote advantage is significantly lower for a two-deme model for both type I and type II fitness sets when compared to a single-deme model (Bonferroni post hoc test for multiple comparisons, P-values <0.0005 for all comparisons) (Figure 4). Furthermore, there are significant interaction effects on average levels of heterozygote advantage between the types of fitness set and both the number of alleles (ANOVA, F3, 29941 = 1433, P < 0.0005) and the migration rate (ANOVA, F6, 29941 = 33.3, P < 0.0005). There is also a significant interaction effect between the number of alleles and the migration rate (ANOVA, F18, 29941 = 4.41, P < 0.0005). Overall, the two-deme model does not require such high levels of heterozygote advantage compared to a single-deme model to maintain complete variation and therefore it maintains variation for a wider range of fitness values.

Figure 4.—

Figure 4.—

Open in a new tab

Average heterozygote advantage for type I (a) and type II (b) fitness sets maintaining variation in two demes as a function of migration rate. The error bars are 95% confidence intervals. The shaded symbols indicate the average heterozygote advantage for fitness sets maintaining variation in a single deme.

Cross-deme correlation of heterozygote fitness values:

Pearson's correlation coefficient between the heterozygote fitness values of the two demes was calculated for both types of fitness sets that maintained all alleles for 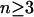Inline graphic as a measure of disruptive selection between the demes. For a given fitness set heterozygote correlation of fitness values between the two demes is given by

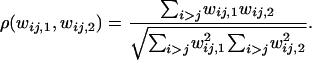graphic file with name M16.gif

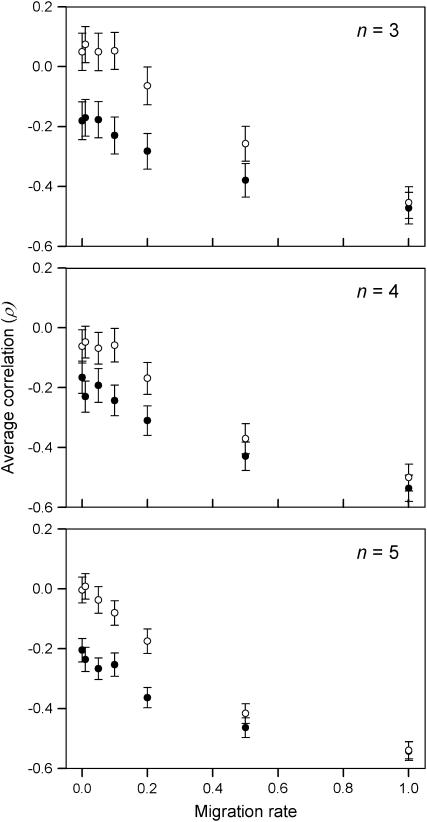
A significant positive correlation indicates that heterozygote fitness values are more similar than can be expected by random chance, while a significant negative correlation indicates the opposite and fitness sets with more negative correlation have stronger disruptive selection. The correlation data were analyzed using ANOVA with the number of alleles, migration rate, and type of fitness sets as factors and 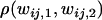Inline graphic as a response variable. The type of fitness set and the migration rate have a significant interaction effect on correlation between the demes (ANOVA, F6, 13958 = 20.2, P < 0.0005). Type II fitness sets have higher correlation for lower levels of migration compared to type I fitness sets, but as the migration rate increases correlation decreases for both types (Figure 5). There is also a significant interaction effect between the type of fitness set and the number of alleles (ANOVA, F2, 13958 = 4.948, P = 0.007). In all, these results indicate that disruptive selection is important for polymorphism when the migration rate is high.

Figure 5.—

Figure 5.—

Open in a new tab

Pearson's correlation coefficient (ρ) between heterozygote fitness values as a function of migration rate. Values were calculated for type I (solid circles) and type II (open circles) fitness sets with three, four, and five alleles. The error bars are 95% confidence intervals.

Equilibrium allele-frequency distributions:

The skew of allele frequencies was determined by calculating I, the sum of squared differences of the frequencies from the mean (Lewontin et al. 1978). This index was calculated using both the allele-frequency vector (pi,d) taken from one of the two demes and a pooled allele-frequency vector using the frequencies from both demes. The pooled allele-frequency vector is analyzed to investigate what frequency patterns emerge if the underlying spatial structure is ignored. I is given by 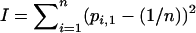Inline graphic for the frequencies in a single deme and by 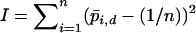Inline graphic for the pooled allele frequencies over both demes. 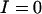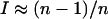If all alleles have equal frequency, Inline graphic, and if one allele is close to fixation Inline graphic.

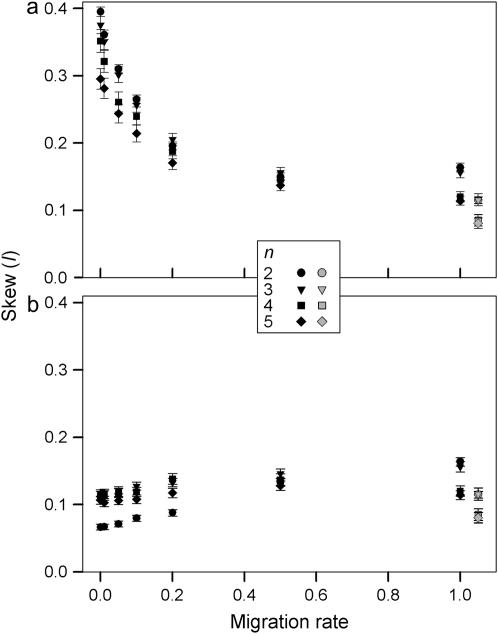
Since maximum I-values are different for different total numbers of alleles, single-factor ANOVA was performed separately for both measures of I and each number of alleles with migration rate as a factor and I as response. Gene flow has a significant effect on skew for both measures and all numbers of alleles as all P-values were <0.0005. Skew measured by I in a single deme is significantly higher in the two-deme model than in the single-deme model especially for lower migration rates (Figure 6a). The high levels of skew for lower migration rates are a direct result of the total number of alleles being maintained as a combination of different alleles in each deme. If skew is measured by I using the pooled frequencies from both demes, an opposite trend is observed and simulations with lower migration rates have significantly lower skew (Figure 6b). At lower migration rates, the allele frequencies are skewed for different alleles in each of the demes and the averaged allele frequencies therefore become more equal. Overall, the level of migration in the two-deme model has a very significant effect on the equilibrium frequency distributions. The magnitude and direction of this effect depends on whether samples are taken from one of the demes or from both demes.

Figure 6.—

Figure 6.—

Open in a new tab

Average skew of equilibrium allele frequencies measured by I (see text for an explanation) as a function of migration rate. I was calculated using allele frequencies from one of the demes (a) or using pooled allele frequencies from both demes (b). The shaded symbols indicate average skew in a single-deme model. The error bars are 95% confidence intervals.

Neutrality:

Following the procedure in Marks and Spencer (1991) and Spencer and Marks (1992), the Ewens–Watterson test was used to examine if the equilibrium allele-frequency vectors were detectably different from those found under the neutral hypothesis using both the allele-frequency vector (pi,d) taken from one of the two demes and the pooled allele-frequency vector from both demes. From both of these allele-frequency vectors per polymorphic equilibrium, 200 sample frequency vectors were taken, each with a sample size of 200 genes. The sample homozygosity (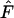Inline graphic) was calculated for each of these sample frequency vectors and compared to the lower and upper critical points of Ewens sampling distributions (Ewens 1972; Watterson 1977, 1978). Thus each allele-frequency vector is tested 200 times to see whether 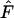Inline graphic was in either critical region. Each single sample from the allele-frequency vector was a binomial experiment with a constant probability of being rejected or not. If significantly >5% of the samples from a single final allele-frequency vector are rejected, which occurs when >9% of the samples are rejected (binomial distribution with N = 200 and P = 0.05), that frequency vector was considered significantly nonneutral. We also recorded the overall proportion of significant tests in either region, which indicates how often samples are rejected for a particular allele-frequency vector.

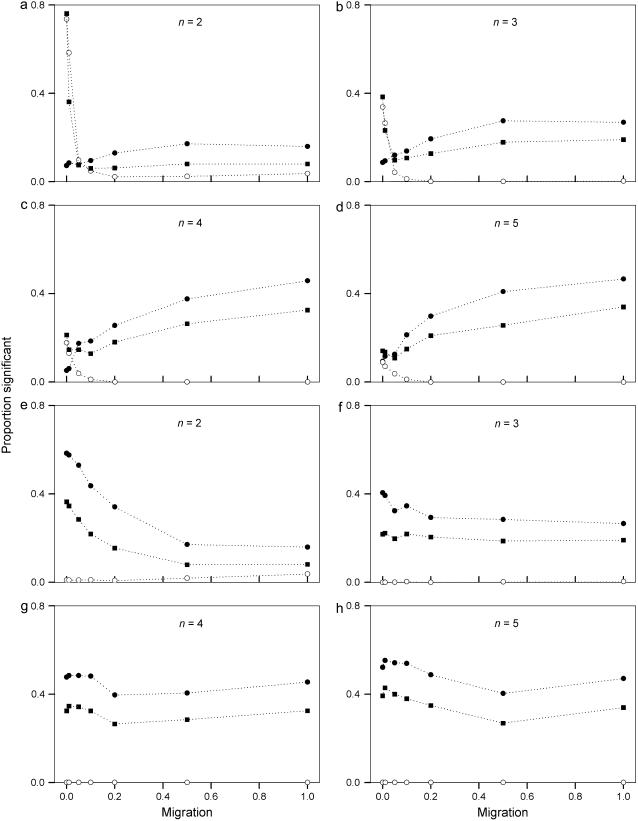
Allele-frequency vectors that significantly deviate from neutrality with 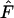Inline graphic in the upper critical region (usually taken to indicate purifying selection) were detected only in the vectors taken from one of the demes at low migration rates (Figure 7, a–d). The individual samples for these significant vectors were rejected almost every time as is indicated by the high overall proportion of significant tests for these vectors. The proportion of allele-frequency vectors that are significantly nonneutral due to 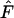Inline graphic -values in the lower critical region (usually interpreted as showing balancing selection) increases with decreasing levels of skew of allele-frequency vectors (Figure 7, a–g). As seen previously in Figure 6, the allele-frequency vectors become less skewed with higher levels of migration for vectors taken from one of the two demes, and they further become less skewed with lower levels of migration for pooled frequency vectors. As the allele-frequency vectors become less skewed the probability of calculating lower 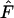Inline graphic -values increases. The individual samples for these vectors were not rejected constantly as is indicated by the lower overall proportion of significant tests. The levels of migration and the way in which the allele-frequency vectors are sampled (i.e., frequency vectors taken from one of the demes or pooled frequency vectors) both have an important effect on the outcome of the Ewens–Watterson test as they influence the levels of skew in the allele-frequency vectors.

Figure 7.—

Figure 7.—

Open in a new tab

Proportion of allele-frequency vectors that were significantly different from neutral according to the Ewens–Watterson test for neutrality. Samples were taken from frequency vectors taken from one of the demes (a–d) and from pooled frequency vectors from both demes (e–h) for two, three, four, and five alleles. Allele-frequency vectors were rejected if 18 or more of the generated sample homozygosity (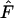Inline graphic) values were lower (solid circles) or higher (open circles) than the critical points of Ewens sampling distribution (see text for explanation). Also shown is the overall proportion of significant tests in either region (solid squares).

DISCUSSION

Numerical simulations in our simple two-deme model show that the volume of fitness space that maintains full polymorphism in a spatially heterogeneous environment is significantly larger compared to the volume in the single-deme model described by Lewontin et al. (1978) for a wide range of parameters (e.g., multiple alleles, different levels of gene flow, and more general selection schemes). In particular, fitness sets with higher numbers of alleles have a relatively larger region of fitness space maintaining all alleles than fitness sets with a lower number of alleles. Thus the simulated heterogeneous environment in our model is more efficient in maintaining variation for higher numbers of alleles. Furthermore, if variation is maintained, the successful viability fitness sets have a wider range of fitness values. Nevertheless, the total proportion of fitness sets that maintain all the variation is still small for higher numbers of alleles, indicating that successful fitness sets for these parameters must still have very particular structures.

Type II fitness sets (i.e., fitness sets leading to full polymorphism for proper subsets of the initial allele frequencies) are common for diallelic frequency-dependent single-locus and diallelic multilocus models (Asmussen and Basnayake 1990; Gimelfarb 1998). These fitness sets have further been mentioned in spatial single-locus systems (Karlin 1982), but to our knowledge our study is the first to characterize the fitness structures of these sets for different numbers of alleles and migration rates. Type II fitness sets are surprisingly common for higher numbers of alleles and low levels of migration. Crucially, however, the allele frequencies leading to the fully polymorphic equilibrium of a type II fitness set may not include the initial frequencies that a new mutation will have. Therefore the high number of type II fitness sets does not necessarily indicate how likely it is that the frequencies of an evolving population will converge to the locally stable equilibrium of these sets. While higher levels of migration increase the likelihood that a particular type II fitness set will converge to equilibrium, these rates also rapidly decrease the proportion of these fitness sets. Furthermore, random processes such as genetic drift can obviously disturb these locally stable equilibria so that their occurrence in natural populations is unclear.

Only very specific fitness sets successfully maintain full polymorphism and fitness sets with substantial heterozygote advantage are more likely to maintain variation in a single-deme model (Lewontin et al. 1978). As the number of alleles increases, successful fitness sets becomes increasingly constrained (De Boer et al. 2004), requiring larger fitness differences between homozygotes and heterozygotes. The average level of heterozygote advantage, 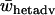Inline graphic, in successful fitness sets is thus a rough measure of how constrained the fitness sets are. Fitness sets in the two-deme model maintain genetic variation with levels of heterozygote advantage less than half than observed in a single-deme model for a wide range of model parameters. Therefore, the two-deme model with spatial heterogeneity substantially reduces the requirement for heterozygote advantage, allowing maintenance for a wider range of fitness values. As the two-deme model is the most simple population subdivision, we suggest that the level of heterozygote advantage will likely be further reduced in a more complex model with multiple demes. We plan to generalize this result to multiple demes in a subsequent article.

Polymorphism for two alleles can be maintained if antagonistic selection is sufficiently strong compared to the levels of migration (Bulmer 1972) and antagonistic selection results in fitness sets that are negatively correlated across the demes. This negative correlation is shown for multiple alleles by the inverse relationship of Pearson's correlation coefficient between heterozygote fitness values and levels of migration in our model (Figure 6). These negative correlations coincide with the highest levels of heterozygote advantage, 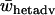Inline graphic in our model. Thus, polymorphism for higher numbers of alleles is most easily maintained by a combination of balancing selection within the demes and disruptive selection between the different demes.

One criticism of balancing selection in the single-deme model is that it tends to produce equilibrium allele frequencies that are fairly equal (Lewontin et al. 1978). In contrast, the two-deme model produces a range of equilibrium frequency distributions depending on the level of migration. This effect of spatial structure is obvious, since at low levels of migration alleles that are maintained in one deme may be present at low frequencies in the other deme, resulting in more skewed frequency distributions. If spatial scale is ignored by pooling the frequency vectors from both demes, the skew of equilibrium allele frequencies is obviously influenced and the frequencies in fact become less skewed for low levels of migration. This result underlines the importance of taking into account the spatial scale of a metapopulation when sampling the different demes. If different demes are incorrectly mistaken for a single population, the skew of equilibrium allele frequencies will be underestimated.

Since gene flow has such a large influence on the skew of frequency distributions, it also has a large influence on the outcome of the Ewens–Watterson test for neutrality that is based on deviations of these patterns (Ewens 1972; Watterson 1977, 1978). Frequency distributions are rejected from neutrality either due to a low sample homozygosity (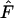Inline graphic), which indicates selection for heterozygotes, or a high sample 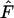Inline graphic, which indicates selection against heterozygotes (Manly 1985; but also see Marks and Spencer 1991). For higher levels of gene flow it is proposed that the Ewens–Watterson test is based on the pooled frequencies of subdivided populations (Ewens and Gillespie 1974; Manly 1985) while for lower levels of gene flow the test should be based on allele-frequency vectors of a single deme (Slatkin 1982). Pooled frequencies at low levels of gene flow result in underestimation of 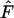Inline graphic, which is shown by our simulations with an increased proportion of frequency vectors rejected from neutrality due to low 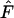Inline graphic at these levels of gene flow. Regardless of which allele-frequency vectors (i.e., those from a single deme or pooled values) the Ewens–Watterson test is based upon, it seems to be more sensitive for detecting deviations from neutrality due to low 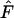Inline graphic with an increasing number of alleles. In contrast, deviations from neutrality due to high 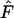Inline graphic decrease with an increasing number of alleles. Interpretation of deviation from neutrality due to either low 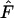Inline graphic or high 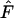Inline graphic in selection for or against heterozygotes should be regarded with caution as most alleles in our simulations seem to be maintained by a combination of balancing selection and disruptive selection. These results are further consistent with previous findings that a variety of selectively maintained polymorphisms often cannot be detected as nonneutral by the Ewens–Watterson test (Gillespie 1991; Marks and Spencer 1991; Spencer and Marks 1992). Overall, these results show that the simulated environmental heterogeneity improves the selective maintenance of genetic variation for a wide range of parameters and resulting patterns of variation are varied. Interestingly, most of these patterns cannot be distinguished from the neutral hypothesis.

Acknowledgments

This work was supported by the Allan Wilson Centre for Molecular Ecology and Evolution and by the University of Otago Postgraduate Scholarships.

References

  1. Asmussen, M. A., and E. Basnayake, 1990. Frequency-dependent selection—the high-potential for permanent genetic-variation in the diallelic, pairwise interaction-model. Genetics 125: 215–230. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bulmer, M. G., 1972. Multiple niche polymorphism. Am. Nat. 106: 254–257. [Google Scholar]
  3. Christiansen, F. B., 1975. Hard and soft selection in a subdivided population. Am. Nat. 109: 11–16. [Google Scholar]
  4. De Boer, R. J., J. A. M. Borghans, M. van Boven, C. Kesmir and F. J. Weissing, 2004. Heterozygote advantage fails to explain the high degree of polymorphism of the MHC. Immunogenetics 55: 725–731. [DOI] [PubMed] [Google Scholar]
  5. Endler, J. A., 1973. Gene flow and population differentiation. Science 179: 243–250. [DOI] [PubMed] [Google Scholar]
  6. Ewens, W. J., 1972. Sampling theory of selectively neutral alleles. Theor. Popul. Biol. 3: 87. [DOI] [PubMed] [Google Scholar]
  7. Ewens, W. J., and J. H. Gillespie, 1974. Some simulation results for neutral allele model, with interpretations. Theor. Popul. Biol. 6: 35–57. [DOI] [PubMed] [Google Scholar]
  8. Eyland, E. A., 1971. Morans island migration model. Genetics 69: 399–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Felsenstein, J., 1976. The theoretical population genetics of variable selection and migration. Annu. Rev. Genet. 10: 253–280. [DOI] [PubMed] [Google Scholar]
  10. Futuyma, D. J., and G. Moreno, 1988. The evolution of ecological specialization. Annu. Rev. Ecol. Syst. 19: 207–233. [Google Scholar]
  11. Gillespie, J. H., 1991. The Causes of Molecular Evolution. Oxford University Press, New York.
  12. Gimelfarb, A., 1998. Stable equilibria in multilocus genetic systems: a statistical investigation. Theor. Popul. Biol. 54: 133–145. [DOI] [PubMed] [Google Scholar]
  13. Gurganus, M. C., J. D. Fry, S. V. Nuzhdin, E. G. Pasyukova, R. F. Lyman et al., 1998. Genotype-environment interaction at quantitative trait loci affecting sensory bristle number in Drosophila melanogaster. Genetics 149: 1883–1898. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Hanski, I., and I. Saccheri, 2006. Molecular-level variation affects population growth in a butterfly metapopulation. PloS Biol. 4: 719–726. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hedrick, P. W., 1986. Genetic-polymorphism in heterogeneous environments—a decade later. Annu. Rev. Ecol. Syst. 17: 535–566. [Google Scholar]
  16. Johannesson, K., J. Lundberg, C. Andre and P. G. Nilsson, 2004. Island isolation and habitat heterogeneity correlate with DNA variation in a marine snail (Littorina saxatilis). Biol. J. Linn. Soc. 82: 377–384. [Google Scholar]
  17. Karlin, S., 1982. Classifications of selection migration structures and conditions for a protected polymorphism. Evol. Biol. 14: 61–204. [Google Scholar]
  18. Kassen, R., 2002. The experimental evolution of specialists, generalists, and the maintenance of diversity. J. Evol. Biol. 15: 173–190. [Google Scholar]
  19. Kawecki, T. J., 2000. Adaptation to marginal habitats: contrasting influence of the dispersal rate on the fate of alleles with small and large effects. Proc. R. Soc. Lond. Ser. B Biol. Sci. 267: 1315–1320. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Lenormand, T., 2002. Gene flow and the limits to natural selection. Trends Ecol. Evol. 17: 183–189. [Google Scholar]
  21. Levene, H., 1953. Genetic equilibrium when more than one ecological niche is available. Am. Nat. 87: 331–333. [Google Scholar]
  22. Lewontin, R. C., L. R. Ginzburg and S. D. Tuljapurkar, 1978. Heterosis as an explanation for large amounts of genic polymorphism. Genetics 88: 149–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Manly, B. F. J., 1985. The Statistics of Natural Selection. Chapman & Hall, London.
  24. Marks, R. W., and S. E. Ptak, 2000. The maintenance of single-locus polymorphism. V. Sex-dependent viabilities. Selection 1: 217–228. [Google Scholar]
  25. Marks, R. W., and H. G. Spencer, 1991. The maintenance of single-locus polymorphism. 2. The evolution of fitnesses and allele frequencies. Am. Nat. 138: 1354–1371. [Google Scholar]
  26. Nagylaki, T., and Y. A. Lou, 2001. Patterns of multiallelic polymorphism maintained by migration and selection. Theor. Popul. Biol. 59: 297–313. [DOI] [PubMed] [Google Scholar]
  27. Schmidt, P. S., M. D. Bertness and D. M. Rand, 2000. Environmental heterogeneity and balancing selection in the acorn barnacle Semibalanus balanoides. Proc. R. Soc. Lond. Ser. B Biol. Sci. 267: 379–384. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Slatkin, M., 1982. Testing neutrality in subdivided populations. Genetics 100: 533–545. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Smith, J. M., 1970. Genetic polymorphism in a varied environment. Am. Nat. 104: 487. [Google Scholar]
  30. Smith, J. M., and R. Hoekstra, 1980. Polymorphism in a varied environment - how robust are the models. Genet. Res. 35: 45–57. [DOI] [PubMed] [Google Scholar]
  31. Spencer, H. G., and R. W. Marks, 1992. The maintenance of single-locus polymorphism. 4. Models with mutation from existing alleles. Genetics 130: 211–221. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Travisano, M., and P. B. Rainey, 2000. Studies of adaptive radiation using model microbial systems. Am. Nat. 156: S35–S44. [DOI] [PubMed] [Google Scholar]
  33. Vieira, C., E. G. Pasyukova, Z. B. Zeng, J. B. Hackett, R. F. Lyman et al., 2000. Genotype-environment interaction for quantitative trait loci affecting life span in Drosophila melanogaster. Genetics 154: 213–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Watterson, G. A., 1977. Heterosis or neutrality. Genetics 85: 789–814. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Watterson, G. A., 1978. Homozygosity test of neutrality. Genetics 88: 405–417. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Weinig, C., and J. Schmitt, 2004. Environmental effects on the expression of quantitative trait loci and implications for phenotypic evolution. Bioscience 54: 627–635. [Google Scholar]

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES