Increasing the Efficiency of Variance Component Quantitative Trait Loci Analysis by Using Reduced-Rank Identity-by-Descent Matrices

Abstract

Recent technological development in genetics has made large-scale marker genotyping fast and practicable, facilitating studies for detection of QTL in large general pedigrees. We developed a method that speeds up restricted maximum-likelihood (REML) algorithms for QTL analysis by simplifying the inversion of the variance–covariance matrix of the trait vector. The method was tested in an experimental chicken pedigree including 767 phenotyped individuals and 14 genotyped markers on chicken chromosome 1. The computation time in a chromosome scan covering 475 cM was reduced by 43% when the analysis was based on linkage only and by 72% when linkage disequilibrium information was included. The relative advantage of using our method increases with pedigree size, marker density, and linkage disequilibrium, indicating even greater improvements in the future.

THE use of variance component models is rapidly increasing in the field of QTL analysis (Lynch and Walsh 1998). As the cost for genotyping decreases, the sizes of the analyzed pedigrees are likely to increase, making full genome scans computationally slow or even infeasible. However, current algorithms commonly used for variance component estimation were not specifically developed for QTL analysis and there is a need to reevaluate the computational efficiency and robustness of these algorithms.

Variance component estimation has been included in general statistical software, such as Proc Mixed in SAS (Littell et al. 1996), where an arbitrary covariance structure of the random effect can be given by the user. These programs have in common that they use iterative procedures, Fisher's scoring or Newton–Raphson, to maximize the likelihood or the restricted likelihood (Pawitan 2001). More specific programs for applications in animal breeding have also been developed over the last two decades such as ASReml, DMU, and VCE (see Druet and Ducrocq 2006 and references therein). These programs use a mixture of Fisher's scoring and Newton–Raphson to maximize the restricted likelihood, called the “average information restricted maximum-likelihood (AI-REML) algorithm.” The most computationally demanding part of AI-REML is the inversion of the variance–covariance matrix (V) of the response vector (y). This inversion has to be performed on each iteration. We study a model with a random QTL effect and a residual effect, with variance–covariance matrix of the form 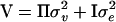, where is the symmetric identity-by-descent (IBD) matrix, 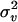is the QTL variance, I is the identity matrix, and 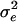is the residual variance. If 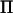is positive definite, then the inversion of V can be simplified by inverting V in parts. This has been implemented in the software package ASReml by setting up the mixed-model equations (MME) (Gilmour et al. 1995; Johnson and Thompson 1995; Jensen et al. 1997).

The AI-REML algorithm can be implemented by combining the MME with sparse matrix techniques (as done in ASReml), which gives fast solutions when the covariance structure of the random effect is sparse and positive definite. In traditional animal breeding applications, the covariance structure is given by the average relationship between individuals (Lynch and Walsh 1998). This covariance structure is usually sparse and always positive definite. The IBD matrix is not necessarily sparse or positive definite, however, and the advantage of using sparse matrix techniques together with inversion of V by means of MME in AI-REML may be questioned. Lee and van der Werf (2006) found that the AI-REML algorithm could be faster and more robust in QTL analysis if direct inversion of V is used, especially in linkage-disequilibrium linkage (LDL) mapping (Meuwissen and Goddard 2000) since the IBD matrices used in LDL are usually dense and positive semidefinite. The reason for this is that a covariance structure is added to the base generation alleles (Meuwissen and Goddard 2000; Hernandez-Sanchez et al. 2006), which increases the number of nonzero elements in .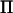

The rank of 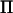at a marker depends on the size of the base generation and how polymorphic the marker is (Rönnegård and Carlborg 2007). In a QTL linkage analysis, the rank of 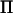is twice the size of the base generation when the marker is fully informative (i.e., all marker alleles are unique) and the rank does not depend on the total pedigree size, whereas the number of rows (and columns) in 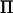equals the total number of individuals in the pedigree, n. Hence, at marker locations, 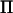will have many eigenvalues equal to zero, and the number of zero-valued eigenvalues increases with the difference between the total number of individuals and the number of base individuals. In nonmarker locations, the number of eigenvalues in 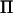that approaches zero, when the distance to the marker decreases, is equal to twice the difference between the total number of individuals and the number of base individuals. Thus, for a dense marker map most eigenvalues in all IBD matrices will be either equal to zero (in marker positions) or close to zero (in nonmarker positions).

In this article we develop a fast genome scan method for variance component QTL analysis using AI-REML. The method utilizes an efficient inversion of V that takes advantage of the fact that 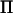has many eigenvalues close to zero.

An efficient inversion of V using the Sherman–Morrison–Woodbury formula:

A simple mixed linear model for QTL detection is given by 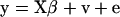, where X and 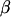are the design matrix and parameter vector, respectively, for the fixed effects, v is the vector of QTL genotype effects (length n), v ∼ MVN (0, Π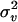), and e ∼ MVN(0, I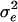). Thus the variance–covariance matrix of y is V = 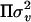+ 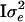. Now let the spectral decomposition of Π be 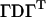, where 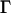is the matrix of eigenvectors and D is the diagonal eigenvalue matrix (superscript T denotes matrix transpose). Using this decomposition, we approximate Π. Let 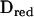be a submatrix of D, where the eigenvalues larger than a threshold value τ are included, and 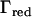be the matrix of eigenvectors corresponding to these eigenvalues. Then an approximate IBD matrix with reduced rank is given by 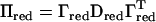. In our applications τ was set equal to λ_i for which the cumulative sum of λ₁ to λ_i divided by the total sum of eigenvalues was 0.8, where λ₁, λ₂, … , λ_n are the ordered eigenvalues from largest to smallest. Using the Sherman–Morrison–Woodbury formula (Golub and van Loan 1996) we then get an efficient equation for inverting V: .

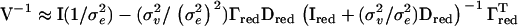Here I_red is the identity matrix of the same size as 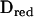. This approximation dramatically decreases the number of mathematical operations needed to invert V. Let k be the rank of 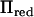; then the number of floating point arithmetic operations (flops) in calculating the approximated inverse is n²k + 3nk², whereas the number of flops to invert V directly is n³/2. The spectral decomposition of 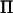requires on the order of n³ flops, but this computation is performed only once in each REML estimation, whereas the inversion of V is performed in each iteration. As an example suppose n = 500, k = 20, and that AI-REML converges in 10 iterations; then the total number of flops for inverting V directly is 6.25 × 10⁸ with the direct method and 1.81 × 10⁸ with the reduced method, giving a 3.5-fold speedup.

Two important questions are then: How are the maximum log-likelihood values and the variance component estimates affected by the approximation? How much is the computational time reduced in a genome scan in practice? To answer these questions we tested the method on chicken chromosome 1 (475 cM) in a Jungle Fowl–White Leghorn F₂ cross, where the measured trait was body weight at 200 days of age. Kerje et al. (2003) reported two QTL for this trait on chromosome 1 at 68 and 420 cM. There were 4 F₀, 41 F₁, and 767 F₂ individuals in the pedigree. In our analysis, population mean and sex were included as fixed effects. There were 14 genotyped markers located at 0, 27.7, 35.3, 91.3, 124.3, 154.2, 189.7, 209.3, 233.0, 258.8, 337.4, 407.9, 425.9, and 475.4 cM. The IBD matrices were estimated at every 1 cM using the Markov chain Monte Carlo-based program package Loki (Heath 1997; Heath et al. 1997). The estimated IBD matrices were dense with >80% nonzero elements (elements were defined as nonzero for values ≥10⁻³). The likelihood-ratio (LR) statistic in AI-REML was calculated as twice the difference between the maximized log(L) and log(L) with 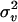= 0. The convergence criterion used was change in log-likelihood <10⁻⁴, with 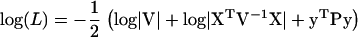and 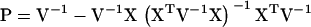, and the starting value of 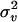was 0.01 times the residual variance. The computer code to calculate 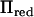and the AI-REML algorithm was implemented in R (R Development Core Team 2004).

Accuracy and efficiency of the method:

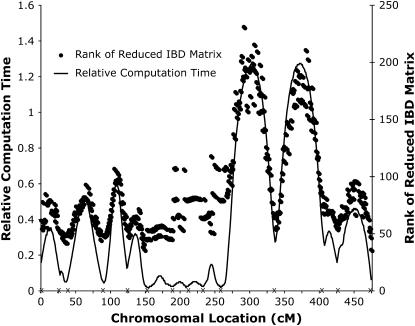
At individual chromosomal locations, our method was up to five times faster than the direct inversion of V and taken over the whole chromosome it reduced the computation time by 43% (Figure 1). It was faster at all tested locations, except at positions >30 cM from the closest marker. The rank of 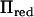was smallest close to marker positions, where also the greatest speedups were achieved.

Figure 1.—

The rank of 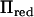(right axis) and the relative computation time (left axis) along chicken chromosome 1. The relative computation time is the ratio of the total number of flops used in AI-REML for the inversion of V by the reduced method and direct inversion. This is [n³ + N_red(n²k +3nk²)]/[N_fulln³/2], where N_red and N_full are the number of iterations until convergence using Π_red and Π, respectively, n is the number of observations, and k is the rank of Π_red. A marker position is given by an “X” along the x-axis.

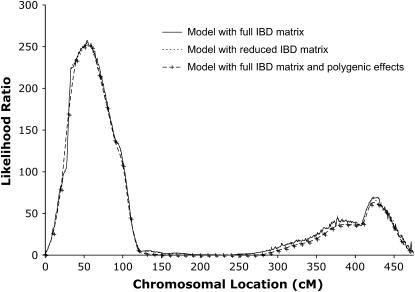
The correlation between the LR values obtained with 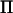and 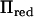was 0.9999. Both methods resulted in maximum LR values at 54 and 426 cM (Figure 2). The relative difference in LR between the two methods was 0.5 and 4.3% at these locations, respectively. In our experience, the shape of the likelihood-ratio curve is not substantially affected by the inclusion of polygenic effects in the variance component QTL model, which was confirmed in our analysis (Figure 2). Both the full model including polygenic effects and our method identified the same two peaks, with a relative difference in LR of 2.7% at 54 cM and 8.1% at 426 cM.

Figure 2.—

QTL likelihood-ratio curves for body weight at 200 days of age along chicken chromosome 1 for three different variance component models.

In LDL mapping, a correlation structure is added to the base generation individuals in a pedigree with a varying degree of positive correlation between alleles. In a second analysis of our chicken data, we computed 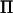assuming fixation within lines. This is an extreme case of LDL mapping, where the base generation alleles are assumed fully correlated within lines. Assuming fixation of QTL alleles within lines is equivalent to fitting a line effect, and for a fully informative marker the rank of 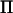will therefore be 2. The rank of 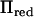was consequently reduced further in this example, where the rank was 2 in all positions except at positions >30 cM from the closest marker. In this case our method was up to five times faster than direct inversion in specific positions and reduced the computations over the whole chromosome by 72%. Both models with eithe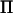r or 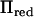gave similar LR values (correlation 0.9999) with QTL at 60 and 430 cM. The relative differences in LR were 1.2 and 0.7%, respectively, for the two QTL.

Conclusions:

Our efficient AI-REML method approximates the likelihood-ratio statistic very well. It is, therefore, a useful method to locate the regions in the genome with the strongest support for a QTL. The efficiency of the method increases when a covariance structure is added to the base generation alleles, which is the case in LDL mapping. This increase in efficacy was illustrated with an extreme covariance structure where the QTL alleles were assumed fixed within lines.

For accurate testing and estimation of the variance components at the QTL identified using this fast method, we suggest that a full model including polygenic effects should be used. Our results indicate that inclusion of polygenic effects is not important in the variance component model when the aim is to detect the location of potential QTL. Other studies have shown that the risk of getting false positives increases in QTL studies if polygenic effects are not included (Kennedy et al. 1992), but this will not be a problem in our suggested application.

Meuwissen and Goddard (2000) did not include polygenic effects in their presentation of their LDL-mapping model, but accounted for different kinds of population substructures by modeling a general residual variance–covariance matrix R, where V = 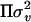+ 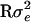. This is also possible in our model, and V may then be inverted using the more general version of the Sherman–Morrison–Woodbury formula (Golub and van Loan 1996) 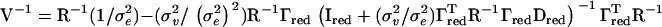. The inversion of R has to be performed only once for the whole genome scan, since it does not change between positions, and the loss in computation time merely depends on how sparse R⁻¹ is.

We have not developed the method for several QTL (see Lee and van der Werf 2006). In principle, the method should be extendable to several QTL, either by developing a more general version of the Sherman–Morrison–Woodbury formula or by developing an orthogonal model where the variance components can be tested one at a time (following Thomsen 1975).

In our analysis we used Loki to estimate . If, however, an approximate decomposition of could be rapidly estimated directly from the marker data, then the spectral decomposition would be redundant and the speed of AI-REML would increase significantly. This decomposition can be made in LDL mapping if the number of possible haplotypes is limited, as shown by Meuwissen and Goddard (2000). Furthermore, Rönnegård and Carlborg (2007) have recently developed a general method for estimating a decomposition of 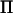directly from marker information. Their method is based on single-marker information, but is in principle extendable to a multiple-marker framework. In our analysis of chicken chromosome 1 the number of flops to invert V would have been decreased by 98% if a decomposition of 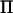had been estimated directly. In Table 1, we have also compared the potential of our method when applied to an existing commercial chicken pedigree (Rowe et al. 2006) and an outbred pig cross (M. S. Lund, personal communication; Danish Institute of Agricultural Sciences).

TABLE 1.

Pedigree structure of a commercial chicken pedigree and an outbred pig cross used for QTL mapping

	Pedigree structure		Computational reduction
	Size of base	Total size	% highly informative markersa	% fully informative markersb
Commercial chicken pedigreec	146	2.708	43	71
Duroc–Landrace/Yorkshire crossd	710	11.000	36	64

The reduction in the number of flops to invert V with our method compared to direct inversion is given for two cases: (1) highly informative and moderately dense markers (<10 cM apart) and (2) a fully informative marker at each tested position.

^aRank of 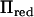is twice the size of the base generation, the number of AI-REML iterations is assumed to be seven, and spectral decomposition of 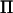is included in calculations.

^bRank of 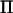is twice the size of the base generation, and decomposition is estimated directly from the data.

^cPedigree structure is from Rowe et al. (2006).

^dPedigree structure is from M. S. Lund (personal communication; Danish Institute of Agricultural Sciences).

In conclusion, the efficiency of our method will increase when the ratio between the total pedigree size and base generation size increases, the density and informativeness of markers increases, and the correlation between base generation alleles increases. Hence, the relative efficacy of the method can be expected to increase in the future as deeper pedigrees and more markers become available.