A server and database for dipole moments of proteins

Abstract

An Internet server at http://bip.weizmann.ac.il/dipol calculates the net charge, dipole moment and mean radius of any 3D protein structure or its constituent peptide chains, and displays the dipole vector superimposed on a ribbon backbone of the protein. The server can also display the angle between the dipole and a selected list of amino acid residues in the protein. When the net charges and dipole moments of ∼12 000 non-homologous PDB biological units (PISCES set), and their unique chains of length 50 residues or longer, were examined, the great majority of both charges and dipoles fell into a very narrow range of values, with long extended tails containing a few extreme outliers. In general, there is no obvious relation between a protein's charge or dipole moment and its structure or function, so that its electrostatic properties are highly specific to the particular protein, except that the majority of chains with very large positive charges or dipoles bind to ribosomes or interact with nucleic acids.

INTRODUCTION

Due to the presence of a significant number of charged residues at neutral pH, proteins are macro-zwitterions whose electrostatic properties are important for their stability and function. A major breakthrough that permitted detailed theoretical and computational examination of the electrostatic properties of proteins was a rapid numerical implementation of the Poisson–Boltzmann equation of electrostatics (PBE) (1), coupled with a computer algorithm to color the solvent-accessible molecular surface or isopotential surfaces by electrostatic potential, as implemented by computer algorithms such as Delphi and GRASP (2). Many proteins are found to have significant surface regions or patches of positive or negative potential that might be important for function. Such regions are indicative of an excess of net positive or negative charge and/or a significant imbalance in the spatial distribution of the charges or, in other words, of a large dipole moment. Many examples of proteins with large net charges or dipole moments have been reported. Ripoll et al. (3) reported a large dipole moment oriented approximately along the deep, narrow, aromatic-lined gorge pointing toward the active site of the enzyme acetylcholinesterase (AChE), corresponding to a region of negative potential around the gorge entrance that is thought to help attract the positively charged substrate, acetylcholine, towards the gorge entrance. This large electrostatic dipole was subsequently confirmed experimentally (4). Structurally related proteins such as cholinesterase-like adhesion molecules (CLAMS) are predicted to have similar electronegative patches (5,6) that could be important in recognition of their oppositely charged partners during nervous system development. Moreover, for the complexes of the potent polypeptide inhibitor, fasciculin II, a neurotoxin isolated from the venom of the green mamba (snake), with both Torpedo californica AChE (7) and mammalian AChEs (8), the dipole moments of the inhibitor and the enzyme are aligned in the same direction. Burley (9) and Gajiwala et al. (10), among many others, have reported large regions of positive potential in the binding regions of proteins that interact with DNA and RNA. Furthermore, many of the proteins of both the ribosome and the nucleosome display a high positive charge. Radditz et al. (11) reported a dipole moment of ∼300–400 D in a thioredoxin from Escherichia Coli with a mass of only 12 000 kDa.

Examination of electrostatic properties is now routinely performed for most new protein structures that are solved. Although rigorous calculations using the PBE are practical, they remain time-consuming both to set up and to implement. Recently, an improved electrostatics algorithm, Adaptive Poisson–Boltzmann Solver (APBS), became available (12) at website http://apbs.sourceforge.net, and a web server is being developed to implement it. Nevertheless, the calculation remains slow and complex. In contrast, calculation of the net charge and dipole moment are much simpler, and can be used to screen proteins rapidly for the presence of interesting electrostatic properties. Furthermore, experimental measurement of protein dipole moments demands sophisticated equipment which is not widely available (4,13,14). Thus, availability of a reliable method for their calculation is of importance. Accordingly, we have constructed a web tool to perform such calculations. In order to address the question of correlation of a protein's dipole moment with its overall shape, this tool also incorporates calculation of a protein's mass moments and mean radius (the geometric average of its three mass moments). The tool developed, which has been named Protein Dipole Moments Server (PDMS), is available at http://bip.weizmann.ac.il/dipol.

METHODS

In order to expedite rapid calculations, which would facilitate ready comparison of large numbers of proteins, we decided to focus on calculating the dipole moments of only the peptide portions of PDB entries. The wide variety of non-peptidyl moieties complexed with the PDB proteins, including DNA, RNA, salts, cofactors, drugs and explicit solvent molecules, many of whose partial atomic charges are not easily amenable to automatic assignment, were ignored, even though they may be expected to contribute significantly to the overall dipole moment of the entire complex.

The major components of protein dipoles are the net charges on individual charged residues, which depend on the location of the given residues relative to the center of the protein and the cooperatively aligned backbone C=O … N-H dipoles of their helices, which are residue-independent.

Owing to the complexities involved in attaching hydrogen atoms, which are absent in most PDB entries, and in particular, the great uncertainty involved in placing those bonded to oxygen and nitrogen atoms, that might contribute to dipole moments, we considered whether it would be possible to calculate reasonably accurate dipole moments without including hydrogens explicitly. To this end, a modified set of Parse partial atomic charges (15), optimized for electrostastic calculations on small molecules, was developed to allow for an implicit treatment of the hydrogens, as follows: The backbone C and O charges were approximately doubled to +/–1 to compensate for the lack of N–H dipoles that are required to reproduce the dipole moments of helices. Alkyl carbons and hydrogens already have zero charges, and those on aromatic rings are small and symmetric, and thus should not contribute to the overall dipole. The charges on hydrogens bonded to side-chain oxygens and nitrogens were transferred to the adjacent (or nearest) carbon atoms. Trial calculations were performed for a number of proteins, for most of which experimentally measured dipole moments are available. As shown in Table 1, the differences between the dipoles calculated with and without hydrogens were <70 D, or 5–8%, within the range of discrepancy between the calculated and measured dipoles, and the calculated dipole vectors pointed in practically the same direction, as measured by the angle between them. Although in the case of 2hhb, the dipoles calculated with and without hydrogens appear to differ significantly, this protein's dipole is very small, so that when considered relative to the large dipoles of other proteins, this difference is, in fact, insignificant. Therefore, it was decided to calculate the dipole moments making use of the modified set of Parse partial charges referred to earlier, without addition of the hydrogen atoms.

Table 1.

Benchmark comparison of calculated dipole moments (Debye) with and without hydrogens, using Parse 3 charges

PDB_id or name	Including hydrogens	Without hydrogens	Anglea	Measured	Description
Snake AChE(22)	1647	1615	3	1000(4)	Snake AChE homology model
1p0i	1718	1636	1		Human butyrylcholinesterase
Glutactin	105	108	8		Drosophila glutactin
5cha	522	494	6	540(14)	Bovine α-chymotrypsin
2gct	453	492	7	465(14)	Bovine γ-chymotrypsin
2hhb	101	48	30	45(13)	Human deoxy-hemoglobin
1hho	210	196	4	271(13)	Human oxy-hemoglobin

^aAngle in degrees between the calculated dipole vectors with and without hydrogens.

The calculation of charge and dipole moment proceeds as follows. Only those atoms comprising the 20 standard amino acid residues of the actual peptide chains are used, without hydrogens. Since most proteins have a net charge, and the calculated dipole moment depends on the placement of a charged entity within the coordinate system, the protein is first centered about the average coordinates of all its heavy atoms (C, N, O, S), d₀ = (Σr_i0)/N, as an approximation to its center of mass, where r_i0 = (x_i0, y_i0, z_i0) are the initial coordinates of atom i, and r_i = r_i0−d₀ is the corresponding centered coordinate. Then, assuming a pH value of 7, partial atomic charges q_i are assigned to all atoms, such that all Arg and Lys residues and the NH₂-terminal residue each have a total net charge of +1, all Glu and Asp residues, and the COOH-terminal residue have a net charge of –1, and all other residues have a zero net charge. If a residue sidechain is incomplete, and it is a charged residue, the entire residue charge is assigned to the last sidechain atom present; otherwise, the atomic charges of all incomplete sidechains are set to zero. Residues completely missing from the ATOM records are ignored.

The next step is the actual calculation of the electrostatic and geometric properties. The net charge on the protein is simply the sum of all the partial atomic charges. The dipole moment, in Debyes, is calculated as the magnitude of the dipole vector D = 4.803*Σr_i q_i, summing over all atoms ‘i ’, where 4.803 converts from Angstrom-electron-charge units to Debyes. The mass moment vector of the protein is calculated as R_x=Σx_i², R_y=Σy_i², and R_z=Σz_i², and the associated mean radius R_M = ((R_x + R_y + R_z)/3)^1/2 is a measure of the overall protein size. As a check on the net charge calculation, the numbers of positive (Lys and Arg) and negative (Glu and Asp) residues are also determined. All summations are over all C, N, O and S peptide atoms in the protein. These quantities can be determined either independently for each peptide chain in the protein, or for all the peptide chains contained within the biological unit of the protein (taken as a single entity), which is that quaternary structure of the protein that is physiologically active, as defined on the PDB website (16).

On the web server, the user can either request the biological unit of any protein in the PDB(16), or its constituent chains, by specifying its ID-code (an obsolete PDB ID is replaced automatically by the updated entry), or read in the coordinates of any protein in PDB format from an external file. This allows not only examination of intact structures, whether or not they are deposited in the PDB, but also of subsets or domains of proteins or novel complexes thereof. A ribbon diagram of the protein with its dipole and mass moment vectors are displayed in a Jmol applet picture (http://jmol.sourceforge.net), thus allowing the dipole moment to be visualized in relation to the overall protein structure. The dipole vector itself is drawn in black with a dark blue arrowhead, while the mass moment vector has no arrowhead. An option is provided to display the angles between the dipole vector and a list of selected residues’ Cβ atoms (Cα for Gly), which might be important binding or catalytic sites, to help estimate whether electrostatic properties play an important role in influencing the binding or catalytic properties of that site. These residues are displayed as green, space-filling structures in the Jmol picture.

In order to identify any possible global correlations between dipole moments and other calculated properties of the proteins, databases containing the geometric and electrostatic calculated properties for a representative, non-homologous set of PDB entries were prepared, for biological units and for their unique, constitutive peptide chains, using the PISCES list of 11 981 non-homologous proteins (comprising 14 053 peptide chains) at the 90% identity level (17), as of December 17, 2006, obtained via the OCA server at http://bioportal.weizmann.ac.il/oca-bin/ocamain. All proteins and chains with <50 residues, or with only Cα atoms, were discarded. Duplicate chains were eliminated from each entry in the database compilation for unique chains, on the basis of their SEQRES records. Two chains were considered to be identical if their sequence identities were >95%. Averages and standard deviations of all the calculated quantities were determined for both the polypeptide chain and biological unit databases, are shown in Tables 2 and 3, and are used to provide a frame of reference for the values calculated for individual proteins by the server. Thus, in addition to the actual values, the server displays the corresponding numbers of standard deviation units (Z-scores) from the database averages.

Table 2.

Database statistics for 14,053 unique chains

	Minimum	Maximum	Mean	Median	SD	Skewnessa	Kurtosisb
Number of atoms	242	12773	1761	1491	1171	1.94	6.59
Number of residues	50	1610	224	188	149	1.92	6.51
Mean radius (Å)	59	1601	261	228	149	1.92	6.78
Net charge	–76	38	–3.19	–3	7.68	–0.83	4.38
Dipole moment (Debye)	5	5563	543	436	420	3.09	18.29
Charge per atom	–0.038	0.036	–0.001	–0.002	0.006	0.55	4.46
Dipole per atom	0.034	4.53	0.370	0.305	0.285	3.46	24,66

^aThe symmetry of the distribution. The skewness of a normal Gaussian distribution is 0.

^bThe sharpness or flatness of the distribution. The kurtosis of a normal Gaussian distribution is 0.

Table 3.

Database statistics for 11,981 biological unit proteins

	Minimum	Maximum	Mean	Median	SD	Skewnessa	Kurtosisb
Number of atoms	321	62495	3004	2994	3431	5.19	48.67
Number of residues	50	8290	383	265	441	5.27	50.71
Mean radius (Å)	59	5946	400	298	380	4.37	33.88
Net charge	–246	446	–5.68	–4	17.27	4.03	141.42
Dipole moment (Debye)	4	34460	639	452	977	14.36	333.26
Charge per atom	–0.038	0.031	–0.002	–0.002	0.005	0.28	3.90
Dipole per atom	0.000	4.486	0.300	0.246	0.248	2.82	20.16

^aThe symmetry of the distribution. The skewness of a normal Gaussian distribution is 0.

^bThe sharpness or flatness of the distribution. The kurtosis of a normal Gaussian distribution is 0.

It should be noted that the server probably overestimates the actual net charge and dipole moment in highly charged regions of the protein, since the net electrostatic potential may be expected to modify the pK_a values of the residues in such regions, which will consequently be <100% ionized, as assumed by the server. Estimation of these modified pK_a values and correction of the net charge values accordingly would involve a complex calculation. It was felt that, even if this effect were ignored, meaningful relative dipole data could still be obtained for comparison purposes, provided that the dipole moment is determined in the same way for all proteins. Indeed, the same assumption is made for the widely used programs Delphi and APBS, which assign the charges by treating the acidic and basic residues, and chain termini in their fully ionized state. For proteins found to display potentially interesting features by use of the PDMS, it may be worthwhile to use Delphi (2) or APBS (12) to generate a detailed potential grid, and subsequently to generate representations showing isopotential surfaces or molecular surfaces colored by potential.

RESULTS AND DISCUSSION

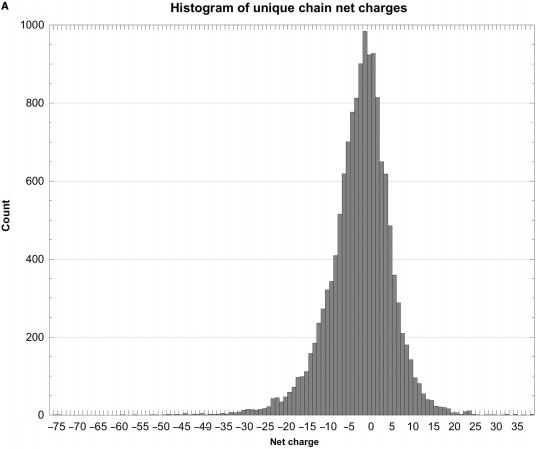
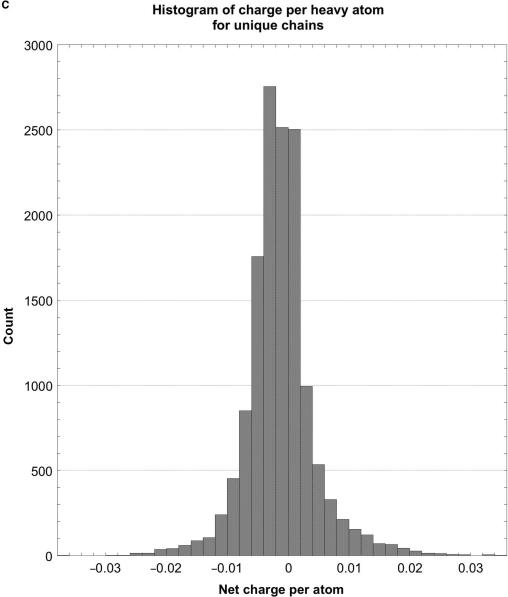
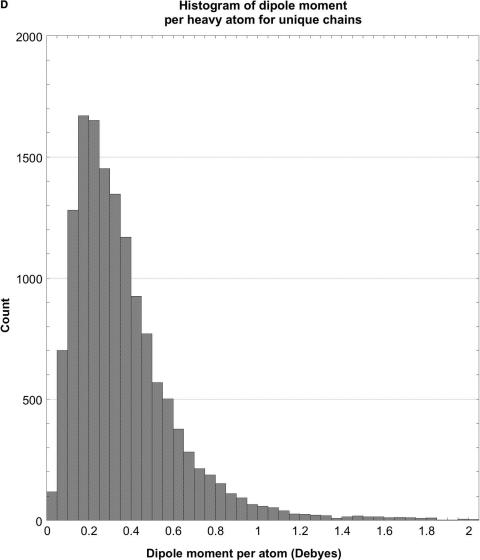
As shown in Tables 2 and 3 and Figure 1, the raw distributions of net charges and dipole moments from the databases and also the corresponding normalized distributions (net charge or dipole per atom), while continuous, are highly skewed and non-Gaussian. They consist of a single sharp peak near the median, and one (dipoles) or two (charges) extended tails containing very few proteins. For example, about 43% of the peptide chain charges lie in the interval –6 to 0 (6% of the range of charges), and 44% of their dipoles are in the interval 250–550 D (about 6% of the range of dipoles). Further evidence of this asymmetry comes from the distributions’ median and peak values (highest counts) being somewhat lower than the mean or average values. The standard deviations are large compared with the mean values, the positive skewness values show that the distributions are fairly asymmetric, and the kurtosis values indicate that the peaks are much sharper than would be expected for a normal Gaussian distribution. The normalized distributions are even more skewed and sharp than the raw ones. Hence, the number of standard deviation units, viz. the Z-score, that a given protein's dipole or charge is above or below the database average provides only a rough estimate of how unusual that protein may be.

Figure 1.

Histograms of net charges and dipole moments for unique protein chains in the PDB. (A) Histogram of the distribution of net charges for 14 053 unique chains, prepared using KalaidaGraph (23). The distribution for 11 981 biological units is very similar. (B) Histogram of the distribution of dipole moments for 14 053 unique chains. For clarity, the histogram had to be truncated at 4000 D, even though the distribution continues to almost 5600 D. Only 14 chains have dipoles larger than 4000 D. The distribution for 11 981 biological units is very similar. (C) Histogram of the distribution of the net charge per atom for unique chains. The distribution for biological units is very similar. (D) Histogram of the distribution of net dipole moment per atom for unique chains. For clarity, the histogram had to be truncated at 2 D, even though the distribution continues almost up to 25 D. The distribution for biological units is very similar.

Analysis of the biological unit distributions is more complicated than for the individual chains. Firstly, the values of raw, un-normalized charges and dipoles are strongly dependent on the precise definition of how many identical chains each biological unit comprises; in some cases, this definition may be uncertain. Secondly, particularly in the past year, a number of extremely large protein complexes, mainly ribosomal subunits and photosystems, have been added to the PDB. Some of them have extremely large calculated net charges and dipoles that tend to distort the database averages and skewness. However, when normalized, the charges and dipoles for these entries are much less extreme; as a consequence, the normalized distributions are much less distorted. For example, large ribosomal subunit entry 1sli has the largest charge, –446, and entry 1jj2 has the largest dipole, 34 660 D. But when normalized, these values become 1.2 and 0.014, respectively, both of which are far from the largest values in the normalized distributions. If these few outliers were to be deleted, the raw biological unit distributions would be very similar to those for the individual chains.

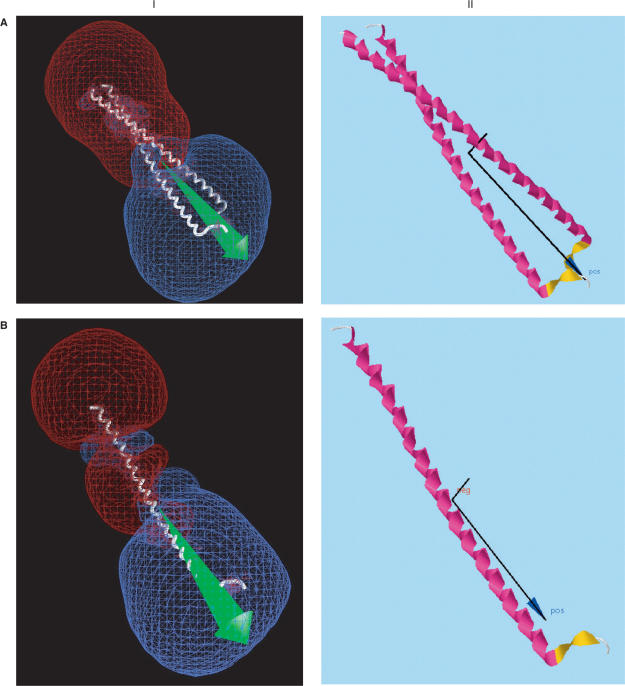
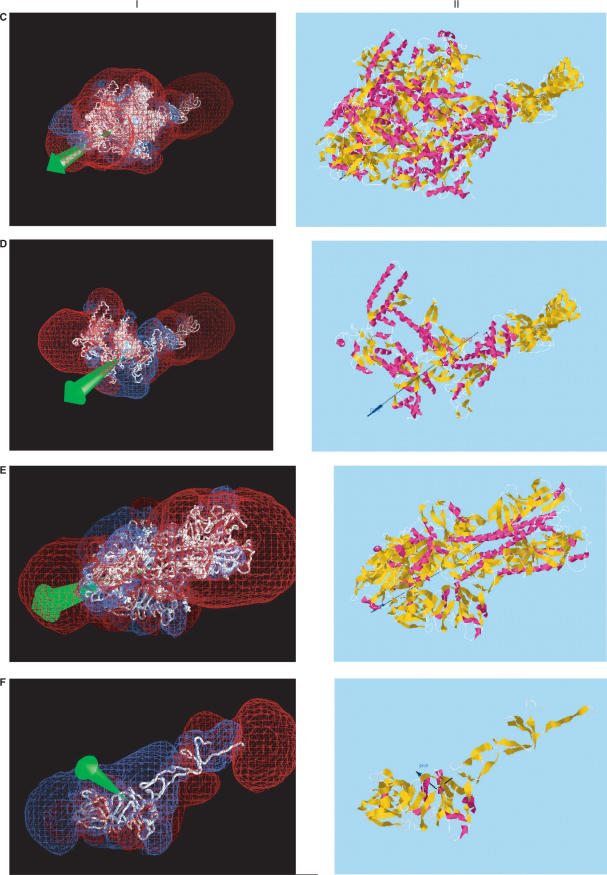
Figure 2 shows a few representative proteins with fairly large dipole moments that may be important for function. Alongside the dipole drawings from the server, drawn by computer application Jmol (http://jmol.sourceforge.net), are corresponding dipole (green) and +/–12 kT/e isopotential surface drawings (blue and red) made by computer application GRASP (2), to provide validation for the accuracy of the server. While the same orientations and partial atomic charges were used without hydrogens, GRASP centers the structures by center of net charge rather than by center of mass, so that the dipole moments are slightly different. Nevertheless, the two methods give similar results in most cases. Furthermore, these figures show that the dipole server provides much of the same information as supplied by GRASP, while requiring much less work on the part of the user, by providing a rough indication of the locations of major positively and negatively charged regions of the protein that might be important for their function. As such, it provides an additional validation of the accuracy of the server's calculations.

Figure 2.

Comparison of dipole moments calculated using (I) GRASP (2), displaying the dipole vector in green and –12 kT/e (red) and +12 kT/e (blue) isopotential surfaces; (II) Protein Dipole Moment Server (PDMS), showing the dipole moment vector in black, with a dark blue arrowhead, and the mass moment vector without an arrowhead. The same molecular orientations and modified Parse 3 partial atom charges were used, without hydrogens. (A) 1gd2: BZIP transcription factor PAP1 bound to DNA; 2 chains, 1051 atoms, 129 residues, mean radius 300 Å, charge +10, dipole moments 3328 D (I, GRASP) and 3032 (II, PDMS), with an angle of 2° between their vectors. This pattern is typical of several DNA-binding proteins, including 2dgc, yeast GCN4 Leu zipper, and 1dh3, mouse CREB BZIP-CRE complex, all of which are highly elongated and project a large region of negative potential into the region binding the positively charged DNA. (B) 1gd2, Chain E: 530 atoms, 65 residues, mean radius 212 Å, charge +4, dipoles 1747 D (I, GRASP) and 1591 D (II, PDMS) D, making an angle of 1°. (C) 1ynj: TAQ RNA polymerase. 6 chains, 24 309 atoms, 2821 residues, mean radius 2821 Å, charge –52, dipoles 6532 D (I, GRASP) and 6541 D (II, PDMS), making an angle of 3°. The putative DNA binding region is near the lower left. (D) 1ynj Chain D. 9602 atoms, 1238 residues, mean radius 1924 Å, charge –13, dipoles 8311 D (I, GRASP) and 9414 D (II, PDMS), making an angle of 6°. (E) 1flc: Hemagglutinin-esterase fusion glycoprotein of influenza virus. 6 chains, 13 700 atoms, 1767 residues, mean radius 1718 Å, charge –21, dipoles 7725 D (I, GRASP) and 7971 D (II, PDMS), making an angle of 1°. The acetylsialic acid binding domain is at the lower left. (F) 1flc Chain A. 3339 atoms, 427 residues, mean radius 598 Å, charge +5, dipoles 411 D (I, GRASP) and 411 D (II, PDMS), making an angle of 1°.

No obvious correlations were observed between net charges and dipole moments, or of either of them with the number of atoms, the number of residues or the mean radius; nor was there any obvious relationship between charge or dipole and function. Even among proteins with very large positive or negative charges or dipoles, there was, in most cases, no clear pattern. The two exceptions relate to chains with very large charges or dipoles, where 24 of the 35 chains (69%) with charges >+20 are either ribosomal proteins or proteins binding to ribosomes, and 17 of 39 chains (43%) with dipoles >3000 D interact with nucleotides or nucleic acids. Among the normalized distributions, 32 of 40 chains (80%) with a charge per atom >0.023 are either ribosomal or bind to ribosomes, and 25 of 42 chains (59%) with dipole per atom values >2.0 D interact with nucleic acids. In this context, Seligmann (18) suggests that dipole moments might explain substitution frequencies of nucleotides of genes coding for the corresponding proteins. Furthermore, it has been suggested that the dipole moments of helices may line up approximately along the gradients of the local electric fields (19). In contrast, when examining the detailed electrostatic potentials of conserved, homologous domains or regions of proteins with similar functions, similar electrostatic patterns or motifs are frequently observed (5,20,21).

In conclusion, it appears that any effect that the net charge or the large dipole moment of a protein may have on its binding properties and function is probably quite specific to that particular protein. Thus, as shown earlier and in Figure 2, the presence of a large net charge or dipole on a given protein suggests that it may play a highly specific role for that protein, such as directing a charged substrate or ligand toward the correct binding site or functional locus. Sometimes, a whole series of related proteins may have a similar dipole, an example being the cholinesterases and CLAMs, where the dipole may guide the substrate, acetylcholine, towards the active-site (3), and the charged motif associated with the dipole moment may be involved in specific interactions with other proteins, in the case of the CLAMs (5,6). In other cases, related proteins with similar functions may have quite different charges or dipoles. For example, influenza C virus hemagglutinin has a net charge of –21, and a dipole of 7271 D, while its swine H9 homolog has a charge of only –4 and a dipole moment of 954 D. Indeed, various factors limit the applicable range of global charge and dipolar interactions. On the one hand, the local electrostatic potential and specific interactions with nearby atoms and groups probably dominate the actual binding of other moieties to a protein's binding sites. On the other hand, over long distances, the reaction monopole and dipole fields induced by the protein charge and dipole moment in the aqueous medium substantially dampen the effect of the latter. Thus, global charges and dipole moments are most likely to be important when the interacting species approach each other close enough to be able to interact significantly, but are still some distance away from the actual binding sites, and thus help to direct them to those sites.