BioBayesNet: a web server for feature extraction and Bayesian network modeling of biological sequence data

Abstract

BioBayesNet is a new web application that allows the easy modeling and classification of biological data using Bayesian networks. To learn Bayesian networks the user can either upload a set of annotated FASTA sequences or a set of pre-computed feature vectors. In case of FASTA sequences, the server is able to generate a wide range of sequence and structural features from the sequences. These features are used to learn Bayesian networks. An automatic feature selection procedure assists in selecting discriminative features, providing an (locally) optimal set of features. The output includes several quality measures of the overall network and individual features as well as a graphical representation of the network structure, which allows to explore dependencies between features. Finally, the learned Bayesian network or another uploaded network can be used to classify new data. BioBayesNet facilitates the use of Bayesian networks in biological sequences analysis and is flexible to support modeling and classification applications in various scientific fields. The BioBayesNet server is available at http://biwww3.informatik.uni-freiburg.de:8080/BioBayesNet/.

INTRODUCTION

Researchers in many biological fields are often confronted with classification problems concerning biological sequences. For example, analyzing promoter sequences often requires the classification in transcription factor binding sites and background sequence parts (1,2). For a given set of exons or splice sites one might be interested in predicting which of these are alternatively spliced (3,4).

State-of-the-art machine-learning approaches extract various features from these sequences and perform classification on the feature vectors instead of the original sequences. Bayesian networks (BN) have recently attracted considerable attention for data modeling and classification (5,6) since they can cope with features of various value ranges and can learn dependencies between features. BNs have been successfully used for modeling of gene expression to derive genetic regulatory networks (7–9), for discovering pathogenic SNPs (10), for identifying missing enzymes in metabolic pathways (11), for protein folding (12), genetics and phylogeny analysis (5), as well as for predicting the effect of missense mutations (13). Another large and rather new application area of BNs are biological sequence data (2,14–17). Compared to profile hidden Markov models (HMMs) (18), which are often used to model conserved sequence families such as protein domains as in the PFAM database (19), they allow for more modeling flexibility w.r.t. the following points. First, they allow a more flexible scheme of dependencies between variables. In profile HMMs, the variables are sorted ‘chronologically’, and dependencies are restricted to the previous variable(s). In contrast, multiple dependencies are allowed in BNs, and there is no fixed ordering of the variables. This has been shown to be especially important to model regulatory like TF binding sites (14). Second, Bayesian network allow to integrate arbitrary features, which is not possible for HMMs. This has been shown to be important to integrate structural properties in the recognition of regulatory sequence (2,20). And third, the network structure (i.e. the set of all dependencies to be considered) must be given as an input to profile HMMs, whereas they are automatically learned in the BN approach.

To the best of our knowledge, there is no web-based application of BN modeling that is tailored to the analysis of biological sequences. To facilitate the use of BNs in this context, we have developed a new web application BioBayesNet. This web application allows to perform a wide spectrum of analysis from automatic feature generation and selection, to BN learning and application of the learned model to new input data and for probabilistic inference. Furthermore, BioBayesNet accepts any user-defined features as input, which extends its application range to various scientific areas.

METHODS

In this section, we briefly describe the methods applied by BioBayesNet in the order in which they occur in the processing chain. We first are concerned with features and their generation from uploaded input sequences. A feature is a measurable property of a single input data sample (e.g. an input sequence). Each feature has its own set of possible values which we denote as the feature range. For each feature, there is a well-defined feature value for each single input data sample. Given that a class label is assigned to each input sample, BioBayesNet tries to detect exactly that feature subset which is optimal in predicting the class label of so far unseen samples.

The typical usage of BioBayesNet assumes that the user defines a large bunch of features which might be useful for characterizing sequences of the different classes. For each sequence the value of every feature is calculated leading to a feature vector for each sequence. All further processing of the user input only requires the feature vectors, not the sequences.

The next step is the search of a subset among all defined features which is optimal with respect to its ability to discriminate between feature vectors of different classes. For this purpose we apply the sequential feature subset selection algorithm (SFFS) (21) which searches the space of feature subsets with respect to a special quality measure. Starting from an initially empty subset, this algorithm successively adds that feature which best improves the quality measure. After each insertion step the algorithm deletes previously added features as long as this does not worsen the quality measure. These deletion steps are necessary for avoiding the search path being trapped in local optima since the whole set of defined features can contain redundant features. For instance, a single feature which has been added in the last step could perform better together with another selected feature and make a formerly selected third feature dispensable. The algorithm stops if neither insertion of another feature nor the deletion of features can improve the quality measure. In order to calculate the quality of a particular feature subset we perform a 10-fold cross validation. Successively, 90% of the feature vectors are used to learn a Bayesian network classifier. For the remaining 10% of the samples the information loss

is calculated. This value expresses the strength of evidence given by a feature vector for predicting its own class. Finally, we obtain the quality measure value by summing up the information loss for the 10 runs of the cross validation.

The core of BioBayesNet is the probabilistic modeling of the resulting feature subset in Bayesian classifiers (BCs) (22) which is a special class of BNs. In general, a BN is a graphical representation of the joint probability distribution over a set of random variables. Each feature F is represented by a discrete random variable which defines a probability distribution over the feature range of F.

Formally, a BN is a pair B = (G, P). Its first component G is an annotated directed acyclic graph whose vertices correspond to random variables F₁, F₂, …,  F_d, and whose edges determine direct dependencies between connected variables. The second component P is a parameter set which quantifies the network. It contains probability parameters p_fi | π_fi = P_B (F_i = f_i | Π_fi = π _fi) for each possible value f_i of random variable F_i and each configuration Πf_i of the set of parent variables Πf_i. Thus, a BN B defines a unique joint probability distribution over all concerned random variables F = {F₁, F₂, …,  F_d} given by

Beside random variables for the features, a BC also contains an additional variable, the class variable C, which is parent of every feature variable. Obviously, the range of this class variable is the set of the different class labels c₁, …,  c_K. For a given feature vector f = f₁, …,  f_d (i.e. observations of values for all considered features), a BC classifies with respect to the conditional probabilities of having a sample of class c_k. Thus, class c′ is predicted so that

We further restrict the structure (i.e. the edges) of the BN in allowing at the most one parent feature variable for each feature. These specially structured networks are called tree-augmented networks (TAN) (21). The restriction is done due to the higher robustness of the learning procedure when confronted with small data sets and the existence of efficient structure learning algorithms for this subclass of BNs.

Learning a Bayesian classifier from a set of feature vectors comprises two steps: (i) the structure learning and (ii) the probability parameter estimation. For structure learning, we apply the algorithm Chow and Liu (23) which reduces that problem to the finding of a minimal spanning tree using the conditional mutual information content (MIC) between the distributions of two features as edge weights. To avoid the insertion of edges between features which only show weak correlation we slightly have modified this procedure by setting up a MIC threshold and only including edges with weights above this threshold. Once the structure of the network is determined, the (conditional) probability distributions over the feature values of each feature given the class label and optionally the value of the parent feature are estimated straightforward from count statistics derived from learning data. Since the usage of BNs requires that there do not occur zero probabilities, we use Dirichlet priors for smoothing the probability distributions.

The conditional probability in the previously illustrated BC-decision rule is an instance of what is called Bayesian inference, the querying of probabilities for some variable value in presence of observed values for other (not necessarily all) variables. It is one advantage of BNs that such queries (marginalizations) can be approximately calculated by efficient algorithms. In BioBayesNet, we apply the technique of variable elimination (24).

SERVER USAGE

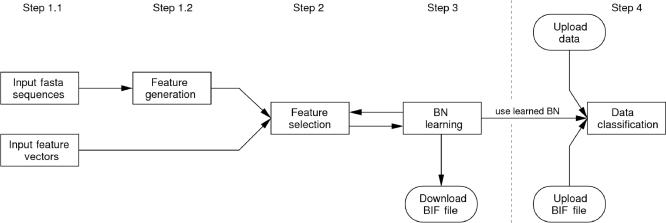
The general workflow of the server is illustrated in Figure 1. The first step comprises the input of data. There are two different kinds of input data.

Figure 1.

The general workflow of the BioBayesNet web-server.

The first possibility is to input sequences in FASTA format (Step 1.1). Each sequence must be associated to a class label. Optionally, one may specify a subsequence (for example, a protein binding site within an entire promoter sequence) which allows to use relative positions in the next step. To generate the features from these sequences, the user is redirected to Step 1.2, where the server allows the selection of a wide range of features. There are five main groups of features:

1. Nucleotides at particular positions: features of this group all have the same range, namely the four different nucleotides. A nucleotide feature for position i is the analogue of the ith column of a position weight matrix (PWM).

2. DNA structural parameters which express the sequence-dependent local variation of geometrical or physiochemical DNA properties at a subsequence. Examples are the average helical twist between two base pairs, the DNA bendability or the average melting temperature of the subsequence. A feature value for a subsequence is calculated as the mean of all dinucleotide steps in this subsequence. Values for dinucleotides were given in literature (25,26). We provide 38 different DNA properties that can be calculated from a user-defined subsequence.

3. RNA single-strandedness measures the probability for a given RNA subsequence to be completely single-stranded (i.e. not part of a secondary structure). For that we use RNAup from the Vienna RNA package (27).

4. Subsequence nucleotide contents: These features measure the fraction a subset of nucleotides in a user-defined subsequence. An example is the fraction of pyrimidines in the subsequence from position 10 to 20.

5. Consensus matches: features of this group decide whether there is a match of a given subsequence to a given consensus sequence. These features can take values true or false.

Features of all groups can be restricted to particular subsequences or positions in the sequences. If a subsequence is specified the positions refer to a location relative to the subsequence. For example, position -5 refers to the 5 nucleotides upstream of the start of the specified subsequence.

Features of groups 2, 3 and 4 describe continuous properties of sequences. In order to derive a finite feature range, the continuous ranges are discretized using the entropy-based, supervized discretization algorithm by Fayyad and Irani (28). This procedure finds a partition of the continuous range which best separates the different classes.

The second possibility is to input user-given feature vectors for each data sample in C4.5 format (29). This allows full flexibility as the user can input any prior computed feature. For example, one might input pre-computed features about protein sequences and/or structures to analyze protein data. The user has to upload two files. The first file contains the class labels and feature names with possible feature values, whereas the second file contains the data samples (Table 1).

Table 1.

An example of user-given feature vectors describing potentially discriminative features of alternatively and constitutively spliced exons

File 1: Class labels and feature names	File 2: Data samples
alternative, constitutive.	3.4, 100, high, yes, alternative.
donor_splice_site_score: continuous.	−5.7, 67, medium, no, alternative.
exon_length: continuous.	7.4, 167, high, yes, alternative.
flanking_intron_conservation: high, medium, low.	13, 231, low, no, constitutive.
length_divisible_by_3: yes, no.	9.5, 189, medium, yes, constitutive.
	7.8, 345, low,no, constitutive.

The first line of the first file has to contain the class labels (alternative and constitutive). The next lines of this file specify feature names and their value ranges. Each line of the second file contains one data sample. The features are given in the order of the first file and the class label is given at the end of each line.

Learning BNs

After the data input, the user can select which features are used to learn the BN (Step 2). Apart from manual selection, this process is assisted by an automatic feature selection method (see ‘Methods’ section), which selects the most discriminative features from all generated or user-given features. This step also provides an overview of the value ranges and the empirical probability distribution.

The selected features are used in the next step (Step 3) to learn a Bayesian classifier with TAN structure. After learning, the BN classification quality is evaluated. This includes two quality measures (information loss function and the average posterior probability for the correct class) and the final classification of the input data. Furthermore, the power of the individual features is estimated by computing the loss of quality if this feature is omitted during learning. The server also produces a graphical representation of the network structure, which allows the exploration of learned dependencies between the features (Figure 2).

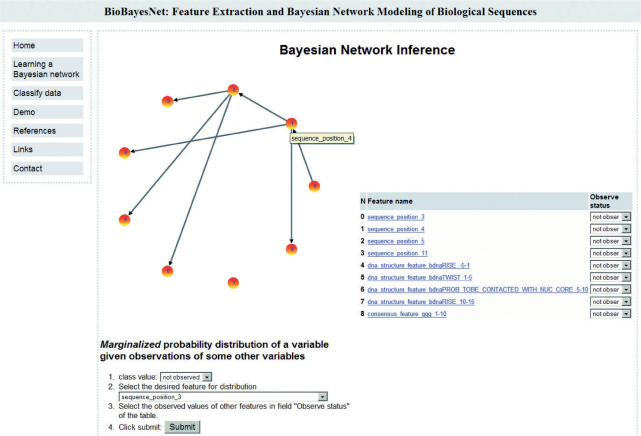
Figure 2.

Graphical overview of a BN and the dependencies between feature variables.

Besides this graphical overview, an interesting information is the distribution of a single feature, given particular values for some of the other features (variables). To this end, our tool allows to set some variables to particular values and query the a posteriori probability distribution of another variable given this setting. Furthermore, one can view the feature values for each data sample and how these samples were classified by the BN. The final BN can be downloaded as a file in the Bayesian Interchange Format (BIF) to use it for further data classification or to use it in Bayesian Network Software such as JavaBayes (30).

Data classification

In the next optional step (Step 4), the user can classify new input data using the learned BN. If a BN has been learned in advance, the server also allows classification after the upload of the BN in BIF format. In each case, the user has to upload new input data (either FASTA sequences or feature vectors).

SERVER IMPLEMENTATION

BioBayesNet is a Java-based three-tier web application. The user interacts with this application via HTML pages which are dynamically generated using Java server pages (JSP). Input given by the user is directed to Java Servlets which validate the input and generate objects which are conducted to the algorithmic layer of the application. The servlets further take the result objects of the algorithmic layer and redirect it to Java server pages which again produce HTML output for the user. As a Java-based web application, BioBayesNet runs in a TOMCAT environment. For handling the biological input of the user, we employ the BioJava API (31). The implementation of the BNs and related algorithms partly rely on third-party APIs, namely JavaBayes (30) and jBNC (32). BioBayesNet runs on a dedicated web compute server with two dual cores.

FUTURE DIRECTIONS

We have developed the web server BioBayesNet that enables an easy use of Bayesian Network models for the analysis of biological sequence data. We are working on extending the set of automatically generated features, especially to include protein-related features and a greater variety of RNA structural features.