KinasePhos 2.0: a web server for identifying protein kinase-specific phosphorylation sites based on sequences and coupling patterns

Abstract

Due to the importance of protein phosphorylation in cellular control, many researches are undertaken to predict the kinase-specific phosphorylation sites. Referred to our previous work, KinasePhos 1.0, incorporated profile hidden Markov model (HMM) with flanking residues of the kinase-specific phosphorylation sites. Herein, a new web server, KinasePhos 2.0, incorporates support vector machines (SVM) with the protein sequence profile and protein coupling pattern, which is a novel feature used for identifying phosphorylation sites. The coupling pattern [XdZ] denotes the amino acid coupling-pattern of amino acid types X and Z that are separated by d amino acids. The differences or quotients of coupling strength C_XdZ between the positive set of phosphorylation sites and the background set of whole protein sequences from Swiss-Prot are computed to determine the number of coupling patterns for training SVM models. After the evaluation based on k-fold cross-validation and Jackknife cross-validation, the average predictive accuracy of phosphorylated serine, threonine, tyrosine and histidine are 90, 93, 88 and 93%, respectively. KinasePhos 2.0 performs better than other tools previously developed. The proposed web server is freely available at http://KinasePhos2.mbc.nctu.edu.tw/.

INTRODUCTION

Protein phosphorylation, which is an important reversible mechanism in post-translational modifications, is involved in many essential cellular processes including cellular regulation, cellular signal pathways, metabolism, growth, differentiation and membrane transport (1). Phosphorylation of substrate sites at serine, threonine and tyrosine residues of eukaryotic proteins is performed by members of the protein kinase family. Additionally, phosphorylation on histidine plays an important role in signal transduction in prokaryotes known as two-component histidine kinase (2). It is estimated that one-third of proteins are phosphorylated and around half of kinome are disease- or cancer-related by chromosomal mapping (3). Experimental identifications of kinase-specific phosphorylation sites on substrates in vivo and in vitro are the foundation of understanding the mechanisms of phosphorylation dynamics and important for the biomedical drug design (4). However, these experiments are often time-consuming, labor-intensive and expensive. Therefore, in silico prediction of phosphorylation sites with high predictive performance could be a promising strategy to conduct preliminary analyses and could heavily reduce the number of potential targets that need further in vivo or in vitro confirmation.

With the recent exponential increase in protein phosphorylation sites identified by mass spectrometry (MS), many researches are undertaken to identify the kinase-specific phosphorylation sites. Our previous work, KinasePhos 1.0, incorporated profile hidden Markov model (HMM) for identifying kinase-specific phosphorylation sites, whose overall predictive accuracy is ∼87% (5,6). NetPhos (7) developed neural networks to predict phosphorylation sites on serine, threonine and tyrosine residues; however, it cannot provide information on the kinases involved and NetPhosK (8) applied an artificial neural network algorithm to predict 17 PK groups-specific phosphorylation sites. DISPHOS (9) took advantage of the position-specific amino acid frequencies and disorder information to improve the discrimination between phosphorylation sites and non-phosphorylation sites. Scansite 2.0 (10) identified short protein sequence motifs that are recognized by modular signaling domains, phosphorylated by protein serine/threonine, tyrosine kinases or mediate specific interactions with protein or phospholipid ligands. PredPh2ospho (11) predicts phosphorylation sites limited to four protein major kinase families, such as CDK, CK2, PKA and PKC, and four protein kinase groups (AGC, CAMK, CMGC and TK) with predictive accuracy 83–95 and 76–91%, respectively. GPS (12,13), is a group-based phosphorylation site predicting and scoring platform which clustered the 216 unique protein kinases in 71 groups. PPSP (4) developed an approach based on Bayesian decision theory for predicting the potential phosphorylation sites accurately for around 70 protein kinase groups.

This work proposes a kinase-specific phosphorylation site prediction server which incorporates support vector machines (SVM) with two features, i.e. protein sequence profiles surrounding the modified sites and coupling patterns surrounding the modified sites. The coupling pattern of proteins, which is first used for analyzing the protein thermostability (14). In this work, we incorporate the protein coupling pattern as a feature for training computer models for identifying phosphorylation sites. After evaluating the computational models by k-fold cross-validation and Jackknife cross-validation, the overall predictive accuracy of KinasePhos 2.0 is ∼91%, which is better than the previous version and the other tools previously developed. The details of the proposed method and predictive performance are described below.

MATERIALS AND METHODS

Data preprocessing

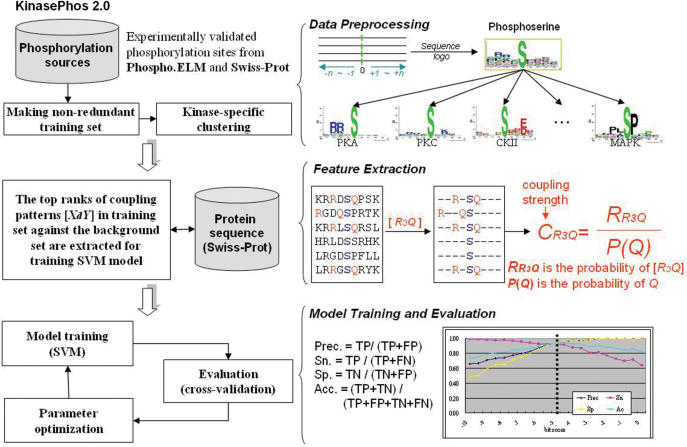
Figure 1 depicts the system flow of the proposed method. The experimentally validated phosphorylation sites are extracted from Phospho.ELM (release 6.0) (15) and Swiss-Prot (release 50) (16), containing 13 612 phosphorylation sites within 3674 proteins and 6832 sites within 3148 proteins, respectively. After removing the redundant sites between Phospho.ELM and Swiss-Prot, the number of serine (S), threonine (T), tyrosine (Y) and histidine (H) substrate are 11 888, 2433, 2179 and 43, respectively, as given in Table 1. Since the flanking sequences (position −4 ∼ +4) of the phosphorylation sites (position 0) are graphically visualized as sequence logos (17), the conservation of amino acids in the phosphorylation sites can be observed. The 9-mer sequences (−4 ∼ +4) of kinase-specific phosphorylation sites are extracted and constructed as training sets. Table S1 (See Supplementary Data) summarizes the statistics of 60 kinase-specific phosphorylation sites in the data set constructed.

Figure 1.

The system flow of KinasePhos 2.0.

Table 1.

The statistics of phosphorylation sites obtained from Phospho.ELM and Swiss-Prot

Data source	Number of phosphorylated proteins	Number of phosphorylation sites
		Serine (S)	Threonine (T)	Tyrosine (Y)	Histidine (H)	Total
Phospho.ELM	3674	9917	1890	1804	1	13 612
Swiss-Prot*	3148	4846	1035	901	42	6832
Combined (non-redundant)	5842	11 888	2433	2179	43	16 551

It notices that the sum of serine, threonine, tyrosine and histidine in Swiss-Prot is not equal to 6832, because there are several phosphorylation sites located on other kinds of residue. *The entries which contain residues annotated as ‘phosphorylation’ in the ‘MOD_RES’ are extracted and the entries annotated as ‘by similarity’, ‘potential’ and ‘probable’ are excluded.

Feature extraction

To avoid the overestimation of the predictive performance, the redundant training sequences should be discarded. After the construction of non-redundant training set of kinase-specific phosphorylation sites, two features, i.e. sequence of surrounding catalytic sites and coupling pattern of surrounding catalytic sites, are extracted. As to sequence surrounding catalytic sites, 9-mer sequences (−4 ∼ +4) of kinase-specific phosphorylation sites are encoded in three ways: BLOSUM62 profile encoding (the corresponding row number of amino acids in BLOSUM62 matrix), reduced alphabet (sparse encoding with fewer letters) (18) and 20-dimensional vector (each amino acid is mapped to a 20-dimensional vector), as given in Table S2. It was found that amino acids have a great variety of properties such as mass, polarity, hydrophobicity, so many groupings are possible (19). With the hydrophobicity (20), for instance, the 20 amino acids are reduced into three classes, such as polar (R,K,E,D,Q,N), neutral (G,A,S,T,P,H,Y) and hydrophobic (C,V,L,I,M,F,W).

The coupling pattern of surrounding catalytic sites is extracted from the flanking sequences of kinase-specific phosphorylation sites. Let [XdZ] denote the coupling pattern of amino acids X and Z that are separated by d amino acids. Since the protein sequence is directional, the sign of d is determined by the relative positions of X and Z. For example, as shown in Figure 1, a coupling pattern [R3Q] occurs in the training set, another coupling pattern [Q-3R] also occurs. Herein, we would not consider the coupling pattern with minus symbol. Let N(XdZ) be the number of occurrences of the coupling pattern [XdZ] in training sequences and the conditional probability R_XdZ is

1

where 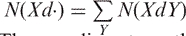and Y ∈ {20 types of amino acid}. The coupling strength C_XdZ between X and Z of the pattern [XdZ] is given by

2

where P(Z) is the probability of the occurrence of amino acid Y. If C_XdZ ≥ 1, then X and Z are positively correlated with respect to the distance d, and they are negatively correlated if C_XdZ < 1.

The differences of coupling strength C_XdZ between the training set of phosphorylation sites and the background set, which is extracted from all 9-mer sequences centering at residue serine, threonine, tyrosine and histidine in Swiss-Prot protein sequences, are computed and used to determine the number of coupling patterns trained by SVM. The higher differences of C_XdZ mean that the coupling pattern [XdZ] is the most important feature for separating the training set from the background set; therefore, the values of differences of the coupling strength C_XdZ between training set and background set should be tuned for determining the number of coupling patterns used to train a SVM model. Each coupling pattern is a dimension of features used in SVM. For instance, when set up the cutoff value of the differences of C_XdZ between training set and background set to 1.5, there are about 400 coupling patterns which is higher than the cutoff; thus, the number of dimensions trained by SVM is about 400, which is equal to the number of selected coupling patterns.

Model creation and evaluation

This work incorporates support vector machine (SVM) with the protein sequences and profiles of coupling pattern for training the predictive models for kinase-specific phosphorylation site prediction. A public SVM library, namely LIBSVM (21), is applied for training the predictive models. The SVM kernel function of radial basis function (RBF) is selected. In general, the experimental kinase-specific phosphorylation sites are defined as the positive set, while all other residues (S, T, Y or H) in the phosphorylated proteins are regarded as the negative set. K-fold cross-validation is used to evaluate the predictive performance of the models trained from the large data sets including PKA, PKC and MAPK, and Jackknife cross-validation is applied for models trained from the data size smaller than 30. We balance the positive set and negative set and the sizes of positive set and negative set are equal during the cross-validation processes. The cross-validation is performed for 30 times. The following measures of predictive performance of the trained models are defined: Precision (Prec) = TP/(TP + FP), Sensitivity (Sn) = TP/(TP + FN), Specificity (Sp) = TN/(TN + FP) and Accuracy (Acc) = (TP + TN)/(TP + FP + TN + FN), where TP, TN, FP and FN are true positive, true negative, false positive and false negative predictions, respectively.

Moreover, several parameters of the models including the values of differences of coupling strengths, the SVM cost values and SVM gamma values are optimized for maximizing the predictive accuracy. Finally, the parameters of the trained model with the highest predictive accuracy in each data set, were selected and used to provide the prediction service on the web.

PREDICTION PERFORMANCE

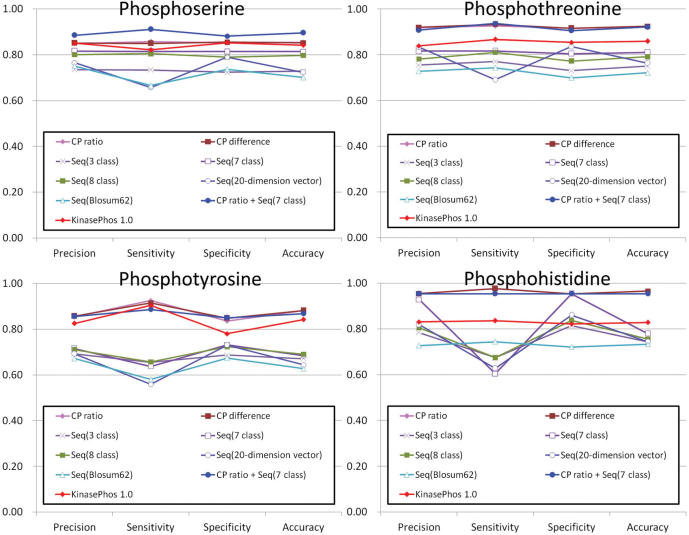
For finding the best predictive performance of SVM models in each kinase-specific group, the SVM models trained with various features such as coupling pattern (CP), sequence and the combination of coupling pattern and sequence are evaluated based on cross-validation. As shown in Figure 2, the average precision (Prec), sensitivity (Sn), specificity (Sp) and accuracy (Acc) of the SVM models trained with various features are calculated for phosphoserine, phosphothreonine, phosphotyrosine and phosphohistidine. Two methods are used to extract the coupling patterns, i.e. ‘CP difference’ and ‘CP ratio’. ‘CP difference’ indicates the coupling strength of training set subtracted the coupling strength of background set, and ‘CP ratio’ indicates the coupling strength of training set divided the coupling strength of background set. As to the feature of sequence profile, there are various coding methods used for encoding amino acids surrounding the phosphorylation sites, such as reduced alphabet (3-classes, 7-classes and 8-classes), BLOSUM62 profile encoding and 20-dimensional vector. Because the average predictive performance of the kinase-specific phosphorylation sites with small training set may be overestimated, the SVM models of kinase-specific group whose data size is smaller than 20 training sequences are not considered. Figure 2 gives the average predictive accuracies of models trained with coupling patterns (CP difference or CP ratio) of phosphoserine, phosphothreonine, phosphotyrosine and phosphohistidine are 86, 93, 88 and 93%, respectively. The overall predictive performance of SVM models trained with the features of coupling patterns, whose accuracy is close to 90%, is performing better than the SVM models trained only with sequence profiles (Seq).

Figure 2.

The comparison for the average precision (Prec), sensitivity (Sn), specificity (Sp) and accuracy (Acc) among the models trained with various features in phosphoserine, phosphothreonine, phosphotyrosine and phosphohistidine.

Since the features of coupling patterns (CP ratio) and sequences (7-classes) with best predictive performance are combined, the average predictive accuracy of SVM models trained with the combined features of phosphoserine is 89%, which is slightly better than the SVM models trained only with coupling patterns. However, the average predictive performance of the SVM models trained with the combined features of phosphothreonine, phosphotyrosine and phosphohistidine is close to the SVM models trained only with coupling patterns. The overall predictive accuracy of SVM models trained with the combined features of coupling patterns and sequences is close to 91%. In addition, the method of KinasePhos 1.0 is evaluated based on the data set constructed in this work. The average predictive accuracies of phosphoserine, phosphothreonine, phosphotyrosine and phosphohistidine are 84, 88, 84 and 83%, respectively.

Since the SVM models trained with various features, the most accurate model of each kinase-specific phosphorylation sites are selected and used to implement a prediction server. As shown in Table S3, the trained features, SVM Cost value, SVM Gamma value, precisions, sensitivity, specificity and accuracy of the selected models are presented for 37 kinase-specific groups with at least 20 experimentally verified phosphorylation sites. In the column of trained features, the value in the parentheses behind the coupling pattern (CP) is the value of difference or quotient of coupling strength between the training set against the background set. The average predictive accuracies of phosphoserine, phosphothreonine, phosphotyrosine and phosphohistidine are 90, 93, 88 and 93%, respectively.

WEB INTERFACE

After evaluating the trained models for identifying kinase-specific phosphorylation sites, the model with the highest predictive accuracy for each data set was selected. Users can submit their uncharacterized protein sequences and select the kinase-specific models for predicting phosphorylated serine, threonine, tyrosine or histidine. Although only 37 kinase groups containing at least 20 experimental phosphorylation sites were used to evaluate the predictive performance, the web server provides 60 predictive models of the kinase-specific groups with at least 10 experimental phosphorylation sites. As depicted in Figure 3, the web server locates the predictive phosphorylation sites and the involved catalytic protein kinases. In order to reveal the characteristics of the phosphorylation sites including the phosphorylated residues and surrounding sequences, the training phosphorylation sites and constructed sequence logos corresponding to each protein kinase are also provided graphically on the web interface. Moreover, users can download the predicted results with tab-delimited format for further analyses. The web server can accurately and efficiently predict the kinase-specific phosphorylation sites in the input protein sequences.

Figure 3.

The web interface of KinasePhos 2.0.

DISCUSSIONS AND CONCLUSION

The models trained with various features, including sequence profiles and coupling patterns, were evaluated by 5-fold and Jackknife cross-validation, the predictive performance of the models trained with coupling patterns are better than the models trained with sequence profiles. In general, the previous works of phosphorylation site prediction focused on residues serine, threonine and tyrosine; like our previous work (KinasePhos 1.0). Herein, KinasePhos 2.0 first considers phosphohistidine from Phospho.ELM and Swiss-Prot, which contain one and 42 phosphorylated histidine, respectively.

Moreover, the proposed web server is compared with several previously developed phosphorylation prediction tools, such as DISPHOS (9), PredPhospho (11), GPS (12,13), PPSP (4) and KinasePhos 1.0 (5,6). As given in Table 2, the number of kinases, sensitivity and specificity of prediction and the overall predictive performance of these tools are compared. GPS, PPSP, PredPhospho, KinasePhos 1.0 and the proposed methods all support the identification of kinase-specific phosphorylation sites. Although only the kinase groups containing at least 20 experimental phosphorylation sites were selected to evaluate the average predictive performance, the web server of KinasePhos 2.0 provided the predictive models of 60 kinase-specific groups with at least 10 experimental phosphorylation sites. Because the average predictive performance of serine, threonine and tyrosine of GPS and PPSP cannot be obtained, the predictive performance of three representative kinases such as PKA, PKC and CK2 are compared. As given in Table 2, the predictive performances of three representative kinases in KinasePhos 2.0 are comparable with PredPhospho, GPS, PPSP and KinasePhos 1.0. In particular, KinasePhos 2.0 provides the predictive model for phosphohistidine, whose predictive accuracy is 93%. The overall predictive accuracy of the kinase-specific groups with at least 20 phosphorylation sites of the proposed method is 91%. However, as given in Table S4, the overall predictive accuracy of the kinase groups which are smaller than 20 experimental phosphorylation sites is 94%.

Table 2.

The comparison among KinasePhos 2.0, DISPHOS, PredPhospho, GPS, PPSP and KinasePhos 1.0

Tools	DISPHOS	PredPhospho	GPS	PPSP	KinasePhos 1.0	KinasePhos 2.0
Method	Logistic regression	SVM	MCL+GPS	BDT	MDD+HMM	CP+SVM
Number of kinases	–	4 groups	71 groups	68 groups	18	58
Kinase PKA	–	Sn = 0.88	Sn = 0.89	Sn = 0.90	Sn = 0.91	Sn = 0.92
		Sp = 0.91	Sp = 0.91	Sp = 0.92	Sp = 0.86	Sp = 0.89
Kinase PKC	–	Sn = 0.79	Sn = 0.82	Sn = 0.82	Sn = 0.80	Sn = 0.84
		Sp = 0.86	Sp = 0.83	Sp = 0.86	Sp = 0.87	Sp = 0.86
Kinase CK2	–	Sn = 0.84	Sn = 0.83	Sn = 0.83	Sn = 0.87	Sn = 0.87
		Sp = 0.96	Sp = 0.88	Sp = 0.90	Sp = 0.85	Sp = 0.86
Serine	Acc = 0.76	Acc = 0.81	–	–	Acc = 0.86	Acc = 0.90
Threonine	Acc = 0.81	Acc = 0.77	–	–	Acc = 0.91	Acc = 0.93
Tyrosine	Acc = 0.83	–	–	–	Acc = 0.84	Acc = 0.88
Histidine	–	–	–	–	–	Acc = 0.93
Overall performance	–	Acc = 0.76 ∼ 0.91	–	–	Acc = 0.87	Acc = 0.91

SVM, support vector machine; MCL, Markov cluster algorithm; GPS, group-based phosphorylation scoring method; BDT, Bayesian decision theory; MDD, maximal dependence decomposition; HMM, hidden Markov model; CP, coupling pattern; Sn, sensitivity; Sp, specificity; Acc, accuracy.

The protein structural properties, such as accessible surface area (ASA) and secondary structure, can be considered in the future to improve the predictive performance of the models. For instance, ASA may be used for reducing the number of false-positive predictions of phosphorylation sites which locate in buried regions. However, the number of experimental phosphorylation sites located in the protein regions with known structure from PDB (22) is few for each kinase-specific group. Although ASA and secondary structure can be predicted by several published tools such as RVP-net (23) and PSIPRED (24), respectively, the predictive performance of phosphorylation sites may be affected by the predictive structural properties.

AVAILABILITY

The web server of KinasePhos 2.0 will be continuously maintained and updated. The web server is now freely available at http://KinasePhos2.mbc.nctu.edu.tw/

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.