MADAP, a flexible clustering tool for the interpretation of one-dimensional genome annotation data

Abstract

A recurring task in the analysis of mass genome annotation data from high-throughput technologies is the identification of peaks or clusters in a noisy signal profile. Examples of such applications are the definition of promoters on the basis of transcription start site profiles, the mapping of transcription factor binding sites based on ChIP-chip data and the identification of quantitative trait loci (QTL) from whole genome SNP profiles. Input to such an analysis is a set of genome coordinates associated with counts or intensities. The output consists of a discrete number of peaks with respective volumes, extensions and center positions. We have developed for this purpose a flexible one-dimensional clustering tool, called MADAP, which we make available as a web server and as standalone program. A set of parameters enables the user to customize the procedure to a specific problem. The web server, which returns results in textual and graphical form, is useful for small to medium-scale applications, as well as for evaluation and parameter tuning in view of large-scale applications, requiring a local installation. The program written in C++ can be freely downloaded from ftp://ftp.epd.unil.ch/pub/software/unix/madap. The MADAP web server can be accessed at http://www.isrec.isb-sib.ch/madap/.

INTRODUCTION

A variety of experimental genome annotation technologies provide counts, probabilities or intensity values for chromosomal positions spread over a complete or partial genome. Such technologies include cDNA and tag-sequencing protocols to map the 5′ and 3′ ends of mRNA (1,2), ChIP–chip analysis to reveal transcription factor binding sites and epigenetic markers, and high-density SNP profiling platforms for various kinds of genotype–phenotype association studies. A recurrent problem in the processing of such data is the identification of individual clusters (alternatively called peaks or islands) by some kind of signal detection and noise-filtering algorithm. The analysis of genome annotation data challenges any clustering software in many respects. Genome coordinates with available quantitative measurements are often not evenly distributed over the analyzed chromosomal range. Furthermore, the horizontal axis is discrete in nature and the size and shape of the target objects are in most cases largely unknown in advance. Moreover, the position-specific readout from the experimental protocol may be a function of several overlaid biological and technical processes For instance, in the case of promoter mapping, the number of cDNA 5′ ends at a given position is thought to reflect primarily transcription initiation events, but technical artifacts or premature termination of cDNA synthesis may also contribute to the signal.

Peak-recognition algorithms exist in many variants (3,4) and their application is described for instance for the analysis of MS data and chromatographic profiles or time series (5). However descriptions of applications of these methods to genome annotation data are sparse. Existing methods frequently lack flexibility and at the example of the package mclust in R (6), implementation of additional constraints is difficult. These methods are typically based on more or less explicit physical assumptions about the signal-generating process and peak shapes, and therefore cannot be directly ported to new applications. Standard clustering algorithms are furthermore prone to be perturbed by atypical distributions. Often, there is no experimental gold standard available for evaluation of the results. In such cases, the ultimate reference remains human intuition applied to representative examples.

We initially developed the program MADAP for the inference of promoters from mRNA 5′ end profiles obtained from the mapping of full-length cDNAs to the genome sequence (7). More recently, we discovered the usefulness of MADAP for the interpretation of ChIP–chip data. Given the potential of an even more general use, the web server presented here is primarily intended to enable a rapid evaluation of the suitability of MADAP for new kinds of data. Finding appropriate parameter settings likely represents the largest obstacle in applying MADAP to a new genome annotation problem. Please note that previously established parameters might not be suited for a novel data set with distinct characteristics such as background noise. The server may also be used for small-scale productive applications. However, for large-scale genome annotations task, we recommend to use a local installation of the program which can be freely downloaded from our FTP site.

USER INPUT AND DESCRIPTION OF ALGORITHM

The MADAP web server takes as input an uploaded file containing a set of tabulator-separated numbers representing for instance positions on a chromosome. The numbers describing the data points occur at a frequency corresponding to the strength (or intensity) of a measure at this given position, for instance the number of times a 5′ end of a full-length transcript (8) is observed at this position. Alternatively, data can be supplied in a file in gff format (www.sequenceontology.org/gff3.shtml). In this case, a frequency score of each feature has to be indicated in column 6 (‘score’) of the gff file.

The function of MADAP is to determine the most likely model describing the input data set. A mixture of normal (Gaussian) distributions with centers, standard deviations and relative frequencies are used to model the data points, an approach also known as a mixture modeling. Although the shape of the distributions of the clusters hidden in the input data is frequently not known and not necessarily resembling a normal distribution, we observe that the algorithm of MADAP as further described later copes remarkably well with most kinds of distributions. Using normal distributions has the advantage that the probability of observing a unit event (e.g. one cDNA 5′ end) at a specific position can easily be computed given the center position and standard deviation of a set of normal distributions. The number, the location of the centers and the relative frequency of the normal distributions are initially deduced from the data. Using a standard Expectation Maximization (EM) approach (4) MADAP optimizes the center positions of zero to many clusters and their standard deviation. A known drawback in this approach is that isolated points distant from the cluster centers (leverage points) can have an undesirable high impact on the selection of the model that best describes the clusters of points. In order to control for disturbing isolated points, we add to the mixture model an additional non-Gaussian, uniform ‘background’ component, thereby reducing the negative influence on the model selection. MADAP thus differs from the standard algorithm (9) in the addition of a background distribution and in the possibility to specify a set of additional constraints explained in the following summary of the optimization steps of the model.

In a first model initialization step, the program generates several initial models for each possible number of clusters. Minimal and maximal numbers of clusters can be defined by user-specified parameters; the initial numbers of clusters are additionally limited by the number of distinct data points in the input data. The center positions of the clusters are initially attributed to data points with the highest frequency. Data points within a neighboring ‘integration range’ are included into each initial cluster. A second parameter for background control subtracts a user-defined constant from all positions for model initialization. The subsequent steps are calculated again with full data.

In next steps, each of the initial models is iteratively evolved using the EM algorithm. The initial centers of clusters are optimized until stabilization of the data likelihood or discarded if a maximal number of iterations is reached. In a third step, models resulting from the EM step are required to comply with user-defined model constraints. Such constraints include a minimal number of data points attributed to a cluster and a minimal distance between peaks of neighboring clusters. Noncompliant clusters in models are removed and the EM step described earlier is repeated with a model with a reduced number of clusters. If there is no cluster left, the model is rejected. Models satisfying all constraints are recorded.

Upon the optimization of all initial models, the final model is chosen as the one with the highest data likelihood. Two variants for likelihood computation are offered: the usual likelihood under a mixture model (4), and a likelihood that is calculated after attributing each data point to the cluster with the highest density at that position (see explanatory document on web server).

Due to limits in computational resources, the web server version of MADAP features a few restrictions, notably in the number of initial clusters. Users are advised to either split up their data sets to ranges putatively containing less than 50 clusters, or to install MADAP on their local computers. For the analysis of larger data sets on our infrastructure, please contact the authors. Further descriptions of the algorithm and its parameters can be found on the site of the MADAP web server.

EXAMPLES AND PARAMETERS DEFINED BY THE USER

In the following we are going to describe with two examples how MADAP can be used for definition of promoters from full-length cDNA data or from ChIP–chip data. Note that this is a partly exploratory (unsupervised) data analysis problem. Given a spectrum of transcription start sites over a genomic range, there is no objective way to answer the question of how many promoters they represent. The consensus answer is likely to come from an interacting learning process with new methods and data. We therefore equipped the MADAP algorithm with a variety of parameters that enable the user to guide the partitioning process in a desired direction. Default parameters on the web server correspond to optimized values for the transcription start site (TSS) task. In particular, we try to relate the parameters chosen in this application to assumptions about the biological signal, in the following presented in the estimated order of importance. Aiming for high robustness and precision of TSS mapping, we required at least 10 counts (here cDNA 5′ ends) per clusters (parameter n = 10). We assumed that in average ∼70% of all full-length transcripts initiate within 20 bp of its ‘main’ TSS, thus being best described by a fixed standard deviation of the initial Gaussian components equal to 20 (d = 20). Alternative promoters were defined as neighboring TSS having a minimal distance of 50 bp (p = 50).

Parameters (m = 1) and (M = 16) specify the range for the number of clusters in the initial models. Computation time increases significantly with increasing ranges, because the more models have to be tested. Parameter (s = 0) defines the background subtraction for model initialization and parameter (e = 0.02) represents an estimate of the proportion of data points that belong to a random point background distribution. Optimal values for these parameters strongly depend not only on the kind of application, but also on the actual data set with, for instance specific noise levels. Parameter (c = 5) defines an integration range within which data points are initially attributed to a cluster center. Parameters (u = 6) and (w = 11) specify extended reporting ranges, for which the number and the fraction of points is reported in the text output, without influence on the clustering. This led to the following parameter settings (default on the web server, resulting output shown in Supplementary Figure 1):

Due to the fact that exact characteristics of the putative clusters in the input data are not known, some parameter settings may appear arbitrary.

A second demo file provided on the web server is derived from a ChIP–chip experiment using the Nimblegen platform with an antibody against a component of the preinitiation complex (10). Data describing a ∼250 kb segment of chromosome 12 was extracted from the GEO database, and the locations of the probes were remapped onto the current human genome assembly (NCBI 36). The intensity of the hybridization signal on the chip was transformed into integers by a simple exponentiation to the power of 10, setting an arbitrary maximum of 200 (the numerical values provided by GEO represent log-intensities). The input file provided in gff format contains 336 genome coordinates associated with a total of 3357 digitized intensity units. This demo gff file was submitted to MADAP with the following parameters:

Changes in parameters c, p, d, u and w relate to the larger cluster width expected for ChIP signals. The background probability (e = 0.002) was adjusted to a lower noise level.

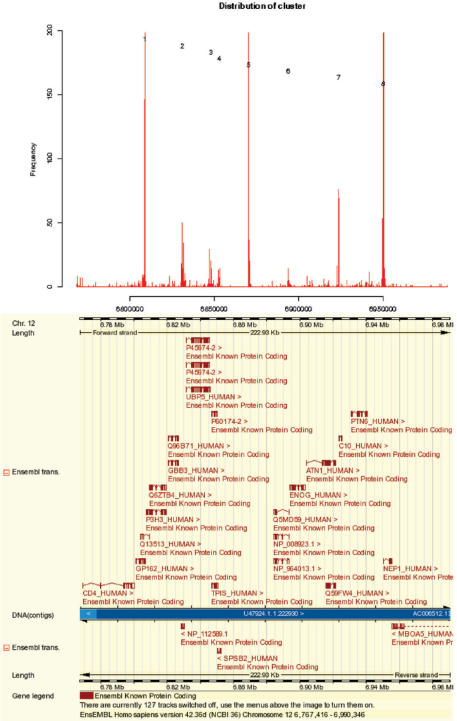
Figure 1 shows the output of the MADAP web server on this second demo file aligned with the corresponding genome annotations visualized by the ENSEMBL genome viewer (11).

Figure 1.

Output of MADAP server aligned with ENSEMBL genome annotations: MADAP executed on data derived from a ChIP–chip experiment using chromatin from IMR90 cells and antibodies against αTAF1. On top, a histogram of the input data is shown, with the x-axis indicating genomic positions on a portion of human chro. 12, and the y-axis representing transformed hybridization intensities of corresponding probes of a Nimblegen whole genome array. MADAP determines the location of 8 clusters of putative promoters, which largely correspond to 5′ ends of annotated transcribed sequences, as visualized in the ENSEMBL ContigView below.

On the MADAP web server, the results are presented graphically on top of histograms of the input data. In an overview plot, the distribution of determined clusters is displayed as numbers plotted at the approximate location of the corresponding cluster. A detailed view of each cluster allows the determination of the center and the estimated standard deviation. In addition to the visual representation of the location of the inferred clusters, the output of the MADAP server includes parseable output files in text format. The main results of MADAP are reported in a file ‘output’ containing a recapitulation of the parameters used and a description of the clusters found under the models described above. Supplementary files are intended to help to track the iteration behavior of MADAP, including the files ‘components’ with an outline of iteration steps, and a ‘summary’ file resuming properties of optimized models. Eventual problems encountered during execution of the program are reported in an ‘error’ file.

CONCLUSIONS

We present here a web server for the clustering program MADAP, which was initially developed for the determination of TSS (7). Although MADAP uses internally normal distributions, it was designed to model non-contiguous distributions of any shape and proved to be remarkable robust in this aspect.

Others have exploited cDNA full-length sequencing data or 5′ tags (5′ SAGE, CAGE) for promoter mapping and have presumably developed alternative solutions to the TSS clustering problem. However, to our knowledge none of these methods has been explicitly described or made public via web servers.

MADAP is in principle versatile enough to interpret data from any source in terms of a finite number of clusters characterized by center positions, volume and extension. In the scope of primary genome annotation data, we envisage an extended usage of MADAP in the analysis of 3′ ends of transcripts and the inference of polyA signals, and on data derived from ChIP–chip, or from tiling arrays.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.