Abstract
Autism is among the most clearly genetically determined of all cognitive-developmental disorders, with males affected more often than females. We have analyzed autism risk in multiplex families from the Autism Genetic Resource Exchange (AGRE) and find strong evidence for dominant transmission to male offspring. By incorporating generally accepted rates of autism and sibling recurrence, we find good fit for a simple genetic model in which most families fall into two types: a small minority for whom the risk of autism in male offspring is near 50%, and the vast majority for whom male offspring have a low risk. We propose an explanation that links these two types of families: sporadic autism in the low-risk families is mainly caused by spontaneous mutation with high penetrance in males and relatively poor penetrance in females; and high-risk families are from those offspring, most often females, who carry a new causative mutation but are unaffected and in turn transmit the mutation in dominant fashion to their offspring.
Keywords: human genetics, neurodevelopmental disorders, population genetics
Autism Spectrum Disorder (ASD) (Online Mendelian Inheritance in Man accession no. 209850) is characterized by language impairments, social deficits, and repetitive behaviors; can occur either sporadically (simplex) or in a familial (multiplex) pattern; occurs far more commonly in males; and has an overall incidence of ≈1 in 150 births (1). Monozygotic (MZ) twins show >70% concordance (2), higher with broader diagnostic criteria, and much higher than observed in dizygotic (DZ) twins, strongly suggesting that autism is genetically determined. Children with affected siblings have a higher risk than the general population, suggesting that autism can be inherited at least partially from preexisting genetic variants in parents.
Autism is likely to involve many genes. Linkage studies find no single locus of major effect but rather a very minor increase in allele sharing over the entire genome among concordant sibs (3–9). Cytogenetic studies (10), and more recently copy number analyses (9, 11, 12), support the idea that many loci may contribute to the disease.
Sibling and DZ concordance rates are perhaps one-tenth of MZ concordance rates, and this discrepancy, plus the suggestion of a large number of risk loci, has led many to expect that autism is attributable to complex multigenic interactions rather than simple dominant or recessive mutations. However, our current knowledge of genetic factors in autism suggests otherwise. Most of what we know about heritable risk factors comes from monogenic disorders, including fragile X syndrome (13–15), Rett syndrome (16), and tuberous sclerosis (17). Furthermore, cytogenetic findings and, more recently, copy number analysis point to a higher incidence of spontaneous mutation in children with sporadic autism (11), presumably occurring in a parental germ line.
An alternate to the multigenic interaction hypothesis is worth considering; most cases of autism are due to de novo mutation in the parental germ line, which can strike any of a number of critical loci. The large discrepancy in concordance rates between MZ twins and siblings can be explained thus: inherited or de novo mutation in the parental germ line affects MZ twins alike, whereas sibling and DZ concordance rates represent a mixture of modalities, sometimes inherited and sometimes de novo mutation.
This hypothesis makes a strong prediction: de novo mutations that can cause autism will also be found in resistant individuals, especially females, and these relatively asymptomatic individuals will mature to form high-risk families transmitting the mutation and hence the disorder in nearly dominant fashion to male offspring. To test one of our predictions, we analyzed autism risk in the multiplex families collected by the Autism Genetic Resource Exchange (AGRE) consortium (18) and find strong statistical evidence for families with a dominant pattern of transmission to their male offspring.
To determine the abundance of such families in the population, we extended our model beyond familial autism by incorporating two widely accepted ranges of parameters: the incidence of autism in the general population and the recurrence rate in siblings. Very simple models have a good fit to three independent databases of autism incidence; the vast majority of families have a low risk and contribute to the majority of autism, and a tiny minority of high-risk families, for whom transmission to male offspring is near 50%, contribute to the majority of the remainder. The high-risk families can be explained readily as generated by the expected number of offspring from low-risk families who have sustained de novo mutation but are themselves relatively asymptomatic.
We therefore propose the following unified model for sporadic and inherited autism. The majority of autisms are a result of de novo mutations, occurring first in the parental germ line. For reasons yet to be determined, female offspring are considerably more resistant to displaying the effects of such mutations than are males. Resistant individuals, but females in particular, carrying a mutation may marry and, with a probability of 50%, pass the mutation to their offspring, who will display the symptoms with high probability if male. The latter process accounts for a minority of autisms, but together these two mechanisms are likely to account for the great majority of cases.
A consequence of this model is the explanation of increased autism incidence as a function of parental age (19); germ-line mutations can be expected to increase with age. The model also leads to other testable deductions and suggests practical approaches in the design of future genetic studies of autism and other disorders with similar epidemiological patterns, which will be discussed in the paper.
Results
The Autism Family Databases.
We first and most thoroughly analyzed the AGRE database, comprising extensive and validated records of families with at least two affected children. Diagnoses are based on the Autism Diagnostic Interview-Revised. In most cases, the Autism Diagnostic Observation Schedule was also administered. These tools were designed to detect deficits in three behavioral domains: (i) reciprocal social interaction skills; (ii) qualitative communication skills; and (iii) restricted, repetitive, and stereotyped patterns of behavior (20, 21). For milder autism cases, the AGRE sample used a “broad-spectrum” category based on the presence of severe deficits in one of three domains of functioning moderate deficits in two of three or milder deficits in all three domains. We use the term “autism” or “Autism Spectrum Disorder” to refer to all three of these patterns.
We used two other independent databases. The first and much smaller from the University of Michigan was collected in part on the referral of families with at least two autistic children. The second, the Interactive Autism Network (IAN) Research Database, is a large and rapidly growing database collected by Internet registry, self referral, and self description (administered by P.L. and K.L.). The summaries of data and further information are in supporting information (SI) Tables 4 and 5 and legends.
For purposes of modeling, in all databases, we counted MZ siblings as one child, assigning the diagnosis of “affected” if even one of the MZ sibs was so diagnosed. In AGRE there was concordance of diagnosis in all 52 MZ male sibs and discordance in 3 cases of 11 female MZ sibs. In IAN, there was ≈80% concordance overall.
Transmission to Males in High-Risk Families.
We look initially at families where the first two children are affected, taking these to be a subset of “high-risk” families, and consider when a third child is born. There are 165 such families in AGRE, and the third-born children can be divided by gender and affected status: 44 unaffected males, 42 affected males, 62 unaffected females, and 17 affected females. It is apparent that the risk to the third-born male child, i.e., his probability of being affected conditional upon the first two children being affected, is nearly 50%, consistent with dominant transmission with high penetrance. There is a lower risk for females (≈20%), consistent with the overall lower incidence in females and explainable as reduced penetrance in that gender.
Note that, by examining only the third-born children of families already having two children with autism, we avoid the potential bias of our risk estimate caused by stoppage. Stoppage refers to the tendency of families to cease having offspring when one of their children has autism. Stoppage can distort basic assumptions of the likelihood method used in the next section but is not operant in this data slice.
Risk estimates are affected by ascertainment bias. If the rate of recruitment for families with three children with autism was higher than the rate of recruitment for families with two, we would see an inflated risk rate. Although there is no effort from AGRE to favor families with more affected children once they meet the basic requirement of having at least two, one could argue that families with more affected children are more likely to self report to the study. However, in that case, we would also expect to see a distortion in the gender ratio of the third born, because autism is more common in males. In fact, the proportion of third-born children that are males is 86:165, or 52.1%, very close to the ratio of males to females in that age group nationally (105/205 = 51.2%) (22).
Based on the above insight, we can estimate the ascertainment bias from the gender and affected status of the third child in the 165 families whose first two children are affected, and simultaneously estimate the risks for each gender, by expressing these parameters in a likelihood equation and searching for the maximum likelihood estimate (MLE) of these parameters. Let pf and pm represent the risk of females and males respectively, and r represent the ascertainment bias. Using a multinomial distribution, we can express the likelihood relating gender bias and ascertainment by the following equation:
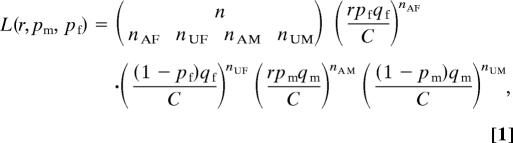 |
where nAF and nUF represent the number of affected and unaffected females, nAM and nUM represent the males, and n = nAF + nUF + nAM + nUM, qm and qf are the proportion of male and female in the population, respectively, which equal 105/205 and 100/205 for this age group in the United States. In Eq. 1, C = rqfpf + qf(1 − pf) + rqmpm + qm(1 − pm) is a normalization factor.
There is a wide range of possible values for the bias r that we cannot rule out because of the small sample size; nevertheless the data do not suggest strong ascertainment bias. For details, see SI Fig. 1. The MLE for r is 1.14, a value we use for additional analysis (see below). With the consideration of ascertaining bias, the MLE for risk of males with autism is 0.46, still consistent with a pattern of dominant transmission with high penetrance.
Estimating Simple Autism Risk Models.
To determine whether the observations consistent with dominant transmission in males would hold under analysis of more of the AGRE data, we sought a mathematical model fitting the data. At the same time, we could estimate the proportion of such high-risk families in the general population under the model by using accepted ranges of autism incidence, R, and sibling recurrence, S, for the general population. In the following, we restrict our analysis to male offspring only.
We assume that each male–female progenitor pair has a characteristic and time invariant risk x of producing male offspring with autism. The distribution of risk x across all progenitor pairs can be described by a density function f(x) on [0, 1]. We choose to model f(x) as having discrete risk components, corresponding to the intuition that there are a fixed number of genetic states for progenitor pairs. Using families of up to five offspring, there is information about the first five moments of f(x), which in principle means that we can explore discrete density functions with as many as five independent parameters, that is, three-component mass functions. As it turns out, a two-component mixture model suffices to fit the available autism data very well.
Consider a family of n children. The probability that this family has m children with autism is given by:
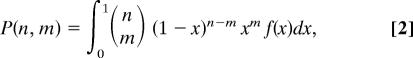 |
a mixture of binomial distributions of n trials. Note that Eq. 2 provides a system of equations for the moments of f(x). The kth moment of f(x) is defined as
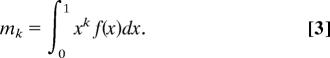 |
Theories and methods for statistical inference of f(x) in binomial mixtures are well developed (23, 24). However, our problem is unique in that families with fewer than two children with autism are not observed in AGRE. Therefore, existing methods do not directly apply to our data. In particular, we cannot infer the first two moments from the AGRE data. Therefore, in our maximum-likelihood approach, we use constraints for the first two moments, derived from R and S, and conditional probabilities for the likelihood function.
Let F(n, m) denote the “shape” of a family with n children of whom m have autism, and let fθ(x) be a density function parameterized by θ. Suppose that only families of shape F(n, m) with m ≥ 2 are observed, and here we consider only those families with at least three offspring. Under the assumption that the diagnoses of children within a family are independent, and that the families are themselves independent, a log-likelihood function of this data is given by
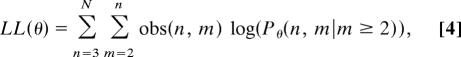 |
where N is the size of the largest sibships, obs(n, m) is the observed number of families of shape F(n, m), and Pθ(n, m|m ≥ 2) denotes the conditional probability Pθ(n, m)/Σk≥2 Pθ(n, k), where Pθ is defined by Eq. 2 with f(x) = fθ(x).
The first and second moments of f are constrained by R and S, the probability that a second child will be diagnosed with autism given that the first was, by the following two equations.
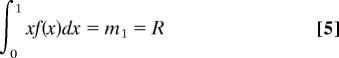 |
Therefore, given the rate of autism R and sibling recurrence rate S, we have two constraints on the first two moments of f(x).
We consider f(x) as a k-component discrete density function
 |
where δ is the Dirac density function and the ai sum to one. Here xi is the probability of an offspring with autism, and ai is the proportion of families with that probability. We consider two- and three-component parameterizations where the parameters θ are determined by ai and xi. To find the MLE for three-component models under the moment constraints, we applied a systematic grid search over all possible combinations of xi with 0 ≤ xi < xj ≤ 1 for 0 ≤ i < j ≤ 2 using a grid with spacing 10−4. For a given combination of the three xi, the corresponding ai are then uniquely determined by using the constraint equations on the first two moments and the constraint that the ai sum to one. For two-component models, the three constraints allow exploration of all 0 ≤ xi ≤ 1 over a grid with the same resolution.
For our standard constraint parameters, we chose an overall autism rate RT of 1/150 and a sibling recurrence rate ST of 10%. Assuming an incidence ratio, males to females, of 3:1, we calculated new parameters for males: an autism rate RM of 1%, and a sibling recurrence rate SM of 15% (males born into a family with a single previous male child, that child having autism). In keeping with the preceding analysis, we make the conservative assumption that the ascertainment bias is 1.14, that is, a family with three or more children with autism is 1.14 times more likely to be recruited to the study than a family with only two affected (see SI Text for the mathematical details of the adjustment).
Table 1 describes the data from which we drew the values for obs(n, m), a total of 145 informative families, from families with up to five male children (female offspring were not counted). By considering families with up to five male children, we have enough data to examine a three-component discrete model (i.e., three risk types of families), but we examine first the parameters of simpler nested models. The MLE for parameters of one- and two-component models for males are shown in Table 2, first and second rows. xi refers to the risk of the ith family type, and ai refers to their proportion in all families. The one-component model 2(m, 0) is in actuality a two-component model with x0, the “rate” of the first component, set to 0. That is, there are families with zero risk, and the rest have high-risk x1. In model 2(m), there is no constraint for x0. That is, there are two types of families, each with uniform risk (x0 and x1). We achieve a much higher likelihood with the two-component model, with a P value equal to 2.59e-12 by χ2 approximation and 0 of 1,000 by Monte Carlo simulation.
Table 1.
Family shapes: Male offspring
| No. of male children | No. of males with autism |
|||
|---|---|---|---|---|
| 2 | 3 | 4 | 5 | |
| 3 | 85 | 26 | ||
| 4 | 19 | 9 | 1 | |
| 5 | 2 | 2 | 1 | 0 |
Data were extracted from the AGRE database, counting the number of male offspring and of affected male offspring for each family.
Table 2.
Maximum-likelihood estimates for several models
| Model type | Data source | a0 | x0 | a1 | x1 | a2 | x2 | LL |
|---|---|---|---|---|---|---|---|---|
| 2(m,0) | AGRE | 0.9333 | 0 | 0.0667 | 0.15 | −112.70 | ||
| 2(m) | AGRE | 0.9923 | 0.0067 | 0.0077 | 0.434 | −88.211 | ||
| 3(m) | AGRE | 0.7961 | 0.0067 | 0.1963 | 0.0068 | 0.0076 | 0.437 | −88.210 |
| 2(m/f/p) | AGRE | 0.9941 | 0.0072 | 0.0059 | 0.501 | −783.02 | ||
| 2(m) | IAN | 0.9932 | 0.0069 | 0.0068 | 0.462 | −38.821 | ||
| 2(m/f/p) | IAN | 0.9913 | 0.0066 | 0.0087 | 0.416 | −326.49 |
Models 2(m) and 3(m) are the two- and three-component models for males only, respectively. Model 2(m,0) is for the model where x0 is set to 0. Model 2(m/f/p) is for mixed gender (see SI Text and text below).
We have explored ranges of the autism rate for males, RM, from 0.5% to 1.2% and ranges of the sibling recurrence rate for males, SM, from 5% to 20% for model 2(m) (see SI Table 6), and it is satisfying to note that, regardless of R and S, the MLE of parameters impute low-risk families with transmission rates ranging from 0.0027 to 0.0111 (first-component rate x0) and high-risk families with transmission rates from 0.429 to 0.519 (second-component rate x1). Obviously, the second-rate component is always close to 0.5, yet nothing about Mendelian inheritance is embodied in our mathematical methods. Thus, we interpret families with high risk as transmitting to males in a dominant pattern with high penetrance, and this conclusion is largely independent for a wide range of incidence and sibling recurrence.
We next looked at MLE for parameters of the three-component model 3(m), males only, shown in Table 2, row 3, using the same constraint parameters, RM and SM. Despite providing a model with two extra parameters, presenting an opportunity to choose another component for risk, the MLE parameters show one high-rate component (x2) that is nearly 50%, and two low-risk components that are essentially indistinguishable. Although there is no evidence for an intermediate-risk component, we examine its possibility below. The maximum likelihood of the three-component model is marginally higher than for the two-component model and not of any statistical significance (P value is 0.999 by χ2 approximation and 0.86 by Monte Carlo simulation). Again, varying the values for rates of autism or sibling recurrence does not change this picture.
In summary, the MLE of the discrete-component models for males only imply a pattern consistent with a clear genetic interpretation; the population mixes two kinds of families: high-risk families, where the probability of a male offspring with autism is near 50%; and low-risk families. We interpret the high-risk families as transmitting the disorder in a dominant manner, with nearly complete penetrance for males.
Goodness of Fit of Simple-Risk Models to AGRE and Other Data Sets.
To assess how well the statistical models fit the observations, we performed goodness-of-fit tests on the AGRE data for the two-component model, male only, listed as 2(m) in Table 2. A similar model that includes female offspring can be constructed from a two-component discrete-density function by postulating a uniform rate of penetrance in females [see 2(m/f/p) in Table 2 and SI Text). We used Pearson χ2 as the test statistics, summarizing the difference between observed number of F(n, m) families and expected number of F(n, m) families from our model, for n = 3,4,5 and 2 ≤ m ≤ n. The P values, obtained empirically from 1,000 random simulations (details described in SI Text), were equal to 0.98 and 0.41 for 2(m) and 2(m/f/p), respectively, suggesting our risk models fit the data well.
We performed goodness-of-fit analysis on two other data sets. For IAN, we used the estimated ascertainment bias of 1.06 (see below); otherwise, we used the same parameters (i.e., the ai and xi) estimated from AGRE data. For the University of Michigan data set, we obtained P values equal to 0.24 and 0.12 for 2(m) and 2(m/f/p), respectively (21 informative families for males only and 40 informative families for mixed gender). An analysis of the IAN database, an ongoing and expanding database, which, like AGRE, is based on self referral, had P values equal to 0.54 and 0.04 for 2(m) and 2(m/f/p), respectively (60 informative families for males only and 154 informative families for mixed gender).
The IAN database was large enough (3,000 families) for us to perform an ascertainment bias based on gender asymmetry, similar to what was described in Eq. 1, and also independent maximum-likelihood estimation. The results yielded a bias of 1.26 for accruing families of size two with two affected children over families of size two with only the first child affected. For families of size three with three affected children over families of size three with only the first two children affected, the bias was only 1.06. These biases are consistent with our analysis of ascertainment bias in AGRE. The model parameters we derived from this database were very similar to those we derived from AGRE, with high-risk transmission equal to 0.46 and 0.42 for the 2(m) and 2(m/f/p) models, respectively (row 5 and row 6, Table 2). The family risk patterns inferred from these data are thus remarkably similar to that from AGRE.
The same simple models of risk fit the three databases well.
Size and Contribution of Risk Classes Using Simple and Complex Density Functions.
Our simple two-component model [2(m) in Table 2] estimates that two-thirds and one-third of autism cases are contributed from low- and high-risk families, respectively. However, our biological conclusions do not depend on such a unique model. Although the data are always insufficient to determine the actual probability distribution of transmission in families, we can explore the likely functions within the same general classes of density functions and examine their properties, such as the size and contribution to autism from the various risk classes. To do this, we capped the risk at 0.5, the maximum expected risk for a dominantly inherited. model. We used our standard values for RM and SM and accepted for analysis those three-component mass functions with log-likelihood given the AGRE data within 1.92 (= 0.5χ1,0.952) of the maximum log-likelihood. We analyzed 10,000 three-component mass functions randomly selected from all such functions found during a grid search. We also broadened the class of allowed density functions beyond just three discrete components by considering the class of 150-component mass functions, thereby approximating the properties of continuous density functions. We used a Markov chain Monte Carlo (MCMC) method (25) to uniformly sample 10,000 150-component mass functions that satisfied the first and second moment constraints and gave a good fit to the data (with P >0.05 in the Pearson χ2 goodness-of-fit test). MCMC samples were collected every 1,000 iterations after an initial 5 million iterations. Details of the sampling method will be presented subsequently, along with some theoretical discussions relating to moment analysis and population genetics.
For each density function, we determined the size and contribution to autism from families with 0 to 0.01 risk (low risk), 0.1 to 0.3 risk (intermediate risk, which would include recessive patterns of transmission), and 0.3 to 0.5 risk (high risk, which would include dominant patterns of transmission with partial to complete penetrance). The mean and standard deviation of these values from each function class are summarized in Table 3. It is clear from our analysis that the major contribution to autism comes from low-risk families, those below the mean expected risk. Also, the contribution from high-risk families in general exceeds the overall contribution from intermediate risk families, whether we inspect 150- or 3-component mass functions.
Table 3.
Mean (standard deviation) of sizes and contributions to autism of various risk classes
| Model type | aL | aI | aH | aLxL/R | aIxI/R | aHxH/R | aHxH>aIxI | aHxH>aBIxBI |
|---|---|---|---|---|---|---|---|---|
| 3-component | 0.9325 (0.0975) | 0.0032 (0.0063) | 0.0071 (0.0019) | 0.474 (0.183) | 0.051 (0.092) | 0.303 (0.051) | 0.921 | 0.653 |
| 150-component | 0.9735 (0.004) | 0.0089 (0.002) | 0.0064 (0.0006) | 0.513 (0.02) | 0.172 (0.03) | 0.260 (0.02) | 0.949 | 0.731 |
Columns aL, aI, and aH are the mean (standard deviation) of sizes of low-, intermediate-, and high-risk classes, respectively. Columns aLxL/R, aIxI/R, and aHxH/R are the mean (standard deviation) of contributions for each class. Columns aHxH/R, aHxH>aIxI, and aHxH>aBIxBI show the proportionate number of times that contribution from the high-risk range exceeds the contribution from the intermediate-risk and the broadly defined intermediate-risk ranges, respectively.
By examining each particular reasonable density function from either class, contribution from the high-risk range exceeds the contribution from the intermediate risk range 92% of the time. Contribution from high-risk families exceeds even more broadly defined intermediate-risk families (range from 0.01 to 0.3) 65% of the time for either function class. We interpret this as evidence that, in a purely genetic model, the families with a dominant pattern contribute more cases than the families with a more complex genetic transmission pattern.
We do not know with certainty that the MCMC process (used for the 150-component mass functions) reached convergence, hence the sampling obtained may not be uniform from the targeted function space. However, our above conclusions are robust to the possibility of nonuniformity. This is because we deliberately chose our starting point for the MCMC to be the 150-component mass function that has the least contribution from the high-risk families. We obtained this function using mathematical programming under two linear constraints for first two moments and a quadratic constraint for the remaining moments using the Pearson χ2 statistic.
Discussion
We must emphasize at the outset that our biological interpretation of the risk models assumes that risk is determined by genetic factors, and thus, except for their appealing simplicity, the risk models themselves should not be taken as evidence for genetic causation. We cannot rule out environmental factors, such as complications during pregnancy, contributing to the observed risk data, and the presence of these factors could impact our biological interpretation and some of our modeling assumptions. Nevertheless, in what follows, we assume a genetic basis for risk, justified largely by MZ and DZ twin studies.
Analysis of three databases shows that a simple-risk model has good fit for the incidence of autism in males, in which families fall into two major types: families for whom the risk of autism in male offspring is nearly 50%, as expected for dominant transmission with high penetrance; and families for whom male offspring have a low risk. The two-component model fits female incidence well if we simply add a penetrance factor of ≈0.3 for females. The two-component model is vastly superior to the single-component model. This latter finding is in keeping with the observation that there are at least two distinct genetic mechanisms for acquiring autism, one through de novo mutation in simplex families, and one through inheritance in multiplex families (11). Indeed, deleterious de novo mutations, which enter the gene pool for only a brief time, may be the simplest way in which to explain the discrepancy between MZ and DZ concordance rates and the origin of low- and high-risk families.
The data in our study do not rule out recessive modes of inheritance or a variety of more-complex genetic states that could give rise to families with gradations of risk. Nevertheless, if we exclude the possibility of families with greater than a dominant risk pattern, examination of simple and complex discrete density functions with plausible likelihood or χ2 measures suggests that intermediate risk families with a recessive pattern of transmission would contribute less to autism incidence than families with a dominant pattern, and overall contribution is greatest from low-risk families.
We need to consider what factors might lead to spurious conclusions. The most obvious are overdiagnosis, stoppage, and ascertainment bias. Overdiagnosis seems to us unlikely. Standardized interviews were performed on each AGRE patient, so assessment is as objective as possible at the present time. Stoppage, the tendency to curtail procreation given affected offspring, could undermine the assumptions of the likelihood model. But stoppage is not relevant in the analysis of the third-born children, which showed evidence of families with the dominant pattern. A criticism of ascertainment bias is harder to rebut, because families with more than two affecteds might have a higher likelihood of being collected than families with just two. However, this potential bias is mitigated by two conditions: recruitment was initiated by self referral of the family, not by the encounter with a proband; and the collection was amassed over a 10-year interval. In addition, we have developed a method based on the asymmetry of gender ratios to estimate ascertainment bias and find only a minor effect in both AGRE and IAN databases.
In the following several paragraphs, we will consider the biological implications if the high-risk families are transmitting an allele in a dominant fashion and with high penetrance in males. Such families raise the question: what sort of mutation can cause autism, can be present in an apparently unaffected parent, and then can be transmitted to an offspring in a dominant manner? This pattern could be explained by X-linked mutations, but we see insufficient evidence of increased sharing of maternal X in concordant siblings in the AGRE data set (7). The most likely remaining explanation is disruptions on a single parental chromosome, with incomplete penetrance creating carrier states. Females are especially resistant and make logical carriers, but discordance between MZ twins suggests an “Autism Spectrum Disorder genotype” can exist in the absence of phenotype in either gender. To explain greater penetrance in males, we need merely consider the hypothesis that autism involves loss of cognitive abilities related to social skills, language, and repetitive behavior that may already be targets of sexual dimorphism (26–28) and hence these traits are already sensitive to perturbation.
Where are these high risk families coming from? We propose that a significant proportion of sporadic autism is caused by de novo mutation, deletions, duplications, other genomic rearrangements, or point mutations in the germ line of one parent that can cause loss-of-function (haploinsufficiency) or gain of function to any of a large number of target genes. This can occur in any family, regardless of genetic background, and can appear in any offspring, regardless of gender. Offspring with mild disorders or asymptomatic carriers such as females, may marry and have children who will inherit the mutation in a dominant fashion. With our standard parameters (RT = 1/150, ST = 10%, 3:1 males to females), the number of asymptomatic females would, by symmetry arguments, be 2 in 300 (0.0067) female newborns. This is the right magnitude needed to explain the proportion of high-risk families, which we estimate as 0.0077 (see Table 2, row 2, value a1).
We observe de novo mutation in 10% of children with sporadic autism, significantly more often than observed in either healthy children or children from multiplex families (11). We believe that 10% is a gross underestimate because of the low resolution of the technique for discovering these copy-number mutations. The true rate of de novo copy number mutations in children with autism could well be three times that number, and we do not yet know the frequency of spontaneous point mutation. Thus the rate of spontaneous mutation of all types reasonably can be expected to account for the majority of sporadic autism. The great majority of de novo mutations we observe in sporadic autism are deletions (11), although other types of mutation, such as duplication, do occur (29). Deletions will most likely create haploinsufficiency. There is no lack of examples of haploinsufficiency affecting neurological development, behavior, and cognition (30). The association of chromosomal abnormalities and submicroscopic deletions with autism supports the idea that gene imbalance can contribute to the disorder.
Our conjecture makes strong predictions, some testable in the short term. One parent in a high-risk family may have a de novo mutation. We predict this will be more commonly observed in the mother, and high risk should follow one parent when they have offspring with another partner.
We have achieved a simple model for autism in large part by focusing on the pattern of inheritance in males and using broad diagnostic criteria, while ignoring the details of the phenotype. Thus, our study does not directly address very important questions: what “modifier” genes influence the phenotypic manifestations of the disorder, the variable severity of autism in siblings, and the penetrance of autism in females. In particular, the high concordance in MZ females and the low penetrance in females suggest that additional genetic factors moderate incidence in that gender. Guided by our model, we propose that, whereas genetic association studies will fail to find causative mutations, such studies can find modifier genes.
Spontaneous mutation should be considered as a cause for any disorder clearly genetic in origin that reduces fecundity yet recurs in the population and particularly if the incidence is related to the age of the parents at conception. Besides autism, this potentially includes other severe developmental, metabolic, or neuropsychiatric disorders such as congenital heart disease, cerebellar dysfunction, morbid obesity, and severe mood and cognitive disabilities. The overall rate of de novo mutation in humans per generation is not a well determined figure and could be surprisingly high in light of our previous work (11). Finding de novo mutations by examining parent–child trios should become increasingly powerful over the next few years.
Supplementary Material
Acknowledgments
We thank Jim Simons, David Donoho, Terry Speed, Michael Zhang, Mary-Claire King, Gerry Fischbach, and Nat Heintz for helpful discussions and suggestions and Conrad Gilliam, Jonathan Pritchard, David Botstein, and Leonid Kruglyak for a critical reading of the manuscript. We gratefully acknowledge the resources provided by the AGRE Consortium and the participating AGRE families. AGRE is a program of Cure Autism Now and is supported, in part, by National Institute of Mental Health Grant MH64547 (to D.H.G.). [The AGRE Consortium: D.H.G.; Maja Bucan (University of Pennsylvania, Philadelphia, PA); W. Ted Brown (Institute for Basic Research in Developmental Disabilities, Staten Island, NY); Rita M. Cantor (University of California School of Medicine, Los Angeles, CA); John N. Constantino (Washington University School of Medicine, St. Louis, MO); T. Conrad Gilliam (University of Chicago, Chicago, IL); Martha Herbert (Harvard Medical School, Boston, MA); C. Lajonchere; David H. Ledbetter (Emory University, Atlanta, GA); Christa Lese-Martin (Emory University, Atlanta, GA); Janet Miller (Cure Autism Now); Stanley F. Nelson (University of California School of Medicine, Los Angeles, CA); Gerard D. Schellenberg (University of Washington, Seattle, WA); Carol A. Samango-Sprouse (George Washington University, Washington, DC); Sarah Spence (University of California School of Medicine, Los Angeles, CA); Matthew State (Yale University, New Haven, CT); and Rudolph E. Tanzi (Massachusetts General Hospital, Boston, MA).] This work was supported by a grant from the Simons Foundation.
Abbreviations
- MZ
monozygotic
- DZ
dizygotic
- AGRE
Autism Genetic Resource Exchange
- MLE
maximum likelihood estimate
- IAN
Interactive Autism Network
- MCMC
Markov chain Monte Carlo.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/cgi/content/full/0705803104/DC1.
References
- 1.Centers for Disease Control Prevention. MMWR Surveill Summ. 2007;56:12–28. [Google Scholar]
- 2.Bailey A, Le Couteur A, Gottesman I, Bolton P, Simonoff E, Yuzda E, Rutter M. Psychol Med. 1995;25:63–77. doi: 10.1017/s0033291700028099. [DOI] [PubMed] [Google Scholar]
- 3.Risch N, Spiker D, Lotspeich L, Nouri N, Hinds D, Hallmayer J, Kalaydjieva L, McCague P, Dimiceli S, Pitts T, et al. Am J Hum Genet. 1999;65:493–507. doi: 10.1086/302497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.International Molecular genetic Study of Autism Consortium. Am J Hum Genet. 2001;69:570–581. [Google Scholar]
- 5.Liu J, Nyholt DR, Magnussen P, Parano E, Pavone P, Geschwind D, Lord C, Iversen P, Hoh J, Ott J, Gilliam TC. Am J Hum Genet. 2001;69:327–340. doi: 10.1086/321980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Auranen M, Vanhala R, Varilo T, Ayers K, Kempas E, Ylisaukko-Oja T, Sinsheimer JS, Peltonen L, Jarvela I. Am J Hum Genet. 2002;71:777–790. doi: 10.1086/342720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Yonan AL, Alarcon M, Cheng R, Magnusson PK, Spence SJ, Palmer AA, Grunn A, Juo SH, Terwilliger JD, Liu J, et al. Am J Hum Genet. 2003;73:886–897. doi: 10.1086/378778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ylisaukko-oja T, Alarcon M, Cantor RM, Auranen M, Vanhala R, Kempas E, von Wendt L, Jarvela I, Geschwind DH, Peltonen L. Ann Neurol. 2006;59:145–155. doi: 10.1002/ana.20722. [DOI] [PubMed] [Google Scholar]
- 9.Szatmari P, Paterson AD, Zwaigenbaum L, Roberts W, Brian J, Liu XQ, Vincent JB, Skaug JL, Thompson AP, Senman L, et al. Nat Genet. 2007;39:319–328. doi: 10.1038/ng1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Vorstman JA, Staal WG, van Daalen E, van Engeland H, Hochstenbach PF, Franke L. Mol Psychiatry. 2006;1:18–28. doi: 10.1038/sj.mp.4001781. [DOI] [PubMed] [Google Scholar]
- 11.Sebat J, Lakshmi B, Malhotra D, Troge J, Lese-Martin C, Walsh T, Yamrom B, Yoon S, Krasnitz A, Kendall J, et al. Science. 2007;316:445–449. doi: 10.1126/science.1138659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jacquemont ML, Sanlaville D, Redon R, Raoul O, Cormier-Daire V, Lyonnet S, Amiel J, Le Merrer M, Heron D, De Blois MC, et al. J Med Genet. 2006;43:843–849. doi: 10.1136/jmg.2006.043166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Oberle I, Rousseau F, Heitz D, Kretz C, Devys D, Hanauer A, Boue J, Bertheas MF, Mandel JL. Science. 1991;252:1097–1102. doi: 10.1126/science.252.5009.1097. [DOI] [PubMed] [Google Scholar]
- 14.Verkerk AJ, Pieretti M, Sutcliffe JS, Fu YH, Kuhl DP, Pizzuti A, Reiner O, Richards S, Victoria MF, et al. Cell. 1991;65:905–914. doi: 10.1016/0092-8674(91)90397-h. [DOI] [PubMed] [Google Scholar]
- 15.Yu S, Pritchard M, Kremer E, Lynch M, Nancarrow J, Baker E, Holman K, Mulley JC, Warren ST, Schlessinger D, et al. Science. 1991;252:1179–1181. doi: 10.1126/science.252.5009.1179. [DOI] [PubMed] [Google Scholar]
- 16.Amir RE, Van den Veyver IB, Wan M, Tran CQ, Francke U, Zoghbi HY. Nat Genet. 1999;23:185–188. doi: 10.1038/13810. [DOI] [PubMed] [Google Scholar]
- 17.The European Chromosome 16 Tuberous Sclerosis Consortium. Cell. 1993;75:1305–1315. doi: 10.1016/0092-8674(93)90618-z. [DOI] [PubMed] [Google Scholar]
- 18.Geschwind DH, Sowinski J, Lord C, Iversen P, Shestack J, Jones P, Ducat L, Spence SJ. Am J Hum Genet. 2001;69:463–466. doi: 10.1086/321292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Reichenberg A, Gross R, Weiser M, Bresnahan M, Silverman J, Harlap S, Rabinowitz J, Shulman C, Malaspina D, Lubin G, et al. Arch Gen Psychiatry. 2006;63:1026–1032. doi: 10.1001/archpsyc.63.9.1026. [DOI] [PubMed] [Google Scholar]
- 20.Lord C, Rutter M, Goode S, Heemsbergen J, Jordan H, Mawhood L, Schopler E. J Autism Dev Disord. 1989;19:185–212. doi: 10.1007/BF02211841. [DOI] [PubMed] [Google Scholar]
- 21.Lord C, Rutter M, Le Couteur A. J Autism Dev Disord. 1994;24:659–685. doi: 10.1007/BF02172145. [DOI] [PubMed] [Google Scholar]
- 22.Mathews TJ, Hamilton BE. Natl Vital Stat Rep. 2005;53:1–17. [PubMed] [Google Scholar]
- 23.Lindsay BG. Mixture Models: Theory, Geometry and Applications. Hayward, CA: IMS; 1995. [Google Scholar]
- 24.Wood N. Ann Stat. 1999;27:1706–1721. [Google Scholar]
- 25.Lovász L. Math Prog. 1999;86:443–461. [Google Scholar]
- 26.Skuse DH. J Lab Clin Med. 1999;133:23–32. doi: 10.1053/lc.1999.v133.a94575. [DOI] [PubMed] [Google Scholar]
- 27.Skuse DH. Hum Mol Genet 14 Spec No. 2005;1:R27–R32. doi: 10.1093/hmg/ddi112. [DOI] [PubMed] [Google Scholar]
- 28.Baron-Cohen S, Knickmeyer RC, Belmonte MK. Science. 2005;310:819–823. doi: 10.1126/science.1115455. [DOI] [PubMed] [Google Scholar]
- 29.Veenstra-VanderWeele J, Cook EH., Jr Mol Psychiatry. 2004;9:819–832. doi: 10.1038/sj.mp.4001505. [DOI] [PubMed] [Google Scholar]
- 30.Lee JA, Lupski JR. Neuron. 2006;52:103–121. doi: 10.1016/j.neuron.2006.09.027. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


