Abstract
Bacteria of the genus Wolbachia are among the most common endosymbionts in the world. In many insect species these bacteria induce a sperm-egg incompatibility between the gametes of infected males and uninfected females, commonly called unidirectional cytoplasmic incompatibility (CI). It is generally believed that unidirectional CI cannot promote speciation in hosts because infection differences between populations will be unstable and subsequent gene flow will eliminate genetic differences between diverging populations. In the present study we investigate this question theoretically in a mainland-island model with migration from mainland to island. Our analysis shows that (a) the infection polymorphism is stable below a critical migration rate, (b) an (initially) uninfected “island” can better maintain divergence at a selected locus (e.g. can adapt locally) in the presence of CI, and (c) unidirectional CI selects for premating isolation in (initially) uninfected island populations if they receive migration from a Wolbachia-infected mainland. Interestingly, premating isolation is most likely to evolve if levels of incompatibility are intermediate and if either the infection causes fecundity reductions or Wolbachia transmission is incomplete. This is because under these circumstances an infection pattern with an infected mainland and a mostly uninfected island can persist in the face of comparably high migration. We present analytical results for all three findings: (a) a lower estimation of the critical migration rate in the presence of local adaptation, (b) an analytical approximation for the gene flow reduction caused by unidirectional CI, and (c) a heuristic formula describing the invasion success of mutants at a mate preference locus. These findings generally suggest that Wolbachia-induced unidirectional CI can be a factor in divergence and speciation of hosts.
Introduction
Reproductive parasites like intracellular bacteria Wolbachia manipulate the reproductive system of their hosts to their own benefit. Most commonly, Wolbachia cause sperm-egg incompatibilities, known as cytoplasmic incompatibility (see [1], [2] for reviews). In concert with geographic or genetic barriers to gene flow, such cytoplasmic incompatibility (CI) could promote the evolution of reproductive isolation, a crucial component in speciation [3]–[6]. Wolbachia are widely distributed in arthropods, with an estimate of 20% to 70% insect species infected with the bacteria [7]–[9]. Hence, addressing whether Wolbachia affects the speciation processes of its hosts is an important question. Here, we investigate theoretically the effect of unidirectional CI on speciation. Our modeling approach is in line with the theoretical literature on both speciation by reinforcement and the invasion of modifiers of mating (e.g. [10]–[13]).
Cytoplasmic incompatibility (CI) is a mating incompatibility induced by Wolbachia (see [14] for a review). It is called cytoplasmic because Wolbachia is transmitted from the mother through the cytoplasm of the egg to the offspring. There are two basic forms. Unidirectional CI involves one Wolbachia strain. If the father is infected with Wolbachia then matings with uninfected females (or females infected with a different strain) have a reduced number of surviving offspring in comparison to other possible matings. This is due to an incompatibility between egg and sperm [15]. Bidirectional CI is caused by two Wolbachia strains and can occur when mating partners are infected with different strains.
Cytoplasmic incompatibility has attracted attention as a possible mechanism for rapid speciation [1], [3], [4], [6], [16]–[18]. The basic idea is that CI reduces gene flow between populations, permitting genetic divergence and selecting for premating isolation. In the case of bidirectional CI there is both empirical and theoretical evidence supporting this view. Field studies show that many insect species harbor different strains of Wolbachia, often in different geographic regions [19]–[22]. Further, crossing experiments suggest that bidirectional CI is a major isolation factor between some strains and closely related species [4], [5], [17], [23]–[25]. Theoretically, it has been shown that two Wolbachia strains can stably coexist in parapatric host populations in the face of substantial migration [26], and that bidirectional CI reduces the gene flow of locally adapted alleles and selects for premating isolation even if the transmission of Wolbachia and the level of incompatibility are incomplete [6], [27], [28].
However, the view that Wolbachia are significant factors in arthropod speciation is controversial [3], [18], [29]–[32]. Common criticisms are that bidirectional CI (the mode that most obviously can promote reciprocal reductions in gene flow) will be uncommon in nature, that levels of CI are insufficient to allow genetic divergence, and that CI is not effective in promoting the evolution of premating isolation.
Unidirectional CI is likely to be more common in nature, since it requires that only one population be infected with Wolbachia. However, unidirectional CI is generally not believed to promote speciation in hosts because maintenance of infected and uninfected populations is expected to be unstable in the presence of migration. Therefore, CI differences would not persist and gene flow would eliminate differences between diverging populations. A prominent example for the instability of unidirectional CI is the rapid spread of Wolbachia in Drosophila simulans of California [33]. However, in other field studies mixed infections have been observed between populations of a species [5], [34], [35]. One example is the absence of Wolbachia in invasive populations of fire ants in North America, but presence of infections in source populations in South America [5]. The converse pattern is also found, presence of Wolbachia in globally distributed Culex pipiens but its absence in a smaller potential source population in South Africa [35]. Further, in mushroom feeding Drosophila unidirectional CI between a closely related infected and uninfected species may be a major factor of genetic isolation [5], [36]. Reinforcement of reproductive isolation appears to be occurring in the contact zone. These experimental studies indicate that further modeling of the dynamics of unidirectional CI and its possible role in promoting reproductive isolation is needed. The basic question is whether there are conditions under which unidirectional CI can create a stable infection pattern and whether this selects for genetic divergence and premating isolation. So far there is one theoretical study addressing this question. Flor et al. [37] demonstrated analytically that infected and uninfected parapatric host populations can stably coexist if migration is below a critical migration rate. The critical migration rate was shown to be positive if Wolbachia causes either a fecundity reduction in the host or its transmission is incomplete.
In the present study we investigate the role of Wolbachia-induced unidirectional CI on host speciation more generally. We first consider the conditions that permit maintenance of infection differences between an infected mainland and an initially uninfected island population in the presence of unidirectional migration and local adaptation. We then follow Telschow et al. [6] and combine models for the Wolbachia dynamics [27], [38] with a well-studied reinforcement model [13]. This new model allows us to investigate the effect of unidirectional CI on genetic divergence of the host. We consider selection acting on a small (initially uninfected) island population experiencing migration from a large (infected) mainland population. The model includes a mate preference locus, a male trait locus undergoing divergent selection in the two populations, and cytoplasmic incompatibility. In the present study we demonstrate that island populations with low Wolbachia infection frequencies are able to maintain local adaptation in the face of migration better than can island populations with an infection. When combined, locally adapted alleles and differences in infection are both stable at higher rates of migration than either would be alone. In addition the infection difference between mainland and island allows premating isolation to evolve more readily. The results suggest that, if recurrent peripheral populations occur, it is the ones that lose their Wolbachia that are more likely to diverge into new species, and that unidirectional CI can select for premating isolation by reinforcement of mate discrimination.
Model
Our model is similar to Dobzhansky's classical model of speciation by reinforcement (fig. 1, [39]). We assume that an ancestral host population has split into two populations, a large mainland and a small island. The scenario is analogous to a large central population with a small peripheral isolated population. The populations remain for some time in allopatry and diverge during that time at a locus which controls a male trait used in female mate choice. Further, the mainland is infected with Wolbachia but there is no infection on the island. After the establishment of these genetic differences the populations restore contact via migration from the mainland to the island (secondary contact). For low migration rates and if either Wolbachia transmission is incomplete or the infection reduces female fecundity, this infection pattern of infected mainland and (mostly) uninfected island is stable and, further, unidirectional CI acts as a postzygotic isolation mechanism. We first determine the stability of the infection difference between the populations, and then investigate whether postzygotic isolation selects for premating isolation and thus reinforces the genetic differences between the populations. To analyze when reinforcement takes place, we introduce mutants at a locus for female mating preference and study under which circumstances such mutants can invade, and whether this results in divergence at the preference locus.
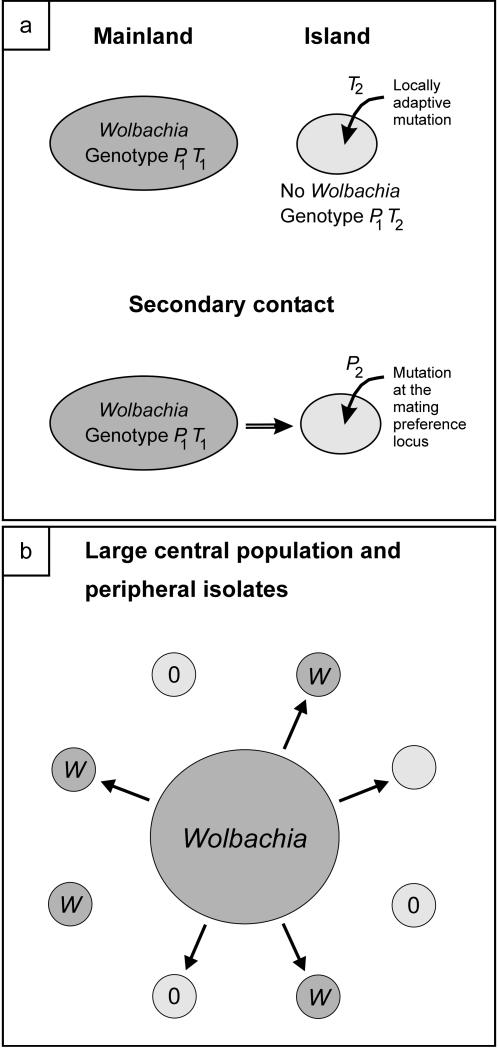
Figure 1. Model scenario.
Graph (a): The ancestral situation is a large mainland population infected with Wolbachia and a small peripheral island population without Wolbachia. Further, the populations have diverged at a phenotypic trait locus T, with local adaptation in the island population of the T 2 allele. After migration from mainland to island is restored (secondary contact), a new allele at the mating preference locus, P 2, is introduced at low frequency in the island population. Females with P 2 prefer T 2 males relative to T 1 males. We investigated the stability of infection differences between the populations, probability of local adaptation at the selected locus in the presence of migration, under what conditions mutants at the mate preference locus can invade and result in genetic divergence and prezygotic isolation. Graph (b): The mainland-island model analyzed in this article applies to a situation with a large central population and small peripheral isolates. The peripheral isolates might face migration from the infected mainland or not. Some of the isolates are infected with Wolbachia while others have lost the infection. Our results suggest that it is the ones that lose their Wolbachia that are more likely to diverge into new species.
For simplicity, we assume haploid sexual organisms, an assumption that often has been made for theoretical analyses involving multiple interacting loci (e.g. [13], [40]). Generations are discrete and non-overlapping. Individuals reproduce sexually with a primary sex ratio of 1∶1. The life cycle consists of four steps: migration, viability selection, sexual selection, and reproduction. It is assumed that the first three steps happen in the haploid phase of the organism. The diploid phase occurs during reproduction and ends with the production of the male and female gametes.
Organisms are characterized by their cyto-genotype. Individuals can be either infected with Wolbachia or not. Two nuclear loci are considered which recombine fully, a locus P for female mating preference, and a locus T for a male trait. Although we have not analyzed intermediate rates of recombination in this study it is worth noting that linkage between trait and preference locus will assist the spread of mutants at the preference locus and, further, increase the frequencies of the preferred male trait.
The life cycle starts with migration of the haploid organisms. Migration occurs only from the mainland to the island. Each generation a fraction m on the island is replaced by mainland organisms. After migration, viability selection takes place. We assume that selection on male trait alleles acts differently in mainland and island. On the mainland, T 1 is favored and therefore fixed. On the island, however, T 2-individuals have a (1+s)-times higher viability than T 1-individuals. Therefore, there is differential selection for the trait on the island relative to the mainland.
Mating is nonrandom due to female mating preferences. We assume that females of genotype P 1 and P 2 have characteristic mating preference strengths, a 1 and a 2, respectively. In all simulations shown below, females with genotype P 1 show no mating preference, i.e. a 1 = 1, whereas P 2 genotype females favor mating with T 2 males, i.e. a 2>1. Mating of P 1 females is random and the frequency of mating with T 1 and T 2 males is proportional to the relative abundance of the two male traits. P 2 females, however, mate a 2-times more often with T 2-males than P 1 females do. The frequency of mating with the different male types is proportional to the relative abundance of the respective male trait weighed by the strength of mating preference. Normalization ensures the same overall number of matings for P 1 and P 2 genotype females (see Text S1 for a mathematical description). This structure using differential selection at a trait locus and a preference for that trait is similar to other modeling efforts of mate preference (e.g. [6], [13]).
After sexual selection the haploid individuals produce gametes that fuse to a diploid zygote. In this diploid phase some individuals suffer from Wolbachia-induced unidirectional CI. Following Fine [38], we describe the Wolbachia dynamic by three parameters: (a) the level of cytoplasmic incompatibility, l CI, defined as the fraction of offspring that die in matings between infected males and uninfected females, (b) the fecundity reduction, f, of infected females relative to uninfected females, and (c) the transmission rate, t, defined as the fraction of offspring which inherit the infection from their mother. Note that Wolbachia is transmitted only maternally through the cytoplasm of the egg.
The verbal description of the life cycle can be formalized. The corresponding mathematical model consists of a system of 8 coupled difference equations. A precise mathematical description is given in the supplementary material (Text S1). Table 1 summarizes the definitions of the parameters and symbols. In general, the model is too complex to be solved analytically. Therefore analytical results are only given for special cases and computer simulations were performed to analyze the general model (see [6] for details concerning the simulations).
Table 1. Definitions of the parameters and symbols used in the model.
| Parameter | Description |
| m | migration rate |
| lCI | level of cytoplasmic incompatibility |
| F | fecundity reduction of infected females |
| T | transmission rate of Wolbachia |
| S | viability selection coefficient at locus T |
| a 1; a 2 | mating preference strength coefficient |
| T 1; T 2 | alleles at male trait locus T |
| P 1;P 2 | alleles at mating preference locus P |
Note that on the island individuals with genotype T 2 have a (1+s)-times higher probability to survive than T 1 individuals. Furher, females of genotype P 2 mate a 2 times more often with T 2 males than with T 1 males. In our simulations P 1 females show no mating discrimination (a 1 = 1).
Results
Throughout the following sections we assume complete Wolbachia-transmission, i.e. t = 1. The case of incomplete transmission is considered in the supplementary material (Text S5).
Stability of Postzygotic Isolation
In the first part of the results section we investigate under which circumstances the island remains at low infection frequencies in the face of migration from an infected mainland. In this situation there is an infection polymorphism between the infected mainland and the (mainly) uninfected island, and unidirectional CI causes postzygotic isolation between the two populations. We analyze the stability of this postzygotic isolation just after secondary contact and in the absence of sexual selection.
Critical Migration Rate
Previously, it was shown for both bidirectional CI and nuclear based mating incompatibilities that the stability of postzygotic isolation can be described in terms of a critical migration rate [6], [26]. It was shown that postzygotic isolation between two populations is stable if migration is below a critical value. However, if this critical migration rate is exceeded, postzygotic isolation gets inevitably lost. This is because selection is frequency dependent on the mating incompatibilities. Here, we follow Flor et al. [37] and use the term critical migration rate in the context of unidirectional CI and define the critical migration rate as the highest migration rate below which an infection polymorphism between an infected mainland and a (mainly) uninfected island can stably persist. The critical migration rate is a function of the parameters describing the Wolbachia dynamic as well as of the selection coefficient associated with the male trait and is denoted by mc = mc(l CI, f, s).
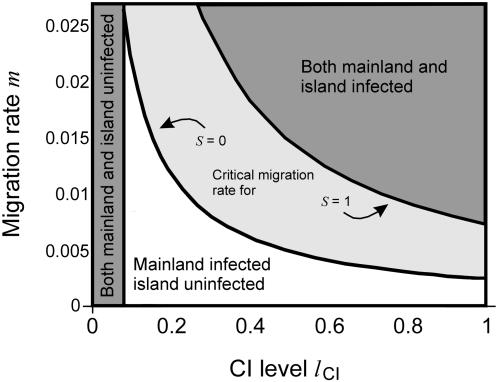
Flor et al. [37] analyzed the stability of the infection polymorphism and unidirectional CI in the absence of local adaptation. It was demonstrated analytically that the parameter space spanned by the CI level and the migration rate consists of three qualitatively different regions: (a) a region where Wolbachia goes to extinction in both populations, (b) a region where Wolbachia spreads to fixation in both populations, and (c) a region where an initially uninfected island remains at low infection frequencies despite migration from an infected mainland (fig. 2). The critical migration rate separates the third region from the other two. For low CI levels of l CI <f, critical migration rates are zero because CI is not sufficiently strong to offset the fecundity reduction. However, if CI levels are larger than the fecundity reduction, positive critical migration rates are observed. An interesting finding from that study is that high critical migration rates are reached for rather low levels of CI and is the highest for l CI = f.
Figure 2. Critical migration rates.
Shown are the critical migration rates (highest migration rates below which post-zygotic isolation stably persists) as a function of the CI level for f = 0.1 and s = 0 or s = 1. The parameter space consists of three regions. If l CI<f then Wolbachia is lost in both populations. If l CI≥f then Wolbachia persists on the mainland and can spread on the island only if migration is above the critical migration rate but cannot if migration is below this threshold. The critical migration rate separates the latter region from the other two and increases with increasing selection coefficient s.
In the present study we investigate how local adaptation affects the stability of infection polymorphism and unidirectional CI. Our results demonstrate that generally the critical migration rate increases with increasing selection coefficient s. This is because local adaptation favors residents in comparison to migrants, and the infection type and selected locus tend to be coupled in association disequilibrium, which imparts a selective advantage to both in the resident population (uninfected cytotypes are associated with the selectively favored allele T 2 in the island population). Local adaptation can result in comparatively high critical migration rates (fig. 2). If, for example, the CI level is l CI = 0.5 and f = 0.1 then the critical migration rate for s = 0 is mc = 0.5%, but for s = 1 it is mc = 1.6%. Note that s = 1 corresponds to a two-fold fitness advantage for the resident allele. This shows that local adaptation significantly stabilizes postzygotic isolation induced by unidirectional CI.
Analytical Analysis
Telschow et al. [26] determined analytically critical migration rates in a two population model with bidirectional CI using standard fixpoint analysis. This method can be applied to unidirectional CI if no viability selection at the trait locus is considered (for details see [37]). For the mainland-island scenario considered in the present study the critical migration rate is
| (1) |
if l CI≥f. If l CI <f then the Wolbachia infection cannot persist stably on the mainland and the critical migration rate is zero (see also fig. 2).
Formula (1) does not incorporate the effects of local adaptation. In this case, it is not possible to determine the critical migration rate analytically. However, we were able to derive analytically a lower estimation of mc (see Text S2 for a proof). For l CI≥f and s≥0 it holds that
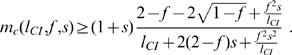 |
(2) |
Note that the right-hand side of equation (2) reduces for s = 0 to formula (1).
Three conclusions can be drawn from inequality (2). First, adding a locus under local selection results generally in an increase of the critical migration rate. A straightforward calculation shows that mc(l CI, f, s)>mc(l CI, f, 0) for all s>0. Second, linearization of mc around s = 0 reveals that mc (lCI, f, s)≈(1+s)mc (lCI, f, 0) if s is small. Third, the critical migration rate converges to one if s goes to infinity. The important implication here is that large s result in large critical migration rates.
Gene Flow Reduction and Local Adaptation
Next we investigate how the infection polymorphism and unidirectional CI affect the genetic divergence at the locus under differential selection and interpret the results in terms of the concept of the effective migration rate [27], [41], [42].
Effective Migration Rate
We follow Telschow et al. [42] and use a definition of the effective migration rate that was introduced to measure gene flow on weakly selected loci. Considering a locus under local adaptation, the effective migration rate between two populations, where one is infected with Wolbachia, is defined as the migration rate that-in a scenario without Wolbachia-would result in the same equilibrium frequencies at that locus. Note that the scenario where both populations are infected yields the same divergence at the selected locus as the scenario without Wolbachia, and the effective migration rate is equal to the real migration rate.
Telschow et al. [27] derived for bidirectional CI an analytical approximation for the effective migration rate. Here, we point out that this approach is applicable to the case of unidirectional CI (see supplementary material (Text S3) for details). Under the assumption that migration rate m and selection coefficient s are small the effective migration rate between an infected mainland and an uninfected island is in good approximation
| (3) |
The key point for deriving this formula is to consider the matriline of female migrants over successive generations. Formula (3) shows that a CI level of 0.5 results in a reduction of the effective migration rate of more than 50%, a CI level of 1 results in zero gene flow. This is counterintuitive because only infected male migrants suffer from CI. However, the recursive nature of reduction in effective migration rate shows that gene flow is inhibited in the matriline too because each generation sons of female migrants inherit the infection and therefore suffer from CI, thus further reducing input of genes from migrant descendants into the population.
Local Adaptation
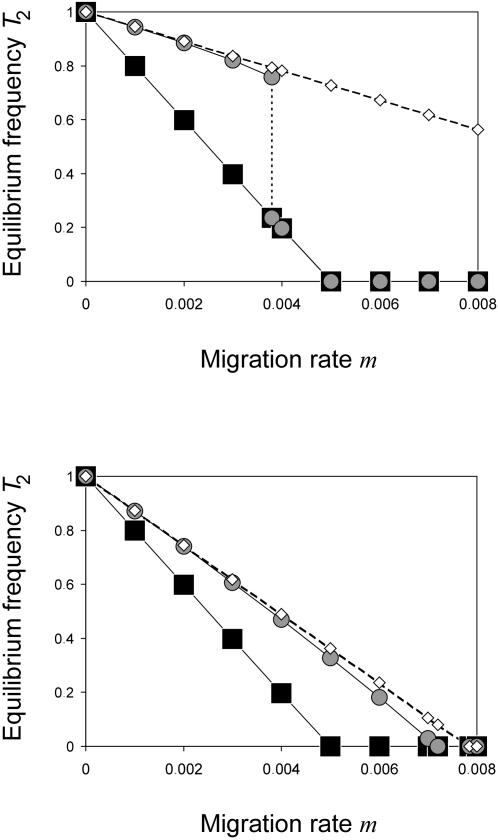
We calculated the frequencies of the locally adapted T 2 allele on the island for the scenario where the mainland is infected but the island not, and compared them with the scenario where both mainland and island are infected. Figure 3 shows that the former scenario results in higher genetic divergence between the populations at the selected locus over a broad range of migration rates. This holds true for varying selection coefficients (results not shown). The basic reason is that the selected locus and the cytotype are in linkage disequilibrium. On the island, the positively selected allele T 2 is associated with uninfected individuals. Because uninfected individuals suffer less from CI, this linkage disequilibrium boosts the frequency of the T 2 allele. However, these linkage disequilibria occur only as long as Wolbachia cannot spread on the island. If migration is above the critical migration rate, Wolbachia spreads on the island and no differences in T 2 allele frequencies are seen (fig. 3a). Figure 3b shows that there is a range where local adaptation disappears entirely on the island in the absence of CI, but is maintained in the presence of CI. For example, if m = 0.005 and s = 0.005 then the T 2 allele goes to extinction when the island is infected but reaches high frequencies of 37.7% when the island is uninfected.
Figure 3. Equilibrium frequencies of T 2 on the island.
Black symbols indicate that both mainland and island are infected with Wolbachia. The frequencies were calculated analytically with formula (5). Gray symbols show numerically determined equilibrium frequencies for starting conditions with an infected mainland and an uninfected island. White diamonds show approximations of the latter case using formula (8). Parameters are f = 0.1, s = 0.005 in both graphs, l CI = 0.7 in (a), and l CI = 0.3 in (b).
Analytical Analysis
The dynamics of the T
2 allele can be investigated analytically using the effective migration rate introduced above. First, let us consider the simplest situation where both mainland and island are uninfected. Note that the resulting dynamics do not differ from the situation where both populations are infected. Let 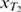 and
and 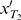 denote the frequencies of the T
2 allele on the island in subsequent generations. Then it holds that
denote the frequencies of the T
2 allele on the island in subsequent generations. Then it holds that
| (4) |
To determine the equilibrium frequency
of the system, we solve equation (4) for
. This yields
| (5) |
Next, we consider the general case which includes the situation with an infected mainland and an uninfected island. The dynamics are now more complex and cannot be solved analytically anymore. However, good analytical approximations can be achieved using the effective migration rate. Our simple approach is to substitute m by me in equations (4) and (5). This yields the following approximation of the dynamics of T 2 and its equilibrium frequencies,
| (6) |
| (7) |
Combining (3) and (7) under the assumption that m is small results in the following approximation for the equilibrium frequencies of T 2
| (8) |
As illustrated in figure 3, formula (8) yields good approximations of the real equilibrium frequencies of T 2 calculated by computer simulations. Note that formula (8) applies only to the situation where migration is below the critical migration rate (see fig. 3a). If migration is above this critical value, the equilibrium frequencies are given by (5).
A comparison of formula (5) and (8) demonstrates that T
2 always reaches higher frequencies in the scenario with an uninfected island than in the scenario with an infected island (see also fig. 3). Taking the difference of both we see that the increase in frequency of the T
2 allele is linear in l
CI and computes for small m to 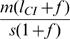 . Moreover, the results demonstrate that unidirectional CI significantly enlarges the range of parameters where local adaptation on the island is possible. In the scenario with both mainland and island infected the T
2 allele gets lost on the island if m≥s/(1+s), whereas it can persist on an uninfected island as long as me≈m(1−l
CI)/(1+f)<s/(1+s) .
. Moreover, the results demonstrate that unidirectional CI significantly enlarges the range of parameters where local adaptation on the island is possible. In the scenario with both mainland and island infected the T
2 allele gets lost on the island if m≥s/(1+s), whereas it can persist on an uninfected island as long as me≈m(1−l
CI)/(1+f)<s/(1+s) .
Premating Isolation
In the third part of the results section we investigate under which circumstances postzygotic isolation (caused by unidirectional CI) selects for premating isolation. Generally, the migration rate is chosen to be below the critical migration rate.
Equilibrium Frequencies
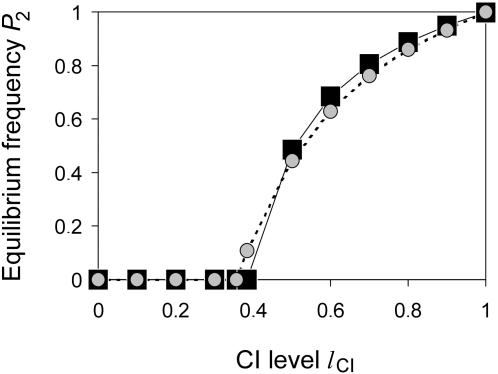
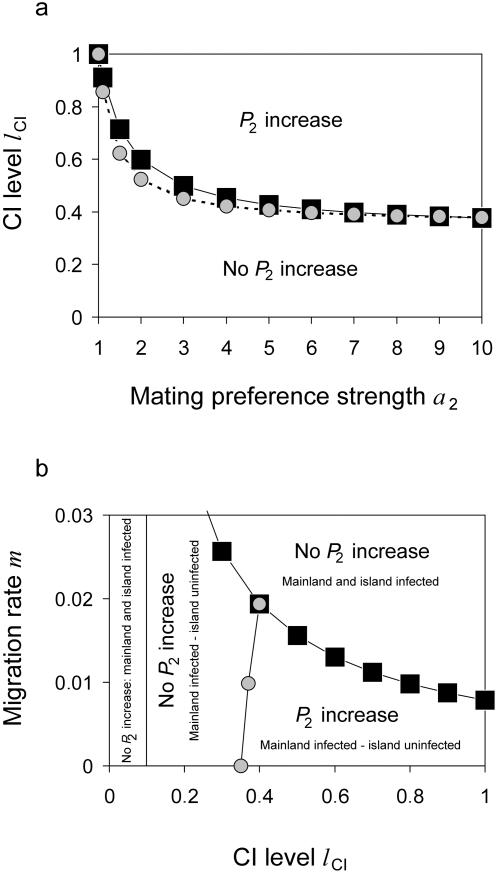
To investigate the impact of unidirectional CI on genetic divergence we first determined equilibrium frequencies of the system after introduction of the preference allele P 2. In all simulations performed, a minimal level of CI was necessary for P 2 to spread. If the mating preference strength is a 2 = 10, as shown in figure 4, then P 2 goes to extinction if the CI level is below 0.384 but spreads on the island if CI is above this threshold. The frequencies of P 2 increase with increasing CI level and reach high frequencies close to one for high levels of CI.
Figure 4. Equilibrium frequencies of P 2 after introduction on the island with the low frequency of 0.1%.
Black squares indicate simulation results, gray circles values determined by formula (16). The figure illustrates the finding that P 2 spreads on the island if the CI level is above a threshold but goes to extinction if the CI level is below. Parameters are a 2 = 10, f = 0.1, s = 0.1, m = 0.003.
The minimal CI level for P 2 to spread has its roots in two opposing forces. CI creates a selective advantage for P 2 but in order to spread this advantage must be sufficient to offset the gene flow from the mainland. Note that choosiness itself creates a double advantage for P 2 females. First, mating with the locally better adapted T 2 males results in locally better adapted offspring. Second, matings with T 2 males result less often in CI because T 2 males are less likely to be infected with Wolbachia. The latter can be a huge advantage because P 2 females are mostly not infected with Wolbachia. From the female's perspective, the advantage of being choosy is therefore not only to find a male that fits the environment but also to find a male that is compatible with one's own cytotype. Because the selected allele and cytotype are in association, female choice of the selected allele enhances chances of mating with a compatible cytotype.
Thresholds for Divergence at the Preference Locus
In what follows we screened the parameter space more generally. Figure 5a shows the plane spanned by the preference strength and the CI level. The mutant at the preference locus P 2 cannot spread for low CI levels no matter how strong the mating preference is. However, if the CI level is above a threshold, P 2 spreads on the island. The threshold CI level decreases with increasing preference strength a 2. Both increasing viability selection and decreasing migration reduce this threshold further (results not shown). Qualitatively similar results were presented by Servedio [13] for a mainland-island model of reinforcement where postzygotic isolation is caused by nuclear epistatic interactions.
Figure 5. Thresholds for the spread of the mating preference mutant.
Graph (a): The parameter plane spanned by the preference strength and the CI level consists of two areas. For low levels of CI, P 2 cannot spread no matter how strong the mating preference is. For CI levels above a certain threshold, however, P 2 spreads on the island. Black squares indicate simulation results, gray circles values determined by formula (17). Graph (b): The parameter space spanned by the CI level and the migration rate consists of four areas. First, if l CI<f then mainland and island are uninfected and P 2 cannot spread. Second, if m>mc then both mainland and island are infected and P 2 cannot spread. Third and fourth, if l CI>f and m<mc then P 2 can spread if the CI level is above a threshold but cannot if the CI level is below. Parameters are f = 0.1 in both graphs, m = 0.001, s = 0.1 in (a), and a 2 = 10, s = 1 in (b).
Figure 5b shows the plane spanned by the CI level and the migration rate. Four areas can be seen. First, if l CI<f then both mainland and island are uninfected and P 2 cannot spread. Second, if m>mc then both mainland and island are infected and P 2 cannot spread. Third and fourth, if l CI>f and m<mc then P 2 can spread if the CI level is above a threshold but cannot if the CI level is below. The important implication of figure 5b is that moderate CI levels select for premating isolation in a larger part of the parameter space than high CI levels. This is because infection differences between the mainland and island population are maintained for higher m when the CI level is not too high.
Analytical Analysis
As discussed above, there are two opposing forces acting on the preference mutant P 2. On the one side, P 2 individuals have a selective advantage over P 1 individuals because they are less often involved in incompatibility matings. On the other side there is permanent gene flow of the P 1 allele from the mainland. Here, we formalize the verbal reasoning and derive heuristic formulae for the calculation of P 2 allele frequencies.
We use the above defined function F = F(x, m, s) to describe selection and migration acting on the preference locus. In order to apply the function F to the P 2 dynamics we will define an “effective selection coefficient” se that describes the selective advantage of P 2 over P 1. In addition, we take into account that gene flow is appropriately described by the effective migration rate me. As we will show, the following equations are good approximations for the dynamics and equilibrium frequencies of the P 2 allele,
| (9) |
| (10) |
Here, 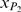 and
and 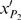 denote the frequencies of the P
2 allele on the island in subsequent generations, and
denote the frequencies of the P
2 allele on the island in subsequent generations, and 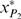 its equilibrium frequency.
its equilibrium frequency.
In order to define an effective selection coefficient for a rare P
2 allele in a P
1 population we determine the average fitness of the respective alleles. First, we consider the case that P
2 females mate exclusively with T
2 males, i.e. a
2 = ∞. Under this assumption, there is strong linkage disequilibrium between P
2 and T
2. Let xW denote the frequency of Wolbachia on the island. Then the average fitness of P
1 is 1−l
CI
xW. The fitness of P
2 individuals is 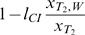 , where
, where 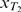 denotes the frequency of T
2 on the island and
denotes the frequency of T
2 on the island and 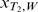 the frequency of infected T
2 individuals. As the effective selection coefficient we take the difference of both,
the frequency of infected T
2 individuals. As the effective selection coefficient we take the difference of both,
| (11) |
In order to get a useful approximation of se, we assume that 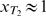 . This is justified for small m. Denoting the frequency of infected T
1 individuals with
. This is justified for small m. Denoting the frequency of infected T
1 individuals with 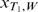 we get
we get
| (12) |
As shown in the supplementary material (Text S4), a good approximation of 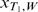 for small s is 2m/(1+f). Substitution into formula (12) yields the following useful approximation for the effective selection coefficient which depends only on the parameters of the system,
for small s is 2m/(1+f). Substitution into formula (12) yields the following useful approximation for the effective selection coefficient which depends only on the parameters of the system,
| (13) |
In a next step, we consider the case where a
2<∞. In general, the selective advantage of P
2 over P
1 is reduced by smaller a
2. This is because P
2 females are more likely to be involved in incompatibility matings if a
2 is low, whereas the fitness of P
1 individuals stays the same. For finite a
2 the fitness of a rare P
2 allele is 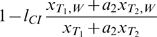 . This expression simplifies to
. This expression simplifies to 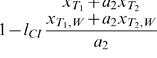 if we assume, as above, that
if we assume, as above, that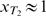 . Again, we set as the effective selection coefficient se the fitness difference of the two mating preference alleles. This results in
. Again, we set as the effective selection coefficient se the fitness difference of the two mating preference alleles. This results in
| (14) |
Note that if a 2 goes to infinity, formula (14) correctly reduces to formula (13). To achieve approximations for P 2 equilibrium frequencies, we substitute (3) and (14) in (10). This yields
| (15) |
For small m formula (15) reduces to
| (16) |
A consequence of formula (16) is that P 2 can spread into the population only if
| (17) |
but goes to extinction if the CI level is below this threshold value. Note that the threshold CI level decreases with increasing preference strength and converges to 1/3 if a 2 goes to infinity. Figure 4 and 5a illustrate formulae (16) and (17) and demonstrate that they approximate the numerically determined values well. The approximations are especially good when mating preference is strong.
Discussion
In this article we investigated the role of Wolbachia-induced unidirectional CI on genetic divergence and reinforcement using a mainland-island model. We demonstrated analytically that (a) the infection polymorphism between populations is stabilized by local adaptation, (b) gene flow between the populations is reduced but divergence at a selected locus enhanced, and (c) unidirectional CI selects for premating isolation in a mostly uninfected island population receiving migration from a Wolbachia-infected mainland. Interestingly, premating isolation is most likely to evolve if levels of incompatibility are intermediate, if the infection causes fecundity reductions or Wolbachia transmission is incomplete. This is because under these circumstances an infection pattern with an infected mainland and a mostly uninfected island can persist in the face of comparably high migration. We anticipate that if additional locally adapted alleles accumulate in the island population then stability will persist at even higher levels of CI.
These findings generally support the view that Wolbachia-induced unidirectional CI could be a factor in host divergence and speciation, but only under certain conditions. The role of Wolbachia would be to reduce gene flow between populations, allowing genetic divergence for locally adaptive traits, and to select for premating isolation. Furthermore, the association of infection status with locally adapted alleles and local male traits creates positive selection for females with local mate preference, both because of the advantages of local adapted genotypes and of mating with compatible cytotype males.
Our results suggest that peripheral populations that have lost their Wolbachia infection are able to maintain local adaptation in the face of migration better than peripheral populations that maintain their infection (fig. 1b). The threshold migration rate for maintenance of the infection difference is therefore increased, and premating isolation more readily evolves. This means that if recurrent peripheral populations occur, it is the ones that lose their Wolbachia that are more likely to diverge into new species. This could be considered a form of population selection, where populations that lose their infections are better able to “resist” gene flow and therefore locally adapt and evolve into new species. The scenario is not simply hypothetical. North American populations of the fire ant Solenopsis invicta, which were established by presumably small founding populations due to human transport, are devoid of Wolbachia, whereas South American source populations show infection polymorphisms [43], [44]. Similarly, Atlantic coast populations of the beetle Chelymorpha alternans are infected with two Wolbachia strains, whereas some Pacific coast populations have lost one of the Wolbachia [22]. Thus, the scenarios envisioned here could occur in nature. A counter example is the spread of Wolbachia in uninfected populations of Drosophila simulans in uninfected North American populations [33].
Our results also have important ramifications for classical reinforcement theory. A standard critique in reinforcement is that gene flow might overwhelm the selective advantage of being choosy [45]. Although previous work has shown that reinforcement is possible (e.g. [12], [13], [46]), most of the studies are purely simulation based (but see [47]). In the present study we developed a new method to analyze the reinforcement dynamics analytically. In this approach gene flow is modeled by an effective migration rate and the advantage of being choosy by an effective selection coefficient. We believe that this approach is also applicable to other reinforcement scenarios, i.e. with postzygotic isolation caused by nuclear mating incompatibilities.
The possible role of Wolbachia in host speciation has generated some controversy over the past decade [3], [6], [18], [29], [48]. One major criticism against Wolbachia-induced speciation is that in most systems Wolbachia cannot totally prevent gene flow because both levels of cytoplasmic incompatibility and transmission rates are incomplete [49]. Our results show that unidirectional CI is most likely to select for premating isolation if levels of incompatibility are intermediate, if the infection causes fecundity reductions or Wolbachia transmission is incomplete (see Text S5). The fact that in most systems cytoplasmic incompatibility is incomplete broadens therefore the conditions under which unidirectional CI selects for premating isolation and is, based on our analysis, rather an argument for a role of Wolbachia in host speciation than against it.
A second criticism is that unidirectional CI is unlikely to be stable. Crucial in our speciation scenario is that infected and uninfected host populations can stably persist in the face of migration. In a previous study we have demonstrated that both fecundity reduction and incomplete transmission rate can prevent Wolbachia from spreading [37]. The observed critical migration rates, however, are relatively low, thus narrowing the range where unidirectional CI as a single factor could promote host speciation. We expect that unidirectional CI is most likely to promote speciation if it acts in concert with other genetic factors that stabilize infection differences and enhance critical migration rates. In the present study we have shown that locally adapted alleles substantially stabilize postzygotic isolation (fig. 2). Other factors that will likely stabilize infection differences and postzygotic isolation are cytoplasmic sex ratio distorters [50], nuclear based mating incompatibilities (Telschow, unpublished results), and the accumulation of multiple adaptive genes within the diverging populations. The latter would be particularly important when epistatic interactions among adapted loci occur. As shown for the single adapted locus case and for pairwise genetic incompatibilities [27], [28, here], these effects further enhance the association of infection type with adapted loci, increasing the frequencies of each in the presence of immigration.
A third criticism of the possible role of unidirectional CI in divergence and speciation is that nuclear gene flow is reduced or prevented only in one direction (from the infected to the uninfected population), whereas nuclear genes flow freely from the uninfected to the infected population. We have not analyzed this effect in this article, since we considered only one-way migration from the mainland to the island population. Therefore, the model presented here is likely to apply only to conditions where migration from a small island population to a large mainland population is much lower than in the other direction. However, we also investigated an extended model with two populations and migration in both directions (see [51] for details). For this extended model the effective migration rate from an uninfected population to an infected population can be approximated by m/(1+l CI) (see formula (1) in [27]); a CI level of l CI = 1, for example, results in 50% gene flow reduction. As shown in the results, the effective migration rate from an infected to an uninfected population is approximately m(1−l CI) and therefore generally results in higher gene flow reduction. If the CI level is one then gene flow is prevented totally. These results together show that gene flow between an infected and an uninfected population is reduced in both directions but that this reduction is asymmetric. The resulting asymmetric gene flow reduction between the populations, however, affects the pattern of adaptation in the Wolbachia host; adaptation is favored in the uninfected population but impeded in the infected population. A comparison of the mainland-island model with the two-way migration model reveals that back migration facilitates local adaptation and the spread of mating preference mutants on the island. Under certain parameter values, asymmetric gene flow and runaway sexual selection leads to an increase of the introduced female preference allele and fixation of the preference mutant or the preferred male trait in both populations, whereas under other parameter values it leads to divergence in the two populations in preference and male trait alleles. This is in concordance with previous theoretical studies [6], [13]).
The full impact of unidirectional CI on host speciation in nature will likely involve more complex population structures than modeled here. The results on the critical migration rates suggest that Wolbachia infections might occur in mosaic patterns with infected and uninfected patches close by. We have shown that under these circumstances unidirectional CI selects for female mating preferences in uninfected patches facing migration from infected patches. This observation lets us state the general prediction that species infected with Wolbachia (causing unidirectional CI) will evolve premating discrimination more rapidly than their uninfected sibling species. So far there is one case in concordance with this view. The mushroom feeding Drosophila recens is infected with unidirectional CI inducing Wolbachia and shows, when allopatric populations are considered, significantly stronger mating discrimination than the uninfected sibling species D. subquinaria [5], [36]. Of course, this case alone is not sufficient to test our hypothesis. Therefore we suggest a comparative study similar to the work of Coyne and Orr [52], [53]. These authors screened over 171 pairs of Drosophila species and concluded that sym-or parapatric pairs show larger mate discrimination than allopatric pairs. A re-analysis of these data with infection status added may reveal whether earlier evolution of mate discrimination is associated with closely related species pairs where one is infected with Wolbachia.
Our model scenario involves a full allopatric phase during which the locally adapted allele spreads on the island. The mutant at the preference locus is introduced after secondary contact is established. An alternative model setting would allow a certain amount of migration from the start. It is important to remark that the full allopatry at the beginning is not a necessary condition for reproductive isolation to evolve. A modification of our model with migration from the start does not change the results qualitatively as long as migration is below the critical migration rate.
In this study we analyzed the question whether a single Wolbachia strain causing unidirectional CI can select for local adaptation and premating isolation. Previously, it was shown that two Wolbachia strains causing bidirectional CI promote local adaptation and select for rapid premating isolation under a broad variety of conditions [6]. This is mainly because bidirectional CI can persist up to high critical migration rates of over 15% per generation [26]. As shown in this study, critical migration rates for unidirectional CI are much lower, resulting in a comparatively weak selection for premating isolation. These results suggest that once bidirectional CI is established in a system, its impact on host speciation is much stronger than that of unidirectional CI. Nevertheless, the full significance of unidirectional CI for host speciation might be bigger than that of bidirectional CI. First of all, unidirectional CI is much more common in nature because it requires that only one population is infected whereas bidirectional CI requires different infections in both populations. Furthermore, in case of bidirectional CI, one Wolbachia strain is inevitably eliminated if postzygotic isolation is destroyed. Postzygotic isolation can be reestablished only if the system becomes infected again with a second Wolbachia strain, a rather unlikely event. In the unidirectional CI scenario, however, reestablishment of postzygotic isolation involves only the loss of the infection in an island population, an event which is much more likely to reoccur. In fact recurrent establishment of peripheral isolate populations from a central source population could produce the circumstances for repeated opportunities for local adaptation and speciation. Our results suggest that when these conditions occur, those peripheral populations that have lost their infections are more likely to maintain locally adapted alleles and to evolve reinforcement of mate discrimination.
In summary, our results demonstrate that a stable coexistence between infected and uninfected host populations is possible if migration is below a critical migration rate. Under these circumstances unidirectional CI acts as a postzygotic isolation mechanism and selects for local adaptation and premating isolation under a variety of conditions. These results generally suggest that unidirectional CI could be a factor in speciation processes of arthropods.
Supporting Information
Model description.
(0.05 MB DOC)
Lower estimation of the critical migration rate.
(0.04 MB DOC)
Formula for the effective migration rate.
(0.02 MB DOC)
Equilibrium Frequencies of infected T 1 Individuals
(0.03 MB DOC)
Incomplete transmission.
(0.03 MB DOC)
Acknowledgments
We thank Menno Schilthuizen, Norman A. Johnson, Sergey Gavrilets, Andy Gardner and Jan Engelstädter for many helpful comments and their constructive critics.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: The study was funded by the Deutsche Forschungsgemeinschaft (SFB 618), the National Science Foundation (NSF: EF-0328363), the Grant of Biodiversity Research 21COE (A14), and the Japanese Society for the Promotion of Science (JSPS).
References
- 1.Werren JH. Biology of Wolbachia. Annual Review in Entomology. 1997;42:587–609. doi: 10.1146/annurev.ento.42.1.587. [DOI] [PubMed] [Google Scholar]
- 2.Bourtzis K, Miller T. Boca Raton: CRC Press; 2003. Insect Symbiosis. [Google Scholar]
- 3.Werren JH. Wolbachia and speciation. In: Howard D, Berlocher S, editors. Endless Forms: Species and Speciation. Oxford University Press; 1998. pp. 245–260. [Google Scholar]
- 4.Bordenstein SR, O'Hara FP, Werren JH. Wolbachia-induced bidirectional incompatibility precedes other hybrid incompatibilities in Nasonia. Nature. 2001;409:707–710. doi: 10.1038/35055543. [DOI] [PubMed] [Google Scholar]
- 5.Shoemaker DD, Katju V, Jaenike J. Wolbachia and the evolution of reproductive isolation between Drosophila recens and Drosophila subquinaria. Evolution. 1999;53:1157–1164. doi: 10.1111/j.1558-5646.1999.tb04529.x. [DOI] [PubMed] [Google Scholar]
- 6.Telschow A, Hammerstein P, Werren JH. The Effect of Wolbachia versus genetic incompatibilities on reinforcement and speciation. Evolution. 2005;59:1607–1619. [PubMed] [Google Scholar]
- 7.Werren JH, Zhang W, Guo LR. Evolution and phylogeny of Wolbachia-reproductive parasites of arthropods. Proceedings of the Royal Society B. 1995;261:55–63. doi: 10.1098/rspb.1995.0117. [DOI] [PubMed] [Google Scholar]
- 8.Jeyaprakash A, Hoy MA. Long PCR improves Wolbachia DNA amplification: wsp sequences found in 76% of sixty-three arthropod species. Insect Molecular Biology. 2000;9:393–405. doi: 10.1046/j.1365-2583.2000.00203.x. [DOI] [PubMed] [Google Scholar]
- 9.Werren JH, Windsor DW. Wolbachia infection frequencies in insects: evidence of a global equilibrium? Proceedings of the Royal Society B. 2000;267:1277–1285. doi: 10.1098/rspb.2000.1139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gavrilets S. Monographs in Population Biology. Vol. 41. Princeton, NJ: Princeton Univ. Press; 2004. Fitness landscapes and the origin of species. [Google Scholar]
- 11.Sanderson Can gene flow prevent reinforcement? Evolution. 1989;43:1223–1235. doi: 10.1111/j.1558-5646.1989.tb02570.x. [DOI] [PubMed] [Google Scholar]
- 12.Liu LW, Price TD. Speciation by reinforcement of premating isolation. Evolution. 1994;48:1451–1459. doi: 10.1111/j.1558-5646.1994.tb02187.x. [DOI] [PubMed] [Google Scholar]
- 13.Servedio MR. Reinforcement and the genetics of nonrandom mating. Evolution. 2000;54:21–29. doi: 10.1111/j.0014-3820.2000.tb00003.x. [DOI] [PubMed] [Google Scholar]
- 14.Bourtzis K, Braig HR, Karr TL. Cytoplasmic Incompatibility, In: Bourtzis K, Miller T, editors. Insect Symbiosis. Boca Raton: CRC Press; 2003. pp. 217–246. [Google Scholar]
- 15.Hoffmann AA, Turelli M. Cytoplasmic incompatibility in insects, In: O'Neill SL, Hoffmann AA, Werren JH, editors. Influential Passengers. New York: Oxford University Press; 1997. pp. 42–80. [Google Scholar]
- 16.Laven H. Speciation by cytoplasmic isolation in the Culex pipiens complex. Cold Spring Harbor Symp. Quant. Biol. 1959;24:166–73. doi: 10.1101/sqb.1959.024.01.017. [DOI] [PubMed] [Google Scholar]
- 17.Breeuwer JAJ, Werren JH. Microorganisms associated with chromosome destruction and reproductive: isolation between two insect species. Nature. 1990;346:558–560. doi: 10.1038/346558a0. [DOI] [PubMed] [Google Scholar]
- 18.Bordenstein SR. Symbiosis and the Origin of Species, In: Bourtzis K, Miller T, editors. Insect Symbiosis. Boca Raton: CRC Press; 2003. pp. 283–304. [Google Scholar]
- 19.Mercot H, Llorente B, Jacques M, Atlan A, Montchamp-Moreau C. Variability within the Seychelles cytoplasmic incompatibility system in Drosophila simulans. Genetics. 1995;141:1015–1023. doi: 10.1093/genetics/141.3.1015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Clancy DJ, Hoffmann AA. Cytoplasmic incompatibility in Drosophila simulans: evolving complexity. TREE. 1996;11:145–146. doi: 10.1016/0169-5347(96)30006-2. [DOI] [PubMed] [Google Scholar]
- 21.Baudry E, Emerson K, Whitworth T, Werren JH. Wolbachia and genetic variability in the birdnest blowfly Protocalliphora sialia. Molecular Ecology. 2003;12:1843–1854. doi: 10.1046/j.1365-294x.2003.01855.x. [DOI] [PubMed] [Google Scholar]
- 22.Keller GP, Windsor DM, Saucedo J, Werren JH. Reproductive effects and geographical distribution of two Wolbachia strains infecting the Neotropical beetle, Chelymorpha alternans (Chrysomelidae, Cassidinae). Molecular Ecology. 2004;13:2405–2420. doi: 10.1111/j.1365-294X.2004.02213.x. [DOI] [PubMed] [Google Scholar]
- 23.Laven H. Speciation and evolution in Culex pipiens, In: Wright JW, Pai R, editors. Genetics of Insect Vectors of Diseases. Elsevier, North Holland: 1967. pp. 251–275. [Google Scholar]
- 24.Perrot-Minnot MJ, Guo LR, Werren JH. Single and double infections of Wolbachia in the parasitic wasp Nasonia vitripennis: Effects on compatibility. Genetics. 1996;143:961–972. doi: 10.1093/genetics/143.2.961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Guillemaud T, Pasteur N, Rousset F. Contrasting levels of variability between cytoplasmic genomes and incompatibility types in the mosquitoe Culex pipiens. Proceedings of the Royal Society B. 1997;264:245–251. doi: 10.1098/rspb.1997.0035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Telschow A, Yamamura N, Werren JH. Bidirectional cytoplasmic incompatibility and the stable coexistence of two Wolbachia strains in parapatric host populations. Journal of Theoretical Biology. 2005;235:265–274. doi: 10.1016/j.jtbi.2005.01.008. [DOI] [PubMed] [Google Scholar]
- 27.Telschow A, Hammerstein P, Werren JH. Effects of Wolbachia on genetic divergence between populations: models with two way migration. American Naturalist. 2002;160:S54–S66. doi: 10.1086/342153. [DOI] [PubMed] [Google Scholar]
- 28.Telschow A, Hammerstein P, Werren JH. Effects of Wolbachia on genetic divergence between populations: mainland-island model. Integrative Comp. Biol. 2002;42:340–351. doi: 10.1093/icb/42.2.340. [DOI] [PubMed] [Google Scholar]
- 29.Hurst GDD, Schilthuizen M. Selfish genetic elements and speciation. Heredity. 1998;80:2–8. [Google Scholar]
- 30.Turelli M, Barton NH, Coyne JA. Theory and speciation. TREE. 2001;16:330–343. doi: 10.1016/s0169-5347(01)02177-2. [DOI] [PubMed] [Google Scholar]
- 31.Weeks AR, Reynolds KT, Hoffmann AA, Mann H. 2002. Wolbachia dynamics and host effects: what has (and has not) been demonstrated? [Google Scholar]
- 32.Coyne JA, Orr HA. Sunderland, Massachusetts, USA: Sinauer Associates; 2004. Speciation. [Google Scholar]
- 33.Turelli M, Hoffmann AA. Rapid spread of an inherited incompatibility factor in California Drosophila. Nature. 1991;353:440–442. doi: 10.1038/353440a0. [DOI] [PubMed] [Google Scholar]
- 34.Vala F, Egas M, Breeuwer JAJ, Sabelis MW. Wolbachia affects oviposition and mating behavior of its spider mite host. Journal of Evolutionary Biology. 2004;17:692–700. doi: 10.1046/j.1420-9101.2003.00679.x. [DOI] [PubMed] [Google Scholar]
- 35.Rasgon JL, Cornel AJ, Scott TW. Evolutionary history of a mosquito endosymbiont revealed through mitochondrial hitchhiking. Proceedings of the Royal Society B. 2006;273:1603–1611. doi: 10.1098/rspb.2006.3493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jaenike J, Dyer KA, Cornish C, Minhas MS. Asymmetrical reinforcement and Wolbachia infection in Drosophila. PLOS Biology. 2006;4:1852–1862. doi: 10.1371/journal.pbio.0040325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Flor M, Hammerstein P, Telschow A. Wolbachia-induced unidirectional cytoplasmic incompatibility and the stability of infection polymorphism in parapatric host populations. Journal of Evolutionary Biology. 2007;20:696–706. doi: 10.1111/j.1420-9101.2006.01252.x. [DOI] [PubMed] [Google Scholar]
- 38.Fine PEM. On the dynamics of symbiont dependent cytoplasmic incompatibility in Culicine mosquitoes. Journal of Invertebrate Pathology. 1978;30:10–18. doi: 10.1016/0022-2011(78)90102-7. [DOI] [PubMed] [Google Scholar]
- 39.Dobzhansky T. Speciation as a stage in evolutionary divergence. American Naturalist. 1940;74:312–321. [Google Scholar]
- 40.Hartl DL, Clark AG. Sunderland, Massachusetts: Sinauer Associates, Inc.; 1989. Principles of Population Genetics. [Google Scholar]
- 41.Barton NH, Bengtsson BO. The barrier to genetic exchange between hybridizing populations. Heredity. 1986;56:357–376. doi: 10.1038/hdy.1986.135. [DOI] [PubMed] [Google Scholar]
- 42.Telschow A, Engelstaedter J, Yamamura N, Hammerstein P, Hurst GDD. Asymmetric gene flow and constraints on adaptation caused by sex ratio distorters. Journal of Evolutionary Biology. 2006;19:869–878. doi: 10.1111/j.1420-9101.2005.01049.x. [DOI] [PubMed] [Google Scholar]
- 43.Shoemaker DD, Ross KG, Keller L, Vargo EL, Werren JH. Wolbachia infections in native and introduced populations of fire ants (Solenopsis spp.). Insect Molecular Biology. 2000;9:661–673. doi: 10.1046/j.1365-2583.2000.00233.x. [DOI] [PubMed] [Google Scholar]
- 44.Shoemaker DD, Ahrens M, Sheill L, Mescher M, Keller L, Ross KG. Distribution and prevalence of Wolbachia infections in native populations of the fire ant Solenopsis invicta (Hymenoptera: Formicidae). Environmental Entomology. 2003;32:1329–1336. [Google Scholar]
- 45.Mayr E. Cambridge, MA: Harvard University Press; 1963. Animal Species and Evolution. [Google Scholar]
- 46.Spencer HG, McArdle BH, Lambert DM. A theoretical investigation of speciation by reinforcement. American Naturalist. 1986;128:241–262. [Google Scholar]
- 47.Kirkpatrick M, Servedio M. The Reinforcement of Mating Preferences on an Island. Genetics. 1999;151:865–884. doi: 10.1093/genetics/151.2.865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.De Crespigny FEC, Butlin K, Wedell N. Can cytoplasmic incompatibility inducing Wolbachia promote the evolution of mate preferences? Journal of Evolutionary Biology. 2005;18:967–977. doi: 10.1111/j.1420-9101.2005.00909.x. [DOI] [PubMed] [Google Scholar]
- 49.Wade MJ. Infectious speciation. Nature. 2001;409:675–677. doi: 10.1038/35055648. [DOI] [PubMed] [Google Scholar]
- 50.Engelstaedter J, Telschow A, Hammerstein P. Infection dynamics of different Wolbachia-types within one host population. Journal of Theoretical Biology. 2004;231:345–355. doi: 10.1016/j.jtbi.2004.06.029. [DOI] [PubMed] [Google Scholar]
- 51.Telschow A. Berlin: Humboldt University; 2004. Wolbachia, Reproduktionsparasitismus und Artbildung. Ph.D. diss. [Google Scholar]
- 52.Coyne JA, Orr HA. Patterns of speciation in Drosophila. Evolution. 1989;43:362–381. doi: 10.1111/j.1558-5646.1989.tb04233.x. [DOI] [PubMed] [Google Scholar]
- 53.Coyne JA, Orr HA. Patterns of speciation in Drosophila revisited. Evolution. 1997;51:295–303. doi: 10.1111/j.1558-5646.1997.tb02412.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Model description.
(0.05 MB DOC)
Lower estimation of the critical migration rate.
(0.04 MB DOC)
Formula for the effective migration rate.
(0.02 MB DOC)
Equilibrium Frequencies of infected T 1 Individuals
(0.03 MB DOC)
Incomplete transmission.
(0.03 MB DOC)