Learning reward expectations in honeybees

Abstract

The aim of this study was to test whether honeybees develop reward expectations. In our experiment, bees first learned to associate colors with a sugar reward in a setting closely resembling a natural foraging situation. We then evaluated whether and how the sequence of the animals’ experiences with different reward magnitudes changed their later behavior in the absence of reinforcement and within an otherwise similar context. We found that the bees that had experienced increasing reward magnitudes during training assigned more time to flower inspection 24 and 48 h after training. Our design and behavioral measurements allowed us to uncouple the signal learning and the nutritional aspects of foraging from the effects of subjective reward values. We thus found that the animals behaved differently neither because they had more strongly associated the related predicting signals nor because they were fed more or faster. Our results document for the first time that honeybees develop long-term expectations of reward; these expectations can guide their foraging behavior after a relatively long pause and in the absence of reinforcement, and further experiments will aim toward an elucidation of the neural mechanisms involved in this form of learning.

Modern views on associative learning acknowledge that classical as well as instrumental conditioning depend upon associations between external cues or behavioral responses and internal representations of reward (Rescorla 1987). Within this context, the term “expectation,” or “expectancy,” denotes an activation of an internal representation of reward in the absence of reinforcement by the cues and events predicting such a reward (Tolman 1959; Logan 1960). According to theory, the reward value associated with a stimulus is not a static, intrinsic property of the stimulus. Thus, for example, animals can assign different appetitive values to a stimulus as a function of both their internal state at the time when the stimulus is encountered and the background of their previous experience with such stimulus. This means that specific neural mechanisms have evolved not only to detect the presence of reward but also to predict its occurrence and magnitude based on internal representations from past experiences, in turn activated by the subject’s current motivational status (Schultz 2000).

Studying this form of learning is critical for understanding how reward controls behavior, how it leads to the formation of reward expectations, and how the brain uses reward-related information to control goal-directed behavior. Studies on reward expectations, however, sometimes appear to be paradoxical in assessing the cognitive complexity underlying such processes, as well as the basic principles of planning and decision-making. The reason is probably to be found in the fact that an anticipatory imagery or idea aroused by learned associations is thought to underlie these phenomena. In principle, however, neither highly complex cognitive abilities nor consciousness phenomena are assumed to be the bases for the development of reward expectations (Hebb and Donderi 1987).

In invertebrate species, as opposed to vertebrate species, reward expectations have not been systematically addressed. Here, we ask whether and how the behavior of a highly social insect depends upon the development of reward expectations. Our focus is on Apis mellifera bees, animals that form large societies, appear to have evolved multiple forms of communication in the course of evolution, including the famous waggle dance (von Frisch 1967), and whose ability to associate an initially neutral stimulus (as a conditioned stimulus, or CS) with a sugar reward (as an unconditioned stimulus, or US) is at the heart of the behavioral flexibility that they exhibit during foraging (Menzel 1990, 1999). For example, honeybees perform complex time-dependent sequences of actions (e.g., Zhang et al. 2006), and learn, for example, the place and time of the day when food is available (von Frisch 1967). They also adjust their foraging efforts to the quality and quantity of available resources, and it is reasonable to ask whether they “expect” specific rewards at particular locations and times of the day, although it has not yet been proven whether they can store and retrieve multiple combinations of “what, when, and where” attributes (Menzel et al. 2006). In the present study, we addressed reward expectations in the context of honeybee foraging, because this form of learning can be revealed under conditions mimicking natural situations as closely as possible.

Our approach was straightforward: We presented bees with two variable and three constant reinforcement schedules, and observed their later behavior in the absence of reinforcement. In the variable schedules, the reward magnitude either increased (small-medium-large) or decreased (large-medium-small), whereas in the constant schedules we used three different levels of reward magnitude (small, medium, and large) equivalent to those of the variable schedules. In our experiment, the bees first had to forage individually on a relatively large patch of flowers giving off two different color signals, and learn which of these two colors was actually offering rewards. Our set-up, in addition, did not allow the bees to have immediate access to the offered reward: Each animal first needed to discriminate between the two types of flowers, then enter and walk inside a tubular flower in order to find and drink a small amount of sugar solution, and, finally, repeat this procedure several times in order to obtain a certain amount of sugar reward before returning to the hive. The use of flowers giving off two different colors demanding a certain amount of handling allowed us to separately quantify two different, still-connected aspects of the animals’ responses in the absence of reinforcement: the “correctness” of choice and the overall length of their searches for reward, or “persistence.” The first component is usually applied to measure learning and retention scores, whereas the latter might be capable of reflecting a reward-related component.

We predicted that (1) the bees from all series will show both high learning scores and significant retention scores, because they learn flower colors very fast (Menzel 1967), and only three learning trials are needed to form long-term color memories, which last for a lifetime (Menzel 1968), and (2) that in the absence of reinforcement and in an otherwise similar context, the animals would search for reward more intensively after having experienced an increasing reward schedule than after having experienced a decreasing reward schedule. The first prediction refers to the “correctness” of choice, whereas the second refers to the animals’ “persistence.” If the results fit the second prediction, they might be accounted for by means of rather simple “stimulus–response” mechanisms, without reference to expectations of reward. For example, if the bees from the different groups had differentially associated the related predicting signals during training, they might assign a different proportion of time to inspect the flowers that had previously yielded reward, as calculated from the total amount of time assigned to flower inspection, even if they show similar retention scores. Moreover, the bees’ responses during testing might reflect their most recent experience during training. By this argument, the bees in the decreasing series might retain information only on the small volume, and the bees in the increasing series might retain information only on the large volume; next, the later behavior during testing is controlled by this information. If this were the case, similar results must be expected between the large and the increasing series, and the small and decreasing series. Finally, had the bees differentially associated the related predicting signals because they were fed more or faster, one should expect differences in the animals’ responses across the constant series, because in these groups the animals received different amounts of reward, and also experienced different rates of nectar intake.

On the other hand, if the bees from the increasing series search for reward more intensively than those from the decreasing series, and, in addition, their responses cannot be accounted for by simple “stimulus–response” mechanisms, their later behavior in the absence of reinforcement will be explained only by reference to reward expectations. In other words, they behaved differently because they learned that reward magnitude either increased or decreased over time, and, therefore, expected more or less reward during testing.

Results

In our experiment, foraging bees first had to forage individually on a relatively large patch of flowers consisting of 12 yellow and 12 blue artificial feeders (“flowers”), and learn which of these two colors was actually rewarding. During the variable series, we offered either increasing (small-medium-large) or decreasing (large-medium-small) volumes of unscented sugar solution during nine successive visits by the single bees. Hence, both series offered the same total volume of sugar solution at the end of these visits. Three additional series, called the constant series, offered the same volume (small, medium, or large) of sugar solution throughout all the visits to the patch by the single bees. The bees’ foraging behavior was then observed in the absence of reward (extinction tests) 24, 25, and 48 h after the animals finished foraging on the patch. Our set-up did not allow the bees to have immediate access to the sugar reward, meaning that each bee first needed to discriminate between the two flower types, then handle a tubular flower in order to find and drink a small amount of solution, and systematically repeat this procedure in order to fill its crop as much as possible before flying back to the hive.

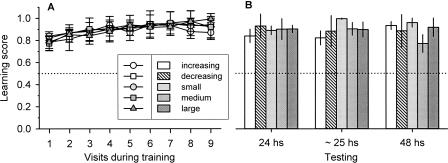
The bees showed similar learning scores for yellow and blue colors (data not shown), and we therefore pooled the data from both training situations. Hence, as we expected on the basis of previous results (Menzel 1967, 1968), the bees from all series showed both high learning scores (which developed even during the first visit to the patch) and significant retention scores at 24, 25, and 48 h after training (Fig. 1A,B; the proportion of correct choices was higher than that expected by random choices, one-sample t-test, P < 0.02). Learning scores, in addition, slightly increased throughout the successive visits, and were similar in all five experimental series (Fig. 1A, one-way ANOVA, P = 0.6), even when the total number of successful (SI) and unsuccessful inspections (UI) differed across series (Table 1). Likewise, retention scores did not differ during testing across the five experimental series (Fig. 1B, Kruskal–Wallis test, P > 0.1). Hence, color learning as related to the animals’ choices did not vary across series, meaning that any possible effect of the strength of reinforcement was saturated for this type of learning.

Figure 1.

Learning (A) and retention (B) scores (mean ± SEM), measured as the ratio between the number of inspections of the rewarded color and the total number of inspections of both colors, for the increasing (white circles and bars), decreasing (white squares and dashed bars), small (light gray circles and bars), medium (gray squares and bars), and large (dark gray triangles and bars) series. (Dotted lines) The score that would be expected via random choices: one-sample t-test, for learning score: increasing, t₍₆₎ = 8.3, P = 0.0002, N = 8; decreasing, t₍₇₎ = 4.6, P = 0.002, N = 9; small; t₍₈₎ = 8.4, P < 0.001, N = 9; medium; t₍₈₎ = 3.8, P = 0.005, N = 9; large; t₍₇₎ = 5.0, P = 0.001, N = 8; for retention score: increasing, 24 h, t₍₇₎ = 5.6, P = 0.0008, N = 8, ∼25 h, t₍₇₎ = 5.0, P = 0.0015, N = 8, 48 h, t₍₆₎ = 11.92, P < 0.0001, N = 7; decreasing, 24 h, t₍₈₎ = 11.5, P < 0.0001, N = 9, ∼25 h, t₍₆₎ = 5.4, P = 0.002, N_∼25h = 7, 48 h, t₍₄₎ = 5.2, P = 0.007, N = 5; small, 24 h, t₍₈₎ = 9.9, P < 0.0001, N = 9, ∼25 h, t₍₈₎ = 93.5, P < 0.0001, N = 9, 48 h, t₍₆₎ = 11.3, P < 0.0001, N = 7; medium, 24 h, t₍₈₎ = 12.4, P < 0.0001, N = 9, ∼25 h, t₍₇₎ = 6.9, P = 0.0002, N = 8, 48 h, t₍₄₎ = 3.3, P = 0.02, N = 5; large, 24 h, t₍₇₎ = 12.0, P < 0.0001, N = 8, ∼25 h, t₍₇₎ = 5.8, P = 0.0006, N = 8, 48 h, t₍₃₎ = 5.0, P = 0.01, N = 4. One-way ANOVA for cumulative score learning (see Materials and Methods), F_(4,37) = 0.7, P = 0.6. Kruskal–Wallis test for retention score, 24 h: H = 1.9, P = 0.7; ∼25 h: H = 7.8, P = 0.1; 48 h: H = 5.2, P = 0.3.

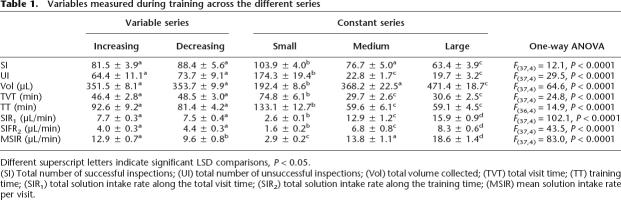
Table 1.

Variables measured during training across the different series

Different superscript letters indicate significant LSD comparisons, P < 0.05.

(SI) Total number of successful inspections; (UI) total number of unsuccessful inspections; (Vol) total volume collected; (TVT) total visit time; (TT) training time; (SIR₁) total solution intake rate along the total visit time; (SIR₂) total solution intake rate along the training time; (MSIR) mean solution intake rate per visit.

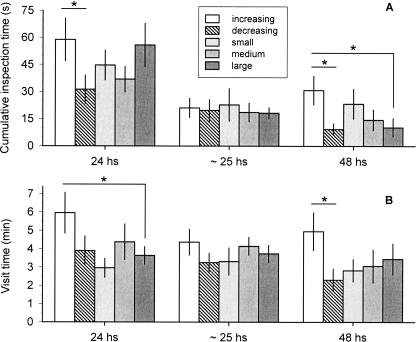
We then compared the time that the bees spent inspecting both types of empty flowers during testing (cumulative inspection time, or CIT), as well as the visit time, which included the CIT, but also took into account the time that the bees spent outside the tubes while flying over the flowers (see Materials and Methods). We found a greater CIT in the increasing series than in the decreasing series during the first test, performed 24 h after training (Fig. 2A, planned comparison, t_{I vs. D} = 2.1, P < 0.05). It decreased and did not differ across series during the second test, performed ∼25 h after training (Fig. 2A, one-way ANOVA, P = 0.9). Finally, we found a greater CIT in the increasing series than in the decreasing and the large series during the third test, performed 48 h after training (Fig. 2A, planned comparisons, t_{I vs. D} = 2.4, P < 0.05 and t_{I vs. L} = 2.1, P < 0.05). The visit time was also greater in the increasing series than in the large series during the first test (Fig. 2B, planned comparisons, t_{I vs. L} = 2.2, P < 0.05). It decreased and did not differ across series during the second test (Fig. 2B, one-way ANOVA, P = 0.6), and, finally, it was greater in the increasing series than in the decreasing series during the third test (Fig. 2B, planned comparison, t_{I vs. D} = 2.7, P < 0.05). It is important to note that the bees were not rewarded in the first test, and that, over a short period of time (i.e., between the first and the second test), extinction learning might have overridden the differences in inspection time. However, 24 h later (i.e., during the third test) the animal’s original response was partially re-established, indicating a recovery from extinction, and led to clear differences for these measures between the increasing and decreasing series. In summary, when first tested 24 and 48 h after training, the animals searched for reward more intensively after having experienced an increasing reward schedule than after having experienced a decreasing reward schedule, as revealed by the higher scores of either one or both of the two measures of “persistence.” This result matched our second prediction (see above), and suggested that subjective reward values controlled the animal’s behavior during testing. Other studies have also found that time-based measurements seem to be more sensitive to subjective reward values than choice-based measurements (e.g., Sage and Knowlton 2000; Schoenbaum et al. 2003).

Figure 2.

Cumulative inspection time (mean ± SEM) (A) and visit time (mean ± SEM) (B) during testing for the increasing (white bars), decreasing (dashed bars), and the constant series: small (light gray bars), medium (gray bars), and large (dark gray bars). One-way ANOVA: for cumulative inspection time, 24 h, F_(4,38). = 1.6, P = 0.19; ∼25 h, F_(4,37). = 0.1, P = 0.9; 48 h, F_(4,26). = 2.1, P = 0.11; for visit time: 24 h, F_(4,38). = 1.9, P = 0.1; ∼25 h, F_(4,36). = 0.7, P = 0.6; 48 h, F_(4,26). = 1.9, P = 0.13. We made the following planned comparisons for each test: increasing vs. decreasing series, increasing vs. large series, decreasing vs. small series, small vs. medium series, small vs. large series, and medium vs. large series. (Asterisks) Statistical differences, P < 0.05. Sample size across tests: increasing series, N_24h = 8, N_∼25h = 8, N_48h = 7; decreasing series, N_24h = 9, N_∼25h = 8, N_48h = 8; small, N_24h = 9, N_∼25h = 9, N_48h = 7; medium, N_24h = 9, N_∼25h = 8, N_48h = 5; large, N_24h = 8, N_∼25h = 8, N_48h = 5.

These results might be due to the fact that the bees from the increasing series had differentially associated the related predicting signals during training. Thus, they might have assigned proportionally more time to inspect the flowers that had previously yielded reward, as related to the total amount of time assigned to flower inspection. We calculated the proportion of time that the bees assigned to inspect the flowers that had previously yielded reward, and found it similar in all groups during all three tests (one-way ANOVA, 24 h: F_(4,38) = 0.4, P = 0.8; 25 h: F_(4,35) = 2.1, P = 0.1; 48 h: F_(4,23) = 0.8, P = 0.6). Still, the differences in performance between the increasing and decreasing series could be accounted for by assuming that the bees’ behavior on the test reflects their most recent experience during training. Behavior controlled in this way could be learned through simple “stimulus–response” mechanisms, without reference to reward expectations. However, the differences in the animals’ “persistence” between the increasing and the large series 24 and 48 h after training, and the similar performance of the bees from the three constant series (Fig. 2A,B), argue against the results being a simple reflection of the most recent reward experience, and in favor of a learned expectation of relative reward magnitude.

Finally, the differences between the increasing and decreasing series might be due to changes in the energy balance of their foraging excursions. That is, they might have differentially associated the related predicting signals derived from the entire patch because they were fed more or faster. Hence, we also analyzed the bees’ experiences with the offered reward on the basis of the energy balance of their successive foraging trips during training. At the end of training, the bees from the increasing, decreasing, and medium series had collected similar volumes of sugar solution; these volumes were greater than those of the small series, and smaller than those of the large series (Table 1). In addition, the total visit time (TVT) and training time (TT) (see Materials and Methods) gave minimal values for the large and the medium series, intermediate values for both variable series, and maximal values for the small series (Table 1). As a result, the bees’ solution intake rate clearly varied across series. SIR₁ and SIR₂ were the ratios between the total volume collected and the TVT and the TT, respectively (see Materials and Methods). Both the SIR₁ and SIR₂ gave a series of decreasing values for the different groups (from maximum to minimum): large, medium, variable, and small series (see Table 1). We also computed the mean solution intake rate (MSIR) that the bees experienced throughout their single visits to the patch (see Materials and Methods), and found maximal values for the large series, intermediate values for both the increasing and the medium series, and minimal values for the decreasing and the small series (Table 1). The difference observed between the increasing and the decreasing series is due to the fact that the bees from the decreasing series collected a lower volume of solution and required a larger amount of time while searching for the offered reward during their first visit to the patch. In summary, the bees from the increasing and the decreasing series collected the same amount of sugar solution and experienced the same overall intake rate during training. We found differences between these series in the mean solution intake rate per visit, although we also found differences for this variable across the constant series, where the bees behaved similarly during testing (Table 1; Fig. 2).

Taken together, our results show that simple “stimulus–response” mechanisms cannot account for the differences in “persistence” found in the increasing and decreasing series, meaning that these differences can only be explained by reference to reward expectations.

Discussion

In our experiment, bees first learned to associate colors with a sucrose reward in an array of artificial flowers closely resembling a natural foraging situation. We evaluated whether and how the sequence of the animals’ experiences with different reward magnitudes changed their later foraging behavior in the absence of reinforcement and under an otherwise similar context. In addition to the usual measure of correctness of choice, we also evaluated the bees’ “persistence” during their searches for sugar reward. We found that the animals that had experienced increasing volumes of sugar reward during training assigned more time to flower inspection (i.e., showed greater “persistence”) when tested 24 and 48 h after training. We found that the animals behaved differently neither because they had more strongly associated the related predicting signals nor because they were fed more or faster. Instead, they appear to have changed their “persistence” based on the variations in reward magnitude they had previously experienced during training. This becomes evident if one considers (1) the proportion of time that the bees from the different groups assigned to inspect the flowers that previously yielded sugar reward, as related to the total time assigned to flower inspection, (2) the relationship between the most recent experience with the offered reward during training and the animals’ responses during testing, and, finally, (3) the results of the constant series as related to the energy balance of the animals’ foraging trips during training (see Results). The latter issue, for example, is well-illustrated by comparisons across the constant series: The bees from the large series collected approximately twice as much sugar solution as the bees from the small series, and they did it in approximately half the time; both groups, however, showed similar values for their measures of “persistence” during testing (Fig. 2B; Table 1).

Hence, our results indicate that the animals from both variable series developed different long-term reward expectations, and that these expectations eventually led to differences in test performance in the absence of reward, and did so even 48 h after training. The term “expectation” denotes an effect on behavior at a later time that reflects specific past experiences with the offered reward. These variations at a later time presumably depend upon the activation of a memory about specific properties of the experienced reward, which differs from and exists in addition to a memory arising from the contingency between a given stimulus (such as the flower color), the animal’s response (such as the inspection of the flower), and the offered reward. Thus, according to theory, the bees’ later behavior at the patch must have been modulated by different subjective reward values learned during training.

Our reward schedule somehow resembles those of experiments addressing incentive phenomena, exemplified by the early studies of Crespi (1942). He trained rats to feed at the end of a straight alley, and found that the animals shifted from a large to a small reward size ran more slowly for the small reward size than did the animals trained only with the small reward size, while the animals shifted from a small to a large reward size ran faster than did those trained with the large reward size. Both types of responses are usually referred to as “Crespi effects,” or, more specifically, as successive “negative” and “positive” contrast effects, respectively (Flaherty 1982). Considering the results from our first test, for example, we found that the bees from the increasing series spent more time in the patch than the bees from the large series (Fig. 2B), somehow resembling the successive positive contrast effect found in rats (Flaherty 1982). In contrast, we found no evidence of successive negative contrast effects during the first test (Fig. 2A,B). This is intriguing because positive contrast effects seem to be much more elusive than negative contrast effects (Flaherty 1982). Contrast effects are often linked with reward expectations. Our experiment was not designed to tackle such effects, but it unambiguously shows that bees make use of long-lasting subjective reward values. Moreover, expectations in laboratory animals are usually investigated by means of the so-called reward devaluation procedure, in which reward values are manipulated outside the learning situation by using satiation or conditioned taste aversion (e.g., Holland and Straub 1979; Rescorla 1987; Gallagher et al. 1999; Sage and Knowlton 2000). This approach might also be considered in future experiments on reward expectations with free-flying and restrained bees.

Reward expectations are a key product of acquired knowledge about reward properties. Studies on reward learning and the subsequent development of reward expectations are critical for understanding the rules controlling goal-directed behaviors, and for the assessment of the cognitive complexity underlying decision making and planning. Reward expectations and incentive phenomena have systematically been addressed only in vertebrate species, probably because such phenomena are frequently linked to complex cognitive abilities only ubiquitous in animals with large brains. Studies of rodents (e.g., Gallagher et al. 1999), nonhuman primates (e.g., Schultz 2000), and humans (e.g., O’Doherty et al. 2001), indicate that neural interaction between the basolateral complex of the amygdala and the orbitofrontal cortex are crucial for the development and subsequent use of reward expectations involved in various goal-directed behaviors (Holland and Gallagher 2004). Here, we document for the first time that honeybees also develop long-term reward expectations. These expectations can guide their foraging behavior after a relatively long pause and in the absence of reinforcement, and further experiments will aim toward an elucidation of the neural mechanisms involved.

It has been reported that foraging honeybees develop a form of short-term reward expectation (Greggers and Menzel 1993; Bitterman 1996; Greggers and Mauelshagen 1997). This form of expectation becomes evident through the analysis of an animal’s intra- and inter-patch choices across its successive visits to an array of multiple feeders, and depends upon the amount and concentration of the solution offered by these feeders; bees match their choices to these properties. Moreover, they also appear to be sensitive to variance of reward (Real 1981; Shafir et al. 1999; Shapiro et al. 2001; Waddington 2001; Drezner-Levy and Shafir 2007). These short-term reward expectations seemingly help the animal in anticipating the level of reward, and suggest that the value of the appetitive stimulus depends on what the animal expects to experience next in a given situation and, therefore, on the background of its experience under a similar situation (Waddington and Gottlieb 1990; Real 1991; Greggers and Menzel 1993; Fülöp and Menzel 2000; Wiegmann et al. 2003). No attempts have been made, however, to distinguish between the strength of signal learning and learning about subjective values of reward, let alone the possible development of long-term reward expectations. Interestingly, evidence has been reported indicating that honeybee dance behavior, an intriguing example of multisensory convergence and central processing, also depends upon the magnitude of past rewards (Raveret-Richter and Waddington 1993; De Marco and Farina 2001; De Marco et al. 2005).

Honeybees seem to critically rely on their memory store in deciding when and where to forage. A honeybee’s working memory can track the rewarding properties of several, simultaneous feeding stations, integrating critical components of the animal’s reward experience over a time span of several minutes (Greggers and Menzel 1993). Here, we show that honeybees also develop persisting forms of subjective reward values. It might be interesting to evaluate how these persisting memories are subsequently retrieved by specific constellations of stimuli, and how their contents are appropriately integrated with a number of current conditions based on the time of the day and the animal’s general motivational state. This may allow further dissociation between stimulus–response association, incentive phenomena, and basic forms of planning.

Materials and Methods

A colony of Apis mellifera carnica bees was placed indoors in a two-frame observation hive. A small group of labeled bees was trained to collect an unscented 50% w/w sucrose solution at an artificial flower patch placed 145 m from the hive. These bees (henceforth, recruiting bees) were not used as experimental animals; they only recruited nest-mates to the foraging place. The newcomers arriving at the feeding place were trapped before they got in contact with any sugar reward. They were cooled, marked with plastic tags, and released. Upon returning to the hive, these animals became potential experimental bees. Those that returned underwent a pre-training phase and became experimental bees. The artificial flower patch consisted of 24 Eppendorf tubes (4 cm deep) (henceforth, “flowers”) regularly distributed over the surface of a foraging arena (28 cm × 28 cm) made of two superposed plastic squares, both of which presented 24 holes (1 cm diameter). The lower part of the arena was a 0.7-cm thick opaque acrylic plastic, while the upper square was a 0.2-cm thick transparent Plexiglas. The tubes were placed inside the holes and raised 1.8 cm above the upper surface of the transparent Plexiglas. The flowers gave off one of two signaling colors, either yellow or blue. We presented 24 color circles, 12 yellow and 12 blue, centered around the single holes holding the flowers. Each circle had a diameter of 3.8 cm. These 24 colored circles, set onto a gray cardboard offering a homogeneous background, were visible to the bees through the upper transparent Plexiglas square. Since the flowers were held by the upper surface of the patch and the colored circles were set below this surface, both the flowers and their corresponding visual stimuli could easily be replaced between the successive visits of the experimental bees. In between the successive visits by the experimental bees, we randomly changed the relative position of the 24 visual stimuli, thus minimizing visual orientation based on the position of the single flowers relative to the entire patch. Since (1) the patch consisted of a relatively large number of flowers whose signaling colors were regularly distributed, (2) the bees had no access to the surface of the visual stimuli, (3) all flowers were replaced between visits, and (4) the relative position of the visual stimuli changed across visits, any putative influence of chemosensory cues that bees may produce and benefit from while foraging (Núñez 1967) were minimized and restricted to the single visits by the animals.

The labeled bees had to learn how to handle the flowers in order to efficiently access the offered reward. They were allowed to forage on the patch twice before training (pre-training phase). During these two visits, each flower offered a 50% w/w sugar solution (ad libitum), and the bees were exposed to a homogeneous gray background. After the beginning of this pre-training phase, in addition, the recruiting bees (see above) and the newcomers present at the patch, with the exception of the single experimental bee, were captured and kept inside small cages until the end of the experiment. Training started when the experimental bee returned to the feeding place after its last pre-training visit. It consisted of nine successive visits to the patch, always presenting 12 yellow and 12 blue flowers. Throughout the experiments, half of the bees were rewarded at yellow flowers, the other half at the blue flowers. Different volumes of an unscented, 20% w/w sugar solution were used as a sugar reward; these volumes correspond to the different reward magnitudes used during the experiment, and were defined according to the different experimental series described below. The foraging arena was removed from the feeding location after training. The volume of sugar solution (or reward magnitude) offered by the single flowers of the patch changed across the five different experimental series. The first two series presented a variable volume, either increasing or decreasing, throughout the nine visits by the single bees. In the increasing series, the volume per flower was 2 μL during visits one through three, 5 μL during visits four through six, and 10 μL during visits seven through nine. In the decreasing series, the volume per flower was 10 μL during visits one through three, 5 μL during visits four through six, and 2 μL during visits seven through nine. Hence, the mean volume per flower as well as the total volume of sugar solution offered by the patch at the end of the nine successive visits by the single bees (5.67 and 612 μL, respectively) was the same in both series. The remaining three series (henceforth, the small, medium, and large series) offered a constant volume of sugar solution per flower throughout the nine visits by the single bees: either 2 μL, 5.67 μL, or 10 μL, respectively. The total volume of sugar solution offered to the bees in the small, medium, and large series was 216 μL, 612.4 μL, and 1080 μL, respectively.

The behavior of each experimental bee foraging at the patch was evaluated three times after training. The flowers offered no sugar reward during testing. The first, second, and third tests took place 24, 25, and 48 h after training, respectively. The second test began when the experimental bee returned spontaneously to the patch after having performed the first test; the time elapsed between the first and the second test clearly varied across individuals, and was ∼1 h.

The entire sequence of behaviors performed by the experimental bees at the flower patch was video recorded during both training and testing. The following variables were analyzed: (1) Learning score: defined as the ratio between the number of inspections of the flowers signaled by the rewarded color and the total number of inspections of both types of flowers (those of the rewarded as well as the unrewarded color) that the single bees performed during each of their visits to the patch. The cumulative learning score, computed for the sake of comparisons across series, is the total proportion of inspections of the rewarded color throughout the nine successive visits; it equals the sum of the individual learning scores. (2) Retention score: defined as the ratio between the number of inspections of the rewarded color and the total number of inspections of both colors. (3) Total number of successful inspections (henceforth, “SI”): the number of times that the experimental bee found sugar reward during its multiple inspections of the flowers. (4) Total number of unsuccessful inspections of the rewarded color (henceforth, “UI”): corresponds to the number of times that the experimental bee did not find sugar solution upon inspecting a flower signaled by the rewarded color. These events occurred either when the inspected tube was already emptied or when the length of the inspection did not allow the animal to reach the offered sugar solution. (5) Cumulative inspection time (henceforth, “CIT”), in seconds: the amount of time that the experimental bee spent searching for sugar reward inside the tubes—both rewarded and unrewarded—during each test session. (6) Visit time (henceforth, “VT”), in minutes: the time the experimental bee spent foraging on the arena during each single visit. We also calculated a total VT (henceforth, “TVT”), as the sum of the single VT values recorded during the nine successive visits. (7) Training time (henceforth, “TT”), in minutes: the sum of the total visit time (TVT) and the time the experimental bee spent inside the hive in between its successive foraging visits to the arena. It therefore computes the time interval between the beginning and the end of training. (8) Total volume collected during training (henceforth, “Vol”), in microliters: the sum of the volumes of sugar solution that the experimental bee collected during each of the nine successive visits to the patch. (9) Solution intake rate throughout the total visit time (henceforth, “SIR₁”), in μL/min: the ratio between Vol and TVT. (10) Solution intake rate throughout the training time (henceforth, “SIR₂”), in μL/min: the ratio between the Vol and TT. (11) Mean solution intake rate per visit to the patch (henceforth, “MSIR”), in μL/min. We computed the ratio between the collected volume and the VT for each of the nine visits to the patch, and then averaged these values in order to calculate the mean solution intake rate.

Data were analyzed by means of one-sample t-tests, one-way ANOVAs, Kruskal–Wallis tests (when the data did not fulfill the requirements of parametric tests), LSD tests, and planned comparisons. While performing planned comparisons, we used the Bonferroni adjustment to set a level per comparison so that the overall alpha level was 0.05.