Nearest-neighbor non-additivity versus long-range non-additivity in TATA-box structure and its implications for TBP-binding mechanism

Abstract

TBP recognizes its target sites, TATA boxes, by recognizing their sequence-dependent structure and flexibility. Studying this mode of TATA-box recognition, termed ‘indirect readout’, is important for elucidating the binding mechanism in this system, as well as for developing methods to locate new binding sites in genomic DNA. We determined the binding stability and TBP-induced TATA-box bending for consensus-like TATA boxes. In addition, we calculated the individual information score of all studied sequences. We show that various non-additive effects exist in TATA boxes, dependent on their structural properties. By several criterions, we divide TATA boxes to two main groups. The first group contains sequences with 3–4 consecutive adenines. Sequences in this group have a rigid context-independent cooperative structure, best described by a nearest-neighbor non-additive model. Sequences in the second group have a flexible, context-dependent conformation, which cannot be described by an additive model or by a nearest-neighbor non-additive model. Classifying TATA boxes by these and other structural rules clarifies the different recognition pathways and binding mechanisms used by TBP upon binding to different TATA boxes. We discuss the structural and evolutionary sources of the difficulties in predicting new binding sites by probabilistic weight-matrix methods for proteins in which indirect readout is dominant.

INTRODUCTION

The identity of eukaryotic cells is defined by the correct temporal and spatial expression of specific genes. The first step in the selective expression of any gene is the ability to single it out from among all the others genes in the genome. This ability, which lies at the heart of many cellular processes, invariably requires the interactions of proteins with DNA molecules. Protein–DNA interactions proceed through an induced-fit mechanism, similar to the induced-fit mechanism of enzyme action (1). Both the DNA and the protein are not passive players, but have active roles, dictated by their structural plasticity. The ability of the DNA to deform upon interaction with proteins (‘deformability’) is determined by the preferred stacking interactions between adjacent base pairs (2) and gives an indirectly recognized structural signature (3). Sequence selectivity, in most sequence-specific DNA-binding proteins, is based on direct hydrogen bonds between amino acid residues and the donor and acceptor groups primarily in the major groove of DNA [‘direct readout’, (4)]. In addition, the sequence-dependent features of intrinsic DNA structure and its deformability contribute to specific recognition [‘indirect readout’, (3)]. In several specific protein/DNA complexes, DNA conformation is used to the extreme case and there are indications for interaction mainly through indirect readout. The TBP/TATA-box system is such a system (5–10). The formation of the TBP/TATA-box complex is the first step in the assembly of the preinitiation complex on promoters of genes that are transcribed by RNA polymerase II. TBP binds to an eight-base-pair segment of DNA, which thus defines the core TATA box (5–10). The TATA-box consensus sequence is T₁-A₂-T₃-A₄-W₅-A₆-W₇-R₈ (W = A, T; R = A, G) (11,12). The crystal structures of various TBP/TATA-box complexes show that the formation of the complex results in a severe bend of the DNA towards the major groove (80–100°), as well as untwisting, which exposes a very wide and shallow minor groove on its convex side where TBP engages (5–10).

We have previously studied the indirect readout mechanism of TATA-box recognition by TBP (13). Based on this study, we proposed several possible signals for TBP recognizing TATA boxes through indirect readout: The first signal was the helical twist angle in the middle of TATA boxes (base pairs 4 and 5, the only two base pairs with direct hydrogen bonds to the protein). Second signal was the identity of base pairs 7 and 8 and third, recognition of global DNA flexibility (13).

In TATA boxes containing alternating (T-A)_n runs (similar to the sequence of the AdE4 TATA box) binding affinity and stability to TBP was recently shown to be significantly dependent on the nature of the sequences flanking the core TATA box (14). We suggested that this is a novel form of indirect readout (14). The structure of (T-A)_n runs is polymorphic (15) and context dependent (16). Consequently, this pliable structure can be altered by the DNA structure at the flanking sequences, thereby indirectly influencing the interaction with TBP. The variability observed in TBP binding to E4-like TATA boxes, as a function of changing the flanking sequences, is comparable to that observed when the sequences within the core TATA box itself are changed (14).

Indirect readout of DNA sequences can sometime manifest itself through non-additivity effects in protein–DNA interactions. By this it is meant that protein-binding affinity cannot be accounted for by successive contributions from individual nucleotide pairs within the target sequence. Such non-additivity has been observed in several systems, notably the Mnt system (17) and the EGR1 Zn-finger system (18). However, in both cases it was concluded that the additive, mononucleotide-based assumption, was good enough for most purposes (19). Recently, O’Flanagan et al. (20) observed non-additive effects in the TBP system, but in this study a theoretical approach has been used to obtain binding-site data.

We study here the binding properties of TBP to all consensus-like TATA boxes. We show that grouping consensus-like TATA boxes by their structural properties reveal differences in the indirect readout of these TATA boxes by TBP, and in TBP-binding mechanism. Statistical analysis indicate that TATA boxes that have a context-independent cooperative structure are best described by a nearest-neighbor non-additive model, whereas TATA boxes that have a flexible context-dependent conformation cannot be described by either an additive model or by a nearest-neighbor non-additive model.

MATERIAL AND METHODS

Protein

The c-terminal domain of yeast TBP (yTBPc) was a kind gift from S. Juo (Yale University). The overexpression and purification of the protein were as described by Kim et al. (5). The fraction of yTBPc active for DNA binding was determined as previously described (13) and found to be 50%.

DNA

All TATA-box variants in this study were chemically synthesized on an automated DNA synthesizer at the Keck Foundation Resource Laboratory (Yale University) or by Sigma Genosys (Israel), and purified using standard protocols (21). TATA-box variants for dissociation kinetics experiments were chemically synthesized as hairpin constructs with 20-base-pair (bp) double-stranded stems and five cytosines in the loop (Table 1). TATA-box variants for phasing analysis were chemically synthesized as linear duplexes 21-bp long. They are identical in sequence to the stem of the hairpin variants except for an additional T at the 5′ side, used to create an AvaI site for cloning the fragments as described previously (13). These linear duplexes were also used as specific competitors in the dissociation kinetics experiments.

Table 1.

Various analyses of the TATA boxes studied here

Name	sequencea 12345678	yTBPc- induced TATA-box bendingb	half life of fraction B (minutes)c	‘A’ fractionc	‘B’ fractionc	EPD occur. (8 bp)d	EPD frequency@ positions 7–8e	Dinuc. slide flexibility (KJ/mol)f	Tetranuc. conform. energy@ positions 6–9g	Total conform. tetranuc. energy (KJ/mol)h	Helical twist@ A4A5 or A4T5i	Z statistics for positions 6–9j	Inf. score monok	Inf. score dinuck
I. MLP-like TATA boxes:
MLP*	CGGGCTATAAAAGGGGGTGG	65(±4)°	255(±24)	0.17(±3)	0.83(±3)	184	0.243	7.58	−166.8	−2662	11.4°	2.7	0.0	0.0
T7A8*	CGGGCTATAAATAGGGGTGG	63(±3)°	230(±12)	0.19(±8)	0.81(±8)	142	0.222	7.13	−170.3	−2666		5.0	0.32	0.21
A8	CGGGCTATAAAAAGGGGTGG	53(±2)°	239(±4)	0.13(±1)	0.87(±1)	74	0.085	13.72	175.6	−2679	4.9°	−4.1	0.02	0.68
T8	CGGGCTATAAAATGGGGTGG	50(±3)°	122(±8)	0.74(±3)	0.26(±3)	27	0.021	11.69	−171.6	−2672	13.5°	−2.3	1.27	2.33
T7	CGGGCTATAAATGGGGGTGG	45(±4)°	110(±5)	0.75(±3)	0.25(±3)	19	0.036	1.35	−163.1	−2656	14.0°	−4.0	0.30	1.89
II. E4-like TATA boxes:
T5*	CGGGCTATATAAGGGGGTGG	76(±4)°	139(±13)	0.29(±4)	0.71(±4)	99	0.266	7.58	−166.8	−2648	8.3°	4.0	0.71	0.71
(TA)4*	CGGGCTATATATAGGGGTGG	65(±4)°	163(±6)	0.26(±4)	0.74(±4)	75	0.190	7.13	−170.3	−2652	1.5°	1.9	1.03	0.92
T5A8	CGGGCTATATAAAGGGGTGG	63(±3)°	332(±16)	0.19(±3)	0.81(±3)	91	0.370	13.72	−175.6	−2664	4.8°	1.6	0.73	1.39
T5T8	CGGGCTATATAATGGGGTGG	53(±3)°	195(±8)	0.20(±2)	0.80(±2)	9	0.027	11.69	−171.6	−2657	8.3°	−1.0	1.98	3.04
T5T7*	CGGGCTATATATGGGGGTGG	43(±3)°	78(±6)	0.13(±2)	0.87(±2)	12	0.033	1.35	−163.1	−2641		−3.1	1.01	2.6

Numbers in parenthesis are the SE of the mean. It includes the experimental error between the different independent experiments and the difference between the experimental points and the curve-fitting model.

^aThe 20-bp sequence in the stem of the hairpin constructs. The letters in bold are the 8-bp core TATA box.

^bBend angles determined at 30°C. The bend center is between the 5th and the 6th bp, or on the 6th bp, and is pointing into the major groove at the bend center. Bend angles for sequences with an asterisk are from Bareket-Samish et al. (13).

^cEquation used: F(0)/F(t) = Ae^−k₁^t + Be^−k₂^t. A and B are the fraction of molecules dissociating with macroscopic rate constants k₁ and k₂, respectively.

The half-life was determined from t_1/2B = ln2/k₂. Asterisk denotes sequences for which dissociation kinetics data was measured by Bareket-Samish et al. (13) and re-analyzed here by this equation.

^dNumber of occurrences of 8-bp TATA boxes in EPD release 89.

^eFrequency of occurrence of dinucleotide in position 7/8 in the EPD release 89, calculated separately from the YWTAAADN and YWTATADN datasets, for groups I and II, respectively.

^fSlide flexibility (in KJ mol⁻¹) of the dinucleotide at position 7/8, determined from the curvature of the slide/shift stacking potential at the minimum energy Packer et al. (54).

^gMinimum conformational energy (in KJ/mol) for the tetranucleotides at positions 6–9, calculated from the data of Packer et al. (39).

^hMinimum tetranucleotide conformational energy (in KJ/mol) summed along each sequence. Calculations are based on the data of Packer et al. (39).

ⁱObserved in TBP/TATA-box co-crystal structures having these TATA-box sequences.

^jZ statistics, the deviation of the observed frequency of DNA tracts from that expected based on mononucleotide composition. See text for details.

^kIndividual information score calculated from either mononucleotide or dinucleotide weight matrices. See text for details.

Dissociation kinetics experiments

Radiolabeled hairpin duplexes (0.4 nM) and yTBPc (27 nM active protein) were incubated for 60 min at 30°C in the binding buffer before adding unlabeled 21-bp linear duplex competitor of the same DNA sequence (1.76 μM, 65-fold excess of the cold competitor over active protein and 4400-fold over labeled DNA targets). We used these experimental conditions to concur with those of our previous study (13). The rational for using short hairpin duplexes as DNA targets and short linear duplexes as DNA competitors was previously described (13). At the time points indicated in Figures 2 and 4, samples were removed and immediately frozen in liquid nitrogen (22). After the final time point, the samples were thawed and immediately loaded on native gels (10%, acrylamide/bisacrylamide ratio 75:1, 10% glycerol) while the gels were running. The gels were run at 450 V and 30°C, in a running buffer containing 0.5× TG (25 mM Tris.HCl, 190 mM Glycine, pH 8.3) and 5 mM MgAc, until the BPB dye migrated 5.5 cm.

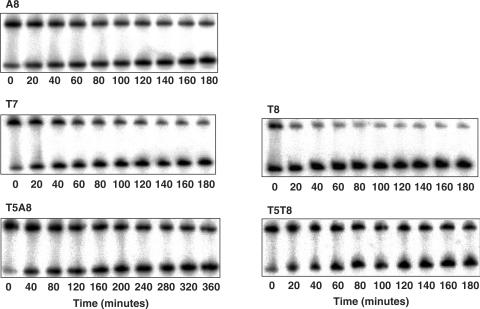
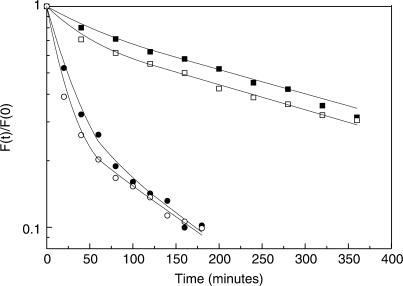
Figure 2.

Dissociation kinetics of yTBPc (27 nM) from consensus-like TATA-box variants embedded in hairpin constructs (0.4 nM). The number below each gel denotes the time after adding competitor DNA (1.76 μM).

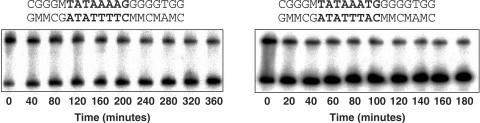
Figure 4.

Dissociation kinetics experiments using methylated DNA targets. Left: double-stranded stem of DNA hairpin containing the MLP target with methylated cytosine residues (denoted by M). Right: stem of DNA hairpin containing the T₇ target with methylated cytosine residues. For other details see Figure 2.

Phasing analysis

yTBPc-induced DNA bending was analyzed by phasing analysis using radiolabeled DNA targets, 569–579 bp long, as previously described (13). These DNA probes (0.4 nM) were incubated with 25–200 nM yTBPc for 60 min at 30°C. The relative mobilities of the complexes were analyzed on native gels (6%, acrylamide/bisacrylamide 75:1, 10% glycerol). Gels were run at 450 V and 30°C, in a running buffer containing 0.5× TG (25 mM Tris.HCl, 190 mM Glycine, pH 8.3) and 5 mM MgAc, until the XC dye migrated 12 cm.

Analysis of dissociation kinetics experiments

All gels were dried and quantified using a Fujii Bas-1000 phosphoimager. For the analysis of the kinetic experiments, boxes were defined surrounding each band on the gel. To account for dissociation of the complex during electrophoresis, the band corresponding to the protein/DNA complex was defined as extending from its main band to the free-DNA band (23). A similar box in a lane containing the unbound target only defined the background. The fractions of bound DNA at the different time points, F(t), were calculated from the equation: F(t) = (PSL − bg)_complex(t)/[(PSL − bg) _complex(t) + (PSL − bg)_free(t)], where PSL is the photostimulated luminescence and bg is the background. ln[F(t)/F(0)] was plotted as a function of time (t) after the addition of the unlabeled competitor.

The data was analyzed by a two-phase first-order kinetic equation: F(t)/F(0) = Ae^−k_At+ Be^−k_Bt, where A and B are fractions of molecules dissociating with rate constants k_A and k_B, respectively. Half-life of complexes dissociating by A and B processes were calculated from: t_1/2A = ln2/k_A and t_1/2B = ln2/k_B.

Structural analysis

Analysis to determine the local helical parameters in crystal structures of TBP/TATA-box complexes was carried out using the web version of 3-DNA (24). However, in structures containing Hoogsteen base pairs this analysis yielded erroneous parameters. These structures were then analyzed using curves (25).

Statistical analysis of TATA boxes

We have downloaded from the eukaryotic promoter database [EPD, (26,27)] sequences corresponding to the degenerate consensus sequence YWTAWADN. This consensus sequence corresponds to all TATA-box variants that appear with at least moderate frequency (>10%) in eukaryotic promoters, according to the TATA-box consensus of Bucher (12). We have filtered the sequences to exclude unidentified preliminary bulk sequences (as defined in the EPD, i.e. sequences with the ‘OS_bA’ identifier), and those derived from high-throughput studies, which cannot be assigned to a defined homology group. We define a homology group, as in the EPD, as sequence similarity due to common phylogenetic origin. In the EPD, and here, two promoters are considered homologous if they exhibit >50% sequence similarity between −79 and +20. However, as the definition of homologous promoters is based only on similarity of DNA sequence in the promoter region, they can be either orthologs or paralogs. We then deleted from each set multiple sequences coming from the same homology group, as well as TATA boxes in the transcribed region. Thus, the dataset now corresponds to a representative set of not closely related promoters. Similarly, we downloaded sequences corresponding to the more restricted consensus sequences, YWTATADN and YWTAAADN. All datasets were aligned by the program MEME (28), using only the one strand given in the EPD.

From the YWTAWADN dataset (457 sequences) we constructed mononucleotide position-specific weight matrices whose elements are the log-odds weights:

where f_lB is the observed frequency of each base B in position l of the binding site, and P_B is the frequency in the whole genome (29). P_B is taken here to be 0.25 for each base. These matrix elements are a maximum probability estimate for the binding energy contribution of each base at each position, assuming that each position contributes independently to the total binding energy (29). The base frequencies are corrected here for small sample errors as described by Berg and von Hippel (30). To score individual sequences, the weight matrix is multiplied by a matrix (s_lB) containing only 0's and 1's, corresponding to sequences for which binding data was experimentally determined in this study. The summation of this multiplication yields an individual information score for each sequence (20,29):

To the summation we add a constant (C₀), chosen such that the best binding site scores zero and poorer sites score positively.

To test for nearest-neighbor non-additive effects we need to calculate dinucleotide information scores, for which we need to add to mononucleotide information scores the following term (20,31):

where the numerator is the observed frequencies of the doublet B_lB_l+1 in positions l and l + 1 and the denominator is the observed frequencies of its monomeric components. Here again a constant is added to each result to make the score of the best binder zero.

We have also calculated the Z statistics of tetranucleotide motifs at position 6–9 in TATA boxes. It is calculated by subtracting from the observed number of occurrences of each motif the expected number of occurrences based on the mononucleotide frequency of the component base pairs, and then dividing this value by the expected SD (31).

In testing the strength of relationships between variables, we calculated Spearman's rank correlation coefficient (denoted by ρ) as a non-parametric measure of correlation (32).

RESULTS AND DISCUSSION

Differential DNA flexibility divides the TATA boxes to two unique groups

We have grouped the ten TATA boxes studied here to two groups. The first group contains sequences that resemble the Adeno virus major late promoter (MLP) sequence, TATAAAAG (Table 1). All sequences in this group have a central A₄-A₅ step. The second group contains sequences that resemble the Adeno virus E4 promoter, TATATATA (Table 1). All sequences in this group have a central A₄-T₅ step. Initially, we made this division based on our previous observations (13) that TATA boxes having a central A₄-A₅ step have higher twist angle (around 13°) than TATA boxes with a central A₄-T₅ step (around 3°), even though both angles are untwisted relative to the canonical value, which is 34° for generic B-DNA in solution (33). This observation is still valid, but is less distinctive, when we analyze co-crystal structures corresponding to the present ten sequences (Table 1). The average twist angle at the central A₄-A₅ position in TBP/DNA complexes identical to those of group I (pdb codes: 1qne or 1cdw for MLP; 1ngm for A₈, 1qn4 for T₈ and 1qnb for T₇) is 11°± 2°, whereas the A₄-T₅ twist angle in TBP/DNA complexes corresponding to group II sequences (pdb codes: 1qn7 for T₅; 1tgh for (TA)₄; and 1yth for T₅A₈) is 6° ± 2°.

Looking at Table 1, we observe that sequences belonging to group I all harbor an A-tract, defined as a DNA region consisting of four or more A's in a row (34). T₇A₈ and T₇ have only an A₃-tract, but it has been shown that A_xT_y tracts have similar structural properties to A_n tracts [x + y = n ≥ 4, (35,36)]. A-tracts are known to adopt a dominant unique structure, distinct from that of generic B-DNA (37), which is invariant and sequence-context independent (38,39). A-tract may even confer unique structural properties to sequence adjacent to them (40). On the other hand, alternating (T-A)_n runs are known to be a conformationally flexible DNA element, relative to B-DNA in general and A-tracts in particular (39,41,42). Thus, the sequences of group I have on the whole a more rigid DNA structure than those of group II. This suggestion is supported by looking at variability in roll angle, between same steps in different structures, especially the steps at positions 4/5 and 5/6. Roll angle at the 4/5 position vary between 23.5° ± 0.6°, for group I and 26° ± 3°, for group II. At the 5/6 position the variability is 23° ± 1°, for group I and 22° ± 5°, for group II. Thus, the variability in roll angle at these positions is 5-fold larger for group II sequences than those of group I sequences (compare the SD values of group I to those of group II, i.e. 0.6° to 3° and 1° to 5°). Moreover, the average deviation of the roll angle along any one crystal structure corresponding to those studied here is also larger for sequences of group II than those of group I, 13.2 ± 0.5° for group II, versus 12.1 ± 0.1° for group I. Large roll fluctuations are commonly associated with conformational flexibility.

Packer et al. (39) have argued that when DNA bending is non-planar, such as in the nucleosome (43) and in the TBP/TATA-box complex (5–10), the bending motion requires shearing by slide and shift, in addition to utilizing changes in roll, tilt and twist, and that slide and shift are better studied on the tetranucleotide level. We have used the values given by Packer et al. (39) for the flexibility of tetranucleotides with respect to slide, to compare group I to II. We calculated the flexibility with respect to slide of the ten sequences studied here by summing the components tetranucleotides in a sliding window along the core 8-bp of each sequence. We then averaged the values from each 5-sequence group. Group I has average flexibility of 71 ± 7 KJ/mol Ų, whereas group II has an average flexibility of 35 ± 7 KJ/mol Ų. Thus, group I is significantly more rigid than group II, also with respect to slide.

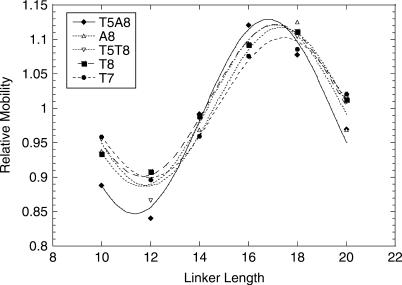
TBP-induced TATA-box bending

We measured the bend angles induced on TATA boxes upon binding of yTBPc (Figure 1) by phasing analysis (13,23,44,45). The results (Table 1) show that when we divide the set to two groups (MLP-like versus E4-like), we can arrange the sequences within each group with the same order of base-pair steps at position 7/8, going from complexes with a large induced bend angle to complexes with smaller bend angles. In both groups sequences with the A₇-G₈ step harbors the largest TBP-induced bend angle, followed by T-A, A-A, A-T and T-G, spanning the range from 76 (±4)° for TATATAAG to 43 (±4)° for TATATATG (Table 1). Thus, the bend angles induced on the TATA box by TBP binding are not only sequence dependent (13,46), but they depend only on the identity of the dinucleotide at position 7/8.

Figure 1.

Phasing analysis of yTBPc-induced TATA-box bending. Shown are the relative mobilities of the bound DNA divided by the relative mobilities of the free DNA as a function of the linker length. The values shown are of one representative experiment (of 3–4 independent experiments). The line is from the best fit to a cosine function (44).

These results are similar to those obtained in the study of Wu et al. (46) who measured the solution bend angles for TBP complexes with different AdMLP-related TATA-box variants, using fluorescence resonance energy transfer (FRET). The values of the bend angles in the study of Wu et al. (46) ranged from 76° for the complex of TBP with MLP to 30° for the complex of TBP with an A₃ variant (TAAAAAAG). These results contrast with the crystallographic study of Patikoglou et al. (10), who observed a similar structure of the wild-type TBP complexes with eleven naturally occurring variants of the AdMLP, including the T₇ and T₈ sequences. Two different explanations are possible for this discrepancy. First, the difference may be due, at least partly, to the writhed DNA structure observed in the crystalline state, as discussed in (13). Variations in electrophoretic mobility, between DNA fragments of the same length, are related to differences in the mean square end-to-end distance of the molecules. Bend angles derived from phasing analysis, or from FRET measurements, are 2D entities, determined from the differences in mobility between the cis and trans isomers, or distance differences between the 5′-dye and the 3′-dye. Therefore, the difference between the crystallographic and solution results may thus be partly attributed to the difference in the outcome of projecting a 3D curve onto a 2D plane in the two methods. However, no sequence-dependent differences in writhe have been observed in the crystallographic studies (5–10). Second, it has been shown by Wu et al. (47) that the osmolytes used to crystallize TBP/TATA-box complexes increase the bend angle of the DNA in the complex to the bend angle observed in the crystalline structures. The data presented here support this option and points to the last base-pair step, position 7–8, as the origin of the sequence-dependent pattern.

Differential biphasic dissociation kinetic behavior and mechanism of TBP binding

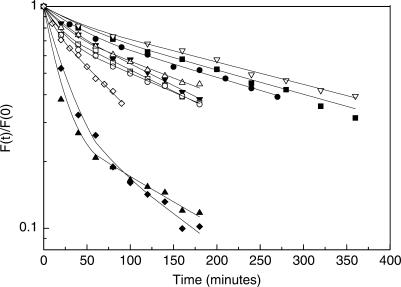
We have determined the rate of dissociation of yTBPc from all variants studied here by gel electrophoresis (Figure 2), as previously described (13). However, we could not fit well the data of two of the variants (T₇ and T₈) to a one-phase dissociation equation, as in our previous study (13). Hence, we analyzed these two variants by a two-phase kinetic equation (Figure 3). Consequently, we have also re-analyzed the remaining data by a two-phase kinetic equation (Figure 3). This analysis shows (Table 1) that for all variants there are two macroscopic dissociation processes occurring simultaneously—a fast process (termed ‘A’ in Table 1), which is poorly defined in terms of a rate constant (ranging approximately between 7 and 20 min for different TATA boxes, but with a curve-fitting error of the same magnitude or larger in some cases), and a slow process (termed ‘B’ in Table 1), with a low curve-fitting error. However, whereas in all variants except T₇ and T₈ the molecules mainly undergo the slow process (∼80%), for the T₇ and T₈ variants the picture is different. A significant part of T₇ and T₈ molecules undergo mainly the fast process (∼75%).

Figure 3.

Plot of the fraction of molecules bound to consensus-like TATA-box variants at time (t) divided by the fraction of molecules bound at time zero is plotted as a function of time. The lines are from the best fit to a double exponential curve. Solid squares, MLP; solid circles, T₇A₈; solid down triangles, A₈; solid up triangles, T₈; solid diamonds, T₇; open squares, T₅; open circles, (TA)₄; open down triangles, T₅A₈, open up triangles, T₅T₈; open diamonds, T₅T₇. The shown experimental points are those from only one experiment, out of 3–6 independent experiments conducted with each DNA target. Hence, they may deviate slightly from the averaged values presented in Table 1.

There are a priori two likely interpretations for the observed behavior. First, the two events could arise from dissociation from non-specific DNA versus dissociation from the TATA box (48). According to this hypothesis the T₇ and T₈ variants have very low sequence specificities, and thus dissociation from the TATA-box region of the T₇ and T₈ variants and dissociation from the sequence flanking them has similar (and short) half-life. Second possible explanation is that the kinetics of dissociation could proceeds through a complex mechanism with several intermediates (49–52). Parkhurst et al. (50) proposed that these intermediates are different intercalation states of TBP on TATA boxes.

To differentiate between these two possibilities, we have studied TATA-box variants with methylated cytosines in their flanking sequences. If the different biphasic behavior observed for the T₇ and T₈ variants are due to dissociation from specific sequences (core TATA box) versus nonspecific sequences (the flanking sequences), i.e. if there is sliding of TBP on the TATA box prior to dissociation (48), then we would expect different behavior of methylated and unmethylated targets, because we expect that methyl groups, being a bulky side group on cytosine residues, will inhibit this lateral movement by TBP, or else that the methyl group on the flanking sequences will inhibit binding of TBP to these regions. However, if the biphasic behavior of the T₇ and T₈ variants is due to different dissociation events from the TATA box itself, then we would expect similar dissociation behavior of methylated and unmethylated sequences. To address these issues we have studied two representative TATA-box variants, MLP and T₇, embedded within sequences with methylated cytosines in the region upstream and downstream to the TATA box (Figure 4). MLP represents the TATA-box variants that undergo mainly the slow process, whereas T₇ represents the variants that undergo mainly the fast process.

Figure 4 shows the results of dissociation kinetic experiments using methylated T₇ and MLP TATA-box variants. Analysis by a two phase kinetic equation (Figure 5) shows that the stability of yTBPc complexes with methylated and unmethylated sequences is similar for the T₇ variants (123 ± 4 and 110 ± 5 min, respectively) as well as for the MLP variants (267 ± 17 and 255 ± 24 min, respectively). The fraction of molecules undergoing the slow process did not change significantly upon methylation (29 ± 2% of the methylated T₇ and 25 ± 3% of the unmethylated T₇ variants; 72 ± 5% for the methylated MLP and 83 ± 3% for the unmethylated MLP sequences). These results indicate no significant difference between the dissociation kinetic behavior of yTBPc complexes with regular TATA boxes versus with TATA boxes containing methylated cytosines in their flanking sequences. Thus, we can conclude that the two processes are dissociation events from complexes having different intercalation states.

Figure 5.

Comparison between the dissociation kinetics of yTBPc from methylated and non-methylated TATA boxes. Fraction of yTBPc molecules bound at time (t) divided by the fraction of molecules bound at time (0) is plotted as a function of time. Solid squares, MLP; open squares, methylated MLP; solid circles, T₇; open circles, methylated T₇. For other details see Figure 3.

Powell et al. (51) suggested that the overall energy profile for the reaction between either AdMLP or AdE4 with yTBP is similar, but that they are composed of different energetic intermediates. Both binding events are composed of three distinct steps, of which the initial step is the interaction of the similar 5′ TATA part of the TATA box with yTBP, i.e. binding, bending and insertion of the 5′ phenylalanines from the stirrup loops between nucleotides T₁ and A₂. In the AdE4 target, the next step is ordering of the flexible T-A steps, and intercalation of the second phenylalanine pair between the nucleotides at position 7 and 8 (51). The interaction is basically over before the final step, which consists of further structural and energetic adjustments. In the more rigid AdMLP target, the second step is not as facile, and thus the intercalation step is delayed until the final step (51).

We suggest that this overall view is in accord with the results obtained with our extended set of TATA boxes, which are all either MLP-like or E4-like (Table 1). We propose that in group I, the second intercalation event is delayed relative to that in group II. Thus, when the equilibrium TBP/TATA-box mixture is challenged with a large excess of competitor DNA the members of group I that are bound with the least binding stability (T₇ and T₈), will be found to a larger extent stuck at the second step of the binding reaction. Hence, these sequences will not have the second pair of phenylalanine intercalated at the 3′-side of the TATA box, and as a result a larger percentage of these complexes dissociate fast.

The two TATA-box groups show different correlations between binding stability and structural properties

Within the group of MLP-like TATA boxes (group I) the values of the dissociation half-life and the global bending induced by TBP binding are correlated to each other (Table 1). The TBP/MLP complex is the complex with the longest half-life, and it is also the one with the highest DNA bend induced by the binding of TBP. This trend is followed for the rest of group I sequences (ρ = 1). This is similar to the relationship found by Starr et al. (53). On the other hand, no correlation between global induced TATA-box bending and half-life of the complex with TBP is observed in E4-like TATA boxes (group II, ρ = 0.1). However, in group II other structural correlations emerge. First, there is a correlation (ρ = 0.9) between binding stability and dinucleotide flexibility with respect to slide, when we use parameters taken from the study of Packer et al. (54). Here the most rigid dinucleotide (A-A) forms the most stable complex with TBP, and the most flexible dinucleotide (T-G) forms the weakest complex. Similarly, a strong correlation is observed between the conformational energy of tetranucleotides at position 6–9 and binding stability for group II sequences (ρ = 1), but no such correlation is found for group I sequences (ρ = 0.2), when we use parameters taken from the study of Packer et al. (39). In group II tetranucleotides with the lowest conformational energy (minimized with respect to all six base-pair step parameters for the central dinucleotide) form the most stable complexes with TBP. This correlation holds for group II sequences also when we sum the minimal tetranucleotide conformational energy along the entire sequence of each of our target sites, including the flanking sequences (ρ = 1).

Since sequences in group II are on the whole more flexible than canonical B-DNA, and in particular more flexible relative to group I, it is logical that binding stability correlates with lower conformational energy, as well as with more rigid sequences with respect to slide. In group I, the sequences are on the whole more rigid. After the first intercalation event TBP needs very little re-orientation for the second intercalation event, and thus the binding stability correlates with the ability to intercalate into the dinucleotide at position 7/8. Thus, the most stable binder is also the most bent one, which probably forms the most intimate interface. However, sequences in group II being highly flexible, and thus found in a variety of conformations, need a firm anchor to grip to after the first intercalation event, for the second intercalation event to occur, since they may not be rightly oriented at that step, and thus the most rigid sequence, that with the AAA tract is the most stable binder. Hence, in this more flexible group the correlation is between rigidity (relative to other group members) and binding stability.

Nearest-neighbor interaction versus long-range effects in TATA-boxes

Berg and von-Hippel (30,31) were the first to link between the statistics of binding sites occurrences and their binding free energy. In group I we see such correlations, both at the 8-bp level as well as on the dinucleotide level (Table 1). Binding stability is correlated with the number of occurrences of the 8-bp core TATA box in the EPD (ρ = 1), as well as the frequency of occurrence in EPD of dinucleotides at position 7/8 in A₄-A₅-containing TATA boxes (ρ = 0.9). No such correlation is observed among group II sequences. Moreover, we have calculated an informational theoretical weight matrix from sequences that conform to the YWTAWADN consensus. The matrix elements are the log-odds ratio per base pair and per position. This degenerate consensus sequence includes all high and moderate probability mononucleotide combinations appearing in the base frequency table of Bucher (12). There are 457 such sequences in the EPD, when we take only identified sequences belonging to known homology groups, and we take only one sequence per homology group, i.e. only sequences that are not from closely related promoters (see Material and Methods section for details).

The matrix elements are the maximum probability estimate for the binding energy contribution of each base at each position, when we assume that each position contributes independently to the total binding energy (29). The sum of the dot product between this matrix and a matrix (containing only 0's and 1's as its elements) corresponding to a sequence studied here gives an informational score for that sequence, which is the calculated total binding energy for that sequence (29). If the additivity assumption holds true for the studied binding sites the informational score for these sequences should correlate with their measured binding affinity. When we have indications for non-additivity in protein–DNA interactions, we can correct for nearest-neighbor interactions by calculating the dinucleotide information score for these sequences (31). This is done by adding to the term based on independent mononucleotide contributions a term that takes into account doublet correlations (20,31).

We have measured the binding stability of ten TATA boxes to yTBPc, and not the binding affinity, which is the more direct measure of the binding free energy. However, Hoopes et al. (55) found a direct correlation between binding affinity and binding stability for yTBP. Based on their experimental results, Hoopes et al. (55) concluded that the primary difference among TBP/TATA-box complexes is the dissociation rate, and that the difference in association rate between various yTBPc/TATA-boxes complexes is small. These results are in accord with the study by Grove et al. (56). Grove et al. (56) found that increased affinity of yTBP to TATA boxes that are more flexible, because of various sequence mismatches or because of various replacements of T with 5-hydroxymethyluracil, is due almost exclusively to an increase in complex stability rather than in the rate of complex formation. In addition, Starr et al. (53) found that the binding kinetics determined for yTBP, paralleled those for yTBPc. In Table 1, we present the mononucleotide and dinucleotide information scores for each of the sequences studies here. When we calculate the rank-order correlation coefficient, we observe that at the mononucleotide level there is no link between the measured binding stability and the individual information score of the 10 sequences studied here (ρ = 0.16). When we look at each group of five sequences separately, we find a very weak correlation between the binding stability of group I members and their individual mononucleotide information score (ρ = 0.5), and no such correlation among group II members (ρ = 0.2). If we include a nearest-neighbor doublet correlation term in the individual information score, the overall correlation among all 10 sequences is still very weak (ρ = 0.48). However, among group I members the correlation is now very high (ρ = 0.9), whereas for group II sequences no correlation is found (ρ = 0.2). We suggest that this behavior is due to the different structural properties of the two groups. Group I sequences all have A-tracts in them, a known cooperative-built structural unit that forms in sequences of the form A_n or A_xT_y [n ≥ 4, x + y = n, (34,35,36,38)]. Thus, the non-additivity in group I is due to the presence of cooperative A-tract motifs in these sequences. Berg and von Hippel (31) suggested that non-additivity will be observed above the scatter in the calculated and experimental binding energy only if at least half of the binding site is involved in the non-additive effect. In our case, the A-tract motifs are 4-bp long, and thus comprise half of the 8-bp core TATA box.

A different long-range cooperative structure exists in group II sequences. Here it is the cooperative structure of the flanking sequences that determines the structure in the core sequences (14). Thus, the non-additivity in group II is of different origin than that of group I. In group II sequences we have non-additivity, but it is not influenced by nearest-neighbor interactions within the TATA box, but instead stems from the effects of the flanking sequences on the core TATA box. Thus, no correlation is found between binding stability and individual information score that is based on weight matrices build from probability of occurrences of either mononucleotides or dinucleotides in TATA boxes (see further discussion below).

Long-range correlations and TBP-induced bend angles

We have calculated the Z statistics for tetranucleotides at position 6–9 from the dataset of sequences of the form YWTAWADN. It measures the deviation of the observed tetranucleotide motif from that expected based on additive mononucleotides. Shorter sequence motifs appear both in the MLP-like sequences as well as in the E4-like group. Hence, calculating the Z statistics of motifs shorter than tetranucleotide is biased by the higher occurrence of MLP-like sequences relative to E4-like sequences in eukaryotic genomes (∼2:1 ratio). In Table 1 it can be observed that there is a relationship between the Z statistics for the tetranucleotide at position 6–9 and the bend angle induced on TATA boxes by TBP binding in both groups. Larger induced bend angles (63–76°) are linked to tetranucleotides with positive Z-score, whereas those with smaller bend angles (43–53°) have negative Z-scores. This indicates that the latter sequences appear in natural sequences less than their mononucleotide occurrences, i.e. that they are being avoided in natural promoters. This may mean that TATA boxes in which TBP induces smaller bend angles are avoided in natural sequences regardless of the binding stability in complexes with TBP. Since the homology groups, as defined in the EPD and used here, are related to the DNA sequence of the promoter only, and not to its attached gene, it is impossible at this point to deduce whether this property is observed when looking across phylogenetic trees, namely, whether an alternative explanation to these observations is that sequences that incur small bend angle are selected for this property (or a related one) and are equally well conserved but are used less frequently.

TATA-box evolution and implications for locating new binding sites in genomic DNA

Specificity is not maximized in evolution. Instead, as Berg and von-Hippel suggested (31), evolution minimizes the maximum loss of specificity. Thus, specificity will tend towards a situation where mutational drift have relatively small effects. Hence, if we take a dataset of strong TATA boxes, such as that composed of the sequences conforming to the YWTAWADN consensus, we do get a correlation to binding stability, when we calculate the individual information score for sequences having the context-independent A-tract motif in them, or when we simply take the 8-bp occurrences of these sequences in the EPD, as expected based on the statistical–mechanical selection theory of Berg and von Hippel (31) (Table 1). This is not the case when we look at sequences containing a flexible context-dependent (A-T)_n motif. There are some indications that E4-like TATA boxes may be more sensitive to base changes within the core TATA box. First, they are more sensitive to base changes at position 7 and 8, as can be observed from the half-life in Table 1. Second, the change of T₃ to A₃ has larger effect (greater reduction in binding stability) going from TATATAAG to TAAATAAG, than from TATAAAAG to TAAAAAAG (53). However, in addition to the sensitivity to mutation within the TATA box, E4-like TATA boxes are sensitive to base changes in the sequences flanking them. Only in these sequences the role played by the flanking sequences in determining the structure of the core TATA box is dominant (14). Thus, E4-like TATA boxes are probably more sensitive to mutational errors than MLP-like TATA boxes, if only for the extended DNA region in which mutations can have an effect on TBP binding This may be the reason why evolution did not select these binding sites to be strong promoters, even though TBP can form very stable complexes with such sites, and in optimal sequence context TBP can form stronger complexes to these sites, than those it forms with the known strong basal promoter MLP. An additional structural rational why evolution did not frequently select E4-like sequences to be strong TBP-binding targets may be that stated in our previous publication (14). The pliability of E4-like sequences makes it quite easy to modulate their binding properties using their flanking sequences, whereas for the MLP TATA box these changes are not possible, and it is invariably a strong binding site. Thus, one can extend the specificity of TBP/TATA-box interaction by the use of flanking sequences of certain TATA boxes only.

For proteins that recognize their target sites mostly or exclusively by indirect readout, as is the case with TBP, mononucleotide weight-matrix methods do not work well in locating new binding sites. Including nearest-neighbor doublet correlation does significantly improve the correlation to binding free energy. However, as observed here, this is true only for sequences in which non-additivity is local. Sequences, in which non-additivity is of longer range than successive base pairs, are not represented well by probabilistic methods based on frequency of occurrence of base pairs in genomic DNA. For such sequences, we need to use methods that are based on experimental data on binding-site strength, which may soon be available more easily from high-throughput studies (57–59).