Short- and long-range effects of Sonic hedgehog in limb development

Abstract

The secreted protein Sonic hedgehog (Shh) and its transmembrane receptor Patched (Ptc) control a major signal transduction pathway in early vertebrate limb development. Ligand-free Ptc interacts with the transmembrane protein Smoothened (Smo) and blocks expression of Smo-controlled genes including ptc. Ligand-bound Ptc removes the block and leads to further expression of ptc, which in turn restricts the range of Shh transport. Currently it is not certain that Shh functions as a morphogen on the 300-μm scale of early chick limb development, because it has been difficult to determine how far different forms of Shh are transported. We develop a model to study the effects of two forms of Shh used experimentally and propose a mechanism for Shh signal transduction based on a two-state model for the Ptc-Smo interaction. Recent bead- and tissue-implant experiments can be explained by using this model without postulating different diffusivities for the two forms of Shh; a difference in other parameters such as the rate of release of Shh from the bead or transplant can explain the results equally well. The model also predicts that lower concentrations of Shh in a bead will produce a response similar to that after a tissue transplant. Our results provide an explanation for the counterintuitive experimental results and show that the same signal transduction mechanism can explain both short- and long-range Shh signaling. We conclude that Shh can function as a long-range morphogen.

Chick limb development is a widely used model system for the study of vertebrate pattern formation, and much is known about the signaling networks involved, the spatiotemporal patterns of gene expression, and the outcome of surgical interventions (1-3). The limb bud first appears as a small protrusion from the flank of the embryo that elongates along the proximo-distal axis, flattens along the dorsal-ventral (≈ top-to-bottom) axis, and develops an asymmetric pattern of cartilage condensations along the anterior-posterior (AP, ≈ “thumb”-to-smallest-digit) axis during outgrowth. Recent evidence suggests that there is a prepattern in the limb field before outgrowth (4), but later growth and patterning along the three axes depend on the establishment and maintenance of three distinct signaling regions within the limb bud: (i) the apical ectodermal ridge (AER), a group of columnar cells at the distal edge of the bud at the dorsal-ventral boundary; (ii) the zone of polarizing activity (ZPA), a region of specialized mesenchymal cells beneath the posterior boundary of the bud; and (iii) the nonridge ectoderm of the bud (5, 6).

Some of the molecules produced by the signaling centers have been identified. Fibroblast growth factors (FGFs) produced by AER cells are required for outgrowth and continued production of Sonic hedgehog (Shh), which is produced in the ZPA (7). The expression of FGFs in the AER is in turn up-regulated by Shh through Gremlin, which suppresses FGF inhibition by Bmp-2 (8). Several observations suggest that Shh regulates patterning along the AP axis (9): (i) its expression is detected first during initiation of limb-bud outgrowth, and thereafter expression colocalizes with the ZPA (10) both in position and in intensity; (ii) Shh replicates polarizing activity by inducing digit duplication when misexpressed in the anterior limb bud (1); and (iii) Shh is essential for the specification of digit identity (8).

Shh, FGFs, and their downstream effectors regulate limb outgrowth and coordinate the patterns of gene expression, in particular the Hox family (2, 11). This morphogenetic landscape of signals is “interpreted” by a population of proliferating, undifferentiated cells just below the AER. Before the model developed in ref. 12, patterning along the three axes of the limb was treated separately and growth was omitted. The model (12) considers a 2D section defined by the AP and proximo-distal axes and employs a simple positive-feedback kinetic scheme wherein Shh (respectively, FGF) production in the ZPA (respectively, AER) depends on the concentration of the other factor, and growth depends on the concentration of FGF. By postulating plausible interpretation functions for gene expression, the known patterns of Hox expression can be reproduced. The results demonstrated the dramatic effect of growth on the morphogenetic landscape and showed that the effects on patterning of the coupled, spatially separated signaling from the ZPA and AER can be predicted by the computational model.

It was assumed in ref. 12 that Shh is freely diffusing, but there was doubt until recently as to whether Shh functions directly as a long-range morphogen or whether it acts via secondary intermediates. In principle, the long-range effects could result from free diffusion of Shh, cell-to-cell relay, or directed transport via cytonemes (13). Shh undergoes cleavage to yield an N-terminal and a C-terminal portion, and in vivo the former is covalently linked with cholesterol to produce the active signal N-Shh_p (14). This linkage may lead to tethering to the membrane and perhaps restricted movement. However, recent evidence demonstrates long-range N-Shh diffusion (13, 15).

It has been suggested that the unmodified form N-Shh, which can be introduced ectopically, may diffuse more rapidly because it lacks the cholesterol tether (16, 17). To explore this, patched (ptc) expression was used to monitor the spatial and temporal aspects of Shh signaling in response to an ectopic Shh source (16). N-Shh-loaded beads were implanted in the anterior tissue of wing buds in stage 19/20 chick embryos, and ectopic expression of ptc was first observed 2 h postimplant (PI) in the posterior wing bud. The leading edge of high ptc expression moved anteriorly, covering the posterior half at 6 h PI and the entire wing bud at 16 h PI (16). Eighteen hours PI, ectopic ptc expression dropped in the central region along the AP axis, leaving an expression domain surrounding the bead in addition to the posterior expression domain controlled by the ZPA. In a second experiment, cell aggregates derived from ZPA tissue were grafted to the anterior margin of the wing bud. Here additional ptc expression was first induced around the implant at 4 h PI, then subsided in this region but was reestablished at 16 h in the host tissue surrounding the graft. There was little discernible change in the ptc expression in the posterior region. Thus two very different patterns of ptc expression were observed in the bead- and tissue-implant experiments, namely a ptc expression wave from the posterior end in response to the anterior bead implant, and a more complex rise and fall of ptc expression for the tissue implant. These results were explained by postulating a two-phase signaling model wherein Shh acts at a long range in the initial phase and short range in the later phase.

The major objectives here are to investigate the role of Shh diffusion and in particular to demonstrate that the results in ref. 16 can be explained without invoking different diffusivities for N-Shh_p and N-Shh and without postulating temporal changes in the mechanism of Shh signaling. We will (i) develop a mechanistic model for the interaction of free and Shh-bound Ptc with Smoothened (Smo), (ii) incorporate this in a model for reaction and transport in one space dimension that will shed light on the role of Shh diffusion on patterning, (iii) incorporate the expanded transduction scheme into the existing 2D model and analyze the spatiotemporal distributions of FGF, Shh, and Ptc, and (iv) use the computational model to study the effects of bead and tissue implants on the FGF, Shh, and Ptc distributions. Our results show that by changing only the effective rate of release of Shh from a transplant or bead, the model reproduces the traveling wave of posterior-anterior ptc expression after the bead implant as well as the anteriorly restricted ectopic ptc expression after the tissue implant. By analyzing the effect of key parameters in a geometrically realistic model of a limb bud we can suggest an explanation for these experiments, which show very different results for tissue and bead implants.

Model Development

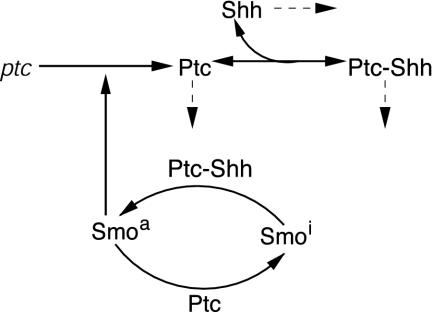
The transmembrane protein Smo mediates Shh signaling through phosphorylation of the Gli family of transcription factors (18, 19). There is evidence to suggest that the effect of Shh signaling on patterning and FGF production in the AER is mediated through Gli3 (8). Phosphorylated transcription factors then can affect expression of ptc and other genes, but the detailed mechanism is not known. Ptc represses Smo signaling, and ptc null mutants exhibit a constitutive Shh response phenotype (20). Binding of Shh to Ptc relieves the repression of Smo by Ptc, but neither the mechanism for Ptc repression of Smo nor the mechanism by which Shh-Ptc relieves this repression have been defined completely. However, it is known that Ptc acts catalytically to inactivate Smo, possibly via its role as a transporter of a molecule that interacts with Smo (21) or by promoting activity of a phosphatase that dephosphorylates Smo in the absence of Shh (22).

We assume that the total amount of Smo is fixed but can exist in either of two states: an active state, Smo^a, in which it activates transcription factors and an inactive state, Smoⁱ. We further assume that the Shh-Ptc complex catalyzes Smo activation, whereas Ptc catalyzes the transition of Smo from the active to the inactive state. The catalytic inactivation is based on previously cited evidence, but the activation step has not been demonstrated experimentally; all that is known is that binding of Shh to Ptc is not sufficient to relieve the repression (23). Finally, Ptc is produced at a rate proportional to the active Smo concentration.

The Shh-Ptc-Smo interactions are shown in Fig. 1. Ptc, both forms of Shh, and the Ptc-Shh complex are assumed to degrade at rates proportional to their respective concentrations. It has been shown that Shh degradation is enhanced by proteolytic targeting of the Shh-Ptc complex (24), and this is incorporated into the model through first-order degradation of the complex.

Fig. 1.

The kinetic model for the Shh-Ptc-Smo interactions. Solid lines denote primary steps, and dashed lines denote first-order decay.

There are conflicting reports that show that Shh is either capable (25) or not capable (26) of long-range diffusion, but it has been shown that native Shh diffuses across the chick limb bud (27). Other proteins such as tout velu, disp (28), and Hip (29) have been shown to affect Shh transport but are not considered in our model. In our model Shh is assumed to diffuse freely and binds to Ptc receptors reversibly. To accommodate both tissue and limb implant experiments, we introduce two forms of Shh: one that corresponds to the N-terminal peptide of Shh, designated N-Shh, and the native form with cholesterol attached, designated N-Shh_p. We allow for the possibility that N-Shh_p has a significantly lower diffusion rate by virtue of the fact that it may be transiently tethered to the membrane via cholesterol.

Our model thus incorporates the essential elements of Shh signal transduction while simplifying interactions (e.g., the pathway leading from Smo^a to activation of ptc transcription) whose exact molecular mechanism is not yet fully understood. All but one of the steps in the proposed mechanism are supported by experimental studies, the only postulated mechanism being the catalytic activation of Smo by the Shh-Ptc complex. Alternate mechanisms such as stoichiometric effects caused by decreased availability of free Ptc due to binding are rejected because the predictions conflict with results from experimental studies.

The 1D Model for AP Pattern Formation

To facilitate our understanding of the experimental results described above, we first consider a 1D domain. Later we demonstrate that this does not significantly alter the explanation of the results using simulations on a 2D domain.

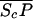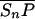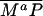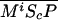Let S_c (S_n) represent N-Shh_p (N-Shh), both of which bind reversibly to free Ptc (P) to form the corresponding complex (). P and the Shh-Ptc complex catalyze the interconversion of active (M^a) and inactive (Mⁱ) forms of Smo through the formation of complexes and or 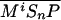. The rate of Ptc production is assumed to be a linear function of the active Smo concentration, and k^*_P is the associated proportionality constant. Uppercase letters represent the corresponding concentrations of species. k^sub_sup represents the rate constants for the reactions shown in Fig. 1, where sub denotes the complex formed and degraded as a result of the association (sup =+) or dissociation (sup =-) of the constituents. Absence of a superscript denotes a first-order rate constant for irreversible conversion or degradation.

Let D_c (D_n) represent the diffusivities of S_c (S_n), a_s the cell surface area per unit of total tissue volume, and θ_f the ratio of the extracellular volume to the total volume. X_Z and X_T are used to denote the fraction of the 1D domain occupied by the ZPA and tissue implant respectively, f_Z and f_T represent the rate of Shh production in the ZPA and in the tissue implant, respectively, and f_P is the basal rate of Ptc production.

We can now write the equations for transport and reaction of the proteins involved in the Shh signal transduction as follows. For a bead implant both the diffusion equations are needed, because both forms of Shh are present, but for a tissue transplant only the diffusion equation for the native form is used. In the 2D simulations an equation for the diffusion of FGF is added to those below (see The 2D Model).

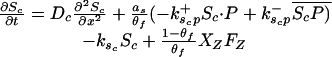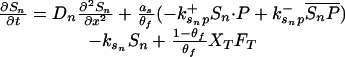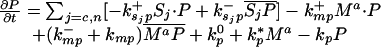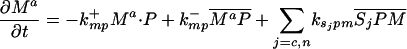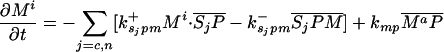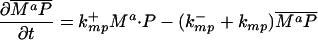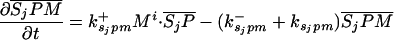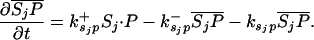A detailed derivation of the nondimensional forms of these equations used for numerical simulations and the values of the kinetic constants are given in Detailed Derivation of 1D and 2D Models, which is published as supporting information on the PNAS web site, www.pnas.org. These equations are supplemented with initial conditions for all species and zero-flux boundary conditions on the diffusible species. The specific values of the initial conditions are immaterial because, in the numerical simulations, the equations are integrated to reach a steady state before introducing a transplant.

The 2D Model

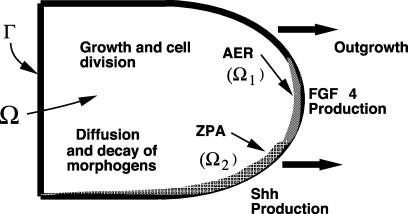
In ref. 12 the tissue was modeled as a viscous, incompressible fluid, the volume of which increases by virtue of growth and cell division (see Fig. 2). The two diffusible proteins (Shh and FGF) are produced only in the predefined ZPA and AER regions. Details of the formulation of the model and the numerical scheme, which is based on the immersed boundary method (30), are given in ref. 12.

Fig. 2.

A schematic of the growing limb and the processes involved in the limb. Ω, interior of the limb; Ω₁, AER region; Ω₂, ZPA region; Γ, boundary of the limb (from ref. 12).

The equations for the fluid motion comprise the continuity equation, the momentum equation, and the equations for the motion of the boundary. The continuity equation takes the form

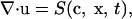wherein u is the local fluid velocity. The fluid motion is described by the Navier-Stokes equations, which provide the simplest description of a viscous fluid. These are (31)

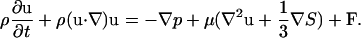Here ρ is the fluid density, u is the fluid velocity vector, p is the pressure, μ is the fluid viscosity, and F is the force density that ectoderm exerts on the surrounding fluid. The configuration of the boundary is given by X(s, t), where s is a Lagrangian label for a point on the boundary. We specify that X(s, t) moves at the local fluid velocity, and therefore

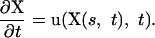The limb-bud boundary forces are transmitted directly to the fluid via the force density F, which is given by

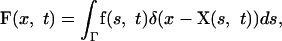where f is the force density at the boundary elements.

In the interior Ω of the limb the evolution of the protein concentrations, c, is described by a system of reaction-diffusionconvection equations of the form

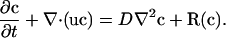The diffusion matrix D is a diagonal matrix, the only nonzero elements of which are the diagonal elements corresponding to Shh and FGF. We assume that the diffusion coefficients are constant, but we could easily incorporate dependence on the protein concentrations to describe control of cell-cell communication. The reaction rate vector R comprises reaction rates for each protein described previously in the 1D model with the exception that Shh production is restricted to Ω₂ and depends on the concentration of FGF there. FGF production in turn is restricted to Ω₁ and depends on the Shh level there (see ref. 12). On the boundary Γ we specify no-flux boundary conditions for all diffusible species. Details of the model equations and the parameters used are given in Detailed Derivation of 1D and 2D Models.

Numerical Simulations

Simulations were done for a time interval corresponding to 24 h PI. The 1D simulations were used to test the effects of changes in parameter values, and the results were confirmed with the 2D simulations.

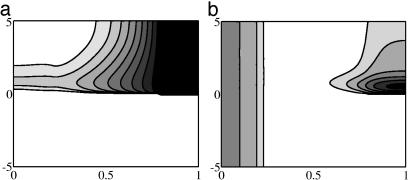
In the 1D simulations we model the ZPA as a region at the posterior end in which f_Z ≠ 0. Implantation of a Shh-filled bead at the anterior end is modeled as a region wherein Shh is held constant PI at a value of 100 nM.∥ An alternate way to model bead implants is to consider a finite amount present initially in the bead and let this concentration decrease as the Shh diffuses into the tissue. The Shh and Ptc profiles presented here can also be obtained by using such a representation and the initial concentration in the bead equal to that reported in ref. 16. For computational convenience in the 2D simulations we use the model of a fixed Shh concentration in the bead-implant region. For the tissue implant, the Shh production rate at the implant site is initially decreased from its value of f_Z in the ZPA to 1% of this and then increased to f_Z. Fig. 3 shows that the 1D simulations can reproduce the effect of the posterior-anterior Ptc wave during the bead implant and localized ectopic expression during the tissue implant. In Fig. 3a the increased Ptc concentration after the bead implant at the anterior end begins at the posterior end, as is observed experimentally (16). This is in contrast with Fig. 3b, wherein the ectopic Ptc concentration triggered by the tissue implant is localized near the implant. We found that we do not observe the decrease and increase in Ptc concentration at the tissue-implant site in the 1D simulation without first decreasing and then increasing the Shh production rate at the implant site. Later we suggest that this is a result of interactions with the AER that cannot be captured by the 1D model.

Fig. 3.

Contours of the computed Ptc distribution for bead (a) and tissue (b) implants. Dimensionless distance from the posterior end is shown on the x axis, and the PI time in hours is shown on the y axis. Contour lines are equally spaced from 0.1 to 0.5 nM (a) and 0.05 to 0.5 nM (b). Here and in Figs. 4 and 5 white denotes the lowest concentration and black the highest. In a, the rightmost portion of the domain corresponds to the bead, where there is no ptc expression.

How does one understand the long-range effect of the bead and the more localized effect of the tissue implant? Fig. 4 shows the Shh profile 5 h before and after the implant. Before the implant, there exists an (identical) Shh concentration profile across the AP axis, with highest levels at the posterior end where the ZPA is located and an exponentially decreasing concentration toward the anterior end. The change in Shh concentration profile after a bead or tissue implant depends on the type of implant. A high Shh concentration in the bead and higher N-Shh diffusivity lead to the delivery of a large bolus of Shh in the posterior region. This is seen in Fig. 4a near the posterior border shortly after implant. In contrast, a tissue implant with a lower diffusivity of N-Shh_p produces a significant increase in Shh concentration near the tissue implant but not in the posterior region (compare with Fig. 4b). At a location with high initial Ptc and Shh concentrations (the posterior end), the machinery for Shh signal transduction is in place, and the additional bolus of Shh immediately produces a corresponding increase in ptc expression levels. At a location with very low steady-state Shh and Ptc levels (the anterior region), even after a large Shh bolus, time is required for the Ptc concentration to increase such that the Shh signal is fully transduced and ptc expression is further up-regulated. This is the reason for the immediate up-regulation of ptc expression at the anterior end after a bead implant and the time lag before the ptc expression near the implant site is up-regulated. Later, the high Ptc levels near the implant site result in restricted spread of Shh, and hence the Shh from the implant has a negligible effect at long distances. Of course a very low Shh bolus results in negligible ptc up-regulation irrespective of the initial Shh and Ptc concentration. For a tissue implant, the posterior region sees a very low bolus of Shh, and hence there is no ectopic ptc expression at the posterior end after the implant. The anterior end is subjected to high Shh concentrations, and ptc expression is up-regulated to corresponding levels. However, because of the very low initial (preimplant) Ptc concentration at the anterior end, there is a time lag before ptc expression is up-regulated.

Fig. 4.

Shh profiles before and after bead (a) and tissue (b) implants as a function of distance from ZPA (x axis) and PI time (y axis). Contours range from 10 to 100 nM (a) and 2 to 12 nM (b).

We investigated the possibility that higher N-Shh diffusivity may not be responsible for the observed Ptc concentration profiles by doing a 1D simulation of a bead implant with Shh diffusivity equal to the diffusivity of native N-Shh_p and with lower concentrations of Shh in the implant. Fig. 5 shows the result of reducing the Shh diffusivity for several different initial Shh concentrations in bead implants. It is seen that at implant Shh concentration of 100 nM, decreasing the diffusivity does not qualitatively change the nature of the ptc expression kinetics (Fig. 5a), i.e., there is still a Ptc wave that starts from the posterior end. However, at low (10 nM) implant Shh concentrations, a low diffusivity results in local ptc expression around the implant site and no significant long-range effect, as in the response to a tissue transplant (Fig. 5b). Using the model developed here we can also predict the observed Ptc profiles that would result from implantation of cells that cannot covalently attach the cholesterol molecule to Shh. The simulations show that the effect of increased Shh diffusivity on Ptc concentration is similar to the bead response shown earlier, as one expects (results not shown). Thus there is no fundamental difference in the response to bead and tissue implants.

Fig. 5.

1D simulation of Ptc concentration on application of a bead containing 100 nM (a) and 10 nM (b) Shh with a Shh diffusivity corresponding to N-Shh_p. Note the similarity of a to the bead-implant simulation (Fig. 3a) and the similarity of b to the tissue-implant simulation (Fig. 3b). Contours range from 0.1 to 0.5 nM (a) and 0.05 to 0.5 nM (b).

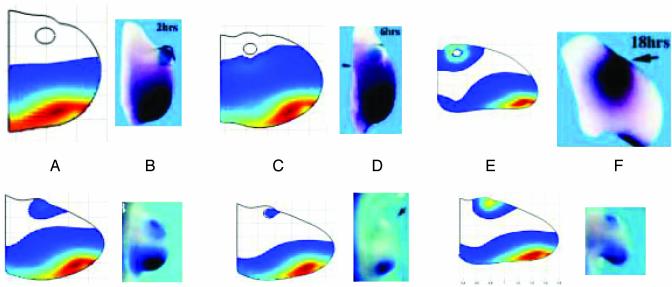
Numerical simulation of the 2D model shows that it can qualitatively reproduce not only the reported bead implant but also the decrease and reestablishment of Ptc concentration observed in the tissue-implant experiments. In Fig. 6, we show simulation results from the 2D model using identical diffusivities of N-Shh in the bead and tissue implants. As in the 1D simulations, the evolution equations are integrated to an approximate steady state before the bead or tissue implant. The simulation results shown here include a delay of 30 min between the active Smo concentration and the onset of the corresponding Ptc production. This is an approximation of the time lag in signal transduction from the activation of Smo to the phosphorylation of the transcription factors, transcription factor binding, ptc transcription, translation, posttranslational processing, and transport to give the final transmembrane form of the Ptc protein. From tests with the 1D model we observed that the magnitude of the time delay does not qualitatively affect the Ptc profiles in response to implants. The anterior-to-posterior wave of Ptc, followed by localized ectopic Ptc after a bead implant, is observed in the model simulations. There is also quantitative agreement with the observed PI expression time. In the tissue-implant simulation, initial increase in ectopic Ptc concentration near the implant site, followed by a reduction and reestablishment of ectopic expression, is qualitatively reproduced by the model, although the simulations shown here are chosen at PI times that are different from the reported values. This phenomena could not be explained by the 1D model but was observed when interactions with the AER were taken into account in the 2D model. The alteration in the morphology of the limb bud due to growth, surgical interventions and ectopic Shh sources can also be seen in the 2D simulations.

Fig. 6.

(Upper) Computational and experimental Ptc responses to bead implants. (Lower) Ptc response to tissue implants. (Upper) Numerical simulations of Ptc concentration 2, 6, and 18 h after bead implants (A, C, and E, respectively). (Lower) Ptc concentration 12, 16, and 20 h after tissue implant. (A, C, and E, respectively). Experimental results are from ref. 16 for ptc transcript concentration 2, 6, and 16 h after bead implants PI and for tissue implants, 4, 8, and 16 h PI. (B, D, and F, respectively). [Reproduced with permission from Drossopoulou et al. (16) (Copyright 2000, Company of Biologists Ltd.).] The simulation shows the experimentally observed posterior-anterior ptc expression wave followed by restriction of expression near the implant site. Tissue implant simulations show the initial expression near the implant site followed by a decrease and subsequent reestablishment of ectopic ptc expression. The figures for numerical simulations have been rescaled. The unscaled length of the proximal boundary in each of the numerical simulations is identical. The rescaling with respect to A Upper is as follows: C Upper, 1.8:1; E Upper, 3:1; A Lower, 1.9:1; C Lower, 2.1:1; E Lower, 2.7:1. The unscaled version of C Upper, for example, is 1.8 times larger than shown.

Discussion

We developed a model of Ptc-Smo interaction and incorporated it into a model for tissue-level behavior in response to bead or tissue implants. Several reports support elements of the proposed mechanism. It has been shown recently that Ptc catalytically suppresses Smo activity (21). Studies with Shh variants reveal that mere binding of Shh to Ptc does not lead to the induction of gli-1 or ptc. Thus there is a decoupling between the Ptc binding activity and signaling activity of Shh (23). In the model we postulate that the Shh-Ptc complex catalytically activates Smo. One possible function of the Ptc-Shh binding might be to localize the Shh near inactive Smo such that the signaling domain (thought to be the N-terminal cysteine) can relieve the inhibition of Smo. The present model does not describe ptc^-/- mutants because the activation and inactivation of Smo is catalyzed by the Ptc-Shh complex and Ptc, respectively. However, they can be treated simply by assuming that all Smo exists in its active form initially. Alternatively, one could model Ptc mutants or functional inactivation experiments by postulating a slow basal rate of interconversion between the two forms of Smo.

The model simulations involve several parameters with values that are not available. We have chosen values from comparable systems wherever possible (for example ligand-receptor binding constants for the protein-binding steps in our model). Details of the parameter values used are given in Tables 1 and 2, which are published as supporting information on the PNAS web site. The 2D model involves several parameters for the rheological properties of the limb tissue that have been arbitrarily assigned so as to replicate the limb morphology in the absence of implants (the control experiments; ref. 16). Our 1D model simulations reveal that the experimentally observed Ptc response to bead implants can be fully explained by the 1D fixed-domain model, which suggests that the results obtained are not sensitive to the growth kinetics and hence the parameter values used for the growth rates and rheological properties. However, the moving-boundary 2D model presented here is necessary to model limb morphology and to model cell-tracking experiments. It can be seen from the values of the dimensionless parameters that the values of the reaction rate constants multiplied by γ are significantly higher than the dimensionless values of the diffusion constants. Consistent with this fact, we observed that increased diffusion rate constants lead to a faster Ptc wave from the anterior region in response to a bead implant and more tissue-implant-like behavior when the diffusion rates are lowered.

We have seen that a 1D model can give significant insight into the Shh signal transduction process but cannot capture all the observed ptc expression dynamics resulting from a tissue implant. The reason lies in the fact that although the phenomena we seek to explain involves ptc expression only along the AP axis, the ZPA and tissue-implant activity is modulated by interactions with FGFs produced by the distally located AER. After a tissue implant, the Shh production in the implant varies as a function of the FGFs and is reinitiated because of interactions established with the AER. This conclusion is supported by reports that shh expression in the implant is higher at regions near the AER (16). However, the bead implant, being physiologically inert, can be qualitatively simulated by using the 1D simulations.

We have demonstrated that a geometrically and biochemically realistic model of the bead and transplant experiments reported by Drossopoulou et al. (16) can reproduce the observations described therein without invoking different diffusion coefficients for the modified and unmodified forms of Shh. The nature of the spatio-temporal profile of ptc expression depends on the magnitude of the additional Shh that is experienced by various regions in the tissue due to the implant. Of course, as we have shown, a difference in diffusion coefficients may contribute to the effect, but it is not an essential component. Thus Shh can function as a morphogen in limb development, and its long- and short-range signaling activities can be explained via a single mechanism for Shh signal transduction.

The mechanistic model leads to testable predictions of ptc expression profiles under different implant conditions. The model predicts that bead implants with very low Shh concentrations but high Shh diffusivity will lead to ptc expression profiles of the type seen in tissue implants. Bead implants with a high concentration of Shh will exhibit the same response irrespective of the Shh diffusivity. Tissue implants producing N-Shh that is incapable of cholesterol modification will result in a bead-implant-like response if the rate of production of N-Shh is sufficiently large.

Here we have described Shh transport using Fickian diffusion kinetics, but other modes such as “bucket-brigade” transport may have a very similar mathematical representation and lead to similar predictions. Here and in ref. 12 we treat the limb as a viscous fluid, but cellular aggregates display elastic behavior as well (32). Moreover, the cells are growing and dividing in a matrix comprising collagens, proteoglycans such as hyaluronic acid, and possibly various adhesion molecules. To better represent the mechanical forces that shape the limb, a better theoretical model for the tissue is needed.