Role of across‐muscle motor unit synchrony for the coordination of forces

Abstract

Evidence from five‐digit grasping studies indicates that grip forces exerted by pairs of digits tend to be synchronized. It has been suggested that motor unit synchronization might be a mechanism responsible for constraining the temporal relationships between grip forces. To evaluate this possibility and quantify the effect of motor unit synchrony on force relationships, we used a motor unit model to simulate force produced by two muscles using three physiological levels of motor unit synchrony across the two muscles. In one condition, motor units in the two muscles discharged independently of one another. In the other two conditions, the timing of randomly selected motor unit discharges in one muscle was adjusted to impose low or high levels of synchrony with motor units in the other muscle. Fast Fourier transform analysis was performed to compute the phase differences between forces from 0.5 to 17 Hz. We used circular statistics to assess whether the phase differences at each frequency were randomly or non‐randomly distributed (Rayleigh test). The mean phase difference was then computed on the non‐random distributions. We found that the number of significant phase‐difference distributions increased markedly with increasing synchronization strength from 18% for no synchrony to 65% and 82% for modest and strong synchrony conditions, respectively. Importantly, most of the mean angles clustered at very small phase difference values (∼0 to 10°), indicating a strong tendency for forces to be exerted in a synchronous fashion. These results suggest that motor unit synchronization could play a significant functional role in the coordination of grip forces.

Introduction

Evidence from five‐digit grasping studies indicates that normal forces exerted by digits tend to be synchronized across a variety of task constraints (Santello and Soechting 2000; Rearick and Santello 2002; Rearick et al. 2002, 2003). The consistency with which force synchronization patterns are observed during different types of multi‐digit grasping tasks would suggest a mechanism that operates in a default‐like fashion. In fact, the biomechanical architecture of extrinsic hand muscles (i.e., superficial and deep digit flexors) might account for force covariations across multiple digits (Schieber 1991, 1995). However, Santello and Soechting (2000) observed that the coupling between multiple normal forces is not obligatory. Specifically, force covariations were disrupted when subjects were asked to lift one of the fingers during object hold. A recent study (Rearick et al. 2003) was designed to further investigate the extent to which force coordination patterns are task dependent. When subjects gripped an object without holding it against gravity, force synchronization was greatly reduced compared to that when subjects held the object after lifting it above a support surface. These findings strongly suggest that force synchronization is not an obligatory consequence of multi‐digit force production. Such task dependency also suggests that finger muscle biomechanical constraints alone cannot fully account for multi‐digit force synchronization. These results further suggest that force synchronization is not simply an epiphenomenon of force production.

Several non‐mutually exclusive mechanisms might be responsible for the coordinated force fluctuations observed across pairs of digits during grasping. One of these mechanisms might be the activation of motor units innervating different functional subdivisions of finger flexor muscles, e.g., flexor digitorum profundus (FDP; Kilbreath et al. 2002). Coordinated force fluctuations might also be a consequence of synchronous firing of motor units belonging to different hand muscles, i.e., FDP and the flexor pollicis longus, or different FDP compartments (Winges et al. 2003; Reilly et al. 2004). The present study focuses on motor unit synchrony.

We have previously suggested that motor unit synchronization might be a mechanism responsible for constraining the temporal relationships between grip forces observed during multi‐digit grasping (Santello and Soechting 2000; Rearick and Santello 2002; Rearick et al. 2002, 2003). Early observations of motor unit firing patterns suggested a higher than chance tendency for pairs of motor units to fire synchronously (Sears and Stagg 1976) particularly among muscles that control the digits (Datta and Stephens 1990; Bremner et al. 1991a; Nordstrom et al. 1992). Sears and Stagg (1976) proposed that the above‐chance coincident discharges of motor units occurring within a few milliseconds of each other (shortterm synchronization) arises from shared inputs from branched axons of last‐order neurons. This increases the probability of simultaneous discharge in the target neurons sharing these inputs. Later work in cats (Kirkwood and Sears 1978) and humans (Datta and Stephens 1990) gave further quantitative support to this hypothesis. Synchrony of broader duration is likely due to synchronization of separate pre‐synaptic inputs to the motoneurons (Kirkwood 1979).

It should be noted that most motor unit studies have focused on within‐muscle motor unit synchrony, i.e., pairs of motor units belonging to the same muscle. However, the above evidence from multi‐digit grasping studies prompts questions that must be addressed by studying the behavior of motor units belonging to different muscles. Although several studies have reported across‐muscle synchronization (Bremner et al. 1991a, 1991b, 1991c; Gibbs et al. 1995; Huesler et al. 2000; Hockensmith and Fuglevand 2000), this phenomenon deserves further investigation. In particular, what needs to be determined is the functional consequences of across‐muscle synchronization. The purpose of the present investigation was to examine the extent to which across‐muscle motor unit synchronization can affect the relationship between muscle forces. To address this issue, we used a motor unit model to simulate force produced by two muscles using three physiological levels of motor unit synchrony across the two muscles. In one condition, motor units in the two muscles discharged independently of one another. In the other two conditions, the timing of randomly selected motor unit discharges in one muscle was adjusted to impose low or high levels of synchrony with motor units in the other muscle. The results of the present investigation indicate that synchrony among motor units in different muscles can account for a large part of coordinated force fluctuations across digits during gripping tasks. Preliminary accounts of these results have been published as an abstract (Fuglevand and Santello 2002).

Methods

Motor unit model

Isometric forces developed concurrently in two muscles were simulated using a motor unit model (for details, see Fuglevand et al. 1993). Each muscle consisted of 120 motor units and the properties of the motor units in the two muscles were the same. Motor unit twitches were modeled as the impulse response of a critically damped 2nd order system (Fig. 1). Each motor unit was assigned a unique twitch amplitude and twitch contraction time. The distribution of motor units based on twitch amplitude was skewed such that many motor units had small twitch forces and relatively few motor units had large twitch forces. Forces were scaled relative to the twitch force of the weakest motor unit and twitch forces ranged from 1.0 to 100.0 arbitrary force units. Contraction times were assigned as an inverse function of twitch amplitude and ranged from 30 ms for the strongest unit to 90 ms for the weakest unit (Fig. 1).

Fig. 1.

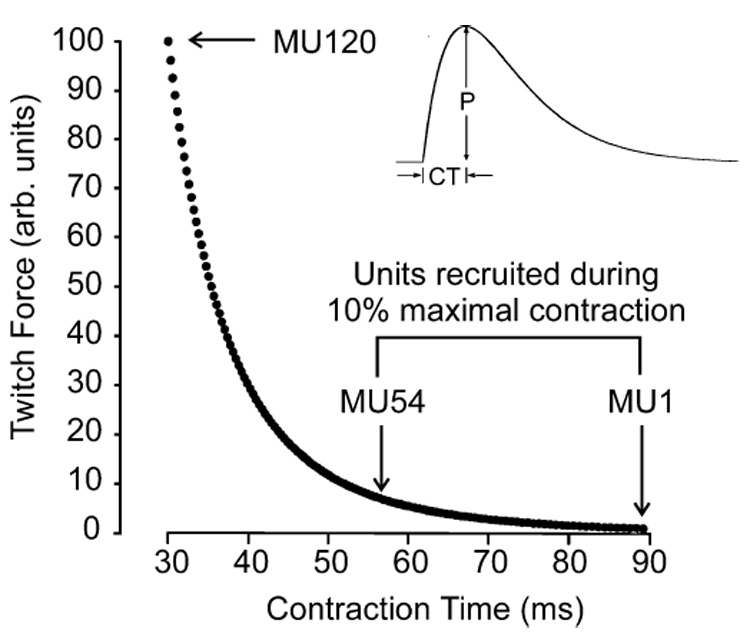
Twitch properties of simulated motor units based on the model of Fuglevand et al. (1993). The twitch force of each motor unit was simulated as the impulse response of a critically damped 2nd order system (inset). Each of the 120 motor units within the simulated muscle was assigned unique values of twitch contraction time (CT) and peak twitch force (P) such that weakest motor unit (MU1) had the longest contraction time and the strongest motor unit (MU120) had the briefest contraction time. For the present simulations, excitatory drive to the motor neuron pool was set at 10% of the maximum excitation, which caused the weakest 54 motor units to be recruited

All motor neurons within a pool received the same level of excitatory drive. Recruitment thresholds were determined as an exponential function which assigned many neurons to have low thresholds and few to have high thresholds. Motor neurons supplying weaker muscle units were assigned lower recruitment thresholds than motor neurons innervating stronger muscle units. Recruitment thresholds varied by 30‐fold across the motor neurons comprising a pool. A motor unit (i) was recruited when the excitatory drive equaled or exceeded the recruitment threshold excitation (RTE_i) assigned to its motor neuron. At threshold, motor units discharged at a minimum firing rate (MFR) of 8 impulses (imp)/s. Firing rate of a motor unit (FR_i) increased linearly with increased excitation beyond the threshold level up to an assigned maximum rate. The gain (g) of the excitatory drive‐firing rate relationship was assigned the same value for all motor neurons. Therefore, the mean firing rate of a motor neuron in response to an excitatory drive function, E(t), was modeled as: FR_i(t)=g×[E(t)−RTE_i]+MFR for E(t) 3 RTE_i (Fuglevand et al. 1993). Maximum discharge rates were inversely related to recruitment threshold and varied from 25 imp/s for the highest threshold unit to 35 imp/s for the lowest threshold unit. To emulate the stochastic nature of motor neuron activity, the discharge times of individual motor units predicted from the above equation were then adjusted to simulate a Gaussian random process with a coefficient of variation (standard deviation/mean × 100) in the interdischarge intervals of 20%. Prior to imposition of synchrony (see below), each motor unit discharged independently of every other motor unit and successive interdischarge intervals were uncorrelated within a motor unit. Motor unit force was modeled as a sigmoid function of discharge rate. This was accomplished by including a gain factor that amplified the motor‐unit impulse response based on the instantaneous discharge rate of the unit (Fuglevand et al. 1993). Total muscle force was determined as the linear sum of the active motor unit forces.

Simulation procedures

Motor unit activities and associated isometric forces were simulated for the two muscles when both muscles were driven at 10% of maximum excitation. Maximum excitation was defined as the excitatory drive required to just bring the highest threshold motor unit to its assigned maximal discharge rate (Fuglevand et al. 1993). At 10% maximum excitation, 54 motor units were recruited (Fig. 1) and the discharge rates ranged from 8 to ∼12 imp/s. This relatively low level of excitation was chosen to mimic the type of contractions typically used to study motor unit synchrony in human subjects. Forces were simulated at 1,000 samples/s for a period of 10 s. A total of ten trials were simulated for each condition and muscle.

Within‐muscle synchrony

In order to simulate a level of synchrony that normally occurs among motor units within individual hand muscles, we used an approach modified from that described in detail previously by Yao et al. (2000). In general, this process involved adjusting discharge times of some units to coincide with selected discharges of other units. As shown in Fig. 2A, each motor unit was paired with every other motor unit for this process. For each pairing, one unit was designated as the reference unit and the other unit was identified as the test unit. Then, a proportion of the discharges of the reference unit were randomly selected to which the test unit had its nearest discharge shifted to coincide with the selected discharge of the reference unit (Fig. 2B). Some variability in the alignment of adjusted discharges was included such that the average duration separating synchronized discharges was 0 ms with a standard deviation of ±2 ms (Yao et al. 2000). The number of reference‐unit discharges selected to serve as events to which the test unit had discharges aligned was based on the frequency of extra (i.e., above chance) synchronous discharges observed for motor unit pairs within human hand muscles (∼0.5–0.7 extra synchronous discharges/s, Nordstrom et al. 1992; Keen and Fuglevand 2004). We chose a value of 0.6 extra synchronous discharges/s to represent the typical level of synchrony among motor units within a hand muscle. Therefore, on average, 0.6 discharges/s were randomly selected from the reference‐unit discharge train to which the test unit had its nearest discharges aligned. This level of within‐muscle synchrony was used for all pairs of active motor units and was maintained for all simulation conditions.

Fig. 2A, B.

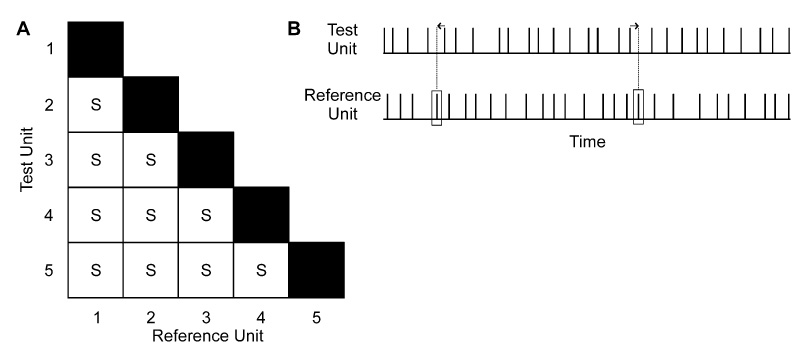
Schematic diagram depicting method used to add synchrony to motor unit activity. A shows matrix of motor‐unit pair combinations to which synchrony (S) was added within a muscle. For each combination, one unit was designated as the reference unit and the other as the test unit. For randomly selected discharges of the reference unit (rectangles, B), the nearest discharge of the test unit was shifted (arrows) to coincide with the reference unit discharge. The average frequency of these adjustments to impose synchrony within a muscle was 0.6 adjustments/s, a value that roughly corresponds to the frequency of extra synchronous discharges observed for pairs of motor units in human hand muscles

Across‐muscle synchrony

In order to evaluate the effect that synchronized activity among motor units lying in different muscles might have on the temporal relationship between forces generated by separate muscles, three levels of across‐muscle synchrony were tested in the simulations. In one condition, no across‐muscle synchrony was added. In a second condition, modest across‐muscle synchrony was imposed upon the discharge patterns previously created for the two muscles. For this condition, 0.3 extra synchronous discharges/s were randomly selected from the discharges of reference units in Muscle 1 to which discharges of test units in Muscle 2 were aligned according to the method described above. Each unit in Muscle 1 was paired with every unit in Muscle 2 for the addition of synchrony. In the third condition, strong across‐muscle synchrony (0.6 extra synchronous discharges/s) was added between reference units in Muscle 1 and test units in Muscle 2. These values of across‐muscle synchrony were used to approximate the levels of synchrony observed between pairs of motor units residing in different compartments of extensor digitorum (0.40±0.22 extra synchronous discharges/s, Keen and Fuglevand 2004) and between motor units in flexor pollicis longus and the index finger compartment of flexor digitorum profundus (0.52±0.27, Hockensmith and Fuglevand 2000; 0.49±0.14, Winges et al. 2003).

The probability that a discharge of one unit was synchronized to a discharge of a second unit can be estimated by dividing the imposed level of synchrony (extra synchronous discharges/s) by the discharge rate of the first unit. The average discharge rate of units in these simulations was about 10 discharges/s. Therefore, for the two levels of synchrony of 0.3 and 0.6 extra synchronized discharges/s, the probability that the discharge of one unit was synchronized with the discharge of a unit, p(s), in the other muscle was ∼0.03 and 0.06, respectively. Furthermore, it is possible to estimate the likelihood that a discharge of one unit was synchronized with the discharge of any unit in the other muscle. For example, for the moderate level of synchrony used (0.3 extra synchronous spikes/s with a probability of ∼0.03) the probability that a discharge of a unit is not synchronized, p(ns), with the discharge of another unit is given as: p(ns)=1.0−p(s)=0.97. Then, based on the multiplication rule for the law of total probability, the probability that a discharge of a unit is not synchronized with any of the 54 units in the other muscle, P(NS), is given by the product of the individual probabilities, namely, P(NS) = p1(ns) × p2(ns) × … p54(ns) = p(ns)⁵⁴ = 0.97⁵⁴ = 0.19. Therefore, the probability that the discharge of a unit will be synchronized with the discharge of at least one unit in the other muscle, P(S), is given as P(S)=1.0−P(NS)=1.0−0.19=0.81. Consequently, even for the modest level of synchrony used in these simulations, nearly every spike of a unit was synchronized with a spike of at least one unit (and often more) in the other muscle.

Analysis of simulated forces

We computed the average normalized force and the coefficient of variation over the period of steady force production for simulated forces F₁ and F₂ produced by Muscle 1 and Muscle 2, respectively. The relationship between F₁ and F₂ was analyzed in the time and frequency domain as done previously on forces recorded during 5‐digit grasping tasks (see “Introduction”). In these tasks, we analyzed normal forces exerted by all pairs of digits during object hold (2 s). To allow comparison with results from grasping tasks, we selected a time period of 2 s during the ‘steady state’ of simulated force produced by two muscles. Details of the analysis are given below.

We performed linear regression analysis to assess the extent to which the pair of simulated forces (F₁ vs. F₂) covaried in the time domain for each condition. To better illustrate force covariation at particular frequencies, we performed a Fast Fourier Transform analysis (FFT) on the simulated forces over a period of 2,048 s (i.e., 2,048 force samples).

From the FFT, we computed the phase response (α) by calculating the arctangent (arctan) of the ratio of the imaginary and real components of the Fourier transform. The phase difference between F₁ and F₂ (∠) was calculated at each frequency as: ∠=αF₁−αF₂. This yielded a value for each trial indicative of the temporal relationship between the two simulated forces at a particular frequency. For example, if increasing the amount of synchrony caused fluctuations in F₁ and F₂ at a particular frequency to occur at similar times, then ∠ would tend to be ∼0°, i.e., an in‐phase force relationship. At the other extreme, if F₁ increased while F₂ decreased, then ∠ would tend to be ∼±180°, i.e., an out‐of‐phase relationship. For comparison with previous grasping studies, ∠’s were calculated over frequencies from 0.5 to 17 Hz in 0.5 Hz frequency increments (n=34). For each frequency, a distribution of 10 ∠ values was generated, i.e., one ∠ value per trial.

Circular statistics

We performed the present study to test the hypothesis that there is a relationship between motor unit synchronization strength and force synchronization (see “Introduction”). To assess the existence of such a relationship and quantify its strength we used circular statistics (Batschelett 1981). This analysis has been described in detail elsewhere (Santello and Soechting 2000; Rearick et al. 2002). Briefly, for each frequency we tested whether phase differences (n=10) tended to cluster at a particular angular value or to be distributed uniformly a across a ±180° range of phase differences, i.e., whether the phase difference distributions were non‐random or random, respectively. If the distribution was non‐random, it would reveal a tendency for consistent relationships (i.e., phase difference) between forces across trials.

For each phase difference distribution, we computed three parameters: the length of the mean vector (r), the mean angle of the sample (ϕ), and the angular deviation (s). The components of the vector r are the x‐ and y‐coordinates associated with each phase difference, i.e., cos∠ and sin∠, respectively. The length of the vector r ranges from a minimum of 0 to a maximum of 1 for phase difference distributions that are evenly distributed (random distributions) or that cluster at a particular angular value (non‐random distribution), respectively. The parameters ϕ and s are analogous to the mean and standard deviation used in linear statistics. Therefore ϕ indicates the mean phase difference of the distribution and s indicates the amount of dispersion around ϕ. The means of x‐ and y‐coordinates (x and y) associated with each phase difference were used to compute r as: (x²+y²)^1/2, and the mean angle of the sample (ϕ) was computed as: arctan(x/y). The parameter s was computed as: [2(1−r)]^1/2. Randomness of phase difference distributions was tested using the Rayleigh test, which is based on the amplitude of the parameter r (Batschelett 1981). The mean angle was computed only for the non‐random phase difference distributions.

Results

Example cross‐correlation histograms depicting the relative timing of discharges of one unit with respect to another are shown for randomly selected pairs (one unit from each muscle) for each across‐muscle synchrony condition in Fig. 3. Above each histogram is shown the cumulative sum (cusum), which was calculated by adding successive differences between the count of each bin in the histogram and the mean bin count (Ellaway 1978). A rise in the cusum near time 0 was used to delineate a synchronous peak in the cross‐correlation histogram. The number of counts in the peak region of the histogram above that expected due to chance (i.e. in excess of the mean count in the off‐peak region) divided by the duration of the trial (for these examples, trial duration was extended to 30 s) yields the number of extra synchronous discharges/s for the pair of selected units. In the case of the no‐synchrony condition in which no peak was evident in the cusum, synchrony calculation was based on an 11‐ms window centered on time 0. For the moderate‐synchrony condition (Fig. 3, middle panel), a small peak is evident near time 0 in the histogram, which yielded a synchrony value of 0.32 extra synchronized discharges/s. A larger peak is evident in the cross‐correlation histogram for the strong synchrony condition (Fig. 3, right panel), from which a synchrony value of 0.66 extra synchronized discharges/s was calculated. These calculated values of synchrony derived from the cross‐correlation histograms were close to the imposed levels of synchrony set by the simulations.

Fig. 3.

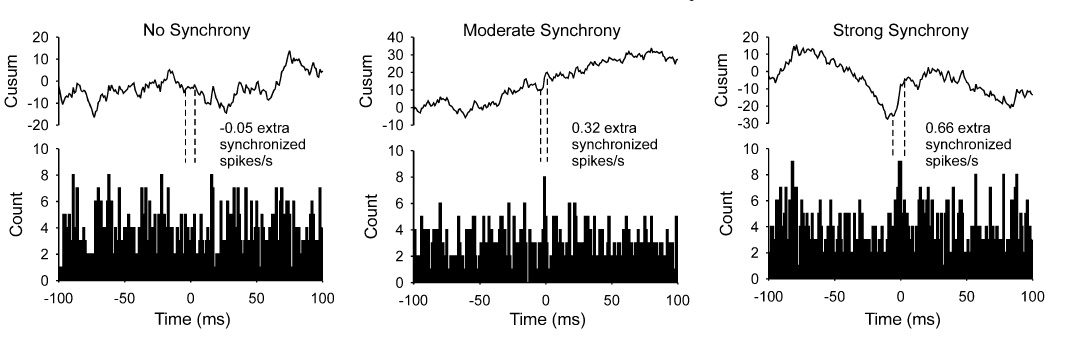
Example cross‐correlation histograms. Cross‐correlation histograms (lower row) and associated cumulative sum (cusum, upper row) for randomly selected pairs of motor units (one unit from each muscle) for the three across‐muscle synchrony conditions: no synchrony, moderate synchrony, strong synchrony. The duration of the trials used for these examples was 30 s. Dashed vertical lines indicate the limits of the peak in the histogram as estimated from the cusum for the moderate and strong synchrony conditions. For the no‐synchrony condition, the dashed lines denote an 11‐ms window centered on time 0. The number of counts within the delimited region in excess of the mean level were divided by the duration of the trial to obtain the rate of extra synchronous spikes/s

Figure 4A shows example trials of the simulated force output for the two muscles. The amplitude of both forces increased over the initial ∼500 ms and then remained relatively constant for the remainder of the simulation. Figure 4B shows the simulated forces for the two muscles for three levels of across‐muscle synchronization, i.e., 0, 0.3, and 0.6 extra synchronous discharges/s. Note that synchrony was adjusted by altering the firing pattern of motor units belonging to Muscle 2 (Fig. 4B, thick line). The motor unit population of Muscle 1 served as the reference units to which selected discharges of Muscle 2 were adjusted. Consequently, the force profile for Muscle 1 (Fig. 4B, thin line) remained the same for a given trial across all synchrony levels (see “Methods”).

Fig. 4A, B.

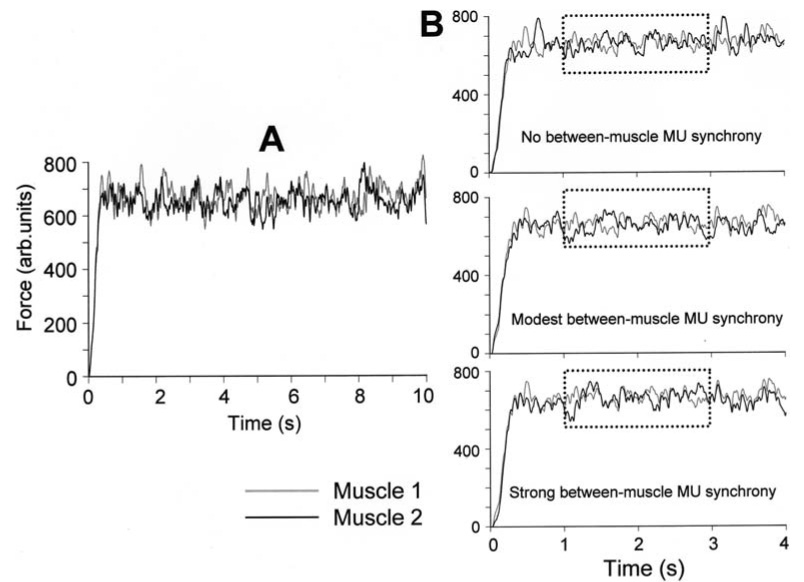
Force output of two simulated motor unit populations. A shows the forces generated by the two populations of motor units (Muscle 1 and Muscle 2, respectively) over the entire period of simulation (10 s) (modest synchrony condition). Force amplitude is expressed in normalized units. B shows the two forces simulated under three conditions: no across‐muscle motor unit synchrony (top panel); modest across‐muscle motor unit synchrony (middle panel); and strong across‐muscle motor unit synchrony (bottom panel). Please note that motor unit synchrony was added by changing the motor unit firing behavior of Muscle 2 only. The dashed box indicates the time period over which time and frequency domain analyses were performed

Amplitude and variability of simulated force

The normalized force averaged during the plateau ranged from 510 to 715 across all trials and had similar values for the two muscles across the three conditions. The average coefficient of variation across trials ranged from 5 to 7% with approximately the same amount of variability for both muscles and across conditions. This amount of force variability is comparable to that observed experimentally in a recent study where the coefficient of variation of normal fingertip forces during static object hold ranged from 5 to 9% (Rearick et al. 2002).

Linear regression and Fast Fourier Transform analysis

We quantified the temporal relationship between F₁ and F₂ by performing linear regression analysis. On average, the R value tended to increase with increasing synchrony. The mean of the z‐transformed R values ± standard deviation found for the no synchrony condition was −0.01 (±0.12), whereas for the modest and high synchrony conditions R was 0.28 (±0.08) and 0.30 (±0.08). These R values are within the range of those reported for correlations between normal forces exerted by pairs of fingers during object hold, e.g., from 0.22 (middle finger vs. little finger) to 0.57 (index finger vs. little finger; Santello and Soechting 2000).

To further quantify the relationship between the simulated forces, we performed Fast Fourier Transform analysis (FFT; see “Methods”) over a 2 s time period (Fig. 4B, dashed box). Phase differences between the forces were then computed over the 0.5–17 Hz frequency range as most of the power (∼75%) of both forces was found within this frequency range. Figure 5A–Figure 5C shows the distribution of phase differences associated with each frequency for across‐muscle synchrony values of 0, 0.3 and 0.6 extra synchronous discharges/s, respectively. For each frequency, a single phase‐difference value was determined for each of ten trials. A histogram was generated that indicated the number of trials possessing a particular phase difference value (binned in 0.5 degree increments) for a given frequency. Therefore, the vertical axes in Fig. 5A–Fig. 5C indicate the number of trials having a specified phase difference at a particular frequency. For the no‐synchrony condition (Fig. 5A), phase differences tended to be uniformly distributed across the −180° to +180° range. This indicates that the temporal relationship between the two forces was characterized by a high between‐trial variability. However, when we imposed modest synchrony across the two muscles (0.3 extra synchronous discharges/s; Fig. 5B), phase differences tended to cluster toward near 0° phase difference at most frequencies, as indicated by larger central peaks of the distributions. This tendency was further enhanced when we imposed high across‐muscle synchrony (0.6 extra synchronous discharges/s; Fig. 5C).

Fig. 5A–F.

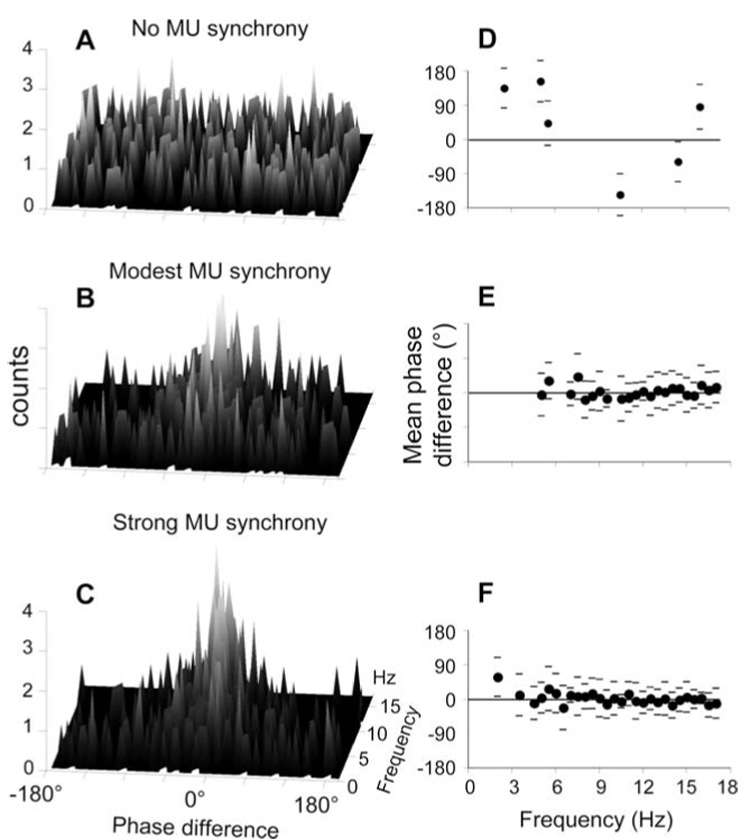
Between‐forces phase differences and circular statistics. A, B and C show the phase differences between the pair of simulated forces for no motor unit synchrony, modest motor unit synchrony and strong motor unit synchrony, respectively. Phase differences from all trials (n=10) are plotted as 3‐D histograms for each frequency (n=34) from 0.5 to 17 Hz. For graphical purposes, phase differences were binned into 5° intervals. D, E and F show the mean phase difference ± angular deviation (filled circles and horizontal lines, respectively) computed on phase difference distributions shown in A, B and C, respectively. Note that mean phase difference values are shown only for significant phase difference distributions

The results shown in Fig. 5A–Fig. 5C were subjected to circular statistics analysis (see “Methods”). Figure 5D–Figure 5F shows the mean phase difference computed from phase difference distributions shown in Fig. 5A–Fig. 5C, respectively. Please note that we computed the mean phase difference only from non‐random phase difference distributions (Rayleigh test; see “Methods”). Hence, missing values in the plots indicate that the phase difference distribution at a particular frequency was random. It can be noticed that for the no synchrony condition (Fig. 5D), only 6 out of 34 phase difference distributions were non‐random, the mean angle ranging from −145° to 153°. However, when we imposed a modest level of across‐muscle motor unit synchrony (Fig. 5E), two phenomena were observed: (1) most phase difference distributions (65%) became nonrandom; and (2) the mean angle of such distributions tended to cluster at very small values ranging from −18° to 42°. Hence, the introduction of a modest amount of across‐muscle motor unit synchrony caused more consistent relationships between forces across trials as well as in‐phase (synchronous) relationships.

When we imposed strong across‐muscle motor unit synchrony (Fig. 5F), we found an even larger number of significant phase difference distributions (82%) with a similar range of mean phase differences, i.e., from −22° to 59°, as for the modest synchrony condition. The additional significant phase differences in the strong synchrony condition were found primarily at low frequencies, i.e., from 2.5 to 5 Hz. For the modest and high synchrony conditions the percentages of significant phase difference distributions as well as the ranges of mean phase differences are comparable to those observed experimentally for multi‐digit grasping (−20° to 39°, Rearick and Santello 2002; −14° to 23°, Rearick et al. 2003).

Discussion

The results of our motor unit simulation suggest that the introduction of modest and physiologically realistic levels of synchrony between motor units lying in different muscles can markedly affect the relationship between forces. These results are discussed below in relation to the functional significance of motor unit synchrony and the coordination of force fluctuations during grasping.

Motor unit synchrony and its functional significance

The phenomenon of within‐muscle motor unit synchronization has been thoroughly studied in the past several decades. The most widely accepted theory for the underlying mechanisms is that short‐term motor unit synchronization arises from shared inputs from branched axons of last‐order neurons (Sears and Stagg 1976; Kirkwood and Sears 1978). It should be pointed out, however, that the functional significance of motor unit synchronization is still being debated. Recent experimental (Semmler et al. 2000) and modeling (Yao et al. 2000) approaches have shown that within‐muscle motor unit synchronization contributes little, or does not contribute at all, to the production of larger forces. This controversy on whether within‐muscle motor unit synchrony serves a functional role for the control of movement is an important issue also for situations where synchrony is found on motor units belonging to different muscles (Bremner et al. 1991b; Huesler et al. 2000) or muscle compartments of the digits (Reilly et al. 2003; Winges et al. 2003; Keen and Fuglevand 2004).

Although within‐ and across‐muscle motor unit synchrony are likely to share the same mechanisms (see above), the functional outcome of these phenomena is very different. Specifically, within‐muscle motor unit synchrony of a given muscle can only affect the magnitude and temporal characteristics of force generated by the same muscle. In contrast, across‐muscle motor unit synchrony has the potential to affect the temporal relationships between the forces generated by pairs of muscles or muscle compartments. These relationships are particularly important in tasks requiring a fine temporal coordination of multiple forces such as multi‐digit grasping (see below).

Across‐muscle motor unit synchrony and multi‐digit forces during grasping

The focus of the present study was to quantify the effect of different levels of motor unit synchrony on the temporal coordination of forces. To do so we used a motor unit model based on physiological parameters to simulate forces with behaviorally plausible features. Indeed, the simulated forces captured the essential features of behavioral data reported by a number of studies of multi‐digit grasping, i.e., within‐trial coefficient of variation of force amplitude and amount of power within the same frequency ranges.

Our results demonstrate that modest across‐muscle motor unit synchrony can account for a number of experimental observations on force coordination during multi‐digit grasping. Specifically, adding modest synchrony caused a marked increase in the number of significant phase differences between the simulated forces (Fig. 5D, Fig. 5E). This result indicates that the temporal force relationships became more consistent across‐trials, although this finding did not necessarily imply in‐phase relationships per se. Indeed, the most important result was that the added synchrony caused most mean phase differences to approach values close to 0°. The number of significant phase differences and in‐phase force relationships further increased when we added strong synchrony to the motor unit populations (Fig. 5F). It should be noted that the value for modest synchrony that we used in the simulations was lower or equal to that found across all digit pairs during 5‐digit object hold (Winges et al. 2003).

The above results on in‐phase force relationships are in strong qualitative and quantitative agreement with observations from multi‐digit grasping performed under a variety of task conditions, i.e., object hold using the dominant (Santello and Soechting 2000) and non‐dominant hand (Rearick and Santello 2002) in healthy subjects and in subjects with Parkinson’s disease (Rearick et al. 2002). All of these studies have shown that in‐phase force relationships occur with very minor differences across subjects and digit pairs. The phenomenon of force synchronization is not well understood and deserves further investigation. However, the fact that in‐phase force relationships occur to a greater extent when holding an object against gravity than when exerting the same forces without holding the object (Rearick et al. 2003) suggests some degree of task dependency and argue against force synchrony as a mere by‐product of force production.

The present results allow us to consider across‐muscle motor unit synchrony as a plausible mechanism accounting for a large part of the coordinated force fluctuations observed during multi‐digit grasping tasks.