Reaction coordinate of an enzymatic reaction revealed by transition path sampling

Abstract

The transition path sampling method previously applied in our group to the reaction catalyzed by lactate dehydrogenase was used to generate a transition path ensemble for this reaction. Based on analysis of the reactive trajectories generated, important residues behind the active site were implicated in a compressional motion that brought the donor–acceptor atoms of the hydride closer together. In addition, residues behind the active site were implicated in a relaxational motion, locking the substrate in product formation. Although this suggested that the compression-relaxation motions of these residues were important to catalysis, it remained unproven. In this work, we used committor distribution analysis to show that these motions are integral components of the reaction coordinate.

The relationship between enzymatic structure and function remains an area of intense research. Many studies have demonstrated that factors such as electrostatic and entropic effects are significant to enzyme function (1). The role of dynamics in catalysis, however, is less well understood. Protein motions such as conformational fluctuations on the millisecond timescale have been shown to influence substrate binding and the height of the barrier to reaction. The role of vibrational motions on the femtosecond to picosecond timescale and their connection to catalysis remain controversial. It has been suggested that the vibrational motions that exist within the protein are in equilibrium with the reaction and thermally averaged along the reaction coordinate (2, 3). But we and others have suggested that vibrational motions within the protein may in fact be coupled to the reaction coordinate (4). Previous work in our group has suggested the coupling of these vibrational motions to the reaction coordinate and has developed methods to study their effect on enzyme reactions (5).

The search for these subpicosecond motions (“protein promoting vibrations”) was first applied to the enzyme horse liver alcohol dehydrogenase. This work suggested there existed motions, protein-promoting vibrations (PPVs), that coupled directly to the reaction coordinate and that were on the timescale of barrier crossing (6). The algorithm was then tested on another enzyme system lactate dehydrogenase (LDH), and similar PPVs were identified that, along with conformational fluctuations, helped explain the preference of the heart isoform to produce pyruvate and of muscle isoform to produce lactate (7).

Further investigation into the mechanism of LDH was achieved with the transition path sampling (TPS) method (8). TPS is a computational method that can simulate rare events in complex systems. Using a Monte Carlo approach, a reactive path ensemble connecting reactants to products can be defined without prior knowledge of the reaction coordinate. This method allows mechanistic details to be identified from reactive paths generated with no bias (9). A reactive path ensemble was generated for LDH, and it was found that, in all reactive trajectories, there were important residues outside the active site that exhibited significant motion during the reaction on the subpicosecond timescale. These residues are located along the donor/acceptor axis of the hydride and extend as far as 40 Å away from the active site (Fig. 1). The residues located behind the hydride donor (Val-31, Gly-32, Met-33, Leu-65, and Gln-66) exhibited a compressional motion bringing the cofactor close its acceptor, whereas Arg-106 located behind the hydride acceptor exhibited relaxational motions that seem to lock the substrate in product formation. Previous work suggested that inhibition of these residue motions resulted in an incomplete reaction (8) but did not prove these motions to be part of the reaction coordinate.

Fig. 1.

A monomer of LDH with atoms in the active site highlighted, specifically, the nicotinamide ring, substrate, active site histidine (red), and donor/acceptor axis residues (green and blue). Val-31, Gly-32, Met-33, Leu-65, and Gln-66 (in green) compressed toward the active site bringing the NC4 of the nicotinamide ring and substrate carbon closer together, whereas Arg-106 (blue) relaxes away, locking the substrate in product formation. These residues span the entire length of the monomer to the edge of the protein.

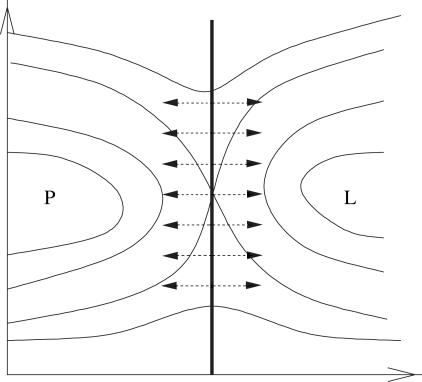
A reaction coordinate includes all of the collective variables that contribute to catalysis. Defining a complete reaction coordinate can be difficult in a complex system such as an enzyme because of the many degrees of freedom that are available. The transition state ensemble represents the “bottleneck” of a reaction, the region of phase space that all paths must cross from reactants to products. This region of phase space, the separatrix, is a reduced dimensionality manifold that separates the reactant portion of phase space from the product region (Fig. 2). When the transition surface is properly defined, all motions that are part of the reaction coordinate are orthogonal to the separatrix. Transition states can be found in a statistical manner, as configurations that, given random velocities, have equal probabilities of committing to reactants or products. Once a group of transition states is found, putative reaction coordinates can be tested to determine whether such parameters are indeed orthogonal to the separatrix. If a complete reaction coordinate is defined, committor values sampled along the coordinate should peak at 0.5. The transition state ensemble has been found in systems such as ion dissociation in water (10), DNA binding (11), protein folding (12, 13), and isomerization of alanine dipeptide in vacuum and water (14). In each of these systems, through transition-state analysis, details of the mechanisms were obtained. In this paper, we determine the reaction coordinate for LDH. It is shown to include the compression and relaxation motions from residues outside the active site. Through committor distribution analysis, we provide proof of the coupling of these motions to the reaction coordinate.

Fig. 2.

One possible visualization of reactive trajectory space. Regions P and L represent stable regions of phase space for pyruvate and lactate. The solid black line represents the transition surface. All of the relevant degrees of freedom that describe the reaction coordinate are orthogonal to this surface. If we appropriately identify the reaction coordinate, any configuration located on this surface should equally commit to the pyruvate and lactate regions.

Results

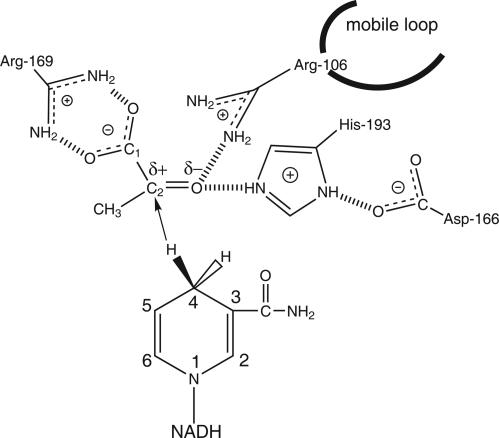
Our studies focus on the enzyme LDH, which catalyzes the interconversion of the keto-acid pyruvate to the hydroxy-acid lactate with the coenzyme NADH. The reaction catalyzed involves the transfer of a proton between an active site histidine and the C2 substrate oxygen, as well as a hydride transfer between NC4 atom of the coenzyme and C2 of the substrate (Fig. 3). Although the biologically active form of this enzyme is a tetramer, we used the monomer for computational efficiency. Six hundred initial reactive trajectories were generated for the transition path ensemble. A calculation of the trajectory autocorrelation function (8) showed that the reactive paths decorrelated after ≈30 paths. Throughout the ensemble, a stepwise mechanism dominated with the hydride transferring from the substrate to the NADH before the proton transferring from the substrate to the reactive nitrogen of the active site histidine (pyruvate to lactate direction). The lag time between the two mass transfers varied from 15–150 fs.

Fig. 3.

Diagram of the binding site of LDH with bound NADH and pyruvate showing hydrogen bonds between the substrate and catalytically important residues of the protein. The catalytic event involves the hydride transfer of the C4 hydrogen of NADH from the pro-R side of the reduced nicotinamide ring to the C2 carbon of pyruvate and proton transfer from the imidozole group of His-193 to pyruvate's keto oxygen substrate

Commitment probabilities for lactate (pL) and pyruvate (pP) were calculated for configurations along the transition paths. We searched for configurations that had an equal probability of reaching the lactate and pyrvuate regions of phase space. Transition states were identified where the values pL and pP were within the 0.4–0.6 range. Once transition to products took place, there was no recrossing of the transition surface observed in the time scale studied. A 1-ns trajectory confirmed that once the system had crossed the transition surface to products, it remained in the product region of phase space. This lack of recrossing confirms our previous supposition that conformational relaxation is used by the enzyme to “lock in” product formation. The hydride remained tightly bonded to the reactive carbon, and the proton remained tightly bonded to the reactive nitrogen of the active site histidine. Consistently, among each of the transition states found, the state of the hydride transfer was more advanced as compared with the state of proton transfer in the pyruvate to lactate direction.

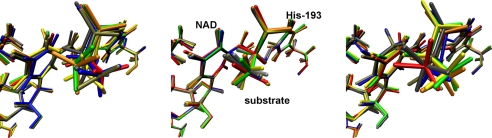
Fig. 4 shows snapshots of configurations of the enzyme/cofactor/substrate complex at initial, transition state, and final structures from eight transition paths. The paths chosen are from separate regions of phase space so that each represents a unique way to cross the barrier from reactants to products. Table 1 shows the rmsd values comparing the initial, transition state, and final configurations from one trajectory to the remaining seven. The transition states identified, although not identical, are very similar in structure. Thus, indeed there is a narrowing in phase space as reactive trajectories approach the transition region. These transition states begin to define the “transition surface” in trajectory space. The common motions that guide each of these paths orthogonal to this surface define the reaction coordinate.

Fig. 4.

Shown above are snapshots of the active site of LDH from eight transition paths at 10 fs, the transition state, and 500 fs. Although each path represents a unique approach to crossing the separatrix from reactants to products, the common motions that guide each path over the transition surface are evident in the strong overlap of the configurations at the transition state.

Table 1.

rmsd values of configurations at initial, transition, and final regions

Trajectory	Initial	Transition	Final
1	0.222	0.154	0.211
2	0.246	0.109	0.243
3	0.235	0.118	0.226
4	0.239	0.142	0.229
5	0.244	0.136	0.228
6	0.244	0.099	0.231
7	0.252	0.122	0.247

We chose to study three putative reaction coordinates, each increasing in complexity and calculated committor distributions based on each. The first reaction coordinate follows the progress of the chemical reaction at the active site. It consisted of following the hydride and proton from their respective donors and acceptors. The second trial coordinate included two additional parameters, the dihedral angle of the substrate as defined by C1-C2-C(from methyl)-O(from carbonyl) atoms, and the dihedral of the NADH ring defined by NC5-NC4-NH4-NC3 atoms (see Fig. 3). We chose to include these parameters in the second coordinate because they, too, describe the progress of the chemistry at the NC4 carbon of the nictotinamide ring and the C2 carbon of the substrate, the atoms that exchange a hydride during reaction. The third and final trial reaction coordinate included the residues that were previously implicated as having compression/relaxation motions along the donor/acceptor axis of the hydride. Transition states from each reactive path were isolated, and an ensemble of configurations constrained with a putative reactive coordinate was generated from that transition state configuration. The details regarding these constraints are given in Methods. If the degrees of freedom constrained were indeed part of the reaction coordinate, then the new ensemble generated from propagation along the separatrix would yield committor values with a peak ≈0.5. We note that in this approach, constraints are placed on position space definitions of the reaction coordinate. Averaging over all reactive trajectories then yields a committor distribution. Previous work has generated this averaging in free energy computations (10, 14). The results should yield equivalent information.

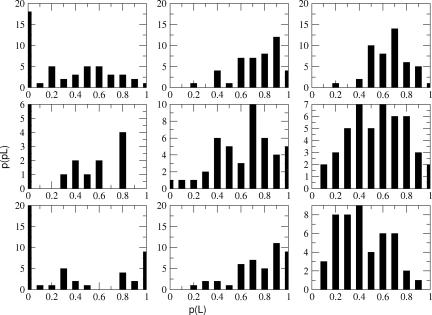
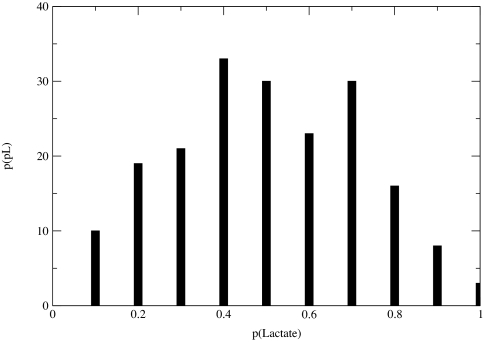
Fig. 5 shows committor distributions obtained from the constrained ensembles appropriate to the three putative reaction coordinates described above. Each column displays the results of three constrained ensembles, each constrained from a different transition state. However, within each column, the level of constraints is the same. The motions of each putative reaction coordinate are constrained so that evolution of a trajectory starting from the transition state should propagate along the transition surface. Committor values of configurations along the constrained trajectory were calculated with 100 individual trajectories free from any bias, initiated from each configuration. As the committor distributions in the first column of Fig. 5 show, there are sharp peaks ≈0 and/or 1. These distributions represent the putative reaction coordinate that simply follows the hydride and the proton. In the absence of a peak in the center of the distribution, we have confirmed there must be additional parameters important to the reaction, and the hydride and proton alone are not sufficient to define a complete reaction coordinate. Shown in the second column of Fig. 5 are the committor distributions for the reaction coordinate, which included dihedral parameters. We begin to discern a peak in the distribution; however, it is not centered ≈0.5, but rather ≈0.8. While adding more information about the atoms in the active site to the reaction coordinate, the results from the distribution reveal that the total reaction coordinate must include parameters beyond those related directly to the transferring atoms of the reaction. Shown in the last column of Fig. 5 are the committor distributions which include the compression motions of the residues along the donor/acceptor axis. The peak in the center of the distributions demonstrates that including the motions of these residues in the reaction coordinate improves the definition of the transition surface. Fig. 6 shows the results for the committor distribution for the third trial reaction coordinate, including the residue motions along the donor/acceptor axis of the hydride. This distribution represents results from a larger sampling of constrained ensembles generated from five different transitions states along the transition surface. As compared with the distributions from Fig. 5, this distribution has a sharper peak in the center of the distribution, indicating better statistical sampling. Further details of the generation of the committor distributions are given in Methods.

Fig. 5.

Committor distributions from three putative reaction coordinates (from left to right): the first reaction coordinate describes the motions of only the hydride and proton from their respective donors and acceptors; the next reaction coordinate includes a dihedral of the NADH including NC5-NC4-NH4-NC3 atoms and a dihedral of the substrate; and the final reaction coordinate includes motions of the residues (Val-31, Gly-32, Met-33, Leu-65, and Gln-66) behind the cofactor and residue Arg-106 behind the substrate, along the donor/acceptor axis beyond the active site. These distributions are based on results tested on three individual trajectories where transition states were identified, and constrained trajectories were constructed from them. As the reaction coordinate is improved, the peak of the committor distribution approaches 0.5.

Fig. 6.

Committor distribution of five constrained trajectories where the reaction coordinate included the dynamic motions of the outside residues along the donor/acceptor axis (Val-31, Gly-32, Met-33, Leu-65, Gln-66, and Arg-106). Note that sampling a larger group of constrained ensembles significantly improves the distribution.

Conclusions

We have studied a chemical reaction catalyzed by an enzyme system with many degrees of freedom. Upon identification of the separatrix that divides reactants and products in phase space, a reaction coordinate orthogonal to the separatrix was validated through a committor distribution that peaked at 0.5. These results reveal that the compression/relaxation motions of residues along the donor/acceptor axis of the hydride are in fact part of the reaction coordinate. Although it is possible that a reaction coordinate that includes the farther residues (Gly-32, Met-33, Leu-65, and Gln-66) in addition to Val-31 could be overdefined, it is clear that all these residues move in all reactive trajectories. The architecture of the protein is such that restraining the interior residues will likely effectively restrain the exterior ones as well. Still, these residue motions, although likely not the only motions important to catalysis, expand the definition of the reaction coordinate to include dynamic effects as integral parts of the reaction coordinate.

Although the distributions in the third column of Fig. 5 are broad, this could in part be due to the fact that the initial transition states identified did not have committor values of exactly 0.5 but were within the values of 0.4–0.6. Part of the reason that it is difficult to identify the total reaction coordinate is that the dividing surface between reactants and products is narrow and it is easy to “fall off” the surface into more stable regions of phase space. This was confirmed by taking configurations from a reactive path only a few femtoseconds away from the transition state from both the lactate and pyruvate regions of the trajectory and creating new constrained ensembles constraining the motions that defined the third trial reaction coordinate. The committor distributions (not shown) did not peak at 0.5 but instead peaked either at 1 or 0, depending on whether the starting configuration was on the lactate region or the pyruvate region of the trajectory.

The committor distribution in Fig. 6 represents probability values calculated from configurations generated from five constrained trajectories. The computation needed to first locate a transition state along a reactive path required thousands of trajectories. In addition, for each committor distribution in Fig. 5, 5,000 independent trajectories were generated. For the committor distribution in Fig. 6, 25,000 trajectories were generated. The computation needed to obtain the transition state ensemble was 3,000 central processing unit (CPU) hours, whereas the committor distributions required 13,500 CPU hours. Because of the significant computation required with this approach, we were limited in the number of trial coordinates we could test. An automatic method has been developed that finds reaction coordinates more efficiently (15); however, this method has not yet been applied on a system larger than alanine dipeptide. In addition, the residues motions that we have identified as part of the reaction coordinate present obvious choices for mutagenesis experiments. Future work will investigate the mutations' effect on structure and dynamics and will complement experimental rate studies as well.

Methods

Simulation Details.

We use the crystal structure of the homotetramic human heart isozyme, h-H4LDH, in a ternary complex with NADH and oxamate solved by Read et al. (16) at a 2.1-Å resolution (Brookhaven National Laboratory; Protein Data Bank ID no. 1I0Z). To generate reactive potential energy surfaces, quantum mechanical/molecular mechanical calculations were performed on a Linux Cluster by using the CHARMM/MOPAC interface with the CHARMM27 (17), all-hydrogen force field, and the AM1 semiempirical method. The CHARMM27 force field includes specific parameters for NAD+/NADH. Oxamate (NH2COCOO), an inhibitor of LDH, is an isosteric isoelectronic mimic of pyruvate with similar binding kinetics. Changes to the Protein Data Base file included substitution of the oxamate nitrogen with carbon to create pyruvate and replacement of the active site neutral histidine with a protonated histidine to establish appropriate starting conditions with pyruvate and NADH in the active site. A total of 39 atoms were treated with the AM1 potential; 17 or 16 atoms of the NADH or NAD+ nicotinamide ring, 13 or 12 atoms of the protonated or neutral histidine imidazole ring, and 9 or 11 atoms of the substrate pyruvate or lactate, respectively. The generalized hybrid orbital (GHO) (18) method was used to treat the two covalent bonds that divide the quantum mechanical and molecular mechanical regions. The two GHO boundary atoms are the histidine Cα atom and the NC1′ carbon atom of the NAD+/NADH adenine dinucleotide structure that covalently bonds to the nicotinamide ring.

The reactive trajectory surface was divided into three regions, pyruvate, lactate, and transition. The details of the order parameters that differentiate these regions are described elsewhere (8). A reactive trajectory was defined as a single simulation that connected the pyruvate region to the lactate region or vice versa. A nonreactive trajectory connected the same basin or connected pyruvate or lactate to a transition region.

Transition Path Ensemble.

The transition path sampling algorithm was implemented within CHARMM. A microcanonical ensemble of reactive trajectories was generated by using deterministic dynamics. This algorithm is summarized in detail elsewhere (19) but will briefly be described here. An initial 500-fs trajectory, including both coordinates and momenta, was used as in input for further trajectories. New trajectories were generated through the use of the shooting algorithm on randomly chosen time slices from the 500-fs trajectory. The momenta were altered and rescaled to conserve linear momentum, angular momentum, and energy. Dynamics were run forward and backward in time to complete a 500-fs trajectory. The initial and final conformations were determined to be in the pyruvate, lactate, or transition region through inspection of the order parameter values. If the new trajectory was reactive, it was used as an input for generation of a new trajectory. If the trajectory was not reactive, a new time slice was randomly chosen from the old trajectory until a new trajectory was generated.

Transition State Analysis.

Each reactive path in the path ensemble was 500 fs in length, sufficient time to observe the chemical event. One transition state was found for each reactive path, and no recrossing was observed. This was confirmed by examining a 1-ns trajectory, and no recrossing of the transition surface was observed.

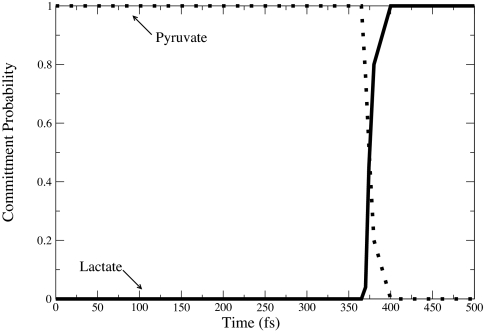
To find a transition state, we calculated the likelihood of a configuration along the trajectory to commit to reactants or products given random velocities (20). Fig. 7 shows the commitment probability values from a reactive path starting in pyruvate and ending in lactate. In the reactant region, pP = 1, whereas pL in this region = 0. As the trajectory progresses, the value of pP decreases to 0, and the value of pL increases to 1. The configuration at which the values of pP and pL are equal is considered the transition state of the path.

Fig. 7.

Commitment probability values were calculated for both lactate and pyruvate along a sample trajectory from the reactive path ensemble. The solid line represents probability values for lactate, and the dotted line represents probability values for pyruvate. The transition state was found at the 374-fs time slice.

To be truly unbiased, each configuration along each 500-fs trajectory from reactants to products should be considered as a potential transition state; however, this would be computationally expensive, and configurations far from the transition surface can be ruled out quickly. Our approach has instead been to evaluate the committor values in regions around where either the hydride, the proton, or both transfer, meaning the region of the trajectory where the hydride and proton are equidistant from the donors and acceptors, respectively. This significantly narrowed the search region.

The shooting algorithm was used to determine committor values along the trajectory. A random velocity chosen from a Maxwell Boltzmann distribution was assigned to a configuration and dynamics were run for 250 fs. Up to 100 trajectories were run per time slice. The configuration where pL and pP were both in the 0.4–0.6 region was considered the transition state. We note that the high value of the derivative in the transition region of Fig. 7 makes localization to exactly 0.5 impossible.

Reaction Coordinate and Transition Surface.

To determine which degrees of freedom are relevant to the reaction coordinate, an ensemble of configurations constrained with the putative reaction coordinate was generated from transition states identified from transition paths. The motions of the hydride and proton were constrained by constraining the distances of the hydride and proton to their respective donors and acceptors at the transition state. The motions of residues 31–33, 65–66, and 106 were constrained by constraining the distances of the Cα of each residue to the NC4 carbon of NADH at the transition state. Distance constraints were imposed by using the RESDISTANCE command, and dihedral constraints added by using CONS DIHEDRAL command within CHARMM.

If a correct reaction coordinate is chosen, then the constrained trajectory should be propagated along the separatrix. This constrained trajectory contained an ensemble of configurations from which committor values along the trajectory should be 0.5. Committor values of configurations from the constrained trajectory were calculated by shooting 100 trajectories from a configuration free from any constraint. A committor distribution was then acquired from a sampling of configurations along the constrained trajectory. For a given committor distribution from Fig. 5, 5,000 individual trajectories were generated to construct this histogram. Fig. 6 represents a larger sampling of the transition surface whereby five constrained trajectories were generated from five different transition states along the transition surface. The constraints were the same for each starting transition state. This distribution required ≈25,000 trajectories.

Abbreviations

LDH

lactate dehydrogenase

pL

commitment probability for lactate

pP

commitment probability for pyruvate.