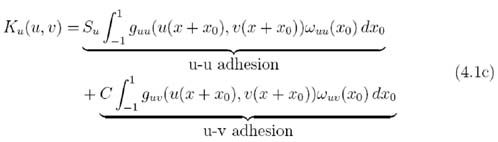A Continuum Approach to Modelling Cell-Cell Adhesion

Abstract

Cells adhere to each other through the binding of cell adhesion molecules at the cell surface. This process, known as cell-cell adhesion, is fundamental in many areas of biology, including early embryo development, tissue homeostasis and tumour growth. In this paper we develop a new continuous mathematical model of this phenomenon by considering the movement of cells in response to the adhesive forces generated through binding. We demonstrate that our model predicts the aggregation behaviour of a disassociated adhesive cell population. Further, when the model is extended to represent the interactions between multiple populations, we demonstrate that it is capable of replicating the different types of cell sorting behaviour observed experimentally. The resulting pattern formation is a direct consequence of the relative strengths of self-population and cross-population adhesive bonds in the model. While cell sorting behaviour has been captured previously with discrete approaches, it has not, until now, been observed with a fully continuous model.

1 Introduction

1.1 Cell adhesion

Cell-cell adhesion is a fundamental biological phenomenon describing the binding of one cell to another through cell surface proteins known as cell-adhesion molecules (CAMs). This process is largely responsible for tissue formation, tissue stability and tissue breakdown. Tissue and organ formation occurs early in embryo development. Selective adhesion of embryonic cells allows the cells to move and organise themselves into the patterns that develop into tissues and organs. This same process is responsible for the stability of the tissues post-development as new cells move in to replace those that have died to maintain the tissue structure. In addition, selective adhesion is thought to be responsible for certain types of tissue breakdown, as a change in cell adhesion is recognised as a factor in the invasion and metastasis of tumour cells.

The dependence of cell sorting on cell-cell adhesion was shown experimentally several decades ago. The knowledge that the adhesive bonds between embryonic amphibian cells break down when placed in alkaline solutions was exploited by Townes and Holtfreter to conduct experiments with disassociated cells (Townes and Holtfreter, 1955). By mixing disassociated cells of different types and then returning to a normal pH, they found that not only do the cells reaggregate, but they also sort such that cells of the same type are found in the same region. This rearrangement returned the cells to their original embryonic configuration.

Further experiments by Steinberg (Steinberg, 1962a,b,c) showed that if two embryonic cell types are mixed then they will always rearrange to the same configuration, but this configuration will vary according to the cell types. For example, one cell type might always aggregate centrally when interacting with a second cell type, but peripherally when interacting with a third cell type. Moreover if cell type A always envelops cell type B, and cell type B always envelops cell type C, then A will always envelop C. Steinberg proposed the differential adhesion hypothesis to explain these experimental results.

This hypothesis is based on a thermodynamic model which explains sorting of cell populations as a result of differences in cell surface tensions. These differences are in turn the consequence of differences in the adhesion properties of the cells. It suggests that the cells behave like a mixture of two immiscible liquids, such as oil and water. In the same way that the relative surface tensions determine the configuration to which the liquid system will evolve, the adhesion properties of the cell types will determine the arrangement to which the cells will evolve. The differential adhesion hypothesis and evidence for the model are reviewed by Foty and Steinberg (2004). Other proposed mechanisms for cell sorting have been investigated but only the differential adhesion hypothesis has correctly predicted the experimental results (Foty and Steinberg, 2005).

Cell-cell adhesion is clearly important for understanding many biological processes. While traditional experiments offer valuable insight into cellular interactions and their final outcomes, other important information is harder to assess. The speed at which sorting occurs, the precise dependence of interactions and outcomes on individual cells adhesion properties, and the relationships between all of the experimental variables are difficult to measure experimentally. It is here that a theoretical approach can offer an invaluable addition to experimental work. Mathematical modelling allows cell properties to be varied independently of one another, allowing measurement of the sensitivity of the system to variations in parameters. It also allows the interactions of any combination of cell types to be investigated. In addition, theoretical models allow parameters such as speeds and rates of change to be measured far more easily. Given these benefits and the importance of cell-cell adhesion and cell sorting there is a clear argument for the mathematical modelling of this behaviour.

1.2 Previous Modelling Work

The experimental evidence summarised above indicates that cell-cell adhesion is intrinsically linked to the cell sorting behaviour fundamental to many biological processes. Mathematical modelling can be used as a tool to further understand these processes. The experimental results show that the configuration to which a mixture of two cell types may evolve is directly related to the relative self-adhesive and cross-adhesive strengths of the cells (Steinberg, 1962c). Replication of these results has previously been successfully achieved with discrete models, but to the authors' knowledge not with a continuous model. Before we discuss our new model we give an overview of some of those in the current literature.

A variety of discrete approaches have been developed, a large proportion of which are based on some form of the extended Potts model. A population of cells is arranged on a grid with rules imposed to govern the movement of each cell according to the cell density at surrounding positions. These models have been used to show cell sorting, replicating some of Steinberg's experimental findings (e.g. Glazier, 1996; Glazier and Graner, 1993; Graner and Glazier, 1992; Mombach et al., 1995; Stott et al., 1999; Sulsky, 1984). A second discrete method is to employ a Lagrangian approach in which each cell is tracked as it moves through continuous space. This approach was employed by Palsson and Othmer (2000) to replicate cell sorting by modelling each cell as a deformable ellipsoid responding to the adhesive interactions with neighbouring cells.

The success of discrete models in replicating the dynamics of adhesive populations has led to a number of applications, for example the modelling of tumour cell invasion into the surrounding tissue through altered cell-cell/cell-matrix adhesion (Turner and Sherratt, 2002; Turner et al., 2004a), the modelling of aggregation and slug development in the cellular slime mould Dictyostelium discoideum (Palsson and Othmer, 2000; Maree and Hogeweg, 2001) and the early morphogenesis of embryonic cell populations (Drasdo and Forgacs, 2000). While discrete models of cell adhesion offer a number of distinct advantages, for example the ease of incorporation of specific movement “rules” and the ability to track individual cells, there are two main reasons for a continuous mathematical model being desirable. Firstly, solving large scale discrete models is computationally intensive, leading to a limitation on the scale of the problem that can be explored. Secondly, for realistic numbers of cells, analytical results are difficult, if not impossible, to obtain from a discrete model. A continuum model, in principle at least, can allow the calculation of quantities such as cell group velocity without the need for numerical solutions.

Despite this, modelling cell-cell adhesion with a continuum approach is problematic and there are relatively few papers on the subject. One method is to take a discrete model to its continuous limit, the route taken by Turner et al. (2004b). While the authors show that this method is possible, the resulting model is too complicated to be feasibly applied in specific applications. An alternative approach was employed by Byrne and Chaplain (1996), who modelled the influence of cell adhesion on the growth of a solid tumour. They modelled adhesion phenomelogically by considering the surface forces on a tumour spheroid; however, it is unclear whether their model is capable of replicating the behaviour of the sorting experiments. Another continuous method used by several authors is to employ a non-linear diffusion term in which cells have restricted movement in regions of high density (e.g. Perumpanani et al., 1996). This approach only reflects one aspect of cell adhesion, such approaches do not show the active aggregation required for cell sorting.

A final approach found in the literature is to combine discrete and continuous methods. Recognising the need for a continuous model while acknowledging the importance of the behaviour of individual cells, Anderson (2005) uses a hybrid discrete-continuum model for cell adhesion. This involves a discrete representation of cell behaviour and a continuous approach for other factors in the system such as chemical concentration. Fundamentally though this is still a discrete model of cell adhesion and as such is still limited for the reasons discussed above.

In this paper we take a continuous approach and consider the force balance of adhesive forces acting on the cells. This approach leads to a non-local term for the directed movement of cells due to cell-cell adhesion. The resulting model presented in this paper provides a method of modelling cell adhesion which is applicable on a macroscopic scale and still replicates the behaviour seen experimentally and in discrete models.

1.3 Layout of the Paper

We begin in §2 by describing the derivation of the model investigated throughout the paper. We consider the behaviour of the model for a single adhesive population in one space dimension in §3 and demonstrate the ability of the model to form cell aggregations. In §4 we extend the model to consider multiple populations with different adhesive interactions, and demonstrate its ability to predict different types of sorting. The model is extended again in §5 to consider cell-cell adhesion in two dimensions and in §6 we discuss our findings, applications and our plans for future work. For reference we include an appendix which summarises each variation of the model and gives a description of the parameters.

2 Derivation of the Model

Cells are known to move in response to chemical stimuli (chemotaxis) and in response to fixed environmental factors such as the extracellular matrix (haptotaxis). They may also move due to adhesive forces between the cells. The latter is the behaviour we will be concerned with here as we assume that the breaking and forming of adhesive bonds exerts forces on the cells. To derive our model for cell-cell adhesion we first consider the movement of a single and uniform population of cells in one dimension although generalisation to multiple populations and higher dimensions is straightforward. We follow an approach employed by Pate and Othmer (1986) to describe Dictyostelium cell interactions.

We can derive the model by considering the forces acting on the cells in a conservative system. If we assume there is no cell birth or death in our system, then mass conservation implies

$$\frac{\partial u(x,t)}{\partial t}=-\frac{\partial J}{\partial x}$$ (2.1)

where u(x, t) is the population density at time t and position x, and J is the flux of the cells. Assuming there is some random movement of the cells as well as the movement due to adhesive forces, the total flux will be

$$J=J_d+J_a,$$ (2.2)

where J_d is the flux due to diffusion and J_a is the adhesive flux.

We expect that cells experiencing cell-cell adhesion are less likely to be able to move in regions of high cell density. Therefore an appropriate form of diffusive flux may be non-linear and decreasing with cell density. However, we find that the results reported in this paper are the consequence of the adhesion term and are not greatly affected by the form of diffusive flux used, to the extent that the results can be obtained even without a diffusion term in the model. Since our results do not appear to depend on a realistic form of diffusive flux we assume Fickian diffusion, i.e. $J_d=-D\frac{\partial u}{\partial x}$ where D is the diffusion coefficient. This has the advantage of not requiring any specific assumptions on a nonlinearity, as well as making the numerical calculations significantly more straightforward.

Movement due to adhesion occurs as a result of the forces produced when adhesive bonds between cells are formed or broken. We therefore assume that the adhesive flux is proportional to the density of the cells and the forces between them and inversely proportional to cell size, such that

$$J_a=\frac{\varphi }{R}\mathit{uF}$$ (2.3)

where ϕ is a constant of proportionality related to viscosity, F is the total force acting on the cells and R is the sensing radius of the cells. The notion of a sensing radius will be discussed later; for now we can consider it to be a measure of cell size. This form of adhesive flux follows from Newton's law on assuming that inertia is negligible and that drag is proportional to velocity and cell size, both of which are reasonable assumptions for cell movement at low speeds.

The total force, F , acting on cells at position x will be the sum of local forces, f, created by cells at position x with cells a distance x₀ away. We term the maximum x₀ the ‘sensing radius’, R, of the cells. Biologically this represents the range over which cells can detect their surroundings. For adhesion, forces are created through the binding of adhesion molecules at the cell membrane and the sensing radius would therefore represent the physical extent of the cell, although this may be greatly larger than the average radius through the extension of cell protrusions such as filopodia. The magnitude of the local forces will depend on the number of adhesive attachments made, and hence the local cell density. The direction of the local forces will depend on the position of the cells at x₀ with respect to x. Thus, we assume

$$f=\alpha g\left(u(x+x_0)\right)\omega \left(x_0\right)$$

where g(u(x + x₀)) describes the nature of the forces and their dependence on the local cell density, ω(x₀) describes how the direction and magnitude of the force alters according to x₀ and α is a positive parameter reflecting the strength of adhesive force between the cells. Examples of each of these functions will be given later. The total force, F, is therefore

$$F={\int }_{-R}^R\alpha g\left(u(x+x_0)\right)\omega \left(x_0\right){\mathit{dx}}_0.$$ (2.4)

Substituting this into (2.3), the equation for the adhesive flux is

$$J_a=\frac{\varphi }{R}u{\int }_{-R}^R\alpha g\left(u(x+x_0)\right)\omega \left(x_0\right){\mathit{dx}}_0.$$ (2.5)

and our mass conservation equation, (2.1) is given by

$$\frac{\partial u}{\partial t}=D\frac{{\partial }^{2}u}{\partial x^2}-\frac{\partial }{\partial x}\left(\mathit{uK}\left(u\right)\right)$$ (2.6a)

where

$$K\left(u\right)=\frac{\varphi }{R}{\int }_{-R}^R\alpha g\left(u(x+x_0)\right)\omega \left(x_0\right){\mathit{dx}}_0.$$ (2.6b)

To consider suitable forms for g(u(x + x₀)), consider the configuration shown in figure 2. Both the magnitude and the direction of the force generated by the cells at x₁ on the cell at x may depend on the cell density at x₁, depending on the physical forces present. For example, to model an adhesive force, we would assume the force is directed towards x₁ and increasing with the cell density (this simple assumption would reflect the attractive nature of the adhesive force and the increased likelihood of making adhesive bonds at higher densities). At its simplest, we could assume a linear form

$$g\left(u(x+x_0)\right)=u(x+x_0).$$ (2.7)

However, if we also wanted to include a “population pressure” in which cells are only attracted to regions below a threshold density, then we would instead expect the force to eventually decrease as the cell density increases, using for example the following logistic type function

$$g\left(u(x+x_0)\right)=\{\begin{array}{cc}u(x+x_0)(1-u(x+x_0)∕M)\hfill & \text{if}u(x+x_0)<M\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (2.8)

where M represents the crowding capacity of the population.

Fig. 2.

A schematic illustration of cell movement under an attractive force towards cells at position x.

Let us now consider the form of ω(x₀). For convenience, let us suppose that g(u(x + x₀)) is given by (2.7) above. The force generated at position x₁ will be positive while that at x₂ will be negative due to the “pulling” nature of the adhesive force. Further, the size of the force may vary according to the distance of x₁ and x₂ from x — cells further away may generate a weaker force as result of a diminished possibility of forming adhesive bonds with distance. Thus ω(x₀) should be an odd function of x₀ with ω(x₀) > 0 for x > 0 and ω(x₀) < 0 for x < 0. At its simplest we could assume a step function

$$\omega \left(x_0\right)=\{\begin{array}{cc}-1\hfill & -R<x_0<0\hfill \\ 1\hfill & 0<x_0<R\hfill \end{array}\phantom{\}}$$ (2.9)

though as we remark above, more realistic forms may vary smoothly with x₀.

Finally we rescale to give a nondimensional model. We let

$$x^{\ast }=\frac{x}{R}{t}^{\ast }=t\frac{D}{R^2}{u}^{\ast }=\frac{u}{\widehat{u}}\text{and}\alpha =\frac{\alpha }{\widehat{\alpha }}.$$

where û and $\widehat{\alpha }$ are determined by the form of g(u). If g(u) is given by (2.7) then $\widehat{\alpha }=1$ and û = D/Rϕ. If g(u) is given by (2.8) then $\widehat{\alpha }=D∕\mathit{MR}\varphi$ and û = M. Using these rescalings, dropping the stars for notational convenience, the nondimensional model for the movement of a single population in one dimension, due to diffusion and cell-cell adhesion is

$$\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x^2}-\frac{\partial }{\partial x}\left(\mathit{uK}\left(u\right)\right)$$ (2.10a)

where

$$K\left(u\right)=\alpha {\int }_{-1}^{1}g\left(u(x+x_0)\right)\omega \left(x_0\right){\mathit{dx}}_0,$$ (2.10b)

under the condition that ω(x₀) is an odd function. We note that α is now a nondimensional parameter representing the adhesion strength of the cells and g(u(x + x₀)) is the rescaled version of the force function. After rescaling the linear form of g(u) remains as (2.7) however the logistic form (2.8) will become g(u) = u(1 − u).

Here we have derived only the simple one population model, but the derivation of higher-dimensional models is straightforward: see Hillen et al. (2006) for the derivation and analysis of such a model in the context of chemotaxis.

3 One Population Model

We begin by considering a single cell population with uniform adhesive properties. For an initially dispersed population of cells with sufficiently strong cell-cell adhesion, we expect to observe the formation of cell clusters or aggregations (see figure 1). Thus our basic model should demonstrate the formation of cell aggregations from an initially randomly distributed population. To model this behaviour we use the simple model derived in section 2, that is

$$u_t=u_{\mathit{xx}}-{\left(\mathit{uK}\left(u\right)\right)}_x$$ (3.1a)

where

$$K\left(u\right)=\alpha {\int }_{-1}^{1}g\left(u(x+x_0)\right)\omega \left(x_0\right){\mathit{dx}}_0.$$ (3.1b)

Here u(x, t) is the population density at time t and position x and K(u) is the non-local adhesion term. α represents the adhesion strength of the cells. In section 2 we showed that K(u) describes the movement of cells through adhesive forces acting on the cells. In this section we assume the simple linear form for g(u) as given by (2.7). The model equations and parameters are summarised in appendix A.1.

Fig. 1.

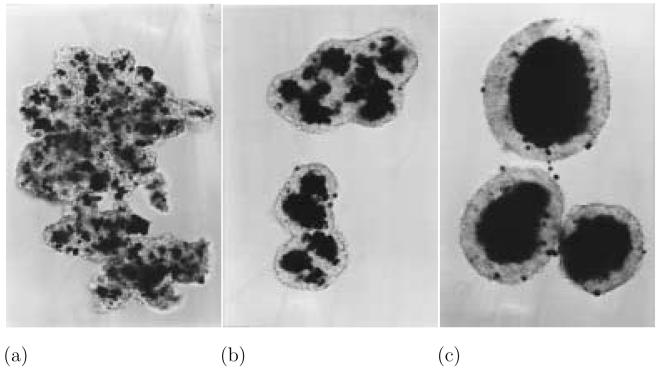
Illustrative figures of cell adhesion and sorting showing aggregations observed in experiments mixing 7 day old chick embryo neural retinal cells (light cells) and pigmented retinal epithelial cells (dark cells). (a) After 5 hours cells form randomly mixed aggregates. (b) After 19 hours the pigmented retinal cells are almost exclusively located in the interior of the aggregates. (c) After 2 days the pigmented retinal cells have formed central masses, completely surrounded by the neural retinal cells. The few pigmented cells seen on the surface are thought to be dead cells. (From Armstrong (1971), courtesy of P.B. Armstrong.)

3.1 PDE Approximation

The novelty in our model lies in the non-local advection term, K(u). Although non-local terms have been used in the modelling of other areas of biology, their effects are not immediately obvious. To obtain some intuition we can approximate the model by a partial differential equation (PDE). This approximation can then be compared to PDE models whose behaviour has been previously studied.

A PDE approximation to the model can be achieved by expanding the density term within the integral, u(x + x₀), as a Taylor series. We let

$$u(x+x_0)=u\left(x\right)+x_0{u}_x+\frac{x_0^2}{2}{u}_{\mathit{xx}}\cdots$$

and substitute this into the adhesion term, (3.1b) with (2.7)

$$u_t=u_{\mathit{xx}}-A\alpha [{\mathit{uu}}_x{]}_x-B\alpha [{\mathit{uu}}_{\mathit{xxx}}{]}_x+\varnothing \left(x_0^5\right),$$ (3.2)

where $A={\int }_{-1}^1{x}_0\omega \left(x_0\right){\mathit{dx}}_0$ and $B=\frac{1}{6}{\int }_{-1}^1{x}_0^3\omega \left(x_0\right){\mathit{dx}}_0$ are both positive. We note that terms with odd order derivatives in (3.2) disappear since ω(x₀) is odd.

In the second order term of (3.2) there is a dependence on the first spatial derivative, u_x, showing similarity with PDE models of taxis. It indicates directed movement up gradients of cell density, thus implying that aggregating behaviour may be possible in this model. However, a second order PDE model for cell-cell adhesion based on such terms is impractical due to their tendency to form singularities. The fourth order term has a dampening effect, and we can therefore speculate that the effect of the non-local term will be to allow aggregations to form without blow-up. This is supported by the results in Hillen et al. (2006), where a non-local model for chemotaxis was demonstrated to have globally existing solutions.

3.2 Stability

As we discussed previously, a model for cell-cell adhesion should demonstrate evolution of a randomly distributed cell population into a pattern of aggregations. To indicate whether this is possible in the model we perform a standard linear stability analysis about the homogeneous steady state U. Specifically, we let $u(x,t)=U+\stackrel{-}{u}(x,t)$ where $\stackrel{-}{u}$ is a small perturbation. Substituting this into our governing equation (3.1), and neglecting non-linear terms in $\stackrel{-}{u}$, our linearised model becomes

$${\stackrel{-}{u}}_t=D{\stackrel{-}{u}}_{\mathit{xx}}-\alpha U{\left[{\int }_{-1}^1\stackrel{-}{u}(x+x_0)\omega \left(x_0\right){\mathit{dx}}_0\right]}_x.$$ (3.3)

Substituting solutions of the form $\stackrel{-}{u}\propto e^{\mathit{ikx}+\lambda t}$ into (3.3), where k and λ are the wavenumber and frequency respectively, yields the dispersion relation

$$\lambda \left(k\right)=-k^2-i\alpha \mathit{Uk}\widehat{w}\left(k\right),$$ (3.4)

where $\widehat{w}\left(k\right)={\int }_{-1}^1{e}^{{\mathit{ikx}}_0}\omega \left(x_0\right){\mathit{dx}}_0$.

For aggregations to develop we require Re(λ(k)) > 0 for some k. The wave numbers, k, for which this occurs will clearly depend on the form of w(x₀). Assuming the simple form for ω(x₀) given by (2.9) the dispersion relation now becomes

$$\lambda \left(k\right)=-k^2-2\alpha U(\cos \left(k\right)-1).$$ (3.5)

For Re(λ(k)) > 0, we have the condition

$$1-\cos \left(k\right)>\frac{1}{2\alpha U}{k}^2.$$ (3.6)

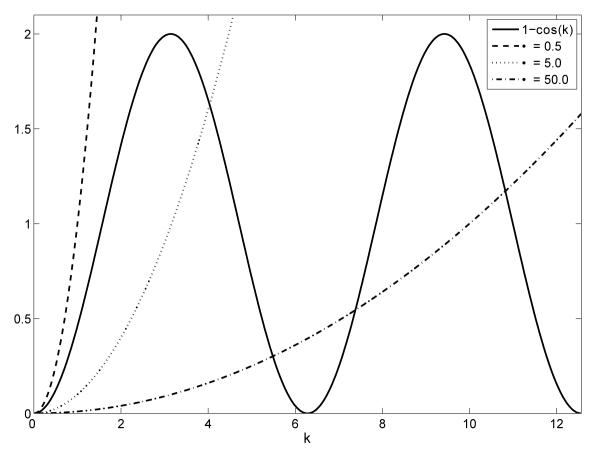
The inequality, (3.6), highlights that the magnitude of the adhesion strength, α, is critical in determining whether aggregations are possible. We can explore the possibility of aggregations by evaluating both sides of (3.6) for different values of α. In figure 3 we plot the two sides of (3.6) for three values of α. Clearly, for certain α wavenumbers exist for which Re(λ(k)) > 0. The figure suggests the existence of a minimum strength of adhesive force below which aggregations do not occur. This is in fact the case and aggregating behaviour is possible in the model when α > α_crit where α_crit is the smallest value of α at which the two sides of (3.6) touch when considered as functions of k. Straightforward calculation gives

$${\alpha }_{\mathit{crit}}=\frac{1}{U{\cos }^2(k_{\mathit{crit}}∕2)}$$

where k_crit is the first non-zero solution to tan(k/2) = k/2.

Fig. 3.

An illustration of the inequality, (3.6). We let the initial population density across the domain be U = 1. The solid line curve is the right hand side of (3.6), 1 − cos(k). The other three lines are plots of the left hand side of (3.6), k²/2αU, for three values of α. We can see that for α = 0.5 there is no region where the inequality holds and so aggregations will not occur. When α = 5.0 and α = 50.0 aggregations are possible for wavenumbers in regions where the solid line is above the dotted and dash-dotted line respectively. This indicates the importance of the adhesion strength on the model behaviour.

3.3 Numerical Simulations

Having confirmed analytically that the model may display aggregating behaviour we investigate this further through numerical simulation. The numerical scheme employs an explicit finite volume method to discretise the PDEs into a system of ODEs. We use a central differencing scheme for diffusion and high order upwinding with flux limiting for the advection term. The integral is calculated directly by summing over the enclosed points and the time integration uses an explicit trapezoidal scheme. The choice of boundary conditions is dependent on the cell types and problem in question. Here we are investigating a modelling technique and so we have only considered generic cell populations. As the domain over which these cells interact is unknown we assume periodic boundary conditions for numerical simplicity.

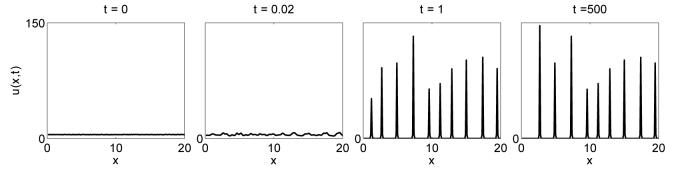
From (3.6) and figure 3 we expect aggregating behaviour to occur when the adhesion strength, α, is greater than some critical value. Figure 4 shows a time evolution of our model for a cell population with adhesion strength α = 10. The population of cells is initially assumed to be uniformly distributed, perturbed by a small amount of noise. Over time the population develops a number of peaks in cell density. As time progresses, these peaks are seen to coarsen, becoming steeper and more widely spaced. The numerics clearly confirm the ability of the model to produce cell aggregations in certain parameter regimes.

Fig. 4.

Confirmation that aggregating behaviour can be seen in this model under certain parameter assumptions. The model, (3.1), is solved on a domain of length 20 discretised into 200 mesh points. Here we choose α = 10. Initially the cell population is distributed evenly across the domain. With time the system evolves into a pattern of peaks showing aggregations of cells.

4 Two interacting populations

Having confirmed that aggregations are possible in the model for one population, we now consider the modelling of two populations, u and v, interacting through adhesion. The derivation follows directly that for a one population model in section 2, with the exception that we must now consider the different types of adhesive interactions. For each of the cell types, we assume two types of adhesive force: one representing adhesion between cells of the same type (self-population adhesion) and the other representing adhesion between cells of different type (cross-population adhesion). Biologically, these different types may arise though different levels and types of cell adhesion molecule at the cell membrane.

Thus we assume that the diffusion terms remain as for the one population case, but that adhesion terms will now be replaced by the sum of two terms representing self-population and cross-population adhesion. We will make no initial assumption about adhesion dependence on cell density and so for now all adhesion terms will include a function of both cell densities. The extended nondimensional model equations are therefore

$$u_t=u_{\mathit{xx}}-{\left({\mathit{uK}}_u(u,v)\right)}_x$$ (4.1a)

$$v_t=v_{\mathit{xx}}-{\left({\mathit{vK}}_v(u,v)\right)}_x$$ (4.1b)

where

and

Here u(x, t) and v(x,t) are the population densities of the two cell types at time t and position x; and K_u,v(u, v) are the adhesion terms, encompassing both self-population adhesion and cross-population adhesion. S_u, S_v and C represent the self-adhesive strength of population u, self-adhesive strength of population v, and the cross-adhesive strength between the populations respectively. Note that both cells are assumed to have the same sampling radius, however population variations due to differences in cell geometry can be modelled through the choices of S_u, S_v, C, g_uu, g_vv, g_uv and ω_uu,vv,uv(x₀). To describe the varying strengths of self- and cross-population adhesion, S_u, S_v and C should clearly be distinct. C appears in both (4.1c) and (4.1d) to reflect the anticipated symmetry of the u – v and v – u bonds. The model equations and the parameters are summarised in appendix A.2.

4.1 Are aggregations possible?

In the one population case we investigated the possibility of aggregating behaviour in the model by considering both a PDE approximation and a stability analysis. We can use the same techniques to investigate possible behaviour in the model for two interacting populations, (4.1).

We begin by making the simplifying assumption that each of the force functions are given by linear forms

$$g_{\mathit{uu}}=u,g_{\mathit{vv}}=v,g_{\mathit{uv}}=v,g_{\mathit{vu}}=u.$$ (4.2)

This implies that the strength of the adhesive forces will increase linearly with cell density and so adhesive forces are stronger where cell density is greater. This simplifies the adhesion terms (4.1c) and (4.1d) to

$$K_u(u,v)={\int }_{-1}^1{S}_{u}u(x+x_0){\omega }_{\mathit{uu}}\left(x_0\right)+\mathit{Cv}(x+x_0){\omega }_{\mathit{uv}}\left(x_0\right){\mathit{dx}}_0$$ (4.3a)

and

$$K_v(u,v)={\int }_{-1}^1{S}_{v}v(x+x_0){\omega }_{\mathit{vv}}\left(x_0\right)+\mathit{Cu}(x+x_0){\omega }_{\mathit{uv}}\left(x_0\right){\mathit{dx}}_0.$$ (4.3b)

Using the technique described in section 3.1 we can find the PDE approximation to this model. We find that, as in the one population case, there is a dependence in the advection terms on the first spatial derivatives of both cell populations, indicating directed movement along population gradients. As before we speculate that singularities are avoided through the damping effect of higher order terms.

The second technique we use to investigate possibilities of aggregating behaviour is to look at the model's stability. We follow the method described in section 3.2 to find the dispersion relation, λ(k), for the system. To simplify the analysis of the dispersion relation we consider the case where ω_uu,vv,uv(x₀) are all equal and are given by the simple step function form (2.9). In addition we assume that both cell types have the same homogeneous steady state, U = V = N. The condition for instability, Re(λ) > 0, is then

$$-(S_u{S}_v+C^2)X^2-N(S_u+S_v)X-1>0$$ (4.4)

where

$$X=\frac{1}{k^2}(\cos k-1).$$

While it is difficult to obtain a firm grasp on the parameter regions for which aggregations are possible, we can use the above to provide some broad predictions on the effect of S_u, S_v and C on patterning instability. Clearly, since X ≤ 0, patterning is only possible for a sufficiently large S_u + S_v. Further, increasing C decreases the first term, and thus we can predict that a sufficiently large cross-population adhesion should prevent aggregations from forming. Figure 5 shows the left hand side of inequality (4.4) as a function of k, the wavenumber, for a specific set of parameter values. We can see that for this set of parameter values there is a range of k for which aggregating behaviour is possible in the model.

Fig. 5.

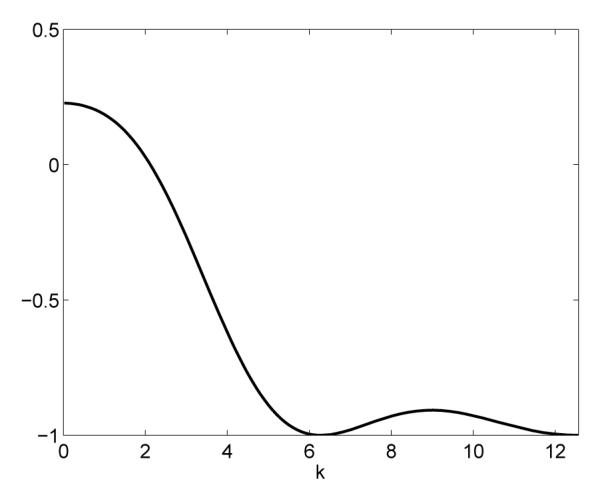
A plot of the left hand side of inequality (4.4) as a function of k showing that there are values of k where the inequality holds and hence wavenumbers for which aggregations are possible. The initial cell density is taken to be N = 1, and the adhesion parameters are S_u = 3.0, S_v = 1.0 and C = 0.3

To confirm this we solve the model numerically using the method described in section 3.3. Typical numerical solutions are shown in figure 6. We can see that, as in the one population case, time evolution of the numerical solutions shows a pattern of peaks developing across the domain. The two figure rows demonstrate the behaviour for zero cross-population adhesion, (figure 6 (a)), and non-zero cross-population adhesion (figure 6 (b)). With no interactions, the two populations form separate peaks: effectively they are unaware of each others existence. With the inclusion of cross-population adhesion, the peaks that form are a mixture of both cell types. These numerics clearly demonstrate that the model displays aggregating behaviour and that the relative sizes of the different adhesion strengths in the model can be linked to different types of pattern formation. We investigate this further in the following section.

Fig. 6.

Confirmation of aggregations in the two population model in one dimension. The model is solved on a domain of length 20, discretised into 200 mesh points. The model parameters are set at S_u = 25, S_v = 7.5 and (a) C = 0.0, (b) C = 12.5. We can see in (a) that separate aggregations occur when there is no interaction between cell types. In (b) there are interactions between cell types. Aggregations occur but we are unable to distinguish between the cell populations as all cells aggregate in the same spatial regions.

4.2 Numerical Simulation of the Steinberg Experiments

Numerical methods allow us to use our model to investigate the outcome of interactions between cell populations with different adhesion properties. Experimental evidence shows that a mixture of two cell types may evolve to one of four configurations depending on the relative strengths of self-adhesion and cross-adhesion of the cell populations (Steinberg, 1962c). In figure 7 we show the configurations that are seen experimentally and summarise the adhesion properties of the experimental cell types whose interactions result in the formation of each pattern.

Fig. 7.

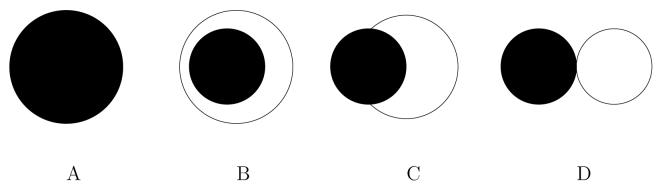
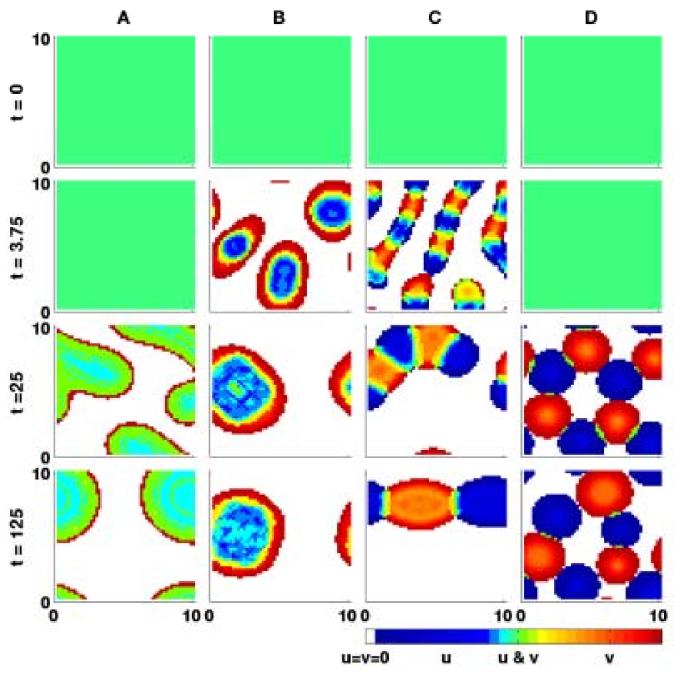
The possible configurations to which a system of two cell populations may evolve. The more cohesive population, u, is shown here in black and the less cohesive population, v, in white. S_u, S_v and C represents the cohesive strength of population u, the cohesive strength of population v and the cross-population adhesive strength respectively. A: Mixing (Preferential cross adhesion). The cross adhesion strength of the cells is greater than the average of the two self adhesion strengths, $C>\frac{S_u+S_v}{2}$. The cells form mixed population aggregates. B: Engulfment (Intermediate cross adhesion). The cross adhesion strength is greater than the self adhesion strength of the less cohesive population but less than the self adhesion strength of the more cohesive population, S_v < C < S_u. The more cohesive population is engulfed by the less cohesive population. C: Partial Engulfment (Relatively weak adhesion). The cross adhesion strength is less than both the self adhesion strengths, C < S_u and C < S_v. The more cohesive population is partially engulfed by the less cohesive population. D: Complete Sorting (No cross adhesion). If there is no cross adhesion between the two populations and C = 0 the two cell types form separate aggregations. (Figure adapted from Foty and Steinberg (2004).)

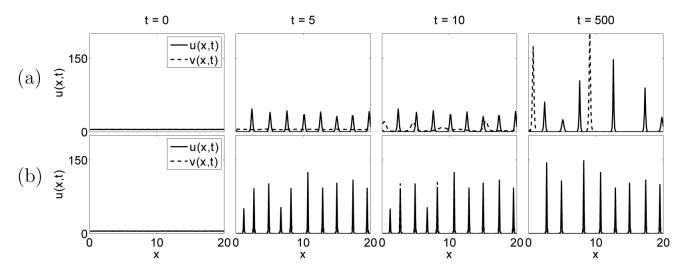
In section 4.1 we solved the model numerically, both for a system with no interaction between cell types (figure 6(a)), and with an interaction between cell types (figure 6(b)). The cell types used in these simulations obey the conditions C = 0 and S_v < C < S_u corresponding to scenarios D and B detailed in figure 7 respectively. While the pattern formation seen in figure 6(a) matches that seen experimentally for these cell types, (part D, figure 7), the pattern formation seen in figure 6(b) represents a “mixing” scenario, A, rather than the engulfment scenario B. To model all types of configurations we consider the assumptions made in developing the model.

For mathematical simplicity, thus far we have assumed linear forms for the functions g_uu,vv(u, v) and g_uv,vu(u, v). These are somewhat unrealistic since they imply that higher cell densities always generate stronger adhesive force, leading to the sharp aggregation peaks seen in the numerics thus far. A more realistic assumption would be to assume at higher cell densities, population pressure limits the ability to aggregate, see (2.8). Thus we replace our linear functions by nondimensional logistic equations of the form

$$\begin{array}{cc}\hfill & g_{\mathit{uu}}(u,v)=g_{\mathit{vu}}(u,v)=\{\begin{array}{cc}u(1-u-v)\hfill & \text{if}u+v<1\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}\hfill \\ \hfill & g_{\mathit{vv}}(u,v)=g_{\mathit{uv}}(u,v)=\{\begin{array}{cc}v(1-u-v)\hfill & \text{if}u+v<1\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.\hfill \end{array}$$

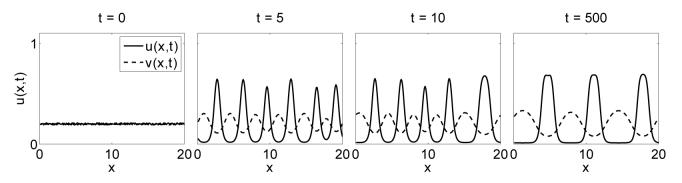
To demonstrate the effect of introducing the logistic functions, we repeat the numerical simulations described in section 4.1 using the above logistic functions together with (2.9) for each of the ω-functions in (4.1c) and (4.1d). Figure 8 shows the equivalent results to figure 6(a) when logistic functions are taken instead of the linear form. A comparison of figures 8 and 6(a) shows that the introduction of the logistic term results in aggregations which cover a larger spatial area but with a lower maximum cell density. This is more biologically realistic than the small, high density aggregations seen in figure 6. Separate aggregations are seen once again but this is now genuine cell sorting as the cells are aware of each others existence.

Fig. 8.

Aggregations in the two population logistic model in one dimension. Parameters are set at S_u = 25, S_v = 7.5 and C = 0.0, corresponding to scenario D in figure 7. The model is solved on a domain of length 20, discretised into 200 mesh points. This is a repeat of the simulation shown in figure 6(a) with the introduction of a logistic form for g(u, v). By comparison the aggregations are smoother, cover a larger spatial area and have a lower maximum density than those in figure 6(a). In addition cell sorting is now seen.

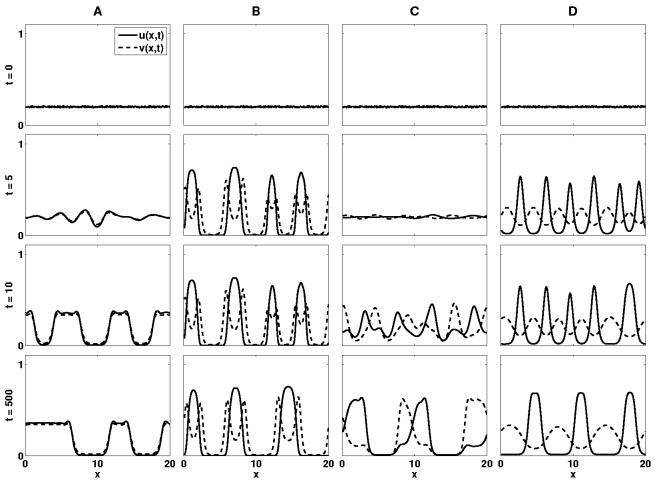
We now test the ability of the model to reproduce the experimental findings outlined in figure 7 by choosing the relative values of the adhesive strengths, S_u,v and C, in line with the properties of the experimental cells used in each scenario from figure 7. The results of these simulations are shown in figure 9. With the introduction of a logistic function into the model, we can replicate each of the four types of pattern formation seen experimentally with equivalent relations between the strengths of self- and cross-population adhesion. We therefore have a model capable of replicating the experimental cell sorting results, something not previously achieved with a continuum model.

Fig. 9.

The results of numerical simulations in one dimension using adhesive strengths relating to the experiments by Steinberg (1962c). In each case the model is solved on a domain of length 20, discretised into 200 mesh points. Initial conditions are shown along with the pattern formation seen at time steps t = 5, t = 10 and finally at t = 500. Results (A)-(D) use the adhesion properties detailed in figure 7. (A):Mixing, S_u = 25, S_v = 7.5 and C = 22.5. (B):Engulfment, S_u = 250, S_v = 25 and C = 50. (C):Partial Engulfment, S_u = 25, S_v = 25 and C = 12.5. (D):Complete Sorting, S_u = 25, S_v = 7.5 and C = 0.0.

5 Two dimensions

In section 4 it was shown that for two interacting populations in one dimension, our model can reproduce Steinberg's experimental results on cell sorting. In this section, we extend our model to investigate whether these results extend to the two-dimensional scenario more relevant to the actual biological process. We begin by extending the one population model and then consider interacting populations with different adhesion properties.

5.1 Extension of the Model to Two Dimensions

Derivation of the equations in 2D is a reasonably straightforward extension of the method used in 1D and described in section 2. Our two dimensional governing equation is given by

$$u_t={\nabla }^{2}u-\nabla \cdot \left(\mathit{uK}\left(u\right)\right)$$ (5.1)

(after nondimensionalisation).

For the adhesion term, K(u), we apply the same biological considerations as for the original derivation in section 2. Cells will be affected by the forces generated through adhesive binding with other cells within a circle of sensing radius R, scaled to be 1, and thus the integral now uses ${\int }_0^1{\int }_0^{2\pi }\mathit{rd}\theta \mathit{dr}$. Within the integral, cells now have a two dimensional position, x. The position of other cells within the sensing radius can be specified by x + ηr, where η is the outer unit normal to the circle. Thus, the adhesive strength is now determined by g(u(x + rη)), while we replace ω(x₀) by ηΩ(r), where η is the direction and Ω(r) the dependence of the adhesion strength on the radial distance. α remains the nondimensional adhesive strength parameter. The adhesion term therefore reflects the dominant direction of movement due to adhesive forces:

$$K\left(u\right)=\alpha {\int }_0^1{\int }_0^{2\pi }g\left(u(\underset{-}{x}+r\underset{-}{\eta })\right)\Omega \left(r\right)\underset{-}{\eta }\mathit{rd}\theta \mathit{dr}.$$ (5.2)

To demonstrate the capabilities of the model we initially choose g(u) = u, and Ω(r) = 1. Analytical investigation of this model gives similar criteria for aggregations as were derived in section 3. The model equations and parameters are summarised in appendix A.3.

Numerical Solutions

The numerical scheme is adapted from the method used by Hillen et al. (2006). To summarise, we discretise the diffusion and advection terms in conservative flux form, employ a second order central differencing scheme for the diffusion term and a high order upwinding method with a flux limiting function for the advection term. The non-local advection term requires calculation of the integral over the circle of radius 1, centred on the mid-point between adjacent mesh points. To do this we first discretise the radial component to give concentric circles of radius r, 0 < r < 1. We then discretise each circular surface into grid points and use linear interpolation from the surrounding domain grid points to find the densities at the surface. The time integration uses an explicit trapezoidal scheme and we assume periodic boundary conditions.

Numerical results for the simplified model are given in figure 10 for α = 1. Solutions evolve from an initially random distribution and cluster together forming high density aggregates, confirming the aggregative capability of the model.

Fig. 10.

An illustration of aggregating behaviour in the two dimensional model for one cell population. The model is solved on a domain of size 5×5 which is discretised into 50×50 mesh points. The adhesion strength of the cells is assumed to be linear with respect to cell density, g(u) = u, and constant with respect to radial distance, Ω(r) = 1.0. We choose the adhesion strength parameter to be α = 1. In these panels cell density from zero to 2 is shown on a scale running from white to black. All densities greater than 2 are shown in black. We can see that with time the system evolves from an almost homogeneous distribution to a pattern of aggregations.

5.2 Two interacting populations

Having confirmed that aggregating behaviour is possible in the two dimensional model we extend the model (5.1) to consider interacting populations. The two population model is

$$u_t={\nabla }^{2}u-\nabla \cdot \left({\mathit{uK}}_u(u,v)\right)$$ (5.3a)

and

$$v_t={\nabla }^{2}v-\nabla \cdot \left({\mathit{vK}}_v(u,v)\right)$$ (5.3b)

where

$$\begin{array}{cc}\hfill K_u(u,v)={\int }_0^1& {\int }_0^{2\pi }r\underset{-}{\eta }[S_u{g}_{\mathit{uu}}(u(\underset{-}{x}+r\underset{-}{\eta }),v(\underset{-}{x}+r\underset{-}{\eta })){\Omega }_{\mathit{uu}}\left(r\right)\hfill \\ \hfill & +{\mathit{Cg}}_{\mathit{uv}}(u(\underset{-}{x}+r\underset{-}{\eta }),v(\underset{-}{x}+r\underset{-}{\eta })){\Omega }_{\mathit{uv}}\left(r\right)]d\theta \mathit{dr}\hfill \end{array}$$ (5.3c)

and

$$\begin{array}{cc}\hfill K_v(u,v)={\int }_0^1& {\int }_0^{2\pi }r\underset{-}{\eta }[S_v{g}_{\mathit{vv}}(u(\underset{-}{x}+r\underset{-}{\eta }),v(\underset{-}{x}+r\underset{-}{\eta })){\Omega }_{\mathit{vv}}\left(r\right)\hfill \\ \hfill & +{\mathit{Cg}}_{\mathit{vu}}(u(\underset{-}{x}+r\underset{-}{\eta }),v(\underset{-}{x}+r\underset{-}{\eta })){\Omega }_{\mathit{uv}}\left(r\right)]d\theta \mathit{dr}.\hfill \end{array}$$ (5.3d)

Here u(x,t), v(x,t) are the cell densities at position x and time t; and K_u,v are the non-local adhesion terms. As before the functions Ω_uu,vv,uv represent the dependence of the strength of adhesive binding on the radial distance and S_u, S_v and C are the self-adhesive strength of population u, the self-adhesive strength of population v and the cross-adhesive strength between the populations respectively. For simplicity we shall assume Ω_uu,vv,uv = 1. The model equations and parameters are summarised in appendix A.4.

We omit the details of the stability analysis for brevity. The methods used follow from those employed in the one dimensional investigation and result in a complicated dispersion relation for the system. The important implication of the expression is that aggregations are possible in this case and again this can be confirmed by numerical means. For the adhesive strength functions, we use the same nondimensional logistic equations as applied previously:

$$\begin{array}{cc}\hfill & g_{\mathit{uu}}(u,v)=g_{\mathit{vu}}(u,v)=\{\begin{array}{cc}u(1-u-v)\hfill & \text{if}u+v<1\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}\hfill \\ \hfill & g_{\mathit{vv}}(u,v)=g_{\mathit{uv}}(u,v)=\{\begin{array}{cc}v(1-u-v)\hfill & \text{if}u+v<1\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.\hfill \end{array}$$

Typical numerical solutions are shown in figure 11.

Fig. 11.

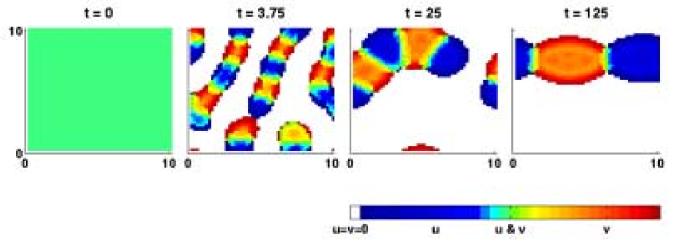
Confirmation that aggregating behaviour is possible in the model for two populations in two dimensions. The model is solved on a domain of size 10×10, discretised into 50×50 mesh points. Here u density is shown in blue, v density is shown in red and regions where both cell types are present are green/yellow depending on the relative densities of u and v. At t = 0 there is a mixture of cells across the domain. At t = 3.75 some reorganisation of cells can be observed. At t = 25 there is evidence of pattern formation and by t = 125 the cells have sorted into two overlapping aggregations. The adhesion strength parameters here are set at S_u = 10, S_v = 10 and C = 5, corresponding to scenario C in figure 7.

5.3 2D Numerical Simulations of the Steinberg Experiments

The final test of our model is to determine whether we can reproduce the different types of configurations from Steinberg's cell sorting experiments shown in figure 7 in the 2D model. To summarise, these experiments show the following patterning types according to the relationship between S_v, S_u and C:

$$C>(S_u+S_v)∕2\Rightarrow \text{Mixing},$$ (5.4a)

$$\begin{array}{cc}\hfill S_v<C<S_u\Rightarrow & \text{Engulfment of population}u\hfill \\ \hfill & \text{by population}v,\hfill \end{array}$$ (5.4b)

$$\begin{array}{cc}\hfill C<S_u\text{and}C<S_v\Rightarrow & \text{Partial engulfment of population}u\hfill \\ \hfill & \text{by population}v,\hfill \end{array}$$ (5.4c)

$$C=0\Rightarrow \text{Complete sorting}.$$ (5.4d)

We simulate our model with values of S_u, S_v, and C corresponding to those in conditions (5.4). The results of these numerical simulations can be seen in figure 12. Clearly, we can demonstrate excellent agreement between our model and the cell sorting experiments. We can thus conclude that our model is able to successfully capture this important characteristic of adhesive populations.

Fig. 12.

The results of numerical simulations in two dimensions using adhesive strengths relating to the experiments by Steinberg (1962c). In each case the model is solved on a domain of size 10×10, discretised into 50×50 mesh points. Results (a)-(d) use the adhesion properties detailed in figure 7. (a):Mixing, S_u = 10, S_v = 3 and C = 9. (b):Engulfment, S_u = 100, S_v = 10 and C = 20. (c):Partial Engulfment, S_u = 10, S_v = 10 and C = 5. (d):Complete Sorting, S_u = 10, S_v = 3 and C = 0.

6 Discussion

In this paper we have presented a new continuum model for cell-cell adhesion. We assume adhesion creates an active directed movement in response to the bonds formed between nearby cells. Our derivation results in an integro-partial differential equation in which adhesion is modelled by a non-local term. We employ both analytical and numerical methods to demonstrate the ability of the model to replicate fundamental behaviour associated with cell-cell adhesion in biology, namely, the ability of disassociated cells to “aggregate” and the active sorting process of two or more cell types from a randomly distributed mixture. As far as we are aware, no continuous model has previously captured this behaviour.

A number of discrete approaches have replicated the sorting dynamics of adhesive cell populations (e.g. Palsson and Othmer, 2000; Glazier, 1996; Glazier and Graner, 1993; Graner and Glazier, 1992; Mombach et al., 1995; Stott et al., 1999; Sulsky, 1984). While these models have proved an important tool for modelling, there are two main reasons why a continuous approach is desirable. Firstly, solving discrete models can be computationally prohibitive for large cell numbers. Secondly, continuous models admit a degree of analytical insight that is difficult, if not impossible, to obtain from a discrete model. For example, through application of standard stability techniques in this paper, we have determined the dependence of aggregating behaviour on different model parameters.

This model has been developed primarily in response to the lack of a technique for including cell-cell adhesion in a continuous model for interacting cell populations. As such, the main thrust of the paper has been to elucidate the modelling approach with a subsequent simplification of many terms. We have chosen just two forms for the dependence of the size of force on cell density. In the first we assumed the adhesive force increases linearly with cell density. While the resulting analysis and numerics clearly demonstrated the ability to predict aggregations, the peaks were extremely sharp and we were unable to resolve the different types of sorting patterns observed experimentally. To overcome this, we considered a logistic function in which the force becomes repulsive above a critical density. A natural interpretation for this would be adhesion dominating at low densities while population pressure dominates at high densities. In this case, the resulting aggregations plateau at a maximum density. Importantly, by solving the model numerically, we can reproduce Steinberg's cell sorting results with equivalent relations between the relative strengths of self-population and cross-population adhesion.

A second assumption was to consider very simple functional forms for the adhesive force variation with distance. Naturally, these functions may be considerably more complicated, for example due to the reduced likelihood of making contact with more distant cells. Further, while we considered our different cell populations to be of similar type, cells may show considerable physical variation according to the range and type of cell processes (e.g. lamellipodia, filopodia) they extend.

A natural extension on the modelling side would be to include other cues affecting cell movement, for example chemotactic and cell-matrix interactions. A non-local model similar to the one studied here has previously been developed to model chemotactic cell movement (Hillen et al., 2006). Combining the different types of interactions that influence cell movement may help us to analyse their relative importance under different conditions and indicate the circumstances under which terms can safely be neglected. Further work may include the extension to three dimension and the inclusion of cell kinetics.

Clearly, there is great scope for the application of the methods developed here to specific biological applications. Cell-cell adhesion is essential for both embryonic development and subsequent tissue homeostasis. During embryonic development, regulated control of the adhesive properties of cells has been implicated in a variety of processes, including gastrulation, neural crest migration and vasculogenesis (Thiery, 2003). Furthermore it plays a key role in the malignant progression of cancers. Numerous studies have implicated altered cell-cell and cell-matrix adhesion properties with an increased ability to invade surrounding tissue (e.g. Mareel and Leroy, 2003). Previous continuous mathematical models have largely neglected the role of cell-cell adhesion in areas such as cancer invasion, although a number of discrete approaches have been employed (e.g. Anderson, 2005; Turner and Sherratt, 2002; Drasdo and Hohme, 2005). Largely, the omission is a result of the difficulties in modelling this type of behaviour, rather than the assumption that cell-cell adhesion is unimportant. The cell populations we have considered here are generic and do not relate to a specific application. Clearly for specific cell types alterations would be required to account for other mechanisms involved in cell movement. Changes may also be required in the assumptions underlying the choice of force functions used here. We acknowledge that there are adjustments to be made which will be dependent on the application but we hope that this model may provide a basis for introducing cell-cell adhesion into mathematical models in these areas.

A Appendix

Here we summarise each of the models discussed in this paper along with parameters used in each case.

A.1 One Population in One Dimension

$$\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x^2}-\frac{\partial }{\partial x}\left(\mathit{uK}\left(u\right)\right)$$ (A.1a)

where

$$K\left(u\right)=\alpha {\int }_{-1}^{1}g\left(u(x+x_0)\right)\omega \left(x_0\right){\mathit{dx}}_0.$$ (A.1b)

Table A.1.

Model parameters for one population in one dimension.

	Description
u(x, t)	Density of population u at position x and time t.
K(u)	Non-local adhesion term.
α	Adhesion strength coefficient Taken to be a non-negative constant.
g(u)	This function defines the dependence of the adhesive force on cell density. To represent an attractive force we require that g(u) is non-negative. For simplicity we assume g(u) = u.
ω(x0)	This function defines the dependence of the adhesive forces on the position of the cells. The direction of the force will depend on the relative positions of the cells. To model an attractive force we require ω(x0) is an odd function and ω(x0) ≥ 0 for 0 < x0 < 1. It is reasonable that the magnitude of the force may also depend on the distance between cells but for simplicity we assume this is not the case and take $$\omega \left(x_0\right)=\{\begin{array}{cc}-1\hfill & -1<x_0<0\hfill \\ 1\hfill & 0<x_0<1\hfill \end{array}\phantom{\}}$$

A.2 Two Populations in One Dimension

$$u_t=u_{\mathit{xx}}-{\left({\mathit{uK}}_u(u,v)\right)}_x$$ (A.2a)

$$v_t=v_{\mathit{xx}}-{\left({\mathit{vK}}_v(u,v)\right)}_x$$ (A.2b)

where

$$\begin{array}{cc}\hfill K_u(u,v)=S_u& {\int }_{-1}^1{g}_{\mathit{uu}}(u(x+x_0),v(x+x_0)){\omega }_{\mathit{uu}}\left(x_0\right){\mathit{dx}}_0\hfill \\ \hfill & +C{\int }_{-1}^1{g}_{\mathit{uv}}(u(x+x_0),v(x+x_0)){\omega }_{\mathit{uv}}\left(x_0\right){\mathit{dx}}_0\hfill \end{array}$$ (A.2c)

and

$$\begin{array}{cc}\hfill K_v(u,v)=& S_v{\int }_{-1}^1{g}_{\mathit{vv}}(u(x+x_0),v(x+x_0)){\omega }_{\mathit{vv}}\left(x_0\right){\mathit{dx}}_0\hfill \\ \hfill & +C{\int }_{-1}^1{g}_{\mathit{vu}}(u(x+x_0),v(x+x_0)){\omega }_{\mathit{uv}}\left(x_0\right){\mathit{dx}}_0.\hfill \end{array}$$ (A.2d)

Table A.2.

Model parameters for two populations in one dimension.

	Description
u(x, t) v(x, t)	Population densities at position x and time t.
Ku(u, v) Kv(u, v)	Non-local adhesion terms.
Su, Sv, C	Self-population adhesion strength coefficient of population u, self-population adhesion strength coefficient of population v and cross-population adhesion strength coefficient respectively. Each taken to be a non-negative constant.
guu(u, v) guv(u, v) gvv(u, v) gvu(u, v)	These functions define the dependence of the adhesive force on cell density. To represent attractive forces we require that g(u, v) are non-negative. We consider two simple forms, $$1.g_{\mathit{uu}}=g_{vu}=u,g_{\mathit{vv}}=g_{uv}=v$$ $$\begin{array}{cc}\hfill 2.& g_{\mathit{uu}}=g_{\mathit{vu}}=\{\begin{array}{cc}u(1-u-v)\hfill & 0<(u+v)\le 1\hfill \\ 0\hfill & (u+v)>1\hfill \end{array}\phantom{\}},\hfill \\ \hfill & g_{\mathit{vv}}=g_{\mathit{uv}}=\{\begin{array}{cc}v(1-u-v)\hfill & 0<(u+v)\le 1\hfill \\ 0\hfill & (u+v)>1\hfill \end{array}\phantom{\}}.\hfill \end{array}$$ We find that the linear form (1) permits aggregating behaviour but that the density limiting form (2) is required to show cell sorting.
ωuu(x0) ωuv(x0) ωvv(x0)	These functions define the dependence of the adhesive forces on the position of the cells. The direction of the force will depend on the relative positions of the cells. To model an attractive force we require ω(x0) is an odd function and ω(x0) ≥ 0 for 0 < x0 < 1. The magnitude of the force may depend on the distance between cells but for simplicity we assume this is not the case. We assume that ωuu,uv,vv(x0) all take the same form, $$\omega \left(x_0\right)=\{\begin{array}{c}-1-1<x_0<0\hfill \\ 10<x_0<1\hfill \end{array}\phantom{\}}$$

A.3 One Population in Two Dimensions

$$u_t={\nabla }^{2}u-\nabla \cdot \left(\mathit{uK}\left(u\right)\right)$$ (A.3a)

$$K\left(u\right)=\alpha {\int }_1^0{\int }_0^{2\pi }g\left(u(\underset{-}{x}+r\underset{-}{\eta })\right)\Omega \left(r\right)\underset{-}{\eta }\mathit{rd}\theta \mathit{dr}.$$ (A.3b)

Table A.3.

Model parameters for one population in two dimensions.

	Description
u(x,t)	Density of population u at position x and time t.
K(u)	Non-local adhesion term.
α	Adhesion strength coefficient Taken to be a non-negative constant.
g(u)	This function defines the dependence of the adhesive force on cell density. To represent an attractive force we require that g(u) is non-negative. For simplicity we assume g(u)= u.
Ω(r)	This function defines the dependence of the adhesive strength on the position of the cells. To model an attractive force we require Ω(r) is a positive function. For simplicity we assume Ω(r) = 1.0.
η	The outer unit normal, η = (cos θ, sin θ). Inclusion ensures force has direction.

A.4 Two Populations in Two Dimensions

$$u_t={\nabla }^{2}u-\nabla \cdot \left({\mathit{uK}}_u(u,v)\right)$$ (A.4a)

and

$$v_t={\nabla }^{2}v-\nabla \cdot \left({\mathit{vK}}_v(u,v)\right)$$ (A.4b)

where

$$\begin{array}{cc}\hfill K_u(u,v)={\int }_0^1& {\int }_0^{2\pi }r\underset{-}{\eta }[S_u{g}_{\mathit{uu}}(u(\underset{-}{x}+r\underset{-}{\eta }),v(\underset{-}{x}+r\underset{-}{\eta })){\Omega }_{\mathit{uu}}\left(r\right)\hfill \\ \hfill & +{\mathit{Cg}}_{\mathit{uv}}(u(\underset{-}{x}+r\underset{-}{\eta }),v(\underset{-}{x}+r\underset{-}{\eta })){\Omega }_{\mathit{uv}}\left(r\right)]d\theta \mathit{dr}\hfill \end{array}$$ (A.4c)

and

$$\begin{array}{cc}\hfill K_v(u,v)={\int }_0^1& {\int }_0^{2\pi }r\underset{-}{\eta }[S_v{g}_{\mathit{vv}}(u(\underset{-}{x}+r\underset{-}{\eta }),v(\underset{-}{x}+r\underset{-}{\eta })){\Omega }_{\mathit{vv}}\left(r\right)\hfill \\ \hfill & +{\mathit{Cg}}_{\mathit{vu}}(u(\underset{-}{x}+r\underset{-}{\eta }),v(\underset{-}{x}+r\underset{-}{\eta })){\Omega }_{\mathit{uv}}\left(r\right)]d\theta \mathit{dr}.\hfill \end{array}$$ (A.4d)

Table A.4.

Model parameters for two populations in two dimensions.

	Description
u(x,t) v(x,t)	Population densities at position x and time t.
Ku(u, v) Kv(u, v)	Non-local adhesion terms.
Su, Sv, C	Self-population adhesion strength coefficient of population u, self-population adhesion strength coefficient of population v and cross-population adhesion strength coefficient respectively. Each taken to be a non-negative constant.
guu(u, v) guv(u, v) gvv(u, v) gvu(u, v)	These functions define the dependence of the adhesive force on cell density. To represent an attractive force we require that g(u, v) are non-negative. We consider the density limiting functions, $$\begin{array}{cc}\hfill & g_{\mathit{uu}}=g_{\mathit{vu}}=\{\begin{array}{cc}u(1-u-v)\hfill & 0<(u+v)\le 1\hfill \\ 0\hfill & (u+v)>1\hfill \end{array}\phantom{\}},\hfill \\ \hfill & g_{\mathit{vv}}=g_{\mathit{uv}}=\{\begin{array}{cc}v(1-u-v)\hfill & 0<(u+v)\le 1\hfill \\ 0\hfill & (u+v)>1\hfill \end{array}\phantom{\}}.\hfill \end{array}$$
Ωuu(r) Ωuv(r) Ωvv(r)	These functions define the dependence of the strength of the adhesive forces on the position of the cells. To model an attractive force we require that Ω(r) are positive functions. For simplicity we assume that Ωuu(r) = Ωuv(r) = Ωvv(r) = 1.0
η	The outer unit normal, η = (cos θ, sin θ). Inclusion ensures force has direction