Abstract
It is unclear whether the thermal denaturation of staphylococcal nuclease is a two state, three state, or variable two state process. The thermal denaturation of wild-type staphylococcal nuclease was followed by tryptophan fluorescence and circular dichroism signal at 222 nm, forty-two and fourteen times respectively. Analysis of this data using a simple two state model gave melting temperatures of 53.0 ± 0.4°C (fluorescence) and 52.7 ± 0.6°C (CD) and van't Hoff enthalpies of 82.4 ± 2.6 kcal/mol and 88.6 ± 4.2 kcal/mol. Ninety-seven mutants also had these parameters determined by both fluorescence and CD. The average difference between the melting temperatures was 1.05 ± 0.75° and the average difference between van't Hoff enthalpies was 1.6 ± 4.8 kcal/mol. These very similar results for the two spectroscopic probes of structure are discussed in the context of the different models that have been proposed for nuclease denaturation. It is concluded, for most nuclease variants, that the errors introduced by a two state assumption are negligible and either virtually all helical structure is lost in any initial unfolding event or any intermediate must have low stability.
Keywords: Thermal unfolding, residual structure, melting temperature, van't Hoff enthalpy
Introduction
The thermodynamic parameters of protein stability can be determined by solvent and thermal denaturation experiments. Typically, however, only one or the other technique is used. We were interested in comparing the solvent and thermal denaturation of staphylococcal nuclease, a model protein used by ourselves and others for studies of mutational effects upon protein stability. There is evidence that at least some mutants of nuclease, in particular the V66W mutant, unfold during solvent denaturation in three states, rather than the two state model normally used for data analysis [1-13]. Maki et al. showed that a proline-minus variant of nuclease could have no more than 5% of an equilibrium intermediate at any urea concentration, while a F76W mutant of this proline-minus variant has nearly 50% of the protein populating an equilibrium intermediate at moderate urea concentrations. Bolen's group has argued convincingly [13, 14] that neither a simple two or three state model fully explains the data for wild-type nuclease and the majority of mutants that have been studied. They generally favor the variable two state model proposed by Shortle [15, 16], wherein the character of the denatured state changes with mutation, denaturant concentration, or temperature. However, they point out several disagreements between this model and experimental data [12-14].
Similar questions can be raised about whether a two, three, or variable two state model is more appropriate for analysis of thermal denaturation of nuclease. Carra and Privalov, proponents of the three state model for solvent denaturation [17], have concluded that thermal denaturation of wild-type nuclease is two state [17, 18]. On the other hand, Eftink's group has shown that V66W mutant with tryptophan or tryptophan analogues, appears to be better fit by a three state thermal unfolding model [7]. Therefore, as a necessary first step before comparing the thermal and solvent denaturation behavior of many staphylococcal nuclease mutants, we present here data comparing the thermal denaturation of staphylococcal nuclease and 97 mutants monitored by two different probes of structure, tryptophan fluorescence and the circular dichroism (CD) helical signal at 222 nm.
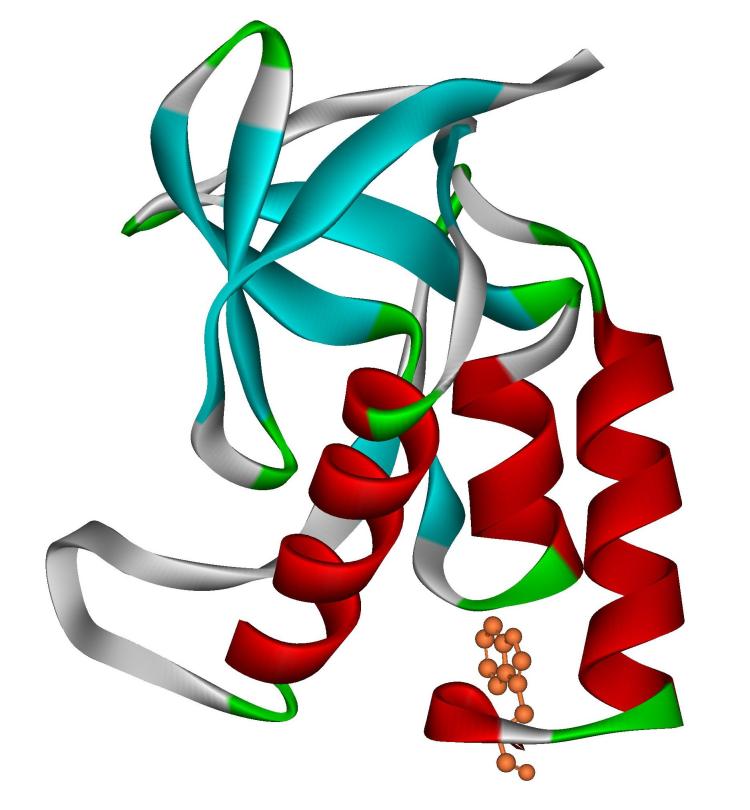
Tryptophan fluorescence is a fairly local probe of structure, monitoring the degree of solvent exposure of the single tryptophan found in staphylococcal nuclease at position 140. (Figure 1) The CD signal at 222 nm, on the other hand, monitors the amount of helix found throughout the protein. The physical model for three state denaturation in nuclease is that the C-terminal helix, which ends with tryptophan 140, unfolds in the first transition. Carra and Privalov propose that the other helices unfold in this transition as well, leaving only the beta barrel structure, an idea supported by some hydrogen exchange data [16, 19, 20]. The remaining structure then breaks down cooperatively in a subsequent step. The putative intermediate is indistinguishable by tryptophan fluorescence from the more fully unfolded form as the 140 side chain is fully exposed in both. The loss of all helical content would not allow CD to distinguish between the partially and fully denatured states. While it seem certain that the C-terminal helix breaks down easily, it seems less clear whether the other helices would in fact break down in any initial unfolding step. NMR [21-25], CD [26], and mass spectrometry [27, 28] study of denatured nuclease have identified residual helical structure in both of the first two helices, which are not proximal to the C-terminal helix in primary or, for the case of the first helix, tertiary structure. Further, Bolen's group has shown that the denatured state becomes more compact at lower concentrations of denaturants [13, 14] and compactness is commonly held to lead to an increase in secondary structural content. If a similar trend were true for high and low temperatures, mutants denaturing at lower temperatures might have a more compact denatured state with a higher helical content that breaks down at higher temperature. Thus, one would predict that the two probes of structure, fluorescence and CD, might give different results if a three state denaturation or a variable two state model more closely reflects the reality of the thermal denaturation than does a simple two state model.
Figure 1.
Ribbon diagram of staphylococcal nuclease (PDB 1EY0) with tryptophan 140 shown in orange. Helical secondary structure is shown in red.
Theory
A more detailed theoretical analysis bears this out, but points out important limitations on what the two probes of structure can differentiate. In past work staphylococcal nuclease denaturation behavior has been analyzed by a two state model. The apparent equilibrium constant, Kapp, for the two state reaction native state Ý denatured state is calculated using the equation:
| 1) |
where [N] and [D] are the concentration of the native and denatured states, respectively, IN is the fluorescence or circular dichroism of the native state, ID the fluorescence or circular dichroism of the denatured state, and I is the fluorescence or circular dichroism intensity at a given temperature. In practice, both IN and ID for both fluorescence and CD decrease as temperature increases in a generally linear fashion.
Let us suppose that the denaturation behavior of nuclease is, instead, a three-state equilibrium.
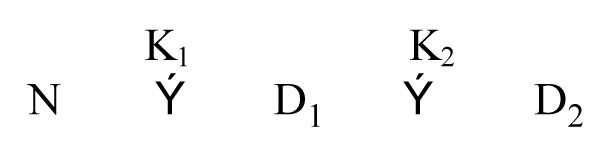
The equilibriums, defined by K1 and K2, in the absence of evidence to the contrary, will be assumed to be two-state and [N], [D1] and [D2] are the concentrations of protein in, respectively, the N, D1 and D2 states. We adopt the nomenclature of D1 and D2 for the partially unfolded and the more completely unfolded state, respectively, to emphasize that the intermediate state is not completely folded, is presumably enzymatically inactive, and to avoid some of the connotations associated with the term “intermediate.” Therefore:
| 2) |
and
| 3) |
The overall, total equilibrium, KT, for native state Ý denatured states is then given by
| 4) |
The fraction of the protein in each state can be expressed terms of these equilibrium constants as well.
| 5) |
| 6) |
| 7) |
The overall intensity, I, of any spectral probe of the protein is related to the fraction of the protein in a given state and the intensity of the protein in that state, IN, ID1, ID2, respectively representing the intensity of the N, D1, and D2 states.
| 8) |
Rearranging we find that
| 9) |
| 10) |
The physical evidence indicates that the fluorescence intensity of tryptophan 140 (W140) is identical in both the D1 and D2 states,[1] in other words ID1 is equal to ID2. Therefore, the overall equilibrium between the native state and the denatured states, KT, at a particular temperature, in equation 10 simplifies to the relationship
| 11) |
where I140 is the measured fraction weighted intensity of W140, is the intensity of W140 in the native state and is its intensity (assumed to be equal) in either the D1 or D2 state. This is just a restatement of equation 1 and thus the fluorescence intensity of W140 gives an accurate measurement of the overall equilibrium constant between the native states and the denatured state(s) at a given temperature, regardless of whether the relationship between these states is best described by a two state or three state model. This is also true for CD if all helical signal is lost in the first transition.
A variable two-state model is similar to the two state treatment. The most significant difference is that the character of the denatured state changes with temperature, but in a second order manner rather than the first order manner of the three state model. In the case of fluorescence monitoring of staphylococcal nuclease thermal denaturation, the value of ID is not affected by the character of the denatured state since tryptophan 140 is apparently fully solvent exposed in any denatured state. However, the possibility exists that residual helix exists in the denatured state, particularly at lower temperature. This helix would break down as the temperature increases, but in a non-cooperative fashion. How this would be reflected in the denaturation curve is hard to model since many assumptions about precisely how the helix breaks down have to be made. Qualitatively, however, Bolen's data [13, 14] show a rapid expansion in denatured state size at low denaturant concentrations followed by a much slower one at high denaturant concentrations. If a similar pattern holds for temperature, then one might expect for mutants which denature at lower temperatures a rapid, but non linear loss of CD signal due to denatured state changes to be overlaid upon a native state denaturation, leading to disagreement between CD and fluorescence curves. For mutants that denature at higher temperatures, the slower loss of any smaller amount of helix left would be blended into the normal linear loss of CD signal with temperature in ID and there would not be any significant difference between fluorescence and CD determined Tm.
On the other hand, the three state denaturation can be well modeled. Suppose the CD signal is different for each of the native, D1 and D2 states. While IN and ID2 are easily measured from the native and denatured baselines, ID1 is much harder to determine. The value of K1 is also unknown and therefore a solution of equation 11 to determine KT is not possible. Alternatively, if either K1 or ID1 is known, then the other could be determined using the KT values as determined by fluorescence, but we, unfortunately, do not know either. Nevertheless, we can use this relationship to estimate important parameters of any possible three state denaturation. Rearranging equation 9 in a different way we find that the intensity of any spectral probe can be described as follows.
| 12) |
If one compares CD and fluorescence data, examination of equation 12 shows that the key term in the disagreement between the two techniques is the value of K1/(1 + KT), if one assumes there is a significant difference in the values of ID1 and ID2 in the CD. Such an assumption seems reasonable if the physical model for the first denaturation step is just the loss of the C-terminal helix. The second transition would be the breakdown of the beta barrel and the long and short helix it contains. We estimate that in this case the loss of helical intensity would be roughly equal in each transition. It may be more realistic to assume that much more helical intensity is lost in the first transition than the second, a point we shall return to later. For now though, the question is whether K1/(1 + KT) is of appropriate value to be detectable. The larger K1 and/or the smaller KT, the larger the difference in the intensity. However, recall from equation 5 that KT is equal to K1(1 + K2). Further, K1 and K2 must both generally trend upwards or down together as the temperature is raised or lowered. In other words, it is a difficult condition to fulfill that K1 is large and KT small.
The practical effect of this is most clear at the temperature of overall melting, when KT is 1. At this temperature K1 = 1/(1 + K2). Near the overall melting temperature, K1 must be comparable to or less than K2, otherwise the D1 state is never significantly populated and the reaction is really more simply described as a two state unfolding mechanism. However, the value of K1/(1 + KT) is maximized the closer to equality that K1 and K2 are. This happens the closer the value of the melting temperature of the first transition is to the second. In other words, if there is a large difference in the melting temperatures for the two transitions, there will be less difference between the transition as monitored by CD and fluorescence. If the two transitions are similar in melting temperature, i.e. both D1 and D2 are well populated near the overall melting temperature, where KT is 1, there will be a larger difference in intensity. This translates into a difference in the melting temperature measured by the two techniques when analyzed by the two state model.
Experimental
Therefore we followed thermal denaturations of wild-type staphylococcal nuclease and 97 mutants by fluorescence and CD. Mutagenesis and protein expression and purification were carried out as described elsewhere [29]. Each mutant, at protein concentration of approximately 50 μg/ml in a buffer consisting of 25 mM phosphate, 100 mM NaCl, pH 7.0, was subjected to a thermal denaturation in our Aviv ATF-101 fluorometer (296 nm excitation, 325 nm emission), as previously described in detail [30, 31]. Thermal denaturations using circular dichroism (CD) at 222 nm as a probe of structure were performed using a Jasco 700 spectropolarimeter equipped with a Peltier thermocontrol unit in the same buffer but at protein concentrations of approximately 80 μg/ml in a standard 1 cm cuvette with stirring. Thermal ramps were generally performed from 20 to 70°C at a rate of 50°C/hr for CD and 60°C/hr for fluorescence. Less stable mutants were started at lower temperatures. Temperatures in both instruments were calibrated throughout the range to the same NIST traceable thermometer. One difference of note is that temperatures in the fluorometer are measured directly in the solution by a Teflon coated thermocouple, while those in the CD instrument are measured from a thermocouple in the wall of the cuvette holder, since the CD software was not capable of recording an additional temperature input. The temperature of the solution in the cuvette presumably lags behind that of the wall, but we have not attempted to apply a correction factor for this effect.
Analysis of the data yields two thermodynamic parameters of unfolding; the temperature at which half of the protein molecules are unfolded (Tm) and the van't Hoff enthalpy of the unfolding reaction (ΔHvH) at the midpoint temperature. The data was processed by first doing linear fits of the native and denatured baselines. Tryptophan fluorescence is not actually linear with temperature, but as shown by Eftink [32, 33], the assumption of baseline linearity usually introduces negligible error. However, it is possible this assumption or other differences in fitting of the baselines of fluorescence versus CD data are responsible for some of the slight systematic differences discussed later between Tm and ΔHvH values returned by the two probes of structure. Native baselines for wild-type nuclease were usually fit over a ten degree range starting at 25 to 28°C and denatured baselines over a 8-9 degree range, starting at 66 to 67°C. Similar ranges were used for mutants, but starting points were adjusted appropriately. To find the Tm, temperature in Kelvin was fit over the range of lnKapp <2 and >−2 as a linear function of lnKapp, calculated by a two state model. A second order least squares fit of lnKapp, again over the range of lnKapp <2 and >−2, was made to 1/T to determine the van't Hoff enthalpy of the unfolding reaction.
Results and Discussion
Average values for wild-type
In order to determine the error in each of these values we have repeatedly followed the thermal denaturation of wild-type nuclease by fluorescence and CD; forty-two and fourteen times respectively. The fluorescence denaturations have taken place over a period of twelve years and have been performed by a number of different individuals using multiple preparations of wild-type staphylococcal nuclease. The denaturations that were monitored by CD took place over only an eighteen month period, were largely performed by one individual and, although multiple protein preparations were used, the number was not as great. The average value of the melting temperature as determined by fluorescence was 53.0°C with a standard deviation of 0.4°C and 52.7 ± 0.6°C when determined by CD. The average van't Hoff enthalpy value determined by fluorescence was 82.4 ± 2.6 kcal/mol and 88.6 ± 4.2 kcal/mol when determined by CD. For the fluorescence data, it appears that variations between protein preparation, presumably related to the level of purity, are the largest source of variation in the value of Tm and ΔHvH. This potential source of variation is not discernable in the noisier CD data. The higher melting temperature for wild-type staphylococcal nuclease measured by fluorescence is statistically insignificant, but is the opposite of what would be expected if a three state denaturation were observed by CD but not by fluorescence. The difference in van't Hoff enthalpies, 6.2 kcal/mol, is slightly greater than the square root of the sum of the squared standard deviations, 4.9, but here again the higher value for the CD data is opposite what one would expect if the CD transition were broader than that measured by the fluorescence probe.
Comparison of mutants
Wild-type was examined multiple times, but mutants were typically measured only once unless the initial experimental run was obviously flawed, which if it occurred was most commonly due to noise at high temperatures caused by gas bubbles forming on the cuvette wall in the beam path. Mutants with fluorescence midpoint temperatures that were less than 35°C were excluded from this study as these mutants are too unstable to give a true native baseline. The values for Tm and ΔHvH for each mutant are available in a table in the supplementary material.
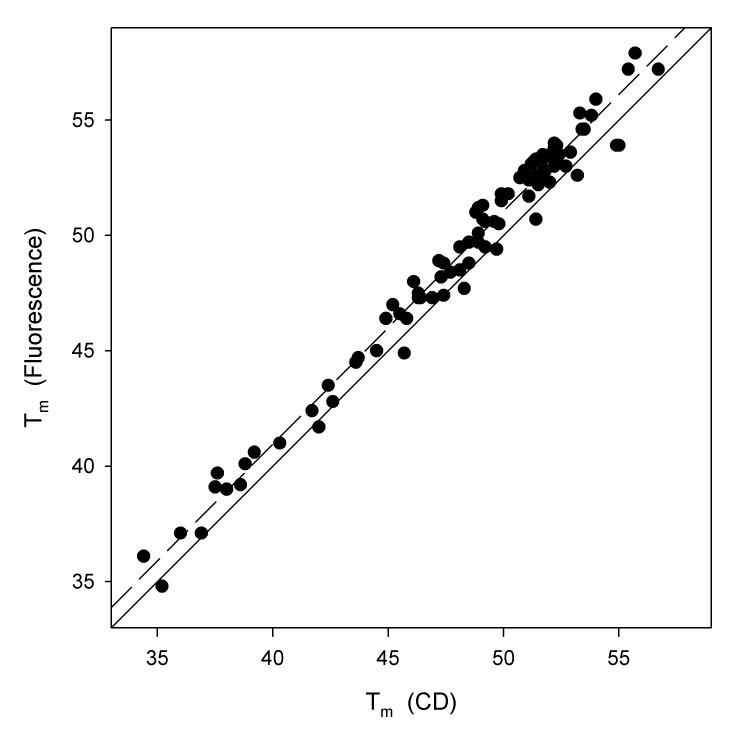
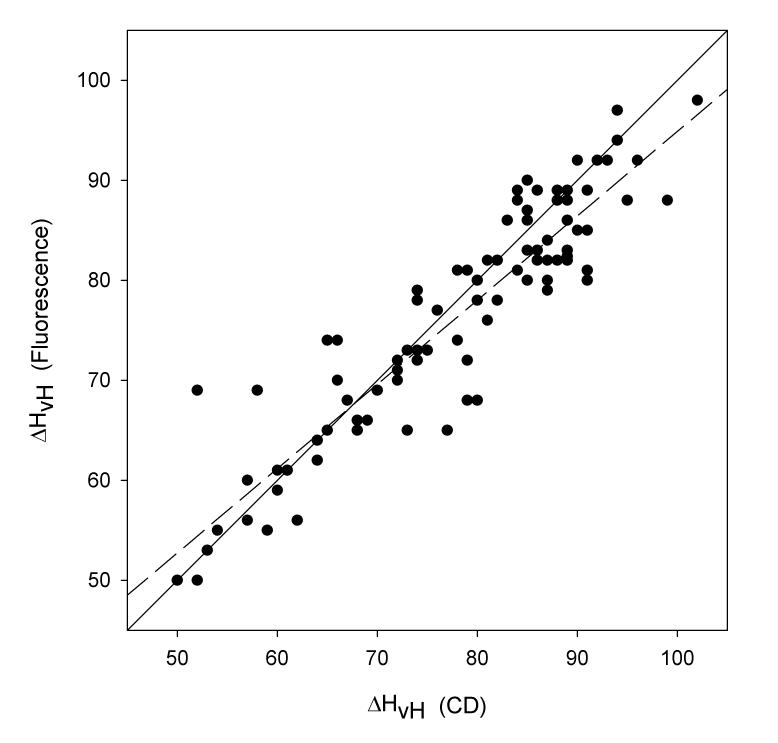
Even though data obtained from a CD thermal denaturation is inherently more noisy than tryptophan fluorescence, there is a very strong correlation (r2 = 0.9787, Figure 2) between the midpoint temperatures of staphylococcal nuclease mutants calculated by both techniques using a two-state model of analysis. Also, the slope of the regression line is 1.012, negligibly different from a 1:1 dependence. Similarly, the agreement between the van't Hoff enthalpies is good (r2= 0.8441, Figure 3) and again the slope of the regression line is very close to one (0.8452), although there are several prominent outliers.
Figure 2.
Plot of midpoint temperature in units of °C calculated from fluorescence thermal denaturations as a function of midpoint temperature calculated from circular dichroism thermal denaturations. The solid line is that upon which all points would fall if there were perfect correspondence in the two values. The dashed line is the result of a least square fit. The slope of this regression line is 1.012, the Y-intercept is 0.463, and the value of r2 is 0.9787.
Figure 3.
Plot of van't Hoff enthalpies in units of kcal/mol calculated from fluorescence thermal denaturations versus those calculated from circular dichroism thermal denaturations. The solid line is that upon which all points would fall if there were perfect correspondence in the two values. The dashed line is the result of a least square fit. The slope of this regression line is 0.8441, the Y-intercept is 10.436, and the value of r2 is 0.8441.
In regard to the variable two state model, we suggested above that the Bolen data [13, 14] showing more compact denatured states at low denaturant concentrations might, by analogy, mean that denatured states were more compact at lower temperatures. If this compactness leads in turn to more helical structure, one might expect to see a greater divergence in CD and fluorescence values for Tm and ΔHvH for mutants that denature at lower temperatures than those that denature at higher temperatures. In fact, Figure 2 does not show such a general trend. Two outliers in Figure 3 do have quite significantly higher fluorescence ΔHvH values but given the larger error in ΔHvH and the number of other mutants not showing this behavior, it does not constitute a statistically significant trend.
The strong correlation in midpoint temperatures and van't Hoff enthalpies evaluated from two different probes suggests that either wild-type nuclease and mutants thermally unfold by a two state mechanism or, at the very least, if unfolding is better reflected by a variable two state or three state model, that the errors introduced by calculating thermodynamic parameters based on two-state assumptions are very low.
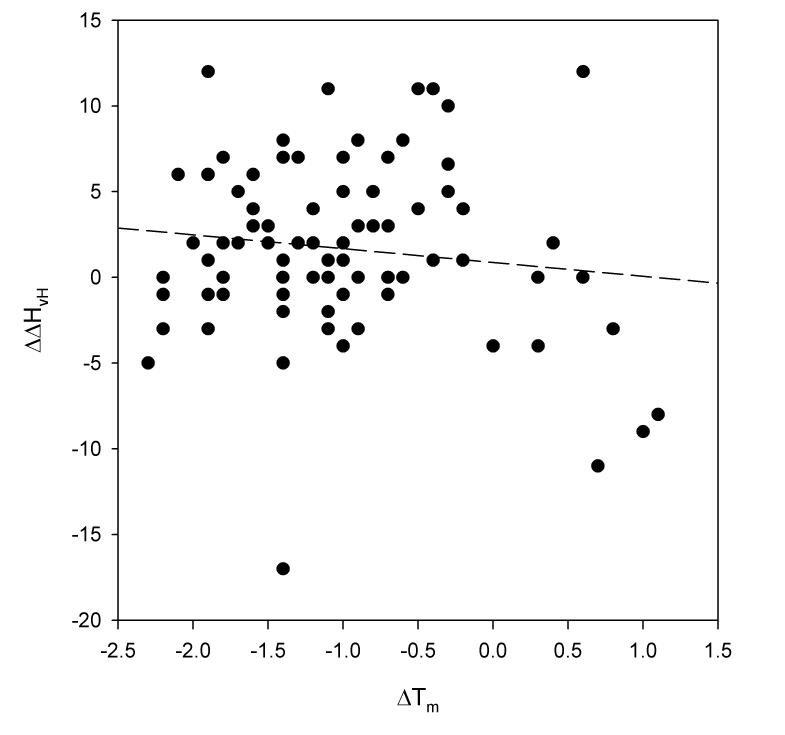
An examination of the differences in Tm and ΔHvH measured by the two probes of structure offers further support for this supposition. These two parameters are plotted against one another in Figure 4. First, note that differences in Tm and ΔHvH are poorly correlated with one another. This is significant because it suggests that these differences are due to random experimental error, rather than any systematic error introduced by incorrect modeling and data analysis.
Figure 4.
Plot of the difference in midpoint temperatures from fluorescence and circular dichroism thermal denaturations (in units of °C) versus the difference in van't Hoff enthalpies for the same denaturations (in units of kcal/mol). The dashed line is the result of a least square fit. The slope of this regression line is −0.88, the Y-intercept is 0.73, and the value of r2 is 0.019.
Further, a three state and possibly a variable two state denaturation would tend to lead to higher Tm values in a two state analysis of CD data, since the second transition, observable by CD but not by fluorescence, would occur at a higher temperature. Similarly, a broader transition generally equates to lower ΔHvH values from the CD data. The difference in Tm for each these variant forms of nuclease is on average is fairly small, 1.05°C with a standard deviation of 0.75. Still, this implies that there is a systematic difference between the two values with some statistical significance. However the fluorescence data generally gives the higher value for Tm, which is not what we expect if the two state model used for analysis is deeply flawed. As noted above, we calibrated the steady state temperatures on both instruments over the range in question and the differences in the way sample temperatures are measured would tend to result in higher recorded temperatures for the CD. We have been unable to isolate the reason for this difference but believe, because it has a sign opposite from that expected from modeling error, that it is an experimental systematic error. On the other hand, this raises the possibility that this systematic experimental error is disguising another systematic error (of opposed sign) arising from the incorrect assumption of the two state model.
We doubt this for two reasons. First, this would mean that any experimental systematic error was in fact larger by the amount of the cancelled analytical systematic error. We believe that the measures we have taken to calibrate the instruments make an even larger systematic experimental error very unlikely to have evaded our notice. Second, any systematic error in temperature will have a minor impact on the van't Hoff enthalpy, defined as −R(d(lnKapp)/d(1/T)), and T is, at the smallest, 308°K. A one degree systematic error in T changes a 60 kcal/mol value of ΔHvH at this temperature by a negligible 0.2 kcal/mol. That this is the case is supported by the poor correlation of differences in Tm and ΔHvH noted above. In fact, the average value for the difference in the van't Hoff enthalpies for wild-type and each mutant is −1.6 kcal/mol with a standard deviation of 4.8. Not only is the average difference statistically insignificant, the sign indicates that the CD van't Hoff enthalpy is higher on average than the fluorescence van't Hoff enthalpy, in the opposite direction of that expected if the CD were recording a broader transition. In short, after detailed examination of the data, there is no experimental evidence in this body of work that the use of a two state model for staphylococcal nuclease thermal denaturation monitored by CD introduces measurable or meaningful error relative to the fluorescence data. This, as the discussion above describes, means that only relatively low levels of the intermediate D1 can accumulate and/or that most helix is lost in the initial breakdown of structure.
This is a qualitative statement, but we can approach it more quantitatively for the three state model. As shown in equation 5, the overall equilibrium, KT is equal to K1(1 + K2). Each equilibrium can be related to the free energy difference for that transition by the equation ΔG = −RTlnK. In turn, the Gibbs-Helmholtz equation expresses how each ΔG changes as a function of temperature, T, and the constants, ΔHm, the enthalpy of unfolding at the melting temperature, Tm, and ΔCp, the difference in heat capacity between the states in question. Expressing KT in this fashion leads to a rather complex equation for which no single solution is possible, but we examined the range of ΔHm, Tm, and ΔCp values for each of the two transitions that reproduce the experimentally measured ΔHm and Tm values for the overall transition of wild-type. The CD and fluorescence monitored denaturations were modeled as described above and we first assumed that half the overall CD helical signal was lost in each of the two transitions or, in other words, that ID1 was equal to (ID2 + IN)/2. The simulated CD intensity generated by an underlying three state model was then analyzed with a two state assumption and the difference between Tm in the modeled fluorescence and CD data was allowed to be as much as 1.5 degrees, a difference that we would be able to detect. The range of values of ΔHm, Tm, and ΔCp for each of the two transitions that meet these restrictions proves to be quite limited. As the discussion above makes clear, the most important parameter is the difference between the two transition Tm values. We found that this difference had to be, generally speaking, 10°K or greater and, notably, that the Tm for the second transition had to be lower than that of the first, otherwise we found a large difference in the apparent Tm returned by two state analysis of the simulated fluorescence and CD data. If this condition is met, then the required values for ΔHm and ΔCp for the second transition were low, under 25 kcal/mol and 0.7 kcal/(mol·K), anything higher would be readily detected. Higher values for ΔHm and ΔCp of the second transition are possible only if the Tm for the second transition is low, in other words, if the denaturation goes straight from N to D2 at higher temperature without populating D1. In terms of the population of D1, any accumulation greater than 20% of total protein would be readily detectable and, depending on the values of the other parameters, in most cases, much less than this would be detected. If two-thirds of the CD signal is lost in the first transition, i.e., ID1 was equal to (ID2 + IN)/3, then the Tm for the two transitions could be roughly equal with values for ΔHm and ΔCp for the second transition similar to those cited above, and as much as 40% of the protein could accumulate in the D1 state, before we could be reasonably certain of detecting it. If ID1 is equal to (ID2 + IN)/4, the values for the second transition ΔHm and ΔCp can be comparable to the first transition and the Tm for the second transition higher approximately 15 degrees, with nearly 80% of the protein accumulating in the D1 state, before detection is likely.
Conclusions
Fluorescence data returns values for melting temperature and van't Hoff enthalpy of the overall denaturation of staphylococcal nuclease that are not dependent upon whether a two state, variable two state, or three state thermal denaturation is occurring, although in the latter two cases the character of the denatured state is assumed to vary from mutant to mutant. Comparison of the CD and fluorescence data for staphylococcal nuclease indicate that if a three state thermal denaturation is occurring, with comparable amounts of CD signal lost in each transition, the transition between the two denatured states has a significantly lower unfolding temperature than the transition between the native state and the first denatured state. In addition, the values of ΔHm and ΔCp for any postulated transition between the two denatured states must be quite low if as little as 20% of the protein ever populates the D1 state. However, if three-quarters or more of the CD signal is lost in a first transition, it would be very difficult to detect any difference between CD and fluorescence determined values, and we can not rule out a multi-state denaturation. Lastly, we find no evidence that mutants with lower Tm values have more compact denatured states with significantly greater amounts of helix. The results presented here do not rule out the possibility that some mutants of staphylococcal nuclease thermally denature by other than a two state mechanism, indeed, we regard that as likely. However, for wild-type and the mutants examined here, a two state model for thermal denaturation fits the data well and, within the bounds of our assumptions, a three state denaturation mechanism appears unlikely. In future communications, we will present data that further defines the possible ranges of thermodynamic parameters of different models of denaturation of nuclease and its mutants.
Supplementary Material
Acknowledgments
We thank Deepika Talla for reading the manuscript and helpful discussion. This work was supported by NIH grant NCRR COBRE P20 RR15569. We thank the referee for pointing out the issue of baseline curvature as a possible explanation for Tm discrepancies.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Gittis AG, Stites WE, Lattman EE. The phase transition between a compact denatured state and a random coil state in staphylococcal nuclease is first-order. J Mol Biol. 1993;232:718–724. doi: 10.1006/jmbi.1993.1425. [DOI] [PubMed] [Google Scholar]
- 2.Xie D, Fox R, Freire E. Thermodynamic characterization of an equilibrium folding intermediate of staphylococcal nuclease. Protein Sci. 1994;3:2175–2184. doi: 10.1002/pro.5560031203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Carra JH, Anderson EA, Privalov PL. Three-state thermodynamic analysis of the denaturation of staphylococcal nuclease mutants. Biochemistry. 1994;33:10842–10850. [Google Scholar]
- 4.Carra JH, Privalov PL. Energetics of denaturation and m values of staphylococcal nuclease mutants. Biochemistry. 1995;34:2034–2041. doi: 10.1021/bi00006a025. [DOI] [PubMed] [Google Scholar]
- 5.Eftink MR, Ionescu R, Ramsay GD, Wong CY, Wu JQ, Maki AH. Thermodynamics of the unfolding and spectroscopic properties of the v66w mutant of staphylococcal nuclease and its 1-136 fragment. Biochemistry. 1996;35:8084–8094. doi: 10.1021/bi9530090. [DOI] [PubMed] [Google Scholar]
- 6.Wong CY, Eftink MR. Biosynthetic incorporation of tryptophan analogues into staphylococcal nuclease: Effect of 5-hydroxytryptophan and 7-azatryptophan on structure and stability. Protein Sci. 1997;6:689–697. doi: 10.1002/pro.5560060318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wong CY, Eftink MR. Incorporation of tryptophan analogues into staphylococcal nuclease: Stability toward thermal and guanidine-hcl induced unfolding. Biochemistry. 1998;37:8947–8953. doi: 10.1021/bi971863g. [DOI] [PubMed] [Google Scholar]
- 8.Walkenhorst WF, Green SM, Roder H. Kinetic evidence for folding and unfolding intermediates in staphylococcal nuclease. Biochemistry. 1997;36:5795–5805. doi: 10.1021/bi9700476. [DOI] [PubMed] [Google Scholar]
- 9.Ye K, Jing G, Wang J. Interactions between subdomains in the partially folded state of staphylococcal nuclease. Biochim Biophys Acta. 2000;1479:123–134. doi: 10.1016/s0167-4838(00)00060-1. [DOI] [PubMed] [Google Scholar]
- 10.Maity H, Eftink MR. Perchlorate-induced conformational transition of staphylococcal nuclease: Evidence for an equilibrium unfolding intermediate. Arch Biochem Biophys. 2004;431:119–123. doi: 10.1016/j.abb.2004.07.023. [DOI] [PubMed] [Google Scholar]
- 11.Maki K, Cheng H, Dolgikh DA, Shastry MC, Roder H. Early events during folding of wild-type staphylococcal nuclease and a single-tryptophan variant studied by ultrarapid mixing. J Mol Biol. 2004;338:383–400. doi: 10.1016/j.jmb.2004.02.044. [DOI] [PubMed] [Google Scholar]
- 12.Ferreon AC, Bolen DW. Thermodynamics of denaturant-induced unfolding of a protein that exhibits variable two-state denaturation. Biochemistry. 2004;43:13357–13369. doi: 10.1021/bi048666j. [DOI] [PubMed] [Google Scholar]
- 13.Yang M, Liu D, Bolen DW. The peculiar nature of the guanidine hydrochloride-induced two-state denaturation of staphylococcal nuclease: A calorimetric study. Biochemistry. 1999;38:11216–11222. doi: 10.1021/bi9909400. [DOI] [PubMed] [Google Scholar]
- 14.Baskakov IV, Bolen DW. Monitoring the sizes of denatured ensembles of staphylococcal nuclease proteins: Implications regarding m values, intermediates, and thermodynamics. Biochemistry. 1998;37:18010–18017. doi: 10.1021/bi981849j. [DOI] [PubMed] [Google Scholar]
- 15.Dill KA, Shortle D. Denatured states of proteins. Annu Rev Biochem. 1991;60:795–825. doi: 10.1146/annurev.bi.60.070191.004051. [DOI] [PubMed] [Google Scholar]
- 16.Wrabl J, Shortle D. A model of the changes in denatured state structure underlying m value effects in staphylococcal nuclease. Nat Struct Biol. 1999;6:876–883. doi: 10.1038/12338. [DOI] [PubMed] [Google Scholar]
- 17.Carra JH, Privalov PL. Thermodynamics of denaturation of staphylococcal nuclease mutants: An intermediate state in protein folding. Faseb J. 1996;10:67–74. doi: 10.1096/fasebj.10.1.8566550. [DOI] [PubMed] [Google Scholar]
- 18.Carra JH, Anderson EA, Privalov PL. Thermodynamics of staphylococcal nuclease denaturation. I. The acid- denatured state. Protein Sci. 1994;3:944–951. doi: 10.1002/pro.5560030609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wooll JO, Wrabl JO, Hilser VJ. Ensemble modulation as an origin of denaturant-independent hydrogen exchange in proteins. J Mol Biol. 2000;301:247–256. doi: 10.1006/jmbi.2000.3889. [DOI] [PubMed] [Google Scholar]
- 20.Walkenhorst WF, Edwards JA, Markley JL, Roder H. Early formation of a beta hairpin during folding of staphylococcal nuclease h124l as detected by pulsed hydrogen exchange. Protein Sci. 2002;11:82–91. doi: 10.1110/ps.28202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hilser VJ, Freire E. Structure-based calculation of the equilibrium folding pathway of proteins. Correlation with hydrogen exchange protection factors. J Mol Biol. 1996;262:756–772. doi: 10.1006/jmbi.1996.0550. [DOI] [PubMed] [Google Scholar]
- 22.Alexandrescu AT, Abeygunawardana C, Shortle D. Structure and dynamics of a denatured 131-residue fragment of staphylococcal nuclease: A heteronuclear nmr study. Biochemistry. 1994;33:1063–1072. doi: 10.1021/bi00171a004. [DOI] [PubMed] [Google Scholar]
- 23.Wang Y, Shortle D. Residual helical and turn structure in the denatured state of staphylococcal nuclease: Analysis of peptide fragments. Fold Des. 1997;2:93–100. doi: 10.1016/S1359-0278(97)00013-8. [DOI] [PubMed] [Google Scholar]
- 24.Wallqvist A, Smythers GW, Covell DG. Identification of cooperative folding units in a set of native proteins. Protein Sci. 1997;6:1627–1642. doi: 10.1002/pro.5560060804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Loh SN, Prehoda KE, Wang J, Markley JL. Hydrogen exchange in unligated and ligated staphylococcal nuclease. Biochemistry. 1993;32:11022–11028. doi: 10.1021/bi00092a011. [DOI] [PubMed] [Google Scholar]
- 26.Wang Y, Shortle D. The equilibrium folding pathway of staphylococcal nuclease: Identification of the most stable chain-chain interactions by nmr and cd spectroscopy. Biochemistry. 1995;34:15895–15905. doi: 10.1021/bi00049a004. [DOI] [PubMed] [Google Scholar]
- 27.Yang F, Cheng Y, Peng J, Zhou J, Jing G. Probing the conformational state of a truncated staphylococcal nuclease r using time of flight mass spectrometry with limited proteolysis. Eur J Biochem. 2001;268:4227–4232. doi: 10.1046/j.1432-1327.2001.02337.x. [DOI] [PubMed] [Google Scholar]
- 28.Huang S, Zou X, Guo P, Zhong L, Peng J, Jing G. Probing the subtle conformational state of n138nd2-q106o hydrogen bonding deletion mutant (asn138asp) of staphylococcal nuclease using time of flight mass spectrometry with limited proteolysis. Arch Biochem Biophys. 2005;434:86–92. doi: 10.1016/j.abb.2004.10.011. [DOI] [PubMed] [Google Scholar]
- 29.Byrne MP, Manuel RL, Lowe LG, Stites WE. Energetic contribution of side chain hydrogen bonding to the stability of staphylococcal nuclease. Biochemistry. 1995;34:13949–13960. doi: 10.1021/bi00042a029. [DOI] [PubMed] [Google Scholar]
- 30.Schwehm JM, Stites WE. Application of automated methods for determination of protein conformational stability. Methods Enzymol. 1998;295:150–170. doi: 10.1016/s0076-6879(98)95039-x. [DOI] [PubMed] [Google Scholar]
- 31.Stites WE, Byrne MP, Aviv J, Kaplan M, Curtis PM. Instrumentation for automated determination of protein stability. Anal Biochem. 1995;227:112–122. doi: 10.1006/abio.1995.1259. [DOI] [PubMed] [Google Scholar]
- 32.Eftink MR. The use of fluorescence methods to monitor unfolding transitions in proteins. Biochemistry (Mosc) 1998;63:276–284. [PubMed] [Google Scholar]
- 33.Eftink MR. The use of fluorescence methods to monitor unfolding transitions in proteins. Biophys J. 1994;66:482–501. doi: 10.1016/s0006-3495(94)80799-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.