Structure and Energetics of Channel-Forming Protein–Polysaccharide Complexes Inferred via Computational Statistical Thermodynamics

Abstract

The ion channel protein α-hemolysin (αHL) forms supramolecular complexes with the polysaccharide β-cyclodextrin (βCD). This system has potential uses in nanoscale device engineering. It has been found recently that βCD formed longer- or shorter-lived complexes with some engineered αHL mutants then with a wild type protein (Gu et al. J. Gen. Physiol. 2001, 118, 481–493). However, how changes in the protein sequence affect complex lifetime was not completely understood in part due to the lack of knowledge of structures of these metastable complexes. In this paper, we present an extensive molecular modeling study of the βCD–αHL and selected mutant complexes to gain insights into the βCD–αHL interaction mechanisms and to predict possible structures and energetics of the complexes. Thermodynamic integration (TI) and umbrella sampling (US) techniques (with the weighted histogram analysis method (WHAM)) were used to calculate the relative binding affinities of the complexes formed with the wild type αHL and the M113N, M113E, M113A, and M113V mutants. Our results are in excellent agreement with experiment. While βCD–M113N and βCD–M113A complexes were stable in the configuration of the wild type complex, the equilibrium configuration of the βCD–M113V and βCD–M113E complexes was significantly different. In these cases, TI alone was insufficient to accurately calculate the corresponding free energy differences. By utilizing a TI/US combination in a novel manner, we were able to accurately calculate free energy changes in these flexible systems. The βCD–M113A and βCD–M113E complexes, which exhibited shorter lifetimes than other complexes in an experiment, in simulations exhibited greater flexibility and higher water solvation of the βCD adapter. MD simulations of the βCD–M113N complex with βCD in a downward orientation were also performed.

Introduction

Recent successes in miniaturizing electronic devices have made reaching a nanometer scale a realistic technological goal. Self-assembling supramolecular complexes may soon play an important role in such technologies. Biological macromolecules constitute one such class of nanoscale objects that are designed (as a result of evolution) to perform a variety of functions. Thus, using biomolecular building blocks for designing nanoscale devices has recently become an area of active investigation.^1–6 A fundamental molecular level understanding of the interactions that are responsible for the properties of such systems is not only a question of scientific curiosity but also a problem of technological necessity. Theoretical approaches such as molecular modeling techniques can provide insightful information on the nature of molecular interactions that lead to assembly and functioning of macromolecular complexes, which is often difficult to infer from experimental observations. As one example of utility and adequacy of computational approaches to study metastable bio-macromolecular assemblies, we present here a theoretical analysis of complexes formed by the cyclic polysaccharide β-cyclodextrin and the bacterial ion channel protein α-hemolysin and its mutants.

An α-hemolysin (αHL) protein, secreted by the bacteria Bacillus brevis, forms a water-filled pore in an otherwise hydrophobic cell membrane and facilitates transport of electrolyte ions in and out of a cell. The three-dimensional structure of αHL has been resolved via X-ray crystallography⁷ to reveal a mushroom-shaped heptameric protein complex with its transmembrane domain formed as a β-barrel (Figure 1a). Recently, αHL has become a target of protein engineering aiming at designing a variety of nanoscale devices. Some possible future applications of modified α-hemolysins include DNA sequencing,^8,9 heavy ion detection,^10–12 and sensing trace amounts of organic matter.^4,13,14 In the latter case, it was discovered that β-cyclodextrin (βCD), a heptameric cyclic polysaccharide, spontaneously lodges in the channel pore while preserving its well characterized ability to form host–guest complexes with small organic molecules.¹⁵ Gu et al.^16–18 proposed building a molecular-sized single molecule sensor based on the βCD–αHL complex. Ion current measured when a guest complex occupies (blocks) the αHL channel pore was found to be highly sensitive to the nature of the blocker. Further mutagenesis studies have been performed to understand the mechanism of βCD binding within the protein pore and to engineer systems with the prolonged complex lifetimes. On the basis of indirect experimental evidence that βCD binds (non-covalently) in the vicinity of Met113 of the αHL protein (supported also by our recent MD simulation study¹⁹), Bayley and co-workers²⁰ studied a series of M113X mutants (X represents here any naturally occurring amino acid). Some of the observed βCD–M113X complex lifetimes were longer than the lifetime of the wild type βCD–αHL complex. However, it remained unclear why certain αHL mutants formed longer-lived complexes while others did not. For example, asparagine (M113N) and valine (M113V) substitution both prolonged complex lifetime, while the alanine (M113A) and glutamate (M113E) mutants resulted in a shorter-lived complex. While it is easy to rationalize the complex-forming behavior of the M113N mutant, with Asn being a polar residue that may form hydrogen bonds with the βCD hydroxyl side groups, both Val and Ala have small nonpolar side chains for which direct interaction with βCD is not expected. To understand in detail the βCD–αHL complex binding mechanism and its dependence on the nature of a residue at position 113, we performed molecular modeling (MM) of the Met113 (wild type), M113N, M113V, M113A, and M113E complexes with the βCD polysaccharide molecule and calculated their relative binding affinities which can be directly compared with experimentally measured complex lifetimes.²⁰ Our results compare well with the experimental observations. Further analysis of the resulting complex structures allowed us to provide a rationale for the observed behavior of these complexes and reveal subtleties of intermolecular interactions that result in complex formation or prevent it.

Figure 1.

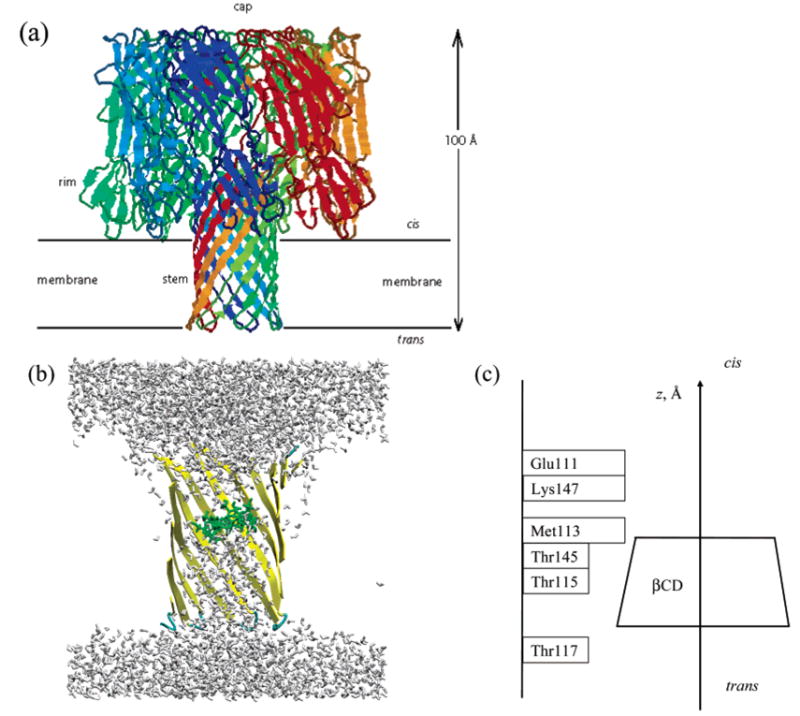
(a) α-Hemolysin structure. Different colors are used for the peptide monomers. A probable position and orientation of a membrane is indicated. (b) The initial model structure for the α-hemolysin–β-cyclodextrin (αHL–βCD) complex in water solvent. βCD is shown in green; water atoms are shown in gray; the backbone (yellow) is shown in ribbon representation; and side chains, model membrane, dummy atoms, and counterions are not displayed. (c) A schematic diagram of the stem domain of αHL with βCD inside the pore. Residues Met113, Lys147, and Glu111 form a constriction impermeable for βCD. The z-axis is shown as it is referred to elsewhere in the paper.

In biomolecular simulations, thermodynamic integration (TI) is the most widely employed technique for calculating the free energy differences, for example, a change in binding affinities upon a point mutation or introduction of a different ligand. This technique is particularly useful when a chemical transformation is involved. However, when chemical transformation involves subsequent configurational reorganization of reacting species, for example, diffusion along a reaction coordinate, TI alone is no longer adequate. We discovered that in such cases, a combination of TI with a sampling enhancing technique is needed to adequately estimate free energy changes. Similar approaches have been previously reported albeit not in bio-molecular simulations.^21,22 One such sampling enhancing technique, umbrella sampling (US),²³ is widely used in simulations of small flexible chemical systems to compute a potential of mean force (PMF),²⁴ a free energy of a system with a given configuration of reactants.²⁵ In combination with the weighted histogram analysis method (WHAM),^26,27 this approach becomes useful for estimating the unbiased density distribution function and minimizing statistical error even in such large biomolecular systems as the one presented here. US/WHAM has recently became practically applicable in biomolecular simulations.^28–30 In the present work, we use the standard TI and the combined TI/US/WHAM methodology to examine the relative binding affinities in βCD–αHL complexes. One important result of this paper is to demonstrate a feasibility of the TI/US/WHAM technique for relatively large and weakly bound supramolecular assemblies. This technique may also prove useful for calculating differences in the binding affinities of ligands in proteins, in cases where the conformational changes or diffusional reconfiguration of a ligand and a protein may not be adequately described by TI alone.

This article is organized as follows: modeled systems are described in the Models and Methods section. Protocols of molecular dynamics simulations and free energy calculations via the TI and TI/US/WHAM techniques are also presented in this section. The Results and Discussion sections present the results of our calculations, comparison with experimental data, discussion of the behavior of different βCD–αHL complexes, and analysis of methods performance. The Conclusions section summarizes the major results.

Models and Methods

The simulated system consisted of a β-cyclodextrin (βCD) bound to a truncated α-hemolysin (αHL) channel (Figure 1a), which was placed in a model membrane and solvated in TIP3P water such that the solvent formed 10 Å thick layers above and below the membrane (as shown in Figure 1b). The details of our model system setup for molecular dynamics (MD) simulations have been previously described by Shilov et al.¹⁹ For each protein mutant, two independent systems were constructed: one containing βCD inside the αHL pore and one without βCD. The initial structure of the βCD–αHL complex was taken from ref 19, as shown in Figure 1b. The model protein structure consisted of the 230 residues. A lipid bilayer was represented via a simple model layer formed out of 1215 heavy (100 amu) hydrophobic dummy particles (interacting via the Lennard-Jones potential). The parameters of these particles were reported elsewhere.¹⁹ To ensure charge neutrality of the simulated system, seven Na⁺ counterions were added. The overall size of the resulting system was 78 × 67 × 78 ų. To prevent the system from diffusing during the simulation, weak position restraints were applied in all simulations to the protein backbone atoms (k = 0.5 kcal/mol/Å). These restraints did not alter the dynamics of the protein backbone, which in the case of the β-barrel pore protein is known to be fairly rigid (see, e.g., refs ³¹ and ³²). Dummy atoms and counterions were restrained with the harmonic force with the strength of k = 200 kcal/mol/Å. All water molecules were free to move.

Model systems with no βCD were constructed by removing the ligand and performing NPT ensemble MD simulations to re-equilibrate the density of the system. In NPT MD, the pressure was kept constant via coupling to a 1 atm hydrostatic bath.³³ After the equilibration period, the simulation was performed with constant volume using a time step of 2 fs. Bonds to hydrogen atoms were constrained via the SHAKE algorithm.³⁴

All MD simulations were performed using the Sander module of the AMBER 7 package.³⁵ Trajectories were collected every 0.5 ps. Temperature was controlled using the Berendsen thermostat.³³ Constant temperature simulations were performed at 300 K. A nonbonded forces cutoff of 12 Å was used in all cases, and the long-range nonbonded forces were evaluated via particle mesh Ewald as implemented in AMBER 7. Force-field parameters for β-cyclodextrin were previously developed and reported in ref 19; the Cornell et al. force field³⁶ was used otherwise.

Calculation of Relative Binding Energies

Predictions of the relative binding free energy, ΔΔG_binding = ΔG_mut − ΔG_wt, where ΔG_wt is the binding free energy of a complex formed by the αHL protein and βCD and ΔG_mut is the binding free energy of a complex formed by the M113X mutant and the βCD adapter, were based on the thermodynamic cycle shown in Figure 2. In the figure, ΔG_A denotes a change in the free energy for mutating the methionine residue to a valine or an asparagine in the βCD–αHL complex. Likewise, ΔG_B is the free energy change corresponding to the αHL → M113X mutations in the free αHL channel (empty of βCD). The simulations were carried out using the TI protocol described in detail below. ΔΔG_binding was then computed as ΔΔG_binding = ΔG_A − ΔG_B. Thus, computed ΔΔG_bind represents the effect of the mutation on the free energy of a complex formation.

Figure 2.

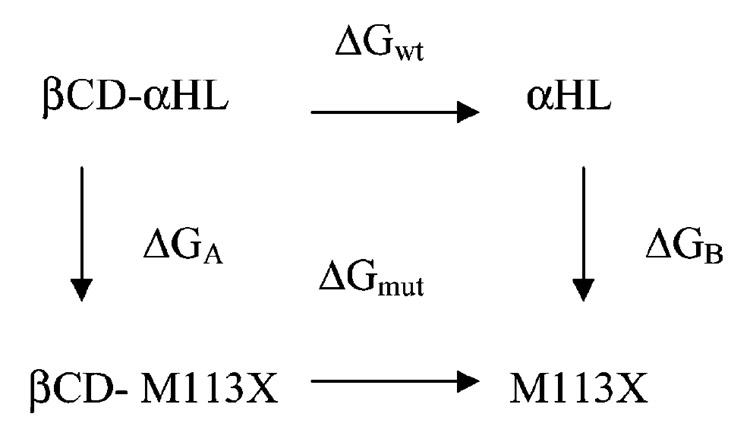
Thermodynamic cycle utilized in the free energy calculations to determine the relative binding affinities between βCD and the mutated α-HL channel. M113X stands for either M113V, M113E, M113A, or M113N mutants.

MD Thermodynamic Integration

TI calculations were performed to evaluate free energy change, ΔG, upon conversion of the wild type αHL protein to the M113V, M113E, M113A, or M113N mutant. The calculations were performed according to the following equation

$$\mathrm{\Delta }G={\int }_0^1\text{d}\lambda \langle \frac{\partial E}{\partial \lambda }\rangle$$ (1)

where E is the potential energy of a system. The mixing parameter, λ, is used to interpolate between “unperturbed”, in this case the wild type protein, and “perturbed”, in this case a M113X mutant (X is used for either V, E, A, or N). Mutants M113X were constructed using the Leap program (a part of the AMBER package). In each simulation, a system was minimized for 500 steps, and then, a 0.4 ns equilibration MD simulation was performed. The forward αHL → M113X mutations were carried out for the 12 λ points spaced between λ = 0 and λ = 1 according to the Gaussian quadrature scheme to approximate the integral in eq 1. All TI simulations were done using the AMBER 7 Sander module in which TI is implemented (see the AMBER manual and references therein for details). At the end of the forward simulations (λ = 0 to λ = 1), an additional 0.2 ns of equilibration was performed; all simulations were also carried out in the reverse (λ = 1 to λ = 0) direction. In Figure 3, a calculated 〈∂E/∂λ〉 is shown as a function of the perturbation parameter, λ, for the forward and reverse simulations of the βCD–αHL → βCD–M113N mutation. Figure 3 is representative of all TI simulations performed in this work. Relatively high errors occurred for small values of λ, when perturbations were significant. Note that starting at λ = 0.437 the convergence of the forward and reverse perturbation is very good. The overall integral difference between forward and reverse mutations did not exceed 10%. Forward and reverse simulation results were averaged to reduce net error. MD-TI simulations were carried out using a 1 or 0.5 fs time step. The equilibration period varied from 100 to 300 ps, and data were collected from a 1 ns trajectory. After completing the TI simulation procedure, further extensive equilibrium MD simulations of the βCD–M113V, M113A, and βCD–M113N, M113E, complexes (λ = 1) were carried out for 2 and 1 ns, respectively.

Figure 3.

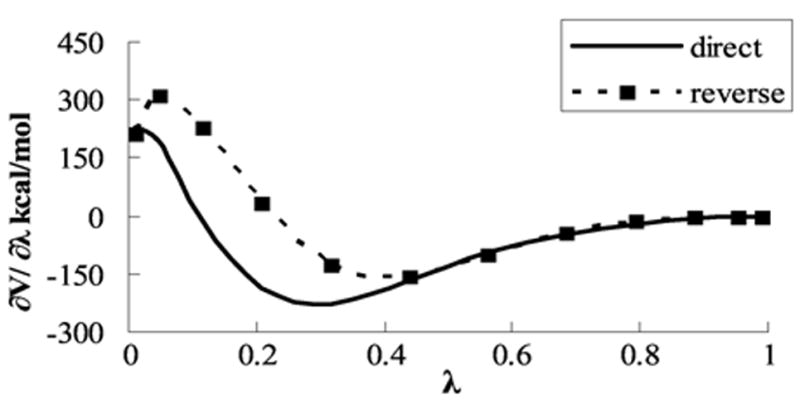
Calculated free energy differences as a function of the perturbation parameter, λ. The state with λ = 0 corresponds to βCD–αHL, and λ = 1 represents the βCD–M113N complex (direct TI).

MD Umbrella Sampling Simulations

To evaluate the potential of mean force (PMF) for both the βCD–M113V and βCD–M113E complexes, we used umbrella sampling molecular dynamics^25,37–39 with the weighted histogram analysis method (US/WHAM)²⁶ implemented in the WHAM program.⁴⁰ These simulations were initiated from the structure formed after approaching the final stage in the thermodynamic perturbation simulations for the forward mutation of βCD–αHL to βCD–M113V and βCD–αHL to βCD–M113E described in the previous section. For both mutants, the subsequent MD simulation (2 and 1 ns, respectively) resulted in a rapid diffusion of βCD away from its initial position at the 113 residue. However, calculating a free energy change via TI in this case is impractical. Instead, we used the spontaneous βCD trajectory from its initial configuration to the final configuration to define a reaction coordinate, r, for the subsequent US simulation. In US, a system is constrained to a narrow range of reaction coordinates by applying a quadratic biasing potential

$$V(r)=\frac{1}{2}k{(r–r_0)}^2$$ (2)

where k is a constant and r₀ is a position along the reaction coordinate, r. In the case of a M113V mutant to cover the range of interest of r₀ = 41.7–47.12 Å along the channel axes (see Figure 1c), seven umbrella windows with a step from 0.5 to 1 Å were used. An equilibrium MD simulation was performed for each window. To construct V(r), harmonic constraints were applied to the βCD backbone atoms. The choice of constraints was window dependent to ensure adequate sampling of the reaction coordinate. For the first window (r₀ = 41.7 Å), the positions of all βCD backbone atoms were constrained with the force constant k = 0.5 kcal/mol/Ų to force the ligand to remain in the initial configuration (and specific orientation) (see the Results and Discussion section for the rationale of our choices). In all other windows, V(r) was applied with a force constant of k = 2.0 kcal/mol/Ų to the two βCD atoms located at the opposite sides of the heptamer ring, one on the wide rim and the other one on the narrow rim. To create several biasing windows close to the top of the energy barrier, harmonic constraints were placed at three or four βCD atoms. For each window, 200 ps equilibration MD was followed by 400 ps of data collection. In all US simulations, the coordinates of the protein and the ligand were stored every 10 fs. To calculate the PMF from the US simulations, data from all simulation windows were combined. Upon completion of all simulations, we used WHAM^26,27 to eliminate contribution to the calculated energy due to the restraining potential. In this method, an optimal estimate of the unbiased distribution function is found as a weighted sum calculated using data extracted from all windows and determines the functional form of the weight factors that minimizes statistical error.

To estimate uncertainties in the free energy values calculated from the TI simulations, an average free energy value was calculated along each MD trajectory. The largest deviation from a value obtained by averaging free energy estimates in the direct and reverse simulations is reported as an uncertainty of the simulation. Uncertainties for the US method have been estimated as the largest deviation from a value obtained by averaging free energy estimates in the simulations.

Results

Energetics of Mutated Complexes

One major goal of the present study was to theoretically predict the relative stability of four M113X mutant complexes with the βCD adapter bound in the channel lumen with respect to the αHL–βCD complex. The summary of these calculations and the experimentally deduced relative binding energies are given in Table 1.

TABLE 1.

Experimental²⁰ and Calculated Free Energy Differences (in kcal/mol)

				ΔΔGbinding
mutant	ΔGexp	ΔΔGTI	ΔGUS	experiment	calculateda
WT	−3.35 ± 0.4
M113V	−7.50b ± 0.8	38.9 ± 3.1	−41.40 ± 1.5	−4.15 ± 0.9	−2.4 ± 3.4
M113N	−9.30b ± 4.3	−5.5 ± 1.1		−5.95 ± 4.3	−5.5 ± 1.1
M113A	−3.32b ± 0.3	3.4c ± 0.7		0.03 ± 0.5	1.0 ± 3.5
M113E	−2.59b ± 0.4	5.7 ± 1.1	−1.0 ± 0.2	0.76 ± 0.6	4.7 ± 1.1

^aΔΔG_binding = ΔΔG_TI + ΔG_US (see text).

^bThese experimental measurements correspond to ΔG_mut (as defined in the text and shown in Figure 2).

^cCalculated ΔΔG_TI corresponds to the mutation from M113V to M113A.

βCD–M113N and βCD–M113A Complexes

We performed the mutation of the methionine 113 to asparagine or methionine 113 to alanine using TI MD as described in the Models and Methods section. Free energy changes, ΔG_A and ΔG_B, corresponding to mutations of βCD–αHL → βCD–M113N and αHL → M113N or βCD–αHL → βCD–M113A and αHL → M113A, respectively, were calculated according to eq 1 (see the Models and Methods section for details). The resulting affinity change, ΔΔG_binding, was calculated as ΔΔG_binding = ΔG_A − ΔG_B according to the thermodynamic cycle shown in Figure 2. Thus, the calculated ΔΔG_binding values for both mutants are in good agreement with the experimentally determined values also reported in Table 1.

Next, we carried out a 1 and 2 ns equilibrium MD simulation of the βCD–M113N and βCD–M113NA complexes, respectively, to allow the structure of the mutant complex to relax fully. The starting conformation for this simulation corresponded to conformations of βCD–M113N and βCD–M113A at the end of the TI simulation (λ = 1). Both complexes were stable during these equilibrium MD simulations, and no significant changes in ligand conformation were observed. Thus, in this case, the TI simulation was sufficient to fully account for the free energy differences between the wild type αHL and its M113N or M113A mutants. Apparent stabilization of the M113N–βCD complex and destabilization of the M113A–βCD complex with respect to the αHL–βCD complex can be partially understood by looking into protein–βCD interatomic interactions. These will be discussed in further sections. By comparison with the simulations of the M113V and M113E mutants described below, the M113N and M113A mutants present a simpler and easier modeled case.

βCD–M113V and βCD–M113E Complexes

ΔΔG_TI free energy differences for the M113V and M113E mutant complexes calculated using the procedure as described for the M113N and M113A complexes above are given in Table 1. For the M113V mutant, this difference is quite large and positive, indicating that the mutation should reduce the affinity of βCD to the protein. At the end of the TI procedure, βCD appeared to interact more favorably with the wild type Met than with Val at position 113. The configuration of the αHL–βCD complex is shown in Figure 4a, and the M113V–βCD complex configuration at the end of the TI simulation is shown in Figure 4b. During the additional 2 ns equilibrium MD simulation of the complex with the M113V mutant, βCD moved further into the channel and away from V113. In this simulation, βCD assumed a new equilibrium position in the channel after approximately 0.5 ns. A snapshot of a complex after 2 ns of simulation is shown in Figure 4c with βCD in the new equilibrium position. However, calculated ΔΔG_TI did not reflect this significant configurational rearrangement.

Figure 4.

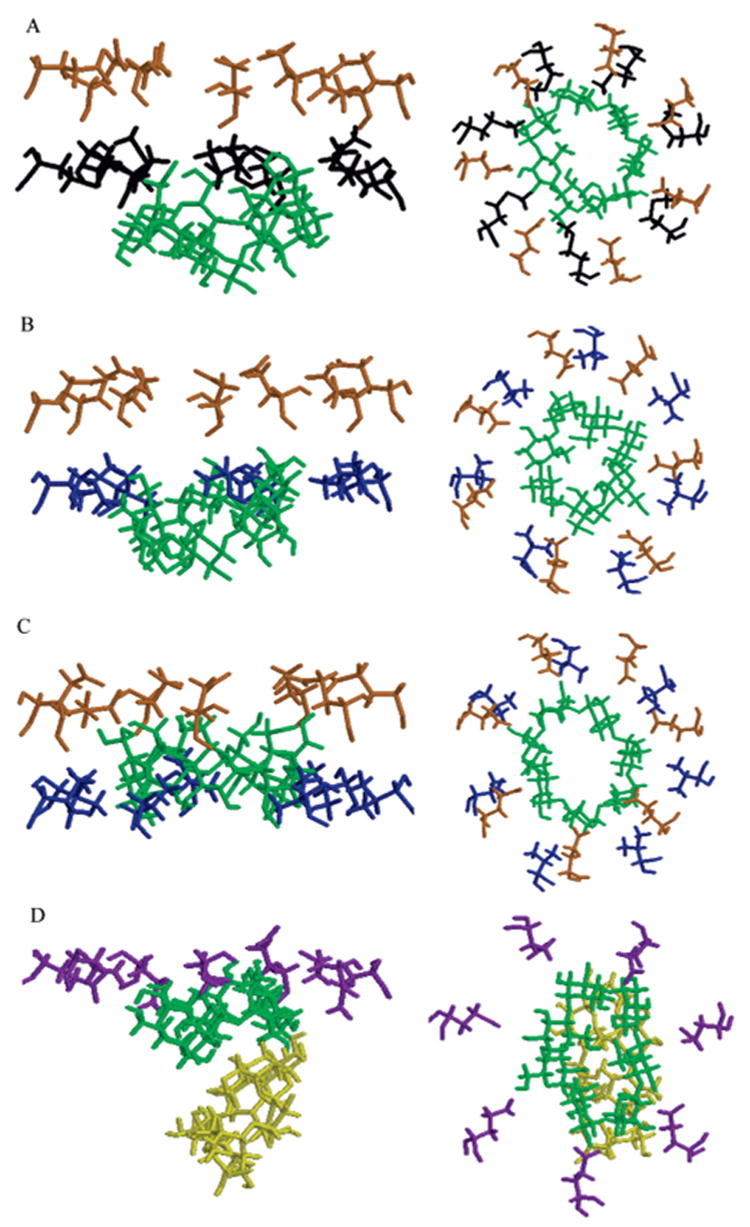
Fragments of the βCD–M113X complex structure from the MD simulations of the wild type (A), βCD–M113V mutated complex at the end of TI (B), and after further extensive equilibrium MD simulation (C); M113 is shown in black, V113 is shown in blue, E111 is shown in orange, and βCD is shown in green. The βCD–M113E mutated complex after TI and additional MD simulations (D); E113 is shown in purple; βCD after TI is shown in green, and βCD after further 1 ns MD simulation is shown in dark yellow. The rest of the protein, water molecules, and dummy atoms are not displayed. In the left panels, the z-axis is oriented as in Figure 1c; in the right panels, the z-axis is oriented normal to the paper toward the reader; that is, the top view of the channel from the cis side of the membrane (Figure 1a) is shown.

The M113E mutation reduced the affinity of βCD to the protein.²⁰ In our simulations, after the M113E mutation had been performed, βCD diffused away from the 113E site during the first 30 ps of the MD simulation. A new equilibrium position of βCD in the channel is shown in Figure 4d, and the initial configuration of the wild type βCD–αHL complex is shown for comparison (Figure 4a). Configurational rearrangement of the complexes during MD simulations after the TI procedure had no additional effect on the ΔΔG_TI of mutation estimated by the TI procedure along the chosen reaction coordinate.

We attribute this problem to the fact that due to the rapid diffusion of the βCD along the reaction coordinate toward the new energy minimum configurations with higher energies were not properly sampled. While a significantly longer simulation may help to ensure adequate sampling of the reaction coordinate, it is clearly impractical for a system of this size.

Various sampling enhancing techniques have been developed^22,30 with umbrella sampling (US) pioneering most of these. In this technique, reactants are moved along a predefined reaction coordinate in an adiabatic fashion, which is ensured by a set of biasing potentials during an MD simulation (see Models and Methods for details of our implementation). The potential of mean force (PMF), which corresponds to a free energy change, ΔG, along a reaction coordinate, can then be calculated using data from such simulations. We used US to calculate ΔG of the βCD diffusion to a new equilibrium position in the channel following the TI mutation simulation. The vectors connecting the βCD atoms in the initial and final states of the system were chosen to be the reaction coordinate. In an approximate manner, this transition can be characterized by a one-dimensional reaction coordinate, r, coaxial with the channel.

ΔG_US was then obtained via the WHAM procedure (see Models and Methods for details). In Figure 5a, calculated ΔG_US is plotted as a function of r for the M113V mutant complex. The minimum of ΔG_US is −41.4 kcal/mol at r = 47.12 Å, while the maximum is at the initial configuration, which corresponds to the βCD–M113V complex at the configuration of the βCD–αHL complex. The complete calculated path of a transformation of the βCD–αHL complex into the βCD–M113V complex can thus be described as a two-step process in which a mutation of the protein is performed initially (corresponds to the uphill energy change) followed by a diffusional reorganization of the complex toward the final equilibrium configuration (corresponds to the downhill energy change). This process is shown as an energy diagram in Figure 5b. The overall ΔΔG_binding can thus be calculated as ΔΔG_binding = ΔΔG_TI + ΔG_US. As seen in Table 1, the total ΔΔG_binding of βCD with αHL and M113V mutant is negative favoring the complex with the mutant and compares well with the experimentally determined ΔΔG value.

Figure 5.

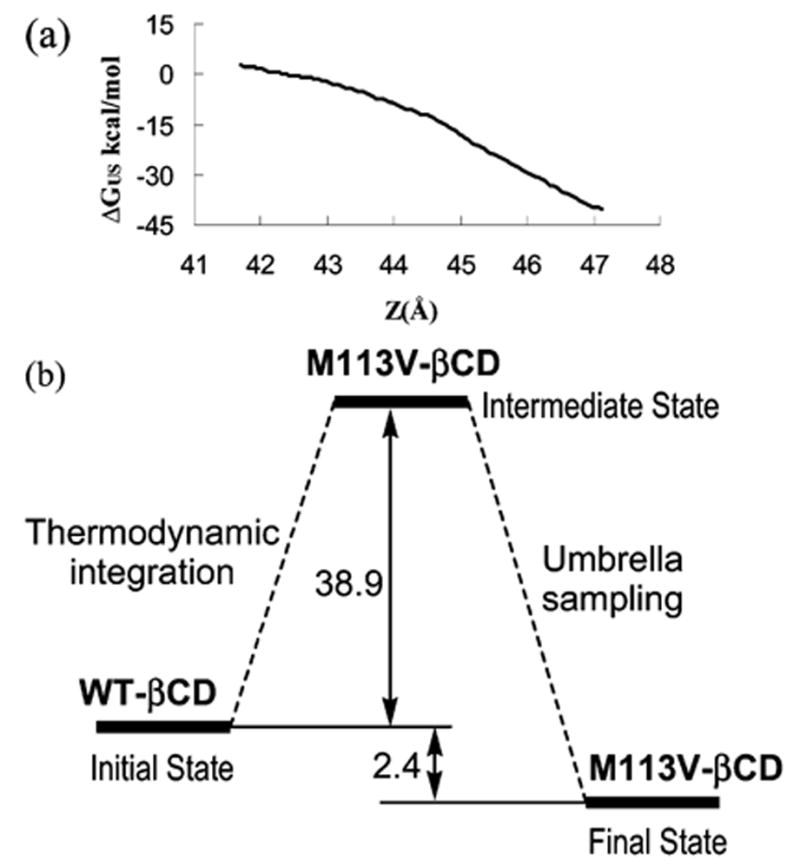
(a) Calculated PMF ΔG_US profile along the reaction coordinate, r, for the βCD–M113V system. (b) A complete schematic energy diagram for perturbation of βCD–αHL to βCD–M113V. Note that the transformation WT → M113V performed via TI proceeds uphill in free energy landscape, while the βCD diffusion assessed via US is a downhill energetic process.

Uncertainty in calculated ΔG_TI and ΔG_US is due to statistical uncertainty (sampling error) and the usual MD simulation deficiencies, such as inadequate parametrization of the force field, inadequate force field, accumulation of integration errors during the long simulations, and boundary condition errors. Statistical error can be reduced somewhat by performing longer simulations and varying the parameters and conditions of simulations. For the purpose of this work, however, the quality of our results is good.

A mechanism by which Val113 or Glu113 provokes adapter–protein reconfiguration can be rationalized by comparing local interactions (such as hydrogen bonds and interaction energy with nearest protein side chains) of βCD with the protein in the initial position near site 113 and in its final position (see the subsection “Analysis of Molecular Mechanisms of Complex Formation” for further discussion).

M113N–βCD Complex with the Downward Adapter Orientation

βCD has the shape of a truncated cone. In all simulations reported above, βCD was oriented with its narrow rim toward the cis side of the channel; see Figure 1a (the upward orientation). In our previous study of the αHL–βCD complex,¹⁹ the structure with an upward orientation of βCD had a slightly lower total energy, indicating that this orientation of the adapter is preferable energetically. However, no direct estimate of relative binding affinities has been made. Considering that protein mutants may have a different preference to the orientation of an adapter, we performed additional equilibrium MD simulations of the βCD–M113N complex with a downward orientation of βCD. The initial position of βCD inside the channel was chosen to be 2 Å below the N113 site. The initial structure of the simulated system is shown in Figure 6a. The “downward” oriented βCD molecule was allowed to move freely inside the mutant pore in the course of the 2.5 ns MD simulation. The system relaxed to an equilibrium configuration after approximately 0.5 ns. During the last 2 ns of the simulation, the system was stable with no apparent diffusion of βCD in the channel. The equilibrium position of the downward oriented βCD in the M113N channel is shown in Figure 6b. Thus, the simulation resulted in an equilibrium location of the downward oriented βCD in the vicinity of M113N residues. The total energy of the complex with βCD in the downward orientation was somewhat lower than the total MD energy of the complex with βCD in the upward orientation. In our earlier work, a wild type αHL complex with an upward orientation of βCD had a lower total MD energy.¹⁹ Thus, our simulations indicate that the residence time of upward and downward oriented βCD inside the channel may be sensitive to the methionine → asparagine mutation, and the binding affinity of the downward oriented βCD to the M113N mutant may be higher than that for the upward oriented βCD. The lower energy of the system with the downward orientation of βCD is probably due to the better geometric fit of protein Asn groups and βCD hydroxyl groups of the wider rim of the polysaccharide ring. An analysis of protein polysaccharide hydrogen bonds and direct free energy difference calculations is needed to better understand this result.

Figure 6.

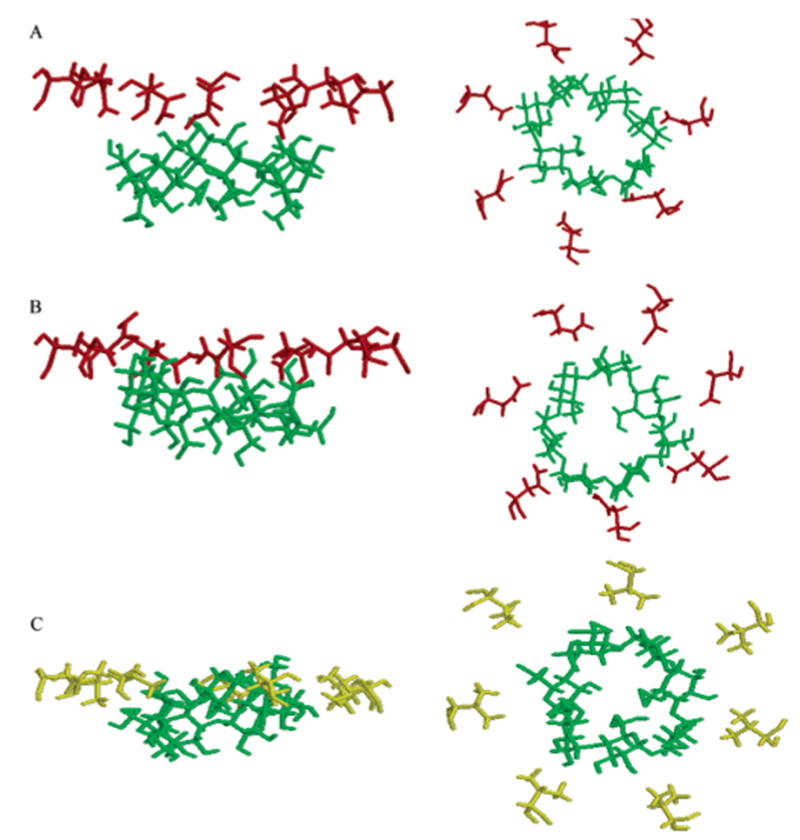
Fragments of the βCD–M113N and βCD–M113A complexes: (A) initial position of the downward oriented βCD in βCD–M113N; (B) after the 2 ns equilibrium MD simulation of βCD–M113N; (C) after the 2 ns equilibrium MD simulation of βCD–M113A. The M113N residues (red), M113E (yellow), and βCD (green) are shown as the stick model. Protein, water molecules, and dummy atoms are not displayed. The z-axis scale is the same as that in Figure 1a,b.

Discussion

Analysis of Molecular Mechanisms of Complex Formation

We looked into mechanisms of protein βCD interaction in all the complexes studied. First, hydrogen-bond formation between a M113X protein and βCD was analyzed. A hydrogen bond was defined as a donor–hydrogen-acceptor assembly in which all of the following geometric criteria were satisfied: the donor–acceptor distance d < 3.6 Å, the hydrogen-acceptor distance r < 2.6 Å, and the donor–hydrogen-acceptor angle 90° < Θ < 180°.⁴¹ Shown in Figure 7 is the typical behavior of a distance and an angle between a potential hydrogen-bond donor atom and a potential acceptor atom as functions of time. As seen in Figure 7, both a distance and an angle may significantly fluctuate in the course of the MD. We considered a particular hydrogen bond to be stable if the geometric criteria described above have been satisfied for 90% of the trajectory duration (1 ns).

Figure 7.

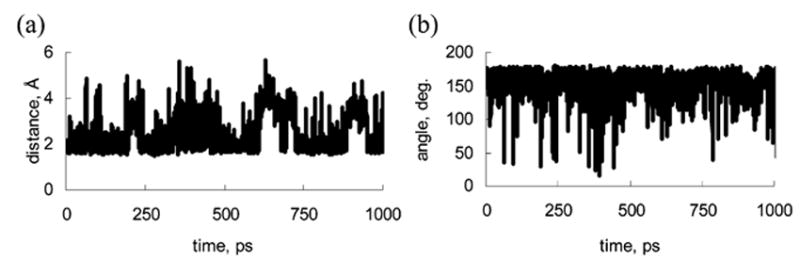
(a) Distance between βCD HO6 and Glu169 OE1 oxygen. (b) Angle between O6–HO6···OE1. The names of the βCD atoms are the same as those in our previous work¹⁹ (see appendix Figure 1A in ref. 19).

Second, we analyzed the interaction energy between βCD ligand and protein residues in its vicinity. Interaction energy was calculated as the time average of the sum of Coulombic and Lennard-Jones (van der Waals) interactions between all atoms of corresponding residues and βCD (see ref 19 for details). In the WT α-hemolysin, the residues responsible for 85% of the total interaction energy between βCD and αHL were shown to be Glu111, Met113, Thr115, Thr145, and Lys147.¹⁹ The relative location of these residues in the channel pore is shown in Figure 1c. Table 2 summarizes contributions to the protein–adapter interaction energy from several amino acid residues for (a) βCD–αHL, (b) βCD–M113V, (c) βCD–M113N, (d) βCD–M113A, and (e) βCD–M113E complexes. Note that the relative values of the total interaction energy for all complexes (Table 2) correlate well with the relative length of the experimentally observed complex lifetimes and are indicative of the predicted relative ΔΔG_binding discussed above. Namely, complexes with the lower absolute total interaction energy were relatively shorter-lived and vice versa. In view of the above observation, we find it instructive to look in detail at local interactions of βCD with different mutants and water in order to better understand the mechanistic implications of protein structure on complex formation.

TABLE 2.

Interaction Energy of βCD, E_int, with Residues of αHL and Its Mutants Averaged over MD Trajectories (van der Waals, E_vdw, and Electrostatic, E_ele, Contributions to the Energy Are Also Shown; E_int = E_vdw + E_ele Reported is the Average Value ± Standard Deviation in kcal/mol)^a

(a) βCD–αHLa
residue	Evdw	Eele	Eint
Glu111	−0.9 ± 0.1	1.9 ± 6.2	1.0 ± 6.2
Met113	−21.0 ± 2.0	−2.8 ± 2.0	−23.8 ± 2.8
Thr115	−12.3 ± 1.4	−1.6 ± 3.3	−13.9 ± 3.2
Thr145	−17.1 ± 1.7	−6.9 ± 3.4	−24.0 ± 3.3
Lys147	−3.0 ± 0.5	−4.0 ± 7.3	−7.0 ± 7.2
total	−54.3 ± 2.9	−13.5 ± 6.3	−67.8 ± 6.9
(b) βCD–M113V (final configuration)
residue	Evdw	Eele	Eint
Glu111	−6.8 ± 2.4	−40.6 ± 15.5	−47.4 ± 15.3
Met113	−17.4 ± 1.4	−1.1 ± 0.6	−18.5 ± 1.5
Thr115	−1.5 ± 0.3	0.9 ± 0.7	−0.6 ± 0.9
Thr145	−9.8 ± 1.0	−1.6 ± 1.0	−11.4 ± 1.4
Lys147	−28.0 ± 2.7	4.3 ± 10.7	−23.7 ± 9.8
total	−63.5 ± 3.8	−38.0 ± 9.6	−101.5 ± 10.2
(c) βCD–M113N
residue	Evdw	Eele	Eint
Glu111	−1.5 ± 1.5	5.5 ± 8	4.0 ± 8
Met113	−17.1 ± 1.8	−12.8 ± 4.5	−29.9 ± 4.4
Thr115	−12.3 ± 1.0	−2.8 ± 2.8	−15.1 ± 2.8
Thr145	−17.1 ± 1.3	−3.8 ± 2.5	−20.9 ± 2.6
Lys147	−5.0 ± 0.9	−12.6 ± 12.3	−17.6 ± 12.6
total	−52.9 ± 2.3	−26.5 ± 8.2	−79.4 ± 8.2
(d) βCD–M113A
residue	Evdw	Eele	Eint
Glu111	−1.0 ± 0.3	0.98 ± 6.6	−0.05 ± 6.6
Ala113	−1.0 ± 0.3	0.50 ± 0.3	−4.3 ± 1.0
Thr115	−12.6 ± 1.3	−3.2 ± 2.6	−15.8 ± 2.9
Thr145	−16.7 ± 2.2	−6.6 ± 3.6	−23.3 ± 4.3
Lys147	−4.1 ± 1.2	−5.7 ± 10.7	−9.7 ± 11.2
total	−39.3 ± 3.5	−14.0 ± 7.4	−53.3 ± 9.2
(e) βCD–M113E
residue	Evdw	Eele	Eint
Thr117	−12.3 ± 1.3	−2.7 ± 2.7	−14.9 ± 3.0
Glu113	−1.4 ± 0.7	−6.4 ± 8.0	−7.7 ± 8.0
Thr115	−6.4 ± 1.6	−1.4 ± 2.1	−7.7 ± 2.8
Thr145	−2.3 ± 0.9	−0.1 ± 1.0	−2.4 ± 1.5
Lys147	−0.2 ± 0.7	4.0 ± 3.7	3.8 ± 3.7
total	−22.3 ± 3.4	−6.4 ± 7.7	−28.9 ± 6.6

^aData are calculated on the basis of the MD trajectory in this work. They compare well with our previous work.¹⁹

Wild Type αHL

In the wild type αHL, only one stable direct hydrogen bond was observed between βCD and the Met113 side chain.¹⁹ A lack of a direct electrostatic interaction between Met residues and βCD is somewhat compensated by strong van der Waals interactions, as was shown in our previous study¹⁹ and presented in Table 2a. Several hydrogen bonds between βCD and five Thr145 and two Thr115 amino acid residues were formed. Hydrogen bonds are formed with O2, O3, or O6 βCD atoms as donors and OG1 atoms of the threonine residues as acceptors. Apparently O–H_βCD···OG1_Thr hydrogen bonds contribute significantly to the βCD stabilization.

M113V

Val at position 113 prolongs complex lifetime by facilitating diffusion of a largely desolvated βCD deeper into the channel lumen. By comparison, in the wild type αHL, the methionine side chains, which are bulkier than valine, block the βCD path. At the final configuration (Figure 4c), βCD formed a strong hydrogen-bond network with three (out of seven) glutamate residues (Glu111), which resulted in a stable βCD–M113V complex (Figure 8). Formation of hydrogen bonds in this case is also manifested in a strong electrostatic contribution of the Glu111 residues to the interaction energy (see Table 2b). In this case, βCD acts as an O–H donor and carboxylate oxygens of the glutamate residues are acceptors. The movement of βCD in the channel is strongly correlated with the dynamics of the Glu111 residues of protein chains A, B, and F as the distances between the ligand and the three residues remain nearly constant during the simulation. The hydrogen-bond network seems to be well maintained in the simulation, with these three residues remaining in a stable conformation. Additional stabilization of βCD in the channel at this position is facilitated by favorable packing against Lys147 and Val113 residues which resulted in significant van der Waals attraction (Table 2b).

Figure 8.

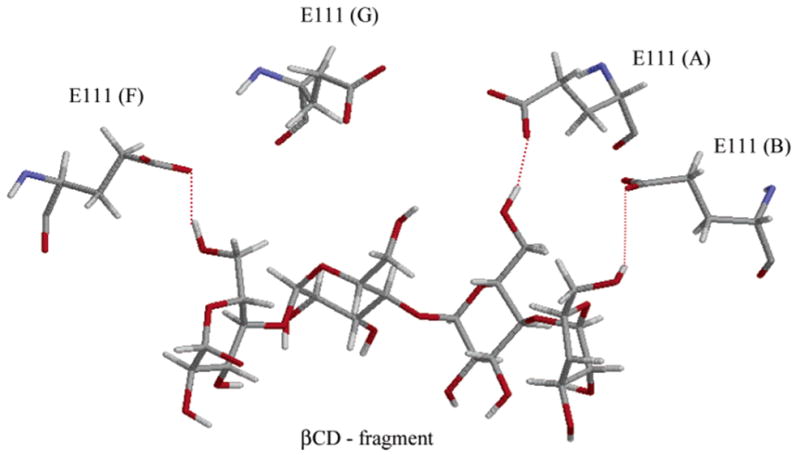
Fragment of a hydrogen-bond network formed by βCD with the E111s of four protein chains (A, B, E, and F). Dotted lines indicate HO6_βCD···OE2 E111 hydrogen bonds.

The energy barrier shown in Figure 5b corresponds to the βCD position near site 113, in which it cannot establish hydrogen bonds with the side chains of the nonpolar valine residue. At the same time, Val is bulky enough to prevent water molecules from providing adequate solvation of the adapter, thus effectively forming a hydrophobic environment near βCD. When βCD diffuses further into the channel, a new free energy minimum is located in the vicinity of the glutamate residues at position 111 with which βCD can form multiple favorable hydrogen bonds.

M113N

The prolonged βCD–M113N complex lifetime can be attributed to an ability of the asparagine residue to stabilize the adapter via hydrogen bonding. In MD simulations, the hydrogen-bond network with βCD was formed in the first 250 ps of the simulation and was stable during the subsequent 1 ns. Electrostatic interactions between βCD hydroxyl groups and polar atoms of asparagine (see Table 2c) result in multiple close contacts between the ligand and the mutated αHL. The side chain of an asparagine residue is polar, providing both hydrogen-bond donors and acceptors. The side-chain donor capabilities of Asn result in N–H···O5_βCD and N–H···O6_βCD bonds. At the same time, HO6_βCD acts as a donor and forms a hydrogen bond with the asparagine carbonyl –CO– to increase the stability of the βCD–M113N complex. An additional contribution to this hydrogen-bond network is due to both βCD–Thr145 and βCD–Thr1115 interactions (Table 2c,d). In this case, hydrogen bonds are formed by hydrogens of the O2, O3, and O6 atoms of βCD. These interactions help reduce the conformational flexibility of βCD¹⁹ when bound in the channel.

M113A

A 2 ns equilibrium MD simulation of the βCD–M113A complex has been performed. During this simulation, βCD remained close to the initial position but exhibited a mobility and a flexibility that were greater than those of other complexes. In agreement with experiments,²⁰ our results indicate weak interaction between βCD and M113A mutant (Table 2d). Decomposition of interaction energy into contributions from several residues revealed an importance of the van der Waals interactions between βCD and Thr145 and Thr115 (Table 2d). For the βCD–M113A complex, we observed virtually no direct ligand–protein H-bonds. On the contrary, the number of the ligand–water hydrogen bonds was significant. The high number of the βCD–water interactions can be explained by the fact that the alanine residue has a smaller surface area than methionine, and hence, there is enough space between βCD and A113 for a water molecule. Water molecules form hydrogen bonds with the ligand where βCD oxygen atoms of O2, O3, and O6 are acceptors or water oxygens are acceptors. However, most hydrogen bonds formed with water were short-lived (less than 20 ps). It appears that water shields interaction between βCD and the M113A protein resulting in decreased βCD affinity to this mutant with respect to the affinity to the wild type protein.

βCD shows the lowest affinity to αHL when the Met113 residues are replaced with Glu. The weakest total binding energy (Table 2e) and shortest experimental lifetime²⁰ were observed for this mutated complex. According to our simulation results, this mutation facilitates diffusion of βCD away from the 113E site (Figure 4d). As a result, we have not expected to find significant interaction between βCD and M113E (Table 2e). The van der Waals interactions between βCD and Thr115 and Thr117 (Table 2e) contribute most to the total binding energy of this complex. The hydrogen-bond network stabilized βCD somewhat near the threonine (Thr145, Thr115, and Thr117) and Ser141 residues, H-bonds were detected between the ligand and both the protein and water. During 1 ns equilibrium simulation βCD remained close to its position in the channel but exhibited significant flexibility.

Radial Distribution Functions

The radial distribution functions of the water oxygen atoms and the βCD oxygen atoms are shown in Figure 9 for all complexes described above, as well as for the βCD simulation in the bulk TIP3P water (see ref 19 for details on this 8 ns MD simulation). All lines in Figure 9 show a first solvation shell peak at 3.25 Å, which can be identified as a typical βCD–water hydrogen-bond length. The RDF g_OO(r) for the βCD–water distribution in the bulk water (solid line in Figure 9) demonstrates the structure of water in the vicinity of the fully solvated βCD. One can see that the height of the first solvation peak of βCD for various mutant complexes is indicative of the degree of its solvation. The M113N and M113V peaks are similar or smaller than those in the WT complex and are indicative of tighter binding in the channel and longer complex dwell times, while the peak for the M113A mutant in significantly higher than that for the WT complex and closer to the bulklike and is indicative of better solvation of βCD in this case and, as a result, a weaker complex.

Figure 9.

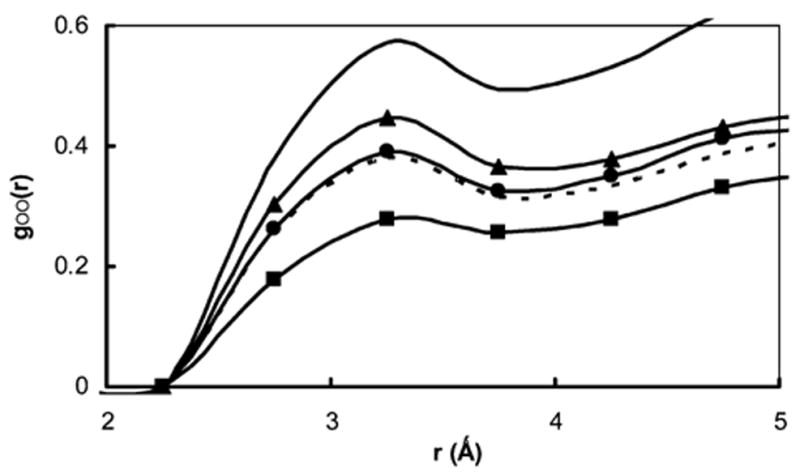
Calculated radial distribution function, g_oo(r), for the water oxygens and βCD oxygens. g_OO(r) for βCD in bulk water (solid line) are compared with result for βCD in WT (dashed line), M113V βCD–αHL (line with squares), M113N βCD–αHL (line with circles), and M113A βCD–αHL (solid line with triangles) complexes.

Conclusions

Developing stable self-assembling supramolecular complexes that can serve as a base for chemical nanodevices requires a detailed understanding of molecular mechanisms which govern complex stability. One purpose of this work was to demonstrate that molecular modeling can provide useful insights in the structure and energetics of large weakly bound supramolecular complexes. We have performed thorough calculations of relative binding affinities of the wild type αHL and its four mutants M113V, M113N, M113E, and M113A to a β-cyclodextrin adapter. Excellent agreement of our calculations with the direct experimental data on a variety of mutants demonstrates that modern empirical models (such as those used in MD simulations, e.g., the Cornell et al. force field used in this study) are capable of adequately representing the main features of the intermolecular interactions. When the statistical sampling is performed with sufficient accuracy and along all relevant degrees of freedom calculated relative binding energies were in nearly quantitative agreement with the experimentally measured values. In this study, we successfully combined two methods of a thermodynamic following of a reaction coordinate: thermodynamic integration and umbrella sampling. Such a nonstandard combination of methods allowed us to follow a nontrivial reaction coordinate (a mutation resulting in a conformational rearrangement as in M113V and M113E mutants).

Two mutants (M113V, M113N) exhibited improved affinity to the βCD adapter in experiment as well as in our simulations. The mechanisms by which these mutants prolong complex lifetimes as well as resulting complex structures are, however, different. Substituting methionine for asparagine resulted in the pore with similar geometric parameters (methionine and aspar-agine are similar in size) but with stronger hydrogen-bonding propensities at the 113 protein site. In both upward and downward orientations of the adapter, polar asparagine provided well positioned hydrogen-bond acceptor groups for the βCD hydroxyl groups to interact with. As indicated by our equilibrium MD simulations, the downward orientation of the adapter is somewhat preferred in the M113N mutant. The M113V mutant protein has a less bulky side chain and thus forms a wider pore near position 113; the βCD adapter was able to “slip through” this pore higher into the channel lumen, where it can interact directly with the E111 group via hydrogen bonding as well as through the electrostatic attraction. Thus, valine facilitates binding of βCD by removing the channel constriction at position 113 and preventing βCD from forming favorable hydrogen bonds with water.

Calculating free energy differences is a computationally demanding problem. The success of a TI technique, when applied to large biomolecular systems, depends strongly on the degree to which differences between an initial and a final system are local. Examples presented in this study are radically different in this respect. For the βCD–M113N or βCD–M113A mutation, an adapter remained in approximately the same position and conformation as in a wild type complex. In this case, the TI simulation alone was sufficient to adequately describe free energy changes upon a molecular transformation. In contrast, TI simulation of βCD–αHL transformation to βCD–M113V or βCD–M113E resulted in an unstable complex and was unable to account for a free energy change upon subsequent complex reorganization, which occurred spontaneously during the equilibrium MD simulation.

The βCD–M113V or βCD–M113E mutants provided us with an illustration of the fact that the TI method alone becomes inadequate in cases when either a ligand or a protein undergoes large conformational changes or subsequent diffusional motion upon mutation (this can also be viewed as a motion along an additional independent reaction coordinate not controlled by an a priori chosen lambda in eq 1). As we demonstrated in this paper, calculating free energy differences between the two systems in such cases is possible by combining TI transformation with the PMF calculations along a coordinate, which describes geometric restructuring of a system after (or during) a mutation. In this work, we used umbrella sampling with the weighted histogram analysis (US/WHAM) technique to enhance sampling and estimate free energy differences in a complicated case of M113V or M113E mutations, in which βCD underwent rapid diffusional relocation to a new binding position at the end of the mutation. Thus, the range of applicability of the traditional TI method, which is widely used in biomolecular simulations, can be significantly extended when combined with US/WHAM, as demonstrated successfully in this study. The proposed combination of methods is a subject of limitations of validity and applicability of both techniques which is widely discussed elsewhere (cf. ref 34). In addition, statistical errors are amplified when an integration path goes over a barrier and a final value is found via subtraction of two relatively big numbers as is the case here (for M113V and M113E mutant complexes). This can be remedied to a certain degree by accumulating more data, but we could only recommend this course of action when it is unavoidable, as seems to be the case here.

While direct calculation of free energy differences from molecular simulations is still a relatively expensive (in terms of the CPU time required) exercise, equilibrium MD simulations are plausible for many molecular systems. Analysis of hydrogen bonds and direct interaction energies between protein side chains and the βCD adapter in MD simulations allowed us to explain the mechanistic differences in the formation of complexes with αHL and its mutants M113V, M113N, M113E, and M113A which resulted in different complex lifetimes observed experimentally.²⁰ In this case, stability of the direct protein–adapter hydrogen bonds monitored in the course of the simulation correlated well with the stability of the complex. For example, in both long-lived M113N and M113V mutants, a βCD adapter formed several stable hydrogen bonds with the protein groups, while, in shorter-lived complexes with the wild type αHL, M113A, or M113E, βCD formed little or no long-lived hydrogen bonds. In the M113A complex, βCD exhibited the greatest conformational mobility and was largely solvated in water unlike in other more stable complexes, in which βCD conformational freedom is strongly restricted by the protein and water solvation is limited.¹⁹