REGIONAL DISTRIBUTION OF MEASUREMENT ERROR IN DTI

Abstract

The characterization of measurement error is critical in assessing the significance of diffusion tensor imaging (DTI) findings in longitudinal and cohort studies of psychiatric disorders. We studied 20 healthy volunteers each one scanned twice (average interval between scans of 51 ± 46.8 days) with a single shot echo planar DTI technique. Inter-session variability for fractional anisotropy (FA) and Trace (D) was represented as absolute variation (standard deviation within subjects: SDw), percent coefficient of variation (CV) and intra-class correlation coefficient (ICC). The values from the two sessions were compared for statistical significance with repeated measures ANOVA or a non-parametric equivalent of a paired t-test. The results show good reproducibility for both FA and Trace (CVs below 10% and ICCs at or above 0.70 in most regions of interest) and evidence of systematic global changes in Trace between scans. The regional distribution of reproducibility described here has implications for interpretation of regional findings and for rigorous pre-processing. The regional distribution of reproducibility measures was different for SDw, CV and ICC. Each one of these measures reveals complementary information that needs to be taken into consideration when performing statistical operations on groups of DTI images.

INTRODUCTION

Diffusion tensor imaging (DTI) has been evolving rapidly and gaining increasing popularity in psychiatric research. There has been a rapid increase in publications particularly in the field of schizophrenia where 8 original papers were published between 1998 and 2002 and 23 between 2003 and May 2005.

Despite this, the measurement error of this technique has not been fully characterized. The information regarding measurement error is critical in assessing the significance of DTI findings in longitudinal studies and when comparing patient groups. This is particularly true in the case of psychiatric disorders where differences from controls may be quite subtle.

Pfefferbaum et al. (Pfefferbaum et al., 2003) were the first to address reproducibility of FA and Trace images in detail. They studied normal controls three times with a minimum time interval between scans of one day. They reported CVs between 1.23 and 2.35% for FA and of 0.84–3.73% for Trace. Their analysis was based either on large collections of voxels (such as all the voxels in the in the white matter of the supratentorium) or on a single large region of interest (ROI) placed over the entire corpus callosum on a midline slab of tissue with thickness of 5 mm. Thus, the estimates of reproducibility and measurement error derived from this study are likely to be quite liberal as compared to common approaches to DTI data analysis which would include either smaller ROIs or voxel-by-voxel approaches with programs such as statistical parametric mapping (SPM). Moreover, this study did not provide any information on the regional distribution of measurement error, which is important since reproducibility may not be equal across the whole image due to the complex statistical properties of the calculated DTI measures and many other factors. For example, recently claims were made regarding differences in anisotropy between patients with schizophrenia and normal controls in small ROIs of gray matter in the entorhinal cortex (Kalus et al., 2005) and the hippocampus (Kalus et al., 2004). How are we to judge the strength of these findings without knowing if the reproducibility of gray matter ROIs is similar to that found in the corpus callosum?

Also Kubicki et al. (Kubicki et al., 2004) studied the reproducibility of single shot planar imaging (EPI) with ROIs applied to four scans (acquired in separate sessions, with unspecified time interval between sessions) of the same subject. The CV varied between 1.4% and 12% for various regions of white matter and reached 25% for a gray matter ROI. However, the EPI acquisition employed was highly susceptible to artifacts due to the use of a fairly high time of echo and the lack of corrections for eddy current distortions. Moreover, the scans were acquired with gaps in between slices and no effort to register scans acquired on different sessions was described. Hence, the estimates of measurement error presented in this study are likely to be conservative when compared with what would be obtained with more state of the art acquisition and processing schemes.

The gap in knowledge left by these two studies provided the rationale for the current study, where we use two methods commonly employed in statistical analysis of DTI images (ROIs and SPM based techniques) and describe the regional variation in FA and Trace (D) (henceforth referred to as Trace) associated with each strategy. We also discuss some factors that might contribute to increased inter-session variability.

MATERIALS AND METHODS

We studied 20 healthy volunteers (ages 21–36, mean 26 ± 4.4 SD, three females), each one scanned twice, with an average interval between scans of 51 ± 46.8 days. All scans were performed with the head immobilized by a vacuum cushion. All subjects gave written informed consent according to procedures approved by the NIMH institutional review board.

DTI sessions were conducted on a 1.5T GE Signa magnet (Waukesha, WI) and consisted of an axial single-shot echo planar imaging (EPI) sequence with six different gradient directions with b-value ~ 1100 s/mm² plus one acquisition with b-value ~ 0 s/mm2, eight replicates, full brain coverage with 2 mm isotropic resolution, cardiac gating, TE 82.7ms, TR > 10s. The average duration of each session was about 20–25 min. No high order shimming was performed because this software option was not available on the scanner at the time of the studies. No correction for B0 inhomogeneity was applied. Images were corrected for distortion caused by eddy currents and for head motion during the acquisition (Rohde et al., 2004) and, prior to tensor computation, all the raw images (images obtained after reconstruction, prior to any processing) were registered to a T2 weighted template available in SPM (http://www.fil.ion.ucl.ac.uk/spm/) with a rigid body transformation. This was done in order to calculate the tensor matrix at each voxel in a frame of reference that would be similar for all subjects (although this is not relevant to the measures addressed in this paper). Moreover, prior to tensor calculation, the background and skull of the images was removed using an adaptation of the BET software (Smith, 2002, http://www.fmrib.ox.ac.uk/) in order to exclude areas of no interest.

Within subject registration

the two sessions from the same individual were registered to each other with a rigid-body algorithm, using the b=0 acquisition of the first scan as a template for the other. This procedure was applied to the raw diffusion weighted images prior to tensor calculation. After the registration was performed, we calculated the normalized mutual information between the images, a measure of similarity that varies between 0 and 2 (the normalized mutual information will be equal to 2 if the two images are identical). All subjects had normalized mutual information above 1.5, except for one who had a value of 1.38. We therefore excluded this subject, while observing that the poor registration had occurred due to high signal in the sinuses that had interfered with the BET procedure. All the results refer to 19 subjects.

The tensor matrix was then calculated at each voxel and Trace and fractional anisotropy (FA) images (Basser and Pierpaoli, 1996) were derived.

Characterization of Reproducibility

We used two approaches to characterize reproducibility: ROIs placed on the images in “native space” (the space of initial tensor calculation, not the acquisition frame, see above) and inspection of whole brain images of reproducibility parameters. In both cases, we calculated three indexes of reproducibility as described in Bland & Altman (Bland and Altman, 1996) and Bartko & Carpenter (Bartko and Carpenter, 1976). Briefly, the 40 scans were entered in a one-way ANOVA, with “scanning session” as the sole two-level factor. The residual mean square within subjects (MSW) gave an estimate of variance within subjects and the residual mean square between subjects (MSB) an estimate of variance across subjects. We used the square root of the MSW (i.e. the standard deviation) to obtain an absolute measure of variation within subjects (SDw: Standard Deviation within subjects). Dividing this quantity by the mean of a particular ROI or voxel across all subjects and all repeated sessions and multiplying by 100 yielded a percent coefficient of variation (CV). This is the most commonly reported relative measure of reproducibility in the literature. Values of CV below 10% are usually desirable for biological variables related to imaging. We also calculated the intra-class correlation coefficient (ICC) as

$$\text{ICC}=[\text{MSB}-\text{m\hspace{0.17em}}\text{MSW}]/[\text{MSB}+\text{m\hspace{0.17em}}({\text{R}}_0-1)\text{MSW}]$$

where m=N(R₀−1)/[N (R₀−1)−2] with N=total number of subjects and R₀= the total number of scanning sessions (Bartko and Carpenter, 1976). This is a measure of correlation between the two scanning sessions, and values above 0.70 are considered measures of high reproducibility.

We looked for evidence against the null hypothesis of the two scanning sessions being equal (i.e. being reproducible) by using a repeated measures ANOVA with ROI (14 levels) and scanning session (2 levels) as repeated measures (α a was set to 0.05). In addition, we also compared the first to the second DTI session for each of the 14 ROIs with a Wilcoxon matched-pairs test. α a was set to 0.05/14 = 0.0036 (Bonferroni corrected). An analogous test was performed on the whole images using the two conditions (replications) permutation plug-in from statistical non-parametric mapping (SnPM2b: Nichols and Holmes, 2002, http://www.sph.umich.edu/ni-stat/SnPM/). This software was used because since the distribution of the data is calculated based on the data themselves, there is no requirement for high levels of smoothing of the images in order to satisfy random fields theory requirements for smoothness of variance across the image. Moreover, the distribution of FA and of Trace values may not be Gaussian, therefore non-parametric statistics may be more adequate. Other parameters used for this analysis were: 2000 permutations, no smoothing of variance, volumetric image processing, supra-threshold statistics collected, and an absolute threshold of 500 mm²/sec was used for Trace and of 0.05 for FA (i.e. values below these were not considered in the analysis in order to analyze only voxels inside the brain. When such a value was encountered in one scan, no other scan was analyzed at that location. This procedure allowed to ignore areas at the edge of the brain where the BET procedure may have identified slightly different contours for the first and second scans). Significant results were displayed when they achieved a p value below 0.05 after family-wise error rate correction for multiple comparisons or a cluster extent threshold with p<0.01.

ROIs were drawn using Medx (Medical Numerics, Inc., Sterling, VA) using the FA maps from the first scan of each individual as a visual guide. To minimize partial volume effects, care was taken that the ROI would be centered in the structure of interest, with no part of the ROI overlapping areas of transition between low and high FA. The size of all ROIs was 64 mm³. For areas such as gray matter and insula where the low values of FA could not be clearly distinguished from the background, gray matter maps were obtained with SPM using the amplitude, trace and FA images of each subject as the input. These gray matter maps were used as guides to position the ROIs. They were drawn on the following structures: splenium (SCC) and genu (GCC) of the corpus callosum, cerebral peduncles, cerebellar peduncles (CblPeduncles), posterior limb of the internal capsule (PLIC), orbito-frontal white matter (OFWM), centrum semiovale (CSO), stem of the hippocampus (Hippo), low anisotropy white matter (LAWM), thalamus (Thal), cerebellar cortex (CblCtx), insula (Ins), putamen (Put), and frontal gray matter (FrG). The positioning of the ROIs is illustrated in figure 1. For each ROI, the SDw, the CV and the ICC were calculated, based on the mean ROI value in the two repeated examinations.

FIGURE 1. ROIs used in the study.

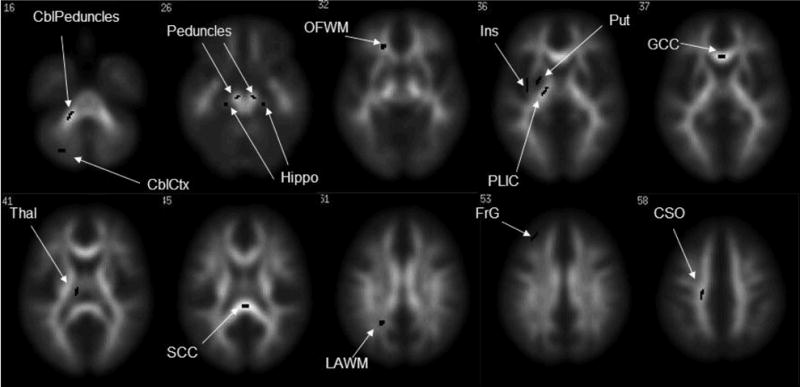
ROIs are shown here superimposed on the FA template, but they were drawn on the FA maps from the first scan of each individual. Abbreviations: cerebellar peduncles (CblPeduncles), cerebellar cortex (CblCtx), cerebral peduncles (Peduncles), stem of the hippocampus (Hippo), orbito-frontal white matter (OFWM), insula (Ins), putamen (Put), posterior limb of the internal capsule (PLIC), genu of the corpus callosum (GCC), thalamus (Thal), splenium of the corpus callosum (SCC), low anisotropy white matter (LAWM), frontal gray matter (FrG) and centrum semiovale (CSO).

We also measured the average signal to noise ratio (SNR) for each ROI by sampling the same ROIs on the amplitude (b=0) images and dividing by the noise measured in a large ROI on the top slice of two T2 weighted raw images (the first one having b=0 and the second one b=1200). The noise was calculated according to Henkelman (Henkelman, 1985).

Across subject Registration

To calculate images of SDw (standard deviation within subjects), CV and ICC, and to perform SnPM (statistical non-parametric mapping) analysis of on-off scans, all images were normalized to a FA template and the same calculations that were used for the mean ROI values were applied voxel-by-voxel. The FA template was constructed using one scan from each subject. It was obtained by registering the T2-weighted image without diffusion weighting (b=0 or “amplitude” image) to the T2 MNI template available in the statistical parametric mapping (SPM2) software distribution (the MNI template was modified by removing the skull). SPM2 normalization defaults (no template weighting, 25 mm cutoff [7x9x7 basis functions], medium regularization, 16 nonlinear iterations) were used for this procedure. The transformation obtained by this procedure was then applied to the FA images. The FA images were then averaged and the resulting image was smoothed with an 8mm FWHM filter, thus yielding the template. A similar procedure for template creation was followed by Toosy et al. (Toosy et al., 2004). All FA images were normalized to this template with the same parameters as above. There are two reasons to use a FA template rather than the first normalization to the T2 weighted template: 1) FA images are more detailed than T2 weighted images and may therefore result in slightly more accurate normalization, 2) iterating the normalization procedure (a first normalization obtained from registering the b=0 images to a T2 template and a second one obtained by registering the FA images to a FA template) allows the template to be more specific to the group under analysis (i.e. to lose some of the features of the MNI group used as reference), and this may also increase the accuracy of normalization. The transformation matrix obtained from the normalization of the FA images was then applied to the Trace images so that all SnPM-based analyses occurred in the same normalized space.

RESULTS

Typical images of FA and Trace obtained during this study are shown in figure 2.

FIGURE 2.

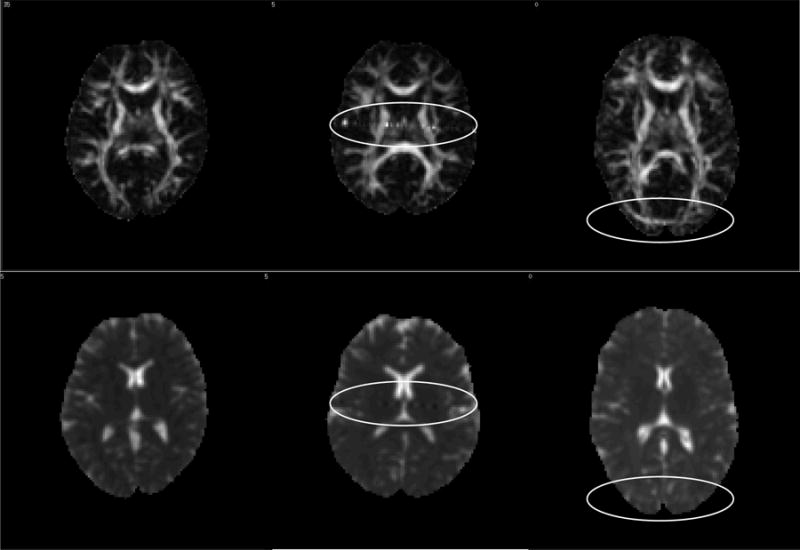
Representative FA and Trace images included in the study. Top row: FA images, bottom row: Trace images. Some artifacts are indicated by white ovals. From left to right: no artifacts (left panel), “zipper” artifact caused by noise generated by the gradients (center) and artifact caused by inadequate fat suppression (right).

SNR, SDw, CV and ICC for mean ROI values for FA and Trace are shown in the Table. A notable regional variation in reproducibility was seen. For FA, the SDw was highest in the Peduncles, PLIC and CSO, and lowest in Put, GCC, FrG, Thal and Ins with values in the Peduncles being twice those of the Put. The CV was highest in the CblCtx and the FrG and lowest in the GCC and the SCC. Nine out of 14 ROIs had CVs below 10%. ICCs were about 0.70 or above in eight ROIs out of 14. The highest ICC was found in the CblPeduncles and the lowest in the Putamen. For Trace, SDw was highest in the Peduncles, SCC, and CblCtx and lowest in CSO, Ins, Hippo and OFWM. The CV for Trace was highest in the Peduncles and was below 5% in 12 out of 14 ROIs, with the lowest value in the Ins. ICCs were 0.70 or above in 8 ROIs out of 14.

The repeated-measures ANOVA revealed a significant effect of ROI for both FA (F_{(13, 234)}=462, p<0.00001) and Trace (F_{(13, 234)}=31.6, p<0.00001). no significant effect of scanning session or interaction of ROI by scanning session emerged for FA, while the effect of scaning session was significant for Trace (F_(1,18)=9.88, p<0.006), with the second scan being higher than the first one. Greenhouse-Geisser tests confirmed these findings. The Wilcoxon matched pairs tests showed no ROIs to be significant at the 0.0036 level for FA or Trace. Also, while one subject had a 4% increase in Trace on the second scan, and two others showed increases of 2% and above from scan 1 to scan 2, they did not appear to be frank outliers. Thus, we reasoned that the increase in Trace during the second scan was likely due to a global effect. We plotted the mean values for Trace (calculated as an average of 14 ROIs) for scan 1 and 2 according to the date of scanning and noticed that there was a systematic increase in Trace from the first to the second scan in four subjects around July 2002.

The images of SDw, CV and ICC for FA and Trace are presented figure 3. Several features of these images are of interest. Firstly the SDw images for FA, which represent absolute variability, were quite different from CV images, which represent relative variability between scanning sessions. This difference was not as marked for Trace. The SDw image for FA showed low variability in the center of structures such as the corpus callosum and high variability on the edges of such structures. This pattern could not be recognized as clearly in the corresponding CV image. The SDw and CV images allowed identification of artifacts (illustrated by the black arrows). These are also visible in the ICC images, although to a lesser extent. There was high variability for CSF values in the Trace images, but not uniformly so: only the areas of CSF that were closest to tissue had high variability across scanning sessions. The ICC images reaffirmed the information already present in the CV images that Trace is a more reproducible parameter than FA overall (note that more voxels surpass the 0.5 threshold in the ICC image of Trace as compared to that of FA). The ICC images also highlight areas of low correlation between scanning sessions around the basal ganglia and, unexpectedly, in some areas of white matter such as the optic radiations. Moreover the cortical rim showed areas of low ICC for FA. This was not the case for Trace.

FIGURE 3.

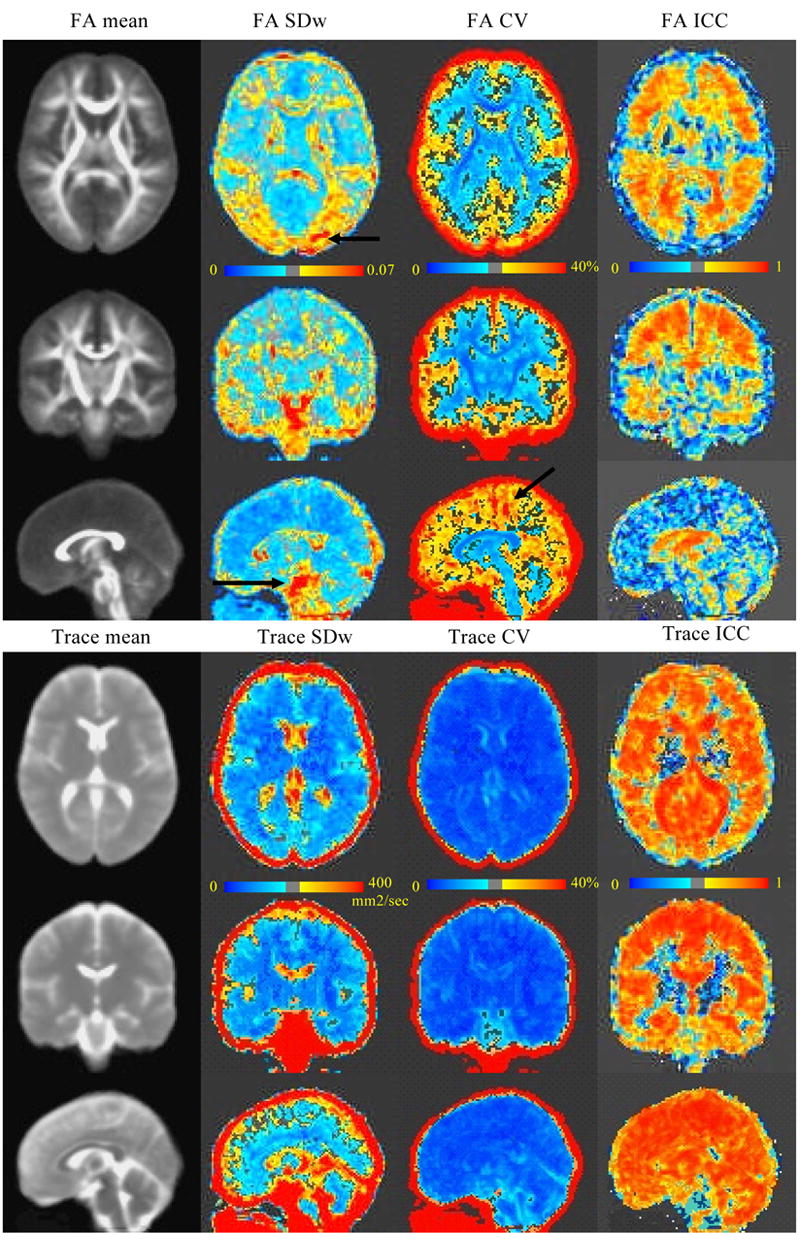
Images of the regional distribution of measurement error for FA and Trace. On the left column mean images for 40 scans are shown, the other columns show SDw, CV and ICC from left to right. FA is shown in the top panel and Trace in the bottom one. The lookup tables indicate the windowing of the various images. For the SDw the represented range of values was chosen in order to recognize the regional structure of the images themselves. CV images are windowed in order to see in blue CVs below 15% approximately. The black arrows indicate the position of artifacts present in some of the acquisitions. The arrow in the axial image of SDw corresponds to the fat suppression artifact in the right panel of figure 2. The arrow in the sagittal CV image for FA indicates the effect of the gradient noise artifact seen in the middle panels of figure 2. The arrow in the sagittal image of FA SDw indicates the effect of artifacts affecting the peduncles.

SnPM comparisons on the normalized images yielded no significant voxels for FA or Trace..

These results emphasize that there is a rather large range of reproducibility across different brain areas for FA and much less so for Trace.

DISCUSSION

Characterizing regional variation in measurement error for DTI is important in order to interpret the results of group comparisons and longitudinal studies. In this paper, we present three different ways of looking at measurement error as they apply to ROI measurements and to voxel-by-voxel analysis. We used different measures of reproducibility because they reveal different and complementary information about the regional distribution of measurement error.

Reproducibility of ROI values

Absolute interscan variability (SDw) for FA varied between 0.019 for some of the ROIs drawn on gray matter and 0.041 for the Peduncles. The high variability in the Peduncles is likely attributable to a n/2 ghost artifact that can interfere with measurements in this area for images acquired with our field of view (Derek K. Jones, oral communication during the ‘Artifacts Gallery’ of the meeting of the Diffusion/Perfusion Study group, 12^th annual meeting of the International Society for Magnetic Resonance in Medicine, Kyoto, Japan, 2004). Note that the CV for FA of the Peduncles was 5.1%, a relatively low value considering that CVs below 10% are generally considered as desirable in the imaging literature. Also, the ICC was 0.70.

CVs for FA were below 10% for most ROIs, with values between 8.6 and 20.5% for most gray matter ROIs. The pattern of regional variation observed with the CV was opposite to the one described by the SDw (i.e. lower variability in areas with low anisotropy).

The ICCs for most regions were at or above 0.70 with particularly low values for CblCtx, Ins, Put and FrG. The ICC is a more stringent test of reproducibility and ideally one would want values of 0.80 or above, but the values reported here are not unreasonable for an imaging study in vivo. ICCs are more difficult to interpret than the other measures included here because their calculation includes the estimation of variance across subjects, not shown in this paper since the focus is on variability within subjects. Generally speaking, values of FA below 0.2 were associated with high CVs and low ICCs.

For Trace values, similar trends emerged as described for FA, however CVs were lower and ICCs were higher than analogous measures for FA.

Repeated measures ANOVA and the Wilcoxon matched pairs test revealed that the ROI mean values for FA did not change significantly from scan one to scan two, though this statistic says nothing about the predictability of one scan based on another. Unexpectedly, Trace values appeared to change significantly from scan 1 to scan 2, most likely due to scanner instability during the period of July 2002. We were not able to retrieve the maintenance records for that time, so we could not identify the cause of this change more specifically. This result alerts us that, despite all the measures of high reproducibility for Trace, this parameter may be sensitive to scanner instability or other unidentified sources of systematic error (such as the body temperature of the subjects).

By inspecting the SNR values reported in the table, one can observe a slight tendency for higher SNR values to be associated with lower mean FA values, probably reflecting the contrast characteristcs of T2 weighted images, with higher signal in gray than white matter and possibly the partial volume effect due to CSF contamination in the ROIs on the cortical rim. This tendency is also consistent with lower SNR resulting in an overestimation of FA (Pierpaoli and Basser, 1996; Bastin et al., 1998), however we believe this effect is minor when compared to the physiological difference in anisotropy between gray and white matter areas. The highest SNR values also corresponded to high CVs for FA. No firm conclusion can be derived from these empirical observations, though, because the interaction between SNR, mean FA values and reproducibility measures is probably complex and not addressed by the current data.

Comparison to values reported in the literature

The CVs reported here for ROIs are higher than those reported by Pfefferbaum et al. (Pfefferbaum et al., 2003) but they calculated a CV for each subject based on all the voxels in the supratentorium and all the voxels in the white matter of the supratentorium. They then averaged all individual CVs, thus generating a more liberal metric than the one reported here. A more comparable figure can be derived from Pfefferbaum’s analysis of the corpus callosum, which revealed CVs for FA and Trace in the same range as the ones reported here (see the Table). Moreover, in that study systematic differences across scanners emerged, especially for Trace. This finding would appear to be consistent with our observation of greater sensitivity of Trace to global changes possibly due to scanner calibration.

Our values seem to indicate better reproducibility for single shot echo-planar imaging (EPI) than found by Kubicki et al. (Kubicki et al., 2004), however, as pointed out in the introduction, this can be attributed to the improved quality of data acquisition and processing in our study.

Another recent paper (Heim et al., 2004) has shown how bootstrapping techniques can be used to assess data quality of FA measures. This paper also derived measures related to intra-session reproducibility. They calculated the CV within a single scan for 15 subjects as a measure of data quality. CVs for FA in gray matter were 25 ± 1% and in white matter 15 ± 1%, a result consistent with our findings of greater intersession CVs in gray vs. white matter, but much higher than the values reported here for across scan variability. They also found that CVs for mean diffusivity (which is one third of the Trace) were lower than for FA, again consistent with our findings related to intersession CVs.

Cassol et al. (Cassol et al., 2004) also studied normal controls with repeated measurements of Trace and FA over the course of three months (three examinations), but the data reported do not allow a comparison with our figures. Similarly, Steens et al. (Steens et al., 2004) studied the reproducibility of whole brain histograms of Trace, but the values reported there are not comparable to ours.

Finally, Ciccarelli et al. (Ciccarelli et al., 2003) studied reproducibility in regions defined by their tract tracing algorithm, finding CVs for FA between 5 (pyramidal tract) and 7% (optic radiations). The ROIs chosen by the tract tracing algorithm were much larger than the ones selected here, though.

Images of Reproducibility

The patterns of regional distribution of measurement error rendered in the images presented in figure 3 reveal some of the multiple contributions to measurement error in repeated sessions. For example, the artifacts that were present in some images emerge in the SDw and CV images. Moreover, the pattern of high variability on the edges of the corpus callosum and of other white matter structures with high FA shown in the SDw images might indicate mis-registration between the scans. The source of this mis-registration could be a combination of EPI distortions, susceptibility artifacts and partial volume effects, which could easily vary from scan one to scan two.

The SDw and CV images for Trace reveal that CSF, in particular at the edge of the ventricles may be more highly variable across scans. This may depend on the combination of several effects: inadequacy of the b-values used here to determine CSF values of Trace accurately, motion of CSF and partial volume effects. Moreover, there may be a regional distribution of measurement error expected on the basis of the signal-to-noise characteristics and the T2 properties of the tissue. This would constitute a baseline uncertainty in the determination of FA or Trace values, possibly a more appropriate denominator for a CV-like measure than the mean value (of FA or Trace, as in the conventionally calculated CV reported here), or may be used as a covariate rather than as the denominator in a ratio.

As for the images of ICC, these give a useful overall view of the regional distribution of measurement error that is independent of the mean value. The regional distribution of across subject variation will be heavily influenced by the accuracy of spatial normalization methods, therefore ICC images will be sensitive to errors in normalization, but sometimes in the opposite direction than expected. An extreme example of this can be seen for the FA images where a smattering of high ICC values can be seen outside the brain. This complex interaction between within and across subject variation may explain the unexpected finding of low ICCs in the optic radiations and in some areas of frontal lobe white matter.

SnPM analysis

No indication of lack of reproducibility emerged from our SnPM analysis. No voxel exceeded thresholds of significance established after stringent (family-wise error rate) and less stringent (false discovery rate) control of for multiple comparisons, although the analysis of Trace came close to significance.

Limitations

The data presented here has been acquired with eight independent acquisitions and 2 mm isotropic voxels, therefore these results do not necessarily apply to the acquisition schemes more commonly present in the literature, where four repetitions and larger and anisotropic voxel sizes are used. Reducing the number of averages decreases signal to noise and will worsen reproducibility, increased partial voluming due to larger voxels will have different effects on reproducibility depending on the homogeneity of the tissue (reproducibility may worsen on the edge of structures, but improve in the middle of homogeneous structures) and anisotropic voxels may cause a bias in the calculation of FA, but is not expected to alter reproducibility per se.

Another potential limitation of the study is the inclusion of some images where artifact was present. This was done to mimic small cohort clinical studies where exclusion of subjects may not be feasible. The fact that good reproducibility was found despite these local artifacts, suggests that DTI measures are quite robust on average.

Conclusions

In summary, FA and even more Trace show good reproducibility by conventional measures. Trace may be sensitive to scanner calibration or other sources of error, resulting in systematic changes in mean values. No evidence for lack of reproducibility emerged for FA or Trace in the SnPM analysis.

Our findings highlight the presence of a regional distribution of measurement error for FA and Trace. Different aspects of this pattern are highlighted by the different measures of reproducibility used in this paper.

Several guidelines for data analysis may be derived from our results: for FA analysis, ROIs to should preferably be drawn on areas of high anisotropy away from the edge of structures such as the corpus callosum. Similarly, findings reported in SPM-like analyses on the edge of white matter areas should be viewed with caution. When analyzing ROIs with mean FA values below 0.2 one should also be cautious about the interpretation of the results. For the analysis of subtle regional changes in Trace, statistical methods should be used to covary out the global mean. This study may also offer a rationale for segmentation of low and high anisotropy images prior to smoothing for SPM-like approaches at least for FA images, where the CV images clearly have higher values in areas of low anisotropy. In fact, the very images of reproducibility reported here may be used as a mask for statistical analyses in normalized space. Such a mask would reduce the voxels analyzed and increase power by making the corrections for multiple comparisons less stringent. We are now developing a framework to understand the relative contribution of the different sources of variability mentioned above to measurement error.

TABLE 1.

Mean FA, Trace (in mm²/sec) and measures of reproducibility for mean ROI values.

ROI	ROI SNR	Grand Mean FA	SDw FA	CV FA	ICC FA	Grand Mean Trace	SDw Trace	CV Trace	ICC Trace
SCC	14.02	0.83	0.031	3.75	0.78	2084	129	6.20	0.74
GCC	13.60	0.81	0.020	2.51	0.80	2255	64	2.85	0.74
Peduncles	16.03	0.81	0.041	5.09	0.70	1821	142	7.82	0.81
CblPeduncles	16.61	0.69	0.031	4.55	0.90	1969	64	3.26	0.62
PLIC	16.38	0.63	0.038	6.10	0.49	2062	78	3.80	0.45
OFWM	13.25	0.54	0.032	5.98	0.74	2272	57	2.49	0.63
CSO	16.27	0.53	0.034	6.32	0.64	2064	43	2.09	0.51
Hippo	17.60	0.43	0.028	6.49	0.77	2342	57	2.42	0.91
LAWM	15.91	0.29	0.030	10.16	0.78	2345	68	2.89	0.75
Thal	17.79	0.26	0.022	8.61	0.78	2271	65	2.86	0.87
CblCtx	18.45	0.16	0.032	20.54	0.37	2408	114	4.71	0.91
Ins	21.23	0.14	0.023	15.89	0.36	2452	50	2.02	0.80
Put	16.16	0.12	0.019	15.37	0.35	2149	59	2.74	0.42
FrG	21.94	0.10	0.021	20.08	0.39	2807	94	3.34	0.69