Dielectric fluctuations and the origins of non-contact friction

Abstract

Dielectric fluctuations underlie a wide variety of physical phenomena, from ion mobility in electrolyte solutions and decoherence in quantum systems to dynamics in glass-forming materials and conformational changes in proteins. Here we show that dielectric fluctuations also lead to non-contact friction. Using high sensitivity, custom fabricated, single crystal silicon cantilevers we measure energy losses over poly(methyl methacrylate), poly(vinyl acetate), and polystyrene thin films. A new theoretical analysis, relating non-contact friction to the dielectric response of the film, is consistent with our experimental observations. This work constitutes the first direct, mechanical detection of friction due to dielectric fluctuations.

The fundamental relationship between random forces and friction plays a pivotal role in physics, chemistry, and biology. Surprisingly, the origin of force fluctuations and friction between objects in close proximity, but not in physical contact, remains poorly understood. Such non-contact friction is important in a variety of seemingly disparate fields, including micro- and nanomechanics, trapped ions for quantum computation, and measurements of quantum gravitation at small length scales. The non-contact friction measurements reported here are motivated by recent advances in the mechanical detection of magnetic resonance [1, 2]; the sensitivity in these measurements has so far been limited by non-contact friction between a cantilever tip and the sample surface [3].

The advent of high sensitivity single crystal silicon cantilevers [4, 5] provides a new opportunity to elucidate the mechanisms of non-contact friction. These cantilevers’ combination of low spring constant and low intrinsic losses enable the detection of non-contact friction with unprecedented sensitivity. Initial work on non-contact friction using high sensitivity cantilevers by Stipe et. al measured dissipation using a conducting probe over metal and quartz substrates at tip-sample separations down to 2 nm and temperatures from 4 – 300K [3]. Friction over Au(111) was found to be 7 orders of magnitude larger than predicted by Coulomb drag theories [6]; several alternative mechanisms have been suggested [7–9]. In this Letter we explore non-contact friction over polymer films.

A single high-sensitivity silicon cantilever was used as shown in Fig. 1(a). The cantilever approached the surface in a perpendicular orientation to avoid snap-in to contact [4] and the motion of the cantilever was parallel to the surface. The cantilever was 250μm long, 5μm wide, and 340 nm thick, with a spring constant k = 7 × 10⁻⁴ N/m, a fundamental resonance frequency ω_c/2π = 7.385 kHz, and a quality factor Q = 31000 (Fig. 1(b)) [5]. The tip region of the cantilever has been thinned from 340 nm to < 100 nm using a reactive ion etch. The cantilever tip has a radius of ~ 30nm and has been coated with a thin layer of platinum using a shadow mask technique [4].

FIG. 1.

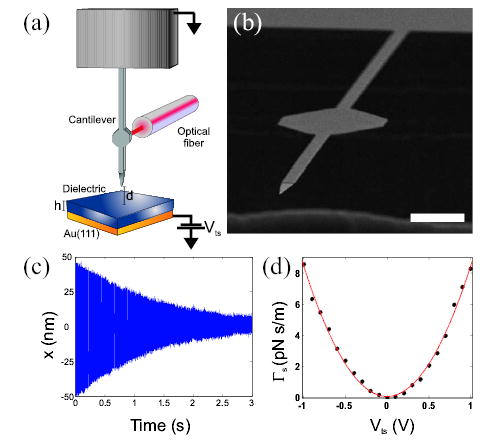
(a) Schematic of the experiment: d is the tip sample separation and h is the thickness of the polymer. The tip-sample voltage (V_ts) is applied to the metal layer underlying the dielectric while the cantilever is grounded. (b) Scanning electron micrograph of a cantilever like the one used in this study. The hexagonal paddle on the shaft of the cantilever provides a target for the fiber optic interferometer. The scale bar is 10μm. (c) Total friction is measured by driving the cantilever at ω_c abruptly turning off the drive signal and recording the ensuing decay to equilibrium shown here. (d) Sample induced friction (dots) for d = 15 nm as a function of the applied tip-sample voltage, with a quadratic fit (red line).

We measure the total friction Γ_t by recording the cantilever ringdown time τ, Fig. 1(c), and calculating Γ_t = 2k/ω_c²τ [3]. The total friction Γ_t = Γ₀ +Γ_s includes losses intrinsic to the cantilever Γ₀ plus any non-contact friction between the cantilever tip and the sample surface Γ_s. In high vacuum (10⁻⁴ Pa) the cantilever has an intrinsic friction of Γ₀ = 6 × 10⁻¹³ Ns/m, as measured far from the sample surface, and is sensitive to non-contact friction as small as 6 × 10⁻¹⁴ Ns/m.

The non-contact friction experienced by the tip can be enhanced by applying a voltage V_ts between the tip and the sample. Since the dependence of the friction on applied bias was quadratic in all samples, Fig. 1(d), and the cantilever Brownian motion agreed with the equipartition theorem, the assumption of linear response is valid [3]. The sample induced friction can therefore be attributed to electric field fluctuations and calculated using the fluctuation-dissipation theorem,

$${\mathrm{\Gamma }}_s=\frac{q^2{S}_E({\omega }_c)}{4k_{B}T},$$ (1)

where q = C(V_ts − φ) is the charge on the tip, C is the tip sample capacitance, φ is the contact potential difference between the tip and the sample, k_B is Boltzmann’s constant, T is the temperature, and

$$S_E({\omega }_c)=4{\int }_0^{\infty }cos({\omega }_{c}t)\langle \delta E_x(t)\hspace{0.17em}\delta E_x(0)\rangle dt$$ (2)

is the power spectrum at the cantilever resonance frequency of the electric field fluctuations experienced by the tip due to the sample. Here δE_x(t) is the electric field component parallel to the sample surface, in the direction of the cantilever motion. Since we observe Γ_s ∞ V_ts², it is reasonable to conclude that the fluctuating field from the sample is small compared to the applied tip-sample field and that the tip can be approximated as having a single contact potential.

For each sample, we begin by locating the sample surface. In order to avoid triboelectric charging, the tip was never allowed to touch the sample surface. We take zero height, d = 0, as the height at which the cantilever quality factor extrapolates to zero. We next measure Γ_t versus (V_ts) at a fixed tip-sample separation of about 30 nm. By fitting the resulting data (Fig. 1(d)) we determine the contact potential difference φ between the tip and the sample to within ±10 mV. We then measured Γ_t as a function of d, observing the same friction at V_ts = φ + 0.5 V and V_ts = φ − 0.5 V in all samples. Since any variation of φ with d would cause the friction to be different at the two voltages, we conclude that the contact potential is not a function of the tip-sample separation. This conclusion was verified by measuring Γ(V_ts) in a few samples as a function of height; the voltage at the Γ(V_ts) minimum, φ, was always independent of the tip-sample separation.

Non-contact friction was measured at room temperature in high vacuum over polymer thin films that were spin-cast onto epitaxial Au(111) substrates (Molecular Imaging). We measured non-contact friction over poly(methyl methacrylate) (PMMA, ε_r (relative dielectric constant) = 3.9, MW = 145, 000, PD(polydispersity) ≤ 1.05, Scientific Polymer Products), poly(vinyl acetate) (PVAc, ε_r = 3.4, MW = 147, 000, PD ≤ 3.1, Sigma-Aldrich), and polystyrene (PS, ε_r = 2.5, MW = 143, 000, PD ≤ 1.09, Scientific Polymer Products). In all samples, friction was measured at different locations and was found to be spatially invariant.

Figure 2 compares friction measured over films of the three polymers as a function of tip-sample separation at V_ts = φ + 0.5 V. PMMA (2(a)) clearly produces higher friction than PVAc (2(b)), and both exhibit dramatically higher friction than PS (2(c)) or Au(111) (2(a)). Since the tip-sample capacitance, and therefore the tip charge, must be larger over the blank Au(111) substrate, we conclude from Eq. 1 that the fluctuating field is dramatically enhanced by the presence of PMMA and PVAc films, but not by PS. Comparing friction over films of the same thickness and relative dielectric constant makes it clear just how dramatically the friction varies between polymers. We find Γ_PMMA/Γ_PS ~ 75 for the 450 nm-thick films over the range d = 8–20nm (see the black symbols in Fig. 2(a) and (c)). We conclude that the electric field fluctuations are strongly polymer dependent.

FIG. 2.

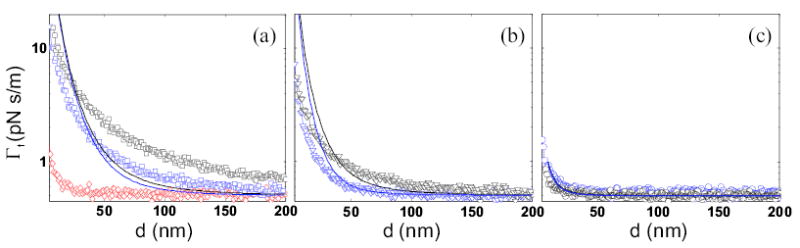
Total friction (Γ_t) at V_ts = φ + 0.5 V for films of different thicknesses on epitaxial Au(111) (symbols) with theoretical predictions based on dielectric spectroscopy measurements and calculated using Eq. 3 (lines). Note the semi-log scale. (a) Poly(methyl methacrylate): 40 nm film (blue squares, blue line) and 450 nm film (black squares, black line), plotted along with measured friction over blank Au(111) (red diamonds). (b) Poly(vinyl acetate): 12nm film (blue triangles, blue line) and 450nm film (black triangles, black line). (c) Polystyrene: 30 nm film (blue circles, blue line) and 450 nm film (black circles, black line).

To prove that the enhanced friction is not purely a surface effect, we vary the thickness h of the polymer films. We observe a decrease in Γ_s with decreasing h for both PVAc and PMMA, and a slight increase in friction upon reduction of the PS film thickness. The change in measured friction due to the reduction in thickness of the film depends on the polymer: for PMMA, Γ_{450 nm}/Γ_{40 nm} = 1.8 ± 0.2, for PVAc, Γ_{450 nm}/Γ_{12 nm} = 1.7 ± 0.1, and for PS, Γ_{450 nm}/Γ_{30 nm} = 0.6 ± 0.4. Since V_ts is applied between the tip and the metal layer underlying the polymer film, the tip-sample capacitance (and therefore the tip charge), increases with decreasing film thickness for a fixed tip-sample separation d. We would therefore expect greater friction at fixed d and V_ts for the thinner film. Instead, we observe a reduction in Γ_s with decreasing h for PMMA and PVAc, leading to the conclusion that S_E(ω_c) must be smaller over thinner films. While PS exhibits a slight increase in friction with decreasing h, we note that the change is not large enough to be explained by increasing tip charge alone, also implying a reduction in S_E(ω_c) with decreasing h. This relation between S_E(ω_c) and film thickness provides unambiguous evidence that the fluctuations responsible for the observed non-contact friction originate within the polymer films.

In order to illustrate this conclusion more clearly, we have determined S_E(ω_c) from the measured friction using Eq. 1 (Fig. 3). The tip charge in this calculation is estimated by approximating the tip-sample capacitance as that of a sphere over a ground plane [10]. The resulting S_E(ω_c) for Au(111) agrees with previous measurements [3]. The significant variation in S_E(ω_c) between polymers clearly indicates that the non-contact friction observed here depends on the chemical composition and, as presented above, the thickness of the film. Figure 3 is the central finding of this Letter.

FIG. 3.

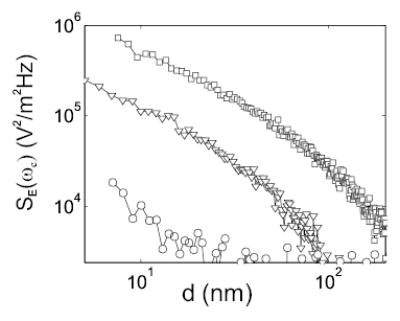
Electric field power spectrum for 450 nm-thick films of PMMA (squares), PVAc (triangles), and PS (circles).

The polymer electric field fluctuations are shielded by a thin layer of gold. In Fig. 4(a) we compare the non-contact friction over 350 nm PMMA spin cast onto Au(111) to that over a 350 nm PMMA spin cast onto quartz and then capped with 40 nm of thermally evaporated gold. The friction observed near uncoated PMMA is significantly larger than that observed over the metal-coated polymer. Since in both measurements V_ts is applied between the tip and the respective gold layer, one might argue that the polymer is not experiencing the tip field in the measurement over gold coated PMMA, making the comparison in Fig. 4(a) ambiguous. However, we have shown that S_E(ω_c) is not a function of the applied bias V_ts, which serves only to charge the tip capacitively. The gold-capped PMMA measurement therefore shows that the metal layer is indeed screening the electric field fluctuations from the polymer.

FIG. 4.

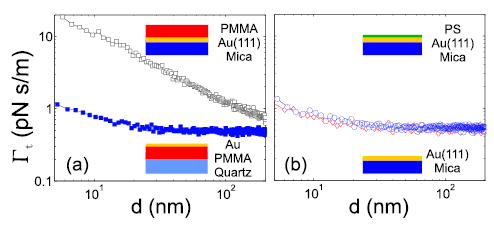
Total friction (Γ_t) at V_ts = φ +0.5V plotted on a log-log scale for (a) 350 nm PMMA on a Au(111)/mica substrate (squares) and 40 nm of Au, thermally evaporated onto 350nm of PMMA on a quartz substrate (filled squares). (b) 150 nm epitaxial Au(111) on mica (diamonds) and 30 nm PS on an Au(111)/mica substrate (circles).

Our data also constrain the possible mechanisms giving rise to the electric field fluctuations seen over bare poly-crystalline gold [3]. Figure 4 shows non-contact friction over two substrates, PMMA capped with 40nm of gold on a quartz substrate (a; blue squares) and 150nm Au(111) on mica (b; red diamonds). The friction is identical to within the noise of the measurement, indicating that friction does not depend on the nature of the underlying substrate [7]. It has been further proposed that acoustic modes in surface adsorbates might dramatically enhance non-contact friction [9]. In the high vacuum measurements presented here, we expect water to be the dominant surface adsorbate. Figure 4(b) compares non-contact friction measured over moderately hydrophilic Au(111) and a 30 nm layer of hydrophobic polystyrene. There is no measurable change in the observed friction, leading us to conclude that adsorbed water is not the source of non-contact friction over gold.

We propose that the non-contact friction produced by our polymer films arises from dielectric fluctuations within the film that produce a time-varying electric field at the capacitively charged tip, resulting in a fluctuating, time-dependent force on the cantilever. The fluctuation-dissipation relation in Eqs. 1 and 2 connects the Fourier transform of the equilibrium autocorrelation function of these field fluctuations to the non-contact friction. By a two-step argument that we defer to a future report [11], we have related Γ_s to the frequency-dependent dielectric response of the polymer film $\widehat{є}(\omega ),$ which may be independently measured. First, the mean-squared electric field fluctuation 〈(δE_x)²〉, the t = 0 limit of the correlation function in Eq. 2, is related, by a linear response argument and continuum electrostatics for a dielectric layer over a conductor [12], to ε, the static dielectric constant of the polymer film. Second, a corresponding dynamical relation between the Fourier transform in Eq. 2 and the complex dielectric function $\widehat{є}(\omega )$ is obtained within a quasistatic approximation [13, 14]. The sample-induced non-contact friction is related to the polymer dielectric function by

$${\mathrm{\Gamma }}_s=\frac{q^2{\widehat{\zeta }}^{″}({\omega }_c)}{8\pi {є}_0{h}^3{\omega }_c}{\int }_0^{\infty }\frac{y^2{e}^{-2yd/h}(1-e^{-4y})}{{(1+{\widehat{\zeta }}^{\prime }({\omega }_c)e^{-2y})}^2+{\widehat{\zeta }}^{″}({\omega }_c)e^{-4y}}dy,$$ (3)

with ε₀ the permittivity of free space and $\widehat{\zeta }(\omega )={\widehat{\zeta }}^{\prime }(\omega )+i{\widehat{\zeta }}^{″}(\omega )\equiv (\widehat{є}(\omega )\hspace{0.17em}-1)/(\widehat{є}(\omega )\hspace{0.17em}+1).$ The result in Eq. 3 thus rests on two approximations: linear response theory for the dielectric, and the adiabatic treatment [13, 14] of dielectric fluctuations.

We have measured $\widehat{є}(\omega )$ required to evaluate Eq. 3 by performing dielectric spectroscopy measurements on 450 nm thick films of PMMA and PVAc at room temperature. For PS, literature values for $\widehat{є}(\omega )$ were used [15]. By using our estimate for the tip sample capacitance and the dielectric response of each film at the cantilever frequency, we can predict the friction measured over each film from Eq. 3. The results are shown in Fig. 2(a)–(c) (lines). A clear agreement between theory and experiment is observed, remarkable given the order-of-magnitude estimate for the tip-sample capacitance and the single free parameter of the fit (the tip radius, which is taken to be 10 nm in all traces in Fig. 2).

We obtain a zero-free-parameter comparison of the measured friction to that predicted from Eq. 3 by taking the ratio of friction coefficients for different polymer films of the same thickness. We find for films where h = 450 nm and d = 8 – 20 nm the following measured (calculated) values: Γ_PMMA/Γ_PVAc = 4.4±0.4 (2.6±0.3), Γ_PMMA/Γ_PS = 75 ± 21 (71 ± 7), and Γ _PVAc/Γ_PS = 18 ± 5 (27±3). Equation 3 also qualitatively predicts the experimentally observed thickness dependence of the non-contact friction, as shown in Fig. 2(a)–(c). Our present analysis treats the polymer film as dynamically homogeneous, so that any variation in polymer dynamics with depth in the film that is dependent on molecular identity or polydispersity is not included in Eq. 3.

Although the non-contact friction observed here results from a coupling between dielectric fluctuations in the sample and charge on the cantilever, in the linear response regime, the fluctuating polarization induced by the cantilever’s electric field is proportional to the fluctuations present in the absence of a perturbing field. The theory employed here could be generalized to include interactions with inhomogeneous tip electric fields likely to be present even at V_ts = φ [3]. In this case, the tip will couple to the same dielectric fluctuations observed here, although other mechanisms may become important [7–9].

We conclude that dielectric fluctuations are dominating the non-contact friction over polymer thin films. While very low frequency dielectric fluctuations have been detected as a slowly varying force-gradient by scanned probe methods before [16], we believe our measurements constitute the first, direct, mechanical detection of non-contact friction due to dielectric fluctuations. This technique, generally applicable to any system exhibiting dielectric fluctuations with appreciable spectral density at ω_c, will enable exploration of dielectric fluctuations at the nanoscale. Equation 3 suggests that one route to minimizing non-contact friction due to dielectric fluctuations is to work with radio-frequency cantilevers. We anticipate that numerous applications, including the direct detection of polymer fluctuations at or around the glass transition, should result from the new view of non-contact friction presented here.