Abstract
Age-related changes in bone quality are mainly manifested in the reduced toughness. Since the post-yield deformation of bone is realized through microdamage formation (e.g., microcracking and diffuse damage), it is necessary to understand the mechanism of microdamage formation in bone in order to elucidate underlying mechanisms of age-related bone fractures. In this study, a two-dimensional shear lag model was developed to predict stress concentration fields around an initial crack in a mineral-collagen composite. In this model, non-linear elasticity was assumed for the collagen phase, and linear elasticity for the mineral. Based on the pattern of the stress concentration fields, the condition for microdamage formation was discussed. The results of our analyses indicate that: (1) an initial crack formed in mineral phase may cause stress concentration in the adjacent mineral layers; (2) the pattern of stress concentration fields depends not only on the spatial but also mechanical properties of the collagen and mineral phases; (3) the pattern of the stress concentration fields could determine either coalescence or scattering of nano cracks around the initial crack.
Keywords: Bone, Nanomechanistic model, Microdamage, Collagen, Mineral
1. Introduction
Age-related bone fracture is a major concern in the health care of the elderly as people live longer. Bone is a natural composite material and comprises approximately 60% mineral (mainly hydroxyapatite), 30% proteins (90% type I collagen), and 10% water by weight (Katz, 1971; Lane, 1979). From mechanics of materials perspectives, the toughness of a material relies mainly on its post-yield behavior because the dissipation of a large amount of energy is possible only through the post-yield deformation process. Thus, elucidating how energy dissipates during the post-yield deformation could provide important insights in the mechanism of osteoporotic and age-related bone fractures. In the past, investigators have attempted to address this issue. For instance, experimental studies suggested that the micro-damage accumulation in bone play a significant role in its post-yield behavior (Akkus and Rimnac, 2001; Burr et al., 1997, 1998; Fazzalari et al., 1998; Forwood and Parker, 1989; Norman et al., 1998; Reilly and Currey, 1999; Timlin et al., 2000; Zioupos et al., 1994). Also, it has been shown that yielding of bone tissues coincides with the formation of diffuse damages (Zioupos et al., 1994), and microcracking may help sustain the toughness of bone (Vashishth et al., 2000, 2003; Zioupos, 2001). Similarly, microdamage accumulation may play a significant role in energy dissipation during fatigue failure or monotonic fracture of bone (Burr, 1993; Burr et al., 1997; Fazzalari et al., 1998; Norman et al., 1998; Schaffler et al., 1995; Zioupos, 2001).
Bone is a quasi-brittle material characterized by the fact that its elastic modulus (or stiffness of the tissue) decreases with increasing microdamage accumulation during the post-yield deformation. Fig. 1 shows a typical stress–strain curve of compact bone in a uniaxial cyclic test. Based on continuum damage mechanics, the energy dissipation in post-yield deformation of bone is associated with microdamage accumulation and could be explained by the increased surface energy due to the formation of new crack surfaces. However, the surface energy by microcrack formation alone cannot explain the energy dissipation by the plastic (residual) and viscoelastic deformation associated with the post-yielding of bone (i.e., εp and hysteresis loop in Fig. 1).
Fig. 1.
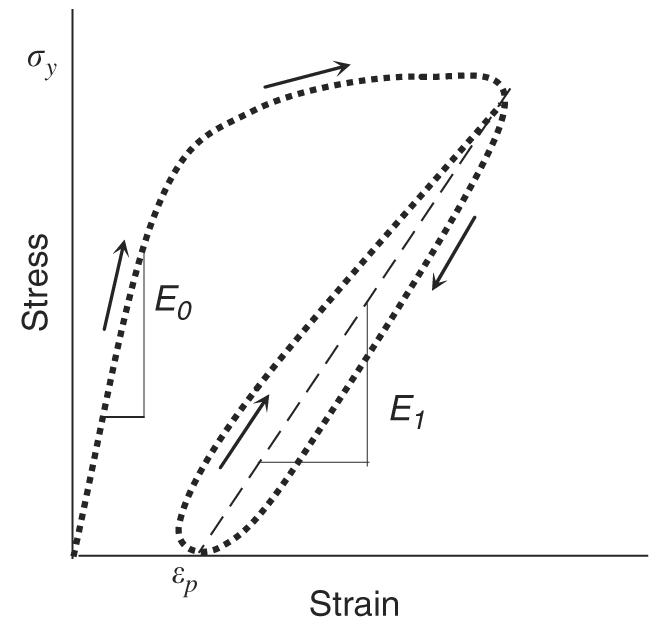
A schematic representation of a typical stress–strain curve of cortical bone: residual strain (εp) and hysteresis (the loop between loading–unloading curves) can be observed after yielding of bone.
So far, very limited information is available in the literature pertaining to the modeling of bone damage formation at the length scales of mineral-collagen fibril composites (i.e., submicron or nanometers). Recently, some investigators developed several micromechanistic models to study the elastic deformation of mineralized collagen fibrils using shear lag approaches, or equivalent inclusion theory, or combination of equivalent inclusion and mean field theories (Harrigan and Reuben, 1997; Jéager and Fratzl, 2000; Kotha and Guzelsu, 2000, 2003; Kotha and Guzeslu, 2002). However, little is known about the post-yield behavior of bone at this length scales.
To address this issue, the present study was intended to investigate the underlying mechanism of micro-damage formation in bone using a shear lag model of mineral-collagen composite. Using this model, the stress concentration around an initial crack was analyzed, and the possible mode of damage formation around the initial crack was discussed based on the pattern of stress concentration.
2. Analytical treatments
2.1. Modes of microdamage formation in bone
Two major types of microdamages in bone are commonly observed: microcracks and diffuse damages. The microcracks are single cracks visible under microscope (Burr et al., 1997; Martin et al., 1996; Schaffler et al., 1994; Zioupos et al., 1995, 1994), whereas diffuse damages are composed of extensive networks of fine ultrastructural-level cracks, which can be observed only by staining (Boyce et al., 1998; Fazzalari et al., 1998). As shown in Fig. 2, microcracks are defined as individual cracks in bone whose size is the range of microns or even longer, whereas diffuse damage is a damaged zone where a large array of nano-cracks are formed (Bentolila et al., 1998). Fig. 3 shows a fluorescence microphotograph of a diffuse damage in cortical bone by laser confocal microscopy.
Fig. 2.
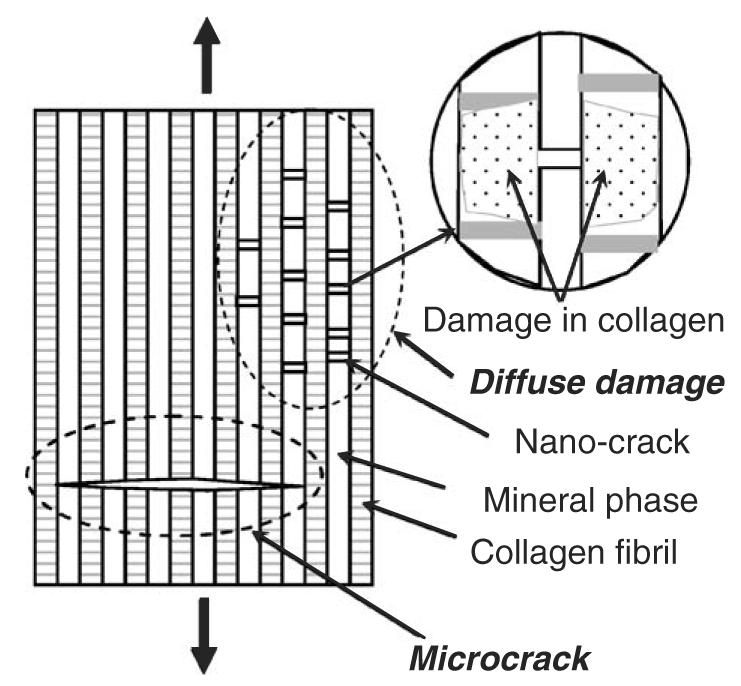
A schematic representation of a microcrack and a diffuse damage in bone: a microcrack runs cross multiple mineral layers, while a diffuse damage is characterized by a distributed array of nano cracks that situate in the mineral layers.
Fig. 3.
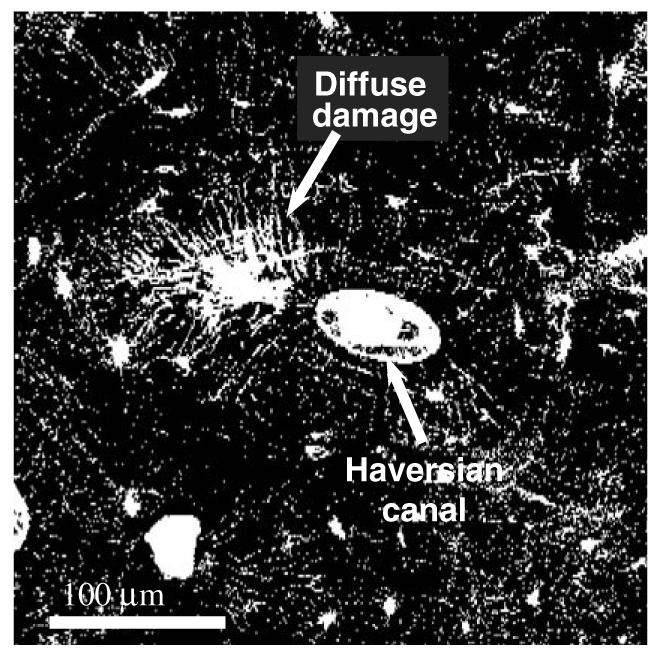
A fluorescence microphotograph (laser confocal microscopy) of a diffuse damage in a transverse cross section of a human cadaveric femur: the bone sample was stained with basic fuchsin following the procedure provided by Burr and Stafford (1990). The fluorescence microphotograph indicates that the diffuse damage comprises a large amount of submicron level defects (nano crack arrays).
Microcracking may function as a toughening mechanism by dissipating energy in the form of surface energy released from the new crack surfaces (Vashishth et al., 2003). In contrast, diffuse damages may lead to energy dissipation through both new crack surface formation and collagenous matrix damage (Fig. 2). Comparing the two types of microdamages, it is obvious that a diffuse damage could absorb more energy than microcracks because it allows for additional energy dissipation. In a diffuse damage zone, it is presumable that the collagen fibrils are readily traumatized by the stress concentration around the tip of the nano-crack (Fig. 2, insert). These cracks in the diffuse damages are reported to be at the order of nano meters (Bentolila et al., 1998).
To study the mechanism of microdamage formation (i.e., microcrack and diffuse damage), it is necessary to know how damages are formed starting from an initial defect in the tissue. Since bone is a natural composite material comprising mineral crystals and collagen fibrils, it is reasonable to study bone tissues using the approaches that have been employed for analyzing engineering composite materials. In the present study, a simplified model was investigated, assuming that an initial crack exists in the mineral phase with a non-linearly elastic collagen phase present.
2.2. Non-linear-elastic model
Fig. 4 shows the schematic representation of the model proposed in this study based on the assumption that bone is a composite of hydroxyapatite mineral reinforced by the collagen fibrils (Hellmich and Ulm, 2002). In this model, an initial crack is assumed to exist in the mineral phase. The cracked layer of mineral phase (Layer 1) is sandwiched between two collagen layers, and then further sandwiched by another two mineral layers (Layer 2). The long axis of the unit is parallel to the longitudinal direction of bone. Considering that the thickness of the whole unit is unity, the two-dimensional and five-component unit model was analyzed using the “shear lag” theory first proposed by Hedgepeth (Hedgepeth, 1961). Based on the shear lag theory, it is assumed that the mineral phase carries normal load only and the collagen phase carries shear load only. Thus, the shear load is exerted only to one side of the mineral layer 2, which is adjacent to the initial crack. Since the collagen phase is much more compliant than the mineral phase, this assumption should be adequate without losing reasonable accuracy. Based on the symmetry of this unit model, the free body diagram of the differential element includes only half of the unit (i.e., half thickness of mineral layer 1 + collagen layer + mineral layer 2). The force equilibrium of the differential element is derived:
| (1) |
where, p1(= σ1d) and p2(= σ2d) are the forces exerted in the cracked (layer 1) and the adjacent (layer 2) mineral layer, respectively, d is the thickness of the mineral layer, and τ is the shear stress exerted in the collagen phase. For ease of discussion, no conversion from the normal loads to stresses is attempted during the following analysis. Assuming that the stress–strain behavior of the mineral phase is linearly elastic, whereas the collagen phase is non-linear-elastic and obeys the power law,
| (2) |
where, Em is the elastic modulus of the mineral phase, γ is the shear strain in the collagen layer, G is the shear stiffness factor and n is a factor greater than unity and determines the non-linearity of the collagen phase, u1 and u2 are the displacements of mineral layer 1 and 2 along the longitudinal direction of the unit model, and h is the thickness of the collagen phase. By introducing two dimensionless numbers α = Emhn/(Gd) and ξ = x/d, the following differential equations of displacements can be obtained:
| (3) |
Solving the above equations for u1 and u2 (see Appendix A), the applied loads in the cracked and the adjacent mineral layers can be obtained as
| (4) |
where and . Using Eq. (4), the stress distribution in the mineral phase can be obtained.
Fig. 4.
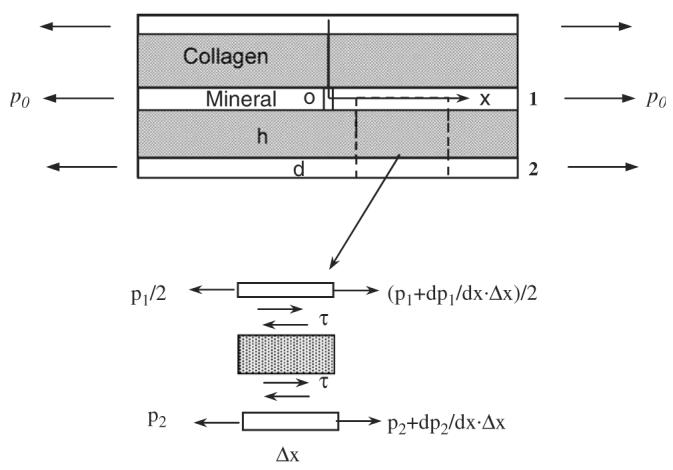
A schematic presentation of the non-linear-elastic model: in this model, three mineral and two collagen layers were included in a unit with the middle mineral layer having a crack perpendicular to the long axis of the mineral-collagen composite. It is assumed that the mineral phase carries only axial load, whereas the collagen phase carries only shear load and behaves non-linear elastically. In the figure, p0 is the nominal load applied, p1 and p2 are the tensile loads exerted in the mineral layers 1 and 2, respectively, and h and d are the thickness of the mineral and collagen phases, respectively.
3. Results
As shown in Figs. 5-7, the normal load (p2) exerted in the mineral layer 2 is greater than the nominal (remote) load, p0, applied to the mineral phase. Also, a stress concentration zone symmetric to the initial crack plane exists in the mineral layer 2, with a maximum load 1.5 times greater than the nominal load (p0). Most importantly, the pattern of stress distribution in the mineral layer 2 is dependent on the spatial and material properties of both the mineral and collagen phases.
Fig. 5.
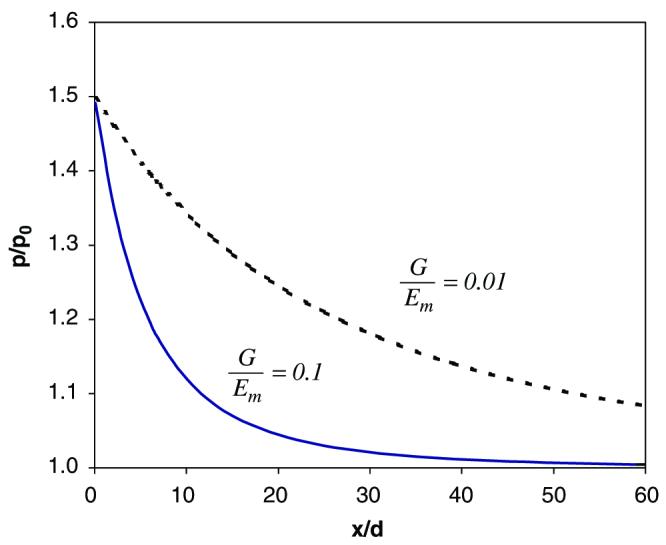
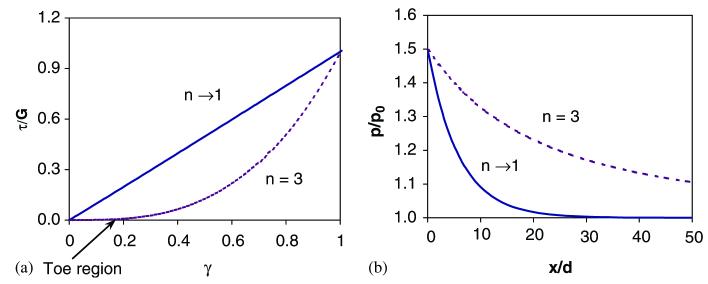
Stress concentration patterns in the mineral layer 2: (a) the linear (n → 1) and non-linear (n = 3) behaviors of the collagen phase used in the analysis; (b) effect of collagen non-linearity on the stress concentration pattern in the adjacent mineral layer to the initial crack. In the linear elastic case (n → 1), stress concentration occurs in a narrows region with respect to the original crack plane, whereas the stress concentration region is greatly expanded in the non-linear elastic case (n = 3). For ease of analysis, the following material and spatial properties of the mineral and collagen phases are employed: G = 1.0 GPa, Em = 100 GPa, h/d = 1.0, where G is the shear stiffness of the collagen phase, Em is the elastic modulus of the mineral phase, n is the collagen non-linearity factor, h and d are the thickness of the collagen and mineral phases, respectively.
Fig. 7.
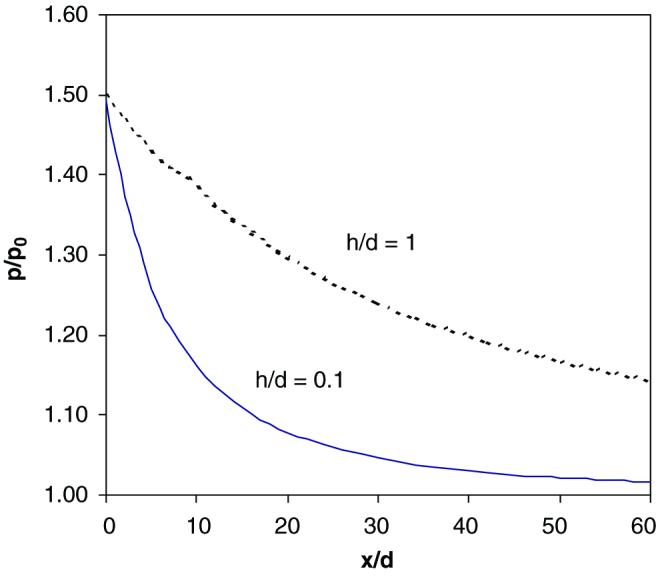
Stress concentration patterns in the mineral layer 2 as a function of the thickness ratio of the collagen phase vs. the mineral phase (h/d) For a thicker collagen phase (h/d = 1), the stress concentration region is significantly expanded compared with the thinner collagen phase (h/d = 0.1) For ease of analysis, the following material and spatial properties of the mineral and collagen phases are employed: G = 1.0 GPa, Em = 100 GPa, n = 3, where G is the shear stiffness of the collagen phase, Em is the elastic modulus of the mineral phase, n is the collagen non-linearity factor, h and d are the thickness of the collagen and mineral phases, respectively.
Effect of non-linearity of the collagen phase
Fig. 5 shows the effect of the non-linearity of the collagen phase on the pattern of stress concentration zone. The non-linearity is determined by the power exponent, n, shown in Eq. (2). The collagen phase behaves in a linear elastic manner when n → 1, and non-linear-elastically when n>1 (Fig. 5a). Also, the “toe region” in the stress–strain curve of the collagen phase expands as the non-linearity increases (n↑). The results show that the stress concentration zone is considerably expanded for a non-linear-elastic collagen phase compared to the linear-elastic one (Fig. 5b).
Effect of the stiffness ratio between the mineral and collagen phases
As exhibited in Fig. 6, the greater the ratio between the stiffness of the collagen and mineral phase (G/Em↑), the sharper the stress concentration zone in the mineral layer 2. In other words, an increase in the stiffness of the collagen phase or a decrease in the stiffness of the mineral phase would lead to sharp stress concentration in the mineral layer 2.
Fig. 6.
Stress concentration patterns in the mineral layer 2 as a function of the stiffness ratio of the collagen phase vs. the mineral phase (G/Em) For a more compliant collagen phase (G/Em = 0.01), the stress concentration region is significantly expanded compared with a stiffer collagen phase (G/Em = 0.1) For ease of analysis, the following material and spatial properties of the mineral and collagen phases are employed: Em = 100 GPa, n = 3, h/d = 1.0, where G is the shear stiffness of the collagen phase, Em is the elastic modulus of the mineral phase, n is the collagen non-linearity factor, h and d are the thickness of the collagen and mineral phases, respectively.
Effect of the thickness ratio of the mineral and collagen phases
The thickness ratio (h/d between the collagen and mineral layers also affects the pattern of stress concentration. As shown in Fig. 7, a decrease in the thickness ratio (h/d ↓) between the mineral and collagen phase results in a sharp tress concentration zone. Since the thickness ratio relates to the volume fraction of these constituents, it is presumable that a higher volume fraction of the collagen phase may lead to an expanded stress concentration zone around the initial crack. This suggests that the spatial arrangement of the mineral and collagen phases is also an influencing factor on micro-damage formation in bone.
4. Discussion
The analytical model proposed in this study is useful for predicting the stress concentration patterns around an initial crack in a nano level construct of mineral-collagen composite. It is anticipated that this nanomechanics model could help relate the spatial and material properties of bone constituents (i.e., the mineral and collagen phases) to the failure behavior induced by an existing crack in the tissue. The results obtained from the proposed model are supported by the experimental results reported in the literature, which have shown that changes in the collagen and mineral phase could lead to significant changes in the post-yield properties of bone (Boskey et al., 1999; Burstein et al., 1975; Catanese et al., 1999; Katz, 1971; Martin, 1993; Opsahl et al., 1982; Oxlund et al., 1995; Vashishth et al., 2001; Wang et al., 2001, 2002; Zioupos et al., 1999). We believe that the present model could provide some insights into the underlying mechanism of microdamage formation in bone.
Failure in the mineral phase could be deemed as a probabilistic event due to the inhomogeneous nature of bone tissues. Thus, the pattern of stress concentration in an adjacent mineral layer to an initial crack would have effect on where failure occurs. As shown in Fig. 8, if a sharp stress concentration occurs, a crack would be induced most likely within the initial crack plane. This in turn would facilitate further formation of cracks in the succeeding mineral layers in the plane and eventually lead to crack coalescence into a microcrack. On the other hand, if the stress concentration zone is expanded (Fig. 8), the probability of scattered crack formation in the neighboring region of the initial crack increases. In such a case, cracks may be formed in a scattered manner around the initial crack and eventually become an array of nano cracks.
Fig. 8.
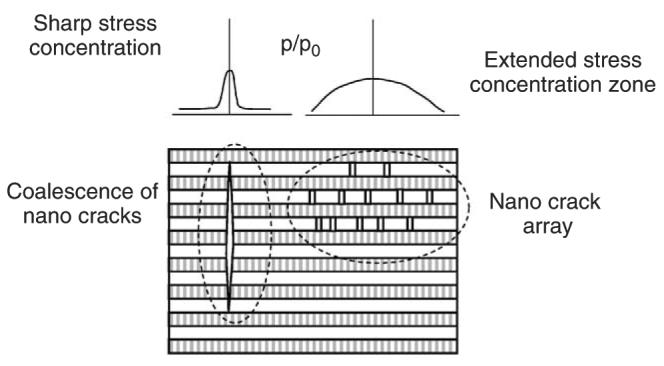
A schematic representation of damage formation as a function of stress concentration pattern around the initial crack: for acute stress concentration, coalescence of cracks most likely occurs, whereas enlarged stress concentration zone facilitates the formation of nanocrack arrays.
From composite materials perspectives, stress concentration induced by an existing crack facilitates further crack formation and/or propagation. The analytical results of the present study indicate that stress concentration exists in the immediately adjacent mineral layer of an initial crack in the mineral-collagen composite model. Additionally, the pattern of stress concentration is not only dependent on the material properties (i.e., collagen non-linearity, n, and stiffness ratio, G/Em), but also on the spatial properties of bone constituents (i.e., thickness ratio, h/d).
An important finding of this study is that collagen non-linearity may significantly alter the stress concentration pattern around the initial crack (Fig. 5). If the collagen phase behaves linear-elastically and exhibits little ‘toe region’ in its stress–strain curve (n → 1) as shown in Fig. 5a, a sharper stress concentration zone would be introduced in the adjacent mineral layer with respect to the initial crack plane (Fig. 5b). In this case, the induced nano cracks is most likely situated along the initial crack plane, thereby facilitating the formation of a much larger and microscopically visible crack (i.e., coalescence of nano cracks). In contrast, if the ‘toe region’ expands or the collagen non-linearity increases, the stress concentration zone expands, thus increasing the chance for crack formation away from the initial crack plane. This would inhibit coalescence of these cracks and facilitate formation of diffuse damages (Fig. 8). The supporting evidence of this mechanism can be found in the literature. A study performed by Vashishth et al. (2001) demonstrated that the collagen phase becomes much stronger and stiffer as glycation induced crosslinks increase and its stress–strain curve shows less non-linearity (or a reduced toe region) compared with the controls. Such changes in the collagen phase were found to be associated with a decrease in the toughness of the tissue. In addition, an early investigation by our group indicated that the collagen phase in bone loses its non-linearity (i.e., a reduced toe region) with increasing age and such changes also are associated with the decreased toughness of bone (Wang et al., 2002).
As shown in Fig. 6, an increase in the stiffness ratio (G/Em ↑) could also result in a sharp stress concentration zone with respect to the initial crack plane, which may facilitate the coalescence of cracks along the plane. Such an effect is observed in the previous experimental data reported. For instance, several studies have shown that the non-enzymatic crosslinks could increase the stiffness of collagen fibrils and subsequently cause reduced toughness of bone (Catanese et al., 1999; Vashishth et al., 2001). The mechanistic model discussed in this study can easily explain the underlying mechanism of these experimental observations. That is, an increased stiffness of the collagen phase (or a decrease in the stiffness of the mineral phase) may cause an increase in the stiffness ratio (G/Em), thereby leading to an acute stress concentration around an existing crack, which would consequently facilitating the coalescence of cracks along the initial crack plane.
In addition, it is interesting to notice that the thickness ratio of the mineral phase versus collagen fibrils may also play a significant role in determining the stress concentration pattern around an initial crack. As shown in Fig. 7, the stress concentration zone becomes acute as the thickness ratio between the mineral and collagen phases increases (h/d ↑). It is presumable that thicker mineral phase (or thinner collagen phase) means greater volume fraction of mineral in bone. Thus, this result suggests that a greater mineral volume fraction may facilitate the coalescence of nano cracks along the initial crack plane, which is consistent with the experimental data reported in the literature. For example, Currey (1984) and Currey et al. (1996) investigated the effect of mineralization on the fracture toughness of bone, and found that a higher mineralization (greater volume fraction of the mineral phase) produces a lower toughness of bone. In addition, Jepsen et al. (2001) investigated the effect of volume changes in bone constituents on the toughness of mice bone, and demonstrated that a reduced collagen content is associated with declining of the toughness of bone. Also, Zioupos et al. (1994) investigated the less mineralized antler bone and ordinary bone tissues, and the results of his study demonstrated that the antler tissue appears to produce more diffuse damages at yielding and is much tougher than the ordinary bone, suggesting that a less dense mineral phase may lead to an increase in the toughness of bone.
However, it should be pointed out that the analyses in this study have limitations. First, we used a two-dimensional model of layered structure of mineral-collagen composite, which is not representative of real structure of bone. Thus, the results of this study only provide qualitative information for predicting the relationship of spatial and material properties of bone constituents with microdamage formation in bone. Second, this model assumed that the initial crack is perpendicular to the collagen fibril direction. In reality, the initial crack may be formed in other orientations, such as parallel to the longitudinal direction of collagen fibrils. To study the damage formation in other orientations, further investigation is required. Also, the contribution of microstructural factors (e.g., cement lines, osteons, etc.) to the microdamage formation was not taken into consideration in this study. Thus, this model is valid only for the mineral-collagen fibril composite discussed in this study. Nonetheless, the information obtained from this study could help understand contributions of ultrastructural and material properties of bone constituents to the toughness of bone reported in the literature (Burr et al., 1985; Martin and Burr, 1982; Muir et al., 1999). Finally, in this study we used the pattern of stress concentration to predict the mode of crack formation (i.e., coalescence or crack array). We assumed that the inhomogeneity in the structure and material properties of bone constituents could lead to probabilistic distributions of failure in the mineral phase. In other word, the failure in the mineral phase may not necessarily occur at the location where the maximum load is applied. Although this assumption is probably true (Bloebaum et al., 1997), further investigations are still needed.
In summary, the shear lag model of a mineral-collagen composite proposed in this study could, for the first time, provide an analytical base for elucidating the mechanism of microdamage formation in bone. The results of our analysis indicate that the stress concentration pattern around an initial crack in bone is dependent upon collagen non-linearity, stiffness and volume fraction of bone constituents. The pattern of stress concentration may eventually determine the mode of microdamage formation in bone (i.e., crack coalescence and crack arrays).
Acknowledgement
The authors are grateful to Dr. Haichao Han for his constructive discussion and comments during the preparation of this paper.
Appendix A. Non-linear-elastic model of a nano crack in a mineral-collagen composite
From Eq. (3)
| (A.1) |
Rearrange it, one obtains
| (A.2) |
where Δ = u1 − u2. Denote
| (A.3) |
a direct calculation yields
| (A.4) |
which, in turn, implies W (ξ) is a constant. Therefore,
| (A.5) |
Under the conditions Δ(∞) = 0 and dΔ/dξ|ξ = ∞ = 0, it can be concluded that c is identical to zero.
As a result,
| (A.6) |
Solving the above equation, we have
| (A.7) |
Substituting Eq. (A.7) into Eq. (A.6), C1 can be determined.
| (A.8) |
By inspecting Eqs. (A.1) and (A.6), and using the following boundary conditions:
| (A.9) |
The solution for Eq. (A.1) can be obtained as
| (A.10) |
The constants can be determined:
| (A.11) |
Finally, we have
| (A.12) |
| (A.13) |
References
- Akkus O, Rimnac CM. Fracture resistance of gamma radiation sterilized cortical bone allografts. Journal of Orthopaedics Research. 2001;19:927–934. doi: 10.1016/S0736-0266(01)00004-3. [DOI] [PubMed] [Google Scholar]
- Bentolila V, Boyce TM, Fyhrie DP, Drumb R, Skerry TM, Schaffler MB. Intracortical remodeling in adult rat long bones after fatigue loading. Bone. 1998;23:275–281. doi: 10.1016/s8756-3282(98)00104-5. [DOI] [PubMed] [Google Scholar]
- Bloebaum RD, Skedros JG, Vajda EG, Bachus KN, Constantz BR. Determining mineral content variations in bone using backscattered electron imaging. Bone. 1997;20:485–490. doi: 10.1016/s8756-3282(97)00015-x. [DOI] [PubMed] [Google Scholar]
- Boskey AL, Wright TM, Blank RD. Collagen and bone strength. Journal of Bone and Mineral Research. 1999;14:330–335. doi: 10.1359/jbmr.1999.14.3.330. [DOI] [PubMed] [Google Scholar]
- Boyce TM, Fyhrie DP, Glotkowski MC, Radin EL, Schaffler MB. Damage type and strain mode associations in human compact bone bending fatigue. Journal of Orthopaedics Research. 1998;16:322–329. doi: 10.1002/jor.1100160308. [DOI] [PubMed] [Google Scholar]
- Burr DB. Remodeling and the repair of fatigue damage. Calcified Tissue International. 1993;53:S75–S80. doi: 10.1007/BF01673407. (discussion S80-1) [DOI] [PubMed] [Google Scholar]
- Burr DB, Stafford T. Validity of the bulk-staining technique to separate artifactual from in vivo bone microdamage. Clinical Orthopaedics. 1990:305–308. [PubMed] [Google Scholar]
- Burr DB, Martin RB, Schaffler MB, Radin EL. Bone remodeling in response to in vivo fatigue microdamage. Journal of Biomechanics. 1985;18:189–200. doi: 10.1016/0021-9290(85)90204-0. [DOI] [PubMed] [Google Scholar]
- Burr DB, Forwood MR, Fyhrie DP, Martin RB, Schaffler MB, Turner CH. Bone microdamage and skeletal fragility in osteoporotic and stress fractures. Journal of Bone and Mineral Research. 1997;12:6–15. doi: 10.1359/jbmr.1997.12.1.6. [DOI] [PubMed] [Google Scholar]
- Burr DB, Turner CH, Naick P, Forwood MR, Ambrosius W, Hasan MS, Pidaparti R. Does microdamage accumulation affect the mechanical properties of bone? Journal of Biomechanics. 1998;31:337–345. doi: 10.1016/s0021-9290(98)00016-5. [DOI] [PubMed] [Google Scholar]
- Burstein AH, Zika JM, Heiple KG, Klein L. Contribution of collagen and mineral to the elastic–plastic properties of bone. Journal of Bone and Joint Surgery American. 1975;57:956–961. [PubMed] [Google Scholar]
- Catanese J, Bank RA, TeKoppele JM, Keaveny TM. Increased cross-linking by non enzymatic glycation reduces the ductility of bone and bone collagen; ASME 1999 Bioengineering Conference. Bioengineering Division; 1999. pp. 267–268. [Google Scholar]
- Currey JD. Effects of differences in mineralization on the mechanical properties of bone. Philosophical Transactions of the Royal Society of London B Biological Sciences. 1984;304:509–518. doi: 10.1098/rstb.1984.0042. [DOI] [PubMed] [Google Scholar]
- Currey JD, Brear K, Zioupos P. The effects of ageing and changes in mineral content in degrading the toughness of human femora. Journal of Biomechanics. 1996;29:257–260. doi: 10.1016/0021-9290(95)00048-8. [DOI] [PubMed] [Google Scholar]
- Fazzalari NL, Forwood MR, Manthey BA, Smith K, Kolesik P. Three-dimensional confocal images of microdamage in cancellous bone. Bone. 1998;23:373–378. doi: 10.1016/s8756-3282(98)00111-2. [DOI] [PubMed] [Google Scholar]
- Fazzalari NL, Forwood MR, Smith K, Manthey BA, Herreen P. Assessment of cancellous bone quality in severe osteoarthrosis: bone mineral density, mechanics, and microdamage. Bone. 1998;22:381–388. doi: 10.1016/s8756-3282(97)00298-6. [DOI] [PubMed] [Google Scholar]
- Forwood MR, Parker AW. Microdamage in response to repetitive torsional loading in the rat tibia. Calcified Tissue International. 1989;45:47–53. doi: 10.1007/BF02556660. [DOI] [PubMed] [Google Scholar]
- Harrigan TP, Reuben JD. Mechanical model for critical strain in mineralizing biological tissues: application to bone formation in biomaterials. Biomaterials. 1997;18:877–883. doi: 10.1016/s0142-9612(97)00006-9. [DOI] [PubMed] [Google Scholar]
- Hedgepeth JM. Stress concentrations in filamentary structures. 1961 NASA-TN-D-882, May 1961. [Google Scholar]
- Hellmich C, Ulm FJ. Are mineralized tissues open crystal foams reinforced by crosslinked collagen? Some energy arguments. Journal of Biomechanics. 2002;35:1199–1212. doi: 10.1016/s0021-9290(02)00080-5. [DOI] [PubMed] [Google Scholar]
- Jéager I, Fratzl P. Mineralized collagen fibrils: a mechanical model with a staggered arrangement of mineral particles. Biophysics Journal. 2000;79:1737–1746. doi: 10.1016/S0006-3495(00)76426-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jepsen KJ, Pennington DE, Lee YL, Warman M, Nadeau J. Bone brittleness varies with genetic background in A/J and C57BL/6J inbred mice. Journal of Bone and Mineral Research. 2001;16:1854–1862. doi: 10.1359/jbmr.2001.16.10.1854. [DOI] [PubMed] [Google Scholar]
- Katz JL. Hard tissue as a composite material. I. Bounds on the elastic behavior. Journal of Biomechanics. 1971;4:455–473. doi: 10.1016/0021-9290(71)90064-9. [DOI] [PubMed] [Google Scholar]
- Kotha SP, Guzelsu N. The effects of interphase and bonding on the elastic modulus of bone: changes with age-related osteoporosis. Medical Engineering and Physics. 2000;22:575–585. doi: 10.1016/s1350-4533(00)00075-8. [DOI] [PubMed] [Google Scholar]
- Kotha SP, Guzelsu N. Effect of bone mineral content on the tensile properties of cortical bone: experiments and theory. Journal of Biomechanical Engineering. 2003;125:785–793. doi: 10.1115/1.1631586. [DOI] [PubMed] [Google Scholar]
- Kotha SP, Guzeslu N. Modeling the tensile mechanical behavior of bone along the longitudinal direction. Journal of Theoretical Biology. 2002;219:269–279. doi: 10.1006/jtbi.2002.3120. [DOI] [PubMed] [Google Scholar]
- Lane JM. American Academy of Orthopaedics and Surgery. Chicago: 1979. Biochemistry of fracture repair. AAOS Monterey Seminar; pp. 141–165. [Google Scholar]
- Martin B. Aging and strength of bone as a structural material. Calcified Tissue International. 1993;53:S34–S39. doi: 10.1007/BF01673400. (discussion S39-40) [DOI] [PubMed] [Google Scholar]
- Martin RB, Burr DB. A hypothetical mechanism for the stimulation of osteonal remodelling by fatigue damage. Journal of Biomechanics. 1982;15:137–139. doi: 10.1016/s0021-9290(82)80001-8. [DOI] [PubMed] [Google Scholar]
- Martin RB, Stover SM, Gibson VA, Gibeling JC, Griffin LV. In vitro fatigue behavior of the equine third metacarpus: remodeling and microcrack damage analysis. Journal of Orthopaedics Research. 1996;14:794–801. doi: 10.1002/jor.1100140517. [DOI] [PubMed] [Google Scholar]
- Muir P, Johnson KA, Ruaux-Mason CP. In vivo matrix microdamage in a naturally occurring canine fatigue fracture. Bone. 1999;25:571–576. doi: 10.1016/s8756-3282(99)00205-7. [DOI] [PubMed] [Google Scholar]
- Norman TL, Yeni YN, Brown CU, Wang Z. Influence of microdamage on fracture toughness of the human femur and tibia. Bone. 1998;23:303–306. doi: 10.1016/s8756-3282(98)00103-3. [DOI] [PubMed] [Google Scholar]
- Opsahl W, Zeronian H, Ellison M, Lewis D, Rucker RB, Riggins RS. Role of copper in collagen cross-linking and its influence on selected mechanical properties of chick bone and tendon. Journal of Nutrition. 1982;112:708–716. doi: 10.1093/jn/112.4.708. [DOI] [PubMed] [Google Scholar]
- Oxlund H, Barckman M, Ortoft G, Andreassen TT. Reduced concentrations of collagen cross-links are associated with reduced strength of bone. Bone. 1995;17:365S–371S. doi: 10.1016/8756-3282(95)00328-b. [DOI] [PubMed] [Google Scholar]
- Reilly GC, Currey JD. The development of microcracking and failure in bone depends on the loading mode to which it is adapted. Journal of Experimental Biology. 1999;202:543–552. doi: 10.1242/jeb.202.5.543. [DOI] [PubMed] [Google Scholar]
- Schaffler MB, Pitchford WC, Choi K, Riddle JM. Examination of compact bone microdamage using back-scattered electron microscopy. Bone. 1994;15:483–488. doi: 10.1016/8756-3282(94)90271-2. [DOI] [PubMed] [Google Scholar]
- Schaffler MB, Choi K, Milgrom C. Aging and matrix microdamage accumulation in human compact bone. Bone. 1995;17:521–525. doi: 10.1016/8756-3282(95)00370-3. [DOI] [PubMed] [Google Scholar]
- Timlin JA, Carden A, Morris MD, Rajachar RM, Kohn DH. Raman spectroscopic imaging markers for fatigue-related microdamage in bovine bone. Analytical Chemistry. 2000;72:2229–2236. doi: 10.1021/ac9913560. [DOI] [PubMed] [Google Scholar]
- Vashishth D, Tanner KE, Bonfield W. Contribution, development and morphology of microcracking in cortical bone during crack propagation. Journal of Biomechanics. 2000;33:1169–1174. doi: 10.1016/s0021-9290(00)00010-5. [DOI] [PubMed] [Google Scholar]
- Vashishth D, Gibson GJ, Khoury JI, Schaffler MB, Kimura J, Fyhrie DP. Influence of nonenzymatic glycation on biomechanical properties of cortical bone. Bone. 2001;28:195–201. doi: 10.1016/s8756-3282(00)00434-8. [DOI] [PubMed] [Google Scholar]
- Vashishth D, Tanner KE, Bonfield W. Experimental validation of a microcracking-based toughening mechanism for cortical bone. Journal of Biomechanics. 2003;36:121–124. doi: 10.1016/s0021-9290(02)00319-6. [DOI] [PubMed] [Google Scholar]
- Wang X, Bank RA, TeKoppele JM, Agrawal CM. The role of collagen in determining bone mechanical properties. Journal of Orthopaedics Research. 2001;19:1021–1026. doi: 10.1016/S0736-0266(01)00047-X. [DOI] [PubMed] [Google Scholar]
- Wang X, Shen X, Li X, Mauli Agrawal C. Age-related changes in the collagen network and toughness of bone. Bone. 2002;31:1–7. doi: 10.1016/s8756-3282(01)00697-4. [DOI] [PubMed] [Google Scholar]
- Zioupos P. Accumulation of in-vivo fatigue microdamage and its relation to biomechanical properties in ageing human cortical bone. Journal of Microscopy. 2001;201:270–278. [PubMed] [Google Scholar]
- Zioupos P, Currey JD, Sedman AJ. An examination of the micromechanics of failure of bone and antler by acoustic emission tests and laser scanning confocal microscopy. Medical Engineering and Physics. 1994;16:203–212. doi: 10.1016/1350-4533(94)90039-6. [DOI] [PubMed] [Google Scholar]
- Zioupos P, Currey JD, Mirza MS, Barton DC. Experimentally determined microcracking around a circular hole in a flat plate of bone: comparison with predicted stresses. Philosophical Transactions of the Royal Society of London B Biological Sciences. 1995;347:383–396. doi: 10.1098/rstb.1995.0031. [DOI] [PubMed] [Google Scholar]
- Zioupos P, Currey JD, Hamer AJ. The role of collagen in the declining mechanical properties of aging human cortical bone. Journal of Biomedical Material Research. 1999;45:108–116. doi: 10.1002/(sici)1097-4636(199905)45:2<108::aid-jbm5>3.0.co;2-a. [DOI] [PubMed] [Google Scholar]