Estimation of pulmonary arterial pressure by a neural network analysis using features based on time-frequency representations of the second heart sound

Abstract

The objective of this study was to develop a non-invasive method for the estimation of pulmonary arterial pressure (PAP) using a neural network (NN) and features extracted from the second heart sound (S2). To obtain the information required to train and test the NN, an animal model of pulmonary hypertension (PHT) was developed and 9 pigs were investigated. During the experiments, the electrocardiogram, the phonocardiogram, and the PAP were recorded. Subsequently, between 15 and 50 S2 were isolated for each PAP stage and for each animal studied. A Coiflet wavelet decomposition and a pseudo smoothed Wigner-Ville distribution were used to extract features from the S2 and train a one-hidden layer NN using 2/3 of the data. The NN performance was tested on the remaining 1/3 of the data. NN estimates of the systolic and mean PAPs were obtained for each S2 and then ensemble averaged over the 15 to 50 S2 selected for each PAP stage. The standard errors between the mean and systolic PAPs estimated by the NN and those measured with a catheter were of 6.0 mmHg and 8.4 mmHg, respectively, and the correlation coefficients were 0.89 and 0.86, respectively. The classification accuracy, using a 23 mmHg mean PAP and a 30 mmHg systolic PAP thresholds between normal PAP and PHT was 97% and 91% respectively.

1 Introduction

Pulmonary hypertension (PHT) is a frequent and serious complication of several cardiovascular or respiratory diseases that is difficult to assess noninvasively (ENRIQUEZSARANO et al., 1997; SNOPEK et al., 1996; GOLAN et al., 1995; FISHMAN; 1994). As the options for treatment of PHT have expanded, the requirement for accurate and noninvasive methods to allow regular and safe estimation of pulmonary arterial pressure (PAP) has increased. In patients necessitating continuous monitoring of PAP or in patients with suspected PHT, the PAP is usually measured using a pulmonary arterial catheter. Even if the occurrences are relatively rare, this method can however cause complications including lesions of the tricuspid valve, pulmonary valve, right ventricle, or pulmonary arteries, cardiac arrhythmia, dislodgment of a thrombus, and infectious complications (KAPLAN; 1987). A pulmonary arterial catheter can be left in place for a few days to allow continuous monitoring of PAP in patients at the critical care unit. However, it is not recommended for repeated measurements (one time every week or month or 6 months depending of the evolution of the disease) because of the potential risks and discomfort for the patient. Nonetheless, regular evaluation of the PAP is very important to follow the evolution of the disease and to assess the efficacy of the treatment. Consequently, non invasive methods have been developed to allow frequent and accurate measurement of PAP. Mainly, two methods have been explored: the first one is based on the measurement of the systolic pressure gradient across the tricuspid valve using Doppler echocardiography, and the second one is based on the spectral analysis of the second heart sound recorded with digital phonocardiography.

1.1 Doppler method

The measurement of PAP by Doppler-echocardiography provides a high degree of correlation (0.89 ≤ r ≤ 0.97) and a standard error (SEE) varying from 7 to 12 mmHg in comparison with pulmonary artery catheterization (YOCK et al., 1984; CURRIE et al., 1985; NAEIJE et al., 1995). However, the PAP cannot be estimated by Doppler in approximately 50% of patients with normal PAP, 10 to 20 % of patients with elevated PAP, and 34 to 76% of patients with chronic obstructive pulmonary disease because of the absence of tricuspid regurgitation, a weak Doppler signal, or a poor signal-to-noise ratio (CURRIE et al., 1985; YOCK et al., 1984; NISHIMURA et al., 1994; NAEIJE et al., 1995). Furthermore, Doppler echocardiography requires an expensive ultrasound system and a highly qualified technician. This method has a limited applicability and is also not practicable for daily measurements of PAP in small clinics or at home.

1.2 Phonocardiographic method

The second heart sound (S2) is composed of 2 basic components (Figure 1). The aortic component (A2), which is generally produced by the vibration of the aortic valve and surrounding tissues after aortic valve closure, is followed by the pulmonary component (P2) resulting from the vibration of the pulmonary valve and surrounding tissues after pulmonary valve closure(REDDY et al., 1985; TILKIAN et al., 1984; STEIN; 1981). It is also well known that the splitting interval between A2 and P2 is increased in the presence of pulmonary hypertension (LEATHAM; 1975; LONGHINI et al., 1991; CHEN et al., 1996). It could therefore be useful feature to estimate the PAP. The basic principle supporting the estimation of the PAP by using spectral features of P2 is based on Laplace’s law which states that the tension of the pulmonary artery wall is proportional to the PAP from the instant corresponding to the onset of the pulmonary valve closure (right ventricular end-systole) up to the end of right ventricular diastole. Similarly to that of a stretched drumhead, it is expected that the resonant frequency of P2 is proportional to the tension in the main pulmonary artery, and thus to the end-systolic PAP.

Figure 1.

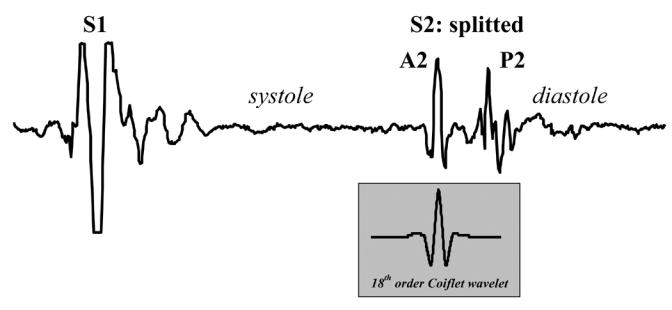
Example of a PCG of one cardiac cycle. The amplitude of S1 was saturated to optimize the amplitude range of S2. The 18^th-order Coiflet wavelet used in our study is presented for visual comparison with A2 and P2.

This hypothesis was confirmed by Longhini et al. and Aggio et al. (AGGIO et al., 1990; LONGHINI et al., 1991) who found in 19 patients with mitral stenosis a high correlation between 2 spectral features of P2 (dominant frequency Fp and quality factor Qp) and the systolic PAP measured by pulmonary artery catheterization. Recently, we have demonstrated that spectral analysis of S2 can provide a reliable estimate (r = 0.84; SEE = ± 5 mmHg) of the systolic PAP when compared with Doppler in patients with a prosthetic heart valve (SHAMSOLLAHI et al., 1997; CHEN et al., 1996). The Longhini study resulted in the following equation: PAP = 0.3 + 0.2 Fp + 18.9 Qp. In our previous study, the use of this equation gave poor results (r = 0.03, p = 0.82, SEE ± 10mmHg). Then, two additional parameters were added: the dominant frequency of S2 (Fs) and the ratio of the dominant frequencies of P2 and A2 (Fp/Fa). The resulting equation was PAP = 47 + 0.68 Fp − 4.4 Qp − 17 Fp/Fa − 0.15 Fs. The main difference between these equations may be partly due to the different patient populations and the different recording devices utilized. It was concluded that additional, more fundamental research was necessary. The main objective of this paper is to evaluate the usefulness of a neural network (NN) using temporal and spectral features extracted from S2 as a noninvasive and low cost method to estimate the PAP in an animal model designed to vary the PAP over a wide range.

2 Method

2.1 Animal model

A phonocardiogram (PCG) and an electrocardiogram (ECG) were recorded in pigs who underwent an experimental protocol based on a pharmacological approach designed to control the PAP. Nine pigs weighing between 30 and 35 kg were anesthetized and ventilated as previously published by Troncy et al. (TRONCY et al., 1996). The PAP measurement was performed using a 7F Swan-Ganz catheter (Model Mikro-tip, MPA-372 T, Millar) inserted into the left jugular vein and flow-directed into the main pulmonary artery. An ARMACO 1306 electret microphone was used to develop a PCG microphone with characteristics similar to those of the electronic stethoscope previously developed by our group (GRENIER et al., 1998). This microphone had a sensitivity of 17 mV/Pa and a flat frequency response (± 3 dB) between 20 Hz and 8 kHz, as determined in a Brüel & Kjaer anechoic chamber (B&K Model 422) coupled to a audio-analyzer (B&K Model 2012). The microphone was positioned and fixed on the thorax of the pigs at the pulmonary area (3rd–4th left intercostal space) to record the thoracic PCG. A first-order high-pass Butterworth filter with a cut-off frequency of 100 Hz was used to de-emphasize the high-intensity low-frequency components of the PCG. According to our previous study (CHEN et al., 1996) and the results of the study of Longhini et al. (LONGHINI et al., 1991), the frequency range of the resonant frequency of P2 is below 200 Hz. Consequently, the overall frequency response of the PCG channel was limited to 300 Hz by using a 5^th order low-pass anti-aliasing Butterworth filter.

After the initial instrumentation of the animal, the study was delayed until a stable and normal physiological state was obtained. The PAP was modulated using the following experimental protocol divided into four stages of 15 min each. 1- Baseline measurements were performed while the systolic PAP was within the normal range (15–20 mmHg), 2- moderate PHT was induced by a continuous intravenous infusion of a thromboxane analogue (U44069, Sigma, USA) at 20 μg/ml diluted in 0.9 % saline (VAN OBBERGH et al., 1996). The infusion rate was adjusted between 5 and 20 μg/min to maintain a stable systolic PAP of approximately 35–40 mmHg for 15 minutes, 3- severe PHT (systolic PAP 45–60 mmHg) was then obtained by increasing the infusion rate (range 10 to 60 μg/min), 4- ‘back to baseline’ measurements were performed after stopping the infusion and allowing sufficient time to ensure that the animal’s PAP had returned to normal. For each stage, the PAP, the ECG and thoracic PCG were digitized at 1 kHz with 12-bit resolution and saved on a 66 MHz 486 personal computer. During PCG recording, the catheter was pulled back into the right ventricle in order to eliminate any potential interaction of the catheter with the pulmonary valve closure and thus with P2.

2.2 Signal processing

Signal processing of the ECG and PCG was performed with Matlab 5.3 (The MathWorks Inc, Boston, USA), in a Windows NT environment, using the Time-Frequency ToolBox (TFTB) developed by le Groupe de Recherche en Information, Signal, Image et Vision (see acknowledgments) and the wavelet toolbox (Wavekit) developed by Harri Ojanen (see also acknowledgments).

First, 256-ms PCG segments containing S2 were automatically extracted from the PCG recordings based on the timing reference of the ECG. The S2 that presented important artifacts or noise were excluded (less than 3% of the data) by visual inspection. Between 15 and 50 S2 were thus obtained for each PAP stage of each pig. The top panel of Figure 2 shows an example of a 256-ms S2 segment selected from one pig recording. Two databases were created. Database A consisted in 514 S2 from 5 pigs, the mean PAP varying between 12 and 47 mmHg and the systolic PAP between 15 and 61 mmHg. The features extracted from this database were used to determine the topology of the NN, i.e. its structure, the number of neurones in the three interconnection levels, and the transfer functions (see Figure 3). Database B was composed of 1250 S2 selected from the PCG of 9 pigs. The mean PAP varied between 12 and 50 mmHg and the systolic PAP between 13 and 61 mmHg (see Table 1). The features extracted from this database were used to train the NN optimized with database A and test its performance to estimate the PAP or to detect PHT using a pressure threshold reference as described later.

Figure 2.

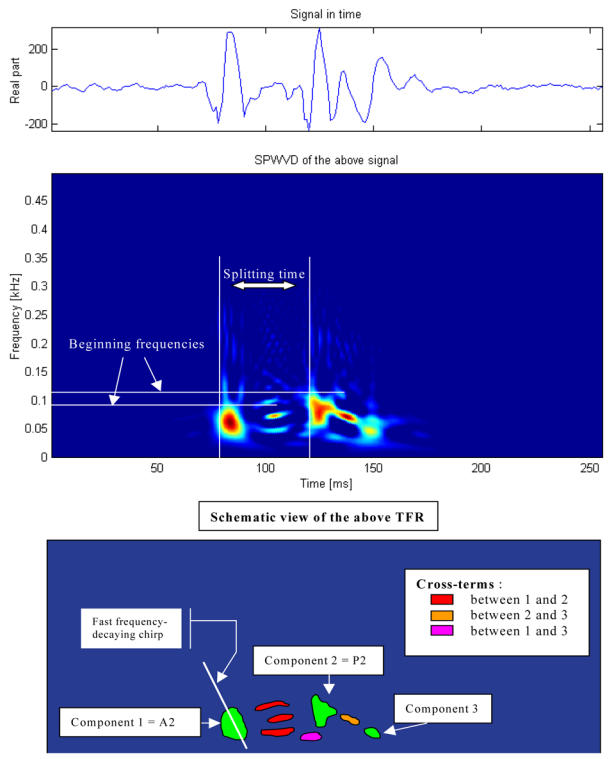
Example of a 256-ms S2 segment selected from one pig recording (top panel) and its time-frequency representation of S2 (middle panel). The splitting time is 40 ms and the maximum instantaneous frequencies of A2 and P2 are 84 Hz and 108 Hz, respectively. A schematic illustration shows examples of auto-terms and cross-terms is shown in the lower panel.

Figure 3.

Basic neuron structure (panel A) and architecture (panel B) of the network selected, which consists in 17 input neurons with a 10 neurons hidden layer (sigmoid transfer functions) and one output neuron (linear transfer function).

Table 1.

Pig description

Pig	stage 1	stage 2	stage 3	stage 4
1	13/19	33/42	40/55	N/A
2	18/22	36/44	45/60	N/A
3	18/25	28/36	40/48	N/A
4	14/17	32/36	44/55	16/18
5	14/18	28/34	38/48	16/19
6	19/21	28/36	41/51	14/17
7	12/15	29/36	37/46	12/15
8	14/15	30/36	26/44	12/13
9	13/16	32/42	47/61	16/21

Pig PAP by stage: values represent mean/systolic PAP in mmHg.

2.3 Time-frequency analysis

The S2 signal is a non-stationary signal. Its temporal representation does not reflect accurately all its basic characteristics since its frequency content is not represented. Computing its power spectrum with the discrete Fourier transform does not take into consideration the dynamic spectral properties of S2. An alternative is therefore the joint time-frequency representations (TFRs). There are a large number of TFR techniques, but an appropriate one should be selected according to the specific characteristics of the S2 signal and the quantitative features to be extracted. For the present application, various TFR techniques were tested and the smoothed pseudo Wigner-Ville distribution (SPWVD) was selected because it provides a good compromise between the time and frequency resolutions while minimizing the cross-terms (FLANDRIN; 1999). Its mathematical definition is:

$${\mathit{SPWVD}}_x(t,\upsilon )=\underset{-\infty }{\overset{+\infty }{\int }}q(\tau )\left[\underset{-\infty }{\overset{+\infty }{\int }}g(s-t)x\left(s+\frac{\tau }{2}\right)x^{\ast }\left(s-\frac{\tau }{2}\right)ds\right]e^{-i2\pi \nu \tau }d\tau ,q(\tau )=h\left(\frac{\tau }{2}\right)h^{\ast }\left(-\frac{\tau }{2}\right),$$

where g and h are the time and frequency smoothing windows. In our application, we used Hamming windows with durations of 25 ms and 16 ms. Three quantitative features were extracted from the SPWVD of S2 by manual selection and utilized to train and test the NN algorithm: the maximum instantaneous frequency of A2, that of P2, and the splitting interval between A2 and P2 (see Figure 2, middle panel).

Since wavelet analysis has been widely and successfully used for signal compression, noise reduction, classification and detection of transient signals, we also evaluate the Orthonormal Wavelet Transform (OWT). Its general expression is:

$${\mathit{OWT}}_x(k,j)=2^{-\frac{j}{2}}\underset{-\infty }{\overset{+\infty }{\int }}x(s)\psi \left(2^{-j}s-k\right)ds,$$

where j and k are integers and 2^−j/2 ψ(2^−j s − k) is the scaled and translated form of the wavelet ψ(s). OWT is an analysis tool that is equivalent to a perfect discrete filter bank based on conjugate mirror filters(MALLAT; 1998). It is a time-scale linear representation that can lead to a reduced cross-term TFR, in which the frequency index “ν” is inversely proportionally to the scale “s”. In the present study, a 18^th order Coifelet wavelet with 6 vanishing moments was chosen because of its resemblance with A2 (see Figure 1) and 7 scales were retained (j ∈ {1,2,…,7}). Each normalized zero-mean S2 signal was decomposed for feature extraction. The associated OWT was squared and for each scale j, the maximum value, its position and the sum of the decomposition coefficients were computed and used as a set of 21 additional features to train and test the NN.

2.4 PAP model

While estimating a physical quantity from several features, one has to make an hypothesis over the type of relationship expected. The most common hypothesis is that of linearity, i.e., the desired quantity can be estimated by a linear combination of the features. In the present case, a preliminary investigation of the time-frequency features of S2 (beginning or mean instantaneous frequencies, splitting interval, etc.) showed no clear linear behavior as a function of the PAP. The relationship between the S2 features and the PAP was thus modeled by the following equation:

$$\mathit{PAP}=\mathrm{\Phi }(D_1,D_2,\dots ,D_N)+\mathrm{\Theta }(F_{\mathit{hemo}},F_{\mathit{anato}})$$

where D_i (0<i<N) are S2 features, F_hemo and F_anato are animal’s hemodynamic and anatomic features (such as systemic pressure, age, sex) and Φ and Θ are non-linear operators. This is a general model; in order to make it useful, we had to make some hypotheses about its different components. Because the pig population used in the present study is quite homogenous, the influence of function Θ was negligible, whereas it may be more important in a patient population. Concerning Φ, we had no a priori assumption, thus a NN was chosen since it is known to be a suited approach to this particular type of situation (LIPPMANN; 1987).

2.5 Topology of the Neural Network

In our particular case, a feed-forward back-propagation NN with one hidden layer was implemented (see Figure 3). The sizes of the input and the hidden layers were determined with Database A. The input vectors (quantitative features extracted from the TFRs) were normalized and a principal component analysis (PCA) performed in order to minimize the redundancy and reduce the number of features of the input layer. A sigmoid transfer function was applied to each neuron of the second hidden layer. The third layer (output) consisted in one neuron with a linear transfer function.

2. 7 Beat-by-beat PAP estimation using the hold-out analysis

Each database was randomly split into three data sets: a training set (5/9 of data), a validation set (1/9 of data) and a testing set (1/3 of data). The NN learning (i.e. estimate of NN weights and biases) was conducted by using the training and validation sets (2/3 of the data) and the test set (remaining 1/3) served to evaluate the performance of the trained NN (hold out method) when applied to a new set of independent data (not used in the learning process).

2.8 Training algorithm

Training is an iterative approach used to determine the parameters (weights and biases) of the NN, in a way that a known input gives a desired output, by minimizing the mean square error over the training set. A potential problem is the over-training of the NN (lack of generalization). In this situation, the NN becomes too specific to the training set and performs poorly on new data. To avoid this drawback, the algorithm was stopped when the estimation error, obtained on the validation set, began to increase for a given number of successive iterations. This early-stopping approach was compared with the approach based on a fixed number of iterations. We also determined the most significant S2 features to be fed into the NN using database A and different combinations of the features (wavelet, TFR or both TFR and wavelet features).

The minimization procedure of the mean square error was performed by the Levenberg-Marquardt algorithm. It is a cost-effective algorithm allowing rapid convergence at the expense of local minima sensitivity (HAGAN et al., 1994). To face the local minima problem, we repeated the random initialization of the Levenberg-Marquardt algorithm 20 times and averaged the output results. This is equivalent to using a 20 NN parallel architecture and to average the estimated 20 PAPs for each heart beat analyzed. The training time is multiplied by 20, but once the algorithm is trained, the calculation time on the testing set is very short, consisting in simple arithmetic computations structured in a parallel architecture.

2.9 Testing approach

The performance of the NN using database B was compared with the catheter measurements of the PAP by using the Pearson’s correlation coefficient (r) and the standard error of the estimate (SEE). The NN attempted to estimate, for each series of 15 to 50 S2, the corresponding mean and systolic PAPs. The classification accuracy (normal PAP vs PHT) was then assessed by using two decision thresholds: 23 mmHg for the mean PAP and 30 mmHg for the systolic PAP. These thresholds corresponded approximately to the median between the maximal PAP recorded in the normal and back to normal stages and the minimal PAP of the moderate PHT stage.

3 Results

3.1 Qualitative analysis of S2

In figure 2, the upper panel is a temporal representation of S2 recorded during a moderate PHT (mean PAP = 29 mmHg) in one pig. The middle panel is a smoothed pseudo-Wigner-Ville representation of the signal and the lowest image is a schematic representation of the main components of this TFR with the most important cross-terms. In this example, there are 3 main components (green in the lower panel), two of relatively high power and long duration and a third, low-power, low-frequency and shorter duration component. The components 1 and 2 are identified as A2 and P2, respectively. In the majority of the S2 signals, a very rapid instantaneous frequency decaying behavior (chirp) could be identified for A2 and P2 (as shown in this example for A2). However, the time-frequency morphology of each component was complex and variable from one PAP condition to another and from one pig to another. The third component might be a remnant of P2, a small (subclinical) S3 or a phonocardiographic component of unknown or artifactual origin.

Besides these 3 main components, there are many other terms in this representation as well as some background noise. Also, all bilinear TFR generate cross-terms. The principal difficulty in eradicating them is that they cannot be identified with precision. Nevertheless, it is known that cross-terms have an oscillatory structure (minimized here by smoothing) with a maximum intensity halfway between the real components. Schematic examples are shown in the lower panel of Figure 2 in relationship with their origins. Cross-terms may also results from the interaction of the different parts of a non linear chirp component (not illustrated in Figure 2). The beginning instantaneous frequencies of A2 and P2 were generally easy to identify visually, as shown in the middle panel of Figure 2.

The examination of the TFRs of representative S2 signals of the two PAP stages of two pigs (Figure 4) confirms that, beside the expected A2 and P2 components, there were other short duration components mostly due to the cross-terms between A2 and P2. The signal complexity seemed to increase with increasing PAP. The beginning instantaneous frequencies of A2 and P2 were generally easy to identify visually. It became more difficult when low frequency components seem to precede the main part of A2 or P2. In such cases, the maximum instantaneous frequency of the component was considered as its instantaneous beginning frequency. No clear linear relationship was found between these beginning instantaneous frequencies and the PAP. Finally, a small but significant difference was observed on the S2 TFRs obtained for the initial and the back-to-baseline conditions (with similar PAPs). This was due to changes in the phases of A2 and P2 that affected both the auto and the cross terms of the signal. Since the splitting interval was generally shorter in the back-to-baseline condition, the A2 and P2 components overlapped more significantly.

Figure 4.

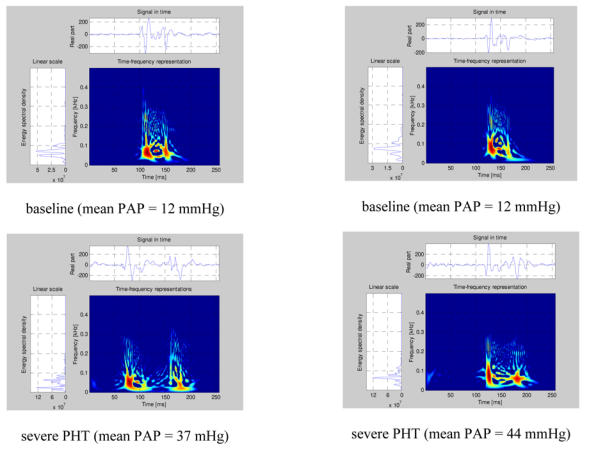
Examples of Pseudo-Smoothed Wigner-Ville Time-frequency representations for two pigs (left panel pig 1, right panel pig 2) for normal pulmonary artery pressure and for pulmonary artery hypertension.

3.2 Training of the NN using database A

As shown in Figure 5, the NN performances using the three TFR features and using both the TFR and the wavelet features were comparable. Also, the differences were not significant for a hidden layer dimension varying between 5 and 15. Nevertheless, we decided to use both the TFR and the Coiflet wavelet features for the rest of the study, considering that the performance of the NN was similar and that, theoretically, the wavelet features should contain relevant information. We also found that a hidden layer with 10 neurons was a stable size providing a very good NN performance. The early stopping approach was compared to the approach stopped after 1000 iterations (see Figure 5). Since the computational speed of the early stopping method was about ten times faster than the other one and its performance was slightly lower, we choose this method even if it was not optimal. In summary, we used the following topology for the study:

Figure 5.

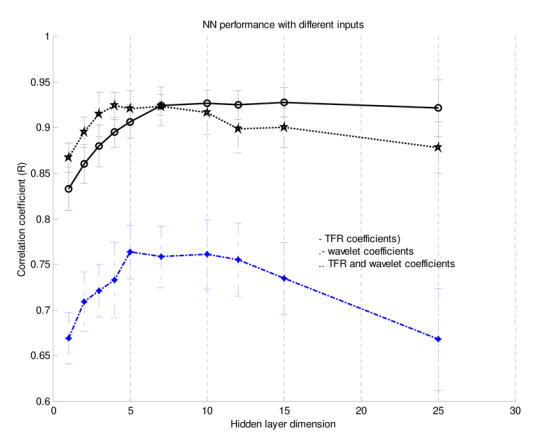
NN performance (based on the correlation coefficient r) for different inputs and varying hidden-layer dimension using Database A (mean performance and standard deviation).

• - The 24 TFR features of the input neurons were reduced to a dimension of 17 by the PCA, using a 1% variance threshold,

• - 10 neurons in the hidden-layer,

• - the catheter measured mean or systolic PAP as the target output,

• - the early stopping approach.

• - averaging the mean and systolic PAPs estimated by the NN over 15 to 50 S2 (heart beats).

3.3 Performance evaluation using database B

Figures 6 show the scattergrams between the catheter-measured and NN estimates of the mean (panel A) and systolic (panel B) PAPs, respectively. The linear regression line is also represented. A correlation coefficient r of 0.89 and a SEE of 6.0 mmHg were obtained for the mean PAP, whereas the correlation coefficient r was 0.86 and the SEE was 8.4 mmHg for the systolic PAP. In this figure, each point corresponds to one PAP condition (i.e. normal PAP, moderate PHT or severe PHT) of each pig, as described in section 2.9. The beat-by-beat classification of the mean PAP (normal vs. PHT) using a threshold of 23 mmHg was 97% accurate; the sensitivity was 100% and the specificity was 93%. For the beat-by-beat classification of the systolic PAP, the accuracy was 91%, the sensitivity 100% and the specificity 79%.

Figure 6.

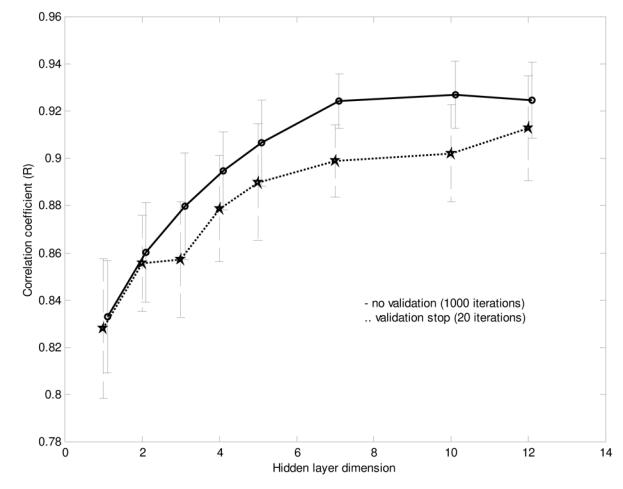
Early stopping effect on NN performance using Database A (mean performance and standard deviation).

4 DISCUSSION ET CONCLUSION

The estimation of the systolic PAP yielded a 40% higher SEE than that of the mean PAP (8.4 mmHg against 6.0 mmHg). Considering that the systolic PAP values were approximately 30% higher than mean PAP, we consider that the SEE results are probably following a statistically insignificant trend. The correlation levels r are following a weaker trend (0.86 for the systolic PAP and 0.89 for the mean PAP). The classification accuracy follows a similar trend, with two more false positives in the systolic PAP case. Although these results might be due to chance alone, it is not excluded that the NN method gives a better estimate of the mean PAP than the systolic PAP. Meanwhile, the small size of our study limits the statistical significance that can be attached to these modest trends. The catheter-measured systolic PAP has a higher variance (being calculated by the maximum of the pressure curve while the mean PAP represents an averaged value) and this might explain a slightly worse correlation with the estimate obtained by the NN from the TFRs of S2.

The NN method thus shows a good robustness and comparable estimation performances for the systolic and mean PAPs. Its performance compares positively with the Doppler echographic method (0.89 ≤ r ≤ 0.97 and SEE varying from 7 to 12 mmHg). In addition, it has the main advantage of being (at least theoretically) applicable to all the patients, while the Doppler method is not feasible in 50% of patients with normal PAP, 20 % of patients with pulmonary hypertension and up to 76% of patients with chronic obstructive pulmonary disease. Defining the PHT as a mean PAP superior to 23 mmHg or a systolic PAP superior to 30 mmHg, the method provided an excellent 91–97% classification accuracy.

The studies performed by Longhini et al. and Chen et al. (LONGHINI et al., 1991a; CHEN et al., 1996a) were based only on spectral features extracted from S2, even if it was well known that the splitting interval was an important indicator of pulmonary hypertension. In addition, the relationships between the mean and systolic PAPs and the spectral features were modeled with linear regression functions, which are probably not the most adequate model. These limitation are compensated to a great extent in the present study because 1-time-frequency representations were used instead of Fourier representations, and 2- of one of the main advantages of the NN is that it can integrate the non linear relationship between the time and frequency features of S2 and the PAP. Consequently, the NN method should provide a more robust PAP estimator when applied to a larger population, especially for the detection of PHT vs. normal PAP.

We are aware that our animal population was small, but four direct pressure measurements at significantly different PAP levels were obtained for most of the nine animals studied. Since almost only the principal variable of interest, the PAP, was modulated, the need for a large animal population was not necessary to develop and test the NN technique. Also, this protocol ensured that the NN was optimised to estimate the mean and systolic PAPs. It is impossible to perform such a study (modulating the PAP) in patients because it would be unethical. Using patients at the intensive care unit or at the catheterization laboratory is possible but may take considerable time to reach a sufficient number of patients in each pressure category: normal PAP, mild, moderate and severe PHT. Since the results of this experimental study are encouraging, it now becomes relevant to evaluate the performance of the NN in patients having right heart catheterization. Our study has thus its own limitations, but is an important one since it provides the basic justification for evaluation the NN method in these patients.

Pulmonary artery catheterization is a routine procedure in cardiology. However, this is an invasive and expensive procedure that is not without risk for the patient. Hence, pulmonary artery catheterization can not be used to measure PAP for a long period of time or on a regular basis (once every week or month). If satisfactory results are obtained in patients, the NN method could potentially replace and/or allow to reduce pulmonary artery catheterization to shorter periods of time since it would allow to pursue the PAP monitoring after the removal of the pulmonary arterial catheter.

Figure 7.

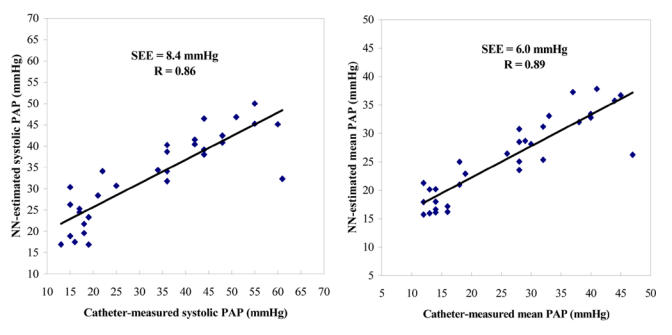
Correlation between the systolic (panel A) or mean (panel B) PAPs estimated using the NN method and directly measured by catheter. Each point represents the average estimate obtained from 15 to 50 S2 recorded during a given PAP condition (normal PAP, moderate hypertension, severe hypertension, back-to-normal PAP) in 9 pigs. The solid line represents the regression line.