Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2008 Jan 1.
Published in final edited form as: J Biomech. 2006 Oct 27;40(8):1716–1722. doi: 10.1016/j.jbiomech.2006.08.009

The Biomechanical Function of the Patellar Tendon During In-vivo Weight-bearing Flexion

Louis E DeFrate 1,*, Kyung Wook Nha 1, Ramprasad Papannagari 1, Jeremy M Moses 1, Thomas J Gill 1, Guoan Li 1
PMCID: PMC1945121  NIHMSID: NIHMS24155  PMID: 17070815

Abstract

Few studies have investigated the function of the patellar tendon in-vivo. This study quantified the three-dimensional (3D) kinematics of the patellar tendon during weight-bearing flexion.

Eleven subjects were imaged using magnetic resonance (MR). Sagittal plane images were outlined to create a 3D model of the patella, tibia, and femur and included the attachment sites of the patellar tendon. Each attachment site was divided into central, medial, and lateral thirds. Next, the subjects were imaged using fluoroscopy from two orthogonal directions while performing a single-leg lunge. The models and fluoroscopic images were used to reproduce the motion of the patella, tibia, and femur. The apparent elongation, sagittal plane angle, and coronal plane angle of each third of the patellar tendon was measured from the relative motion of the attachment sites.

All three portions of the patellar tendon deformed similarly with flexion. The length of the patellar tendon significantly from full extension to 30°. From 30°–110°, no significant change in the length of the patellar tendon was observed. The patellar tendon was oriented anteriorly at flexion angles less than 60° and posteriorly thereafter. From full extension to 60°, the medial orientation of the patellar tendon decreased significantly with flexion. These data may have important implications for anterior cruciate ligament reconstruction using patellar tendon autografts and for the design of rehabilitation regimens for patients of patellar tendon repair.

Introduction

The patellar tendon is an essential component of the extensor mechanism of the knee. Quantifying the function of the patellar tendon under physiological loading conditions is important to understanding the biomechanics of the knee. Numerous studies have investigated patellar tendon biomechanics. The material properties of patellar tendon have been quantified in many studies (Butler, et al., 1989; Haraldsson, et al., 2004; Johnson, et al., 1994). Other investigators have measured the orientation or moment arm of the patellar tendon either in the sagittal plane (Chan and Seedhom, 1995; Smidt, 1973; Tsaopoulos, et al., 2006) or in three dimensions (Krevolin, et al., 2004). More recently, patellar tendon function has been studied in living subjects using various imaging techniques. Ultrasound has been used to measure the elongation of the patellar tendon during in-vivo isometric flexion at 90° (Hansen, et al., 2006). MRI has been used to measure the elongation (Sheehan and Drace, 2000), the orientation (Aalbersberg, et al., 2005), or the moment arm (Wretenberg, et al., 1996) of the patellar tendon during isometric or passive flexion across a limited range of flexion.

Despite the many studies on patellar tendon biomechanics, data on three-dimensional patellar tendon deformation (changes in both length and orientation) during in-vivo weight-bearing flexion is limited. Furthermore, the function of the patellar tendon throughout the range of flexion is unclear. Therefore, the objective of this study was to measure the three-dimensional deformation of the patellar tendon during a quasi-static lunge across a large range of motion (from 0 to 110° of flexion). In order to carry out our objective, we used a combined fluoroscopic and MR imaging technique to measure patellar tendon kinematics in normal subjects. Our hypothesis was that the length and orientation of the patellar tendon changes in three dimensions under physiological activities.

Methods

Eleven healthy subjects (31 ± 8 years old, 5 male and 6 female) participated in this study. The subjects had no history of knee injury or chronic knee pain. Prior to participation, all of the subjects signed a consent form approved by our institutional review board. First, one knee of each subject (for a total of 5 left and 6 right knees) was imaged using a 3.0T MRI scanner (Siemens, Germany) in a relaxed, fully extended position. A water-excitation double-echo sequence was used with a field of view of 160mm and a resolution of 512 by 512 pixels. Approximately 120 sagittal plane 1mm thick slices were obtained.

The MR images were used to create a three-dimensional anatomical model of the knee, as previously described (DeFrate, et al., 2004b; Li, et al., 1999). The contours of each subject’s femur, tibia, and patella were traced within each MR image. In addition to the bony contours, the attachment areas of the patellar tendon on the tibial tubercle and the inferior pole of the patella were delineated. The series of contours was then used to create a model of each patient’s knee joint, including the patella, tibia, femur and the attachment sites of the patellar tendon (Figure 1).

Figure 1.

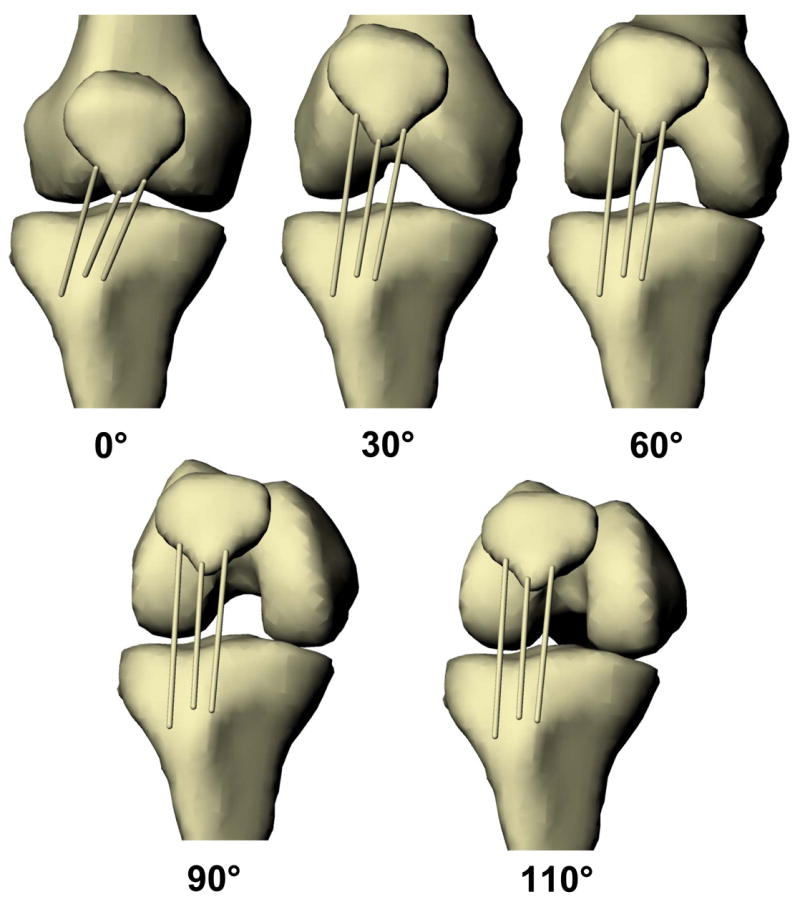
Figure 1

Open in a new tab

The patellar tendon deformed in three dimensions during weight-bearing knee flexion, as demonstrated for one subject. The deformations of the medial, central, and lateral thirds of the patellar tendon were quantified.

Each patient then performed a single-leg lunge to 0, 30, 60, 90, and 110° of flexion. While maintaining a flexed position, the patient was imaged simultaneously from orthogonal directions using two fluoroscopes. Each subject’s flexion angle was measured by a single examiner using a goniometer. The subject was instructed by the examiner to flex accordingly in order to hit each of the targeted flexion angles.

After testing, the fluoroscopic images were imported into a solid modeling software and placed in the appropriate planes, based on the geometry of the fluoroscopes during the imaging of the patient. The contours of the femur, tibia, and patella were outlined on each fluoroscopic image. The 3D model of the patient was then imported into the software and viewed from the two orthogonal directions corresponding to the orthogonal fluoroscopic setup used to acquire the images. The models of the patella, femur, and tibia were independently manipulated in six degrees-of-freedom until the projections of the models matched the bony contours on both imaging planes. After the matching process, the relative positions of the femur, tibia, and patella reproduced those of the patient. This procedure was repeated at each flexion angle, until the motion of the subject’s tibia, femur, and patella was reproduced during flexion from 0 to 110° (Figure 1). This methodology has an error of less than 0.1±0.1mm in measuring joint motion (DeFrate, et al., 2006; Li, et al., 2004c).

Next, the kinematics of the patellar tendon was measured from the series of bone models representing the kinematics of the knee. The attachment sites of the patellar tendon on the patella and tibial tubercle were divided into thirds: a medial portion, a central portion, and a lateral portion. The apparent elongation of each portion of the patellar tendon was defined as the length of the line connecting the attachment sites on the patella and tibial tubercle. The sagittal plane angle was defined as the angle formed between the long axis of the tibia and the projection of the patellar tendon on the sagittal plane of the tibia (Figure 2A). A positive sagittal plane angle corresponded to an anterior orientation of the patellar tendon (patellar attachment anterior to the tibial attachment) relative to the long axis of the tibia and negative values correspond to a posterior orientation. The coronal plane angle was defined as the angle between the long axis of the tibia and the projection of the patellar tendon on the coronal plane of the tibia (Figure 2B). Positive coronal plane angles corresponded to a medial orientation of the patellar tendon (patellar attachment medial to the tibial attachment) relative to the long axis of the tibia, while negative values corresponded to a lateral orientation. In this fashion, the kinematics of the patellar tendon was quantified for each subject as a function of flexion.

Figure 2.

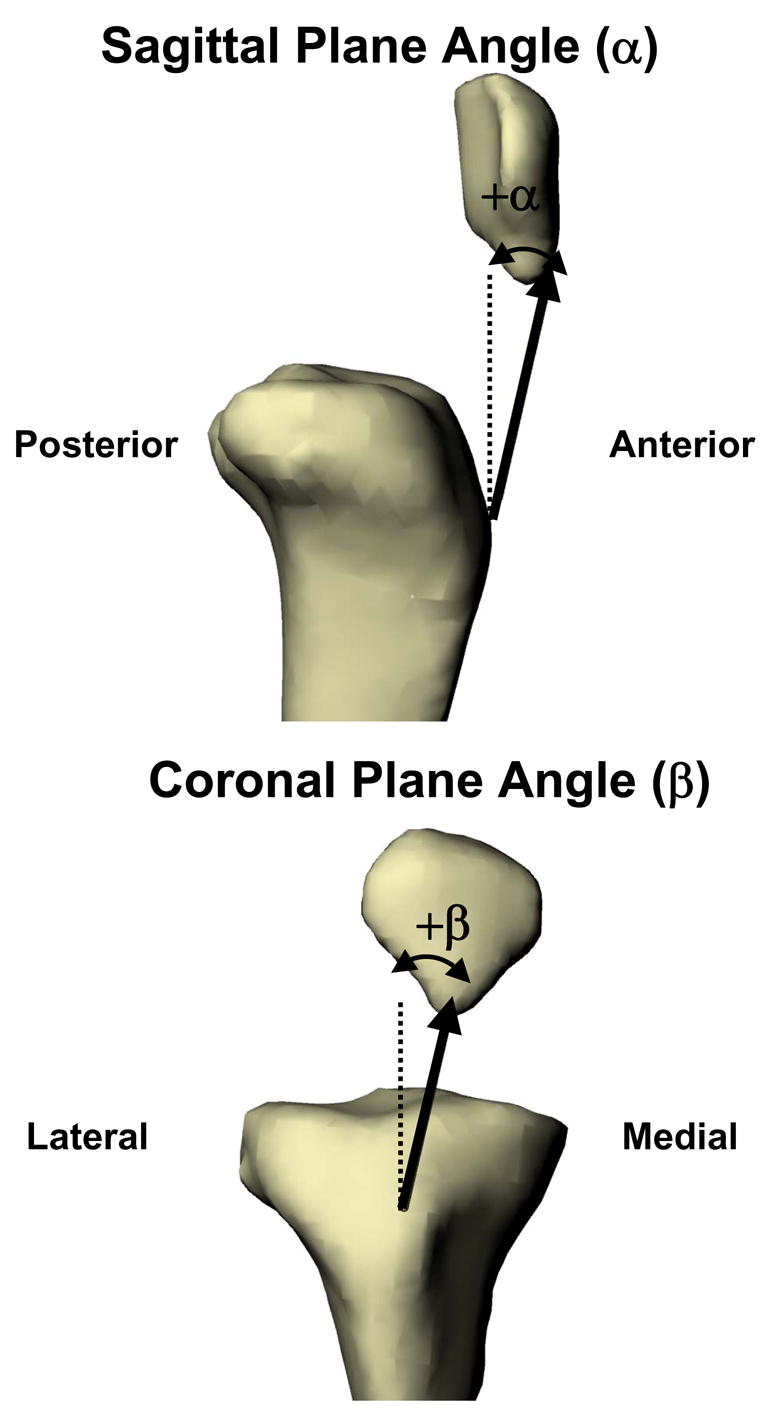
Figure 2

Open in a new tab

The sagittal plane angle was defined as the angle formed between the long axis of the tibia and the projection of the patellar tendon on the sagittal plane of the tibia. The coronal plane angle was defined as the angle between the long axis of the tibia and the projection of the patellar tendon on the coronal plane of the tibia.

Statistical Analysis

Since the apparent elongation, sagittal plane angle, and coronal plane angle were measured in the same individual as a function of flexion, a repeated measures analysis of variance (ANOVA) was used. If the ANOVA detected a statistically significant effect of flexion on any of the variables, the Student-Newman-Keuls (SNK) post-hoc test was used to isolate statistically significant differences between groups. Differences were considered statistically significant where p < 0.05.

Results

Apparent Elongation

The apparent elongation of the three portions of the patellar tendon followed similar patterns with flexion (Figure 3). The length of all three portions sharply increased as the knee flexed from full extension to 30° (p < 0.05). The length of the medial portion increased from 55.5 ± 8.8mm (mean ± standard deviation) at full extension to 61.9 ± 6.5mm at 30° of flexion, while the central portion increased from 49.9 ± 8.1mm to 56.0 ± 5.3mm, and the lateral portion increased from 60.1 ± 6.9 to 65.4 ± 4.3mm. Between 30 and 110°, the length of all three portions remained relatively constant.

Figure 3.

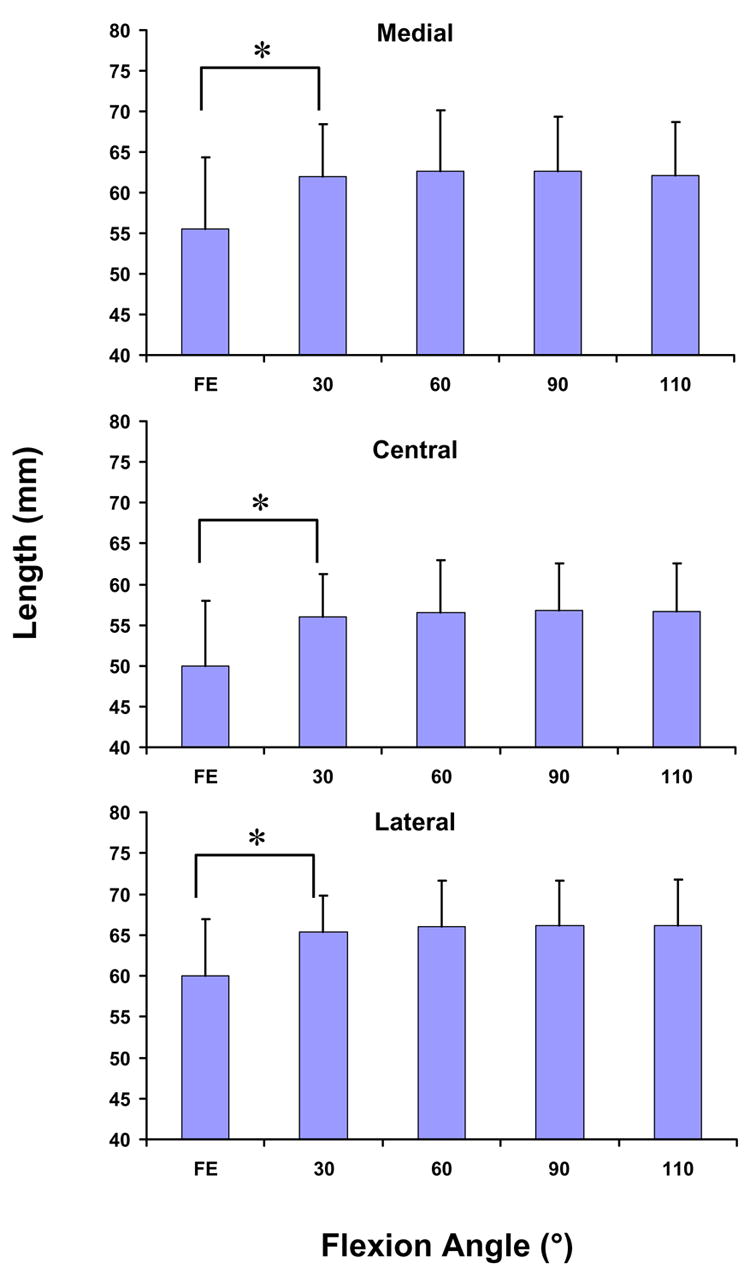
Figure 3

Open in a new tab

The length of the medial, central, and lateral portions of the patellar tendon increased significantly (p < 0.05) from full extension to 30° of flexion. Thereafter, no statistically significant differences in the length of the patellar tendon were observed. (* p < 0.05)

Sagittal Plane Angle

The sagittal plane angle of all three portions of the patellar tendon decreased with increasing flexion (p < 0.05, Figure 4). At full extension, the medial portion was oriented anteriorly relative to the long axis of the tibia by 22.2 ± 7.9°. At 110° of flexion, the medial portion was oriented posteriorly by 8.2 ± 3.4° at 110° of flexion. The central portion ranged from a maximum of 22.9 ± 9.5° at full extension to a minimum of −9.1 ± 4.2° at 110° of flexion. The lateral portion was also oriented anteriorly at full extension (21.6 ± 8.0°), and shifted posteriorly with increasing flexion, reaching a minimum of −11.2 ± 4.0° at 110° of flexion.

Figure 4.

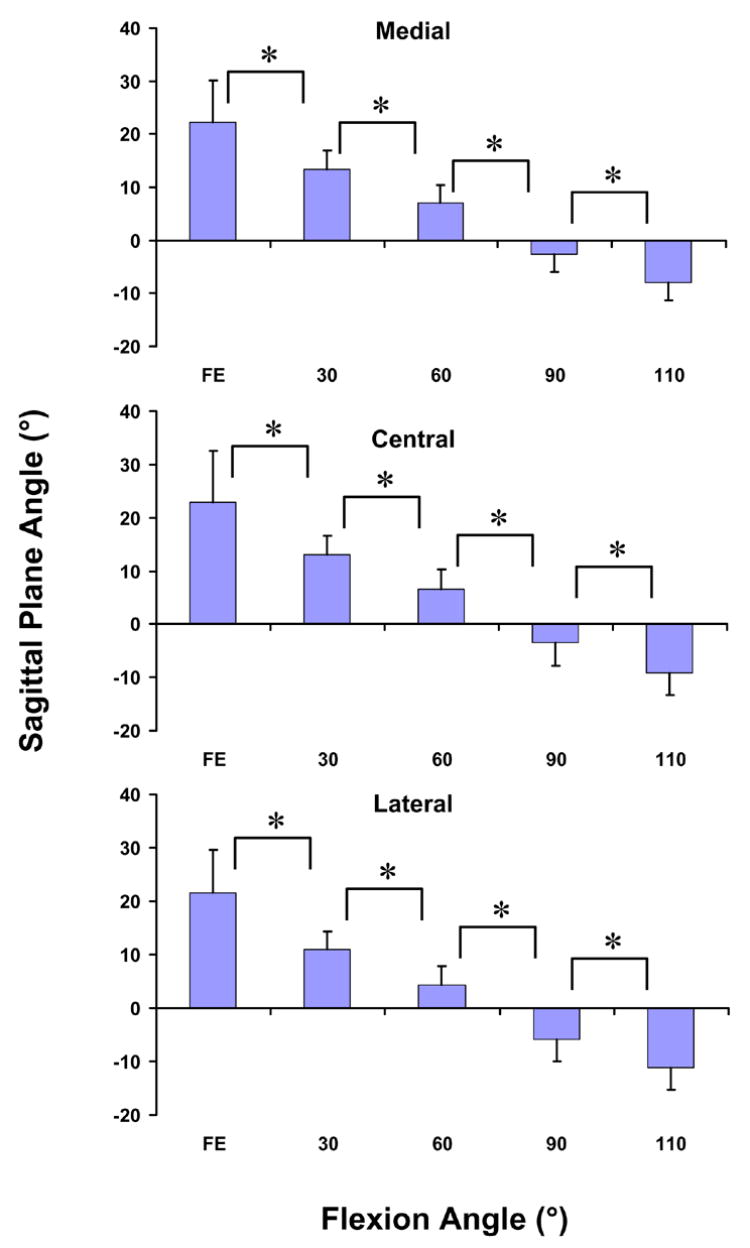
Figure 4

Open in a new tab

The sagittal plane angle of the medial, central, and lateral portions of the patellar tendon decreased significantly (p < 0.05) from full extension to 110°. At low flexion angles, the patellar tendon was oriented anteriorly, and at high flexion angles, the patellar tendon was oriented posteriorly. (* p < 0.05)

Coronal Plane Angle

All three portions of the patellar tendon followed similar changes in the coronal plane angle with flexion (Figure 5). The medial portion was oriented medially by 19.5 ± 6.8° at full extension. At 30° of flexion, there was a statistically significant decrease in the coronal plane angle to 9.9 ± 5.6°. At 60°, there was another statistically significant change of the coronal plane angle to 6.3 ± 5.2°. Beyond 60° of flexion, no statistically significant differences in the coronal plane angle were observed. Similar trends were observed for the central and lateral portions. At full extension, the central portion was oriented medially by 17.5 ± 6.7°. There was a statistically significant decrease in the coronal plane angle to 7.7 ± 5.9° at 30° of flexion and to 4.0 ± 5.3° at 60° of flexion. The lateral portion was oriented by 11.4 ± 5.1° at full extension and decreased significantly to 4.0 ± 5.0° at 30° of flexion and to 1.0 ± 4.7° at 60° of flexion.

Figure 5.

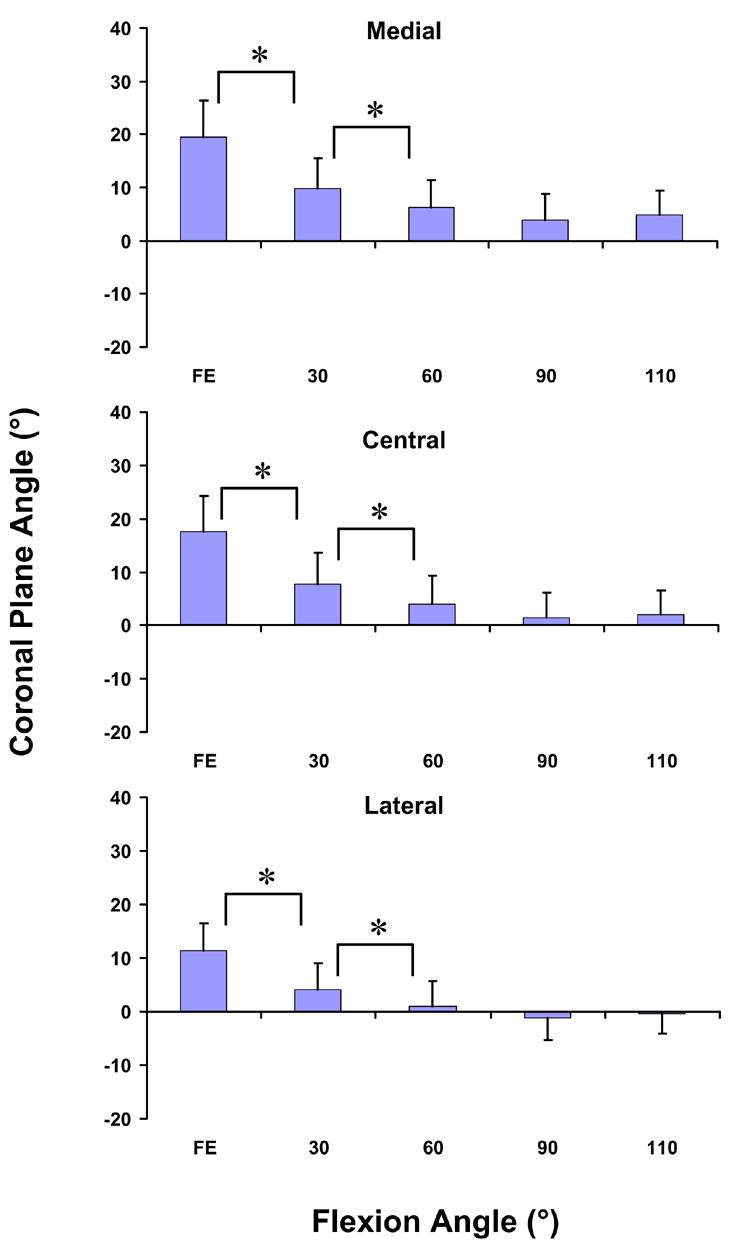
Figure 5

Open in a new tab

The coronal plane angle of the medial, central, and lateral portions of the patellar tendon decreased significantly (p < 0.05) from full extension to 60°. Thereafter, no statistically significant differences in the coronal plane angle of the patellar tendon were observed. At low flexion angles, the patellar tendon was oriented medially (* p < 0.05)

Discussion

In this study, we quantified the in-vivo kinematics of the patellar tendon during weight-bearing flexion. In general, all three portions of the patellar tendon deformed similarly. The length of the patellar tendon increased sharply as the knee flexed from full extension to 30° of flexion. Thereafter, the length of the patellar tendon remained relatively constant until maximum flexion. In the sagittal plane, the patellar tendon was oriented anteriorly relative to the long shaft of the tibia at full extension, and decreased significantly with increasing flexion. The patellar tendon was oriented posteriorly at 90 and 110° of flexion. In the coronal plane, the patellar tendon was oriented medially relative to the tibia at low flexion angle and formed a smaller angle with respect to the long axis of the tibia at higher flexion angles.

Few studies in the literature have quantified the in-vivo elongation of the patellar tendon. Sheehan and Drace used cine phase contrast MRI to measure patellar tendon elongation during flexion and extension from 0 to 35–45° (Sheehan and Drace, 2000). They observed an elongation of 6.6% during this motion. In the present study, we also noted a large apparent elongation of the patellar tendon in this range. Between 30 and 110° of flexion, we observed relatively small changes in the length of the patellar tendon.

The data on the sagittal plane angle are consistent with the observations of previous studies in the literature (Hirokawa, et al., 1992; Li, et al., 2004b; Torzilli, et al., 1994). In the current study, we noted that the sagittal plane angle of the patellar tendon shifted from positive to negative between 60 and 90°. In cadaveric studies, previous investigators have noted that simulated quadriceps loads pull the tibia anteriorly at low flexion angles and posteriorly at high flexion angles (Hirokawa, et al., 1992; Li, et al., 2004b; Torzilli, et al., 1994). The changes in the sagittal plane angle observed in this study might be related to the tibiofemoral kinematics. The decreasing sagittal plane angle of the patellar tendon with flexion might correspond to the posterior translation of the femur relative to the tibia reported during weight-bearing flexion (DeFrate, et al., 2006; Li, et al., 2004c).

The decreasing sagittal plane angle of the patellar tendon is consistent with studies on cruciate ligament function during in-vivo weight-bearing flexion. At low flexion angles, maximal elongation of the anterior cruciate ligament was observed (Li, et al., 2005; Li, et al., 2004a), which might be due to the anterior pull of the patellar tendon on the tibia. At high flexion angles, maximal elongation of the PCL was observed (DeFrate, et al., 2004a; Li, et al., 2004a), which might be due to the posterior pull of the patellar tendon on the tibia.

The data on the coronal plane orientation was also consistent with observations in the literature. At flexion angles less than 60°, previous investigators reported that simulated quadriceps loads elicited a large internal rotation (Hirokawa, et al., 1992; Li, et al., 2004b). Thereafter, only small changes in rotation were observed. In the current study, we observed that as the knee flexes from full extension to 30°, the patellar tendon was oriented medially. A quadriceps contraction, therefore, might dramatically increase the internal rotation the tibia relative to the femur in this range of motion, as observed in other in-vivo studies (DeFrate, et al., 2006; Li, et al., 2004c). At higher flexion angles, the patellar tendon forms a smaller angle with the long axis of the tibia, where a smaller change in rotation with flexion was observed (DeFrate, et al., 2006; Li, et al., 2004c).

Data on the kinematics of the patellar tendon is important for the computational modeling of knee joint function (Aalbersberg, et al., 2005; Imran, et al., 2000; Tsaopoulos, et al., 2006). Many studies have investigated the moment arm of the patellar tendon in two dimensions (Kellis and Baltzopoulos, 1999; Smidt, 1973; Tsaopoulos, et al., 2006). More recently, the moment arm of the patellar tendon has been measured in three dimensions in cadavers (Krevolin, et al., 2004). Others have investigated patellar tendon function during passive or isometric flexion using MRI (Aalbersberg, et al., 2005; Wretenberg, et al., 1996). In many studies, the patellar tendon has been assumed to be inextensible (Gill and O'Connor, 1996; Neptune, et al., 2000; Shelburne, et al., 2004; Yanagawa, et al., 2002). The data of the current study provides three-dimensional data on the line of action of the patellar tendon during in-vivo weight bearing flexion. The patellar tendon changes its orientation in both the sagittal and coronal planes, indicating that it should be modeled as a three-dimensional structure. Furthermore, these data suggest that the patellar tendon experiences large changes in length at low flexion angles. Therefore, the assumption of inextensibility might result in inaccurate predictions of patellar tracking and contact.

The patellar tendon experienced relatively small changes in length during weight bearing flexion between 30 and 110°. Because the quadriceps load has been thought to be relatively large when the knee is flexed (Li, et al., 1998), these data might indicate that the patellar tendon is very stiff in this range. In the linear region of the stress strain curve, Butler et al (Butler, et al., 1986) reported that the patellar tendon has an elastic modulus of approximately 650MPa, while Harraldson (Haraldsson, et al., 2004) reported an average elastic modulus of approximately 900MPa. Hansen et al (Hansen, et al., 2006) recently reported a cross-sectional area of 160mm2 for the patellar tendon. These data imply that for a 1mm change in length, the force in the patellar tendon might change by approximately 1700–2400N. Li et al (Li, et al., 1998) reported that a peak quadriceps force of approximately 3200N during isokinetic extension. Therefore, during weight-bearing flexion between 30 and 110°, the patellar tendon might not experience large changes in length while still transmitting large forces. This information might be useful for computational modeling of knee joint function during weight-bearing flexion.

Our data on the kinematics of the patellar tendon has interesting clinical implications. The shorter length of the patellar tendon at flexion angles less than 30° might correspond to the lower levels of loading of the patella tendon in the toe region of its stress-strain curve. These data might be useful to the design of rehabilitation protocols of patients after patellar tendon repair. For example, in the early stages of healing, rehabilitation exercises should keep the patient at flexion angles less than 30°, so as not to excessively strech the repair.

Surgical procedures that disrupt the patellar tendon might adversely affect the ability of the extensor mechanism to function properly. If the central third of the patellar tendon is removed for an anterior cruciate ligament reconstruction, the stiffness of the patellar tendon might be reduced by one third. This might alter the overall stiffness of the extensor mechanism, altering the articulation between the patella and femur. Furthermore, the perceived weakness of the quadriceps after ACL reconstruction (e.g. reduced ability to exert an extension moment) (Rosenberg, et al., 1992; Tyler, et al., 2004) might be in part due to the reduced stiffness of the patellar tendon after removal of its central third. Future studies should consider the effects of removal of the central third of the patellar tendon on patellofemoral biomechanics in-vivo.

This study has several limitations. The kinematics of the patellar tendon was only measured during one functional activity. Other in-vivo activities such as walking, running, and stair climbing should be considered in future studies. In addition, this study approximated the function of the patellar tendon using three straight lines. However, these lines did not penetrate into the tibia and the differences in deformations between the three regions were relatively small, indicating a uniform deformation of the patellar tendon. Additionally, the unstrained (reference) length of the patellar tendon was not known, so it is difficult to quantify the strains experienced by the patellar tendon from these data. Furthermore, this study did not measure the ground reaction force. Future studies should incorporate a load cell into the system, so that the moment applied to the joint might be estimated. Despite these limitations, this study provides data on the three-dimensional patellar tendon deformation during in-vivo weight-bearing flexion.

In conclusion, this study measured the kinematics of the patellar tendon during in-vivo weight-bearing flexion in normal subjects. All three portions of the patellar tendon experienced similar deformations, indicating that the deformation of the patellar tendon relatively uniform. The length of the patellar tendon increased significantly between full extension and 30° and remained relatively constant between 30 and 110°. The patellar tendon also underwent complex 3D deformations, with its orientation changing in both the sagittal and coronal planes. These data might help to delineate the contribution of the patellar tendon to joint stability.

Acknowledgments

The authors gratefully acknowledge the financial support of National Institutes of Health (R01 AR052408). The authors thank Elizabeth Desouza for her technical assistance.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Aalbersberg S, Kingma I, Ronsky JL, Frayne R, van Dieen JH. Orientation of tendons in vivo with active and passive knee muscles. J Biomech. 2005;38:1780–1788. doi: 10.1016/j.jbiomech.2004.09.003. [DOI] [PubMed] [Google Scholar]
  2. Butler DL, Grood ES, Noyes FR, Olmstead ML, Hohn RB, Arnoczky SP, Siegel MG. Mechanical properties of primate vascularized vs. nonvascularized patellar tendon grafts; changes over time. J Orthop Res. 1989;7:68–79. doi: 10.1002/jor.1100070110. [DOI] [PubMed] [Google Scholar]
  3. Butler DL, Kay MD, Stouffer DC. Comparison of material properties in fascicle-bone units from human patellar tendon and knee ligaments. J Biomech. 1986;19:425–432. doi: 10.1016/0021-9290(86)90019-9. [DOI] [PubMed] [Google Scholar]
  4. Chan SC, Seedhom BB. The effect of the geometry of the tibia on prediction of the cruciate ligament forces: a theoretical analysis. Proc Inst Mech Eng [H] 1995;209:17–30. doi: 10.1243/PIME_PROC_1995_209_313_02. [DOI] [PubMed] [Google Scholar]
  5. DeFrate LE, Gill TJ, Li G. In vivo function of the posterior cruciate ligament during weightbearing knee flexion. Am J Sports Med. 2004a;32:1923–1928. doi: 10.1177/0363546504264896. [DOI] [PubMed] [Google Scholar]
  6. DeFrate LE, Papannagari R, Gill TJ, Moses JM, Pathare NP, Li G. The 6 Degrees of Freedom Kinematics of the Knee After Anterior Cruciate Ligament Deficiency: An In Vivo Imaging Analysis. Am J Sports Med. 2006 doi: 10.1177/0363546506287299. [DOI] [PubMed] [Google Scholar]
  7. DeFrate LE, Sun H, Gill TJ, Rubash HE, Li G. In vivo tibiofemoral contact analysis using 3D MRI-based knee models. J Biomech. 2004b;37:1499–1504. doi: 10.1016/j.jbiomech.2004.01.012. [DOI] [PubMed] [Google Scholar]
  8. Gill HS, O'Connor JJ. Biarticulating two-dimensional computer model of the human patellofemoral joint. Clin Biomech (Bristol, Avon) 1996;11:81–89. doi: 10.1016/0268-0033(95)00021-6. [DOI] [PubMed] [Google Scholar]
  9. Hansen P, Bojsen-Moller J, Aagaard P, Kjaer M, Magnusson SP. Mechanical properties of the human patellar tendon, in vivo. Clin Biomech (Bristol, Avon) 2006;21:54–58. doi: 10.1016/j.clinbiomech.2005.07.008. [DOI] [PubMed] [Google Scholar]
  10. Haraldsson BT, Aagaard P, Krogsgaard M, Alkjaer T, Kjaer M, Magnusson SP. Region Specific Mechanical Properties of the Human Patella Tendon. J Appl Physiol. 2004 doi: 10.1152/japplphysiol.00482.2004. [DOI] [PubMed] [Google Scholar]
  11. Hirokawa S, Solomonow M, Lu Y, Lou ZP, D'Ambrosia R. Anterior-posterior and rotational displacement of the tibia elicited by quadriceps contraction. Am J Sports Med. 1992;20:299–306. doi: 10.1177/036354659202000311. [DOI] [PubMed] [Google Scholar]
  12. Imran A, Huss RA, Holstein H, O'Connor JJ. The variation in the orientations and moment arms of the knee extensor and flexor muscle tendons with increasing muscle force: a mathematical analysis. Proc Inst Mech Eng [H] 2000;214:277–286. doi: 10.1243/0954411001535778. [DOI] [PubMed] [Google Scholar]
  13. Johnson GA, Tramaglini DM, Levine RE, Ohno K, Choi NY, Woo SL. Tensile and viscoelastic properties of human patellar tendon. J Orthop Res. 1994;12:796–803. doi: 10.1002/jor.1100120607. [DOI] [PubMed] [Google Scholar]
  14. Kellis E, Baltzopoulos V. In vivo determination of the patella tendon and hamstrings moment arms in adult males using videofluoroscopy during submaximal knee extension and flexion. Clin Biomech (Bristol, Avon) 1999;14:118–124. doi: 10.1016/s0268-0033(98)00055-2. [DOI] [PubMed] [Google Scholar]
  15. Krevolin JL, Pandy MG, Pearce JC. Moment arm of the patellar tendon in the human knee. J Biomech. 2004;37:785–788. doi: 10.1016/j.jbiomech.2003.09.010. [DOI] [PubMed] [Google Scholar]
  16. Li G, Defrate LE, Rubash HE, Gill TJ. In vivo kinematics of the ACL during weight-bearing knee flexion. J Orthop Res. 2005;23:340–344. doi: 10.1016/j.orthres.2004.08.006. [DOI] [PubMed] [Google Scholar]
  17. Li G, DeFrate LE, Sun H, Gill TJ. In vivo elongation of the anterior cruciate ligament and posterior cruciate ligament during knee flexion. Am J Sports Med. 2004a;32:1415–1420. doi: 10.1177/0363546503262175. [DOI] [PubMed] [Google Scholar]
  18. Li G, DeFrate LE, Zayontz S, Park SE, Gill TJ. The effect of tibiofemoral joint kinematics on patellofemoral contact pressures under simulated muscle loads. J Orthop Res. 2004b;22:801–806. doi: 10.1016/j.orthres.2003.11.011. [DOI] [PubMed] [Google Scholar]
  19. Li G, Gil J, Kanamori A, Woo SL. A validated three-dimensional computational model of a human knee joint. J Biomech Eng. 1999;121:657–662. doi: 10.1115/1.2800871. [DOI] [PubMed] [Google Scholar]
  20. Li G, Kawamura K, Barrance P, Chao EY, Kaufman K. Prediction of muscle recruitment and its effect on joint reaction forces during knee exercises. Ann Biomed Eng. 1998;26:725–733. doi: 10.1114/1.104. [DOI] [PubMed] [Google Scholar]
  21. Li G, Wuerz TH, DeFrate LE. Feasibility of using orthogonal fluoroscopic images to measure in vivo joint kinematics. J Biomech Eng. 2004c;126:314–318. doi: 10.1115/1.1691448. [DOI] [PubMed] [Google Scholar]
  22. Neptune RR, Wright IC, van den Bogert AJ. The influence of orthotic devices and vastus medialis strength and timing on patellofemoral loads during running. Clin Biomech (Bristol, Avon) 2000;15:611–618. doi: 10.1016/s0268-0033(00)00028-0. [DOI] [PubMed] [Google Scholar]
  23. Rosenberg TD, Franklin JL, Baldwin GN, Nelson KA. Extensor mechanism function after patellar tendon graft harvest for anterior cruciate ligament reconstruction. Am J Sports Med. 1992;20:519–525. doi: 10.1177/036354659202000506. discussion 525–516. [DOI] [PubMed] [Google Scholar]
  24. Sheehan FT, Drace JE. Human patellar tendon strain. A noninvasive, in vivo study. Clin Orthop Relat Res. 2000:201–207. [PubMed] [Google Scholar]
  25. Shelburne KB, Pandy MG, Anderson FC, Torry MR. Pattern of anterior cruciate ligament force in normal walking. J Biomech. 2004;37:797–805. doi: 10.1016/j.jbiomech.2003.10.010. [DOI] [PubMed] [Google Scholar]
  26. Smidt GL. Biomechanical analysis of knee flexion and extension. J Biomech. 1973;6:79–92. doi: 10.1016/0021-9290(73)90040-7. [DOI] [PubMed] [Google Scholar]
  27. Torzilli PA, Deng X, Warren RF. The effect of joint-compressive load and quadriceps muscle force on knee motion in the intact and anterior cruciate ligament-sectioned knee. Am J Sports Med. 1994;22:105–112. doi: 10.1177/036354659402200117. [DOI] [PubMed] [Google Scholar]
  28. Tsaopoulos DE, Maganaris CN, Baltzopoulos V. Can the patellar tendon moment arm be predicted from anthropometric measurements? J Biomech. 2006 doi: 10.1016/j.jbiomech.2006.01.022. [DOI] [PubMed] [Google Scholar]
  29. Tyler TF, Nicholas SJ, Hershman EB, Glace BW, Mullaney MJ, McHugh MP. The effect of creatine supplementation on strength recovery after anterior cruciate ligament (ACL) reconstruction: a randomized, placebo-controlled, double-blind trial. Am J Sports Med. 2004;32:383–388. doi: 10.1177/0363546503261731. [DOI] [PubMed] [Google Scholar]
  30. Wretenberg P, Nemeth G, Lamontagne M, Lundin B. Passive knee muscle moment arms measured in vivo with MRI. Clin Biomech (Bristol, Avon) 1996;11:439–446. doi: 10.1016/s0268-0033(96)00030-7. [DOI] [PubMed] [Google Scholar]
  31. Yanagawa T, Shelburne K, Serpas F, Pandy M. Effect of hamstrings muscle action on stability of the ACL-deficient knee in isokinetic extension exercise. Clin Biomech (Bristol, Avon) 2002;17:705–712. doi: 10.1016/s0268-0033(02)00104-3. [DOI] [PubMed] [Google Scholar]

RESOURCES