Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2008 Jan 1.
Published in final edited form as: J Biomech. 2007 Apr 12;40(8):1662–1669. doi: 10.1016/j.jbiomech.2007.01.024

Physical Validation of a Patient-Specific Contact Finite Element Model of the Ankle

Donald D Anderson †,*, Jane K Goldsworthy *, Li Wendy *, M James Rudert †, Yuki Tochigi †, Thomas D Brown †,*
PMCID: PMC1945165  NIHMSID: NIHMS24165  PMID: 17433333

Abstract

A validation study was conducted to determine the extent to which computational ankle contact finite element (FE) results agreed with experimentally measured tibio-talar contact stress. Two cadaver ankles were loaded in separate test sessions, during which ankle contact stresses were measured with a high-resolution (Tekscan) pressure sensor. Corresponding contact FE analyses were subsequently performed for comparison. The agreement was good between FE-computed and experimentally measured mean (3.2% discrepancy for one ankle, 19.3% for the other) and maximum (1.5% and 6.2%) contact stress, as well as for contact area (1.7% and 14.9%). There was also excellent agreement between histograms of fractional areas of cartilage experiencing specific ranges of contact stress. Finally, point-by-point comparisons between the computed and measured contact stress distributions over the articular surface showed substantial agreement, with correlation coefficients of 90% for one ankle, and 86% for the other. In the past, general qualitative, but little direct quantitative agreement has been demonstrated with articular joint contact FE models. The methods used for this validation enable formal comparison of computational and experimental results, and open the way for objective statistical measures of regional correlation between FE-computed contact stress distributions from comparison articular joint surfaces (e.g., those from an intact versus those with residual intra-articular fracture incongruity).

Keywords: ankle, finite element, validation, articular joint contact

INTRODUCTION

Validation of Articular Joint Contact Models

Historically, the methods used and the rigor exercised in finite element (FE) validation studies of articular joint contact analysis have varied substantially. In an FE model of a metal-on-metal hip resurfacing prosthesis, validity was established by comparing pressure distributions from the model with those computed using a Hertzian contact mechanics solution (Udofia et al., 2004). In another study, in which computer-assisted methods were used to calculate contact pressures and areas in dysplastic and normal hips, validity of the computational method was established by comparing contact pressures with those reported in literature (Hipp et al., 1999). In an FE model of patello-femoral contact (reporting contact stress, patellar kinematics and relevant tendon forces), validation metrics involved comparing computed kinematics (resulting from input muscle forces) with kinematics reported from an experimental test, supplemented by comparison of computed patellar tendon force magnitudes with those found in literature (Heegaard et al., 1995). A recent review article went so far as to state that many, if not most numerical models of articular joint contact have been published without any attempt whatsoever at experimental confirmation (Brand, 2005).

While comparing FE results with values cited in previously published work or with corroborative results from other analytical methods serves to establish at least general confidence, comparison with data from a direct physical experiment can provide a more robust and definitive validation. Current experimental capabilities afford relatively high resolution mapping of contact stress distributions in an articular joint, although this is generally restricted to cadaveric specimen testing (Baratz et al., 1996; Brown et al., 2004; McKinley et al., 2004). Most previous studies have chosen to base their validity assessment upon global reduced scalar measures of the three-dimensional contact stress distribution, such as mean or maximum contact stress and/or contact area (Anderson et al., 2005; Haut Donahue et al., 2003; Huber-Betzer et al., 1990). In those few cases where full-field contact stress comparisons have indeed been made, they have generally been only qualitative (Anderson et al., 2005). While arguably reasonable in the past, with the present convergence of biomechanics, mechano-biology, molecular biology and genetics to meaningfully address phenomena at the tissue, cell and even molecular levels, it is critically important now more than ever that the “source” mechanical data be reliable in an absolute and rigorous sense.

The Rationale for Validation: The FE Model

The role of altered contact mechanics in the pathology of post-traumatic osteoarthritis (OA) following intra-articular fracture remains poorly understood. One of several proposed etiologies is that residual incongruities (i.e., anatomical irregularities in the articular surfaces) remaining after the injury and treatment lead to aberrations in the joint contact stress distributions which, over time, predispose to post-traumatic OA (Lefkoe et al., 1993; Wagner et al., 1996). The finite element (FE) method provides an ideal vehicle by which to study joint contact stresses on a patient-specific basis. Toward testing this proposed mechano-pathology, an FE model has been developed to predict patient-specific joint contact stresses in the ankle throughout the entire stance phase of gait (Anderson et al., 2006).

The broader scope of study has involved FE models generated from segmented CT data for fractured and surgically treated ankles, as well as for the uninjured contralateral ankles, from a series of patients with unilateral intra-articular fractures of the tibial plafond. FE meshes of the articulating surfaces have been generated and gait simulation performed, allowing computation of the contact stresses across the articulating ankle surfaces at multiple instances throughout gait. Boundary conditions were applied so as to allow the ankle to rotate not as a fixed hinge, but rather in multiple planes, as dictated by the tibio-talar articulation (Leardini et al., 2000; Tochigi et al., 2005). The resulting ankle motions and computed contact stresses were shown to be consistent with those previously measured experimentally (Bottlang et al., 1999; Vrahas et al., 1994). Computed contact stresses were then summed over time to calculate contact stress exposures for each intact and fractured ankle. For a given patient, differences in contact stress exposures between the healed fractured ankle and the intact contralateral reflect propensity for articular degeneration.

The purpose of the present study was to validate the FE modeling approach used in that work, by direct comparison with physical measurements from corresponding cadaver loading tests. Successful cadaver validation of computed contact stress distributions, across the articular surface, provides a strong base of support for FE model biofidelity.

METHODS

In separate test sessions, two fresh-frozen cadaver ankle specimens (University of Iowa Deeded Body Program) were prepared and loaded in a custom fixture, first to establish a neutral load-bearing joint apposition, then later with a pressure sensor placed within the joint to measure contact stresses. A CT scan of the ankle was acquired to record the precise loaded joint apposition. Stainless steel Kirschner wires (K-wires) were drilled across the joint, piercing the still-loaded pressure sensor, to index sensor orientation relative to the joint surfaces. An FE model of each ankle was generated, with boundary conditions applied to replicate the experimental loading. Finally, experimental and computational contact stress distributions were spatially registered and compared over the entire contact patch.

Specimen Preparation, CT Scan Acquisition, and Physical Testing

The joint capsule and ligaments of the thawed cadaver ankles were left intact. For one specimen, in order to eliminate motion at the talo-calcaneal joint, the talus was rigidly fixed to the calcaneus with two cemented-in fiberglass rods. (This step was omitted in the preparation of the second test specimen, as the influence of this factor was found to be minor.) The calcaneus and forefoot were potted in polymethyl-methacrylate, and rigidly attached to an aluminum base plate.

Each cadaver ankle was placed in a loading fixture in neutral flexion/extension, and a materials testing machine (MTS Bionix 858) was used to apply a 600 N compressive load across the joint (Figure 1). This step was necessary in order to establish the neutral load-bearing apposition for each ankle. Flexion/extension rotations of the foot/talus construct were fixed during force application, but all other translational and rotational degrees of freedom were free. The foot inversion/eversion angle, tibial internal/external rotation angle, and the tibial medial/lateral and anterior/posterior positions were recorded in the loaded apposition. The specimen was then transferred to a plastic mounting fixture (identical to the loading fixture, except machined from plastic), where the apposition was carefully reproduced.

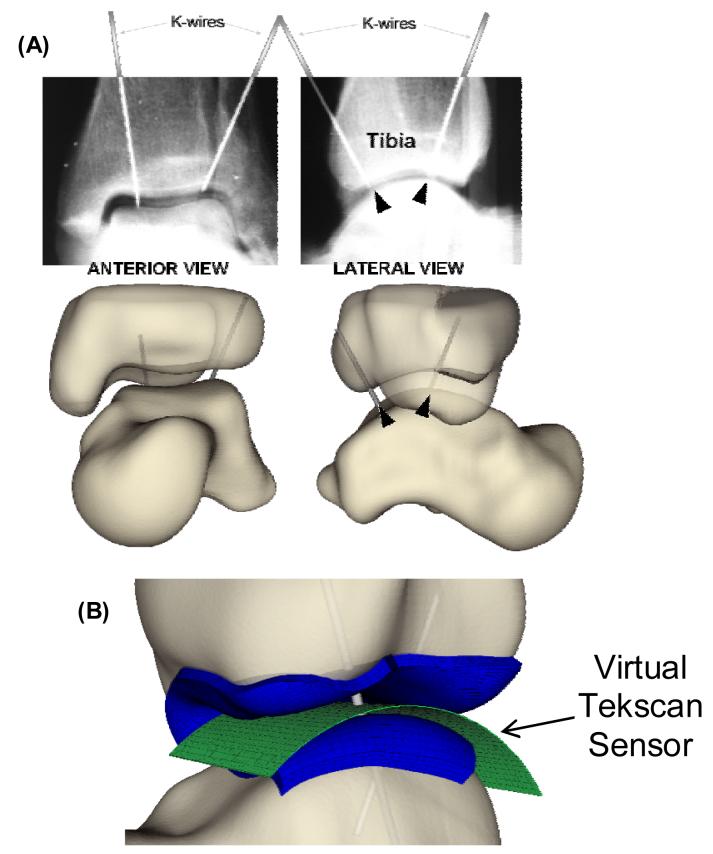
Figure 1.

Figure 1

Open in a new tab

Schematic of ankle loading, showing the bones of an ankle specimen, the Tekscan 5033 pressure sensor, and the loading fixture with noted constraints.

CT scans of the ankles within the plastic fixture were acquired at 0.3 mm slice thickness in a Siemens Sensation 64-slice scanner, with a field of view selected to provide an in-plane spatial resolution of 0.3 mm. The specimens were then returned to the loading fixture and the joint capsule opened. A Tekscan Model #5033 pressure sensor (Tekscan, Inc.; Boston, MA) was calibrated (Baer et al., 2005) and inserted into the tibio-talar joint (McKinley et al., 2004). This sensor measures pressure at 1472 sensing elements (46×32 sensels), with a resolution of 144 sensels/cm2. The 600 N load was once again applied, and the position was recorded to verify restoration of the same neutral load-bearing apposition. Tekscan sensor readings were recorded, obtaining 10 frames at 10 Hz (i.e.,1 second). Two 1 mm diameter stainless steel K-wires were then drilled through the tibia, across the joint piercing the sensor, and into the talus. Bi-planar radiographs were then taken with the K-wires in place to record the relative locations of the tibia, talus, and the Tekscan pressure sensor.

FE Model Generation and Spatial Registration

The CT scan data from each ankle specimen were segmented in MATLAB (The MathWorks, Inc., Natick, MA), using a custom-written program (Anderson et al., 2004), and the results were exported as a bone boundary point cloud for the tibia and for the talus. Geomagic Studio software (Geomagic Inc., Research Triangle Park, NC) was used first to create detailed polygonal surfaces from the bone boundary point cloud data, and subsequently to smooth the noisy surface data. The accuracy of the final smoothed surface fits relative to the original point cloud data were constrained, using Geomagic Studio's tolerance functionality, to be within +/−0.15 mm.

Articular cartilage regions were extruded along local bone surface normals at the tibio-talar articulation to a uniform thickness of 1.7 mm (Anderson et al., 2006). In our intended clinical application of patient-specific contact FE modeling, we are presented with CT studies from ankles for which the distribution of articular cartilage thickness is not known. For this reason, and based on preliminary work with the FE models, we chose to use a uniform cartilage thickness, with the actual thickness value based upon previous work (El-Khoury et al., 2004). Finally, the bone and cartilage surface data were imported into TrueGrid software (XYZ Scientific Applications, Inc., Livermore, CA) to generate an all-hexahedral FE mesh.

The plastic mounting fixture was segmented from CT so that its geometry could be imported into a virtual environment (Data Manager software – Van Sint Jan et al., 2004), along with the bone surfaces, to execute a definitive spatial registration. The bone surfaces were interactively positioned and oriented based upon their known locations with respect to the loading fixture, in order to replicate the loading / rotational axes for FE modeling purposes. Spatial registration of the Tekscan sensor readings and the FE results enabled a comprehensive comparison of the experimentally measured versus computationally predicted contact stress distributions. To facilitate registration, a virtual representation of the Tekscan sensor including the sensor's individual sensels, was imported into Data Manager. The curvature of the virtual sensor was chosen to nominally match the curvature of the tibio-talar articulation (Figure 2), assuming that the highly flexible sensor would conform to the joint surfaces. The two K-wires were modeled in the virtual environment by cylinders of appropriate dimensions, positioned and oriented to match their silhouettes on the bi-planar radiographs. Finally, the Tekscan sensor was rotated and translated so that the K-wires pierced it at the correct locations.

Figure 2.

Figure 2

Open in a new tab

(A) Anterior and lateral view radiographs of the loaded cadaver tibia and talus, with K-wires in place, enabled definitive registration. (B) Antero-lateral view of the Tekscan sensor (green) and the finite element mesh (blue), registered with K-wires (gray) drilled through the tibia and talus (exploded view, for visualization).

Finite element solutions were obtained using a commercially available code (ABAQUS Standard 6.6, ABAQUS, Inc., Providence, RI, USA). Each FE model included a distal segment of the tibia, and the entire talus. Deformable contact zones were defined across the entire apposing tibial and talar articular cartilage surfaces, and the cartilage was assigned isotropic linear elastic material properties (E = 12MPa and ν = 0.42). Boundary conditions of the FE models were selected to replicate the experimental loading. Ankle ligaments were not explicitly included, as only minor relative translation of the two bones was expected in the axial-only loading simulation. Soft tissue constraints across the ankle joint were instead modeled in the FE analysis with a single linear spring (k=50N/mm) placed to resist anterior-posterior translation.

A mesh convergence study was performed in the first of the two validation cases, to ensure that mesh resolution-independent FE results were obtained while exercising a reasonable expenditure of computational resources. The ratio of tibial to talar element size (1:3) was maintained, and the element aspect ratios were held constant, as the number of total elements was varied. Thirteen FE simulations were completed, each with a different number of elements. The minimum number of elements tested was 2,997 and the maximum was 293,402 elements.

The registered Tekscan-measured and FE-computed contact stress distributions were imported into MATLAB to allow formal comparisons of the contact stress distributions. As the two datasets were at different spatial resolutions, and registered to grids that did not coincide, formal comparison required linear interpolation of the data, appropriately re-sampled to a common spatial grid (the Tekscan sensel grid was used for this purpose). Once this was accomplished, point-by-point comparisons between the computed and measured contact stress distributions were made.

Mean and maximum contact stress values, as well as the contact area, were first compared. Next, the contact stress distributions were post-processed to generate area engagement histograms, corresponding to the fractional areas of cartilage experiencing specific ranges of contact stress (0.5 MPa increments – Maxian et al., 1995), and compared. Then absolute point-by-point differences in the computed and measured contact stresses were evaluated, first in terms of their correlation over the 1472 sensel locations, then in terms of the distribution of discrepancies over the surface. Finally, probability density functions were calculated for the differences between the computed and measured contact stress values, allowing confidence intervals to be formulated for each of the two validation ankles.

RESULTS

Using maximum contact stress and total contact area as metrics of convergence, a mesh of approximately 50,000 elements was judged as being adequate to assure a converged FE solution. Computation times (HP rx4640; 4-CPU, 1.5 GHz Itanium (64 bit) system; 12 GB RAM/438 GB disk) ranged from 1.3 minutes for 2,997 elements to nearly 40 hours for 293,402 elements (90 minutes for the converged FE solution). All subsequent FE simulations were run using the 50,000-element converged level of mesh refinement.

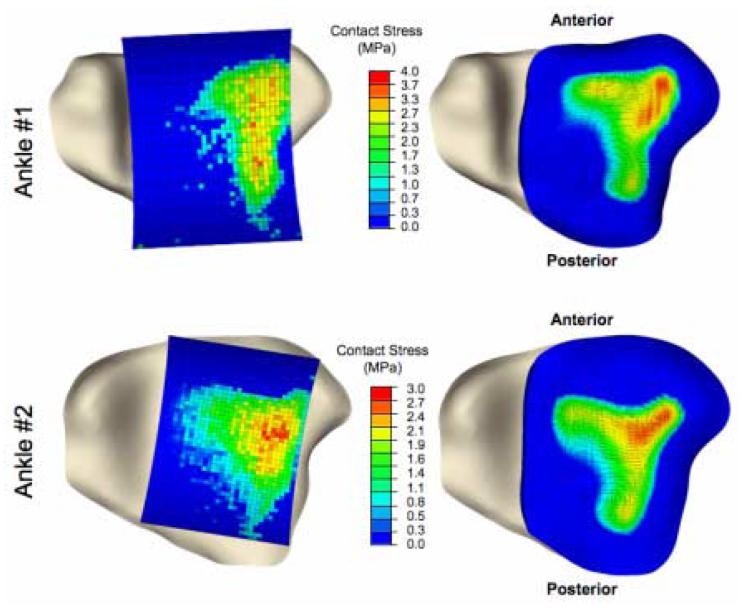
The Tekscan-measured and FE-computed contact stress distributions are shown in Figure 3. In both validation ankles, contact spanned most of the lateral half of the tibial surface. The physical validation established confidence in results from the FE models, beginning with global scalar metrics of contact stress (Table 1). For validation ankle #1, the maximum contact stress computed from the FE simulations was within 1.5% of that measured, the mean computed contact stress was within 3.2%, and the contact area was within 1.7%. For validation ankle #2, the computed maximum contact stress was within 6.2% of that measured, the mean within 18.3%, and the contact area within 14.9%.

Figure 3.

Figure 3

Open in a new tab

Inferior view of tibia, overlaid with spatially aligned Tekscan pressure results (left) and FE results (right) for each validation ankle.

Table 1.

This simple comparison of global metrics for the two cadaver ankles included in the physical validation study establishes general agreement between the Tekscan-measured and FE-computed contact stress distributions.

Ankle #1 Ankle #2
Tekscan Finite
Element		 Tekscan Finite
Element
Maximum Contact Stress (MPa) 3.69 3.74 2.92 2.74
Mean Contact Stress (MPa) 1.96 2.02 1.15 1.36
Contact Area (mm2) 295.1 290.5 493.6 419.9
Open in a new tab

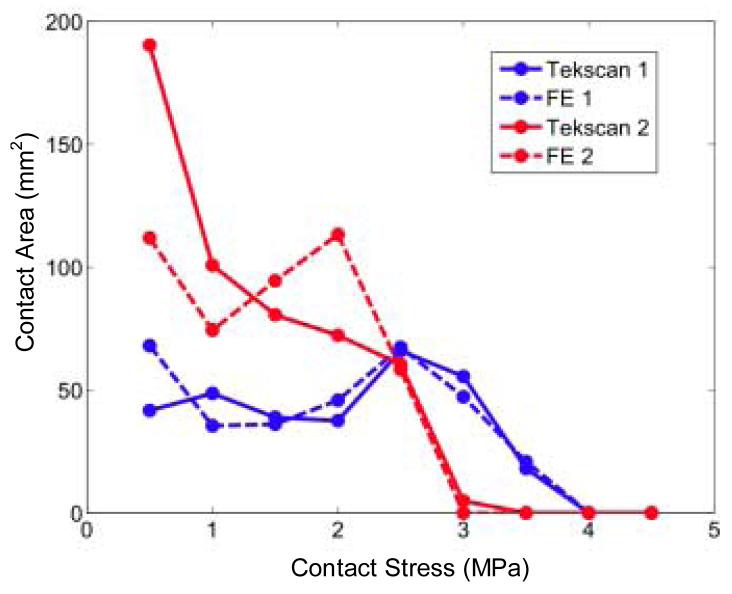
In addition to agreement in these global scalar metrics of contact stress, there was general agreement in the measured versus computed distributions of contact areas across the contact stress levels (Figure 4), especially so at the more physiologically challenging higher contact stress ranges. The area engagement histograms of the two validation ankles varied somewhat, with ankle #1 (presumably more anatomically incongruent) having larger areas with higher contact stresses, and a proportionally smaller area at lower contact stress levels, as compared to ankle #2.

Figure 4.

Figure 4

Open in a new tab

Area engagement histograms of tibio-talar contact for Tekscan and FE results. Each data point represents the high point of that range of contact stress values (e.g., the point at 0.5 MPa reflects regions with stresses > 0.0 MPa and ≤ 0.5 MPa).

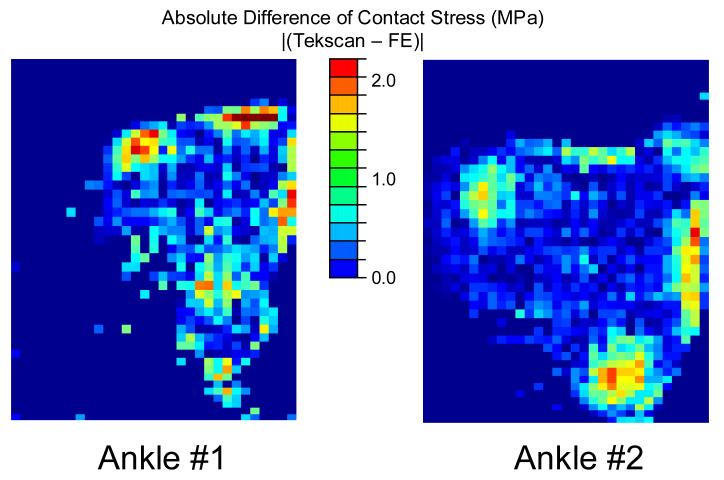
Point-by-point comparisons between the measured and computed contact stress distributions over the surface (Figure 5) showed substantial agreement. There were several small patches of larger discrepancy (>2 MPa), but they were highly focal and near the periphery of contact. The differences were normally distributed, with means and standard deviations of 0.05±0.48 for ankle #1, and −0.02±0.44 for ankle #2. Based upon these putative normal distributions (Figure 6), the probability that differences between the Tekscan-measured and FE-computed contact stress values were less than 0.75 MPa was 88% for ankle #1, and 91% for ankle #2, with correlation coefficients of 90% for ankle #1, and 86% for ankle #2.

Figure 5.

Figure 5

Open in a new tab

Point-by-point absolute differences between the Tekscan-measured and FE-computed contact stress distributions show only minor discrepancies over the majority of the articular surfaces, particularly for the most heavily engaged central regions.

Figure 6.

Figure 6

Open in a new tab

The probability distributions for differences between the Tekscan-measured and FE-computed contact stress values show excellent agreement, with roughly 90% probability that differences are within 0.75 MPa. The two smoothed curves are idealized probability distributions based upon the binned data (n = 1472 samples; μ = mean; σ = standard deviation). Note: A majority of central zero-valued differences are for locations where contact stress values are zero.

DISCUSSION

The present direct comparisons between physical measurements and the FE model of ankle loading convincingly establish the computational model's validity. This validation exercise not only showed reasonable comparison between the global metrics of contact stress and contact area, but also in the regional and spatial distributions of contact stress. Because OA usually initiates regionally, it seems especially important that contact FE models be validated regionally, rather than just in terms of global summary measures. Based upon these validation results, FE stresses could be reported over the whole articulating surface with a very reasonable degree of confidence (conservatively, within 10%-15% of those measured experimentally).

Tekscan was chosen for this study from among a number of other potential pressure sensors. Fuji pressure sensitive film is one type of sensor frequently used because of its reasonable accuracy (±10%), low cost, and ease of use (Brown et al., 1988; Ishii et al., 1998). Fuji film cannot, however, be used to measure dynamic effects, as would be expected in unstable articular joints (McKinley et al., 2004). A Tekscan pressure sensor design (Model #5033) was specifically developed in our laboratory for use in the ankle (Brown et al., 2004). When appropriately calibrated, the Tekscan sensor enables dynamic pressure measurements at spatial resolutions comparable to those from Fuji film (Baer et al., 2005).

There are several plausible explanations for the modest focal discrepancies that were observed between measured and computed contact stress distributions at the periphery of contact. Inserting the Tekscan sensor into the articular joint could potentially disturb the natural contact pattern. Imperfect segmentation of the bones and/or inadequate replication of nonuniform cartilage thickness would influence the computed contact stresses. A final possible explanation would be spatial registration errors between the Tekscan and FE data.

With the articulating surface of the tibio-talar joint being nearly cylindrical in nature, there was no evidence of sensor crinkling in the experimental testing. Since the sensor was very thin and easily conformed to the joint, it was deemed unlikely to interfere substantially with normal joint loading. The sensor was, therefore, not explicitly included in the FE model.

Another limitation was that the articular surface geometry was based on CT source data, where cartilage cannot easily be visualized. For this reason, a constant uniform thickness cartilage layer was extruded from the bony subchondral surfaces along local surface normals. Given the agreement observed between computed and measured contact stress values, this simplification seems reasonable. However, we did find the computed contact stress values to be mildly sensitive to the degree of smoothing utilized in going from CT-derived segmentations to smooth articular cartilage surfaces, an inviting area for further study. Smoothing of segmented point cloud data is a necessary step in obtaining reasonable FE contact solutions, but excessive smoothing would tend to obscure the influence of residual surface incongruity, our point of departure in this study. We chose to err on the conservative side, opting for less smoothing.

The computational investigation of altered contact mechanics associated with clinically observed residual incongruity following treatment and healing of intra-articular fractures depends upon faithful regional reproduction of the prevailing contact stress distributions. Simply establishing general agreement between computed and measured mean and maximum contact stresses and contact areas would not have been sufficient in this regard. In other studies similarly reliant upon accurate local prediction of contact stress, it will likewise be critically important that these “source” mechanical data be validated in an absolute and rigorous sense.

Acknowledgments

The technical assistance of Dr. Douglas Pedersen (Tekscan calibration) and Mr. Thaddeus Thomas (image segmentation) are gratefully acknowledged. Dr. Marco Viceconti and Dr. Fulvia Taddei provided assistance with the Data Manager software. This work was supported by grants from the NIH (AR46601 and AR048939).

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  • 1.Anderson DD, Deshpande BR, Daniel TE, Baratz ME. A three-dimensional finite element model of the radiocarpal joint: distal radius fracture step-off and stress transfer. Iowa Orthop J. 2005;25:108–17. [PMC free article] [PubMed] [Google Scholar]
  • 2.Anderson DD, Goldsworthy JK, Shivanna K, Grosland NM, Pedersen DR, Thomas TP, Tochigi Y, Marsh JL, Brown TD. Intra-articular contact stress distributions at the ankle throughout stance phase – patient-specific finite element analysis as a metric of degeneration propensity. Biomech Model Mechanobiol. 2006;5(23):82–9. doi: 10.1007/s10237-006-0025-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Anderson DD, Muehling VL, Marsh JL, Brown TD. Precise identification of bone fragment boundaries to assist in reduction of highly comminuted fractures. Computer Aided Surgery. 2004;9(3):116. [Google Scholar]
  • 4.Baer TE, Pedersen DR, Rudert MJ, Kallemeyn (Vos) NA, Grosland NM, Brown TD. Traveling-wave calibration of sheet array sensors for intra-articular pressure measurements; 51st Annual Meeting of the Orthopaedic Research Society; February 20–23, 2005; Presentation #1701. [Google Scholar]
  • 5.Baratz ME, Des Jardins J, Anderson DD, Imbriglia JE. Displaced intra-articular fractures of the distal radius: the effect of fracture displacement on contact stresses in a cadaver model. J Hand Surg [Am] 1996;21(2):183–8. doi: 10.1016/s0363-5023(96)80098-0. [DOI] [PubMed] [Google Scholar]
  • 6.Bottlang M, Marsh JL, Brown TD. Articulated external fixation of the ankle: minimizing motion resistance by accurate axis alignment. J Biomech. 1999;32(1):63–70. doi: 10.1016/s0021-9290(98)00143-2. [DOI] [PubMed] [Google Scholar]
  • 7.Brand RA. Joint contact stress: a reasonable surrogate for biological processes? Iowa Orthop J. 2005;25:82–94. [PMC free article] [PubMed] [Google Scholar]
  • 8.Brown TD. Finite element modeling in musculoskeletal biomechanics. J Applied Biomech. 2004;20:336–66. [Google Scholar]
  • 9.Brown TD, Anderson DD, Nepola JV, Singerman RJ, Pedersen DR, Brand RA. Contact stress aberrations following imprecise reduction of simple tibial plateau fractures. J Orthop Res. 1988;6(6):851–62. doi: 10.1002/jor.1100060609. [DOI] [PubMed] [Google Scholar]
  • 10.Brown TD, Rudert MJ, Grosland NM. New methods for assessing cartilage contact stress after articular fracture. Clin Orthop Relat Res. 2004;(423):52–8. doi: 10.1097/01.blo.0000132633.38338.8b. [DOI] [PubMed] [Google Scholar]
  • 11.El-Khoury GY, Alliman KJ, Lundberg HJ, Rudert MJ, Brown TD, Saltzman CL. Cartilage thickness in cadaveric ankles: measurement with double-contrast multi-detector row CT arthrography versus MR imaging. Radiology. 2004;233(3):768–73. doi: 10.1148/radiol.2333031921. [DOI] [PubMed] [Google Scholar]
  • 12.Haut Donahue TL, Hull ML, Rashid MM, Jacobs CR. How the stiffness of meniscal attachments and material properties affect tibio-femoral contact pressure computed using a validated finite element model of the human knee joint. J Biomech. 2003;36(1):19–34. doi: 10.1016/s0021-9290(02)00305-6. [DOI] [PubMed] [Google Scholar]
  • 13.Heegaard J, Leyvraz PF, Curnier A, Rakotomanana L, Huiskes R. The biomechanics of the human patella during passive knee flexion. J Biomech. 1995;28(11):1265–79. doi: 10.1016/0021-9290(95)00059-q. [DOI] [PubMed] [Google Scholar]
  • 14.Hipp JA, Sugano N, Millis MB, Murphy SB. Planning acetabular redirection osteotomies based on joint contact pressures. Clin Orthop Relat Res. 1999;(364):134–43. doi: 10.1097/00003086-199907000-00018. [DOI] [PubMed] [Google Scholar]
  • 15.Huber-Betzer H, Brown TD, Mattheck C. Some effects of global joint morphology on local stress aberrations near imprecisely reduced intra-articular fractures. J Biomech. 1990;23(8):811–22. doi: 10.1016/0021-9290(90)90028-2. [DOI] [PubMed] [Google Scholar]
  • 16.Ishii S, Palmer AK, Werner FW, Short WH, Fortino MD. Pressure distribution in the distal radioulnar joint. J Hand Surg [Am] 1998;23(5):909–13. doi: 10.1016/S0363-5023(98)80172-X. [DOI] [PubMed] [Google Scholar]
  • 17.Leardini A, O'Connor JJ, Catani F, Giannini S. The role of the passive structures in the mobility and stability of the human ankle joint: a literature review. Foot Ankle Int. 2000;21(7):602–15. doi: 10.1177/107110070002100715. [DOI] [PubMed] [Google Scholar]
  • 18.Lefkoe TP, Trafton PG, Ehrlich MG, Walsh WR, Dennehy DT, Barrach HJ, Akelman E. An experimental model of femoral condylar defect leading to osteoarthrosis. J Orthop Trauma. 1993;7(5):458–67. doi: 10.1097/00005131-199310000-00009. [DOI] [PubMed] [Google Scholar]
  • 19.Maxian TA, Brown TD, Weinstein SL. Chronic stress tolerance levels for human articular cartilage: two nonuniform contact models applied to long-term follow-up of CDH. J Biomech. 1995;28(2):159–66. doi: 10.1016/0021-9290(94)00054-8. [DOI] [PubMed] [Google Scholar]
  • 20.McKinley TO, Rudert MJ, Koos DC, Brown TD. Incongruity versus instability in the etiology of posttraumatic arthritis. Clin Orthop Relat Res. 2004;(423):44–51. doi: 10.1097/01.blo.0000131639.89143.26. [DOI] [PubMed] [Google Scholar]
  • 21.Tochigi Y, Rudert MJ, Amendola A, Brown TD, Saltzman CL. Tensile engagement of the peri-ankle ligaments in stance phase. Foot Ankle Int. 2005;26(12):1067–73. doi: 10.1177/107110070502601212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Udofia IJ, Yew A, Jin ZM. Contact mechanics analysis of metal-on-metal hip resurfacing prostheses. Proc Inst Mech Eng [H] 2004;218(5):293–305. doi: 10.1243/0954411041932854. [DOI] [PubMed] [Google Scholar]
  • 23.Van Sint Jan S, Viceconti M, Clapworthy G. Modern Visualization Tools for Research and Education in Biomechanics. Eighth International Conference on Information Visualization (IV'04); IEEE Computer Society.2004. pp. 9–14. [Google Scholar]
  • 24.Vrahas M, Fu F, Veenis B. Intraarticular contact stresses with simulated ankle malunions. J Orthop Trauma. 1994;8(2):159–66. doi: 10.1097/00005131-199404000-00014. [DOI] [PubMed] [Google Scholar]
  • 25.Wagner WF, Jr, Tencer AF, Kiser P, Trumble TE. Effects of intra-articular distal radius depression on wrist joint contact characteristics. J Hand Surg [Am] 1996;21(4):554–60. doi: 10.1016/S0363-5023(96)80003-7. [DOI] [PubMed] [Google Scholar]

RESOURCES