Influence of Electrotonic Structure and Synaptic Mapping on the Receptive Field Properties of a Collision-Detecting Neuron

Abstract

The lobula giant movement detector (LGMD) is a visual interneuron of Orthopteran insects involved in collision avoidance and escape behavior. The LGMD possesses a large dendritic field thought to receive excitatory, retinotopic projections from the entire compound eye. We investigated whether the LGMD’s receptive field for local motion stimuli can be explained by its electrotonic structure and the eye’s anisotropic sampling of visual space. Five locust (Schistocerca americana) LGMD neurons were stained and reconstructed. We show that the excitatory dendritic field and eye can be fitted by ellipsoids having similar geometries. A passive compartmental model fit to electrophysiological data was used to demonstrate that the LGMD is not electrotonically compact. We derived a spike rate to membrane potential transform using intracellular recordings under visual stimulation, allowing direct comparison between experimental and simulated receptive field properties. By assuming a retinotopic mapping giving equal weight to each ommatidium and equally spaced synapses, the model reproduced the experimental data along the eye equator, though it failed to reproduce the receptive field along the ventral-dorsal axis. Our results illustrate how interactions between the distribution of synaptic inputs and the electrotonic properties of neurons contribute to shaping their receptive fields.

INTRODUCTION

The last two decades have given rise to a growing appreciation for the complexities of dendritic integration in single neurons (Koch 1999; Koch and Segev 2000; London and Häusser 2005; Migliore and Shepherd 2005; Stuart et al. 1999). Although most studies are conducted in vitro, several systems, notably insects, have emerged as viable in vivo preparations to study single-neuron computation (Borst and Haag 2002; Jacobs and Theunissen 2000; Ogawa et al. 2006; Pollack 2000). Among these, the locust lobula giant movement detector (LGMD) is particularly interesting because it has been proposed as a model for multiplicative computation (Gabbiani et al. 2002; for review, Gabbiani et al. 2004).

The LGMD is a large, identified neuron located in the third neuropile of the locust optic lobe (O’Shea and Williams 1974). Anatomical and electrophysiological evidence suggests that it receives excitatory retinotopic inputs from the locust eye sensitive to motion (Rowell et al. 1977; Strausfeld and Nässel 1981). The neuron is known to respond most strongly to objects approaching on a collision course with the animal (e.g., Guest and Gray 2006; Hatsopoulos et al. 1995; Rind and Simmons 1992; Schlotterer 1977), although it also exhibits less robust responses to other types of moving stimuli (Krapp and Gabbiani 2005; Rowell 1971; Simmons and Rind 1992). In the protocerebrum, the LGMD contacts the descending contralateral movement detector neuron (DCMD) neuron via a powerful synaptic connection (Killmann and Schürmann 1985; Killmann et al. 1999; O’Shea and Rowell 1975; Rind 1984). The DCMD fires in a 1:1 fashion with the LGMD and projects to thoracic motor centers, synapsing onto neurons involved in the generation of jumps and flight steering maneuvers (Burrows 1996; O’Shea et al. 1974; Simmons 1980). For this reason, the LGMD-DCMD circuit is believed to be involved in mediating collision avoidance and escape (Burrows and Rowell 1973; Gray et al. 2001; O’Shea et al. 1974; Rowell 1971; Santer et al. 2006; Schlotterer 1977). Evidence suggests that its role in collision avoidance involves detecting an angular size threshold as objects approach on a collision course (Gabbiani et al. 1999, 2002; Matheson et al. 2004). This computation is thought to be implemented by multiplying excitatory inputs sensitive to motion with inhibitory inputs sensitive to object size (Gabbiani et al. 2002).

Although previous work has treated the LGMD as a point neuron (Edwards 1982; Rind and Bramwell 1996), recent results suggest it may be electrotonically extensive (Gabbiani and Krapp 2006; Gabbiani et al. 2001; Krapp and Gabbiani 2005). Understanding the electrotonic structure of the LGMD is an important first step in elucidating the mechanisms of dendritic integration underlying its sensitivity to looming objects. For an electrotonically extensive neuron, the synaptic mapping of the neuron’s inputs onto its dendritic compartments will be integral in shaping its response properties (Segev et al. 1995). This is especially interesting in light of recent work demonstrating the sampling of visual space by the locust eye to be highly anisotropic (Krapp and Gabbiani 2005) because the LGMD is believed to receive two inputs from each ommatidium (facet) on the eye in a retinotopically ordered manner (Rowell et al. 1977; Strausfeld and Nässel 1981). Based on this, it has been proposed that the interplay between electrotonic structure and synaptic connectivity of inputs from the eye may underlie the receptive field properties of the LGMD observed in response to local motion stimuli (Krapp and Gabbiani 2005). So far, much work has focused on describing the pattern of synaptic connectivity among neuron classes in the context of networks (Douglas and Martin 2004; Rolls and Treves 1998; Strausfeld and Nässel 1981; White 1989). Apart from a few systems (Borst and Egelhaaf 1992; Borst and Haag 2002; Jacobs and Theunissen 2000; Ogawa et al. 2006), surprisingly little is known about how the detailed mapping between inputs and dendritic compartments influences single-neuron responses to sensory stimuli. To study the interaction between electrotonic structure and synaptic mapping, our study employs a detailed description of the LGMD’s excitatory dendritic field morphology. We first characterize quantitatively the morphology of the LGMD neuron and measure its inter-individual variability. Next, a compartmental model is fit to electrophysiological data to derive the passive electrotonic structure of the neuron. Finally, various connectivity schemes between the distribution of local visual inputs on the eye and the LGMD dendrites are tested in the model to determine how the different mappings shape the neuron’s response properties to local motion stimuli.

METHODS

Experimental

LGMD STAININGS

Five LGMD neurons were impaled with sharp intracellular electrodes (60 – 100 MΩ) containing a solution of 2 M potassium acetate (KAc) and Lucifer yellow (2%; Molecular Probes, Carlsbad, CA). For these experiments, dissection and electrophysiology were identical to those described in Gabbiani et al. (2001; see also below). After iontophoretic injection (20 – 60 min), the brain was dissected out of the head capsule, fixed overnight in Millonig’s buffer, dehydrated through an ascending alcohol series, and cleared (Strausfeld and Miller 1981; chapt. 9). This method has been shown to minimize tissue shrinkage (Bucher et al. 2000). The stained neurons were then viewed through a ×40 objective on a confocal microscope (Zeiss; Göttingen, Germany), and multiple stacks of sections were acquired with 3.88 μm depth resolution. Typically, five to six stacks were required to cover the entire neuron. The number of images per stack varied according to the local complexity of the neuronal morphology and ranged between 5 and 55. All cells were taken from the right optic lobe.

ANATOMICAL EYE RECONSTRUCTIONS

To assess the relationship between the geometry of the LGMD’s excitatory dendritic field and that of the eye, we carefully removed the right eyes of five locusts. The eyes were painted with red nail polish to increase surface reflectance. They were imaged with a 488-nm laser line using a Nikon E350 confocal microscope and a ×2.5 objective (Tokyo). Stacks were acquired with a 50 μm depth resolution and consisted of six images. Six to 10 points were selected at each depth along the perimeter of the eye using a MATLAB interface. In total, ~50 points per eye were used as input to the ellipsoid fitting algorithm described below.

VISUAL STIMULATION EXPERIMENTS

Experiments were performed on adult female locusts (Schistocerca americana), 3 – 4 wk past the final molt. The legs, wings, and antennae were removed, and the animal was secured in a holder using vacuum grease. The head was bathed in cooled locust saline, opened, and cleared of fat and muscles. To improve recording stability, the gut was removed. The head was carefully separated from the thorax with the exception of the ventral nerve cords and four major trachea and rotated 90° about the medial-lateral axis. This procedure allowed for easier access to the optic lobe and minimized mechanical coupling between abdominal respiratory movements and the brain. The right eye was aligned so that the ventral-dorsal axis of the tilted head coincided with the anterior-posterior axis of the thorax and abdomen. The eye was then waxed firmly into position and care was taken to assure that the field of view was unobstructed. The optic lobe was desheathed with fine forceps, and the animal was placed in front of a video monitor. The brain was bathed in room-temperature locust saline. An extracellular hook electrode was placed around the contralateral connective to record from the DCMD. A holder was placed under the brain to minimize movement. Thin-walled borosilicate glass (1.2/0.9 mm OD/ID, World Precision Instruments, Sarasota, FL) was used to make electrodes for intracellular recordings on a horizontal puller (P-97, Sutter Instruments, Novato, CA). The electrodes were filled with 2 M KAc (resistances: 40 – 60 MΩ). The LGMD was identified as the neuron the spikes of which corresponded one-to-one with those of the DCMD. After recording stabilization, the visual stimulation protocol described in the following text was applied. In some recordings, a small hyperpolarizing DC current was injected to stabilize the recording (no greater than −1 nA) that had no impact on the results. An Axoclamp-2B (Molecular Devices, Sunnyvale, CA) in bridge mode was employed for intracellular recording and current injection. The intracellular membrane potential was sampled at 20 kHz and stored via an A/D converter on a personal computer (PC, x86) running QNX6 (QNX Software Systems, Ottawa, Canada). Recording sessions lasted ~1 h.

VISUAL STIMULATION PROTOCOLS

Locusts were positioned so that their anterior-posterior axis was parallel to the front of the video monitor with the right eye 15.8 cm away from and facing the monitor. Visual stimuli were presented at a 200-Hz refresh rate, well above the temporal cut-off frequency of locust photoreceptors (~80 Hz) (Howard et al. 1984). The stimulus consisted of a 7.6° diam black (~0 cd/m²) disk rotating counter-clockwise on a white (~90 cd/m²) background along a 10.4° diam path (Fig. 6A, inset). Rotational velocities of 1 and 4 cycle/s were employed. Each stimulus consisted of a single rotation and thus lasted 1 s and 250 ms, respectively. The stimuli in each trial were presented once in pseudo-random order at nine positions and two velocities for a total of 18 stimulus presentations. The stimuli were centered at each combination of elevations −30, 0, and 30° and azimuths of 60, 90, and 120°. An elevation of 0° corresponded to the eye equator and negative elevations to ventral locations. An azimuth of 0° corresponded to straight in front while an azimuth of 90° was lateral to the animal (e.g., Fig. 4A, bottom inset). In all cases, the stimulus angular size was computed without accounting for distortion as elevation and azimuth grew away from 0 and 90°, respectively (corresponding to the center of the eye and monitor), because the maximal angles employed here resulted at most in a 5% distortion. A delay of 5 s between stimulus presentations was employed and each nine-position trial was separated by a 15-s inter-trial interval. Each stimulus presentation at a given position on the eye was thus separated by ≥1 min. Between 25 and 50 trials were performed in each of five locusts. The eye alignment procedure used in these experiments was not as precise as that employed in the extracellular recordings of Krapp and Gabbiani (2005) but was sufficient for our purposes (see RESULTS). Previous work showed that these visual stimuli are unlikely to activate feed-forward inhibition onto the LGMD (Gabbiani et al. 2005; Krapp and Gabbiani 2005).

FIG. 6.

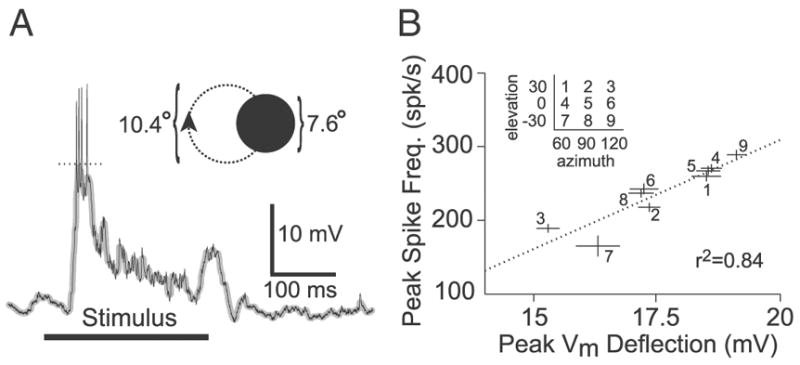
Transformation from peak spike frequency to membrane potential under local visual stimulation. A: example LGMD intracellular recording showing the response to a disk (diameter: 7.6°) rotating on a circular path (diameter: 10.4°; inset) at a speed of 4 cycle/s. The thick black horizontal line denotes the duration of stimulus presentation (250 ms). The thin black line is the membrane potential (V_m), and the superimposed thicker gray line is the median-filtered V_m. The dotted line shows the measured peak deflection in median-filtered V_m. V_m was –56 mV at baseline. B: correlation between peak V_m deflection and peak spike frequency. Every data point corresponds to a different stimulus location (inset), with lines showing SE. Data at each location was pooled across multiple trials (~25 per location-velocity combination, in this animal) and velocities of 1 and 4 cycle/s. The regression (dotted line) in this animal yielded r² = 0.84 (mean r² = 0.69 ± 0.20; n = 5).

FIG. 4.

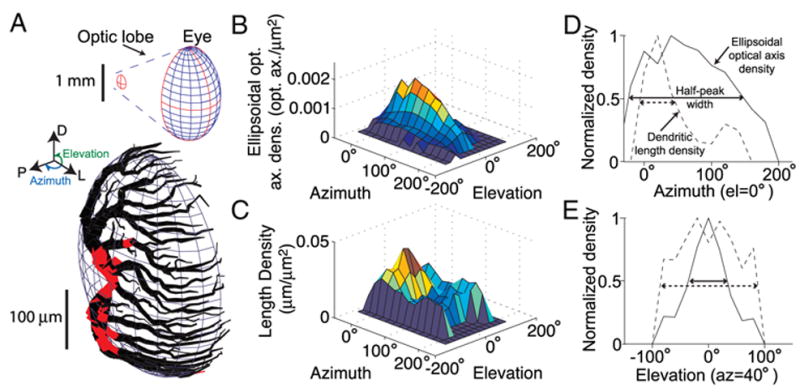
Comparison of dendritic length density with ellipsoidal optical axis density. A: LGMD excitatory dendritic field was fit to an ellipsoid to allow computation of dendritic length density relative to ellipsoid surface area. Red regions depict dendritic segments that are >10% of an ellipsoidal radius away from the ellipsoid surface. Top inset: shape of the eye-fitted ellipsoid, along with the LGMD’s excitatory dendritic field fitted ellipsoid (outlined in red) in the optic lobe. The relative orientation of the ellipsoids reflects their actual anatomical arrangement. Azimuth and elevation angles are illustrated in blue and green, respectively (left inset). An elevation of 0° corresponds to the eye equator with negative and positive elevations being ventral and dorsal relative to the animal, respectively. An azimuth of 0° corresponds to the front of the animal with an azimuth of 90° being perpendicular to the animal’s longitudinal body axis. B: ellipsoidal density of optical axes on the locust eye. Density was calculated by placing a 5° radius cap around every individual optical axis and counting the total number of optical axes in the cap, divided by the surface area of the eye ellipsoid falling into the cap (METHODS). Angular space was subsequently divided into a 20° resolution grid, and the average density of optical axes in each 20 × 20° region is shown in the plot. C: density of dendrite length on lgmd_a ellipsoid. The lgmd_a dendritic field was broken up into ~1,500 5-μm-long segments, and the segment endpoints were used as centers for 5° radius caps originating at the lgmd_a ellipsoid’s center. Density was computed by counting the total number of endpoints falling into the cap and dividing by the surface area of the lgmd_a ellipsoid in the cap. Angular space was subsequently divided into a 20° resolution grid, and the average density of dendrite in each 20 × 20° region is shown. D and E: comparison of ellipsoidal optical axis (solid line) and dendritic length (dashed line) density for a fixed elevation (0°, D) and fixed azimuth (40°, E). The density peaks were normalized to 1 and are equal to 0.069 opt. axes/μm², 0.049 μm dendrite/μm² (D) and 0.069 opt. axes/μm², 0.037 μm dendrite/μm² (E), respectively. The horizontal arrows show the angular width of each density at half-height.

Data Analysis

LGMD RECONSTRUCTIONS AND COMPARTMENTAL MODELING

All neurons were traced using code written in MATLAB (MathWorks, Natick, MA). Specifically, points were selected along the dendrite and radius was computed automatically by detecting edges based on rapid intensity changes between neighboring pixels. The stacks acquired for each cell were aligned using the overlapping segments of dendrite. The five reconstructions, labeled lgmd_a–lgmd_e are illustrated in Fig. 1. Compartmental modeling of the LGMD neuron was performed using the NEURON simulation package (version 5.4) (Hines and Carnevale 1997). Most simulations were carried out using the morphology of a single cell, lgmd_a (Fig. 1B), after converting its 1583 segments to a NEURON-compatible format. In all simulations, a time step of 5 μs was used, and the simulated membrane potential was stored at a sampling frequency of 5 kHz unless otherwise noted. A PC with a 2.4-GHz Intel (Santa Clara, CA) dual-processor running Red Hat Linux 9.0 (Red Hat, Raleigh, NC) was employed for all simulations.

FIG. 1.

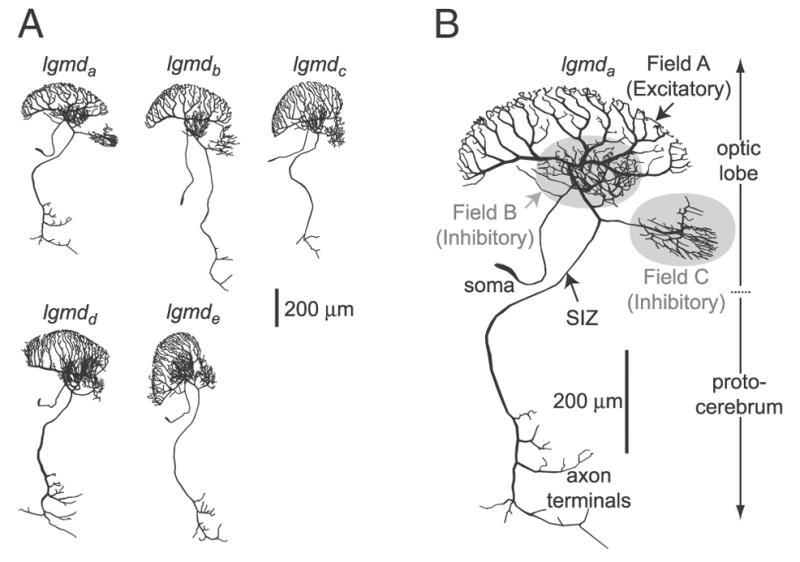
Morphological reconstructions of lobula giant movement detector (LGMD) neurons. A: gallery of 5 neurons stained with Lucifer yellow and reconstructed from confocal stacks. B: enlarged view of the top left neuron (lgmd_a). The morphology of this neuron was employed in the simulations. The inhibitory branches appear on a gray background. The arrow indicates the location of the spike initiation zone (SIZ).

PASSIVE PARAMETER FITS

We used the data set described in Gabbiani and Krapp (2006) to constrain the passive membrane properties of the model. Subsequent simulations employed uniformly distributed passive parameters obtained from these fits. The resting membrane potential was set at − 65 mV (Gabbiani and Krapp 2006). Only the membrane potential deflections to 500-ms-long hyperpolarizing current pulses of −1, −2, and −3 nA were employed because active conductances clearly affected the responses to more negative and positive currents pulses (see Gabbiani and Krapp 2006). The data obtained in response to each current pulse were averaged across six cells (1 penetration per cell, with 2 penetrations for 1 cell; 9 – 10 repetitions per penetration) and median filtered with a 1-ms time window, yielding an average trace.

Because each of the passive parameters (specific membrane resisitivity, R_m; specific membrane capacitance, C_m; axial resistivity R_a) dominates during a different portion of the current injection response (e.g., R_a is prominent during the first ~2 ms) (Major and Evans 1994), we adopted a sequential procedure in which R_m was first fitted, followed by C_m and R_a. The membrane resistivity, R_m, was fit by minimizing the fit error between the simulated and experimental membrane potential deflection during the final 475 ms (i.e., at steady state) of the three current pulses (Fig. 2A). Because the first 25 ms included virtually all transients, the impact of R_a and C_m was negligible. First, the squared difference between the experimental and simulated trace was computed over the 475-ms interval. This quantity was then normalized by the time interval duration (475 ms) and the mean experimental membrane potential, yielding an error measure independent of current injection level. For a fixed R_m value, this normalized error was averaged across the three current values and all the R_a and C_m values considered, giving a fit error. We tested specific membrane resistivity (R_m) values of 2,000, 4,000, 4,500, 5,000, 5,500, 6,000, 8,000, 10,000, 12,000, 15,000, and 20,000 Ω · cm². The tested specific membrane capacitance (C_m) values varied from 0.5 to 1.75 μF/cm² (in steps of 0.25). The axial resistivity (R_a) values ranged from 20 to 100 (in steps of 10), as well as 150 and 200 Ω · cm.

FIG. 2.

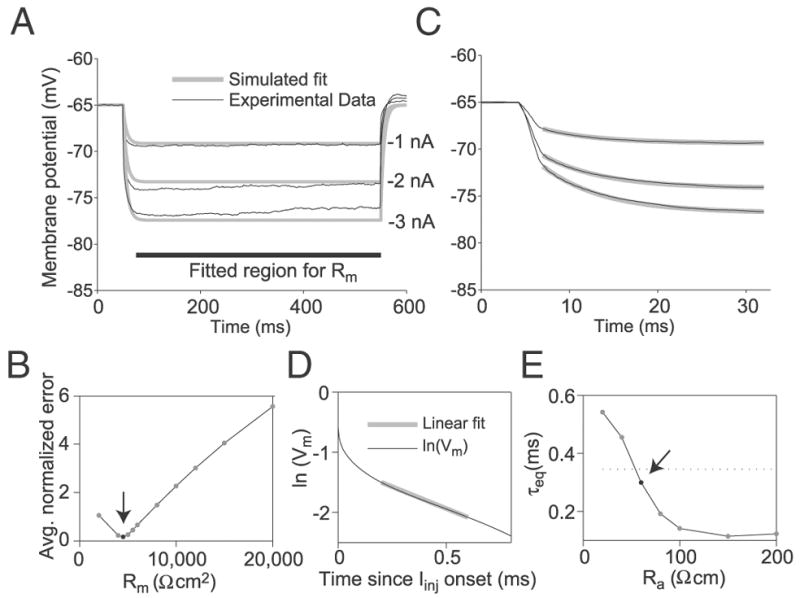
Determination of the LGMD specific membrane resistivity (R_m), specific capacitance (C_m), and axial resistance (R_a). A: R_m was obtained by fitting the steady-state membrane potential deflections to hyperpolarizing current pulses (−1, −2, and −3 nA) simulated in the compartmental model (gray lines) to those obtained experimentally (black lines; mean across 10 cells) (experimental data from Gabbiani and Krapp 2006). The fitted region (thick black bar) excluded transients during the initial 25 ms of the response. The gray curves represent the best fit obtained from the compartmental model, with R_m = 4,500 Ω · cm², C_m = 1.5 μF/cm², and R_a = 60 Ω · cm. These values were determined as illustrated in B–E. B: averaged, normalized error between steady-state experimental and simulated membrane potential as a function of membrane resistivity. The arrow indicates the optimum value (R_m = 4,500 Ω · cm²). Normalized error was measured for a given simulated current step by taking the squared area of the region between the simulated and experimental membrane potential traces and dividing by both the mean experimental membrane potential deflection and the duration of the fitting region (475 ms). Averaged, normalized error for a particular R_m consists of the average of normalized errors across all C_m, R_a, and current injection level values simulated with that R_m. C: determination of the specific membrane capacitance, C_m. The experimental membrane potential transients (black) were fitted with a single-exponential curve (gray) between 2 and 27 ms after current injection onset, yielding a time constant τ_m. The optimal τ_m was 6.6 ms. From τ_m = R_mC_m, we obtain C_m = 1.5 μF/cm². D and E: determination of R_a. The compartmental model was used to simulate membrane potential responses to current pulses for a range of R_a values with R_m and C_m set to the values obtained above. The equalization time constant, τ_eq, was obtained from the simulated current injections by plotting the logarithm of the membrane potential minus the optimal fitting τ_m-based exponential as a function of time during the 1st 0.8 ms of the current pulse (D). A straight line was fit to the linear sub-region of this curve (gray line in D), from which τ_eq was derived (METHODS). E: simulated τ_eq illustrated as a function of R_a. The arrow indicates the point where this curve achieves the value closest to that derived from experimental data (mean τ_{eq-experimental} = 0.34 ms, dotted line; R_a = 60 Ω · cm).

Next we fitted the experimental membrane potential transients between 2 and 27 ms after current pulse onset with a single-exponential curve interpolating between the resting and steady-state membrane potential associated with R_m and the current injection level, yielding the membrane time constant, τ_m. The first 2 ms of each current pulse was omitted because the membrane potential transient was affected by the equalization time constant of the cell in that window (see Fig. 2B) (see also Gabbiani and Krapp 2006). The optimal τ_m was divided with the previously obtained R_m to obtain C_m (τ_m = R_mC_m).

R_a was constrained using the experimental equalization time constant (τ_eq) of the LGMD (Gabbiani and Krapp 2006). In a compartmental model, τ_eq depends primarily on neuronal morphology and R_a (Holmes et al. 1992). We ran current injection simulations and stored the membrane potential at a high sampling rate (200 kHz) using the R_m and C_m values derived in the previous two steps, varying R_a across all 11 values given in the preceding text. Only current injections of −1 nA were employed, but identical results were obtained when −2 and −3nA current pulses were also considered. For each simulated membrane potential trace, we computed the equalization time constant by exponential peeling (see Fig. 2D). The logarithm of the membrane potential deflection minus an exponential curve based on τ_m was plotted and the window between 0.3 to 0.8 ms after current injection onset was used to fit a straight line. The value of the simulated τ_eq was obtained from this line’s slope. The simulated τ_eq was plotted as a function of R_a, and the value of R_a yielding τ_eq in closest agreement with the experimental value was selected.

The simulated electrode was positioned at the junction of the excitatory dendritic field to the main process of the LGMD (see Fig. 1B). Electrodes positioned anywhere along the main segment of the excitatory field as well as in the dendritic segment running from the origin of the excitatory field to the spike initiation zone yielded similar results. Electrodes placed in the thinner dendrites of the excitatory dendritic field, near their tips, or in the inhibitory dendritic fields yielded different passive parameter values (data not shown). The thick dendrites close to the base of the excitatory dendritic field are the most likely penetration sites in the experiments of Gabbiani and Krapp (2006).

SYNAPTIC PARAMETERS

The cholinergic, excitatory synapses impinging on the LGMD’s excitatory dendritic field (Rind and Simmons 1998) were simulated using an alpha function

$$g(t)=g_{max}\cdot (t/{\tau }_{\text{syn}})\cdot e^{-t/{\tau }_{\text{syn}}}$$

where g_max is the maximal conductance (47 nS unless otherwise noted), and τ_syn is the time of peak (0.3 ms). The synaptic reversal potential, E_rev, was set to 0 mV. These parameters were adapted from Bazhenov et al. (2001). The excitatory dendritic field was covered with 7,322 synapses. This number corresponds to the number of ommatidia on a locust compound eye (Krapp and Gabbiani 2005). The conductance, g_max, thus corresponds to the total contribution of a single ommatidium to the excitatory input on the excitatory dendritic field. It is important to note that because our model lacks active conductances and assumes each ommatidium contributes only one synapse, g_max represents an effective synaptic conductance (see DISCUSSION). It is thought that the LGMD actually receives synaptic contacts from at least two afferents per ommatidium (Rowell et al. 1977; Strausfeld and Nässel 1981), although implementing such a modification would not alter the observed results.

ELECTROTONIC STRUCTURE

We studied the electrotonic structure in the model by activating single synapses at various dendritic positions and characterizing the response at the spike initiation zone (SIZ). Specifically, we computed two measures (Fig. 3) described in Zador et al. (1995).

FIG. 3.

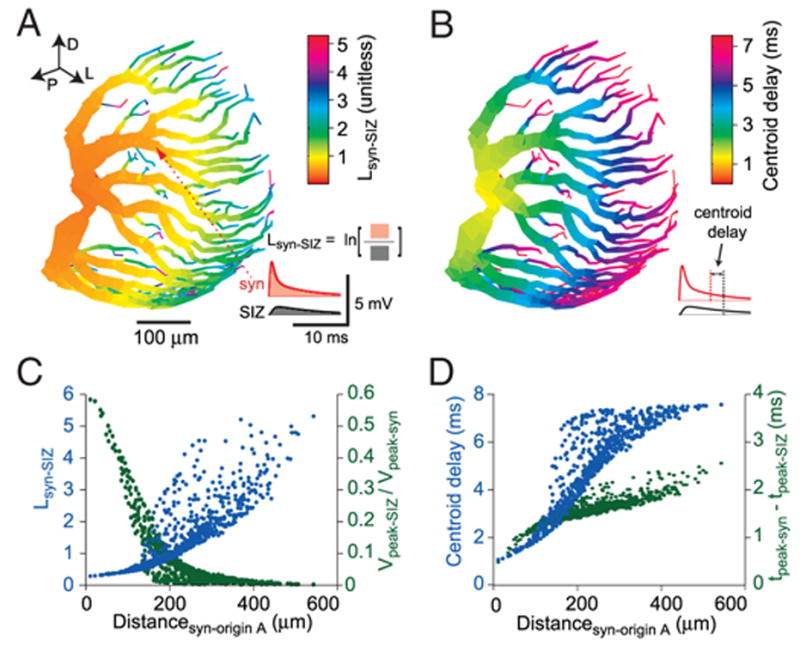
Electrotonic structure of LGMD’s dendritic field A. A: log-attenuation (L_syn-SIZ) between the excitatory postsynaptic potential (EPSP) measured at the synapse and the same EPSP measured at the spike initiation zone (SIZ). The color code reflects the L_syn-SIZ for a synapse placed at that particular spatial location. L_syn-SIZ is equal to the logarithm of the ratio of the membrane potential integrals at the SIZ (inset, black curve) and at the synapse (red curve). The red arrowhead shows the location of the synapse used for the inset. L_syn-SIZ is equivalent to the electrotonic distance for an infinite cylinder and a constant depolarization. The parameters of the alpha synapse wereτ_syn = 0.3 ms, g_max =47 nS, and E_rev = 0 mV. Directional arrows (top left) indicate dorsal, posterior, and lateral directions relative to the animal. B: delay for the arrival of the EPSP centroid at the SIZ relative to the EPSP centroid at the synapse. The centroid is the center of mass of the EPSP: ∫t · V(t)dt/∫ V(t)dt. Each compartment’s color reports the centroid delay for a synapse placed at that compartment. Inset: centroid delay measurement from a given pair of synaptic and SIZ EPSP traces (same sample data as in A). C: attenuation as a function of synaptic distance from origin of field A. L_syn-SIZ (blue) and the ratio of peak SIZ and peak synaptic membrane potential (V_peak-SIZ/V_peak-syn; green) are shown, with each synaptic location in the excitatory dendritic field represented by a point. D: temporal delay as a function of distance from origin of field A. Centroid delay (blue) and delay of membrane potential peak (green) at the SIZ relative to synaptic peak. Each point represents a synaptic location.

The first measure is the log-attenuation (L_syn-SIZ) of the synaptic potential at the spike initiation zone, defined as

$$L_{\text{syn}-\text{SIZ}}=ln\frac{{\int }_0^{50}{V}_{\text{syn}}(t)\text{d}t}{{\int }_0^{50}{V}_{\text{SIZ}}(t)\text{d}t}$$

In this equation, V_syn(t) and V_SIZ(t) represent the membrane potential at the compartment where the synapse is located and the spike initiation zone compartment, respectively, and ln represents the natural logarithm. The integral was taken over the first 50 ms of the response. L_syn-SIZ converges to the electrotonic distance X = x/λ (where x is distance in micrometer and λ is the space constant, also in micrometer) in an idealized infinite cylinder as the frequency of the synaptic membrane potential transient approaches zero (i.e., as it becomes a DC step). The classical electrotonic distance applies only to cylinders, whereas L_syn-SIZ can be applied to complex dendritic morphologies and to more physiological alpha-synapse stimuli.

The second measure is the centroid delay, P_syn-SIZ, a measure of propagation delay along the dendrites. The centroid of the membrane potential transient was computed at the synapse and at the SIZ using the following expression

$$\widehat{t}=\frac{{\int }_0^{50}t\cdot V(t)\text{d}t}{{\int }_0^{50}V(t)\text{d}t}$$

The centroid delay was simply

$$P_{\text{syn}-\text{SIZ}}={\widehat{t}}_{\text{SIZ}}-{\widehat{t}}_{\text{syn}}$$

In addition, we computed the ratio of peak membrane potential at the spike initiation zone to that at the synaptic site as well as the difference in arrival times for the peaks at these two locations (Fig. 3, C and D).

ELLIPSOID FIT OF EYES AND EXCITATORY DENDRITIC FIELDS

Ellipsoid fitting was performed using the same algorithm for both the locust eyes and the LGMD excitatory dendrites (Fig. 4A). The excitatory dendritic field was first converted into a cloud of points, with a point selected for every 5 μm of dendritic length. This resulted in ~1,500 points. Eye data points were obtained as described in Eye reconstructions. The ellipsoid best fitting the data points was specified by nine parameters: three center coordinates, three axes lengths, and three rotation angles between the coordinate and ellipsoid axes. These nine parameters were first selected by an initial guess and then optimized by an iterative algorithm. The initial guess was obtained by computing the centroid of the point cloud and its two dominant axes of symmetry. The centroid was used for the coordinates of the ellipsoid center. The axes of symmetry were used to generate initial lengths of the ellipsoid axes (the 2 shorter axes were set to equal lengths) and the three angles of rotation between the coordinate axes and those of the ellipsoid. For the dendritic fields, this initial procedure was conducted using a 25 μm “coarse” point clouding.

The nine ellipsoid parameters were optimized by minimizing the error function defined as the summed square distance between each data point and the closest point on the ellipsoid surface. The MATLAB least-square fitting function, lsqnonlin, was employed to minimize the fit error, based on the Levenberg-Marquardt method with line search (Moré 1977). During an iteration of the algorithm, the three center coordinates and three axis lengths were first fit simultaneously by a call to the least-squares fitting function. The three rotation angles were then fit by a subsequent call. In both cases, the fitting function typically converged after 50 steps. Five iterations of this procedure were repeated to obtain the final parameters.

OPTICAL AXIS AND DENDRITIC LENGTH DENSITIES

The locust eye consists of ommatidia, each of which samples light from a particular direction—its optical axis. We computed both the density of optical axes on the eye ellipsoid and the dendritic length density on the excitatory dendritic field ellipsoid (Fig. 4, B–E). Dendritic length density represents the amount of dendritic length in a given region of the ellipsoid fitted to the excitatory dendritic field. A comparison of these densities (RESULTS) allowed us to characterize the general properties of the first of the three synaptic mappings between visual space and the LGMD excitatory dendritic field described in the following text. The density of optical axes on the eye was calculated using the density distribution of optical axes in visual space (Krapp and Gabbiani 2005) and the average of the five eye-fitted ellipsoids. For each optical axis, the number of axes falling within a 5° radius cap centered around it was computed (see Krapp and Gabbiani 2005 for details) and divided by the area of the cap on the average eye ellipsoid. The lgmd_a excitatory dendritic field was used to compute dendritic length density. First, the lgmd_a excitatory dendritic field was broken up into 5-μm-long segments. The angular coordinates of each segment’s endpoints were obtained. A 5° cap centered at a particular endpoint was constructed and the number of dendritic segment endpoints bound by the cap was counted. The density was obtained by dividing this number by the corresponding cap surface area on the lgmd_a-fitted ellipsoid. The surface areas of 5° ellipsoidal caps on the eye or on the excitatory dendritic ellipsoid were computed by numerical integration, since no analytic formula exists (Tee 2000).

SYNAPTIC MAPPINGS

Three synaptic mappings were employed to assign inputs from specific regions of visual space to synapses on specific segments of the LGMD’s excitatory dendritic field. The first mapping is based on a neighborhood-preserving transformation between visual space, as sampled by the ommatidia, and the excitatory dendritic field. The remaining mappings were used to investigate the impact of the assumptions made in the first mapping. In all cases, the excitatory dendritic field was broken into 7,322 segments of equal length (0.95 μm), corresponding to the number of ommatidia (optical axes) on the locust eye (Krapp and Gabbiani 2005). An alternative would have been to distribute synapses onto dendritic segments of equal surface area. However, dendritic surface area turned out to be much less well suited for this purpose than dendritic length (RESULTS). Moreover, in anatomical studies, the number of synapses is also commonly characterized per unit length (e.g., White 1989), facilitating comparison with our study (DISCUSSION).

Topographic mapping (Fig. 5C, top)

FIG. 5.

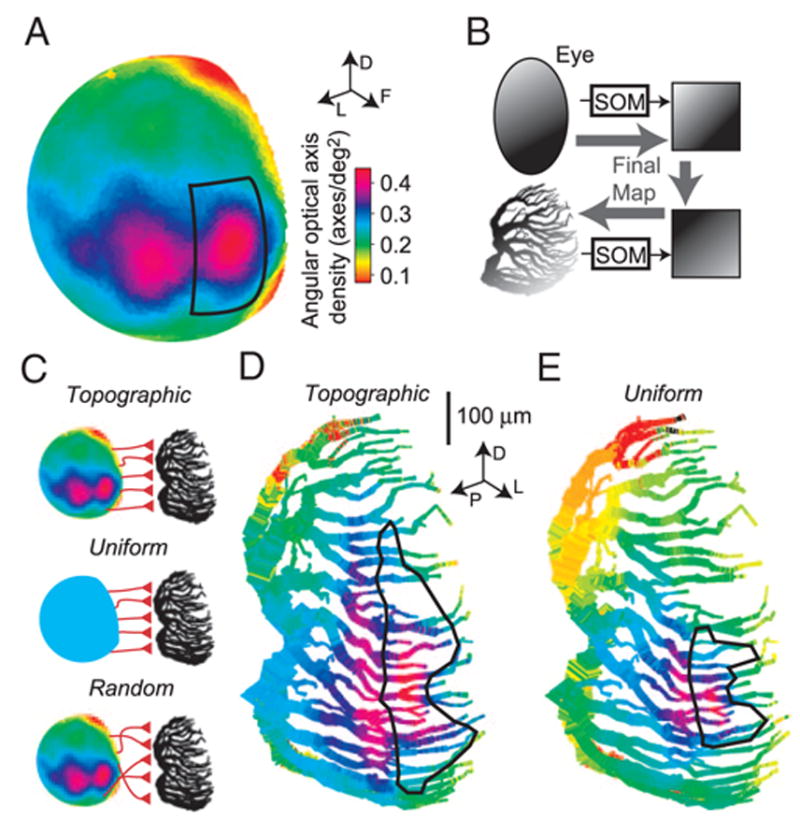
Synaptic mappings from visual space to dendritic space. A: angular density of optical axes in visual space. The sphere representing the directions of optical axes is color-coded according to the angular optical axis density (in axes/°²) at that point in visual space. Adapted from Krapp and Gabbiani (2005). The solid rectangle is bounded at ± 30° in elevation, and azimuths of –10 and 20°. Arrows (top inset) indicate dorsal, frontal, and lateral directions in visual space. B: summary of the mapping process using Kohonen’s self-organizing map (SOM). The optical axes were projected onto a grid using an SOM (top). A 2nd SOM was used to map equal-length dendritic segments of the LGMD excitatory field onto an identical grid (bottom; same number of dendritic segments as optical axes: 7,322 segments of 0.95 μm each). To obtain the final, topographic map, these 2 grids were superimposed, yielding a direct mapping from optical axes to dendrite (lighter, thicker arrows). C: schematic representation of the three synaptic mappings employed. Top: topographic mapping, which is neighborhood-preserving and employs eye-like sampling of visual space. Middle: uniform mapping, which is neighborhood-preserving but samples visual space uniformly. Bottom: random mapping does not preserve neighborhood relationships but employs eye-like sampling of visual space. Color scale bar in A applies. D: topographic synaptic mapping of optical axes onto the LGMD excitatory dendritic field. Each optical axis was mapped to a dendritic point using the SOMs. The color of each dendritic segment reflects the optical axis density at the corresponding position in visual space from which it receives input. The solid outline delineates the region of the dendritic field receiving input from the visual region likewise denoted in A. Directional arrows indicate dorsal, posterior, and lateral directions relative to the animal (inset). E: synaptic mapping with uniform sampling of visual space. Each region of visual space is sampled by an equal number of dendritic segments. Same color code and region outline as in A.

This mapping assumed that the 7,322 ommatidia sampling visual space (represented as optical axes in Fig. 5A) are mapped in a uniform, neighborhood-preserving manner onto the corresponding 7,322 dendritic segments of the LGMD excitatory dendritic field. To the best of our knowledge, no general method to generate such a mapping has been proposed. We thus developed a method based on two Kohonen self-organizing maps (SOMs; Fig. 5B). This algorithm was selected because it was originally designed to yield a neighborhood-preserving mapping from one space onto another. A detailed description of the SOM algorithm can be found in Kohonen (2001; esp. chapt. 3). Two passes of the SOM algorithm were employed, followed by a corrective step to guarantee a one-to-one correspondence between source and target spaces. The first, coarse mapping pass involved 50,000 iterations while the second, refining pass involved 100,000 iterations. In each pass, the two parameters of the SOM, α (learning-rate; unitless) and σ (neighborhood radius; in fraction of target grid side length), determined the mapping. Both parameters were assigned an initial value and decreased linearly to a final value for a given pass.

The first SOM was used to map the ommatidia onto an 86 × 86 equally spaced square grid with 74 points of the last row omitted (total: 7,322 grid points; Fig. 5B, top). In the coarse and refining mapping passes, α decreased from 0.95 to 0.4 and from 0.5 to 0.2, respectively, whereas σ decreased from 0.6 to 0.1 and from 0.05 to 0.005, respectively. The SOM algorithm does not guarantee that two ommatidia will be mapped onto two different grid points (i.e., it is not necessarily 1 to 1) and for ~20% of the ommatidia, several were mapped onto the same target grid point. For these, we applied the following correction algorithm, resulting in a final one-to-one and neighborhood-preserving map. First, a list of ommatidia to be remapped was obtained by going over the sets of ommatidia mapped onto the same target grid point and selecting all but the one with the minimal angle between its optical axis and the optical axes of its four nearest neighbors in the target grid. After this step, there were as many unfilled target points in the target map as unmapped ommatidia in the list. Ommatidia in the list were randomly selected one after the other, and the desired location in the target grid where they would minimize their nearest-neighbor inter-optical axis angle was computed. A line was drawn between the desired location and the closest unoccupied target point in the target grid. The ommatidia assigned to points along that line were successively shifted by one position toward the unoccupied target point, resulting in the desired location being unoccupied. The ommatidium was then assigned to the desired location.

The second SOM was used to map dendritic points onto the same grid (Fig. 5B, bottom). In the coarse and refining mapping passes, α decreased from 0.8 to 0.4 and from 0.5 to 0.2, respectively, whereas σ decreased from 0.6 to 0.05 and from 0.05 to 0.005, respectively. Euclidean distance in dendritic space was computed and the same correction procedure as for the ommatidia was employed. The final map between ommatidia and their corresponding dendritic segments was obtained by combining the two SOMs with the boundaries of both grids aligned so that corresponding locations in visual and dendritic space were in register (see RESULTS and Fig. 4A). Because this map preserves the distribution of ommatidial optical axes in visual space, it can be described as topographic (Fig. 5D). Several runs of the procedure were performed to verify the similarity of the resulting mappings.

Uniform, neighborhood-preserving mapping (Fig. 5C, middle)

The uniform mapping mimicked the synaptic arrangement expected if ommatidia on the locust eye were to sample visual space uniformly which is in sharp contrast to their actual arrangement. Thus this mapping allowed us to test the role that the eye’s sampling of visual space plays in shaping the LGMD’s receptive field to local motion stimuli. For this mapping, only the SOM from dendritic space into the 86 × 86 point grid was employed. The coordinates of points in this grid were then converted into visual coordinates by assigning one grid axis to elevation, ranging from −90 to 90° in equal steps and the other to azimuth (0 – 180°). Because the local neighbor relations of the dendritic field were preserved in the target grid, it was possible to align it realistically with visual space (see RESULTS and Fig. 4A). That is, the grid axis corresponding to the anterior-posterior dendritic axis was assigned to azimuth, and the axis corresponding to the dorso-ventral dendritic axis was assigned to elevation (Fig. 5E).

Random map (Fig. 5C, bottom)

This mapping assumed that the 7,322 optical axes sampling visual space are mapped randomly onto segments of the LGMD’s dendritic tree. Thus this mapping allowed us to test the role that retinotopy plays in shaping the LGMD’s receptive field to local motion stimuli. Ten map instances were generated by a pseudo-random number generator and used in simulations.

RELATION BETWEEN PEAK SPIKE FREQUENCY AND MEMBRANE DEPOLARIZATION DURING VISUAL STIMULATION

We derived a peak spike frequency to membrane potential transform to compare experimental and simulated receptive fields. The intracellular LGMD membrane potential recorded in the visual stimulation experiments (see Experimental methods) was first processed to detect spikes. The shortest inter-spike interval (ISI) within the first 250 ms of stimulation was used to compute the peak instantaneous spike frequency. The intracellular membrane potential was median filtered using a 1-ms window to suppress spikes. The median-filtered trace was used to obtain the peak membrane potential in the first 250 ms of visual stimulation. Peak spike frequency, f̄, and peak membrane potential, V̄_m, were averaged for a given animal across all stimulus presentations at a given location (9 locations total; 20 – 50 presentations per location). A linear regression was then fit to these nine points for each animal, f̄ = αV̄_m + β. The mean slope and intercept of the resulting regressions (n = 5 animals) were used to derive an equivalent peak spike frequency to peak membrane potential transform

$${\overline{V}}_{\text{m}}=\gamma \overline{f}+\delta$$ (1)

where γ = 1/α was found to have a value of 0.05 mV/Hz and δ = −β/α was equal to 5.94 mV (see RESULTS and Fig. 6). The values of f̄ used in Eq. 1 did not fall below 7 Hz.

SIMULATED VISUAL STIMULATION

To conduct simulated visual stimulation in the LGMD model and thereby obtain artificial receptive fields (RFs) for local motion stimuli, the visual hemifield was divided into a uniform grid (150° in elevation by 180° in azimuth). The model’s RF was obtained for each of the three synaptic mappings by “stimulating” it at each location. The stimulus consisted of simultaneous activation of a number of synapses equal to that covered by a disk of 7.6° diameter at that location according to the map under consideration. The surface area of the disk thus matched that used in visual stimulation experiments. To account for local variations in optical axes density, the activated synapses were selected as follows. First, the number of optical axes inside a 20 × 20° rectangle centered at the grid location was counted. The number of activated synapses, n, was obtained by scaling this number by the ratio of disk to rectangle surface area {[π · (7.6/2)²]/20² ≈ 1/9}. Then, n synapses were randomly selected within the set receiving input from the 20 × 20° rectangle, and 10 such simulations were run per stimulus location. The resulting peak membrane potential at the point where the excitatory dendritic field (field A, Fig. 1B) contacts the main process of the LGMD, V̄_origin-A, was recorded and averaged (Fig. 7, B–E). This site was selected because it is presumed to be close to the electrode location in the visual stimulation experiments. For each of the maps illustrated in Fig. 7, the variability of the RF profiles was low within the 10 runs (see in particular Fig. 7E). Thus subsequent simulations (Fig. 8) were conducted using a single set of input synapses.

FIG. 7.

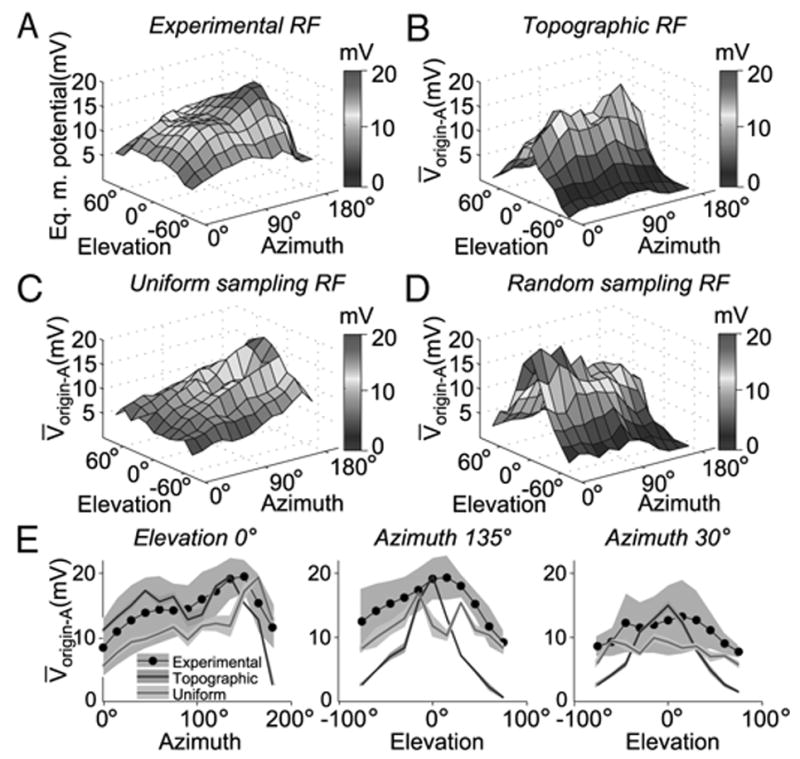
Comparison of the experimental LGMD receptive field (RF) with that obtained using 3 maps of visual to dendritic space in the compartmental model. A: experimental RF obtained by local stimulation at multiple elevations and azimuths (same stimulus as in Fig. 6). The LGMD/DCMD peak spike frequency (obtained from Krapp and Gabbiani 2005) was transformed to an equivalent LGMD peak membrane potential based on the regression depicted in Fig. 6B. B: simulated RF obtained using the topographic synaptic mapping. The plot shows the peak membrane potential at the origin of dendritic field A, V̄_origin-A, elicited by a stimulus centered at a given point in visual space. The responses were simulated by activating a number of synapses equal to those covering the area of the disk at that location (see METHODS). Each synapse’s g_max was set to 47 nS so as to match maximal depolarization in the model to the experimental peak in A. C: simulated RF obtained with the uniform mapping of visual space. The plot reflects V̄_origin-A for a given stimulus center (same stimuli as in B). Each synapse’s g_max was set to 84 nS to match maximal depolarization in the model to the experimental peak in A. D: simulated RF obtained using a random, 1-to-1 mapping from optical axes in visual space to the excitatory dendritic field (g_max = 47 nS). While the wiring scheme was randomized, the local density of optical axes was respected. The plot reflects V̄_origin-A as a function of stimulus center azimuth and elevation. E: cross-sections of the experimental RF and those derived from the topographic, and uniform mappings. The left panel shows the V̄_origin-A observed with stimuli of various azimuths with elevation fixed at 0°. The black line and gray background denote the experimental data mean and 95% confidence interval across animals (t-test; n = 6), respectively. The blue and red line denote the topographic and uniform sampling RF cross-sections, respectively. The shaded regions of the colored lines denote the 95% confidence interval for simulated runs (t-test; n = 10 trials per location). Middle and right: V̄ _origin-A for various elevations with azimuth fixed at 135° (toward posterior end of animal) and 30° (toward anterior end of animal), respectively.

FIG. 8.

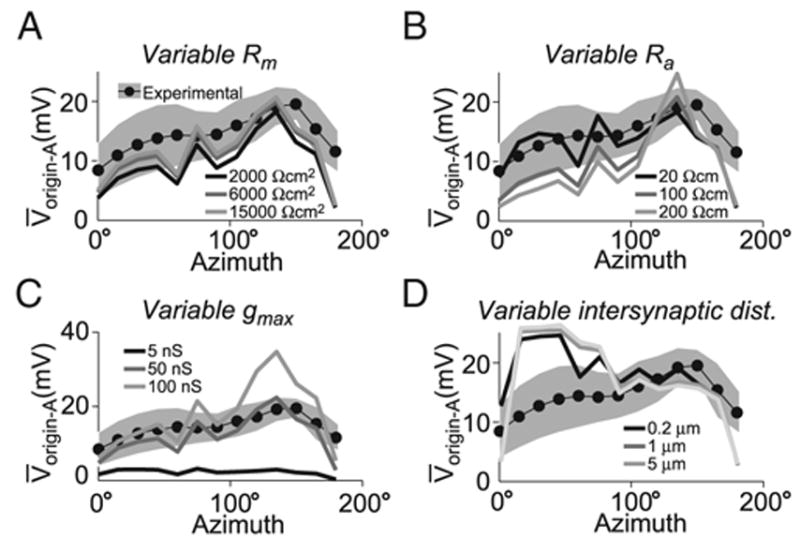
Receptive field robustness to simulation parameters. Each panel shows the V̄ _origin-A observed with stimuli of various azimuths with elevation fixed at 0° for the topographic mapping. Effects seen at other elevations were qualitatively similar. Stimulation was as in Fig. 7. A: RF sensitivity to membrane resistance. The lines show RF cross-sections with R_m values of 2,000, 6,000, and 15,000 Ωcm² (dark, medium, and light gray, respectively). B: RF sensitivity to intracellular resistivity. The lines show simulated RFs with R_a values of 20, 100, and 200 Ωcm (dark, medium and light gray, respectively). C: RF sensitivity to maximal synaptic conductance. Values for g_max were 5, 50, and 100 nS (dark, medium, and light gray, respectively). D: RF sensitivity to inter-synaptic distance. Synapses were spaced at equal increments along a contiguous dendritic segment starting from the dendritic segment closest to the center of mass in dendritic space of the synaptic sites receiving input from the same optical axes in the topographic mapping for a particular stimulus center (see METHODS). Inter-synaptic distance values were 0.2, 1, and 5 μm (dark, medium, and light gray, respectively).

Simultaneous activation of the synapses covering a 7.6° diameter disk was deemed a sufficiently good approximation to the visual stimuli described in the preceding text for the following reasons. First, the quantity compared with experimental data were the peak membrane potential depolarization. In the intracellular visual stimulation experiments, both the peak firing rate and membrane potential typically occurred within the first 20 ms of any detectable response (after a latency of 50 ms; compare stimulus onset with membrane potential response in Fig. 6A). Thus the peak response was most likely determined by the onset of motion. During the initial 20 ms of motion, changes in luminance (dark to light or vice versa) driving the ON-OFF units thought to provide excitatory inputs to the LGMD (Rowell et al. 1997; Strausfeld and Nässel 1981) will occur over the area swept by the edge of the disc during that time period. Assuming a photoreceptor acceptance angle of 2.5° (Wilson 1975), only those ommatidia with an optical axis center within 1.25° (i.e., half of 2.5°) of the disk edge will be stimulated. This corresponds to a stimulated area of ~60°², which did not yield substantially different results from simulations using the area of the disk (45°²). In fact, the sensitivity profile of the RFs plotted in Fig. 7 was only weakly dependent on the typical number of synapses stimulated until the number of synapses reached a much larger value.

EFFECT OF INTER-SYNAPTIC DISTANCE

We investigated the consequences of placing the stimulated synapses at various distances from each other along dendritic segments of the excitatory dendritic field while preserving the overall mapping of visual space defined by the topographic map. For a given stimulus location in visual space, n synapses were selected, as described in the preceding text, based on the topographic map. Their center of mass (COM) was computed in dendritic space and the point closest to the COM on the excitatory dendritic field was determined. The n synapses were then placed along the dendritic branch containing the point closest to the COM. The first synapse was placed at this point and subsequent ones were alternatively placed on each side of the first synapse at fixed distances along the dendrite. The distance values tested were 0.2, 1, and 5 μm.

EFFECT OF SUBLINEAR SUMMATION ON RF SHAPE

We examined the relative impact of sublinear synaptic summation on the simulated RFs of the topographic and uniform synaptic mappings. For this purpose, both models were stimulated by the 7.6° disk at two positions in the visual field: elevation 0°, azimuth 30°, corresponding to the high acuity region of the topographic map, and elevation 0°, azimuth 135°, corresponding to the region of maximal response in the topographic map. The activated synapses were then split into two random subgroups with an equal number of synapses, A and B, and sublinearity was assessed by computing the ratio of V̄_origin-A when both subgroups were activated simultaneously and separately

$$\psi =\frac{{\overline{V}}_{\text{origin}-\text{A}}(A\&B)}{{\overline{V}}_{\text{origin}-\text{A}}(A)+{\overline{V}}_{\text{origin}-\text{A}}(B)}$$

This measure characterizes the fraction of linear summation, and is equal to 1 if the responses to the two subgroup (A, B) stimulations sum linearly to generate the combined response (A & B); if the combined response is less than the sum of the individual subgroups (i.e., summation is sublinear), ψ will be <1. In addition, we split the synapses into subgroups based on the elevation of their corresponding ommatidial optical axes (“high” and “low” elevation subgroups). Simulations were conducted with g_max values of 50 and 100 nS.

RESULTS

Previous work has shown that the LGMD response to local disk motion depends on where the stimulus is presented. If the sensitivity to the stimulus in terms of spike frequency is plotted against stimulus position, an anisotropic sensitivity distribution results: the most vigorous responses are observed for stimuli presented in the caudal region of the visual field at the eye equator, with a gradual decrease in response along the equator toward the front of the animal, as well as away from the equator (Krapp and Gabbiani 2005) (see also Fig. 6A). In contrast, the density of ommatidia sampling visual space is highest in the front, close to the eye equator and gradually decreases along the equator toward the back of the eye, as well as away from the equator (Krapp and Gabbiani 2005) (see also Fig. 5A). To investigate the relative impact of electrotonic structure and synaptic input location on the LGMD sensitivity distribution, we built a compartmental model of the neuron. We used this model to explore the functional consequences of applying different ways of mapping local synaptic inputs onto the excitatory dendritic field.

Morphological properties of the LGMD

Figure 1A illustrates the morphology of five LGMD neurons reconstructed from confocal stacks after staining with a fluorescent dye (METHODS). Qualitatively, the morphologies of the five neurons were very similar. Figure 1B shows a magnified view of the lgmd_a neuron. As first described by O’Shea and Williams (1974), the LGMD possesses three distinct dendritic fields, labeled A–C in Fig. 1B. Anatomical and electrophysiological evidence suggests that dendritic field A receives local excitatory motion sensitive inputs and that dendritic fields B and C receive ON and OFF inhibitory, GABAergic inputs, respectively (see Gabbiani et al. 2004 for review). The LGMD possesses two sites of action potential initiation (O’Shea 1975), one of which is believed to initiate action potentials in response to visual inputs. This site will be referred to as the SIZ (labeled in Fig. 1B). Its location was identified from the reconstructions as a narrowing along the primary process of the LGMD to a minimal diameter of 1.7 μm in lgmd_a (mean: 1.8 μm, SE: 0.3, n = 5). On average, it was located 259 ± 25 (SE) μm away from the origin of dendritic field A (n = 5). The second site of action potential initiation is located in the protocerebrum and is implicated in the generation of spikes in response to auditory inputs (O’Shea 1975). The protocerebrum is also the location of the LGMD axon terminals that can be seen as much less extensive arborizations compared with the dendritic fields at the bottom of Fig. 1B. Some of these axon terminals contact the DCMD neuron (Killmann et al. 1999; O’Shea and Williams 1974). The two inhibitory dendritic fields (B and C in Fig. 1B) were connected to the primary process between the origin of dendritic field A and the SIZ with field C’s site of connection always closer to the SIZ than that of field B (except in 1 case, where both fields shared a common connection site: lgmd_e). The mean distance of the connection sites of fields B and C from the origin of dendritic field A was 102 ± 9 (SE) μm (n = 7) and 131 ± 10 (SE) μm (n = 5), respectively. In two of the five neurons, field B was connected to the primary process at two locations; for these cases, both positions were included in the preceding distance calculation. The soma was always connected to the primary process between the origin of dendritic field A and the connection site of field B [distance to origin of field A: 49.1 ±14.8 (SE) μm, n = 5]. Table 1 reports the total length of dendrites, the number of inter-branch point segments, the average segment radius, and the total dendritic surface areas of the individual dendritic fields. Inter-branch point segments were defined as the sections of dendrite between individual branch points or dendritic tips and branch points. The variability in the number of segments was low for both fields A and C and higher for field B. Field A always contained the most segments, whereas field C always had the least, except for lgmd_c, where field C had the same number of segments as field B (Table 1). The variability in total dendritic length between cells was smaller for fields A and C, relative to field B. For any individual neuron, the order of dendritic field lengths, from highest to lowest, was always A, B, and C (Table 1). The variability in mean radius was substantially greater: a two- to threefold difference in mean radius between the cell with highest mean radii in all fields (lgmd_a) and the lowest ones (lgmd_e) was observed. Mean radius was highest for field A in all cells and lowest for field C. These length and radius relationships were preserved when surface area was computed, though the overall variability was higher in this measure, up to a factor of 3.4. Overall, the morphology of the LGMD was qualitatively conserved across animals, but showed quantitative inter-animal variability.

TABLE 1.

Basic morphological properties of reconstructed neurons

	Dendritic Field	nsegs	Total Length, μm	Mean Radius, μm	Surface Area, μm2
lgmda	A (exc)	183	6938	2.5	134100
	B (ON inh)	149	4485	1.2	43000
	C (OFF inh)	117	2542	1.0	20300
lgmdb	A	183	7784	2.5	149800
	B	98	3079	1.0	23400
	C	90	2368	0.7	12400
lgmdc	A	180	6838	1.3	69700
	B	123	3326	0.7	19200
	C	123	2410	0.7	12200
lgmdd	A	246	8809	1.8	143700
	B	179	6048	0.8	39200
	C	122	2817	0.7	14300
lgmde	A	204	8154	0.7	44700
	B	179	5254	0.4	15900
	C	110	2448	0.5	8200
Mean	A	199 ± 28	7705 ± 832	1.8 ± 0.8	108400 ± 47900
	B	146 ± 35	4438 ± 1259	0.8 ± 0.3	28100 ± 12200
	C	112 ± 14	2517 ± 180	0.7 ± 0.2	13500 ± 4400

The cells are designated as in Fig. 1. Values are means ± SD. The three dendritic fields are labeled A–C following the convention of O’Shea and Williams (1974). Field A receives excitatory inputs (exc); fields B and C are inhibitory (inh), B being closer to A. n_segs is the number of dendritic segments between branch points or tips. lmgd_{a– e}, lobula giant movement detector reconstructions.

Electrotonic parameters of the LGMD

We used responses to hyperpolarizing current pulses obtained in vivo (experimental data from Gabbiani and Krapp 2006) to constrain the passive electrotonic parameters of the LGMD. The final passive model’s responses to current pulses of −1, −2, and −3 nA is compared with the experimental membrane potential traces in Fig. 2A. The fit is best at −1 nA, as inward rectification becomes increasingly apparent for more negative current pulses (Gabbiani and Krapp 2006). The passive model was constructed by finding values for the specific membrane resistivity, R_m, the specific capacitance, C_m, and the axial resistivity, R_a, in that order (see METHODS). Figure 2B shows the fit error as a function of R_m. An optimal fit was obtained for R_m = 4,500 Ωcm² (arrow). This value is comparable to those obtained in other insect visual interneurons in vivo (Borst and Haag 1996). To determine C_m, we used the relation τ_m = R_m · C_m after fitting the membrane potential relaxation to steady state by a single exponential (Fig. 2C). The fit ignored the first 2 ms of the pulse because in that early phase the dynamics of the membrane potential was also affected by the equalization time constant, as explained in the following text. This procedure yielded a membrane time constant (τ_m) of 6.6 ms, close to the average value of 7.3 ms determined from individual LGMD neurons by Gabbiani and Krapp (2006). The equivalent C_m value amounted to 1.5 μF/cm².

Finally, we fit the intracellular resistivity (R_a). This parameter proved more difficult to fit, because it contributes the least to membrane potential responses (see, e.g., Johnston and Wu 1995). We constrained R_a by obtaining estimates for τ_eq as a function of R_a in the model while holding C_m and R_m fixed to the values obtained in the first two fitting steps. The model value of τ_eq was obtained from membrane potential responses to simulated current injection pulses using the standard peeling procedure (METHODS) as depicted in Fig. 2D. The resulting τ_eq versus R_a plot is shown in Fig. 2E. Because the mean experimental τ_eq was found to be 0.34 ms (Gabbiani and Krapp 2006) (dotted line in Fig. 2E), this implied that R_a is approximately equal to 60 Ωcm in our model (using the median τ_eq, 0.26 ms, yielded the same result). We estimated the dependence of passive parameters on morphology by performing the same fits using the lgmd_e and lgmd_b morphologies, the neurons with the largest and smallest surface area, respectively. Overall, the value of R_m ranged from 2,000 to 4,500 Ωcm² with the smallest R_m corresponding to the smallest surface area. The values of R_a ranged from 40 to 60 Ωcm and were only weakly dependent on the particular morphology employed. A C_m value of 1.5 μF/cm² predicted a membrane time constant about twice as fast for the neuron with the smallest surface area. This value lies on the lower end of experimentally observed values (Gabbiani and Krapp 2006).

LGMD is not electrotonically compact

Several lines of evidence suggest that the LGMD is not electrotonically compact in vivo (Gabbiani and Krapp 2006; Gabbiani et al. 2001; Krapp and Gabbiani 2005). We used the passive model derived in the previous section to test this hypothesis quantitatively. Synapses were placed at various locations across the dendritic field and measures of attenuation and delay for dendritic signal propagation were computed. Figure 3A shows the log-attenuation of the membrane potential (L_syn-SIZ, see METHODS) (Zador et al. 1995) between the synapse compartment and the SIZ. The large attenuation of even relatively proximal inputs (red arrowhead and inset in Fig. 3A) demonstrates a significant filtering prior to the SIZ of the LGMD. The log-attenuation converges to the electrotonic distance in an infinite cylinder as stimulus frequency approaches zero (Zador et al. 1995). The dimensionless electrotonic distance, X, is defined as X = x/λ where x is distance (in μm) and λ is the space constant of the cylinder (Johnston and Wu 1995). A neuron is considered electrotonically compact if its dendritic arbors spans ≤0.1λ (i.e., X ≤ 0.1). Functionally, compact neurons exhibit minimal attenuation for inputs coming from even the most distal synapses. The LGMD can be considered electrotonically large as the distal tips typically attain an L_syn-SIZ value of around 3. Figure 3B demonstrates that excitatory postsynaptic potentials propagating along the dendrites experience significant centroid delays: up to 7 ms from the most distal dendritic tips of the excitatory field to the SIZ. Figure 3C depicts L_syn-SIZ and the ratio of peak membrane potential at the SIZ to that at the synaptic location as a function of its distance from dendritic field A’s origin. For synapses beyond 200 μm from the origin of field A, only ~10% of the peak synaptic membrane potential deflection is attained at the SIZ. Figure 3D shows the centroid delay and delay of EPSP peak between the SIZ and the synaptic location as a function of its distance from the origin of field A. EPSP peak delay attains maximal values of ~2.5 ms, about a third that of centroid delay. As explained in the following text, the dendritic tips of field A are expected to sample the frontal visual field and the thicker dendrites the caudal visual field. Thus our results are consistent with experimental findings showing weaker responses to frontal visual stimuli relative to caudal and lateral stimuli, as well as a greater latency of response to frontal stimuli (Krapp and Gabbiani 2005). L_syn-SIZ and centroid delays reached similar maximum values in the inhibitory fields, which are thus also electrotonically extensive (not shown). The noncompactness of dendritic field A may seem surprising when compared with vertebrate neurons with similar dendritic anatomies, such as Purkinje cells, which have been shown to have dendritic fields with average electrotonic sizes of ~0.1 space constants (Roth and Häusser 2001). However, the R_m values reported here and for many other insect visual interneurons are typically an order of magnitude lower than those observed in vertebrate neurons, resulting in a smaller space constant and hence larger electrotonic size (Johnston and Wu 1995). Using the R_m and R_a values derived in the preceding text and a dendritic diameter d of 10 μm to derive λ analytically $(\lambda =\sqrt{\text{d}{R}_{\text{m}}/4R_{\text{a}})}$ yields an estimated value of 1,369 μm for the space constant and an electrotonic distance of <0.5 (dimensionless) for the most distal dendritic tips. This value is still larger than the typical 0.1 value in compact neurons and severely underestimates the attenuation experienced by conductance-based inputs as illustrated in Fig. 3 (see Zador et al. 1995). Indeed, even in the compact Purkinje neuron, attenuation is much greater than the space constant suggests (Roth and Häusser 2001).

Sampling of visual space and dendritic LGMD morphology

Because the LGMD is not electrotonically compact, the distribution of excitatory synapses relaying local visual inputs onto dendritic field A will play a role in shaping its RF properties. To investigate how optical axes may be mapped onto dendritic segments of the excitatory dendritic field, we started by comparing the geometry of the eye with that of the dendritic arborization pattern of field A in the optic lobe. We found that both the eye and dendritic field A have very similar ellipsoidal shapes, suggesting that dendritic field A is well suited to sample retinotopic inputs across the entire visual field. This is illustrated in Fig. 4A, where the excitatory dendritic field of one of the reconstructed neurons (lgmd_a) is plotted together with the ellipsoid fitted to its arborization pattern. The majority of dendritic segments, except those colored in red, lie within a 10% radius of the ellipsoid surface (mean percentage of points outside 10% radius: 7.0 ± 2.0 SE; n = 5). The inset (Fig. 4A, top) shows the ellipsoid that was fitted to the ipsilateral compound eye. The eye ellipsoid fits resulted in 13.7 ± 3.1 (SE) % of points falling outside a 10% radius of the fitted eye ellipsoid surfaces (n = 5). Table 2 reports the ellipsoid axes lengths for all neurons and eyes fitted. The low coefficient of variation (CV) for the ratios of axes lengths (medial-lateral to dorso-ventral: CV_ML:DV = 0.04, anterior-posterior to dorso-ventral: CV_AP:DV = 0.06) across neurons shows that the shape of the excitatory field is conserved across animals. Similarly, the variability of axes ratios among eye ellipsoids was low (CV_ML:DV = 0.05, CV_AP:DV = 0.10). The shape of the eye ellipsoids differed only slightly from the dendritic ellipsoids, as evidenced by very similar ratios between the lengths of the respective axes (last 2 columns in Table 2). The dendritic field ellipsoid and the eye ellipsoid can be transformed into one another by a 90° rotation around the vertical body axis followed by scaling (Fig. 4A, top inset). This arrangement suggests that the distal dendritic tips of field A receive input from afferents sampling information from the frontal visual field, while the thicker proximal (relative to the SIZ) dendrites receive inputs from the caudal visual field.

TABLE 2.

Ellipsoid fits to dendritic field A and locust eyes

	D-V Semi-Axis, μm	M-L Semi-Axis, μm	P-A semi-axis, μm	lenML/lenDV	lenAP/lenDV
lgmda	179	138	89	0.78	0.50
lgmdb	201	152	113	0.76	0.56
lgmdc	190	136	104	0.71	0.55
lgmdd	177	135	86	0.76	0.50
lgmde	178	124	93	0.70	0.52
Mean	185 ± 10	137 ± 10	97 ± 11	0.74 ± 0.03	0.52 ± 0.03
Eye1	1567	1144	901	0.73	0.57
Eye2	1505	1119	895	0.74	0.59
Eye3	1573	1156	976	0.74	0.62
Eye4	1722	1194	1026	0.69	0.60
Eye5	1585	1417	1013	0.89	0.64
Mean	1592 ± 81	1206 ± 118	964 ± 62	0.77 ± 0.08	0.60 ± 0.03

The semi-axes are dorso-ventral (DV), medial-lateral (ML), and anterior-posterior (AP) with respect to the animal. The ratios of ML to DV semi-axis length and AP to DV semi-axis length are in the last two columns. Means and SDs were averaged across cells and eyes.

Dendritic field A spans the entire posterior lobula and intersects over its ellipsoidal surface a bundle of fibers that projects from the medulla to the lobula via the second optic chiasm and is thought to convey local retinotopic inputs to the LGMD (Rowell et al. 1977; Straussfeld and Nässel 1981). Two afferents are thought to contact the LGMD per ommatidium (facet) covering the eye surface. Each of the 7,322 ommatidia sample light intensity at a specific location (optical axis) within the spherical visual space (Krapp and Gabbiani 2005). The simplest assumptions that can be made about the mapping of visual space onto dendritic field A is that inputs corresponding to each ommatidium have the same synaptic strength and synapses are distributed evenly across the dendritic field with a fixed density per unit dendritic length. If, as anatomical evidence suggests, the mapping is retinotopic, these two assumptions and the fact that the eye and dendritic field have the same shape imply that the mapping of visual space onto dendritic field A will be determined by local variations in optical axis density and local dendritic length density. We thus computed and compared the local density of optical axes over the eye ellipsoid, obtained from the corresponding density in visual space (Krapp and Gabbiani 2005), and the local dendritic length density over the dendritic field ellipsoid (OPTICAL AXIS AND DENDRITIC LENGTH DENSITY).

Optical axis density peaks in the frontal, equatorial region of the animal’s eye; i.e., at elevation = azimuth = 0°. As illustrated in Fig. 4B, averaging over 20 × 20° squares yields two peaks: one at 0° and one at 40° azimuth (densities of 0.061 and 0.069 optical axes/μm², respectively). These correspond to the acute zone and the high acuity streak along the equator (Krapp and Gabbiani 2005) (see also Fig. 5A in the following text). The density decayed slowly along this ridge of high acuity, reaching 50% of its peak value at an azimuth of 149° (linearly interpolated; see Fig. 4D, solid line). In contrast, the decay along elevation was sharper, with the optical axes density reaching 50% of its peak for elevations of approx. ± 35°, (Fig. 4E, solid line; for azimuth of 40°).

Figure 4C shows the dendritic length density for the LGMD neuron illustrated in Fig. 4A (lgmd_a). The other reconstructed neurons had similar dendritic length density profiles. Interestingly, the dendritic length density also peaked toward the distal part of the dendritic field, where input from the equatorial region of visual space arrives. Thus the local distribution of dendritic length in field A appears to be in register with the increase in optical axes density at the eye acute zone. This increase in density was due to an increase in branching, as the diameter of dendritic segments decreased distally from the SIZ. In contrast, the dendritic surface area density had a distribution inverted about the 90° azimuth line when compared with length density with a peak toward the proximal region of the dendritic field at 0° elevation and a rapid decay toward the tips (not shown). This was due to the fact that the branches close to the SIZ are considerably thicker than distal branches and thus contributed disproportionally to dendritic surface area. Dendritic length density decayed toward the back of the dendritic field, as the number of dendritic branches decreased. This decay was relatively fast compared with the optical axes density decay (Fig. 4D). In contrast, the decay in dendritic length density was less pronounced along elevation for azimuths ≤40° on the dendritic field ellipsoid. This reflects the fact that dendritic branching depended mainly on distance from the SIZ, which is more closely related to azimuth than elevation. The decrease in dendritic length density was smaller along elevation than that observed for the optical axes density at azimuths ≤40° (Fig. 4E, dashed line). We quantified these differences by computing the width of the distributions of optical axes and dendritic length densities at their half-peak value for 0° elevation and 40° azimuth (double arrows in Fig. 4, D and E). On average across the five reconstructed dendritic fields, the ratio of dendritic length half-peak width to optical axes half-peak width amounted to 2.6 ± 0.22 (SE) (unitless) and 0.40 ± 0.01 (SE) for 0° elevation and 40° azimuth, respectively. Thus, if visual space is mapped according to a constant synaptic density along the dendrites of field A, we expect a deformation of visual space, in spite of the fact that the ellipsoids fitted to the eyes and to the dendritic fields were very similar. Such a deformation is required to compensate for the differences in optical axes and dendritic length densities described above. Specifically, a retinotopy-preserving uniform synaptic density mapping requires a stretching of visual space along the dorsoventral axis of the dendritic field paired with a compression of visual space along the anterior-posterior axis. This corresponds to a stretching and compression along the elevation and azimuth, respectively, of the dendrite-fitted ellipsoid.

Topographic map magnifies dendritic sampling of the acute zone

Figure 5A, adapted from Krapp and Gabbiani (2005), shows the angular density of optical axes sampling visual space. We constructed a one-to-one neighborhood-preserving mapping between ommatidia and equal length dendritic segments of field A based on the SOM algorithm originally introduced by Kohonen (1982). The mapping was based on two steps, as illustrated in Fig. 5B. First, dendritic segments and ommatidia were projected onto equal-sized grids using two distinct SOMs (see METHODS). These two grids were then aligned based on the relative orientation of the eye and dendritic field A (Fig. 4A). Combining the two SOMs resulted in a one-to-one, “topographic” mapping from visual to dendritic space that is illustrated in Fig. 5D (Fig. 5C, top). The color of each dendritic segment of field A corresponds to the optical axis density of the visual region sampled by that particular dendritic segment, obtained from Fig. 5A. The quality of this neighborhood-preserving map was measured by determining the overlap between nearest-neighbors at corresponding locations in dendritic and visual space. For each synapse on a dendritic segment, its hundred nearest spatial neighbors were determined and compared with the corresponding optical axis’ hundred nearest neighbors in visual space. On average, there was a 50.1% overlap between these two sets. A purely random mapping (Fig. 5C, bottom) would be expected to generate an overlap of only 1.4% (100 from a total of 7,322). Thus the SOMs yielded a map that largely preserved, at the dendritic level, the nearest-neighbor relations of optical axes.

As predicted by the analysis carried out in the previous section, the inputs from the acute zone occupied a dendritic region extended along the dorsoventral axis and relatively narrower along the anterior-posterior axis. This is best visualized by observing the mapping to dendritic space of the rectangle delimited by the solid line in Fig. 5A. This rectangle is bounded at ± 30° in elevation, and azimuths –10 to 20°. In the topographic mapping, the visual area corresponding to it contributes input to 12.1% of the total dendritic length of field A. We compared this mapping to another hypothetical mapping illustrated in Fig. 5E. This mapping was obtained by sampling visual space uniformly and mapping the resulting optical axes in a local, neighborhood-preserving manner onto the dendritic surface of field A (see METHODS; Fig. 5C, middle). The resulting contribution from the acute zone is much smaller than in Fig. 5D as can be seen by comparing the areas bounded by the solid lines in both panels. In this case, the rectangle of Fig. 5A provides synaptic input to 4.6% of the dendritic length of field A. The assumption of uniform sampling is in sharp contrast to the highly nonuniform sampling of visual space implemented at the level of the locust eye (Krapp and Gabbiani 2005). This mapping proved useful in subsequent simulations because it allowed us to isolate the effect of nonuniform visual sampling.

Translation of spike-based LGMD spatial sensitivity profiles to equivalent membrane potential RFs

The passive compartmental model and the topographic synaptic mapping derived in the previous sections allowed us to simulate the membrane potential response of the LGMD to local visual inputs. Experimentally, the spatial sensitivity distribution of the LGMD in response to local motion has been characterized in terms of firing rates (Krapp and Gabbiani 2005). To compare simulation results with the experimental data without adding active conductances to the model, we recorded intracellularly from the LGMD and studied the transformation leading from membrane potential to spikes under local visual stimulation. Animals were presented with small discs moving on a circular path, similar to the stimuli employed by Krapp and Gabbiani (2005), whereas the intracellular membrane potential of the LGMD was recorded in the main dendrites of field A (Fig. 6A). These stimuli are not expected to significantly activate feed-forward inhibition onto the LGMD (Gabbiani et al. 2005; Krapp and Gabbiani 2005). During each experiment, the position of the rotating disk was systematically varied across the visual field. This led to systematic changes in the firing rate as expected from the LGMD’s spatially anisotropic sensitivity distribution. We then computed for each stimulus position in each experiment the mean, median-filtered membrane potential and the spikes occurrence times. This allowed us to investigate which variable derived from the median-filtered membrane potential best correlated with the spiking response of the LGMD. Figure 6B shows for a single animal the relation between the mean peak median-filtered membrane potential and the mean peak spike frequency across the nine stimulus positions employed. There was a good correlation between these two variables, r² = 0.84, that was consistent across animals (r² = 0.69 ± 0.09 SE; n = 5). Similar analyses with other variables derived from the median-filtered membrane potential and the spiking response led to weaker correlation coefficients (e.g., integral of membrane potential; not shown). We thus fitted the relation between mean peak median-filtered membrane potential and mean peak spike frequency by a straight line and used it to convert the local motion sensitivities of the LGMD in terms of spike frequency (Krapp and Gabbiani 2005) into a distribution of membrane potentials across visual space (see Eq. 1 in METHODS). This equivalent RF is plotted in Fig. 7A and described in more detail in the next section.

Topographic mapping partially explains LGMD’s RF

The ISI-to-membrane potential transform derived in the previous section was employed to convert the LGMD spike-based RF to an equivalent membrane potential RF. Figure 7A shows the equivalent peak membrane potential as a function of the location of the stimulus. Several characteristic features of the RF are apparent. First, the response increases gradually as the azimuth increases, i.e., as the stimulus is moved toward the caudal part of the visual field. Second, there is a peak around zero elevation with a gradual decline above and below the eye equator.

We explored how the distribution of synaptic inputs on the LGMD’s excitatory dendrites influences its RF structure by simulating the appearance of a visual stimulus of the same size as the experimental stimulus at various locations in visual space and measuring the peak membrane potential response in the simulated neuron (see METHODS). Peak membrane potential was measured at the origin of dendritic field A (denoted by V̄_origin-A) because this location was close to the presumed site of electrode penetration in the experiments described in the preceding text. This location received input from a similar visual position in all simulations (elevation of 0° and azimuth of 165°).

Figure 7B shows that the topographic mapping’s RF replicates the gradual increase of response with increased azimuth. The synaptic conductance was scaled so that the peak membrane potential deflection for the strongest stimulus (centered at elevation of 0° and azimuth of 135°) matched the strongest one observed experimentally (centered at elevation of 0° and azimuth of 150°), yielding a g_max of 47 nS. In the simulated RF, the decline in response along elevation is, however, sharper than observed experimentally. The RF obtained from the map based on a uniform sampling of visual space is shown in Fig. 7C. In this case, matching the stimulus site of peak deflection (centered at elevation of 0°, azimuth of 165°) to experimental data yielded a g_max of 84 nS. The higher single-ommatidium g_max in the uniform relative the topographic mapping resulted from the lower number of ommatidia sampling the caudal equatorial region (the region where the peak response occurred in both mappings) in the uniform mapping. Because the g_max value was derived by matching the peak simulated membrane potential response with the experimental peak, fewer ommatidia meant each ommatidium’s synaptic input had to be greater, resulting in a greater g_max. Like the topographic mapping’s RF, the uniform mapping’s RF replicates the decreased response toward the front of the animal (lower azimuths). In addition, it more successfully reproduces the weaker decline in response along elevation seen in the experimental RF. This result suggests that additional neural mechanisms compensate for the uneven sampling of visual space at the level of the eye, particularly along elevation. The RF resulting from a random mapping of ommatidia onto dendritic field A is shown in Fig. 7D (same g_max was used as for the topographic mapping’s RF). This RF exhibits maximal responses close to the acute zone and thus fails to capture the reduction in response at lower azimuths. The response profile was similar to the optical axis density profile (see Fig. 5A) as randomized synapse location resulted in approximately equal average electrotonic distance to the spike initiation zone for each subset of synapses stimulated. Indeed, a similar RF would be expected from a single-compartment, “point neuron” model lacking electrotonic structure. The maximal variability of the RF between different instances of this random mapping amounted to ≤ 1 mV for any given stimulus location.

A comparison of the RFs illustrated in Fig. 7, B and D, thus shows that preservation of local neighbor relationships and the mapping of ommatidia sampling the frontal visual field to distal dendrites is necessary to replicate experimental results. Figure 7, C and D, also helps clarify the dependence of the topographic mapping’s RF (Fig. 7B) on azimuth and elevation. In Fig. 7C, the RF depends only on electrotonic distance from the origin of field A since visual sampling is uniform, whereas the RF of Fig. 7D is purely determined by visual sampling density. The RF of Fig. 7B depends on both variables: along elevation they have the same effect and combine to cause a rapid decrease in response. In contrast, the increase in density as azimuth decreases partially compensates for the increase in electrotonic distance, leading to a weaker decline in response (see also Fig. 7E in the following text).

To analyze in more detail the difference between the experimental RF and the topographic and uniform mappings’ RFs, several cross-sections were examined. This is shown in Fig. 7E. The first panel depicts the peak response at various azimuths with elevation fixed at 0°. Both RFs reproduced the decline of response with decreasing azimuth and the majority of simulated data points stayed within the 95% confidence intervals (CIs; shown in gray) of the experimental data (n = 6 animals; t-test). The last two panels depict RF cross-sections along fixed azimuths (135 and 30°), showing the rapid decline in response for elevations away from 0° observed with the topographic mapping. The simulated RF mismatch was quantified by examining the fraction of azimuths (of 13 tested) for a given elevation at which the simulated membrane potential fell outside the 95% CI of the experimental data. For the topographic mapping, the match was very good at the equator (elevation 0°; all but 1 azimuth met the criteria), and declined in quality rapidly in both directions away from the equator (at maximal positive and negative elevations, no points satisfied the criteria). In the case of the uniform mapping, the match was slightly worse at the equator (about a third of the azimuths were mismatched), but did not decline in quality away from the equator. Overall, 67 and 35% of simulated RF V̄_origin-A values fell outside the experimental CI for the topographic and uniform mappings, respectively. Hence, we conclude that the uniform mapping yields a better overall fit to the experimental data, while the topographic mapping reproduces better the experimental data at the eye equator (0° elevation).

Influence of physiological parameters on RF shape

To determine the robustness of the results, RFs were reconstructed while systematically varying a single model parameter. In all cases, the topographic mapping was employed. Figure 8 shows a cross-section of the RFs at 0° elevation for systematic variation of several parameters. Similar results were observed along fixed azimuth, variable elevation cross-sections. Figure 8A shows that increasing R_m over an order of magnitude did not qualitatively alter the RF shape. Because the LGMD is electrotonically extensive (see Fig. 3), an eightfold increase in R_m leads to a much smaller shift in the peak membrane potential transient at the origin of field A (V̄ _origin-A). The weak dependence of V̄_origin-A on R_m results from the distribution of current throughout the dendritic arbor via R_a. When R_a was simultaneously decreased by an order of magnitude or more, single synaptic inputs experienced little attenuation at the origin of field A, independent of their location, rendering the neuron electrotonically compact. This in turn led to a significant change in the dependence of V̄ _origin-A on stimulus location and an RF determined by optical axis density (not shown) and resembling the RF obtained with the random synapse distribution of Fig. 7D. This is to be expected, as an RF for an electrotonically compact LGMD should simply reflect the density of optical axes. Thus the dominant factor in shaping the RF of the LGMD was the potential drop over the extensive dendritic tree due to R_a and not R_m. Accordingly, varying R_a over an order of magnitude (Fig. 8B) had a greater effect on RF shape: V̄ _origin-A declined for low azimuths, corresponding to locations far from the recording electrode site. At high azimuths, however, V̄ _origin-A increased with higher R_a. These two effects can be understood by noting that a lower R_a allows greater axial current flow and so increases the influence of distal inputs. Conversely, proximal inputs will have their synaptic current distributed more equally across the dendritic field, causing a decline in response.

Figure 8C shows the effect of systematically varying the maximal synaptic conductance (g_max). Raising g_max increased disproportionately the response at higher azimuths (i.e., close to the origin of field A). Conversely, lower conductance levels flattened the 0° elevation cross-section, resulting in greater responses to low relative to high azimuths. This can be understood by noting that low azimuth stimulation activates the acute zone, and hence a high number of synapses. Because synapses from adjacent visual regions map onto adjacent dendritic segments, increasing g_max gives rise to local membrane potential saturation and thus to sublinear summation. The larger number of synapses activated at the acute zone means that this effect occurs more rapidly as synaptic conductance increases. Sublinear summation also applies for higher azimuth synapses, but their smaller number results in a lower local depolarization and hence reduced sublinearity. Moreover, these synapses are electrotonically closer to the recording site. Thus increasing their conductance results in more pronounced effects at the origin of dendritic field A.

We further investigated the effect of sublinear summation on RF shape by stimulating synapses conveying signals obtained from different locations in visual space for both the topographic and uniform mappings. The first, distal, location was close to the acute zone (elevation 0°; azimuth 30°) and the second, proximal, location was close to the origin of field A (elevation 0°; azimuth 135°). The synapses were first activated simultaneously and then split into two random subgroups, A and B, and V̄_origin-A was recorded for all three conditions. This allowed us to define a linearity index, ψ, varying between 1 (100% linear summation) and 0 (METHODS). For the topographic mapping, stimuli at the proximal location yielded a linearity index of 0.80 for g_max of 50 nS. Not surprisingly, increasing g_max to 100 nS made summation more sublinear (ψ = 0.70). Stimulation at the distal location yielded a lower linearity index of 0.63 (for 50 nS g_max). This is to be expected since far more synapses were activated because of the high density of optical axes close to the acute zone on the eye. For the uniform mapping, the proximal site yielded a linearity index of 0.81 almost indistinguishable from that of the topographic mapping. Summation at the distal location was ~10% more linear than in the topographic map (ψ = 0.74 vs. 0.63), presumably due to the lower number of synapses at this location in the uniform mapping. The decrease in linear summation from distal (ψ = 0.74) to proximal (ψ = 0.81) in the uniform mapping is probably due to decreased dendritic diameter at the distal site, which results in greater local interaction and hence sublinear summation because the number of synapses at both sites was identical for this mapping. Because the acute zone input synapses are dramatically stretched along the elevation of dendritic field A in the topographic mapping relative the uniform mapping (Fig. 5, D and E), we also investigated the effect of splitting synapses into two groups based on the elevation of input ommatidium optical axes. In the topographic map, this led to an increase in linearity at the distal location (ψ = 0.77 vs. 0.63) due to the fact that the synapses of each subgroup had an increased probability of being on the same dendritic branch thus increasing sublinear summation within each subgroup, resulting in lower subgroup responses and hence higher ψ. A similar increase in ψ was observed in the uniform mapping (ψ= 0.86 vs. 0.74). At the proximal location, the increase in linearity was much smaller for the topographic mapping (ψ = 0.81 vs. 0.80) and somewhat larger for the uniform mapping (ψ = 0.90 vs. 0.81). These results suggest that sublinear summation plays a role in determining RF shape, particularly in the topographic map because differences of up to 17% were observed in linear summation across sites. Differences in sublinear summation between the two maps typically amounted to ≤ 10% and thus contributed only moderately to RF shape differences.

We further explored the effects of sublinearity by examining the impact of changes in inter-synaptic distance. We were forced to alter the original synaptic allocation algorithm (see METHODS) because the typical synapse assignment resulted in synapses scattered across the dendritic arbor, whereas enforcing a fixed inter-synaptic distance necessitated the use of a contiguous segment of dendrite. This is the reason for the difference between the 1-μm inter-synaptic distance RF of Fig. 8D with the corresponding topographic mapping’s RF of Fig. 7E (blue). This topographic RF uses an inter-synaptic distance of 0.95 μm, but because the synapses activated are not contiguous along the dendrite, the mean pair-wise inter-synaptic distance along the dendrite is larger and varies with stimulus location. The increase in response observed in Fig. 8D at the acute zone relative the topographic mapping simulations is due to the constraint of contiguity: because the segment of dendrite where synapses were placed was contiguous, synapses had to be placed at locations electrotonically closer to the recording site than the set of synapses used in the Fig. 7, B and E, simulations. Comparing the RFs obtained by varying intersynaptic distance along a single dendritic segment (Fig. 8D), it is apparent that increasing inter-synaptic distance resulted in higher V̄_origin-A for input coming from regions of high synaptic density. This was due to a decrease in sublinear summation, an effect that was more pronounced for simulations triggering a higher number of synapses at the acute zone. Conversely, decreasing inter-synaptic distance resulted in reduced response to acute zone stimulation.

Because the topographic mapping showed the greatest discrepancy from experimental data at high and low elevations, we performed a final set of simulations to determine whether a systematic variation of synaptic strength could reconcile the simulated RF with the experimental data. Specifically, we varied g_max from 5 to 1,000 nS in 5-nS increments and generated an RF for each g_max. For each stimulus location, we then determined the g_max value that yielded the V̄_origin-A value closest to the experimental one. The result showed that it was impossible, without additional assumptions, to account for many of the high and low elevation responses observed experimentally. Specifically, because the input density at these locations was quite low, often only a few synapses were being activated. Increasing g_max pushed the local membrane potential at the synapse site close to its reversal potential, making further response increase impossible. Thus even when some of the high and low elevation sites were assigned very high synaptic conductances, they failed to attain the expected V̄_origin-A. A single synapse placed at the origin of dendritic field A (i.e., the recording site) could attain the necessary membrane potential given a high enough conductance (200 nS for the minimal 6-mV depolarization). Thus placing all high and low elevation synapses close to the dendritic field origin would correct the problem at the expense of a gross distortion of local neighborhood relation preservation. This last result again suggests that additional amplification mechanisms are responsible for the ability of stimuli at low acuity regions to elicit spikes in the LGMD.

DISCUSSION

This study examines the role electrotonic structure and synaptic mapping play in shaping the LGMD’s RF for local motion stimuli. We performed a morphological analysis of this neuron, demonstrating the inter-animal consistency of the excitatory dendritic field geometry and its close relation to eye geometry. In addition, we found that the distribution of dendrite length over the dendritic field-fitted ellipsoid peaks in a location corresponding to where optical axis density is highest on the eye-fitted ellipsoid, suggesting a morphological adaptation for sampling visual inputs retinotopically. To determine if synaptic activation depends on location, and therefore if synaptic integration will be influenced by dendritic geometry, we evaluated the electrotonic structure of the LGMD after fitting a compartmental model to electrophysiological data. This showed the neuron to be electrotonically extensive in vivo, suggesting that the mapping between visual space and dendritic field A will indeed influence synaptic integration. By establishing a relationship between peak membrane potential and firing rate in response to local motion stimuli, we were able to directly compare RFs generated in the passive compartmental model with experimental data. We tested various synaptic mappings from visual inputs onto the excitatory dendritic field. The modeling results, in agreement with anatomical evidence, suggest that the synaptic mapping is retinotopic. Moreover, we showed that a mapping based on an equal contribution from each ommatidium and a constant synaptic density along dendritic length qualitatively reproduces the experimental RF but fails to replicate some of its detailed features. Our results represent a first step toward a biophysically detailed model of synaptic integration in the LGMD. In addition, they provide a set of predictions that can be tested using in vivo functional imaging and other electrophysiological techniques.

Morphological characteristics of the LGMD

Our morphological analysis is based on reconstructions of five LGMD neurons. Although the gross anatomical structure of the LGMD was well conserved across animals (Fig. 1A), we found variability in the three primary morphological parameters of the reconstructions: radius, segment number, and length (Table 1). Some of this variability is likely due to size differences across animals. For example, the coefficient of variation (CV) of eye ellipsoidal axes, which is most likely attributable to size differences, ranged from 0.05 to 0.1 (Table 2). The remaining variability may originate from differences in tissue shrinkage during histological processing or from the determination of primary morphological parameters based on confocal images. We expect tissue shrinkage to account for a small fraction of the variability (16.2%) (Bucher et al. 2000). This suggests that most of the variability not attributable to genuine inter-individual differences is likely to originate in the determination of radii, segment numbers, and lengths. This conclusion is substantiated by the observation that among these three primary morphological parameters, radius had by far the highest coefficient of variation (0.37 on average) when compared with segment number and total length (0.17 and 0.15, respectively). Radius is the most difficult quantity to estimate because it lies close to the resolution limits imposed by light microscopy for small dendrites (Major et al. 1994; Roth and Häusser 2001). In contrast, several geometrical properties of the excitatory dendritic field were well conserved across animals, including the dimension of its ellipsoidal axes (CV = 0.08 on average) and their aspect ratios (CV = 0.05 on average). For these variables, the coefficients of variation were comparable to those obtained for eye ellipsoidal axes and aspect ratios (CV = 0.08 in both cases; Table 2). Thus although there clearly is variability in the detailed branching pattern of dendritic field A in our reconstructions, the geometry of the space it fills in the lobula was almost identical from animal to animal (see Hausen 1984 for a similar observation in fly tangential neurons). Moreover, not only was the eye ellipsoid geometry a simple linear scaling of the dendritic field A ellipsoid, the density of dendritic segments on the LGMD and ommatidia on the locust eye peaked at analogous locations relative to the fitted ellipsoids. This suggests that the geometry of the excitatory dendritic field plays a functional role in sampling afferent fiber inputs. In addition, the insertion position of the dendritic branches along the main process of the LGMD was identical for all neurons studied: the segment between the origin of the excitatory field and the spike initiation zone always intercepted the origins of inhibitory fields B and C, in that order (Fig. 1B). Thus feed-forward inhibition mediated by fields B and C is always on-path relative to the spike initiation zone, an ideal arrangement from a theoretical perspective (Koch et al. 1982; Rall 1964). The ultimate impact of these inhibitory inputs is also likely to depend on the neuron’s conductance load (Williams 2004).

Fitting of passive properties and electrotonic structure

We obtained passive parameters by fits to single-electrode intracellular recordings (Fig. 2) (for a discussion of technical issues related to the recording technique, see Gabbiani and Krapp 2006). In these experiments, the LGMD was penetrated blindly and thus the exact position of the electrode within its dendritic tree was not known. However, an analysis of spike height and width on these data (Gabbiani and Krapp 2006), and subsequent recordings in which electrode position was monitored through fluorescent imaging, confirmed that the data used to constrain our model were most likely obtained from locations close to the origin of dendritic field A. Simulations in which we varied the location of the recording electrode while maintaining proximity to the origin of dendritic field A did not yield substantially different passive fits or sensitivity distributions. Thus we believe that electrode location played a negligible role in the present context. In constructing passive models of neurons, R_m and C_m are known to be more constrainable using single-electrode data than R_a (e.g., Holmes et al. 1992). Indeed, a direct method to characterize R_a requires dual dendritic recordings (Stuart and Spruston 1998). Such an experiment has been performed in the LGMD axon, yielding values of 360 and 650 μm for λ, depending on electrode position (Rind 1984). If these axonal values were employed instead of the λ value of 1,369 μm obtained using our R_m and R_a, it would imply an even more electrotonically extensive dendritic tree. Overall, the fitted values of R_m, C_m, and R_a were comparable to those reported in other insect visual interneurons (Borst and Haag 1996). The variability of R_m and R_a across morphologies reflected the range of experimental input resistances and equalization time constants (Gabbiani and Krapp 2006). R_m is typically higher in mammalian cells (e.g., Spruston and Johnston 1992). This may be due to the fact that most mammalian values were obtained in vitro, a situation where background synaptic activity is likely to be strongly decreased (Bernander et al. 1991). In any case, even a eightfold increase in R_m would not change the RF substantially (Fig. 8A); R_a played a much more dominant role in shaping the RF (Fig. 8B). An important consequence of the R_m and R_a values derived from our fits is that they imply an extensive electrotonic size (Fig. 3). This is consistent with the analysis of earlier intracellular recordings (Fig. 6 of Gabbiani and Krapp 2006) and the fact that the LGMD RF cannot be reproduced with a point neuron. The LGMD’s large electrotonic size had a significant impact on its RF, as discussed in the following text.

Construction of synaptic mappings

By studying the density distribution of dendritic segments on the ellipsoid fits to dendritic field A, we found a sizable increase in dendritic length density at low azimuths toward the tip of the dendrites (Fig. 4C). Because this increase in density is in register with an increase in optical axes density on the eye (Fig. 4B), we interpret this as an adaptation to sample retinotopically inputs from the eye. However, the distributions of optical axes and dendritic length densities were not in exact register (Fig. 4, D and E), suggesting that under the assumption of a neighborhood preserving synaptic mapping with constant synaptic density per unit length, a substantial increase in the dendritic surface occupied by inputs corresponding to the acute zone will occur, particularly along the dorsoventral axis. We confirmed this by constructing such a mapping using Kohonen’s SOM algorithm (Kohonen 2001; esp. chapt. 3). Although this algorithm has been employed in many studies of neural network connectivity (e.g., Piepenbrock and Obermayer 2000), ours is, to the best of our knowledge, the first study applying it to obtain a neighborhood-preserving synaptic connectivity scheme for a single neuron. The mapping produced the predicted compression along the anterior-posterior axis and expansion along the dorsoventral axis (Fig. 5, D and E). The mapping relied on three assumptions. Local neighborhood preservation, the first assumption, is consistent with anatomical data (Rowell et al. 1977; Strausfeld and Nässel 1981) and further supported by our simulations of random synaptic mappings (Fig. 7D). Furthermore, local neighborhood preservation has been demonstrated functionally in lobula plate tangential cells, neurons that occupy a similar position in the visual system of the fly (Borst and Egelhaaf 1992). We adopted the second assumption, a constant synaptic density per unit dendritic length, because it was the most parsimonious. If the LGMD receives two synaptic inputs per ommatidium (Rowell et al. 1977), our synaptic density corresponds to an average of about two synapses per micrometer. The ultrastructure of cholinergic synapses onto dendritic field A of the LGMD has been studied, but no quantitative data on their density are available (Rind and Simmons 1998). Two synapses per micrometer is nonetheless in the range reported for other locust neurons (Killmann et al. 1999; Watson and Burrows 1982, 1985) but may be lower than the actual value for the LGMD (see following text) (Rind and Simmons 1998). A quantitative ultrastructural study of the dendritic synaptic distribution on the neuron postsynaptic to the LGMD, the DCMD, reported that the number of putative excitatory contacts varies with the diameter of dendritic segments, with a peak for segments between 0.5 and 1.5 μm in diameter (Table 3 of Killmann et al. 1999). If this was also the case in the LGMD, we would expect a mapping of visual space closer to that of Fig. 5E than Fig. 5D because the density of synapses would peak in the finer dendrites, which also correspond to the region of maximal dendritic length density (Fig. 4C). The assumption of a constant synaptic input density could be tested by functional imaging: it predicts a considerably larger spatial pattern of activation for a visual stimulus located at the acute zone relative to one positioned, e.g., in the caudal part of the visual field. In any case, a change in synaptic density with dendritic diameter should not affect qualitatively the shape of the simulated LGMD RF: Fig. 8D demonstrates that a reduction of inter-synaptic distance at the acute zone slightly reduces the response, as a consequence of sublinear summation. Furthermore, our synaptic mapping algorithm could be modified to take such a change in synaptic density with dendritic diameter into account. The third assumption made by the mapping, uniform synaptic weight, is discussed in the next section.

Although much work has been done on studying network-level synaptic connectivity, single-neuron connectivity has only been studied in a few systems (Borst and Egelhaaf 1992; Jacobs and Theunissen 2000; Ogawa et al. 2006). The fly lobula plate tangential cells (LPTCs) most resemble the LGMD in terms of synaptic input. Most LPTCs receive retinotopic input from the ipsilateral compound eye, as verified via functional imaging (Borst and Egelhaaf 1992), and the arborization of their main dendrites within the lobula plate indicate where within the ipsilateral visual field motion stimuli have to be presented to result in maximal responses (Borst and Haag 2002; Krapp et al. 1998). In the cricket cercal system, modeling work has tested anatomically derived predictions regarding the connectivity scheme (Jacobs and Theunissen 2000) that are further supported by recent functional imaging results (Ogawa et al. 2006). This system differs from the LGMD in several ways: there are much fewer input afferents, the input afferents overlap, and each afferent presumably contributes a substantial fraction of total synaptic input.

Simulated RFs

The comparison between experimental and simulated RFs revealed several interesting features of the model. First, the topographic mapping required high peak synaptic conductances (~50 nS) to match the experimental peak membrane potential deflections obtained from our spike frequency to peak membrane potential transform (Eq. 1, METHODS). Scaled for surface area, the conductance density (~200 mS/cm²) is far in excess of values used to model fly LPTC neurons (Haag et al. 1999; Single et al. 1997), whereas the actual single-synapse g_max also exceeds values used in models of other excitatory synapses (e.g., Jaeger et al. 1997; Mel et al. 1998; Rudolph et al. 2004). At least three reasons could account for this observation. Synaptic currents could be amplified postsynaptically by active membrane conductances in vivo (Haag and Borst 1996). Recent work suggests that several active conductances are located in the dendrites of the LGMD (Gabbiani and Krapp 2006; Gabbiani et al. 2002). In particular, a persistent sodium current could provide amplification (Astman et al. 2006; Poznanski and Bell 2000a,b). Such active amplification would necessitate a higher peak synaptic conductance to replicate the experimental membrane potential change with our passive model. Thus the peak synaptic conductances used here should be treated as effective ones because they include all possible contributors to membrane potential changes. Another possibility is that the number of afferent fibers contacting the excitatory field per ommatidium is larger than two. Although two distinct types of afferents have been described (Rowell et al. 1977), this does not exclude a larger number. If this was the case, the effective synaptic conductance per actual synaptic contact would be reduced, but conductance density would remain high. Also the number of synaptic contacts per afferent fiber may be larger than one. Indeed, Rind and Simmons (1998) reported a remarkably high density of synapses onto field A with some afferent fibers making three to four contacts onto the LGMD. Finally, any divergence in the pathway presynaptic to dendritic field A would also lead to a higher effective synaptic conductance in the model because this would allow stimulation of any single ommatidium to activate multiple downstream synapses. Although such divergence has not been demonstrated for the locust LGMD, anatomical evidence in the fly optic lobe indicates it is a possibility (Meinertzhagen and Sorra 2001; Strausfeld and Nässel 1981).

The simulated RF of the topographic mapping qualitatively replicated the experimental data (Fig. 7, A and B). Both retinotopy and an extended electrotonic structure were required for this result (Fig. 7D). The model did not, however, quantitatively reproduce the neuron’s sensitivity gradients along the elevation (Fig. 7, B and E). By selectively eliminating the anisotropic sampling of visual space and the extended electrotonic structure of the dendritic tree, we were able to show that both of these features contributed to the observed mismatch (Fig. 7, B and C). On the other hand, these same two features contributed to the satisfactory fit observed along the eye equator (Fig. 7E). Anisotropic sampling caused a drop in sensitivity in the dorsal and ventral visual field where, compared with the equatorial region, the visual sampling density is decreased (Figs. 4B and 5A). In addition, the electrotonic distance between the synapses receiving input from the non-equatorial visual region and the origin of field A further decreased the response. Eliminating the electrotonic component was not sufficient to resolve the mismatch as shown by simulations repositioning the synapses close to the origin of the excitatory field. In light of this, it seems that differences in effective synaptic weights across the visual field might best account for the decrease in the neuron’s sensitivity along elevation. Indeed, the uniform synaptic mapping effectively implements higher synaptic strength away from the equator and so results in a better reproduction of the experimentally obtained RF organization. Physiologically, differential effective synaptic weighting could be implemented either presynaptically, at the synapses themselves, or postsynaptically, through position-dependent amplification of synaptic inputs. A synaptic implementation could be based on local homeostatic mechanisms because visual stimulation at the eye equator will simultaneously activate many more synapses than nonequatorial stimulation, thereby providing a putative signal to such a mechanism (Rabinowitch and Segev 2006; for a general review of homeostatic plasticity, see Turrigiano and Nelson 2004). Another possibility is divergence in the presynaptic network, a mechanism that is anatomically plausible (Meinertzhagen and Sorra 2001). Such a mechanism would disproportionately amplify inputs from regions of low visual acuity—i.e., those coming from nonequatorial regions—and is especially attractive because it would also account for the high-effective single-synapse conductance of the model. The relatively weak response to acute zone stimuli, for which a much higher number of synapses is activated presumably on more distal dendritic segments, suggests that LGMD input synapses are not scaled to achieve uniform effect at the SIZ (Cook and Johnston 1999). This does not rule out nonuniform amplification mechanisms (Migliore and Shepherd 2002).

The simulated RF was robust to local variations in synaptic density and local variability in the synaptic mapping. This was tested in the simulations depicted in Fig. 7E, where activated synapses corresponding to a 7.6° diam disk were selected randomly from a 20 × 20° region (METHODS). The 95% confidence intervals for the simulated maps demonstrate that local variability in intersynaptic distance has little impact on RF structure, provided that coarse retinotopy is maintained.

Clearly further experimental work will be needed to fully characterize the mechanisms of dendritic integration and to fit a quantitative biophysical model to the LGMD’s RF. Especially relevant to this study will be assessing the presence of active conductances and their contribution to RF properties. The present model clarifies the role of electrotonic structure and synaptic mapping in shaping LGMD’s RF, thereby providing a basis for interpreting future experimental results and building subsequent models, as well as a framework for generating novel hypotheses.